Abstract
This paper poses that transition systems constitute a good model of distributed systems only in combination with a criterion telling which paths model complete runs of the represented systems. Among such criteria, progress is too weak to capture relevant liveness properties, and fairness is often too strong; for typical applications we advocate the intermediate criterion of justness. Previously, we proposed a definition of justness in terms of an asymmetric concurrency relation between transitions. Here we define such a concurrency relation for the transition systems associated to the process algebra CCS as well as its extensions with broadcast communication and signals, thereby making these process algebras suitable for capturing liveness properties requiring justness.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Transition systems are a common model for distributed systems. They consist of sets of states, also called processes, and transitions—each transition going from a source state to a target state. A given distributed system \(\mathcal {D}\) corresponds to a state P in a transition system  —the initial state of \(\mathcal {D}\). The other states of \(\mathcal {D}\) are the processes in
—the initial state of \(\mathcal {D}\). The other states of \(\mathcal {D}\) are the processes in  that are reachable from P by following the transitions. A run of \(\mathcal {D}\) corresponds with a path in
that are reachable from P by following the transitions. A run of \(\mathcal {D}\) corresponds with a path in  : a finite or infinite alternating sequence of states and transitions, starting with P, such that each transition goes from the state before to the state after it. Whereas each finite path in
: a finite or infinite alternating sequence of states and transitions, starting with P, such that each transition goes from the state before to the state after it. Whereas each finite path in  starting from P models a partial run of \(\mathcal {D}\), i.e., an initial segment of a (complete) run, typically not each path models a run. Therefore a transition system constitutes a good model of distributed systems only in combination with what we here call a completeness criterion: a selection of a subset of all paths as complete paths, modelling runs of the represented system.
starting from P models a partial run of \(\mathcal {D}\), i.e., an initial segment of a (complete) run, typically not each path models a run. Therefore a transition system constitutes a good model of distributed systems only in combination with what we here call a completeness criterion: a selection of a subset of all paths as complete paths, modelling runs of the represented system.
A liveness property says that “something [good] must happen” eventually [18]. Such a property holds for a distributed system if the [good] thing happens in each of its possible runs. One of the ways to formalise this in terms of transition systems is to postulate a set of good states  , and say that the liveness property
, and say that the liveness property  holds for the process P if all complete paths starting in P pass through a state of
holds for the process P if all complete paths starting in P pass through a state of  [16]. Without a completeness criterion the concept of a liveness property appears to be meaningless.
[16]. Without a completeness criterion the concept of a liveness property appears to be meaningless.
Example 1
The transition system on the right models Cataline eating a croissant in Paris. It abstracts from all activity in the world except the eating of that croissant, and thus has two states only—the states of the world before and after this event—and one transition t. We depict states by circles and transitions by arrows between them. An initial state is indicated by a short arrow without a source state. A possible liveness property says that the croissant will be eaten. It corresponds with the set of states  consisting of state 2 only. The states of
consisting of state 2 only. The states of  are indicated by shading.
are indicated by shading.

The depicted transition system has three paths starting with state 1: 1, \(1\,t\) and \(1\,t\,2\). The path \(1\,t\,2\) models the run in which Cataline finishes the croissant. The path 1 models a run in which Cataline never starts eating the croissant, and the path \(1\,t\) models a run in which Cataline starts eating it, but never finishes. The liveness property  holds only when using a completeness criterion that rules out the paths 1 and \(1\,t\) as modelling actual runs of the system, leaving \(1\,t\,2\) as the sole complete path.
holds only when using a completeness criterion that rules out the paths 1 and \(1\,t\) as modelling actual runs of the system, leaving \(1\,t\,2\) as the sole complete path.
The transitions of transition systems can be understood to model atomic actions that can be performed by the represented systems. Although we allow these actions to be instantaneous or durational, in the remainder of this paper we adopt the assumption that “atomic actions always terminate” [23]. This is a partial completeness criterion. It rules out the path \(1\,t\) in Example 1. We build in this assumption in the definition of a path by henceforth requiring that finite paths should end with a state.
Progress. The most widely employed completeness criterion is progress.Footnote 1 In the context of closed systems, having no run-time interactions with the environment, it is the assumption that a run will never get stuck in a state with outgoing transitions. This rules out the path 1 in Example 1, as t is outgoing. When adopting progress as completeness criterion, the liveness property  holds for the system modelled in Example 1.
holds for the system modelled in Example 1.
Progress is assumed in almost all work on process algebra that deals with liveness properties, mostly implicitly. Milner makes an explicit progress assumption for the process algebra CCS in [20]. A progress assumption is built into the temporal logics LTL [24], CTL [7] and CTL* [8], namely by disallowing states without outgoing transitions and evaluating temporal formulas by quantifying over infinite paths only.Footnote 2 In [17] the ‘multiprogramming axiom’ is a progress assumption, whereas in [1] progress is assumed as a ‘fundamental liveness property’.
As we argued in [10, 15, 16], a progress assumption as above is too strong in the context of reactive systems, meaning that it rules out as incomplete too many paths. There, a transition typically represents an interaction between the distributed system being modelled and its environment. In many cases a transition can occur only if both the modelled system and the environment are ready to engage in it. We therefore distinguish blocking and non-blocking transitions. A transition is non-blocking if the environment cannot or will not block it, so that its execution is entirely under the control of the system under consideration. A blocking transition on the other hand may fail to occur because the environment is not ready for it. The same was done earlier in the setting of Petri nets [26], where blocking and non-blocking transitions are called cold and hot, respectively.
In [10, 15, 16] we worked with transition systems that are equipped with a partitioning of the transitions into blocking and non-blocking ones, and reformulated the progress assumption as follows:
a (transition) system in a state that admits a non-blocking transition will eventually progress, i.e., perform a transition.
In other words, a run will never get stuck in a state with outgoing non-blocking transitions. In Example 1, when adopting progress as our completeness criterion, we assume that Cataline actually wants to eat the croissant, and does not willingly remain in State 1 forever. When that assumption is unwarranted, one would model her behaviour by a transition system different from that of Example 1. However, she may still be stuck in State 1 by lack of any croissant to eat. If we want to model the capability of the environment to withhold a croissant, we classify t as a blocking transition, and the liveness property  does not hold. If we abstract from a possible shortage of croissants, t is deemed a non-blocking transition, and, when assuming progress,
does not hold. If we abstract from a possible shortage of croissants, t is deemed a non-blocking transition, and, when assuming progress,  holds.
holds.
As an alternative approach to a dogmatic division of transitions in a transition system, we could shift the status of transitions to the progress property, and speak of B-progress when B is the set of blocking transitions. In that approach,  holds for State 1 of Example 1 under the assumption of B-progress when \(t\notin B\), but not when \(t\in B\).
holds for State 1 of Example 1 under the assumption of B-progress when \(t\notin B\), but not when \(t\in B\).
Justness. Justness is a completeness criterion proposed in [10, 15, 16]. It strengthens progress. It can be argued that once one adopts progress it makes sense to go a step further and adopt even justness.
Example 2
The transition system on the top right models

Alice making an unending sequence of phone calls in London. There is no interaction of any kind between Alice and Cataline. Yet, we may chose to abstracts from all activity in the world except the eating of the croissant by Cataline, and the making of calls by Alice. This yields the combined transition system on the bottom right. Even when taking the transition t to be non-blocking, progress is not a strong enough completeness criterion to ensure that Cataline will ever eat the croissant. For the infinite path that loops in the first state is complete. Nevertheless, as nothing stops Cataline from making progress, in reality t will occur. [16]
This example is not a contrived corner case, but a rather typical illustration of an issue that is central to the study of distributed systems. Other illustrations of this phenomena occur in [10, Section 9.1], [14, Section 10], [11, Section 1.4], [12] and [6, Section 4]. The criterion of justness aims to ensure the liveness property occurring in these examples. In [16] it is formulated as follows:
Once a non-blocking transition is enabled that stems from a set of parallel components, one (or more) of these components will eventually partake in a transition.
In Example 2, t is a non-blocking transition enabled in the initial state. It stems from the single parallel component Cataline of the distributed system under consideration. Justness therefore requires that Cataline must partake in a transition. This can only be t, as all other transitions involve component Alice only. Hence justness says that t must occur. The infinite path starting in the initial state and not containing t is ruled out as unjust, and thereby incomplete.
In [13, 16] we explain how justness is fundamentally different from fairness, and why fairness is too strong a completeness criterion for many applications.
Unlike progress, the concept of justness as formulated above is in need of some formalisation, i.e., to formally define a component, to make precise for concrete transition systems what it means for a transition to stem from a set of components, and to define when a component partakes in a transition.
A formalisation of justness for the transition system generated by the process algebra AWN, the Algebra for Wireless Networks [9], was provided in [10]. In the same vain, [15] offered a formalisation for the transition systems generated by CCS [20], and its extension ABC, the Algebra of Broadcast Communication [15], a variant of CBS, the Calculus of Broadcasting Systems [25]. The same was done for CCS extended with signals in [6]. These formalisations coinductively define B-justness, where B ranges over sets of transitions deemed to be blocking, as a family of predicates on paths, and proceed by a case distinction on the operators in the language. Although these definitions do capture the concept of justness formulated above, it is not easy to see why.
A more syntax-independent formalisation of justness occurs in [16]. There it is defined directly on transition systems equipped with a, possibly asymmetric, concurrency relation between transitions. However, the concurrency relation itself is defined only for the transition system generated by a fragment of CCS, and the generalisation to full CCS, and other process algebras, is non-trivial.
It is the purpose of this paper to make the definition of justness from [16] available to a large range of process algebras by defining the concurrency relation for CCS, for ABC, and for the extension of CCS with signals used in [6]. We do this in a precise as well as in an approximate way, and show that both approaches lead to the same concept of justness. Moreover, in all cases we establish a closure property on the concurrency relation ensuring that justness is a meaningful notion. We show that for all these algebras justness is feasible. Here feasibility is a requirement on completeness criteria advocated in [1, 16, 19]. Finally, we establish agreement between the formalisation of justness from [16] and the present paper, and the original coinductive ones from [15] and [6].
2 Labelled Transition Systems with Concurrency
We start with the formal definitions of a labelled transition system, a path, and the completeness criterion progress, which is parametrised by the choice of a collection B of blocking actions. Then we define the completeness criterion justness on labelled transition system upgraded with a concurrency relation.
Definition 1
A labelled transition system (LTS) is a tuple \((S, \textit{Tr}, \textit{src},\textit{target},\ell )\) with S and \(\textit{Tr}\) sets (of states and transitions), \(\textit{src},\textit{target}:\textit{Tr}\rightarrow S\) and  , for some set of transition labels
, for some set of transition labels  .
.
Here we work with LTSs labelled over a structured set of labels  , where
, where  . Labels in Act are actions; the ones in
. Labels in Act are actions; the ones in  are signals. Transitions labelled with actions model a state chance in the represented system; signal transitions do not—they satisfy \(\textit{src}(t)=\textit{target}(t)\) and merely convey a property of a state. \( Rec \subseteq Act\) is the set of receptive actions; sets \(B\subseteq Act\) of blocking actions must always contain \( Rec \). In CCS and most other process algebras \( Rec =\emptyset \) and
are signals. Transitions labelled with actions model a state chance in the represented system; signal transitions do not—they satisfy \(\textit{src}(t)=\textit{target}(t)\) and merely convey a property of a state. \( Rec \subseteq Act\) is the set of receptive actions; sets \(B\subseteq Act\) of blocking actions must always contain \( Rec \). In CCS and most other process algebras \( Rec =\emptyset \) and  . Let \(\textit{Tr}^\bullet = \{t \in \textit{Tr}\mid \ell (t)\in Act\setminus Rec \}\) be the set of transitions that are neither signals nor receptive.
. Let \(\textit{Tr}^\bullet = \{t \in \textit{Tr}\mid \ell (t)\in Act\setminus Rec \}\) be the set of transitions that are neither signals nor receptive.
Definition 2
A path in a transition system \((S,\textit{Tr},\) \(\textit{src},\textit{target})\) is an alternating sequence \(s_0\,t_1\,s_1\,t_2\,s_2\cdots \) of states and non-signal transitions, starting with a state and either being infinite or ending with a state, such that \(\textit{src}(t_i)=s_{i-1}\) and \(\textit{target}(t_i)=s_i\) for all relevant i.
A completeness criterion is a unary predicate on the paths in a transition system.
Definition 3
Let \(B\subseteq Act\) be a set of actions with \( Rec \subseteq B\)—the blocking ones. Then \(\textit{Tr}^\bullet _{\lnot B} := \{t\in \textit{Tr}^\bullet \mid \ell (t)\notin B\}\) is the set of non-blocking transitions. A path in  is B-progressing if either it is infinite or its last state is the source of no non-blocking transition \(t \in \textit{Tr}^\bullet _{\lnot B}\).
is B-progressing if either it is infinite or its last state is the source of no non-blocking transition \(t \in \textit{Tr}^\bullet _{\lnot B}\).
B-progress is a completeness criterion for any choice of \(B\subseteq Act\) with \( Rec \subseteq B\).
Definition 4
A labelled transition system with concurrency (LTSC) is a tuple  consisting of a LTS \((S, \textit{Tr}, \textit{src},\textit{target},\ell )\) and a concurrency relation
consisting of a LTS \((S, \textit{Tr}, \textit{src},\textit{target},\ell )\) and a concurrency relation  , such that:
, such that:


Informally,  means that the transition v does not interfere with t, in the sense that it does not affect any resources that are needed by t, so that in a state where t and v are both possible, after doing v one can still do (a future variant u of) t. In many transition systems
means that the transition v does not interfere with t, in the sense that it does not affect any resources that are needed by t, so that in a state where t and v are both possible, after doing v one can still do (a future variant u of) t. In many transition systems  is a symmetric relation, denoted \(\smile \).
is a symmetric relation, denoted \(\smile \).
The transition relation in a labelled transition system is often defined as a relation  . This approach is not suitable here, as we will encounter multiple transitions with the same source, target and label that ought to be distinguished based on their concurrency relations with other transitions.
. This approach is not suitable here, as we will encounter multiple transitions with the same source, target and label that ought to be distinguished based on their concurrency relations with other transitions.
Definition 5
A path \(\pi \) in an LTSC is B-just, for \( Rec \subseteq B\subseteq Act\), if for each transition \(t \in \textit{Tr}^\bullet _{\lnot B}\) with \(s:=\textit{src}(t)\in \pi \), a transition u occurs in the suffix of \(\pi \) starting at s, such that  .
.
Informally, justness requires that once a non-blocking non-signal transition t is enabled, sooner or later a transition u will occur that interferes with it, possibly t itself. Note that, for any \( Rec \subseteq B\subseteq Act\), B-justness is a completeness criterion stronger than B-progress.
Components. Instead of introducing  as a primitive, it is possible to obtain it as a notion derived from two functions
as a primitive, it is possible to obtain it as a notion derived from two functions  , for a given set of components
, for a given set of components  . These functions could then be added as primitives to the definition of an LTS. They are based on the idea that a process represents a system built from parallel components. Each transition is obtained as a synchronisation of activities from some of these components. Now \(\textit{npc}(t)\) describes the (nonempty) set of components that are necessary participants in the execution of t, whereas \(\textit{afc}(t)\) describes the components that are affected by the execution of t. The concurrency relation is then defined by
. These functions could then be added as primitives to the definition of an LTS. They are based on the idea that a process represents a system built from parallel components. Each transition is obtained as a synchronisation of activities from some of these components. Now \(\textit{npc}(t)\) describes the (nonempty) set of components that are necessary participants in the execution of t, whereas \(\textit{afc}(t)\) describes the components that are affected by the execution of t. The concurrency relation is then defined by

saying that u interferes with t iff a necessary participant in t is affected by u.
Most material above stems from [16]. However, there \(\textit{Tr}^\bullet =\textit{Tr}\), so that  is irreflexive, i.e., \(\textit{npc}(t) \cap \textit{afc}(t) \ne \emptyset \) for all \(t\in \textit{Tr}\). Moreover, a fixed set B is postulated, so that the notions of progress and justness are not explicitly parametrised with the choice of B. Furthermore, property (2) is new here; it is the weakest closure property that supports Theorem 1 below. In [16] only the model in which
is irreflexive, i.e., \(\textit{npc}(t) \cap \textit{afc}(t) \ne \emptyset \) for all \(t\in \textit{Tr}\). Moreover, a fixed set B is postulated, so that the notions of progress and justness are not explicitly parametrised with the choice of B. Furthermore, property (2) is new here; it is the weakest closure property that supports Theorem 1 below. In [16] only the model in which  is derived from \(\textit{npc}\) and \(\textit{afc}\) comes with a closure property:
is derived from \(\textit{npc}\) and \(\textit{afc}\) comes with a closure property:

An important requirement on completeness criteria is that any finite path can be extended into a complete path. This requirement was proposed by Apt, Francez and Katz in [1] and called feasibility. It also appears in Lamport [19] under the name machine closure. The theorem below list conditions under which B-justness is feasible. Its proof is a variant of a similar theorem from [16] showing conditions under which notions of strong and weak fairness are feasible.
Theorem 1
If, in an LTSC with set of blocking actions B, only countably many transitions from \(\textit{Tr}^\bullet _{\lnot B}\) are enabled in each state, then B-justness is feasible.
All proofs can found in the full version of this paper [13].
3 CCS and Its Extensions with Broadcast and Signals
This section presents four process algebras: Milner’s Calculus of Communicating Systems (CCS) [20], its extensions with broadcast communication ABC [15] and signals CCSS [6], and an alternative presentation of ABC that avoids negative premises in favour of discard transitions.
3.1 CCS
CCS [20] is parametrised with sets  of agent identifiers and
of agent identifiers and  of (handshake communication) names; each
of (handshake communication) names; each  comes with a defining equation
comes with a defining equation
 with P being a CCS expression as defined below.
with P being a CCS expression as defined below.  is the set of co-names. Complementation is extended to
is the set of co-names. Complementation is extended to  by setting \(\bar{\bar{c}}=c\).
by setting \(\bar{\bar{c}}=c\).
 is the set of actions, where \(\tau \) is a special internal action. Below, c ranges over
is the set of actions, where \(\tau \) is a special internal action. Below, c ranges over  , \(\eta \), \(\alpha \), \(\ell \) over Act, and A, B over
, \(\eta \), \(\alpha \), \(\ell \) over Act, and A, B over  . A relabelling is a function
. A relabelling is a function  ; it extends to Act by
; it extends to Act by  and \(f(\tau ):=\tau \). The set
and \(f(\tau ):=\tau \). The set  of CCS expressions or processes is the smallest set including:
of CCS expressions or processes is the smallest set including:

One often abbreviates \(\alpha .\mathbf{0}\) by \(\alpha \), and \(P\backslash \{c\}\) by \(P\backslash c\). The traditional semantics of CCS is given by the labelled transition relation  , where transitions
, where transitions
 are derived from the rules of Table 1.
are derived from the rules of Table 1.
3.2 ABC—The Algebra of Broadcast Communication
The Algebra of Broadcast Communication (ABC) [15] is parametrised with sets  of agent identifiers,
of agent identifiers,  of broadcast names and
of broadcast names and  of handshake communication names; each
of handshake communication names; each  comes with a defining equation
comes with a defining equation
 with P being a guarded ABC expression as defined below.
with P being a guarded ABC expression as defined below.
The collections  and
and  of broadcast and receive actions are given by
of broadcast and receive actions are given by  for \(\sharp \in \{!,?\}\).
for \(\sharp \in \{!,?\}\).
 is the set of actions. Below, \(A\) ranges over
is the set of actions. Below, \(A\) ranges over  , b over
, b over  , c over
, c over  , \(\eta \) over
, \(\eta \) over  and \(\alpha ,\ell \) over Act. A relabelling is a function
and \(\alpha ,\ell \) over Act. A relabelling is a function  . It extends to Act by
. It extends to Act by  ,
,  and \(f(\tau ):=\tau \). The set
and \(f(\tau ):=\tau \). The set  of ABC expressions is defined exactly as
of ABC expressions is defined exactly as  . An expression is guarded if each agent identifier occurs within the scope of a prefixing operator. The structural operational semantics of ABC is the same as the one for CCS (see Table 1) but augmented with the rules for broadcast communication in Table 2.
. An expression is guarded if each agent identifier occurs within the scope of a prefixing operator. The structural operational semantics of ABC is the same as the one for CCS (see Table 1) but augmented with the rules for broadcast communication in Table 2.
ABC is CCS augmented with a formalism for broadcast communication taken from the Calculus of Broadcasting Systems (CBS) [25]. The syntax without the broadcast and receive actions and all rules except (Bro-l), (Bro-c) and (Bro-r) are taken verbatim from CCS. However, the rules now cover the different name spaces; (Act) for example allows labels of broadcast and receive actions. The rule (Bro-c)—without rules like (Par-l) and (Par-r) with label b!—implements a form of broadcast communication where any broadcast b! performed by a component in a parallel composition is guaranteed to be received by any other component that is ready to do so, i.e., in a state that admits a b?-transition. In order to ensure associativity of the parallel composition, one also needs this rule for components receiving at the same time ( ). The rules (Bro-l) and (Bro-r) are added to make broadcast communication non-blocking: without them a component could be delayed in performing a broadcast simply because one of the other components is not ready to receive it.
). The rules (Bro-l) and (Bro-r) are added to make broadcast communication non-blocking: without them a component could be delayed in performing a broadcast simply because one of the other components is not ready to receive it.
3.3 CCS with Signals
CCS with signals (CCSS) [6] is CCS extended with a signalling operator  . Informally,
. Informally,  emits the signal s to be read by another process.
emits the signal s to be read by another process.  could for instance be a traffic light emitting the signal red. The reading of the signal emitted by
could for instance be a traffic light emitting the signal red. The reading of the signal emitted by  does not interfere with any transition of P, such as jumping to green. Formally, CCS is extended with a set
does not interfere with any transition of P, such as jumping to green. Formally, CCS is extended with a set  of signals, ranged over by s and r. In CCSS the set of actions is defined as
of signals, ranged over by s and r. In CCSS the set of actions is defined as
 , and the set of labels by
, and the set of labels by  , where
, where  . A relabelling is a function
. A relabelling is a function  . It extends to
. It extends to  by
by  for
for  and \(f(\tau ):=\tau \). The set
and \(f(\tau ):=\tau \). The set  of CCSS expressions is defined just as
of CCSS expressions is defined just as  , but now also
, but now also  is a process for
is a process for  and
and  , and restriction also covers signals.
, and restriction also covers signals.
The semantics of CCSS is given by the labelled transition relation  derived from the rules of CCS (Table 1), where now \(\eta ,\ell \) range over
derived from the rules of CCS (Table 1), where now \(\eta ,\ell \) range over  , \(\alpha \) over
, \(\alpha \) over
 , c over
, c over  and
and  , augmented with the rules of Table 3. The first rule is the base case showing that a process
, augmented with the rules of Table 3. The first rule is the base case showing that a process  emits the signal s. The rule below models the fact that signalling cannot prevent a process from making progress.
emits the signal s. The rule below models the fact that signalling cannot prevent a process from making progress.
The original semantics of CCSS [6] featured unary predicates \(P^{\curvearrowright s}\) on processes to model that P emits the signal s; here, inspired by [3], these predicates are represented as transitions
 . Whereas this leads to a simpler operational semantics, the price paid is that these new signal transitions need special treatment in the definition of justness—cf. Definitions 2 and 5.
. Whereas this leads to a simpler operational semantics, the price paid is that these new signal transitions need special treatment in the definition of justness—cf. Definitions 2 and 5.
3.4 Using Signals to Avoid Negative Premises in ABC
Finally, we present an alternative operational semantics ABCd of ABC that avoids negative premises. The price to be paid is the introduction of signals that indicate when a state does not admit a receive action.Footnote 3 To this end, let  be the set of broadcast discards, and
be the set of broadcast discards, and
 the set of transition labels, with Act as in Sect. 3.2. The semantics is given by the labelled transition relation
the set of transition labels, with Act as in Sect. 3.2. The semantics is given by the labelled transition relation  derived from the rules of CCS (Table 1), where now c ranges over
derived from the rules of CCS (Table 1), where now c ranges over  , \(\eta \) over
, \(\eta \) over  , \(\alpha \) over Act and \(\ell \) over
, \(\alpha \) over Act and \(\ell \) over  , augmented with the rules of Table 4.
, augmented with the rules of Table 4.
Lemma 1
[25]
 iff
iff
 , for
, for  and
and  .
.
So the structural operational semantics of ABC from Sects. 3.2 and 3.4 yield the same labelled transition relation \(\longrightarrow \) when transitions labelled  are ignored. This approach stems from the Calculus of Broadcasting Systems (CBS) [25].
are ignored. This approach stems from the Calculus of Broadcasting Systems (CBS) [25].
4 An LTS with Concurrency for CCS and Its Extensions
The forthcoming material applies to each of the process algebras from Sect. 3, or combinations thereof. Let  be the set of processes in the language.
be the set of processes in the language.
We allocate an LTS as in Definition 1 to these languages by taking S to be the set  of processes, and \(\textit{Tr}\) the set of derivations \(t\) of transitions
of processes, and \(\textit{Tr}\) the set of derivations \(t\) of transitions
 with
with  . Of course
. Of course  ,
,  and
and  . Here a derivation of a transition
. Here a derivation of a transition
 is a well-founded tree with the nodes labelled by transitions, such that the root has label
is a well-founded tree with the nodes labelled by transitions, such that the root has label
 , and if \(\mu \) is the label of a node and K is the set of labels of the children of this node then
, and if \(\mu \) is the label of a node and K is the set of labels of the children of this node then
 is an instance of a rule of Tables 1, 2, 3 and 4.
is an instance of a rule of Tables 1, 2, 3 and 4.
We take  in ABC and ABCd: broadcast receipts can always be blocked by the environment, namely by not broadcasting the requested message. For CCS and CCSS we take \( Rec :=\emptyset \), thus allowing environments that can always participate in certain handshakes, and/or always emit certain signals.
in ABC and ABCd: broadcast receipts can always be blocked by the environment, namely by not broadcasting the requested message. For CCS and CCSS we take \( Rec :=\emptyset \), thus allowing environments that can always participate in certain handshakes, and/or always emit certain signals.
Following [15], we give a name to any derivation of a transition: The unique derivation of the transition
 using the rule (Act) is called
using the rule (Act) is called
 . The unique derivation of the transition
. The unique derivation of the transition
 is called
is called
 . The derivation obtained by application of (Comm) or (Bro-c) on the derivations \(t\) and \(u\) of the premises of that rule is called \(t|u\). The derivation obtained by application of (Par-l) or (Bro-l) on the derivation \(t\) of the (positive) premise of that rule, and using process Q at the right of |, is \(t|Q\). In the same way, (Par-r) and (Bro-r) yield \(P|u\), whereas (Sum-l), (Sum-r), (Res), (Rel) and (Rec) yield \(t{+}Q\), \(P{+}t\), \(t\backslash L\), \(t[f]\) and
. The derivation obtained by application of (Comm) or (Bro-c) on the derivations \(t\) and \(u\) of the premises of that rule is called \(t|u\). The derivation obtained by application of (Par-l) or (Bro-l) on the derivation \(t\) of the (positive) premise of that rule, and using process Q at the right of |, is \(t|Q\). In the same way, (Par-r) and (Bro-r) yield \(P|u\), whereas (Sum-l), (Sum-r), (Res), (Rel) and (Rec) yield \(t{+}Q\), \(P{+}t\), \(t\backslash L\), \(t[f]\) and
 . These names reflect syntactic structure: \(t|P \not =P |t\) and \((t|u)|v \not = t|(u|v)\).
. These names reflect syntactic structure: \(t|P \not =P |t\) and \((t|u)|v \not = t|(u|v)\).
Table 3, moreover, contributes derivations  . The derivations obtained by application of the rules of Table 4 are called \(b{:}{} \mathbf{0}\), \(b{:}\alpha .P\), \(t+u\), t|u and A : t, where t and u are the derivations of the premises.
. The derivations obtained by application of the rules of Table 4 are called \(b{:}{} \mathbf{0}\), \(b{:}\alpha .P\), \(t+u\), t|u and A : t, where t and u are the derivations of the premises.
Synchrons. Let  . A synchron is an expression
. A synchron is an expression  or \(\sigma (P^{\rightarrow s})\) or \(\sigma (b{:})\) with
or \(\sigma (P^{\rightarrow s})\) or \(\sigma (b{:})\) with  ,
,  ,
,  ,
,  and
and  . An argument
. An argument  is applied componentwise to a set \(\varSigma \) of synchrons: \(\iota (\varSigma ) := \{\iota \varsigma \mid \varsigma \in \varSigma \}\).
is applied componentwise to a set \(\varSigma \) of synchrons: \(\iota (\varSigma ) := \{\iota \varsigma \mid \varsigma \in \varSigma \}\).
The set of synchrons \(\varsigma (t)\) of a derivation \(t\) of a transition is defined by

Thus, a synchron of \(t\) represents a path in the proof-tree \(t\) from its root to a leaf. Each transition derivation can be seen as the synchronisation of one or more synchrons. Note that we use the symbol \(\varsigma \) as a variable ranging over synchrons, and as the name of a function—context disambiguates.
Example 3
The CCS process \(P=\left( \big (c.Q + (d.R|e.S)\big )|\bar{c}.T\right) \backslash c\)
has 3 outgoing transitions:
 ,
,
 and
and
 . Let \(t_\tau \), \(t_d\) and \(t_e\in \textit{Tr}\) be the unique derivations of these transitions. Then \(t_\tau \) is a synchronisation of two synchrons, whereas \(t_d\) and \(t_e\in \textit{Tr}\) have only one each:
. Let \(t_\tau \), \(t_d\) and \(t_e\in \textit{Tr}\) be the unique derivations of these transitions. Then \(t_\tau \) is a synchronisation of two synchrons, whereas \(t_d\) and \(t_e\in \textit{Tr}\) have only one each:
 ,
,
 and
and
 . The derivations \(t_d\) and \(t_e\in \textit{Tr}\) can be seen as concurrent, because their synchrons come from opposite sides of the same parallel composition; one would expect that after one of them occurs, a variant of the other is still possible. Indeed, there is a transition
. The derivations \(t_d\) and \(t_e\in \textit{Tr}\) can be seen as concurrent, because their synchrons come from opposite sides of the same parallel composition; one would expect that after one of them occurs, a variant of the other is still possible. Indeed, there is a transition
 . Let \(t'_d\) be its unique derivation. The derivation \(t_d\) and \(t'_d\) are surely different, for they have a different source state. Even their synchrons are different:
. Let \(t'_d\) be its unique derivation. The derivation \(t_d\) and \(t'_d\) are surely different, for they have a different source state. Even their synchrons are different:
 . Nevertheless, \(t'_d\) can be recognised as a future variant of \(t_d\): its only synchron has merely lost an argument \(+_R\). This choice got resolved when taking the transition \(t_e\).
. Nevertheless, \(t'_d\) can be recognised as a future variant of \(t_d\): its only synchron has merely lost an argument \(+_R\). This choice got resolved when taking the transition \(t_e\).
We proceed to formalise the concepts “future variant” and “concurrent” that occur above, by defining two binary relations  and
and  such that the following properties hold:
such that the following properties hold:




With  we mean that the possible occurrence of \(t\) is unaffected by the occurrence of v. Although for CCS the relation
we mean that the possible occurrence of \(t\) is unaffected by the occurrence of v. Although for CCS the relation  is symmetric (and \(\textit{Tr}^\bullet =\textit{Tr}\)), for ABC and CCSS it is not:
is symmetric (and \(\textit{Tr}^\bullet =\textit{Tr}\)), for ABC and CCSS it is not:
Example 4
([15]). Let P be the process \(b!|(b?+c)\), and let \(t\) and v be the derivations of the b!- and c-transitions of P. The broadcast b! is in our view completely under the control of the left component; it will occur regardless of whether the right component listens to it or not. It so happens that if b! occurs in state P, the right component will listen to it, thereby disabling the possible occurrence of c. For this reason we have  but
but  .
.
Example 5
Let P be the process  , and let \(t\) and v be the derivations of the a- and \(\tau \)-transitions of P. The occurrence of a disrupts the emission of the signal s, thereby disabling the \(\tau \)-transition. However, reading the signal does not affect the possible occurrence of a. For this reason we have
, and let \(t\) and v be the derivations of the a- and \(\tau \)-transitions of P. The occurrence of a disrupts the emission of the signal s, thereby disabling the \(\tau \)-transition. However, reading the signal does not affect the possible occurrence of a. For this reason we have  but
but  .
.
Proposition 1
Assume (4)–(7). Then the LTS  , augmented with the concurrency relation
, augmented with the concurrency relation  , is an LTSC in the sense of Definition 4.
, is an LTSC in the sense of Definition 4.
We now proceed to define the relations  and
and  on synchrons, and then lift them to derivations. Subsequently, we establish (4)–(7).
on synchrons, and then lift them to derivations. Subsequently, we establish (4)–(7).
The elements \(+_L\), \(+_R\), A : and  of Arg are called dynamic [20]; the others are static. (Static operators stay around when their arguments perform transitions.) For \(\sigma \in Arg ^*\) let \( static (\sigma )\) be the result of removing all dynamic elements from \(\sigma \). For \(\varsigma =\sigma \upsilon \) with
of Arg are called dynamic [20]; the others are static. (Static operators stay around when their arguments perform transitions.) For \(\sigma \in Arg ^*\) let \( static (\sigma )\) be the result of removing all dynamic elements from \(\sigma \). For \(\varsigma =\sigma \upsilon \) with
 let \( static (\varsigma ):= static (\sigma )\upsilon \).
let \( static (\varsigma ):= static (\sigma )\upsilon \).
Definition 6
A synchron \(\varsigma '\) is a possible successor of a synchron \(\varsigma \), notation  , if either \(\varsigma '=\varsigma \), or \(\varsigma \) has the form \(\sigma _1|_D\varsigma _2\) for some \(\sigma _1\in { Arg}^*\), \(D\in \{L,R\}\) and \(\varsigma _2\) a synchron, and \(\varsigma '= static (\sigma _1)|_D\varsigma _2\).
, if either \(\varsigma '=\varsigma \), or \(\varsigma \) has the form \(\sigma _1|_D\varsigma _2\) for some \(\sigma _1\in { Arg}^*\), \(D\in \{L,R\}\) and \(\varsigma _2\) a synchron, and \(\varsigma '= static (\sigma _1)|_D\varsigma _2\).
Definition 7
Two synchrons \(\varsigma \) and \(\upsilon \) are directly concurrent, notation \(\varsigma \smile _d \upsilon \), if \(\varsigma \) has the form \(\sigma _1 |_D \varsigma _2\) and \(\upsilon = \sigma _1 |_E \upsilon _2\) with \(\{D,E\}=\{L,R\}\). Two synchrons \(\varsigma '\) and \(\upsilon '\) are concurrent, notation \(\varsigma '\! \smile \upsilon '\!\), if  .
.
Necessary and Active Synchrons. All synchrons of the form
 are active; their execution causes a transition
are active; their execution causes a transition
 in the relevant component of the represented system. Synchrons \(\sigma (P^{\rightarrow s})\) and \(\sigma (b{:})\) are passive; they are not affecting any state change. Let \(a\varsigma (t)\) denote the set of active synchrons of a derivation t. So a transition t is labelled by a signal, i.e. \(\ell (t)\notin Act\), iff \(a\varsigma (t)=\emptyset \).
in the relevant component of the represented system. Synchrons \(\sigma (P^{\rightarrow s})\) and \(\sigma (b{:})\) are passive; they are not affecting any state change. Let \(a\varsigma (t)\) denote the set of active synchrons of a derivation t. So a transition t is labelled by a signal, i.e. \(\ell (t)\notin Act\), iff \(a\varsigma (t)=\emptyset \).
Whether a synchron \(\varsigma \in \varsigma (t)\) is necessary for t to occur is defined only for \(t\in \textit{Tr}^\bullet \). If \(t\) is the derivation of a broadcast transition, i.e., \(\ell (t)=b!\) for some  , then exactly one synchron \(\upsilon \in \varsigma (t)\) is of the form
, then exactly one synchron \(\upsilon \in \varsigma (t)\) is of the form
 , while all the other \(\varsigma \in \varsigma (t)\) are of the form
, while all the other \(\varsigma \in \varsigma (t)\) are of the form
 (or possibly
(or possibly
 in ABCd). Only the synchron \(\upsilon \) is necessary for the broadcast to occur, as a broadcast is unaffected by whether or not someone listens to it. Hence we define \(n\varsigma (t):=\{\upsilon \}\). For all \(t\in \textit{Tr}^\bullet \) with
in ABCd). Only the synchron \(\upsilon \) is necessary for the broadcast to occur, as a broadcast is unaffected by whether or not someone listens to it. Hence we define \(n\varsigma (t):=\{\upsilon \}\). For all \(t\in \textit{Tr}^\bullet \) with  (i.e.
(i.e.  ) we set \(n\varsigma (t):=\varsigma (t)\), thereby declaring all synchrons of the derivation necessary.
) we set \(n\varsigma (t):=\varsigma (t)\), thereby declaring all synchrons of the derivation necessary.
Definition 8
A derivation \(t'\in \textit{Tr}^\bullet \) is a possible successor of a derivation \(t\in \textit{Tr}^\bullet \), notation  , if \(t\) and \(t'\) have equally many necessary synchrons and each necessary synchron of \(t'\) is a possible successor of one of \(t\); i.e., if \(|n\varsigma (t)| = |n\varsigma (t')|\) and
, if \(t\) and \(t'\) have equally many necessary synchrons and each necessary synchron of \(t'\) is a possible successor of one of \(t\); i.e., if \(|n\varsigma (t)| = |n\varsigma (t')|\) and  .
.
This implies that the relation  between \(n\varsigma (t)\) and \(n\varsigma (u)\) is a bijection.
between \(n\varsigma (t)\) and \(n\varsigma (u)\) is a bijection.
Definition 9
Derivation \(t\in \textit{Tr}^\bullet \) is unaffected by \(u\), notation  , if
, if  .
.
So \(t\) is unaffected by \(u\) if no active synchron of \(u\) interferes with a necessary synchron of \(t\). Passive synchrons do not interfere at all.
In Example 3 one has \(t_d \smile t_e\),  and \(t'_d \smile t_e\). Here \(t \smile u\) denotes
and \(t'_d \smile t_e\). Here \(t \smile u\) denotes  .
.
Proposition 2
5 Components
This section proposes a concept of system components associated to a transition, with a classification of components as necessary and/or affected. We then define a concurrency relation  in terms of these components closely mirroring Definition 9 in Sect. 4 of the concurrency relation
in terms of these components closely mirroring Definition 9 in Sect. 4 of the concurrency relation  in terms of synchrons. We show that
in terms of synchrons. We show that  and
and  , as well as the concurrency relation defined in terms of components in Sect. 2, give rise to the same concept of justness.
, as well as the concurrency relation defined in terms of components in Sect. 2, give rise to the same concept of justness.
A static component is a string \(\sigma \in { Arg}^*\) of static arguments. Let  be the set of static components. The static component \(c(\varsigma )\) of a synchron \(\varsigma \) is defined to be the largest prefix \(\gamma \) of \(\varsigma \) that is a static component.
be the set of static components. The static component \(c(\varsigma )\) of a synchron \(\varsigma \) is defined to be the largest prefix \(\gamma \) of \(\varsigma \) that is a static component.
Let \(\textit{comp}(t) := \{c(\varsigma )\mid \varsigma \in \varsigma (t)\}\) be the set of static components of \(t\). Moreover, \(\textit{npc}(t):=\{c(\varsigma )\mid \varsigma \in n\varsigma (t)\}\) and \(\textit{afc}(t):=\{c(\varsigma )\mid \varsigma \in a\varsigma (t)\}\) are the necessary and affected static components of \(t\in \textit{Tr}\). Since \(n\varsigma (t) \subseteq \varsigma (t)\) and \(a\varsigma (t) \subseteq \varsigma (t)\), we have \(\textit{npc}(t) \subseteq \textit{comp}(t)\) and \(\textit{afc}(t) \subseteq \textit{comp}(t)\).
Two static components \(\gamma \) and \(\delta \) are concurrent, notation \(\gamma \smile \delta \), if \(\gamma = \sigma _1 |_D \gamma _2\) and \(\delta = \sigma _1 |_E \delta _2\) with \(\{D,E\}=\{L,R\}\).
Definition 10
Derivation \(t\in \textit{Tr}^\bullet \) is statically unaffected by \(u\),  , iff
, iff  .
.
Proposition 3
If  then
then  .
.
In Example 3 we have \(t_d \smile t_e\) but \(t_d \,\not \!\smile _s t_e\), for \(\textit{npc}(t_e)=\textit{comp}(t_e)=\textit{comp}(t_d)=\textit{afc}(t_d)=\{\backslash c\, {|_L}\}\). Here \(t \smile _s u\) denotes  . Hence the implication of Proposition 3 is strict.
. Hence the implication of Proposition 3 is strict.
Proposition 4
The functions \(\textit{npc}\) and  satisfy closure property (3) of Sect. 2.
satisfy closure property (3) of Sect. 2.
The concurrency relation  defined in terms of static components according to the template in [16], recalled in Sect. 2, is not identical to
defined in terms of static components according to the template in [16], recalled in Sect. 2, is not identical to  :
:
Definition 11
Let \(t,u\) be derivations. Write  iff \(\textit{npc}(t) \cap \textit{afc}(u) = \emptyset \).
iff \(\textit{npc}(t) \cap \textit{afc}(u) = \emptyset \).
Nevertheless, we show that for the study of justness it makes no difference whether justness is defined using the concurrency relation  ,
,  or
or  .
.
Theorem 2
A path is  -B-just iff it is
-B-just iff it is  -B-just iff it is
-B-just iff it is  -B-just.
-B-just.
6 A Coinductive Characterisation of Justness
In this section we show that the  -based concept of justness defined in this paper coincides with a coinductively defined concept of justness, for CCS and ABC originating from [15]. To state the coinductive definition of justness, we need to define the notion of the decomposition of a path starting from a process with a leading static operator.
-based concept of justness defined in this paper coincides with a coinductively defined concept of justness, for CCS and ABC originating from [15]. To state the coinductive definition of justness, we need to define the notion of the decomposition of a path starting from a process with a leading static operator.
Any derivation \(t\in \textit{Tr}\) of a transition with \(\textit{src}(t)=P|Q\) has the shape
-
u|Q, with \(\textit{target}(t)=\textit{target}(u)|Q\),
-
u|v, with \(\textit{target}(t)=\textit{target}(u)|\textit{target}(v)\),
-
or P|v, with \(\textit{target}(t)=P|\textit{target}(v)\).
Let a path of a process P be a path as in Definition 2 starting with P. Now the decomposition of a path \(\pi \) of P|Q into paths \(\pi _1\) and \(\pi _2\) of P and Q, respectively, is obtained by concatenating all left-projections of the states and transitions of \(\pi \) into a path of P and all right-projections into a path of Q—notation \(\pi \Rrightarrow \pi _1 | \pi _2\). Here it could be that \(\pi \) is infinite, yet either \(\pi _1\) or \(\pi _2\) (but not both) are finite.
Likewise,  with \(\textit{src}(t)=P[f]\) has the shape u[f] with \(\textit{target}(t)=\textit{target}(u)[f]\). The decomposition \(\pi '\) of a path \(\pi \) of P[f] is the path obtained by leaving out the outermost [f] of all states and transitions in \(\pi \), notation \(\pi \Rrightarrow \pi '[f]\). In the same way one defines the decomposition of a path of \(P\backslash c\).
with \(\textit{src}(t)=P[f]\) has the shape u[f] with \(\textit{target}(t)=\textit{target}(u)[f]\). The decomposition \(\pi '\) of a path \(\pi \) of P[f] is the path obtained by leaving out the outermost [f] of all states and transitions in \(\pi \), notation \(\pi \Rrightarrow \pi '[f]\). In the same way one defines the decomposition of a path of \(P\backslash c\).
The following co-inductive definition of the family B-justness of predicates on paths, with one family member of each choice of a set B of blocking actions, stems from [15, Appendix E]—here  .
.
Definition 12
B-justness, for  , is the largest family of predicates on the paths in the LTS of ABC such that
, is the largest family of predicates on the paths in the LTS of ABC such that
-
a finite B-just path ends in a state that admits actions from B only;
-
a B-just path of a process P|Q can be decomposed into a C-just path of P and a D-just path of Q, for some \(C,D\subseteq B\) such that
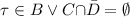 ;
; -
a B-just path of \(P\backslash L\) can be decomposed into a \(B\cup L \cup \bar{L}\)-just path of P;
-
a B-just path of P[f] can be decomposed into an \(f^{-1}(B)\)-just path of P;
-
and each suffix of a B-just path is B-just.
Intuitively, justness is a completeness criterion, telling which paths can actually occur as runs of the represented system. A path is B-just if it can occur in an environment that may block the actions in B. In this light, the first, third, fourth and fifth requirements above are intuitively plausible. The second requirement first of all says that if \(\pi \Rrightarrow \pi _1 | \pi _2\) and \(\pi \) can occur in the environment that may block the actions in B, then \(\pi _1\) and \(\pi _2\) must be able to occur in such an environment as well, or in environments blocking less. The last clause in this requirement prevents a C-just path of P and a D-just path of Q to compose into a B-just path of P|Q when C contains an action c and D the complementary action \(\bar{c}\) (except when \(\tau \in B\)). The reason is that no environment (except one that can block \(\tau \)-actions) can block both actions for their respective components, as nothing can prevent them from synchronising with each other.
The fifth requirement helps characterising processes of the form \(b+(A|b)\) and a.(A|b), with
 . Here, the first transition ‘gets rid of’ the choice and of the leading action a, respectively, and this requirement reduces the justness of paths of such processes to their suffixes.
. Here, the first transition ‘gets rid of’ the choice and of the leading action a, respectively, and this requirement reduces the justness of paths of such processes to their suffixes.
Example 6
To illustrate Definition 12 consider the unique infinite path of the process Alice|Cataline of Example 2 in which the transition t does not occur. Taking the empty set of blocking actions, we ask whether this path is \(\emptyset \)-just. If it were, then by the second requirement of Definition 12 the projection of this path on the process Cataline would need to be \(\emptyset \)-just as well. This is the path 1 (without any transitions) in Example 1. It is not \(\emptyset \)-just by the first requirement of Definition 12, because its last state 1 admits a transition.
We now establish that the concept of justness from Definition 12 agrees with the concept of justness defined earlier in this paper.
Theorem 3
A path is  -B-just iff it is B-just in the sense of Definition 12.
-B-just iff it is B-just in the sense of Definition 12.
If a path \(\pi \) is B-just then it is C-just for any \(C\supseteq B\). Moreover, the collection of sets B such that a given path \(\pi \) is B-just is closed under arbitrary intersection, and thus there is a least set \(B_\pi \) such that \(\pi \) is B-just. Actions  are called \(\pi \)-enabled [14]. A path is called just (without a predicate B) iff it is B-just for some
are called \(\pi \)-enabled [14]. A path is called just (without a predicate B) iff it is B-just for some
 [3, 6, 14, 15], which is the case iff it is
[3, 6, 14, 15], which is the case iff it is
 -just.
-just.
In [3] a definition of justness for CCS with signal transition appears, very similar to Definition 12; it also applies to CCSS as presented here. Generalising Theorem 3, one can show that a path is ( or
or  or)
or)  -just iff it is just in this sense. The same holds for the coinductive definition of justness from [6].
-just iff it is just in this sense. The same holds for the coinductive definition of justness from [6].
7 Conclusion
We advocate justness as a reasonable completeness criterion for formalising liveness properties when modelling distributed systems by means of transition systems. In [16] we proposed a definition of justness in terms of a, possibly asymmetric, concurrency relation between transitions. The current paper defined such a concurrency relation for the transition systems associated to CCS, as well as its extensions with broadcast communication and signals, thereby making the definition of justness from [16] available to these languages. In fact, we provided three versions of the concurrency relation, and showed that they all give rise to the same concept of justness. We expect that this style of definition will carry over to many other process algebras. We showed that justness satisfies the criterion of feasibility, and proved that our formalisation agrees with previous coinductive formalisations of justness for these languages.
Concurrency relations between transitions in transition systems have been studied in [28]. Our concurrency relation  follows the same computational intuition. However, in [28] transitions are classified as concurrent or not only when they have the same source, whereas as a basis for the definition of justness here we need to compare transitions with different sources. Apart from that, our concurrency relation is more general in that it satisfies fewer closure properties, and moreover is allowed to be asymmetric.
follows the same computational intuition. However, in [28] transitions are classified as concurrent or not only when they have the same source, whereas as a basis for the definition of justness here we need to compare transitions with different sources. Apart from that, our concurrency relation is more general in that it satisfies fewer closure properties, and moreover is allowed to be asymmetric.
Concurrency is represented explicitly in models like Petri nets [26], event structures [29], or asynchronous transition systems [2, 27, 30]. We believe that the semantics of CCS in terms of such models agrees with its semantics in terms of labelled transition systems with a concurrency relation as given here. However, formalising such a claim requires a choice of an adequate justness-preserving semantic equivalence defined on the compared models. Development of such semantic equivalences is a topic for future research.
Notes
- 1.
- 2.
Exceptionally, states without outgoing transitions are allowed, and then quantification is over all maximal paths, i.e. paths that are infinite or end in a state without outgoing transitions [5].
- 3.
A state P admits an action \(\alpha \in Act\) if there exists a transition
 .
.
References
Apt, K.R., Francez, N., Katz, S.: Appraising fairness in languages for distributed programming. Distrib. Comput. 2(4), 226–241 (1988). https://doi.org/10.1007/BF01872848
Bednarczyk, M.: Categories of asynchronous systems. Ph.D. thesis, Computer Science, University of Sussex, Brighton (1987)
Bouwman, M.S.: Liveness analysis in process algebra: simpler techniques to model mutex algorithms. Technical report, Eindhoven University of Technology (2018). http://www.win.tue.nl/~timw/downloads/bouwman_seminar.pdf
Coppo, M., Dezani-Ciancaglini, M., Padovani, L., Yoshida, N.: Inference of global progress properties for dynamically interleaved multiparty sessions. In: De Nicola, R., Julien, C. (eds.) COORDINATION 2013. LNCS, vol. 7890, pp. 45–59. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38493-6_4
De Nicola, R., Vaandrager, F.W.: Three logics for branching bisimulation. J. ACM 42(2), 458–487 (1995). https://doi.org/10.1145/201019.201032
Dyseryn, V., van Glabbeek, R.J., Höfner, P.: Analysing mutual exclusion using process algebra with signals. In: Peters, K., Tini, S. (eds.) Proceedings of the Combined 24th International Workshop on Expressiveness in Concurrency and 14th Workshop on Structural Operational Semantics, Electronic Proceedings in Theoretical Computer Science 255. Open Publishing Association, pp. 18–34 (2017). https://doi.org/10.4204/EPTCS.255.2
Emerson, E.A., Clarke, E.M.: Using branching time temporal logic to synthesize synchronization skeletons. Sci. Comput. Program. 2(3), 241–266 (1982). https://doi.org/10.1016/0167-6423(83)90017-5
Emerson, E.A., Halpern, J.Y.: ‘Sometimes’ and ‘Not Never’ revisited: on branching time versus linear time temporal logic. J. ACM 33(1), 151–178 (1986). https://doi.org/10.1145/4904.4999
Fehnker, A., van Glabbeek, R.J., Höfner, P., McIver, A., Portmann, M., Tan, W.L.: A process algebra for wireless mesh networks. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 295–315. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_15
Fehnker, A., van Glabbeek, R.J., Höfner, P., McIver, A.K., Portmann, M., Tan, W.L.: A process algebra for wireless mesh networks used for modelling, verifying and analysing AODV. Technical report 5513, NICTA (2013). http://arxiv.org/abs/1312.7645
van Glabbeek, R.J.: Structure preserving bisimilarity, supporting an operational petri net semantics of CCSP. In: Meyer, R., Platzer, A., Wehrheim, H. (eds.) Correct System Design. LNCS, vol. 9360, pp. 99–130. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-23506-6_9. http://arxiv.org/abs/1509.05842
van Glabbeek, R.J.: Ensuring Liveness Properties of Distributed Systems (A Research Agenda). Position paper (2016). http://arxiv.org/abs/org/abs/1711.04240
van Glabbeek, R.J.: Justness: a completeness criterion for capturing liveness properties. Technical report, Data61, CSIRO (2018). http://www.cse.unsw.edu.au/~rvg/synchrons.pdf. Full version of the present paper
van Glabbeek, R.J., Höfner, P.: CCS: It’s not fair! Acta Inform. 52(2–3), 175–205 (2015). https://doi.org/10.1007/s00236-015-0221-6
van Glabbeek, R.J., Höfner, P.: Progress, fairness and justness in process algebra. Technical report 8501, NICTA (2015). http://arxiv.org/abs/1501.03268
van Glabbeek, R.J., Höfner, P.: Progress, justness and fairness. Survey paper, Data61, CSIRO, Sydney, Australia (2018). https://arxiv.org/abs/1810.07414
Kuiper, R., de Roever, W.-P.: Fairness assumptions for CSP in a temporal logic framework. In: Bjørner, D. (ed.) Formal Description of Programming Concepts II, North-Holland, pp. 159–170 (1983)
Lamport, L.: Proving the correctness of multiprocess programs. IEEE Trans. Softw. Eng. 3(2), 125–143 (1977). https://doi.org/10.1109/TSE.1977.229904
Lamport, L.: Fairness and hyperfairness. Distrib. Comput. 13(4), 239–245 (2000). https://doi.org/10.1007/PL00008921
Milner, R. (ed.): A Calculus of Communicating Systems. LNCS, vol. 92. Springer, Heidelberg (1980). https://doi.org/10.1007/3-540-10235-3
Misra, J.: A Rebuttal of Dijkstra’s position on fairness (1988). http://www.cs.utexas.edu/users/misra/Notes.dir/fairness.pdf
Misra, J.: A Discipline of Multiprogramming—Programming Theory for Distributed Applications. Springer, New York (2001). https://doi.org/10.1007/978-1-4419-8528-6
Owicki, S.S., Lamport, L.: Proving liveness properties of concurrent programs. ACM TOPLAS 4(3), 455–495 (1982). https://doi.org/10.1145/357172.357178
Pnueli, A.: The temporal logic of programs. In: Proceedings of the 18th Annual Symposium on Foundations of Computer Science (FOCS 1977), pp. 46–57. IEEE (1977). https://doi.org/10.1109/SFCS.1977.32
Prasad, K.V.S.: A calculus of broadcasting systems. In: Abramsky, S., Maibaum, T.S.E. (eds.) CAAP 1991. LNCS, vol. 493, pp. 338–358. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-53982-4_19
Reisig, W.: Understanding Petri Nets—Modeling Techniques, Analysis Methods, Case Studies. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-33278-4
Shields, M.W.: Concurrent machines. Comput. J. 28(5), 449–465 (1985). https://doi.org/10.1093/comjnl/28.5.449
Stark, E.W.: Concurrent transition systems. Theor. Comput. Sci. 64(3), 221–269 (1989). https://doi.org/10.1016/0304-3975(89)90050-9
Winskel, G.: Event structures. In: Brauer, W., Reisig, W., Rozenberg, G. (eds.) ACPN 1986, Part II. LNCS, vol. 255, pp. 325–392. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-17906-2_31
Winskel, G., Nielsen, M.: Models for concurrency. In: Abramsky, S., Gabbay, D., Maibaum, T. (eds.) Handbook of Logic in Computer Science, Chap. 1, 4: Semantic Modelling, pp. 1–148. Oxford University Press, Oxford (1995)
Acknowledgement
I am grateful to Peter Höfner, Victor Dyseryn and Filippo de Bortoli for valuable feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
van Glabbeek, R. (2019). Justness. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_29
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)





 and
and  satisfy the properties (
satisfy the properties (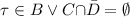 ;
; .
.