Abstract
In 1982, Courcelle and Franchi-Zannettacci showed that the equivalence problem of separated non-nested attribute systems can be reduced to the equivalence problem of total deterministic separated basic macro tree transducers. They also gave a procedure for deciding equivalence of transducer in the latter class. Here, we reconsider this equivalence problem. We present a new alternative decision procedure and prove that it runs in polynomial time. We also consider extensions of this result to partial transducers and to the case where parameters of transducers accumulate strings instead of trees.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Attribute grammars are a well-established formalism for realizing computations on syntax trees [20, 21], and implementations are available for various programming languages, see, e.g. [12, 28, 29]. A fundamental question for any such specification formalism is whether two specifications are semantically equivalent. As a particular case, attribute grammars have been considered which compute uninterpreted trees. Such devices that translate input trees (viz. the parse trees of a context-free grammar) into output trees, have also been studied under the name “attributed tree transducer” [14] (see also [15]). In 1982, Courcelle and Franchi-Zannettacci showed that the equivalence problem for (strongly noncircular) attribute systems reduces to the equivalence problem for primitive recursive schemes with parameters [3]; the latter model is also known under the name macro tree transducer [9]. Whether or not equivalence of attributed tree transducers (ATTs) or of (deterministic) macro tree transducers (MTTs) is decidable remain two intriguing (and very difficult) open problems.
For several subclasses of ATTs it has been proven that equivalence is decidable. The most general and very recent result that covers almost all other known ones about deterministic tree transducers is that “deterministic top-down tree-to-string transducers” have decidable equivalence [27]. Notice that the complexity of this problem remains unknown (the decidability is proved via two semi-decision procedures). The only result concerning deterministic tree transducers that we are aware of and that is not covered by this general result, is the one by Courcelle and Franchi-Zannettacci about decidability of equivalence of “separated non-nested” ATTs (which they reduce to the same problem for “separated non-nested” MTTs). However, in their paper no statement is given concerning the complexity of the problem. In this paper we close this gap and study the complexity of deciding equivalence of separated non-nested MTTs. To do so we propose a new approach that we feel is simpler and easier to understand than the one of [3]. Using our approach we can prove that the problem can be solved in polynomial time.
In a separated non-nested attribute system, distinct sets of operators are used for the construction of inherited and synthesized attributes, respectively, and inherited attributes may depend on inherited attributes only. Courcelle and Franchi-Zannettacci’s algorithm first translates separated non-nested attribute grammars into separated total deterministic non-nested macro tree transducers. In the sequel we will use the more established term basic macro-tree transducers instead of non-nested MTTs. Here, a macro tree transducer is called separated if the alphabets used for the construction of parameter values and outside of parameter positions are disjoint. And the MTT is basic if there is no nesting of state calls, i.e., there are no state calls inside of parameter positions. Let us consider an example. We want to translate ternary numbers into expressions over \(+\), \(*\), \(\text {EXP}\), plus the constants 0, 1, and 2. Additionally, operators s, p, and z are used to represent integers in unary. The ternary numbers are parsed into particular binary trees; e.g., the left of Fig. 1 shows the binary tree for the number 2101.02. This tree is translated by our MTT into the tree in the right of Fig. 1 (which indeed evaluates to \(64.\overline{2}\) in decimal). The rules of our transducer \(M_{\text {tern}}\) are shown in Fig. 2. The example is similar to the one used by Knuth [20] in order to introduce attribute grammars. The transducer is indeed basic and separated: the operators p, s, and z are only used in parameter positions.
Our polynomial time decision procedure works in two phases: first, the transducer is converted into an “earliest” normal form. In this form, output symbols that are not produced within parameter positions are produced as early as possible. In particular it means that the root output symbols of the right-hand sides of rules for one state must differ. For instance, our transducer \(M_{\text {tern}}\) is not earliest, because all three r-rules produce the same output root symbol (\(*\)). Intuitively, this symbol should be produced earlier, e.g., at the place when the state r is called. The earliest form is a common technique used for normal forms and equivalence testing of different kinds of tree transducers [8, 13, 22]. We show that equivalent states of a transducer in this earliest form produce their state-output exactly in the same way. This means especially that the output of parameters is produced in the same places. It is therefore left to check, in the second phase, that also these parameter outputs are equivalent. To this end, we build an equivalence relation on states of earliest transducers that combines the two equivalence tests described before. Technically speaking, the equivalence relation is tested by constructing sets of Herbrand equalities. From these equalities, a fixed point algorithm can, after polynomially many iterations, produce a stable set of equalities.
The proofs of Lemmata 1 and 2 can be found in the appendix of an extended version at http://arxiv.org/abs/1902.03858.
2 Separated Basic Macro Tree Transducers
Let \(\varSigma \) be a ranked alphabet, i.e., every symbol of the finite set \(\varSigma \) has associated with it a fixed rank \(k \in \mathbb {N}\). Generally, we assume that the input alphabet \(\varSigma \) is non-trivial, i.e., \(\varSigma \) has cardinality at least 2, and contains at least one symbol of rank 0 and at least one symbol of rank \(>0\). The set \(\mathcal {T}_\varSigma \) is the set of all (finite, ordered, rooted) trees over the alphabet \(\varSigma \). We denote a tree as a string over \(\varSigma \) and parenthesis and commas, i.e., f(a, f(a, b)) is a tree over \(\varSigma \), where f is of rank 2 and a, b are of rank zero. We use Dewey dotted decimal notation to refer to a node of a tree: The root node is denoted \(\varepsilon \), and for a node u, its i-th child is denoted by u.i. For instance, in the tree f(a, f(a, b)) the b-node is at position 2.2. A pattern (or k-pattern) (over \(\varDelta \)) is a tree \(p\in \mathcal {T}_{\varDelta \cup \{\top \}}\) over a ranked alphabet \(\varDelta \) and a disjoint symbol \(\top \) (with exactly k occurrences of the symbol \(\top \)). The occurrences of the dedicated symbol \(\top \) serve as place holders for other patterns. Assume that p is a k-pattern and that \(p_1,\dots ,p_k\) are patterns; then \(p[p_1,\ldots ,p_k]\) denotes the pattern obtained from p by replacing, for \(i=1,\ldots ,k\), the i-th occurrence (from left-to-right) of \(\top \) by the pattern \(p_i\).
A macro tree transducer (MTT) M is a tuple \((Q,\varSigma ,\varDelta ,\delta )\) where Q is a ranked alphabet of states, \(\varSigma \) and \(\varDelta \) are the ranked input and output alphabets, respectively, and \(\delta \) is a finite set of rules of the form:
where \(q\in Q\) is a state of rank \(l+1\), \(l\ge 0\), \(f\in \varSigma \) is an input symbol of rank \(k\ge 0\), \(x_1,\ldots ,x_k\) and \(y_1,\ldots ,y_l\) are the formal input and output parameters, respectively, and T is a tree built up according to the following grammar:
for output symbols \(a\in \varDelta \) of rank \(m\ge 0\) and states \(q'\in Q\) of rank \(n+1\), input parameter \(x_i\) with \(1\le i\le k\), and output parameter \(y_j\) with \(1\le j\le l\). For simplicity, we assume that all states q have the same number l of parameters. Our definition of an MTT does not contain an initial state. We therefore consider an MTT always together with an axiom \(A = p[q_1(x_1,\underline{T_1}),\ldots ,q_m(x_1,\underline{T_m})]\) where \(\underline{T_1},\ldots ,\underline{T_m} \in \mathcal {T}_\varDelta ^l\) are vectors of output trees (of length l each). Sometimes we only use an MTT M without explicitly mentioning an axiom A, then some A is assumed implicitly. Intuitively, the state q of an MTT corresponds to a function in a functional language which is defined through pattern matching over its first argument, and which constructs tree output using tree top-concatenation only; the second to \((l+1)\)-th arguments of state q are its accumulating output parameters. The output produced by a state for a given input tree is determined by the right-hand side T of a rule of the transducer which matches the root symbol f of the current input tree. This right-hand side is built up from accumulating output parameters and calls to states for subtrees of the input and applications of output symbols from \(\varDelta \). In general MTTs are nondeterministic and only partially defined. Here, however, we concentrate on total deterministic transducers. The MTT M is deterministic, if for every \((q,f)\in Q\times \varSigma \) there is at most one rule of the form (1). The MTT M is total, if for every \((q,f)\in Q\times \varSigma \) there is at least one rule of the form (1). For total deterministic transducers, the semantics of a state \(q\in Q\) with the rule \(q(f(x_1,\ldots ,x_k),y_1,\ldots ,y_l)\rightarrow T\) can be considered as a function

which inductively is defined by:

where \(\underline{S} = (S_1,\ldots ,S_l)\in \mathcal {T}_\varDelta ^l\) is a vector of output trees. The semantics of a pair (M, A) with MTT M and axiom \(A = p[q_1(x_1,\underline{T_1}),\ldots ,q_m(x_1,\underline{T_m})]\) is defined by  . Two pairs \((M_1,A_1)\), \((M_2,A_2)\) consisting of MTTs \(M_1\), \(M_2\) and corresponding axioms \(A_1\), \(A_2\) are equivalent, \((M_1,A_1) \equiv (M_2,A_2)\), iff for all input trees \(t\in \mathcal {T}_\varSigma \), and parameter values \(\underline{T}\in \mathcal {T}_{\varDelta _{in}}^l\),
. Two pairs \((M_1,A_1)\), \((M_2,A_2)\) consisting of MTTs \(M_1\), \(M_2\) and corresponding axioms \(A_1\), \(A_2\) are equivalent, \((M_1,A_1) \equiv (M_2,A_2)\), iff for all input trees \(t\in \mathcal {T}_\varSigma \), and parameter values \(\underline{T}\in \mathcal {T}_{\varDelta _{in}}^l\),  .
.
The MTT M is basic, if each argument tree \(T_j\) of a subtree \(q'(x_i,T_1,\ldots ,T_n)\) of right-hand sides T of rules (1) may not contain further occurrences of states, i.e., is in \(\mathcal {T}_{\varDelta \cup Y}\). The MTT M is separated basic, if M is basic, and \(\varDelta \) is the disjoint union of ranked alphabets \(\varDelta _{out}\) and \(\varDelta _{in}\) so that the argument trees \(T_j\) of subtrees \(q'(x_i,T_1,\ldots ,T_n)\) are in \(\mathcal {T}_{\varDelta _{in}\cup Y}\), while the output symbols a outside of such subtrees are from \(\varDelta _{out}\). The same must hold for the axiom. Thus, letters directly produced by a state call are in \(\varDelta _{out}\) while letters produced in the parameters are in \(\varDelta _{in}\). The MTT \(M_{\text {tern}}\) from the Introduction is separated basic with \(\varDelta _{out}=\{0, 1, 2, 3, *, +, \text {EXP}\}\) and \(\varDelta _{in}=\{p,s,z\}\).
As separated basic MTTs are in the focus of our interests, we make the grammar for their right-hand side trees T explicit:
where \(a\in \varDelta _{out}\), \(q'\in Q\), \(b\in \varDelta _{in}\) of ranks \(m,n+1\) and \(m'\), respectively, and p is an n-pattern over \(\varDelta \). For separated basic MTTs only axioms \(A=p[q_1(x_1,\underline{T_1}),\ldots ,q_m(x_1,\underline{T_m})]\) with \(T_1,\ldots ,T_m \in \mathcal {T}_{\varDelta _{in}}^l\) are considered.
Note that equivalence of nondeterministic transducers is undecidable (even already for very small subclasses of transductions [18]). Therefore, we assume for the rest of the paper that all MTTs are deterministic and separated basic. We will also assume that all MTTs are total, with the exception of Sect. 5 where we also consider partial MTTs.
Example 1
We reconsider the example from the Introduction and adjust it to our formal definition. The transducer was given without an axiom (but with a tacitly assumed “start state” \(q_0\)). Let us now remove the state \(q_0\) and add the axiom \(A=q(x_1,z)\). The new q rule for g is:
To make the transducer total, we add for state \(q'\) the rule
For state r we add rules \(q(\alpha (x_1,x_2),y) \rightarrow *(0,\text {EXP}(3,y))\) with \(\alpha = f,g\). The MTT is separated basic with \(\varDelta _{out}=\{0, 1, 2, 3, *, +, \text {EXP}\}\) and \(\varDelta _{in}=\{p,s,z\}\). \(\square \)
We restricted ourselves to total separated basic MTTs. However, we would like to be able to decide equivalence for partial transducers as well. For this reason we define now top-down tree automata, and will then decide equivalence of MTTs relative to some given DTA D. A deterministic top-down tree automaton (DTA) D is a tuple \((B, \varSigma , b_0, \delta _D)\) where B is a finite set of states, \(\varSigma \) is a ranked alphabet of input symbols, \(b_0\in B\) is the initial state, and \(\delta _D\) is the partial transition function with rules of the form \(b(f(x_1,\ldots , x_k)) \rightarrow (b_1(x_1),\ldots , b_k(x_k))\), where \(b,b_1,\dots ,b_k\in B\) and \(f\in \varSigma \) of rank k. W.l.o.g. we always assume that all states b of a DTA are productive, i.e., \(\mathsf{dom}(b)\ne \emptyset \). If we consider a MTT M relative to a DTA D we implicitly assume a mapping \(\pi : Q \rightarrow B\), that maps each state of M to a state of D, then we consider for q only input trees in \(\mathsf{dom}(\pi (q))\).
3 Top-Down Normalization of Transducers
In this section we show that each total deterministic basic separated MTT can be put into an “earliest” normal form relative to a fixed DTA D. Intuitively, state output (in \(\varDelta _{out}\)) is produced as early as possible for a transducer in the normal form. It can then be shown that two equivalent transducers in normal form produce their state output in exactly the same way.
Recall the definition of patterns as trees over \(\mathcal {T}_{\varDelta \cup \{\top \}}\). Substitution of \(\top \)-symbols by other patterns induces a partial ordering \(\sqsubseteq \) over patterns by \(p\sqsubseteq p'\) if and only if \(p = p'[p_1,\ldots ,p_m]\) for some patterns \(p_1,\ldots ,p_m\). W.r.t. this ordering, \(\top \) is the largest element, while all patterns without occurrences of \(\top \) are minimal. By adding an artificial least element \(\bot \), the resulting partial ordering is in fact a complete lattice. Let us denote this complete lattice by \(\mathcal {P}_\varDelta \).
Let \(\varDelta =\varDelta _{in}\cup \varDelta _{out}\). For \(T\in \mathcal {T}_{\varDelta \cup Y}\), we define the \(\varDelta _{out}\)-prefix as the pattern \(p\in \mathcal {T}_{\varDelta _{out}\cup \{\top \}}\) as follows. Assume that \(T = a(T_1,\ldots ,T_m)\).
-
If \(a\in \varDelta _{out}\), then \(p = a(p_1,\ldots ,p_m)\) where for \(j=1,\ldots ,m\), \(p_j\) is the \(\varDelta _{out}\)-prefix of \(T_j\).
-
If \(a\in \varDelta _{in}\cup Y\), then \(p = \top \).
By this definition, each tree \(t\in \mathcal {T}_{\varDelta \cup Y}\) can be uniquely decomposed into a \(\varDelta _{out}\)-prefix p and subtrees \(t_1,\ldots ,t_m\) whose root symbols all are contained in \(\varDelta _{in}\cup Y\) such that \(t = p[t_1,\ldots ,t_m]\).
Let M be a total separated basic MTT M, D be a given DTA. We define the \(\varDelta _{out}\)-prefix of a state q of M relative to D as the minimal pattern \(p\in \mathcal {T}_{\varDelta _{out}\cup \{\top \}}\) so that each tree  is of the form \(p[T_1,\ldots ,T_m]\) for some sequence of subtrees \(T_1,\ldots ,T_m \in \mathcal {T}_{\varDelta }\). Let us denote this unique pattern p by \(\mathsf{pref}_o(q)\). If \(q(f, y_1,\ldots , y_l) \rightarrow T\) is a rule of a separated basic MTT and there is an input tree \(f(t_1,\ldots , t_k) \in \mathsf{dom}(\pi (q))\) then \(|\mathsf{pref}_o(q)| \le |T|\).
is of the form \(p[T_1,\ldots ,T_m]\) for some sequence of subtrees \(T_1,\ldots ,T_m \in \mathcal {T}_{\varDelta }\). Let us denote this unique pattern p by \(\mathsf{pref}_o(q)\). If \(q(f, y_1,\ldots , y_l) \rightarrow T\) is a rule of a separated basic MTT and there is an input tree \(f(t_1,\ldots , t_k) \in \mathsf{dom}(\pi (q))\) then \(|\mathsf{pref}_o(q)| \le |T|\).
Lemma 1
Let M be a total separated basic MTT and D a given DTA. Let \(t\in \mathsf{dom}(\pi (q))\) be a smallest input tree of a state q of M. The \(\varDelta _{out}\)-prefix of every state q of M relative to D can be computed in time \(\mathcal {O}(|t|\cdot |M|)\).
The proof is similar to the one of [8, Theorem 8] for top-down tree transducers. This construction can be carried over as, for the computation of \(\varDelta _{out}\)-prefixes, the precise contents of the output parameters \(y_j\) can be ignored.
Example 2
We compute the \(\varDelta _{out}\)-prefix of the MTT M from Example 1. We consider M relative to the trivial DTA D that consists only of one state b with \(dom(b) = \mathcal {T}_\varSigma \). We therefore omit D in our example. We get the following system of in-equations: from the rules of state r we obtain \(Y_r \sqsubseteq *(i,\text {EXP}(3,\top ))\) with \(i \in \{0,1,2\}\). From the rules of state q we obtain \(Y_q \sqsubseteq +(Y_q,Y_{q'})\), \(Y_q \sqsubseteq +(Y_r,Y_{q})\) and \(Y_q \sqsubseteq *(i,\text {EXP}(3,\top ))\) with \(i \in \{0,1,2\}\). From the rules of state \(q'\) we obtain \(Y_{q'} \sqsubseteq +(*(0,\text {EXP}(3,\top )),*(0,\text {EXP}(3,\top )))\), \(Y_{q'} \sqsubseteq +(Y_r,Y_{q'})\) and \(Y_{q'} \sqsubseteq *(i,\text {EXP}(3,\top ))\) with \(i \in \{0,1,2\}\). For the fixpoint iteration we initialize \(Y_r^{(0)}\), \(Y_q^{(0)}\), \(Y_{q'}^{(0)}\) with \(\bot \) each. Then \(Y_r^{(1)} = *(\top ,\text {EXP}(3,\top )) = Y_r^{(2)}\) and \(Y_q^{(1)} = \top \), \(Y_{q'}^{(1)} = \top \). Thus, the fixpoint iteration ends after two rounds with the solution \(\mathsf{pref}_o(q) = \top \). \(\square \)
Let M be a separated basic MTT M and D be a given DTA D. M is called D-earliest if for every state \(q \in Q\) the \(\varDelta _{out}\)-prefix with respect to \(\pi (q)\) is \(\top \).
Lemma 2
For every pair (M, A) consisting of a total separated basic MTT M and axiom A and a given DTA D, an equivalent pair \((M',A')\) can be constructed so that \(M'\) is a total separated basic MTT that is D-earliest. Let t be an output tree of (M, A) for a smallest input tree \(t' \in \mathsf{dom}(\pi (q))\) where q is the state occurring in A. Then the construction runs in time \(\mathcal {O}(|t|\cdot |(M,A)|)\).
The construction follows the same line as the one for the earliest form of top-down tree transducer, cf. [8, Theorem 11]. Note that for partial separated basic MTTs the size of the \(\varDelta _{out}\)-prefixes is at most exponential in the size of the transducer. However for total transducer that we consider here the \(\varDelta _{out}\)-prefixes are linear in the size of the transducer and can be computed in quadratic time, cf. [8].
Corollary 1
For (M, A) consisting of a total deterministic separated basic MTT M and axiom A and the trivial DTA D accepting \(\mathcal {T}_\varSigma \) an equivalent pair \((M',A')\) can be constructed in quadratic time such that \(M'\) is an D-earliest total deterministic separated basic MTT.
Example 3
We construct an equivalent earliest MTT \(M'\) for the transducer from Example 1. In Example 2 we already computed the \(\varDelta _{out}\)-prefixes of states \(q, q', r\); \(\mathsf{pref}_o(q) = \top \), \(\mathsf{pref}_o(q') = \top \) and \(\mathsf{pref}_o(r) = *(\top , \text {EXP}(3,\top ))\). As there is only one occurrence of symbol \(\top \) in the \(\varDelta _{out}\)-prefixes of q and \(q'\) we call states \({\langle q,1\rangle }\) and \({\langle q',1\rangle }\) by q and \(q'\), respectively. Hence, a corresponding earliest transducer has axiom \(A=q(x_1,z)\). The rules of q and \(q'\) for input symbol g do not change. For input symbol f we obtain
As there is only one occurrence of symbol \(\top \) related to a recursive call in \(\mathsf{pref}_o(r)\) we call \({\langle r,1\rangle }\) by r. For state r we obtain new rules \(r(\alpha (x_1,x_2),y) \rightarrow 0\) with \(\alpha \in \{f,g\}\) and \(r(i,y) \rightarrow i\) with \(i \in \{0,1,2\}\). \(\square \)
We define a family of equivalence relation by induction, \(\cong _b\ \subseteq ((Q,\mathcal {T}_{\varDelta _{in}}^k) \cup \mathcal {T}_{\varDelta _{in}}) \times ((Q,\mathcal {T}_{\varDelta _{in}}^k) \cup \mathcal {T}_{\varDelta _{in}})\) with b a state of a given DTA is the intersection of the equivalence relations \(\cong ^{(h)}_b\), i.e., \(X \cong _b Z\) if and only if for all \(h \ge 0\), \(X \cong ^{(h)}_b Z\). We let \((q,\underline{T}) \cong ^{(h+1)}_b (q',\underline{T'})\) if for all \(f \in \mathsf{dom}(b)\) with \(b(f(x_1,\ldots ,x_k) \rightarrow (b_1,\ldots , b_k)\), there is a pattern p such that \(q(f(x_1,\ldots , x_k),\underline{y}) \rightarrow p[t_1,\ldots , t_m]\) and \(q'(f(x_1,\ldots , x_k),\underline{y'}) \rightarrow p[t'_1,\ldots ,t'_m]\) with
-
if \(t_i\) and \(t'_i\) are both recursive calls to the same subtree, i.e., \(t_i = q_i(x_{j_i},\underline{T_i})\), \(t'_i = q'_i(x_{j'_i},\underline{T'_i})\) and \(j_i = j'_i\), then \((q_i,\underline{T_i})[\underline{T}/\underline{y}] \cong ^h_{b_{j_i}} (q'_i,\underline{T'_i})[\underline{T'}/\underline{y'}]\)
-
if \(t_i\) and \(t'_i\) are both recursive calls but on different subtrees, i.e., \(t_i = q_i(x_{j_i},\underline{T_i})\), \(t'_i = q'_i(x_{j'_i},\underline{T'_i})\) and \(j_i \ne j'_i\), then
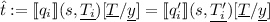 for some \(s \in \varSigma ^{(0)}\) and \((q_i,\underline{T_i})[\underline{T}/\underline{y}] \cong ^{(h)}_{b_{j_i}} \hat{t} \cong ^{(h)}_{b_{j'_i}} (q'_i,\underline{T'_i})[\underline{T}/\underline{y}]\)
for some \(s \in \varSigma ^{(0)}\) and \((q_i,\underline{T_i})[\underline{T}/\underline{y}] \cong ^{(h)}_{b_{j_i}} \hat{t} \cong ^{(h)}_{b_{j'_i}} (q'_i,\underline{T'_i})[\underline{T}/\underline{y}]\) -
if \(t_i\) and \(t'_i\) are both parameter calls, i.e., \(t_i = y_{j_i}\) and \(t'_{i} = y'_{j'_i}\), then \(T_{j_i} = T'_{j'_i}\)
-
if \(t_i\) is a parameter call and \(t'_i\) a recursive call, i.e., \(t_i = y_{j_i}\) and \(t'_i = q'_i(x_{j'_i},\underline{T'_i})\), then \(T_{j_i} \cong ^{(h)}_{b_{j'_i}} (q'_i,\underline{T'_i})[\underline{T'}/\underline{y'}]\)
-
(symmetric to the latter case) if \(t_i\) is a recursive call and \(t'_i\) a parameter call, i.e., \(t_i = q_i(x_{j_i},\underline{T_i})\) and \(t'_i = y'_{j'_i}\), then \((q_i,\underline{T_i})[\underline{T}/\underline{y}] \cong ^{(h)}_{b_{j_i}} T'_{j'_i}\).
We let \(T \cong ^{(h+1)}_b (q',\underline{T'})\) if for all \(f \in \mathsf{dom}(b)\) with \(r(f(x_1,\ldots , x_k))\rightarrow (b_1,\ldots , b_k)\), \(q'(f(\underline{x}),\underline{y}) \rightarrow t'\),
-
if \(t' = y_j\) then \(T = T'_j\)
-
if \(t' = q'_1(x_i,\underline{T'_1})\) then \(T \cong ^{(h)}_{b_i} (q'_1,\underline{T'_1})[\underline{T'}/\underline{y'}]\).
Intuitively, \((q,\underline{T}) \cong ^{h}_b (q',\underline{T'})\) if for all input trees \(t \in \mathsf{dom}(b)\) of height h,  . Then \((q,\underline{T}) \cong _b (q',\underline{T'})\) if for all input trees \(t \in \mathsf{dom}(b)\) (independent of the height),
. Then \((q,\underline{T}) \cong _b (q',\underline{T'})\) if for all input trees \(t \in \mathsf{dom}(b)\) (independent of the height),  .
.
Theorem 1
For a given DTA D with initial state b, let \(M, M'\) be D-earliest total deterministic separated basic MTTs with axioms A and \(A'\), respectively. Then (M, A) is equivalent to \((M',A')\) relative to D, iff there is a pattern p such that \(A=p[q_1(x_1,\underline{T_1}),\ldots , q_m(x_1,\underline{T_m})]\), and \(A'=p[q'_1(x_1,\underline{T'_1}),\ldots , q'_m(x_1,\underline{T'_m})]\) and for \(j=1,\ldots ,m\), \((q_j,\underline{T_j}) \cong _b (q'_j,\underline{T'_j})\), i.e., \(q_j\) and \(q'_j\) are equivalent on the values of output parameters \(\underline{T}_j\) and \(\underline{T}'_j\).
Proof
Let \(\varDelta \) be the output alphabet of M and \(M'\). Assume that \((M,A) \cong _b (M',A')\). As M and \(M'\) are earliest, the \(\varDelta _{out}\)-prefix of  and
and  , for \(t \in \mathsf{dom}(b)\) is the same pattern p and therefore \(A=p[q_1(x_1,\underline{T_1}),\ldots , q_m(x_1,\underline{T_m})]\) and \(A'=p[q'_1(x_1,\underline{T'_1}),\ldots , q'_m(x_1,\underline{T'_m})]\). To show that \((q_i,\underline{T_i}) \cong _{b} (q'_i,\underline{T'_i})\) let \(u_i\) be the position of the i-th \(\top \)-node in the pattern p. For some \(t\in \mathsf{dom}(b)\) and \(\underline{T}\in \mathcal {T}_{\varDelta _{in}}\) let \(t_i\) and \(t'_i\) be the subtree of
, for \(t \in \mathsf{dom}(b)\) is the same pattern p and therefore \(A=p[q_1(x_1,\underline{T_1}),\ldots , q_m(x_1,\underline{T_m})]\) and \(A'=p[q'_1(x_1,\underline{T'_1}),\ldots , q'_m(x_1,\underline{T'_m})]\). To show that \((q_i,\underline{T_i}) \cong _{b} (q'_i,\underline{T'_i})\) let \(u_i\) be the position of the i-th \(\top \)-node in the pattern p. For some \(t\in \mathsf{dom}(b)\) and \(\underline{T}\in \mathcal {T}_{\varDelta _{in}}\) let \(t_i\) and \(t'_i\) be the subtree of  and
and  , respectively. Then \(t_i = t'_i\) and therefore \((q_i,\underline{T_i}) \cong _b (q'_i,\underline{T'_i})\).
, respectively. Then \(t_i = t'_i\) and therefore \((q_i,\underline{T_i}) \cong _b (q'_i,\underline{T'_i})\).
Now, assume that the axioms \(A=p[q_1(x_1,\underline{T_1}),\ldots , q_m(x_1,\underline{T_m})]\) and \(A'=p[q'_1(x_1,\underline{T'_1}),\ldots , q'_m(x_1,\underline{T'_m})]\) consist of the same pattern p and for \(i=1,\ldots ,m\), \((q_i,\underline{T_i}) \cong _b (q'_i,\underline{T'_i})\). Let \(t\in \mathsf{dom}(b)\) be an input tree then

4 Polynomial Time
In this section we prove the main result of this paper, namely, that for each fixed DTA D, equivalence of total deterministic basic separated MTTs (relative to D) can be decided in polynomial time. This is achieved by taking as input two D-earliest such transducers, and then collecting conditions on the parameters of pairs of states of the respective transducers for their produced outputs to be equal.
Example 4
Consider a DTA D with a single state only which accepts all inputs, and states \(q,q'\) with
Then q and \(q'\) can only produce identical outputs for the input a (in \(\mathsf{dom}(b)\)) if parameter \(y_2'\) of \(q'\) contains the same output tree as parameter \(y_1\) of q. This precondition can be formalized by the equality \(y_2'\doteq y_1\). Note that in order to distinguish the output parameters of \(q'\) from those of q we have used primed copies \(y'_i\) for \(q'\). \(\square \)
It turns out that conjunctions of equalities such as in Example 4 are sufficient for proving equivalence of states. For states \(q, q'\) of total separated basic MTTs \(M, M'\), respectively, that are both D-earliest for some fixed DTA D, \(h \ge 0\) and some fresh variable z, we define
where \(\bot \) is the boolean value false. We denote the output parameters in \(\varPsi _{b,q}^{(h)}(z)\) by \(\underline{y}\), we define \(\varPsi _{b,q'}^{\prime (h)}(z)\) in the same lines as \(\varPsi _{b,q}^{(h)}(z)\) but using \(\underline{y'}\) for the output parameters. To substitute the output parameters with trees \(\underline{T}\), \(\underline{T'}\), we therefore use \(\varPsi _{b,q}^{(h)}(z)[\underline{T}/\underline{y}]\) and \(\varPsi _{b,q'}^{\prime (h)}(z)[\underline{T'}/\underline{y'}]\). Assuming that q is a state of the D-earliest separated basic MTT M then \(\varPsi _{b,q}^{(h)}(z)\) is true for all ground parameter values \(\underline{s}\) and some \(T\in \mathcal {T}_{\varDelta \cup Y}\) if  for all input trees \(t\in \mathsf{dom}(b)\) of height at most h. Note that, since M is D-earliest, T is necessarily in \(\mathcal {T}_{\varDelta _{in}\cup Y}\). W.l.o.g., we assume that every state b of D is productive, i.e., \(\mathsf{dom}(b)\ne \emptyset \). For each state b of D, we therefore may choose some input tree \(t_b\in \mathsf{dom}(b)\) of minimal depth. We define \(s_{b,q}\) to be the output of q for a minimal input tree \(t_r \in \mathsf{dom}(b)\) and parameter values \(\underline{y}\)—when considering formal output parameters as output symbols in \(\varDelta _{in}\), i.e.,
for all input trees \(t\in \mathsf{dom}(b)\) of height at most h. Note that, since M is D-earliest, T is necessarily in \(\mathcal {T}_{\varDelta _{in}\cup Y}\). W.l.o.g., we assume that every state b of D is productive, i.e., \(\mathsf{dom}(b)\ne \emptyset \). For each state b of D, we therefore may choose some input tree \(t_b\in \mathsf{dom}(b)\) of minimal depth. We define \(s_{b,q}\) to be the output of q for a minimal input tree \(t_r \in \mathsf{dom}(b)\) and parameter values \(\underline{y}\)—when considering formal output parameters as output symbols in \(\varDelta _{in}\), i.e.,  .
.
Example 5
We consider again the trivial DTA D with only one state b that accepts all \(t \in \mathcal {T}_\varSigma \). Thus, we may choose \(t_b = a\). For a state q with the following two rules \(q(a,y_1,y_2) \rightarrow y_1\) and \(q(f(x),y_1,y_2) \rightarrow q(x,h(y_2),b)\), we have \(s_{b,q} = y_1\). Moreover, we obtain
We observe that \(\varPsi _{b,q}^{(2)}(z) = \varPsi _{b,q}^{(3)}(z)\) and therefore for every \(h\ge 2\), \(\varPsi _{b,q}^{(h)}(z) = \varPsi _{b,q}^{(3)}(z)\). \(\square \)
According to our equivalence relation \(\cong _b\), b state of the DTA D, we define for states \(q,q'\) of D-earliest total deterministic separated basic MTTs \(M,M'\), and \(h \ge 0\), the conjunction \(\varPhi _{b,(q,q')}^{(h)}\) by
\(\varPhi _{b,(q,q')}^{(h)}\) is defined in the same lines as the equivalence relation \(\cong ^{(h)}_b\). \(\varPhi _{b,(q,q')}^{(h)}\) is true for all values of output parameters \(\underline{T}\), \(\underline{T'}\) such that  for \(t \in \mathsf{dom}(b)\) of height at most h. By induction on \(h\ge 0\), we obtain:
for \(t \in \mathsf{dom}(b)\) of height at most h. By induction on \(h\ge 0\), we obtain:
Lemma 3
For a given DTA D, states \(q,q'\) of D-earliest total separated basic MTTs, vectors of trees \(\underline{T}, \underline{T'}\) over \(\varDelta _{in}\), b a state of D. \(s\in \mathsf{dom}(b)\), and \(h\ge 0\) the following two statements hold:
\(\square \)
\(\varPhi _{b,(q,q')}^{(h)}\) is a conjunction of equations of the form \(y_i \doteq y_j\), \(y_i \doteq t\) with \(t \in \varDelta _{in}\). Every satisfiable conjunction of equalities is equivalent to a (possible empty) finite conjunction of equations of the form \(y_{i} \doteq t_{ i}\), \(t_i\in \mathcal {T}_{\varDelta _{in}\cup Y}\) where the \(y_{i}\) are distinct and no equation is of the form \(y_j\doteq y_j\). We call such conjunctions reduced. If we have two inequivalent reduced conjunctions \(\phi _1\) and \(\phi _2\) with \(\phi _1 \Rightarrow \phi _2\) then \(\phi _1\) contains strictly more equations. From that follows that for every sequence \(\phi _0 \Rightarrow \ldots \phi _m\) of pairwise inequivalent reduced conjunctions \(\phi _j\) with k variables, \(m \le k+1\) holds. This observation is crucial for the termination of the fixpoint iteration we will use to compute \(\varPhi _{b,(q,q')}^{(h)}\).
For \(h\ge 0\) we have:
As we fixed the number of output parameters to the number l, for each pair \((q,q')\) the conjunction \(\varPhi _{b,(q,q')}^{(h)}\) contains at most 2l variables \(y_i, y'_i\). Assuming that the MTTs to which state q and \(q'\) belong have n states each, we conclude that \(\varPhi _{b,(q,q')}^{(n^2(2l+1))} \equiv \varPhi _{b,(q,q')}^{(n^2(2l+1)+i)}\) and \(\varPsi _{b,q}^{(n(l+1))} \equiv \varPsi _{b,q}^{(n(l+1)+i)}\) for all \(i \ge 0\). Thus, we can define \(\varPhi _{b,(q,q')} := \varPhi _{b,(q,q')}^{(n^2(2l+1))}\) and \(\varPsi _{b,q} := \varPsi _{b,q}^{(n(l+1))}\). As \((q,\underline{T}) \cong _b (q',\underline{T'})\) iff for all \(h \ge 0\), \((q,\underline{T}) \cong _b^{(h)} (q',\underline{T'})\) holds, observation (3) implies that
Therefore, we have:
Lemma 4
For a DTA D, states \(q, q'\) of D-earliest separated basic MTTs \(M,M'\) and states b of D, the formula \(\varPhi _{b,(q,q')}\) can be computed in time polynomial in the sizes of M and \(M'\).
Proof
We successively compute the conjunctions \(\varPsi _{b,q}^{(h)}(z), \varPsi _{b,q'}^{(h)}(z), \varPhi _{b,(q,q')}^{(h)},\) \(h\ge 0\), for all states \(b,q,q'\). As discussed before, some \(h\le n^2(2l+1)\) exists such that the conjunctions for \(h+1\) are equivalent to the corresponding conjunctions for h—in which case, we terminate. It remains to prove that the conjunctions for h can be computed from the conjunctions for \(h-1\) in polynomial time. For that, it is crucial that we maintain reduced conjunctions. Nonetheless, the sizes of occurring right-hand sides of equalities may be quite large. Consider for example the conjunction \(x_1 \doteq a \wedge x_2 \doteq f(x_1,x_1) \wedge \ldots \wedge x_n \doteq f(x_{n-1},x_{n-1})\). The corresponding reduced conjunction is then given by \(x_1 \doteq a\wedge x_2 \doteq f(a,a)\wedge \ldots \wedge x_n \doteq f(f(f(\ldots (f(a,a))\ldots )\) where the sizes of right-hand sides grow exponentially. In order to arrive at a polynomial-size representation, we therefore rely on compact representations where isomorphic subtrees are represented only once. W.r.t. this representation, reduction of a non-reduced conjunction, implications between reduced conjunctions as well as substitution of variables in conjunctions can all be realized in polynomial time. From that, the assertion of the lemma follows.
Example 6
Let D be a DTA with the following rules \(b(f(x)) \rightarrow (b)\), \(b(g) \rightarrow ()\) and \(b(h) \rightarrow ()\). Let q and \(q'\) be states of separated basic MTTs M, \(M'\), respectively, that are D-earliest and \(\pi \), \(\pi '\) be the mappings from the states of D to the states of M, \(M'\) with \((b,q)\in \pi \) and \((b,q')\in \pi '\).
\(\square \)
In summary, we obtain the main theorem of our paper.
Theorem 2
Let (M, A) and \((M',A')\) be pairs consisting of total deterministic separated basic MTTs M, \(M'\) and corresponding axioms A, \(A'\) and D a DTA. Then the equivalence of (M, A) and \((M',A')\) relative to D is decidable. If D accepts all input trees, equivalence can be decided in polynomial time.
Proof
By Lemma 2 we build pairs \((M_1,A_1)\) and \((M'_1, A'_1)\) that are equivalent to (M, A) and \((M',A')\) where \(M_1\), \(M'_1\) are D-earliest separated basic MTTs. If D is trivial the construction is in polynomial time, cf. Corollary 1. Let the axioms be \(A_1 = p[q_1(x_{i_1},\underline{T_1}),\ldots , q_k(x_{i_k},\underline{T_k})]\) and \(A'_1 = p'[q'_1(x_{i'_1}, \underline{T_1}),\ldots ,q'_k(x_{i'_{k'}},\underline{T_{k'}})]\). According to Lemma 3 \((M_1,A_1)\) and \((M'_1, A'_1)\) are equivalent iff
-
\(p = p'\), \(k = k'\) and
-
for all \(j = 1,\ldots , k\), \(\varPhi _{b,(q_j,q'_j)}[\underline{T_j}/\underline{y},\underline{T_j}/\underline{y'}]\) is equivalent to \(\mathsf{true}\).
By Lemma 4 we can decide the second statements in time polynomial in the sizes of \(M_1\) and \(M'_1\).
5 Applications
In this section we show several applications of our equivalence result. First, we consider partial transductions of separated basic MTTs. To decide the equivalence of partial transductions we need to decide (a) whether the domain of two given MTTs is the same and if so, (b) whether the transductions on this domain are the same. How the second part of the decision procedure is done was shown in detail in this paper if the domain is given by a DTA. It therefore remains to discuss how this DTA can be obtained. It was shown in [4, Theorem 3.1] that the domain of every top-down tree transducer T can be accepted by some DTA \(B_T\) and this automaton can be constructed from T in exponential time. This construction can easily be extended to basic MTTs. The decidability of equivalence of DTAs is well-known and can be done in polynomial time [16, 17]. To obtain a total transducer we add for each pair (q, f), \(q \in Q\) and \(f \in \varSigma \) that has no rule a new rule \(q(f(\underline{x}),\underline{y}) \rightarrow \bot \), where \(\bot \) is an arbitrary symbol in \(\varDelta _{out}\) of rank zero.
Example 7
In Example 1 we discussed how to adjust the transducer from the introduction to our formal definition. We therefore had to introduce additional rules to obtain a total transducer. Now we still add rules for the same pairs (q, f) but only with right-hand sides \(\bot \). Therefore the original domain of the transducer is given by a DTA \(D = (R,\varSigma ,r_0,\delta _D)\) with the rules \(r_0(g(x_1,x_2)) \rightarrow (r(x_1), r(x_2))\), \(r(f(x_1,x_2)) \rightarrow (r(x_1),r(x_2))\) and \(r(i) \rightarrow (\ )\) for \(i = 1,2,3\). \(\square \)
Corollary 2
The equivalence of deterministic separated basic MTTs with a partial transition function is decidable.
Next, we show that our result can be used to decide the equivalence of total separated basic MTTs with look-ahead. A total macro tree transducer with regular look-ahead (\(\text {MTT}^{\text {R}}\)) is a tuple \((Q,\varSigma ,\varDelta ,\delta ,R,\delta _R)\) where R is a finite set of look-ahead states and \(\delta _R\) is a total function from \(R^k \rightarrow R\) for every \(f \in \varSigma ^{(k)}\). Additionally we have a deterministic bottom-up tree automaton \((P,\varSigma ,\delta ,-)\) (without final states). A rule of the MTT is of the form
and is applicable to an input tree \(f(t_1,\ldots ,t_k)\) if the look-ahead automaton accepts \(t_i\) in state \(p_i\) for all \(i = 1,\ldots , k\). For every \(q, f, p_1,\ldots , p_k\) there is exactly one such rule. Let \(N_1 = (Q_1,\varSigma _1,\varDelta _1,\delta _1,R_1,\delta _{R1}), N_2 = (Q_2,\varSigma _2,\varDelta _2,\delta _2,R_2,\delta _{R2})\) be two total separated basic MTTs with look-ahead. We construct total separated basic MTTs \(M_1, M_2\) without look-ahead as follows. The input alphabet contains for every \(f \in \varSigma \) and \(r_1,\ldots ,r_k \in R_1\), \(r'_1,\ldots , r'_k \in R_2\) the symbols \({\langle f,r_1,\ldots ,r_k,r'_1,\ldots ,r'_k\rangle }\). For \(q(f(x_1,\ldots , x_k),\underline{y}) \rightarrow p[T_1,\ldots ,T_m]\ {\langle r_1,\ldots , r_k\rangle }\) and \(q'(f(x_1,\ldots , x_k),\underline{y'}) \rightarrow p'[T'_1,\ldots ,T'_m]\ {\langle r'_1,\ldots , r'_k\rangle }\) we obtain for \(M_1\) the rules
with \(\hat{T}_i = \hat{q}_{i}({\langle x_{j_i}, \hat{r_1},\ldots , \hat{r_l},\hat{r'_1},\ldots , \hat{r'_l}\rangle },Z_{i})\) if \(T_i = q_i(x_{j_i},Z_i)\) and \(q_i(x_{j_i},\underline{y}) \rightarrow \hat{T_i}\ \ {\langle \hat{r_1},\ldots ,\hat{r_l}\rangle }\) and \(q'_i(x_{j_i},\underline{y'}) \rightarrow \hat{T'_i}\ \ {\langle \hat{r'_1},\ldots ,\hat{r'_l}\rangle }\). If \(T_i = y_{j_i}\) then \(\hat{T}_i = y_{j_i}\). The total separated basic MTT \(M_2\) is constructed in the same lines. Thus, \(N_i\), \(i=1,2\) can be simulated by \(M_i\), \(i=1,2\), respectively, if the input is restricted to the regular tree language of new input trees that represent correct runs of the look-ahead automata.
Corollary 3
The equivalence of total separated basic MTTs with regular look-ahead is decidable in polynomial time.
Last, we consider separated basic MTTs that concatenate strings instead of trees in the parameters. We abbreviate this class of transducers by \(\text {MTT}^\text {yp}\). Thus, the alphabet \(\varDelta _{in}\) is not longer a ranked alphabet but a unranked alphabet which elements/letters can be concatenated to words. The procedure to decide equivalence of \(\text {MTT}^\text {yp}\) is essentially the same as we discussed in this paper but instead of conjunctions of equations of trees over \(\varDelta _{in}\cup Y\) we obtain conjunctions equations of words. Equations of words is a well studied problem [23, 24, 26]. In particular, the confirmed Ehrenfeucht conjecture states that each conjunction of a set of word equations over a finite alphabet and using a finite number of variables, is equivalent to the conjunction of a finite subset of word equations [19]. Accordingly, by a similar argument as in Sect. 4, the sequences of conjunctions \(\varPsi _{b,q}^{(h)}(z),{\varPsi '}_{b,q'}^{(h)}(z),\varPhi _{b,(q,q')}^{(h)},h\ge 0\), are ultimately stable. Using an encoding of words by integer matrices and applying techniques as in [19], we obtain:
Theorem 3
The equivalence of total separated basic MTTs that concatenate words instead of trees in the parameters (\(\varDelta _{in}\) is unranked) is decidable.
6 Related Work
For several subclasses of attribute systems equivalence is known to be decidable. For instance, attributed grammars without inherited attributes are equivalent to deterministic top-down tree transducers (DT) [3, 5]. For this class equivalence was shown to be decidable by Esik [10]. Later, a simplified algorithm was provided in [8]. If the tree translation of an attribute grammar is of linear size increase, then equivalence is decidable, because it is decidable for deterministic macro tree transducers (DMTT) of linear size increase. This follows from the fact that the latter class coincides with the class of (deterministic) MSO definable tree translations (DMSOTT) [6] for which equivalence is decidable [7]. Figure 3 shows a Hasse diagram of classes of translations realized by certain deterministic tree transducers. The prefixes “l”, “n”, “sn”, “b” and “sb” mean “linear size increase”, “non-nested”, “separated non-nested”, “basic” and “separated basic”, respectively. A minimal class where it is still open whether equivalence is decidable is the class of non-nested attribute systems (nATT) which, on the macro tree transducer side, is included in the class of basic deterministic macro tree transducers (bDMTT).
For deterministic top-down tree transducers, equivalence can be decided in EXPSPACE, and in NLOGSPACE if the transducers are total [25]. For the latter class of transducers, one can decide equivalence in polynomial time by transforming the transducer into a canonical normal form (called “earliest normal form”) and then checking isomorphism of the resulting transducers [8]. In terms of hardness, we know that equivalence of deterministic top-down tree transducers is EXPTIME-hard. For linear size increase deterministic macro tree transducers the precise complexity is not known (but is at least NP-hard). More complexity results are known for other models of tree transducers such as streaming tree transducers [1], see [25] for a summary.
7 Conclusion
We have proved that the equivalence problem for separated non-nested attribute systems can be decided in polynomial time. In fact, we have shown a stronger statement, namely that in polynomial time equivalence of separated basic total deterministic macro tree transducers can be decided. To see that the latter is a strict superclass of the former, consider the translation that takes a binary tree as input, and outputs the same tree, but under each leaf a new monadic tree is output which represents the inverse Dewey path of that node. For instance, the tree f(f(a, a), a) is translated into the tree f(f(a(1(1(e))), a(2(1(e)))), a(2(e))). A macro tree transducer of the desired class can easily realize this translation using a rule of the form \(q(f(x_1,_2),y)\rightarrow f(q(x_1,1(y)),q(x_2,2(y)))\). In contrast, no attribute system can realize this translation. The reason is that for every attribute system, the number of distinct output subtrees is linearly bounded by the size of the input tree. For the given translation there is no linear such bound (it is bounded by \(|s|\log (|s|)\)).
The idea of “separated” to use different output alphabets, is related to the idea of transducers “with origin” [2, 11]. In future work we would like to define adequate notions of origin for macro tree transducer, and prove that equivalence of such (deterministic) transducers with origin is decidable.
References
Alur, R., D’Antoni, L.: Streaming tree transducers. J. ACM 64(5):31:1–31:55 (2017)
Bojańczyk, M.: Transducers with origin information. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014, Part II. LNCS, vol. 8573, pp. 26–37. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43951-7_3
Courcelle, B., Franchi-Zannettacci, P.: Attribute grammars and recursive program schemes I. Theor. Comput. Sci. 17(2), 163–191 (1982)
Engelfriet, J.: Top-down tree transducers with regular look-ahead. Math. Syst. Theory 10, 289–303 (1977)
Engelfriet, J.: Some open questions and recent results on tree transducers and tree languages. In: Formal Language Theory, pp. 241–286. Elsevier (1980)
Engelfriet, J., Maneth, S.: Macro tree translations of linear size increase are MSO definable. SIAM J. Comput. 32(4), 950–1006 (2003)
Engelfriet, J., Maneth, S.: The equivalence problem for deterministic MSO tree transducers is decidable. Inf. Process. Lett. 100(5), 206–212 (2006)
Engelfriet, J., Maneth, S., Seidl, H.: Deciding equivalence of top-down XML transformations in polynomial time. J. Comput. Syst. Sci. 75(5), 271–286 (2009)
Engelfriet, J., Vogler, H.: Macro tree transducers. J. Comput. Syst. Sci. 31(1), 71–146 (1985)
Ésik, Z.: Decidability results concerning tree transducers I. Acta Cybern. 5(1), 1–20 (1980)
Filiot, E., Maneth, S., Reynier, P., Talbot, J.: Decision problems of tree transducers with origin. Inf. Comput. 261(Part), 311–335 (2018)
Fors, N., Cedersjö, G., Hedin, G.: JavaRAG: a Java library for reference attribute grammars. In: Proceedings of the 14th International Conference on Modularity, MODULARITY 2015, pp. 55–67. ACM, New York (2015)
Friese, S., Seidl, H., Maneth, S.: Earliest normal form and minimization for bottom-up tree transducers. Int. J. Found. Comput. Sci. 22(7), 1607–1623 (2011)
Fülöp, Z.: On attributed tree transducers. Acta Cybern. 5(3), 261–279 (1981)
Fülöp, Z., Vogler, H.: Syntax-Directed Semantics - Formal Models Based on Tree Transducers. Monographs in Theoretical Computer Science. An EATCS Series. Springer, Heidelberg (1998). https://doi.org/10.1007/978-3-642-72248-6
Gécseg, F., Steinby, M.: Minimal ascending tree automata. Acta Cybern. 4(1), 37–44 (1978)
Gécseg, F., Steinby, M.: Tree Automata. Akadéniai Kiadó, Budapest (1984)
Griffiths, T.V.: The unsolvability of the equivalence problem for lambda-free nondeterministic generalized machines. J. ACM 15(3), 409–413 (1968)
Honkala, J.: A short solution for the HDT0L sequence equivalence problem. Theor. Comput. Sci. 244(1–2), 267–270 (2000)
Knuth, D.E.: Semantics of context-free languages. Math. Syst. Theory 2(2), 127–145 (1968)
Knuth, D.E.: Correction: semantics of context-free languages. Math. Syst. Theory 5(1), 95–96 (1971)
Laurence, G., Lemay, A., Niehren, J., Staworko, S., Tommasi, M.: Normalization of sequential top-down tree-to-word transducers. In: Dediu, A.-H., Inenaga, S., Martín-Vide, C. (eds.) LATA 2011. LNCS, vol. 6638, pp. 354–365. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21254-3_28
Lothaire, M.: Algebraic Combinatorics on Words. Cambridge University Press, Cambridge (2002)
Makanin, G.S.: The problem of solvability of equations in a free semigroup. Math. USSR-Sb. 32(2), 129 (1977)
Maneth, S.: A survey on decidable equivalence problems for tree transducers. Int. J. Found. Comput. Sci. 26(8), 1069–1100 (2015)
Plandowski, W.: Satisfiability of word equations with constants is in PSPACE. In: 40th Annual Symposium on Foundations of Computer Science, FOCS 1999, New York, NY, USA, 17–18 October 1999, pp. 495–500. IEEE Computer Society (1999)
Seidl, H., Maneth, S., Kemper, G.: Equivalence of deterministic top-down tree-to-string transducers is decidable. J. ACM 65(4), 21:1–21:30 (2018)
Sloane, A.M., Kats, L.C., Visser, E.: A pure embedding of attribute grammars. Sci. Comput. Program. 78(10), 1752–1769 (2013). Special Section on Language Descriptions Tools and Applications (LDTA 2008 and 2009) & Special Section on Software Engineering Aspects of Ubiquitous Computing and Ambient Intelligence (UCAm I 2011)
Van Wyk, E., Bodin, D., Gao, J., Krishnan, L.: Silver: an extensible attribute grammar system. Sci. Comput. Program. 75(1–2), 39–54 (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Seidl, H., Palenta, R., Maneth, S. (2019). Deciding Equivalence of Separated Non-nested Attribute Systems in Polynomial Time. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_28
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)







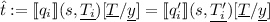 for some
for some 
