Partial and Conditional Expectations in Markov Decision Processes with Integer Weights

Abstract

The paper addresses two variants of the stochastic shortest path problem (“optimize the accumulated weight until reaching a goal state”) in Markov decision processes (MDPs) with integer weights. The first variant optimizes partial expected accumulated weights, where paths not leading to a goal state are assigned weight 0, while the second variant considers conditional expected accumulated weights, where the probability mass is redistributed to paths reaching the goal. Both variants constitute useful approaches to the analysis of systems without guarantees on the occurrence of an event of interest (reaching a goal state), but have only been studied in structures with non-negative weights. Our main results are as follows. There are polynomial-time algorithms to check the finiteness of the supremum of the partial or conditional expectations in MDPs with arbitrary integer weights. If finite, then optimal weight-based deterministic schedulers exist. In contrast to the setting of non-negative weights, optimal schedulers can need infinite memory and their value can be irrational. However, the optimal value can be approximated up to an absolute error of $\epsilon$ in time exponential in the size of the MDP and polynomial in $\log (1/\epsilon )$.

The authors are supported by the DFG through the Research Training Group QuantLA (GRK 1763), the DFG-project BA-1679/11-1, the Collaborative Research Center HAEC (SFB 912), and the cluster of excellence CeTI.

1 Introduction

Stochastic shortest path (SSP) problems generalize the shortest path problem on graphs with weighted edges. The SSP problem is formalized using finite state Markov decision processes (MDPs), which are a prominent model combining probabilistic and nondeterministic choices. In each state of an MDP, one is allowed to choose nondeterministically from a set of actions, each of them is augmented with probability distributions over the successor states and a weight (cost or reward). The SSP problem asks for a policy to choose actions (here called a scheduler) maximizing or minimizing the expected accumulated weight until reaching a goal state. In the classical setting, one seeks an optimal proper scheduler where proper means that a goal state is reached almost surely. Polynomial-time solutions exist exploiting the fact that optimal memoryless deterministic schedulers exist (provided the optimal value is finite) and can be computed using linear programming techniques, possibly in combination with model transformations (see [1, 5, 10]). The restriction to proper schedulers, however, is often too restrictive. First, there are models that have no proper scheduler. Second, even if proper schedulers exist, the expectation of the accumulated weight of schedulers missing the goal with a positive probability should be taken into account as well. Important such applications include the semantics of probabilistic programs (see e.g. [4, 7, 12, 14, 16]) where no guarantee for almost sure termination can be given and the analysis of program properties at termination time gives rise to stochastic shortest (longest) path problems in which the goal (halting configuration) is not reached almost surely. Other examples are the fault-tolerance analysis (e.g., expected costs of repair mechanisms) in selected error scenarios that can appear with some positive, but small probability or the trade-off analysis with conjunctions of utility and cost constraints that are achievable with positive probability, but not almost surely (see e.g. [2]).

This motivates the switch to variants of classical SSP problems where the restriction to proper schedulers is relaxed. One option (e.g., considered in [8]) is to seek a scheduler optimizing the expectation of the random variable that assigns weight 0 to all paths not reaching the goal and the accumulated weight of the shortest prefix reaching the goal to all other paths. We refer to this expectation as partial expectation. Second, we consider the conditional expectation of the accumulated weight until reaching the goal under the condition that the goal is reached. In general, partial expectations describe situations in which some reward (positive and negative) is accumulated but only retrieved if a certain goal is met. In particular, partial expectations can be an appropriate replacement for the classical expected weight before reaching the goal if we want to include schedulers which miss the goal with some (possibly very small) probability. In contrast to conditional expectations, the resulting scheduler still has an incentive to reach the goal with a high probability, while schedulers maximizing the conditional expectation might reach the goal with a very small positive probability.

Previous work on partial or conditional expected accumulated weights was restricted to the case of non-negative weights. More precisely, partial expectations have been studied in the setting of stochastic multiplayer games with non-negative weights [8]. Conditional expectations in MDPs with non-negative weights have been addressed in [3]. In both cases, optimal values are achieved by weight-based deterministic schedulers that depend on the current state and the weight that has been accumulated so far, while memoryless schedulers are not sufficient. Both [8] and [3] prove the existence of a saturation point for the accumulated weight from which on optimal schedulers behave memoryless and maximize the probability to reach a goal state. This yields exponential-time algorithms for computing optimal schedulers using an iterative linear programming approach. Moreover, [3] proves that the threshold problem for conditional expectations (“does there exist a scheduler $\mathfrak {S}$ such that the conditional expectation under $\mathfrak {S}$ exceeds a given threshold?”) is PSPACE-hard even for acyclic MDPs.

The purpose of the paper is to study partial and conditional expected accumulated weights for MDPs with integer weights. The switch from non-negative to integer weights indeed causes several additional difficulties. We start with the following observation. While optimal partial or conditional expectations in non-negative MDPs are rational, they can be irrational in the general setting:

Fig. 1.

Enabled actions are denoted by Greek letters and the weight associated to the action is stated after the bar. Probabilistic choices are marked by a bold arc and transition probabilities are denoted next to the arrows.

Example 1

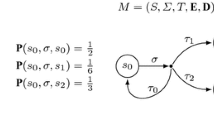
Consider the MDP $\mathcal {M}$ depicted on the left in Fig. 1. In the initial state $s_{ init }$, two actions are enabled. Action $\tau$ leads to $goal$ with probability 1 and weight 0. Action $\sigma$ leads to the states s and t with probability $1{\slash }2$ from where we will return to $s_{ init }$ with weight $-2$ or $+1$, respectively. The scheduler choosing $\tau$ immediately leads to an expected weight of 0 and is optimal among schedulers reaching the goal almost surely. As long as we choose $\sigma$ in $s_{ init }$, the accumulated weight follows an asymmetric random walk increasing by 1 or decreasing by 2 with probability $1{\slash }2$ before we return to $s_{ init }$. It is well known that the probability to ever reach accumulated weight $+1$ in this random walk is $1/\varPhi$ where $\varPhi =\frac{1+\sqrt{5}}{2}$ is the golden ratio. Likewise, ever reaching accumulated weight n has probability $1/\varPhi ^n$ for all $n\in \mathbb {N}$. Consider the scheduler $\mathfrak {S}_k$ choosing $\tau$ as soon as the accumulated weight reaches k in $s_{ init }$. Its partial expectation is $k/\varPhi ^k$ as the paths which never reach weight k are assigned weight 0. The maximum is reached at $k=2$. In Sect. 4, we prove that there are optimal schedulers whose decisions only depend on the current state and the weight accumulated so far. With this result we can conclude that the maximal partial expectation is indeed $2/\varPhi ^2$, an irrational number.

The conditional expectation of $\mathfrak {S}_k$ in $\mathcal {M}$ is k as $\mathfrak {S}_k$ reaches the goal with accumulated weight k if it reaches the goal. So, the conditional expectation is not bounded. If we add a new initial state making sure that the goal is reached with positive probability as in the MDP $\mathcal {N}$, we can obtain an irrational maximal conditional expectation as well: The scheduler $\mathfrak {T}_k$ choosing $\tau$ in c as soon as the weight reaches k has conditional expectation $\frac{k/2\varPhi ^k}{1/2+1/2\varPhi ^k}$. The maximum is obtained for $k=3$; the maximal conditional expectation is $\frac{3/\varPhi ^3}{1+1/\varPhi ^3}=\frac{3}{3+\sqrt{5}}$.

Moreover, while the proposed algorithms of [3, 8] crucially rely on the monotonicity of the accumulated weights along the prefixes of paths, the accumulated weights of prefixes of path can oscillate when there are positive and negative weights. As we will see later, this implies that the existence of saturation points is no longer ensured and optimal schedulers might require infinite memory (more precisely, a counter for the accumulated weight). These observations provide evidence why linear-programming techniques as used in the case of non-negative MDPs [3, 8] cannot be expected to be applicable for the general setting.

Contributions. We study the problem of maximizing the partial and conditional expected accumulated weight in MDPs with integer weights. Our first result is that the finiteness of the supremum of partial and conditional expectations in MDPs with integer weights can be checked in polynomial time (Sect. 3). For both variants we show that there are optimal weight-based deterministic schedulers if the supremum is finite (Sect. 4). Although the suprema might be irrational and optimal schedulers might need infinite memory, the suprema can be $\epsilon$-approximated in time exponential in the size of the MDP and polynomial in $\log (1/\epsilon )$ (Sect. 5). By duality of maximal and minimal expectations, analogous results hold for the problem of minimizing the partial or conditional expected accumulated weight. (Note that we can multiply all weights by ${-}1$ and then apply the results for maximal partial resp. conditional expectations.)

Related Work. Closest to our contribution is the above mentioned work on partial expected accumulated weights in stochastic multiplayer games with non-negative weights in [8] and on computation schemes for maximal conditional expected accumulated weights in non-negative MDPs [3]. Conditional expected termination time in probabilistic push-down automata has been studied in [11], which can be seen as analogous considerations for a class of infinite-state Markov chains with non-negative weights. The recent work on notions of conditional value at risk in MDPs [15] also studies conditional expectations, but the considered random variables are limit averages and a notion of (non-accumulated) weight-bounded reachability.

2 Preliminaries

We give basic definitions and present our notation. More details can be found in textbooks, e.g. [18].

Notations for Markov Decision Processes. A Markov decision process (MDP) is a tuple $\mathcal {M} = (S, Act ,P,s_{ \scriptscriptstyle init }, wgt )$ where S is a finite set of states, $Act$ a finite set of actions, $s_{ \scriptscriptstyle init }\in S$ the initial state, $P : S \times Act \times S \rightarrow [0,1] \cap \mathbb {Q}$ is the transition probability function and $wgt : S \times Act \rightarrow \mathbb {Z}$ the weight function. We require that $\sum _{t\in S}P(s,\alpha ,t) \in \{0,1\}$ for all $(s,\alpha )\in S\times Act$. We write $Act (s)$ for the set of actions that are enabled in s, i.e., $\alpha \in Act (s)$ iff $\sum _{t\in S}P(s,\alpha ,t) =1$. We assume that $Act (s)$ is non-empty for all s and that all states are reachable from $s_{ init }$. We call a state absorbing if the only enabled action leads to the state itself with probability 1 and weight 0. The paths of $\mathcal {M}$ are finite or infinite sequences $s_0 \, \alpha _0 \, s_1 \, \alpha _1 \, s_2 \, \alpha _2 \ldots$ where states and actions alternate such that $P(s_i,\alpha _i,s_{i+1}) >0$ for all $i\ge 0$. If $\pi = s_0 \, \alpha _0 \, s_1 \, \alpha _1 \, \ldots \alpha _{k-1} \, s_k$ is finite, then $wgt (\pi )= wgt (s_0,\alpha _0) + \ldots + wgt (s_{k-1},\alpha _{k-1})$ denotes the accumulated weight of $\pi$, $P(\pi ) = P(s_0,\alpha _0,s_1) \cdot \ldots \cdot P(s_{k-1},\alpha _{k-1},s_k)$ its probability, and $last (\pi )=s_k$ its last state. The size of $\mathcal {M}$, denoted $size (\mathcal {M})$, is the sum of the number of states plus the total sum of the logarithmic lengths of the non-zero probability values $P(s,\alpha ,s')$ as fractions of co-prime integers and the weight values $wgt (s,\alpha )$.

Scheduler. A (history-dependent, randomized) scheduler for $\mathcal {M}$ is a function $\mathfrak {S}$ that assigns to each finite path $\pi$ a probability distribution over $Act ( last (\pi ))$. $\mathfrak {S}$ is called memoryless if $\mathfrak {S}(\pi )=\mathfrak {S}(\pi ')$ for all finite paths $\pi$, $\pi '$ with $last (\pi )= last (\pi ')$, in which case $\mathfrak {S}$ can be viewed as a function that assigns to each state s a distribution over $Act (s)$. $\mathfrak {S}$ is called deterministic if $\mathfrak {S}(\pi )$ is a Dirac distribution for each path $\pi$, in which case $\mathfrak {S}$ can be viewed as a function that assigns an action to each finite path $\pi$. Scheduler $\mathfrak {S}$ is said to be weight-based if $\mathfrak {S}(\pi )=\mathfrak {S}(\pi ')$ for all finite paths $\pi$, $\pi '$ with $wgt (\pi )= wgt (\pi ')$ and $last (\pi )= last (\pi ')$. Thus, deterministic weight-based schedulers can be viewed as functions that assign actions to state-weight-pairs. By $HR ^\mathcal {M}$ we denote the class of all schedulers, by $WR ^\mathcal {M}$ the class of weight-based schedulers, by $WD ^\mathcal {M}$ the class of weight-based, deterministic schedulers, and by $MD ^\mathcal {M}$ the class of memoryless deterministic schedulers. Given a scheduler $\mathfrak {S}$, $\varsigma \, = \, s_0 \, \alpha _0 \, s_1 \, \alpha _1 \ldots$ is a $\mathfrak {S}$-path iff $\varsigma$ is a path and $\mathfrak {S}(s_0 \, \alpha _0 \, s_1 \, \alpha _1 \ldots \alpha _{k-1} \, s_k)(\alpha _k)>0$ for all $k \ge 0$.

Probability Measure. We write $\Pr ^{\mathfrak {S}}_{\mathcal {M},s}$ or briefly $\Pr ^{\mathfrak {S}}_{s}$ to denote the probability measure induced by $\mathfrak {S}$ and s. For details, see [18]. We will use LTL-like formulas to denote measurable sets of paths and also write $\Diamond (wgt \bowtie x)$ to describe the set of infinite paths having a prefix $\pi$ with $wgt(\pi )\bowtie x$ for $x\in \mathbb {Z}$ and $\bowtie \ \in \{<,\le ,=,\ge ,>\}$. Given a measurable set $\psi$ of infinite paths, we define $\Pr ^{\min }_{\mathcal {M},s}(\psi ) = \inf _{\mathfrak {S}} \Pr ^{\mathfrak {S}}_{\mathcal {M},s}(\psi )$ and $\Pr ^{\max }_{\mathcal {M},s}(\psi ) = \sup _{\mathfrak {S}} \Pr ^{\mathfrak {S}}_{\mathcal {M},s}(\psi )$ where $\mathfrak {S}$ ranges over all schedulers for $\mathcal {M}$. Throughout the paper, we suppose that the given MDP has a designated state $goal$. Then, $p_s^{\max }$ and $p_s^{\min }$ denote the maximal resp. minimal probability of reaching $goal$ from s. That is, $p_s^{\max } = \mathrm {sup}_{\mathfrak {S}} \Pr ^\mathfrak {S}_s (\Diamond goal )$ and $p_s^{\min } = \inf _{\mathfrak {S}} \Pr ^\mathfrak {S}_s (\Diamond goal )$. Let $Act^{\max } (s) = \{\alpha \in Act(s) | \sum _{t\in S} P(s,\alpha ,t) \cdot p_t^{\max } = p_s^{\max }\}$, and $Act^{\min } (s) = \{\alpha \in Act(s) | \sum _{t\in S}$ $P(s,\alpha ,t) \cdot p_t^{\min } = p_s^{\min }\}$.

Mean Payoff. A well-known measure for the long-run behavior of a scheduler $\mathfrak {S}$ in an MDP $\mathcal {M}$ is the mean payoff. Intuitively, the mean payoff is the amount of weight accumulated per step on average in the long run. Formally, we define the mean payoff as the following random variable on infinite paths $\zeta =s_0 \alpha _0 s_1 \alpha _1 \dots$: $MP (\zeta ):= \liminf \limits _{k\rightarrow \infty } \frac{\sum _{i=0}^k wgt(s_i,\alpha _i)}{k+1}$. The mean payoff of the scheduler $\mathfrak {S}$ starting in $s_{ init }$ is then defined as the expected value $\mathbb {E}^\mathfrak {S}_{s_{ init }} ( MP )$. The maximal mean payoff is the supremum over all schedulers which is equal to the maximum over all MD-schedulers: $\mathbb {E}^{\max }_{s_{ init }} ( MP )=\max _{\mathfrak {S}\in MD } \mathbb {E}^\mathfrak {S}_{s_{ init }} ( MP )$. In strongly connected MDPs, the maximal mean payoff does not depend on the initial state.

End Components, MEC-Quotient. An end component of $\mathcal {M}$ is a strongly connected sub-MDP. End components can be formalized as pairs $\mathcal {E}= (E,\mathfrak {A})$ where E is a nonempty subset of S and $\mathfrak {A}$ a function that assigns to each state $s\in E$ a nonempty subset of $Act (s)$ such that the graph induced by $\mathcal {E}$ is strongly connected. $\mathcal {E}$ is called maximal if there is no end component $\mathcal {E}' = (E',\mathfrak {A}')$ with $\mathcal {E}\not = \mathcal {E}'$, $E \subseteq E'$ and $\mathfrak {A}(s) \subseteq \mathfrak {A}'(s)$ for all $s\in E$. The MEC-quotient of an MDP $\mathcal {M}$ is the MDP $MEC (\mathcal {M})$ arising from $\mathcal {M}$ by collapsing all states that belong to the same maximal end component $\mathcal {E}$ to a state $s_\mathcal {E}$. All actions enabled in some state in $\mathcal {E}$ not belonging to $\mathcal {E}$ are enabled in $s_\mathcal {E}$. Details and the formal construction can be found in [9]. We call an end component $\mathcal {E}$ positively weight-divergent if there is a scheduler $\mathfrak {S}$ for $\mathcal {E}$ such that $\Pr ^\mathfrak {S}_{\mathcal {E},s}(\Diamond ( wgt \ge n))=1$ for all $s\in \mathcal {E}$ and $n\in \mathbb {N}$. In [1], it is shown that the existence of positively weight-divergent end components can be decided in polynomial time.

3 Partial and Conditional Expectations in MDPs

We define partial and conditional expectations in MDPs. We extend the definition of [8] by introducing partial expectations with bias which are closely related to conditional expectations. Afterwards, we sketch the computation of maximal partial expectations in MDPs with non-negative weights and in Markov chains.

Partial and Conditional Expectation. In the sequel, let $\mathcal {M}$ be an MDP with a designated absorbing goal state $goal$. Furthermore, we collapse all states from which $goal$ is not reachable to one absorbing state $fail$. Let $b\in \mathbb {R}$. We define the random variable $\oplus ^b goal$ on infinite paths $\zeta$ by

$$ \oplus ^b goal (\zeta )={\left\{ \begin{array}{ll} wgt (\zeta ) + b&{} \text {if }\zeta \vDash \Diamond goal \text {,}\\ 0 &{} \text {if }\zeta \not \vDash \Diamond goal \text {.} \end{array}\right. } $$

We call the expectation of this random variable under a scheduler $\mathfrak {S}$ the partial expectation with bias b of $\mathfrak {S}$ and write $PE ^{\mathfrak {S}}_{\mathcal {M},s_{ init }}[b] := \mathbb {E}^\mathfrak {S}_{\mathcal {M},s_{ init }} (\oplus ^b goal )$ as well as $PE ^{\sup }_{\mathcal {M},s_{ init }}[b]:=\sup _{\mathfrak {S}\in HR ^\mathcal {M}} PE ^{\mathfrak {S}}_{\mathcal {M},s_{ init }}[b]$. If $b=0$, we sometimes drop the argument b; if $\mathcal {M}$ is clear from the context, we drop the subscript. In order to maximize the partial expectation, intuitively one has to find the right balance between reaching $goal$ with high probability and accumulating a high positive amount of weight before reaching $goal$. The bias can be used to shift this balance by additionally rewarding or penalizing a high probability to reach $goal$.

The conditional expectation of $\mathfrak {S}$ is defined as the expectation of $\oplus ^0 goal$ under the condition that $goal$ is reached. It is defined if $\Pr ^\mathfrak {S}_{\mathcal {M},s_{ init }} (\Diamond goal )>0$. We write $CE ^\mathfrak {S}_{\mathcal {M},s_{ init }}:= \mathbb {E}^\mathfrak {S}_{\mathcal {M},s_{ init }} (\oplus ^0 goal | \Diamond goal )$ and $CE ^{\sup }_{\mathcal {M},s_{ init }}=\sup _{\mathfrak {S}} CE ^\mathfrak {S}_{\mathcal {M},s_{ init }}$ where the supremum is taken over all schedulers $\mathfrak {S}$ with $\Pr ^\mathfrak {S}_{\mathcal {M},s_{ init }}(\Diamond goal )>0$. We can express the conditional expectation as $CE ^\mathfrak {S}_{\mathcal {M},s_{ init }} = { PE ^\mathfrak {S}_{\mathcal {M},s_{ init }}}/{\Pr ^\mathfrak {S}_{\mathcal {M},s_{ init }}(\Diamond goal )}$. The following proposition establishes a close connection between conditional expectations and partial expectations with bias.

Proposition 2

Let $\mathcal {M}$ be an MDP, $\mathfrak {S}$ a scheduler with $\Pr ^\mathfrak {S}_{s_{ \scriptscriptstyle init }}(\Diamond goal )>0$, $\theta \in \mathbb {Q}$, and $\bowtie \in \{<,\le ,\ge ,>\}$. Then we have $PE ^{\mathfrak {S}}_{s_{ init }}[-\theta ] \bowtie 0 \text { iff } CE ^{\mathfrak {S}}_{s_{ init }}\bowtie \theta$. Further, if $\Pr ^{\min }_{s_{ init }}(\Diamond goal )>0$, then $PE ^{\sup }_{s_{ init }} [-\theta ]\bowtie 0 \text { iff } CE ^{\sup }_{s_{ init }}\bowtie \theta$.

Proof

The first claim follows from $PE ^{\mathfrak {S}}_{s_{ init }}[-\theta ]= PE ^\mathfrak {S}_{s_{ init }}[0]-\Pr ^{\mathfrak {S}}_{s_{ init }}(\Diamond goal ) \cdot \theta$. The second claim follows by quantification over all schedulers.    $\square$

In [3], it is shown that deciding whether $CE ^{\sup }_{s_{ init }}\bowtie \theta$ for $\bowtie \in \{<,\le ,\ge ,>\}$ and $\theta \in \mathbb {Q}$ is PSPACE-hard even for acyclic MDPs. We conclude:

Corollary 3

Given an MDP $\mathcal {M}$, $\bowtie \in \{<,\le ,\ge ,>\}$, and $\theta \in \mathbb {Q}$, deciding whether $PE ^{\sup }_{\mathcal {M},s_{ init }} \bowtie \theta$ is PSPACE-hard.

Finiteness. We present criteria for the finiteness of $PE ^{\sup }_{s_{ init }}[b]$ and $CE ^{\sup }_{s_{ init }}$. Detailed proofs can be found in Appendix A.1 of [17]. By slightly modifying the construction from [1] which removes end components only containing 0-weight cycles, we obtain the following result.

Proposition 4

Let $\mathcal {M}$ be an MDP which does not contain positively weight-divergent end components and let $b\in \mathbb {Q}$. Then there is a polynomial time transformation to an MDP $\mathcal {N}$ containing all states from $\mathcal {M}$ and possibly an additional absorbing state $fail$ such that

• all end components of $\mathcal {N}$ have negative maximal expected mean payoff,

• for any scheduler $\mathfrak {S}$ for $\mathcal {M}$ there is a scheduler $\mathfrak {S}^\prime$ for $\mathcal {N}$ with $\Pr ^\mathfrak {S}_{\mathcal {M},s}(\Diamond goal )=\Pr ^{\mathfrak {S}^\prime }_{\mathcal {N},s}(\Diamond goal )$ and $PE ^{\mathfrak {S}}_{\mathcal {M},s}[b]= PE ^{\mathfrak {S}^\prime }_{\mathcal {N},s}[b]$ for any state s in $\mathcal {M}$, and vice versa.

Hence, we can restrict ourselves to MDPs in which all end components have negative maximal expected mean payoff if there are no positively weight divergent end components. The following result is now analogous to the result in [1] for the classical SSP problem.

Proposition 5

Let $\mathcal {M}$ be an MDP and $b\in \mathbb {R}$ arbitrary. The optimal partial expectation $PE ^{\sup }_{s_{ init }}[b]$ is finite if and only if there are no positively weight-divergent end components in $\mathcal {M}$.

To obtain an analogous result for conditional expectations, we observe that the finiteness of the maximal partial expectation is necessary for the finiteness of the maximal conditional expectation. However, this is not sufficient. In [3], a critical scheduler is defined as a scheduler $\mathfrak {S}$ for which there is a path containing a positive cycle and for which $\Pr ^{\mathfrak {S}}_{s_{ init }}(\Diamond goal )=0$. Given a critical scheduler, it is easy to construct a sequence of schedulers with unbounded conditional expectation (see Appendix A.1 of [17] and [3]). On the other hand, if $\Pr ^{\min }_{\mathcal {M},s_{ init }}(\Diamond goal )>0$, then $CE ^{\sup }_{s_{ init }}$ is finite if and only if $PE ^{\sup }_{s_{ init }}$ is finite. We will show how we can restrict ourselves to this case if there are no critical schedulers:

So, let $\mathcal {M}$ be an MDP with $\Pr ^{\min }_{\mathcal {M},s_{ init }}(\Diamond goal )=0$ and suppose there are no critical schedulers for $\mathcal {M}$. Let $S_0$ be the set of all states reachable from $s_{ init }$ while only choosing actions in $Act^{\min }$. As there are no critical schedulers, $(S_0,Act^{\min })$ does not contain positive cycles. So, there is a finite maximal weight $w_s$ among paths leading from $s_{ init }$ to s in $S_0$. Consider the following MDP $\mathcal {N}$: It contains the MDP $\mathcal {M}$ and a new initial state $t_{ init }$. For each $s\in S_0$ and each $\alpha \in Act(s)\setminus Act^{\min }(s)$, $\mathcal {N}$ also contains a new state $t_{s,\alpha }$ which is reachable from $t_{ init }$ via an action $\beta _{s,\alpha }$ with weight $w_s$ and probability 1. In $t_{s,\alpha }$, only action $\alpha$ with the same probability distribution over successors and the same weight as in s is enabled. So in $\mathcal {N}$, one has to decide immediately in which state to leave $S_0$ and one accumulates the maximal weight which can be accumulated in $\mathcal {M}$ to reach this state in $S_0$. In this way, we ensure that $\Pr ^{\min }_{\mathcal {N}, t_{ init }} (\Diamond goal ) >0$.

Proposition 6

The constructed MDP $\mathcal {N}$ satisfies $CE ^{\sup }_{\mathcal {N},t_{ init }}= CE ^{\sup }_{\mathcal {M},s_{ init }}$.

We can rely on this reduction to an MDP in which $goal$ is reached with positive probability for $\epsilon$-approximations and the exact computation of the optimal conditional expectation. In particular, the values $w_s$ for $s\in S_0$ are easy to compute by classical shortest path algorithms on weighted graphs. Furthermore, we can now decide the finiteness of the maximal conditional expectation.

Proposition 7

For an arbitrary MDP $\mathcal {M}$, $CE ^{\sup }_{\mathcal {M},s_{ init }}$ is finite if and only if there are no positively weight-divergent end components and no critical schedulers.

Partial and Conditional Expectations in Markov Chains. Markov chains with integer weights can be seen as MDPs with only one action $\alpha$ enabled in every state. Consequently, there is only one scheduler for a Markov chain. Hence, we drop the superscripts in $p^{\max }$ and $PE ^{\sup }$.

Proposition 8

The partial and conditional expectation in a Markov chain $\mathcal {C}$ are computable in polynomial time.

Proof

Let $\alpha$ be the only action available in $\mathcal {C}$. Assume that all states from which $goal$ is not reachable have been collapsed to an absorbing state $fail$. Then $PE _{\mathcal {C}, s_{ \scriptscriptstyle init }}$ is the value of $x_{s_{ \scriptscriptstyle init }}$ in the unique solution to the following system of linear equations with one variable $x_s$ for each state s:

$$\begin{aligned}&x_{ goal }=x_{ fail }=0 ,\\&x_s = wgt(s,\alpha )\cdot p_s + \sum _{t} P(s,\alpha ,t)\cdot x_t \text { for }s\in S\setminus \{ goal , fail \}. \end{aligned}$$

The existence of a unique solution follows from the fact that $\{ goal \}$ and $\{ fail \}$ are the only end components (see [18]). It is straight-forward to check that $( PE _{\mathcal {C},s})_{s\in S}$ is this unique solution. The conditional expectation is obtained from the partial expectation by dividing by the probability $p_{s_{ init }}$ to reach the goal.    $\square$

This result can be seen as a special case of the following result. Restricting ourselves to schedulers which reach the goal with maximal or minimal probability in an MDP without positively weight-divergent end components, linear programming allows us to compute the following two memoryless deterministic schedulers (see [3, 8]).

Proposition 9

Let $\mathcal {M}$ be an MDP without positively weight-divergent end components. There is a scheduler $\mathfrak {Max}\in MD ^\mathcal {M}$ such that for each $s\in S$ we have $\Pr ^\mathfrak {Max}_s(\Diamond goal )= p_s^{{\max }}$ and $PE ^{\mathfrak {Max}}_s= \mathrm {sup}_\mathfrak {S} PE ^{\mathfrak {S}}_s$ where the supremum is taken over all schedulers $\mathfrak {S}$ with $\Pr ^\mathfrak {S}_s(\Diamond goal )= p_s^{{\max }}$. Similarly, there is a scheduler $\mathfrak {Min}\in MD ^\mathcal {M}$ maximizing the partial expectation among all schedulers reaching the goal with minimal probability. Both these schedulers and their partial expectations are computable in polynomial time.

These schedulers will play a crucial role for the approximation of the maximal partial expectation and the exact computation of maximal partial expectations in MDPs with non-negative weights.

Partial Expectations in MDPs with Non-negative Weights. In [8], the computation of maximal partial expectations in stochastic multiplayer games with non-negative weights is presented. We adapt this approach to MDPs with non-negative weights. A key result is the existence of a saturation point, a bound on the accumulated weight above which optimal schedulers do not need memory.

In the sequel, let $R\in \mathbb {Q}$ be arbitrary, let $\mathcal {M}$ be an MDP with non-negative weights, $PE ^{\sup }_{s_{ init }}<\infty$, and assume that end components have negative maximal mean payoff (see Proposition 4). A saturation point for bias R is a natural number $\mathfrak {p}$ such that there is a scheduler $\mathfrak {S}$ with $PE ^{\mathfrak {S}}_{s_{ init }}[R]= PE ^{{\sup }}_{s_{ init }}[R]$ which is memoryless and deterministic as soon as the accumulated weight reaches $\mathfrak {p}$. I.e. for any two paths $\pi$ and $\pi ^\prime$, with $last(\pi )=last(\pi ^\prime )$ and $wgt(\pi ),wgt(\pi ^\prime )>\mathfrak {p}$, $\mathfrak {S}(\pi )=\mathfrak {S}(\pi ^\prime )$.

Transferring the idea behind the saturation point for conditional expectations given in [3], we provide the following saturation point which can be considerably smaller than the saturation point given in [8] in stochastic multiplayer games. Detailed proofs to this section are given in Appendix A.2 of [17].

Proposition 10

We define $p_{s,\alpha }^{\max }:= \sum _{t\in S} P(s,\alpha ,t)\cdot p_t^{\max }$ and $PE ^\mathfrak {Max}_{s,\alpha }:= p_{s,\alpha }^{\max }\cdot wgt(s,\alpha ) + \sum _{t\in S} P(s,\alpha ,t)\cdot PE ^\mathfrak {Max}_t$. Then,

$$\begin{aligned} \mathfrak {p}_R:= \mathrm {sup} \left\{ \left. \frac{ PE ^\mathfrak {Max}_{s,\alpha }- PE ^\mathfrak {Max}_{s}}{p^{\max }_s-p^{\max }_{s,\alpha }}\right| s\in S, \alpha \in Act(s)\setminus Act^{\max }(s)\right\} -R \end{aligned}$$

is an upper saturation point for bias R in $\mathcal {M}$.

The saturation point $\mathfrak {p}_R$ is chosen such that, as soon as the accumulated weight exceeds $\mathfrak {p}_R$, the scheduler $\mathfrak {Max}$ is better than any scheduler deviating from $\mathfrak {Max}$ for only one step. So, the proposition states that $\mathfrak {Max}$ is then also better than any other scheduler.

As all values involved in the computation can be determined by linear programming, the saturation point $\mathfrak {p}_R$ is computable in polynomial time. This also means that the logarithmic length of $\mathfrak {p}_R$ is polynomial in the size of $\mathcal {M}$ and hence $\mathfrak {p}_R$ itself is at most exponential in the size of $\mathcal {M}$.

Proposition 11

Let $R\in \mathbb {Q}$ and let $B_R$ be the least integer greater or equal to $\mathfrak {p}_R+ \max _{s\in S,\alpha \in Act(s)} wgt(s,\alpha )$ and let $S^\prime := S\setminus \{ goal ,fail\}$. The values $( PE ^{\sup }_{s_{ init }}[r{+}R])_{s\in S^\prime , 0\le r\le B_R}$ form the unique solution to the following linear program in the variables $(x_{s,r})_{s\in S^\prime , 0\le r\le B_R}$ (r ranges over integers):

Minimize $\sum _{s\in S^\prime ,0\le r\le B_R}x_{s,r}$ under the following constraints:

$$\begin{aligned}&\text {For }r \ge \mathfrak {p}_R: x_{s,r}= p_s^{\max } \cdot (r{+}R) + E^\mathfrak {Max}_s, \\&\text {for }r < \mathfrak {p}_R \text { and }\alpha \in Act(s) :\\&x_{s,r}\ge P(s,\alpha , goal ) \cdot (r{+}R{+} wgt (s,\alpha )) + \sum _{t\in S^\prime } P(s,\alpha ,t) \cdot x_{t,r{+} wgt (s,\alpha ).} \end{aligned}$$

From a solution x to the linear program, we can easily extract an optimal weight-based deterministic scheduler. This scheduler only needs finite memory because the accumulated weight increases monotonically along paths and as soon as the saturation point is reached $\mathfrak {Max}$ provides the optimal decisions. As $B_R$ is exponential in the size of $\mathcal {M}$, the computation of the optimal partial expectation via this linear program runs in time exponential in the size of $\mathcal {M}$.

4 Existence of Optimal Schedulers

We prove that there are optimal weight-based deterministic schedulers for partial and conditional expectations. After showing that, if finite, $PE ^{\sup }_{s_{ init }}$ is equal to $\sup _{\mathfrak {S}\in WD ^{\mathcal {M}}} PE ^\mathfrak {S}_{s_{ init }}$, we take an analytic approach to show that there is a weight-based deterministic scheduler maximizing the partial expectation. We define a metric on $WD ^\mathcal {M}$ turning it into a compact space. Then, we prove that the function assigning the partial expectation to schedulers is upper semi-continuous. We conclude that there is a weight-based deterministic scheduler obtaining the maximum. Proofs to this section can be found in Appendix B of [17].

Proposition 12

Let $\mathcal {M}$ be an MDP with $PE ^{\sup }_{s_{ init }}<\infty$. Then we have $PE ^{\sup }_{s_{ init }}=\sup _{\mathfrak {S}\in WD ^\mathcal {M}} PE ^{\mathfrak {S}}_{s_{ init }}$.

Proof sketch

We can assume that all end components have negative maximal expected mean payoff (see Proposition 4). Given a scheduler $\mathfrak {S}\in HR ^\mathcal {M}$, we take the expected number of times $\theta _{s,w}$ that s is visited with accumulated weight w under $\mathfrak {S}$ for each state-weight pair (s, w), and the expected number of times $\theta _{s,w,\alpha }$ that $\mathfrak {S}$ then chooses $\alpha$. These values are finite due to the negative maximal mean payoff in end components. We define the scheduler $\mathfrak {T}\in WR ^\mathcal {M}$ choosing $\alpha$ in s with probability $\theta _{s,w,\alpha }/\theta _{s,w}$ when weight w has been accumulated. Then, we show by standard arguments that we can replace all probability distributions that $\mathfrak {T}$ chooses by Dirac distributions to obtain a scheduler $\mathfrak {T}^\prime \in WD ^\mathcal {M}$ such that $PE ^{\mathfrak {T}^\prime }_{s_{ init }}\ge PE ^{\mathfrak {S}}_{s_{ init }}$.    $\square$

It remains to show that the supremum is obtained by a weight-based deterministic scheduler. Given an MDP $\mathcal {M}$ with arbitrary integer weights, we define the following metric $d^\mathcal {M}$ on the set of weight-based deterministic schedulers, i.e. on the set of functions from $S\times \mathbb {Z} \rightarrow Act$: For two such schedulers $\mathfrak {S}$ and $\mathfrak {T}$, we let $d^\mathcal {M}(\mathfrak {S},\mathfrak {T}) := 2^{-R}$ where R is the greatest natural number such that $\mathfrak {S}\upharpoonright S\times \{-(R{-}1), \dots , R{-}1\} = \mathfrak {T}~\upharpoonright ~S\times \{-(R{-}1), \dots , R{-}1\}$ or $\infty$ if there is no greatest such natural number.

Lemma 13

The metric space $(Act^{S\times \mathbb {Z}},d^\mathcal {M})$ is compact.

Having defined this compact space of schedulers, we can rely on the analytic notion of upper semi-continuity.

Lemma 14

(Upper Semi-Continuity of Partial Expectations). If $PE ^{\sup }_{s_{ init }}$ is finite in $\mathcal {M}$, then the function $PE : ( WD , d^{ WD }) \rightarrow (\mathbb {R}_\infty ,d^{euclid})$ assigning $PE ^\mathfrak {S}_{s_{ init }}$ to a weight-based deterministic scheduler $\mathfrak {S}$ is upper semi-continuous.

Fig. 2.

All non-trivial transition probabilities are $1{\slash }2$. In the MDP $\mathcal {M}$, the optimal choice to maximize the partial expectation in t depends on the parity of the accumulated weight.

The technical proof of this lemma can be found in Appendix B of [17]. We arrive at the main result of this section.

Theorem 15

(Existence of Optimal Schedulers for Partial Expectations). If $PE ^{\sup }_{s_{ init }}$ is finite in an MDP $\mathcal {M}$, then there is a weight-based deterministic scheduler $\mathfrak {S}$ with $PE ^{\sup }_{s_{ init }}= PE ^\mathfrak {S}_{s_{ init }}$.

Proof

If $PE ^{\sup }_{s_{ init }}$ is finite, then the map $PE : ( WD , d^{ WD }) \rightarrow (\mathbb {R}_\infty ,d^{euclid})$ is upper semi-continuous. So, this map has a maximum because $( WD ,d^{ WD })$ is a compact metric space.    $\square$

Corollary 16

(Existence of Optimal Schedulers for Conditional Expectations). If $CE ^{\sup }_{s_{ init }}$ is finite in an MDP $\mathcal {M}$, then there is a weight-based deterministic scheduler $\mathfrak {S}$ with $CE ^{\sup }_{s_{ init }}= CE ^\mathfrak {S}_{s_{ init }}$.

Proof

By Proposition 6, we can assume that $\Pr ^{\min }_{s_{ init }}(\Diamond goal )>0$. We know that $PE ^{\sup }_{s_{ init }}[- CE ^{\sup }_{s_{ init }}]=0$ and that there is a weight-based deterministic scheduler $\mathfrak {S}$ with $PE ^{\mathfrak {S}}_{s_{ init }}[- CE ^{\sup }_{s_{ init }}]=0$. By Proposition 2, $\mathfrak {S}$ maximizes the conditional expectation as it reaches $goal$ with positive probability.    $\square$

In MDPs with non-negative weights, the optimal decision in a state s only depends on s as soon as the accumulated weight exceeds a saturation point. In MDPs with arbitrary integer weights, it is possible that the optimal choice of action does not become stable for increasing values of accumulated weight as we see in the following example.

Example 17

Let us first consider the MDP $\mathcal {N}$ depicted in Fig. 2. Let $\pi$ be a path reaching t for the first time with accumulated weight r. Consider a scheduler which chooses $\beta$ for the first k times and then $\alpha$. In this situation, the partial expectation from this point on is:

$$ \frac{1}{2^{k+1}}\left( r{-}k \right) + \sum _{i=1}^k \frac{1}{2^i} (r{-}i)= \frac{1}{2^{k+1}}+\sum _{i=1}^{k+1} \frac{1}{2^i} (r{-}i) = \frac{k{-}r+4}{2^{k+1}}+r{-}2. $$

For $r\ge 2$, this partial expectation has its unique maximum for the choice $k=r{-}2$. This already shows that an optimal scheduler needs infinite memory. No matter how much weight r has been accumulated when reaching t, the optimal scheduler has to count the $r{-}2$ times it chooses $\beta$.

Furthermore, we can transfer the optimal scheduler for the MDP $\mathcal {N}$ to the MDP $\mathcal {M}$. In state t, we have to make a nondeterministic choice between two action leading to the states $q_0$ and $q_1$, respectively. In both of these states, action $\beta$ is enabled which behaves like the same action in the MDP $\mathcal {N}$ except that it moves between the two states if $goal$ is not reached. So, the action $\alpha$ is only enabled every other step. As in $\mathcal {N}$, we want to choose $\alpha$ after choosing $\beta$ $r{-}2$ times if we arrived in t with accumulated weight $r\ge 2$. So, the choice in t depends on the parity of r: For $r=1$ or r even, we choose $\delta$. For odd $r\ge 3$, we choose $\gamma$. This shows that the optimal scheduler in the MDP $\mathcal {M}$ needs specific information about the accumulated weight, in this case the parity, no matter how much weight has been accumulated.

In the example, the optimal scheduler has a periodic behavior when fixing a state and looking at optimal decisions for increasing values of accumulated weight. The question whether an optimal scheduler always has such a periodic behavior remains open.

5 Approximation

As the optimal values for partial and conditional expectation can be irrational, there is no hope to compute these values by linear programming as in the case of non-negative weights. In this section, we show how we can nevertheless approximate the values. The main result is the following.

Theorem 18

Let $\mathcal {M}$ be an MDP with $PE ^{\sup }_{\mathcal {M},s_{ init }}<\infty$ and $\epsilon >0$. The maximal partial expectation $PE ^{\sup }_{\mathcal {M},s_{ init }}$ can be approximated up to an absolute error of $\epsilon$ in time exponential in the size of $\mathcal {M}$ and polynomial in $\log (1/\epsilon )$. If further, $CE ^{\sup }_{\mathcal {M},s_{ init }}<\infty$, also $CE ^{\sup }_{\mathcal {M},s_{ init }}$ can be approximated up to an absolute error of $\epsilon$ in time exponential in the size of $\mathcal {M}$ and polynomial in $\log (1/\epsilon )$.

We first prove that upper bounds for $PE ^{\sup }_{\mathcal {M},s_{ init }}$ and $CE ^{\sup }_{\mathcal {M},s_{ init }}$ can be computed in polynomial time. Then, we show that there are $\epsilon$-optimal schedulers for the partial expectation which become memoryless as soon as the accumulated weight leaves a sufficiently large weight window around 0. We compute the optimal partial expectation of such a scheduler by linear programming. The result can then be extended to conditional expectations.

Upper Bounds. Let $\mathcal {M}$ be an MDP in which all end components have negative maximal mean payoff. Let $\delta$ be the minimal non-zero transition probability in $\mathcal {M}$ and $W:= \max _{s\in S, \alpha \in Act(s)} | wgt (s,\alpha )|$. Moving through the MEC-quotient, the probability to reach an accumulated weight of $|S|\cdot W$ is bounded by $1-\delta ^{|S|}$ as $goal$ or $fail$ is reached within S steps with probability at least $1-\delta ^{|S|}$. It remains to show similar bounds inside an end component.

We will use the characterization of the maximal mean payoff in terms of super-harmonic vectors due to Hordijk and Kallenberg [13] to define a supermartingale controlling the growth of the accumulated weight in an end component under any scheduler. As the value vector for the maximal mean payoff in an end component is constant and negative in our case, the results of [13] yield:

Proposition 19

(Hordijk, Kallenberg). Let $\mathcal {E}=(S,Act)$ be an end component with maximal mean payoff $-t$ for some $t>0$. Then there is a vector $(u_s)_{s\in S}$ such that $-t + u_s \ge wgt(s,\alpha ) + \sum _{s^\prime \in S} P(s,\alpha ,s^\prime ) \cdot u_{s^\prime }$.

Furthermore, let v be the vector $(-t,\dots ,-t)$ in $\mathbb {R}^S$. Then, (v, u) is the solution to a linear program with 2|S| variables, 2|S||Act| inequalities, and coefficients formed from the transition probabilities and weights in $\mathcal {E}$.

We will call the vector u a super-potential because the expected accumulated weight after i steps is at most $u_s -\min _{t \in S} u_t - i\cdot t$ when starting in state s. Let $\mathfrak {S}$ be a scheduler for $\mathcal {E}$ starting in some state s. We define the following random variables on $\mathfrak {S}$-runs in $\mathcal {E}$: let $s(i)\in S$ be the state after i steps, let $\alpha (i)$ be the action chosen after i steps, let w(i) be the accumulated weight after i steps, and let $\pi (i)$ be the history, i.e. the finite path after i steps.

Lemma 20

The sequence $m(i):=w(i)+u_{s(i)}$ satisfies $\mathbb {E}(m(i+1)|\pi (0),\dots ,\pi (i)) \le m(i)-t$ for all i.¹

Proof

By Proposition 19, $\mathbb {E}(m(i+1)|\pi (0),\dots ,\pi (i))-m(i) = wgt(s(i),\mathfrak {S}(\pi (i))) + \sum _{s^\prime \in S} P(s(i),\mathfrak {S}(\pi (i)),s^\prime )\cdot u_{s^\prime } -u_{s(i)} \le -t$.    $\square$

We are going to apply the following theorem by Blackwell [6].

Theorem 21

(Blackwell [6]). Let $X_1, X_2, \dots$ be random variables, and let $S_n:= \sum _{k=1}^n X_k$. Assume that $|X_i|\le 1$ for all i and that there is a $u>0$ such that $\mathbb {E}(X_{n+1}|X_1,\dots ,X_n) \le -u$. Then, $\Pr (\sup _{n\in \mathbb {N}} S_n \ge t) \le \left( \frac{1-u}{1+u}\right) ^t$.

We denote $\max _{s^\prime \in S} u_{s^\prime } - \min _{s^\prime \in S} u_{s^\prime }$ by $\Vert u\Vert$. Observe that $|m(i+1)-m(i)|\le \Vert u\Vert +W=:c_{\mathcal {E}}$. We can rescale the sequence m(i) by defining $m^\prime (i) := (m(i)-m(0))/c_\mathcal {E}$. This ensures that $m^\prime (0)=0$, $|m^\prime (i+1)-m^\prime (i)|\le 1$ and $\mathbb {E}(m^\prime (i+1)|m^\prime (0),\dots ,m^\prime (i))\le -t/c_\mathcal {E}$ for all i. In this way, we arrive at the following conclusion, putting $\lambda _{\mathcal {E}}:=\frac{1-t/c_{\mathcal {E}}}{1+t/c_{\mathcal {E}}}$.

Corollary 22

For any scheduler $\mathfrak {S}$ and any starting state s in $\mathcal {E}$, we have $\Pr ^\mathfrak {S}_s (\Diamond wgt \ge (k{+}1)\cdot c_{\mathcal {E}}) \le \lambda _{\mathcal {E}}^{k}$.

Proof

By Theorem 21, $\Pr ^\mathfrak {S}_s (\Diamond wgt \ge (k+1)\cdot c_{\mathcal {E}} ) \le \Pr ^\mathfrak {S}_s (\Diamond wgt \ge \Vert u\Vert + k\cdot c_{\mathcal {E}}) \le \Pr ^\mathfrak {S}_s (\exists i : m(i)-m(0)\ge k\cdot c_{\mathcal {E}}) = \Pr ^\mathfrak {S}_s (\sup _{i\in \mathbb {N}} m^\prime (i)\ge k) \le \left( \frac{1-t/c_{\mathcal {E}}}{1+t/c_{\mathcal {E}}}\right) ^{k}.$    $\square$

Let $MEC$ be the set of maximal end components in $\mathcal {M}$. For each $\mathcal {E}\in MEC$, let $\lambda _\mathcal {E}$ and $c_\mathcal {E}$ be as in Corollary 22. Define $\lambda _{\mathcal {M}} := 1- (\delta ^{|S|}\cdot \prod _{\mathcal {E}\in MEC } (1- \lambda _\mathcal {E}))$, and $c_{\mathcal {M}}:=|S|\cdot W + \sum _{\mathcal {E}\in MEC } c_\mathcal {E}$. Then an accumulated weight of $c_\mathcal {M}$ cannot be reached with a probability greater than $\lambda _\mathcal {M}$ because reaching accumulated weight $c_\mathcal {M}$ would require reaching weight $c_\mathcal {E}$ in some end component $\mathcal {E}$ or reaching weight $|S|\cdot W$ in the MEC-quotient and $1-\lambda _\mathcal {M}$ is a lower bound on the probability that none of this happens (under any scheduler).

Proposition 23

Let $\mathcal {M}$ be an MDP with $PE ^{\sup }_{s_{ init }}<\infty$. There is an upper bound $PE ^{ub}$ for the partial expectation in $\mathcal {M}$ computable in polynomial time.

Proof

In any end component $\mathcal {E}$, the maximal mean payoff $-t$ and the super-potential u are computable in polynomial time. Hence, $c_\mathcal {E}$ and $\lambda _\mathcal {E}$, and in turn also $c_\mathcal {M}$ and $\lambda _\mathcal {M}$ are also computable in polynomial time. When we reach accumulated weight $c_\mathcal {M}$ for the first time, the actual accumulated weight is at most $c_\mathcal {M}+W$. So, we conclude that $\Pr ^{\max }_s(\Diamond wgt\ge k\cdot (c_\mathcal {M}+W))\le \lambda _\mathcal {M}^k$. The partial expectation can now be bounded by $\sum _{k=0}^\infty (k+1)\cdot (c_\mathcal {M}+W)\cdot \lambda _\mathcal {M}^k= \frac{c_\mathcal {M}+W}{(1-\lambda _\mathcal {M})^2}$.    $\square$

Corollary 24

Let $\mathcal {M}$ be an MDP with $CE ^{\sup }_{\mathcal {M},s_{ init }}<\infty$. There is an upper bound $CE ^{ub}$ for the conditional expectation in $\mathcal {M}$ computable in polynomial time.

Proof

By Proposition 6, we can construct an MDP $\mathcal {N}$ in which $goal$ is reached with probability $q>0$ in polynomial time with $CE ^{\sup }_{\mathcal {M},s_{ init }}= CE ^{\sup }_{\mathcal {N},s_{ init }}$. Now, $CE ^{ub}:= PE ^{ub}/q$ is an upper bound for the conditional expectation in $\mathcal {M}$.    $\square$

Approximating Optimal Partial Expectations. The idea for the approximation is to assume that the partial expectation is $PE ^{\mathfrak {Max}}_{s_{ init }}+w\cdot p^{\max }_s$ if a high weight w has been accumulated in state s. Similarly, for small weights $w^\prime$, we use the value $PE ^{\mathfrak {Min}}_{s_{ init }}+w\cdot p^{\min }_s$. We will first provide a lower “saturation point” making sure that only actions minimizing the probability to reach the goal are used by an optimal scheduler as soon as the accumulated weight drops below this saturation point. For the proofs to this section, see Appendix C.1 of [17].

Proposition 25

Let $\mathcal {M}$ be an MDP with $PE ^{\sup }_{s_{ init }}<\infty$. Let $s\in S$ and let $\mathfrak {q}_s:=\frac{ PE ^{ub}- PE ^{\mathfrak {Min}}_s}{p_s^{\min } - \min \limits _{\alpha \not \in Act^{\min }(s)} p_{s,\alpha }^{\min }}$. Then any weight-based deterministic scheduler $\mathfrak {S}$ maximizing the partial expectation in $\mathcal {M}$ satisfies $\mathfrak {S}(s,w)\in Act^{\min }(s)$ if $w\le \mathfrak {q}_s$.

Let $\mathfrak {q}:=\min _{s\in S} \mathfrak {q}_s$ and let $D:= PE ^{ub}-\min \{ PE ^\mathfrak {Max}_s , PE ^\mathfrak {Min}_s |s\in S\}$. Given $\epsilon >0$, we define $R^+_\epsilon := (c_\mathcal {M}+W)\cdot \left\lceil \frac{\log (2D)+\log (1/\epsilon )}{\log (1/\lambda _\mathcal {M})}\right\rceil$ and $R^-_\epsilon := \mathfrak {q}-R^+_\epsilon$.

Theorem 26

There is a weight-based deterministic scheduler $\mathfrak {S}$ such that the scheduler $\mathfrak {T}$ defined by

$$\mathfrak {T} (\pi ) = {\left\{ \begin{array}{ll} \mathfrak {S}(\pi ) &{} \text {if any prefix }\pi ^\prime \text { of }\pi \text { satisfies }R^-_\epsilon \le wgt(\pi ^\prime )\le R^+_\epsilon ,\\ \mathfrak {Max}(\pi ) &{} \text {if the shortest prefix }\pi ^\prime \text { of }\pi \text { with } wgt(\pi ^\prime )\not \in [R^-_\epsilon ,R^+_\epsilon ] \\ &{} \text {satisfies }wgt(\pi ^\prime )>R^+_\epsilon , \\ \mathfrak {Min}(\pi ) &{} \text {otherwise,} \end{array}\right. }$$

satisfies $PE ^\mathfrak {T}_{s_{ init }}\ge PE ^{\sup }_{s_{ init }} - \epsilon$.

This result now allows us to compute an $\epsilon$-approximation and an $\epsilon$-optimal scheduler with finite memory by linear programming, similar to the case of non-negative weights, in a linear program with $R^+_\epsilon + R^-_\epsilon$ many variables and |Act|-times as many inequalities.

Corollary 27

$PE ^{\sup }_{s_{ init }}$ can be approximated up to an absolute error of $\epsilon$ in time exponential in the size of $\mathcal {M}$ and polynomial in $\log (1/\epsilon )$.

If the logarithmic length of $\theta \in \mathbb {Q}$ is polynomial in the size of $\mathcal {M}$, we can also approximate $PE ^{\sup }_{s_{ init }}[\theta ]$ up to an absolute error of $\epsilon$ in time exponential in the size of $\mathcal {M}$ and polynomial in $\log (1/\epsilon )$: We can add a new initial state s with a transition to $s_{ init }$ with weight $\theta$ and approximate $PE ^{\sup }_{s}$ in the new MDP.

Transfer to Conditional Expectations. Let $\mathcal {M}$ be an MDP with $CE ^{sup}_{s_{ init }}<\infty$ and $\epsilon >0$. By Proposition 6, we can assume that $\Pr ^{\min }_{\mathcal {M},s_{ init }}(\Diamond goal )=:p$ is positive. Clearly, $CE ^{sup}_{s_{ init }}\in [ CE ^{\mathfrak {Max}}_{s_{ init }}, CE ^{ub}]$. We perform a binary search to approximate $CE ^{sup}_{s_{ init }}$: We put $A_0:= CE ^{\mathfrak {Max}}_{s_{ init }}$ and $B_0:= CE ^{ub}$. Given $A_i$ and $B_i$, let $\theta _i := (A_i+B_i)/2$. Then, we approximate $PE ^{\sup }_{s_{ init }}[-\theta _i]$ up to an absolute error of $p\cdot \epsilon$. Let $E_i$ be the value of this approximation. If $E_i \in [-2p\cdot \epsilon , 2p\cdot \epsilon ]$, terminate and return $\theta _i$ as the approximation for $CE ^{\sup }_{s_{ init }}$. If $E_i<-2p\cdot \epsilon$, put $A_{i+1}:=A_i$ and $B_{i+1}:=\theta _i$, and repeat. If $E_i>2p\cdot \epsilon$, put $A_{i+1}:=\theta _i$ and $B_{i+1}:= B_i$, and repeat.

Proposition 28

The procedure terminates after at most $\lceil \log ((A_0-B_0)/(p\cdot \epsilon ))\rceil$ iterations and returns an $3\epsilon$-approximation of $CE ^{\sup }_{s_{ init }}$ in time exponential in the size of $\mathcal {M}$ and polynomial in $\log (1/\epsilon )$.

The proof can be found in Appendix C.2 of [17]. This finishes the proof of Theorem 18.

6 Conclusion

Compared to the setting of non-negative weights, the optimization of partial and conditional expectations faces substantial new difficulties in the setting of integer weights. The optimal values can be irrational showing that the linear programming approaches from the setting of non-negative weights cannot be applied for the computation of optimal values. We showed that this approach can nevertheless be adapted for approximation algorithms. Further, we were able to show that there are optimal weight-based deterministic schedulers. These schedulers, however, can require infinite memory and it remains open whether we can further restrict the class of schedulers necessary for the optimization. In examples, we have seen that optimal schedulers can switch periodically between actions they choose for increasing values of accumulated weight. Further insights on the behavior of optimal schedulers would be helpful to address threshold problems (“Is $PE ^{\sup }_{s_{ init }} \ge \theta$?”).