Abstract
This work investigates three notions of program equivalence for a higher-order functional language with recursion and general algebraic effects, in which programs are written in continuation-passing style. Our main contribution is the following: we define a logic whose formulas express program properties and show that, under certain conditions which we identify, the induced program equivalence coincides with a contextual equivalence. Moreover, we show that this logical equivalence also coincides with an applicative bisimilarity. We exemplify our general results with the nondeterminism, probabilistic choice, global store and I/O effects.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Logic is a fundamental tool for specifying the behaviour of programs. A general approach is to consider that a logical formula \(\phi \) encodes a program property, and the satisfaction relation of the logic, \(t\,\models \,\phi \), asserts that program t enjoys property \(\phi \). An example is Hennessy-Milner logic [12] used to model concurrency and nondeterminism. Other program logics include Hoare logic [13], which describes imperative programs with state, and more recently separation logic [28]. Both state and nondeterminism are examples of computational effects [25], which represent impure behaviour in a functional programming language. The logics mentioned so far concern languages with first-order functions, so as a natural extension, we are interested in finding a logic which describes higher-order programs with general effects.
The particular flavour of effects we consider is that of algebraic effects developed by Plotkin and Power [32,33,34]. This is a unified framework in which effectful computation is triggered by a set of operations whose behaviour is axiomatized by a set of equations. For example, nondeterminism is given by a binary choice operation \(or(-,-)\) that satisfies the equations of a semilattice. Thus, general effectful programs have multiple possible execution paths, which can be visualized as an (effect) tree, with effect operations labelling the nodes. Consider the following function or_suc which has three possible return values, and the effect tree of \((\texttt {or\_suc}\ 2\)):

Apart from state and nondeterminism, examples of algebraic effects include probabilistic choice and input and output operations.
Apart from providing a specification language for programs, a logic can also be used to compare two different programs. This leads to a notion of program equivalence: two programs are equivalent when they satisfy exactly the same formulas in the logic.
Many other definitions of program equivalence for higher-order languages exist. An early notion is contextual equivalence [26], which asserts that two programs are equivalent if they have the same observable behaviour in all program contexts. However, this is hard to establish in practice due to the quantification over all contexts. Another approach, which relies on the existence of a suitable denotational model of the language, is checking equality of denotations. Yet another notion, meant to address the shortcomings of the previous two, is that of applicative bisimilarity [1].
Given the wide range of definitions of program equivalence, comparing them is an interesting question. For example, the equivalence induced by Hennessy-Milner logic is known to coincide with bisimilarity for CCS. Thus, we not only aim to find a logic describing general algebraic effects, but also to compare it to existing notions of program equivalence.
Program equivalence for general algebraic effects has been studied by Johann, Simpson and Voigtländer [17] who define a notion of contextual equivalence and a corresponding logical relation. Dal Lago, Gavazzo and Levy [7] provide an abstract treatment of applicative bisimilarity in the presence of algebraic effects. Working in a typed, call-by-value setting, Simpson and Voorneveld [38] propose a modal logic for effectful programs whose induced program equivalence coincides with applicative bisimilarity, but not with contextual equivalence (see counter-example in Sect. 5). Dal Lago, Gavazzo and Tanaka [8] propose a notion of applicative similarity that coincides with contextual equivalence for an untyped, call-by-name effectful calculus.
These papers provide the main starting point for our work. Our goal is to find a logic of program properties which characterizes contextual equivalence for a higher-order language with algebraic effects. We study a typed call-by-value language in which programs are written in continuation-passing style (CPS). CPS is known to simplify contextual equivalence, through the addition of control operators (e.g. [5]), but it also implies that all notions of program equivalence we define can only use continuations to test return values. Contextual equivalence and bisimilarity for lambda-calculi with control, but without general effects, have been studied extensively (e.g. [4, 15, 23, 41]).
In CPS, functions receive as argument the continuation (which is itself a function) to which they pass their return value. Consider the function that adds two natural numbers. This usually has type \(\mathtt {nat}\rightarrow \mathtt {nat}\rightarrow \mathtt {nat}\), but its CPS version is defined as: \(\mathtt {addk} = \lambda (n{:}\mathtt {nat},m{:}\mathtt {nat},k{:}\mathtt {nat}{\rightarrow } \mathtt {R}).\ k\ (n+m)\) for some fixed return type \(\mathtt {R}\). The function \(\texttt {or\_suc}\) becomes in CPS:
A general translation of direct-style functions into CPS can be found in Sect. 5.
We fix a calculus named ECPS (Sect. 2), in which programs are not expected to return, except through a call to the continuation. Contextual equivalence is defined using a custom set of observations \(\mathfrak {P}\), where the elements of \(\mathfrak {P}\) are sets of effect trees. We consider a logic \(\mathcal {F}\) whose formulas express properties of ECPS programs (Sect. 3). For example, or_succ satisfies the following formula: \(\phi = (\{2\},\ (\{3\}\vee \{4\})\mapsto \Box )\mapsto \Diamond .\)
Here, \(\Diamond \) is the set of all effect trees for which at least one execution path succeeds and \(\Box \) is the set of trees that always succeed. So \(\texttt {or\_succ}\,\models _\mathcal {F}\,\phi \) says that, when given arguments 2 and a continuation that always succeeds for input 3 or 4, then or_succ may succeed. In other words, \(\texttt {or\_succ}\) may ‘return’ 3 or 4 to the continuation. In contrast, \({\texttt {or\_succ}\, \models _\mathcal {F}\, \phi ' = (\{2\},\ (\{3\}\vee \{4\})\mapsto \Box )\mapsto \Box }\) says that the program or_succ must return 3 or 4 to the continuation. Thus  because the continuation k might diverge on 2.
because the continuation k might diverge on 2.
Another example can be obtained by generalizing the or_succ function to take a function as a parameter, rather than using addk:

The formula above says that or_succ’ may call f with arguments 2, 2 and k.
The main theorem concerning the logic \(\mathcal {F}\) (Theorem 1) is that, under certain restrictions on the observations in \(\mathfrak {P}\), logical equivalence coincides with contextual equivalence. In other words, \(\mathcal {F}\) is sound and complete with respect to contextual equivalence. The proof of this theorem, outlined in Sect. 4, involves applicative bisimilarity as an intermediate step. Thus, we show in fact that three notions of program equivalence for ECPS are the same: logical equivalence, contextual equivalence and applicative bisimilarity. Due to space constraints, proofs are omitted but they can be found in [21].
2 Programming Language – ECPS
We consider a simply-typed functional programming language with general recursion, a datatype of natural numbers and general algebraic effects as introduced by Plotkin and Power [32]. We will refer to this language as ECPS because programs are written in continuation-passing style.
ECPS distinguishes between terms which can reduce further, named computations, and values, which cannot reduce. ECPS is a variant of both Plotkin’s PCF [31] and Levy’s Jump-With-Argument language [20], extended with algebraic effects. A fragment of ECPS is discussed in [18] in connection with logic.

The only base type in ECPS is \(\mathtt {nat}\). The return type of functions, \(\mathtt {R}\), is fixed and is not a first-class type. Intuitively, we consider that functions are not expected to return. A type in direct style \(A\rightarrow B\) becomes in ECPS:  . In the typing context \((\varGamma ,x:A)\), the free variable x does not appear in \(\varGamma \).
. In the typing context \((\varGamma ,x:A)\), the free variable x does not appear in \(\varGamma \).
First, consider the pure fragment of ECPS, without effects, named CPS:

Variables, natural numbers and lambdas are values. Computations include function application and an eliminator for natural numbers. The expression  is a recursive definition of the function v, which must be applied. If exactly one argument appears in a lambda abstraction or an application term, we will sometimes omit the parentheses around that argument.
is a recursive definition of the function v, which must be applied. If exactly one argument appears in a lambda abstraction or an application term, we will sometimes omit the parentheses around that argument.
There are two typing relations in CPS, one for values \(\varGamma \vdash v:A\), which says that value v has type A in the context \(\varGamma \), and one for computations \(\varGamma \vdash t:\mathtt {R}\). This says that t is well-formed given the context \(\varGamma \). All computations have the same return type \(\mathtt {R}\). We also define the order of a type recursively, which roughly speaking counts the number of function arrows \(\rightarrow \) in a type.

To introduce algebraic effects into our language, we consider a new kind of context \(\varSigma \), disjoint from \(\varGamma \), which we call an effect context. The symbols \(\sigma \) appearing in \(\varSigma \) stand for effect operations and their type must have either order 1 or 2. For example, the binary choice operation  expects two thunked computations. The output operation
expects two thunked computations. The output operation  expects a parameter and a continuation. An operation signifying success, which takes no arguments, is
expects a parameter and a continuation. An operation signifying success, which takes no arguments, is  . Roughly, \(\varSigma \) could be regarded as a countable algebraic signature.
. Roughly, \(\varSigma \) could be regarded as a countable algebraic signature.
We extend the syntax of CPS with effectful computations. The typing relations now carry a \(\varSigma \) context: \({\varGamma \vdash _\varSigma v: A}\) and \({\varGamma \vdash _\varSigma t:\mathtt {R}}\). Otherwise, the typing judgements remain unchanged; we have a new rule for typing effect operations:

In ECPS, the only type with order 0 is \(\mathtt {nat}\), so in fact \(A_i=\mathtt {nat}\) for all i. Notice that the grammar does not allow function abstraction over a symbol from \(\varSigma \) and that \(\sigma \) is not a first-class term. So we can assume that \(\varSigma \) is fixed, as in the examples from Sect. 2.1.
As usual, we identify terms up to alpha-equivalence. Substitution of values for free variables that are not operations, v[w/x] and t[w/x], is defined in the standard way by induction on the structure of v and t. We use \(\overline{n}\) to denote the term \(\mathtt {succ}^n(\mathtt {zero})\). Let \((\vdash _\varSigma )\) be the set of well-formed closed computations and \((\vdash _\varSigma A)\) the set of closed values of type A.
2.1 Operational Semantics
We define a family of relations on closed computation terms \((\longrightarrow )\subseteq (\vdash _\varSigma )\times (\vdash _\varSigma )\) for any effect context \(\varSigma \):

Observe that the reduction given by \(\longrightarrow \) can either run forever or terminate with an effect operation. If the effect operation does not take any arguments of order 1 (i.e. continuations), the computation stops. If the reduction reaches \(\sigma (\overrightarrow{v},\overrightarrow{k})\), the intuition is that any continuation \(k_i\) may be chosen, and executed with the results of operation \(\sigma \). Thus, repeatedly evaluating effect operations leads to the construction of an infinitely branching tree (similar to that in [32]), as we now explain, which we call an effect tree. A path in the tree represents a possible execution path of the program.
An effect tree, of possibly infinite depth and width, can contain:
-
leaves labelled \(\bot \), which signifies nontermination of \(\longrightarrow \);
-
leaves labelled \(\sigma _{\overrightarrow{v}}\), where
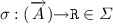 and \((\vdash _\varSigma v_i:A_i)_i\);
and \((\vdash _\varSigma v_i:A_i)_i\); -
nodes labelled \(\sigma _{\overrightarrow{v}}\), where
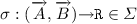 and each \(\vdash _\varSigma v_i:A_i\); such a node has an infinite number of children \(t_0,t_1,\ldots \).
and each \(\vdash _\varSigma v_i:A_i\); such a node has an infinite number of children \(t_0,t_1,\ldots \).
Denote the set of all effect trees by \(\textit{Trees}_\varSigma \). This set has a partial order: \(tr_1 \le tr_2\) if and only if \(tr_1\) can be obtained by replacing subtrees of \(tr_2\) by \(\bot \). Every ascending chain \(t_1 \le t_2 \le \ldots \) has a least upper bound \(\bigsqcup _n t_n\). In fact \(\textit{Trees}_\varSigma \) is the free pointed \(\varSigma \)-algebra [2] and therefore also has a coinductive property [9].
Next, we define a sequence of effect trees associated with each well-formed closed computation. Each element in the sequence can be seen as evaluating the computation one step further. Let  :
:

These are all the cases since well-formed computations do not get stuck. We define the function  as the least upper bound of the chain
as the least upper bound of the chain  :
: 
We now give examples of effect contexts \(\varSigma \) for different algebraic effects, and of some computations and their associated effect trees.
Example 1
(Pure functional computation).  . Intuitively, \(\downarrow \) is a top-level success flag, analogous to a ‘barb’ in process algebra. This is to ensure a reasonable contextual equivalence for CPS programs, which never actually return results. For example,
. Intuitively, \(\downarrow \) is a top-level success flag, analogous to a ‘barb’ in process algebra. This is to ensure a reasonable contextual equivalence for CPS programs, which never actually return results. For example,  runs forever, and
runs forever, and

is a continuation that succeeds just when it is passed zero. Generally, an effect tree for a pure computation is either \(\downarrow \) if it succeeds or \(\bot \) otherwise.
Example 2
(Nondeterminism).  . Intuitively, \(or(k_1,k_2)\) performs a nondeterministic choice between computations \(k_1\ ()\) and \(k_2\ ()\). Consider a continuation
. Intuitively, \(or(k_1,k_2)\) performs a nondeterministic choice between computations \(k_1\ ()\) and \(k_2\ ()\). Consider a continuation  that diverges on 3 and succeeds otherwise. The program or_succ from the introduction is in ECPS:
that diverges on 3 and succeeds otherwise. The program or_succ from the introduction is in ECPS:

Example 3
(Probabilistic choice).  . Intuitively, the operation \(p\text {-}or(k_1, k_2)\) chooses between \(k_1\ ()\) and \(k_2\ ()\) with probability 0.5. Consider the following term which encodes the geometric distribution:
. Intuitively, the operation \(p\text {-}or(k_1, k_2)\) chooses between \(k_1\ ()\) and \(k_2\ ()\) with probability 0.5. Consider the following term which encodes the geometric distribution:

The probability that \(\mathtt {geom}\) passes a number \(n>0\) to its continuation is \(2^{-n}\). To test it, consider  ; then
; then  is an infinite tree:
is an infinite tree:

Example 4
(Global store). \(\mathbb {L}\) is a finite set of locations storing natural numbers and  Intuitively, \(lookup_l(k)\) looks up the value at storage location l, if this is \(\overline{n}\) it continues with \(k\,(\overline{n})\). For \(update_l(v,k)\) the intuition is: write the number v in location l then continue with the computation \(k\, ()\). For example:
Intuitively, \(lookup_l(k)\) looks up the value at storage location l, if this is \(\overline{n}\) it continues with \(k\,(\overline{n})\). For \(update_l(v,k)\) the intuition is: write the number v in location l then continue with the computation \(k\, ()\). For example:

Only the second branch of \(lookup_{l_0}\) can occur. The other branches are still present in the tree because  treats effect operations as uninterpreted syntax.
treats effect operations as uninterpreted syntax.
Example 5
(Interactive input/output).  . Intuitively, the computation input(k) accepts number \(\overline{n}\) from the input channel and continues with \(k\,(\overline{n})\). The computation output(v, k) writes v to the output channel then continues with computation \(k\,()\). Below is a computation that inputs a number \(\overline{n}\) then outputs it immediately, and repeats.
. Intuitively, the computation input(k) accepts number \(\overline{n}\) from the input channel and continues with \(k\,(\overline{n})\). The computation output(v, k) writes v to the output channel then continues with computation \(k\,()\). Below is a computation that inputs a number \(\overline{n}\) then outputs it immediately, and repeats.

2.2 Contextual Equivalence
Informally, two terms are contextually equivalent if they have the same observable behaviour in all program contexts. The definition of observable behaviour depends on the programming language under consideration. In ECPS, we can observe effectful behaviour such as interactive output values or the probability with which a computation succeeds. This behaviour is encoded by the effect tree of a computation. Therefore, we represent an ECPS observation as a set of effect trees P. A computation t exhibits observation P if  .
.
For a fixed set of effect operations \(\varSigma \), we define the set \(\mathfrak {P}\) of possible observations. The elements of \(\mathfrak {P}\) are subsets of \(\textit{Trees}_\varSigma \). Observations play a similar role to the modalities from [38]. For our running examples of effects, \(\mathfrak {P}\) is defined as follows:
Example 6
(Pure functional computation). Define \(\mathfrak {P}=\{{\Downarrow }\}\) where \({\Downarrow }=\{\downarrow \}\). There are no effect operations so the \(\Downarrow \) observation only checks for success.
Example 7
(Nondeterminism). Define \(\mathfrak {P}=\{\Diamond ,\Box \}\) where:
The intuition is that, if  , then computation t may succeed, whereas if
, then computation t may succeed, whereas if  , then t must succeed.
, then t must succeed.
Example 8
(Probabilistic choice). Define \(\mathbb {P}:\textit{Trees}_\varSigma \longrightarrow [0,1]\) to be the least function, by the pointwise order, such that:
Notice that \(\mathbb {P}(\bot )=0\). Then observations are defined as:
This means that  if the probability that t succeeds is greater than q.
if the probability that t succeeds is greater than q.
Example 9
(Global store). Define the set of states as the set of functions from storage locations to natural numbers: \(State=\mathbb {L}\longrightarrow \mathbb {N}\). Given a state S, we write \([S{\downarrow }]\subseteq \textit{Trees}_\varSigma \) for the set of effect trees that terminate when starting in state S. More precisely, \([-]\) is the least State-indexed family of sets satisfying the following:

The set of observations is: \(\mathfrak {P}=\{ [S{\downarrow }] \mid S\in State\}\).
Example 10
(Interactive input/output). An I/O-trace is a finite word w over the alphabet \(\{?n \mid n\in \mathbb {N}\} \cup \{!n \mid n\in \mathbb {N} \}\). For example, \(?1\,!1\,?2\,!2\,?3\,!3\). The set of observations is: \( \mathfrak {P} = \{\langle W\rangle _{\ldots },\ \langle W\rangle {\downarrow } \mid W \text { an I/O-trace}\}.\) Observations are defined as the least sets satisfying the following rules:

and the analogous rules for \(\langle (?n)W\rangle {\downarrow }\) and \(\langle (!n)W\rangle {\downarrow }\). Thus,  if computation t produces I/O trace W, and
if computation t produces I/O trace W, and  if additionally t succeeds immediately after producing W.
if additionally t succeeds immediately after producing W.
Using the set of observations \(\mathfrak {P}\), we can now define contextual equivalence as the greatest compatible and adequate equivalence relation between possibly open terms of the same type. Adequacy specifies a necessary condition for two closed computations to be related, namely producing the same observations.
Definition 1
A well-typed relation \(\mathcal {R}=(\mathcal {R}^\mathfrak {v}_A,\mathcal {R}^\mathfrak {c})\) (i.e. a family of relations indexed by ECPS types where \(\mathcal {R}^\mathfrak {c}\) relates computations) on possibly open terms is adequate if:

Relation \(\mathcal {R}\) is compatible if it is closed under the rules in [21, Page 57]. As an example, the rules for application and lambda abstraction are:

Definition 2
(Contextual equivalence). Let \(\mathbb {CA}\) be the set of well-typed relations on possibly open terms that are both compatible and adequate. Define contextual equivalence  to be \(\bigcup \mathbb {CA}\).
to be \(\bigcup \mathbb {CA}\).
Proposition 1
Contextual equivalence  is an equivalence relation, and is moreover compatible and adequate.
is an equivalence relation, and is moreover compatible and adequate.
This definition of contextual equivalence, originally proposed in [11, 19], can be easily proved equivalent to the traditional definition involving program contexts (see [21, §7]). As Pitts observes [30], reasoning about program contexts directly is inconvenient because they cannot be defined up to alpha-equivalence, hence we prefer using Definition 2.
For example, in the pure setting (Example 1), we have  , because
, because  ; they are distinguished by the observation \(\Downarrow \). In the state example,
; they are distinguished by the observation \(\Downarrow \). In the state example,  , because they are distinguished by the context
, because they are distinguished by the context  and the observation \([S{\downarrow }]\) where \(S(l_1)=\overline{0}\) and \(S(l_2)=\overline{1}\). In the case of probabilistic choice (Example 3),
and the observation \([S{\downarrow }]\) where \(S(l_1)=\overline{0}\) and \(S(l_2)=\overline{1}\). In the case of probabilistic choice (Example 3),  because
because  succeeds with probability 1 (‘almost surely’).
succeeds with probability 1 (‘almost surely’).
3 A Program Logic for ECPS – \(\mathcal {F}\)
This section contains the main contribution of the paper: a logic \(\mathcal {F}\) of program properties for ECPS which characterizes contextual equivalence. Crucially, the logic makes use of the observations in \(\mathfrak {P}\) to express properties of computations.
In \(\mathcal {F}\), there is a distinction between formulas that describe values and those that describe computations. Each value formula is associated an ECPS type A. Value formulas are constructed from the basic formulas \({(\phi _1,\ldots ,\phi _n)\mapsto P}\) and \({\phi =\{n\}}\), where \(n\in \mathbb {N}\) and \(P\in \mathfrak {P}\), as below. The indexing set I can be infinite, even uncountable. Computation formulas are simply the elements of \(\mathfrak {P}\).

The satisfaction relation \(\models _\mathcal {F}\) relates a closed value \(\vdash _\varSigma v : A\) to a value formula \(\phi : A\) of the same type, or a closed computation t to an observation P. Relation \(t\models _\mathcal {F} P\) tests the shape of the effect tree of t.

Example 11
Consider the following formulas, where only \(\phi _3\) and \(\phi _4\) refer to the same effect context:

Given a function  , \(v\models _\mathcal {F}\phi _1\) means that v is guaranteed to call its argument only with \(\overline{3}\) or \(\overline{4}\). The function \(\mathtt {geom}\) from Example 3 satisfies \(\phi _2\) because with probability 1 / 2 it passes to the continuation a number \(n>1\).
, \(v\models _\mathcal {F}\phi _1\) means that v is guaranteed to call its argument only with \(\overline{3}\) or \(\overline{4}\). The function \(\mathtt {geom}\) from Example 3 satisfies \(\phi _2\) because with probability 1 / 2 it passes to the continuation a number \(n>1\).
For example, the following satisfactions hold:  and
and  . The latter formula says that, either f always succeeds, or f evaluated with \(\overline{n}\) changes the state from
. The latter formula says that, either f always succeeds, or f evaluated with \(\overline{n}\) changes the state from  to
to  before calling its continuation. This is similar to a total correctness assertion
before calling its continuation. This is similar to a total correctness assertion  from Hoare logic, for a direct style program. Formula \(\phi _5\) is satisfied by \(\lambda ().\mathtt {echo}\), where \(\mathtt {echo}\) is the computation defined in Example 5.
from Hoare logic, for a direct style program. Formula \(\phi _5\) is satisfied by \(\lambda ().\mathtt {echo}\), where \(\mathtt {echo}\) is the computation defined in Example 5.
Even though the indexing set I in \(\wedge _{i\in I}\) and \(\vee _{i\in I}\) may be uncountable, the sets of values and computations are countable. Since logical formulas are interpreted over values and computations, all conjunctions and disjunctions are logically equivalent to countable ones.
Definition 3
(Logical equivalence). For any closed values \(\vdash _\varSigma v_1:A\) and \(\vdash _\varSigma v_2:A\), and for any closed computations \(\vdash _\varSigma s_1\) and \(\vdash _\varSigma s_2\):
To facilitate equational reasoning, logical equivalence should be compatible, a property proved in the next section (Proposition 3). Compatibility allows substitution of related programs for a free variable that appears on both sides of a program equation. Notice that logical equivalence would not be changed if we added conjunction, disjunction and negation at the level of computation formulas. We have omitted such connectives for simplicity.
To state our main theorem, first define the open extension of a well-typed relation \(\mathcal {R}\) on closed terms as: \({\overrightarrow{x:A}\vdash _\varSigma t \mathrel {\mathcal {R}^\circ } s}\) if and only if for any closed values \({(\vdash _\varSigma v_i:A_i)_i}\), \({t[\overrightarrow{v/x}]\mathrel {\mathcal {R}}s[\overrightarrow{v/x}]}\). Three sufficient conditions that we impose on the set of observations \(\mathfrak {P}\) are defined below. The first one, consistency, ensures that contextual equivalence can distinguish at least two programs.
Definition 4
(Consistency). A set of observations \(\mathfrak {P}\) is consistent if there exists at least one observation \(P_0\in \mathfrak {P}\) such that:
-
1.
\(P_0\not =\textit{Trees}_\varSigma \) and
-
2.
there exists at least one computation \(t_0\) such that
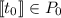 .
.
Definition 5
(Scott-openness). A set of trees X is Scott-open if:
-
1.
It is upwards closed, that is: \(tr\in X\) and \(tr\le tr'\) imply \(tr'\in X\).
-
2.
Whenever \(tr_1\le tr_2\le \ldots \) is an ascending chain with least upper bound \(\bigsqcup tr_i \in X\), then \(tr_j\in X\) for some j.
Definition 6
(Decomposability). The set of observations \(\mathfrak {P}\) is decomposable if for any \(P\in \mathfrak {P}\), and for any \(tr\in P\):

Theorem 1
(Soundness and Completeness of \(\mathcal {F}\)). For a decomposable set of Scott-open observations \(\mathfrak {P}\) that is consistent, the open extension of \(\mathcal {F}\)-logical equivalence coincides with contextual equivalence:  .
.
The proof of this theorem is outlined in Sect. 4. It is easy to see that for all running examples of effects the set \(\mathfrak {P}\) is consistent. The proof that each \(P\in \mathfrak {P}\) is Scott-open is similar to that for modalities from [38]. It remains to show that for all our examples \(\mathfrak {P}\) is decomposable. Intuitively, decomposability can be understood as saying that logical equivalence is a congruence for the effect context \(\varSigma \).
Example 12
(Pure functional computation). The only observation is \({\Downarrow }=\{\downarrow \}\). There are no trees in \(\Downarrow \) whose root has children, so decomposability is satisfied.
Example 13
(Nondeterminism). Consider \(tr\in \Diamond \). Either \(tr= {\downarrow }\), in which case we are done, or \(tr=or(tr'_0,tr'_1)\). It must be the case that either \(tr'_0\) or \(tr'_1\) have a \(\downarrow \)-leaf. Without loss of generality, assume this is the case for \(tr'_0\). Then we know \(tr'_0\in \Diamond \) so we can choose \(P'_0=\Diamond ,P'_1=\textit{Trees}_\varSigma \). For any \(\overrightarrow{p'}\in \overrightarrow{P'}\) we know \(or(\overrightarrow{p'})\in \Diamond \) because \(p'_0\) has a \(\downarrow \)-leaf, so decomposability holds. The argument for \(tr\in \Box \) is analogous: \(P_0'=P_1'=\Box \).
Example 14
(Probabilistic choice). Consider \(tr=p\text {-}or(tr'_0,tr'_1) \in \mathbf {P}_{> q}\). Choose: \(q_0 = \frac{\mathbb {P}(tr'_0)}{\mathbb {P}(tr'_0)+\mathbb {P}(tr'_1)}\cdot 2q\) and \(q_1 = \frac{\mathbb {P}(tr'_1)}{\mathbb {P}(tr'_0)+\mathbb {P}(tr'_1)}\cdot 2q\). From \(\mathbb {P}(tr)= \frac{1}{2}(\mathbb {P}(tr'_0) + \mathbb {P}(tr'_1)) > q\) we can deduce that: \(1\ge \mathbb {P}(tr'_0) >q_0\) and \(1\ge \mathbb {P}(tr'_1) >q_1\). So we can choose \(P'_0=\mathbf {P}_{>q_0},P'_1=\mathbf {P}_{>q_1}\) to satisfy decomposability.
Example 15
(Global store). Consider a tree  . If \(\sigma =lookup_{l}\), then we know \(tr'_{S(l)}\in [S{\downarrow }]\). In the definition of decomposability, choose \(P'_{S(l)}=[S{\downarrow }]\) and \(P'_{k\not =S(l)}=\textit{Trees}_\varSigma \) and we are done. If \(\sigma _{\overrightarrow{v}}=update_{l,\overline{n}}\), then
. If \(\sigma =lookup_{l}\), then we know \(tr'_{S(l)}\in [S{\downarrow }]\). In the definition of decomposability, choose \(P'_{S(l)}=[S{\downarrow }]\) and \(P'_{k\not =S(l)}=\textit{Trees}_\varSigma \) and we are done. If \(\sigma _{\overrightarrow{v}}=update_{l,\overline{n}}\), then  . Choose
. Choose  .
.
Example 16
(Interactive input/output). Consider an I/O trace \(W\not =\epsilon \) and a tree \({tr=\sigma _{\overrightarrow{v}}(tr'_0,tr'_1,tr'_2,\ldots ) \in \langle W\rangle _{\ldots }}\). If \(\sigma =input\), it must be the case that \(W=(?k)W'\) and \(tr'_k\in \langle W'\rangle _{\ldots }\). We can choose \(P'_k=\langle W'\rangle _{\ldots }\) and \(P'_{m\not =k}=\langle \epsilon \rangle _{\ldots }\) and we are done. If \(\sigma _{\overrightarrow{v}}=output_{\overline{n}}\), then \(W=(!n)W'\) and \(tr'_0\in \langle W'\rangle _{\ldots }\). Choose \(P'_0=\langle W'\rangle _{\ldots }\) and we are done. The proof for \(\langle W \rangle {\downarrow }\) is analogous.
4 Soundness and Completeness of the Logic \(\mathcal {F}\)
This section outlines the proof of Theorem 1, which says that \(\mathcal {F}\)-logical equivalence coincides with contextual equivalence. The full proof can be found in [21]. First, we define applicative bisimilarity for ECPS, similarly to the way Simpson and Voorneveld [38] define it for PCF with algebraic effects. Then, we prove in turn that \(\mathcal {F}\)-logical equivalence coincides with applicative bisimilarity, and that applicative bisimilarity coincides with contextual equivalence. Thus, three notions of program equivalence for ECPS are in fact the same.
Definition 7
(Applicative \(\mathfrak {P}\)-bisimilarity). A collection of relations \(\mathcal {R}_A^\mathfrak {v}\subseteq (\vdash _\varSigma A)^2\) for each type A and \(\mathcal {R}^\mathfrak {c}\subseteq (\vdash _\varSigma )^2\) is an applicative \(\mathfrak {P}\)-simulation if:
-
1.
\(v \mathrel {\mathcal {R}^\mathfrak {v}_{\mathtt {nat}}} w \implies v=w\).
-
2.
 .
. -
3.
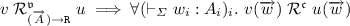 .
.
An applicative \(\mathfrak {P}\)-bisimulation is a symmetric simulation. Bisimilarity, denoted by \(\sim \), is the union of all bisimulations. Therefore, it is the greatest applicative \(\mathfrak {P}\)-bisimulation.
Notice that applicative bisimilarity uses the set of observations \(\mathfrak {P}\) to relate computations, just as contextual and logical equivalence do. It is easy to show that bisimilarity is an equivalence relation.
Proposition 2
Given a decomposable set of Scott-open observations \(\mathfrak {P}\), the open extension of applicative \(\mathfrak {P}\)-bisimilarity, \(\sim ^\circ \), is compatible.
Proof
(notes). This is proved using Howe’s method [14], following the structure of the corresponding proof from [38]. Scott-openness is used to show that the observations P interact well with the sequence of trees  associated with each computation. For details see [21, §5.4]. \(\square \)
associated with each computation. For details see [21, §5.4]. \(\square \)
Proposition 3
Given a decomposable set of Scott-open observations \(\mathfrak {P}\), applicative \(\mathfrak {P}\)-bisimilarity \(\sim \) coincides with \(\mathcal {F}\)-logical equivalence \(\equiv _{\mathcal {F}}\). Hence, the open extension of \(\mathcal {F}\)-logical equivalence \(\equiv _{\mathcal {F}}^\circ \) is compatible.
Proof
(sketch). We define a new logic \(\mathcal {V}\) which is almost the same as \(\mathcal {F}\) except that the \(\textsc {(val)}\) rule is replaced by:

That is, formulas of function type are now constructed using ECPS values. It is relatively straightforward to show that \(\mathcal {V}\)-logical equivalence coincides with applicative \(\mathfrak {P}\)-bisimilarity [21, Prop. 6.3.1]. However, we do not know of a similar direct proof for the logic \(\mathcal {F}\). From Proposition 2, we deduce that \(\mathcal {V}\)-logical equivalence is compatible.
Next, we prove that the logics \(\mathcal {F}\) and \(\mathcal {V}\) are in fact equi-expressive, so they induce the same relation of logical equivalence on ECPS programs [21, Prop. 6.3.4]. Define a translation of formulas from \(\mathcal {F}\) to \(\mathcal {V}\), \((-)^\flat \), and one from \(\mathcal {V}\) to \(\mathcal {F}\), \((-)^\sharp \). The most interesting cases are those for formulas of function type:

where \(\chi _{w_i}\) is the characteristic formula of \(w_i\), that is \(\chi _{w_i}=\bigwedge {\{\phi \mid w_i\,\models _{\mathcal {F}}\,\phi \}}\). Equi-expressivity means that the satisfaction relation remains unchanged under both translations, for example \(v\,\models _\mathcal {V}\,\phi \Longleftrightarrow v\,\models _\mathcal {F}\,\phi ^\sharp \). Most importantly, the proof of equi-expressivity makes use of compatibility of \(\equiv _\mathcal {V}\), which we established previously. For a full proof see [21, Prop. 6.2.3]). \(\square \)
Finally, to prove Theorem 1 we show that applicative \(\mathfrak {P}\)-bisimilarity coincides with contextual equivalence [21, Prop. 7.2.2]:
Proposition 4
Consider a decomposable set \(\mathfrak {P}\) of Scott-open observations that is consistent. The open extension of applicative \(\mathfrak {P}\)-bisimilarity \(\sim ^\circ \) coincides with contextual equivalence  .
.
Proof
(sketch). Prove  in two stages: first we show it holds for closed terms by showing
in two stages: first we show it holds for closed terms by showing  for them is a bisimulation; we make use of consistency of \(\mathfrak {P}\) in the case of natural numbers. Then we extend to open terms using compatibility of
for them is a bisimulation; we make use of consistency of \(\mathfrak {P}\) in the case of natural numbers. Then we extend to open terms using compatibility of  . The opposite inclusion follows immediately by compatibility and adequacy of \(\sim ^\circ \). \(\square \)
. The opposite inclusion follows immediately by compatibility and adequacy of \(\sim ^\circ \). \(\square \)
5 Related Work
The work closest to ours is that by Simpson and Voorneveld [38]. In the context of a direct-style language with algebraic effects, EPCF, they propose a modal logic which characterizes applicative bisimilarity but not contextual equivalence. Consider the following example from [19] (we use simplified EPCF syntax):

where \(\mathtt {?nat}\) is a computation, defined using or, which returns a natural number nondeterministically. Term M satisfies the formula \(\varPhi =\Diamond (true\mapsto \wedge _{n\in \mathbb {N}}\Diamond \{n\})\) in the logic of [38], which says that M may return a function which in turn may return any natural number. However, N does not satisfy \(\varPhi \) because it always returns a bounded number generator G. The bound on G is arbitrarily high so M and N are contextually equivalent, since a context can only test a finite number of outcomes of G.
EPCF can be translated into ECPS via a continuation-passing translation that preserves the shape of computation trees. The translation maps a value \({\varGamma \vdash V:\tau }\) to a value \({\varGamma ^*\vdash V^*:\tau ^*}\). An EPCF computation \({\varGamma \vdash M:\tau }\) becomes an ECPS value  , which intuitively is waiting for a continuation k to pass its return result to (see [21, §4]). As an example, consider the cases for functions and application, where k stands for a continuation:
, which intuitively is waiting for a continuation k to pass its return result to (see [21, §4]). As an example, consider the cases for functions and application, where k stands for a continuation:

This translation suggests that ECPS functions of type  can be regarded as continuations that never return. In EPCF the CPS-style algebraic operations can be replaced by direct-style generic effects [34], e.g. \( input (): \mathtt {nat}\).
can be regarded as continuations that never return. In EPCF the CPS-style algebraic operations can be replaced by direct-style generic effects [34], e.g. \( input (): \mathtt {nat}\).
One way to understand this CPS translation is that it arises from the fact that  is a monad on the multicategory of values (in a suitable sense, e.g. [40]), which means that we can use the standard monadic interpretation of a call-by-value language. As usual, the algebraic structure on the return type \(\mathtt {R}\) induces an algebraic structure on the entire monad (see e.g. [16, 24, §8]). We have not taken a denotational perspective in this paper, but for the reader with this perspective, a first step is to note that the quotient set \(Q{\mathop {=}\limits ^{\mathrm {def}}} (\textit{Trees}_\varSigma )/_{\equiv _{\mathfrak P}}\) is a \(\varSigma \)-algebra, where \(( tr \equiv _{\mathfrak P} tr' )\) if \(\forall P\in \mathfrak P\), \(( tr \in P\iff tr' \in P)\); decomposability implies that \((\equiv _{\mathfrak P})\) is a \(\varSigma \)-congruence. This thus induces a CPS monad \(Q^{(Q^{-})}\) on the category of cpos.
is a monad on the multicategory of values (in a suitable sense, e.g. [40]), which means that we can use the standard monadic interpretation of a call-by-value language. As usual, the algebraic structure on the return type \(\mathtt {R}\) induces an algebraic structure on the entire monad (see e.g. [16, 24, §8]). We have not taken a denotational perspective in this paper, but for the reader with this perspective, a first step is to note that the quotient set \(Q{\mathop {=}\limits ^{\mathrm {def}}} (\textit{Trees}_\varSigma )/_{\equiv _{\mathfrak P}}\) is a \(\varSigma \)-algebra, where \(( tr \equiv _{\mathfrak P} tr' )\) if \(\forall P\in \mathfrak P\), \(( tr \in P\iff tr' \in P)\); decomposability implies that \((\equiv _{\mathfrak P})\) is a \(\varSigma \)-congruence. This thus induces a CPS monad \(Q^{(Q^{-})}\) on the category of cpos.
Note that the terms in (1) above are an example of programs that are not bisimilar in EPCF but become bisimilar when translated to ECPS. This is because in ECPS bisimilarity, like contextual and logical equivalence, uses continuations to test return results. Therefore, in ECPS we cannot test for all natural numbers, like formula \(\varPhi \) does. This example provides an intuition of why we were able to show that all three notions of equivalence coincide, while [38] was not.
The modalities in Simpson’s and Voorneveld’s logic are similar to the observations from \(\mathfrak {P}\), because they also specify shapes of effect trees. Since EPCF computations have a return value, a modality is used to lift a formula about the return values to a computation formula. In contrast, in the logic \(\mathcal {F}\) observations alone suffice to specify properties of computations. From this point of view, our use of observations is closer to that found in the work of Johann et al. [17]. This use of observations also leads to a much simpler notion of decomposability (Definition 6) than that found in [38].
It can easily be shown that for the running examples of effects, \(\mathcal {F}\)-logical equivalence induces the program equations which are usually used to axiomatize algebraic effects, for example the equations for global store from [33]. Thus our choice of observations is justified further.
A different logic for algebraic effects was proposed by Plotkin and Pretnar [35]. It has a modality for each effect operation, whereas observations in \(\mathfrak {P}\) are determined by the behaviour of effects, rather than by the syntax of their operations. Plotkin and Pretnar prove that their logic is sound for establishing several notions of program equivalence, but not complete in general. Refinement types are yet another approach to specifying the behaviour of algebraic effects, (e.g. [3]). Several monadic-based logics for computational effects have been proposed, such as [10, 29], although without the focus on contextual equivalence.
A logic describing a higher-order language with local store is the Hoare logic of Yoshida, Honda and Berger [42]. Hoare logic has also been integrated into a type system for a higher-order functional language with dependent types, in the form of Hoare type theory [27]. Although we do not yet know how to deal with local state or dependent types in the logic \(\mathcal {F}\), an advantage of our logic over the previous two is that we describe different algebraic effects in a uniform manner.
Another aspect worth noticing is that some (non-trivial) \(\mathcal {F}\)-formulas are not inhabited by any program. For example, there is no function  satisfying: \(\psi = (()\mapsto \langle !0\rangle _{\ldots })\mapsto \langle !1\rangle _{\ldots } \ \wedge \ (()\mapsto \langle !1 \rangle _{\ldots })\mapsto \langle !0\rangle _{\ldots }.\)
satisfying: \(\psi = (()\mapsto \langle !0\rangle _{\ldots })\mapsto \langle !1\rangle _{\ldots } \ \wedge \ (()\mapsto \langle !1 \rangle _{\ldots })\mapsto \langle !0\rangle _{\ldots }.\)
Formula \(\psi \) says that, if the first operation of a continuation is \(output(\overline{0})\), this is replaced by \(output(\overline{1})\) and vice-versa. But in ECPS, one cannot check whether an argument outputs something without also causing the output observation, and so the formula is never satisfied.
However, \(\psi \) could be inhabited if we extended ECPS to allow \(\lambda \)-abstraction over the symbols in the effect context \(\varSigma \), and allowed such symbols to be captured during substitution (dynamic scoping). Consider the following example in an imaginary extended ECPS where we abstract over output:

The idea is that during reduction of \((v\ f)\), the output operations in f are captured by \(\lambda output\). Thus, \(output(\overline{0})\) operations from \((f\ ())\) are replaced by \(output(\overline{1})\) and vice-versa, and all other writes are skipped; so in particular \(v\,\models _\mathcal {F}\,\psi \). This behaviour is similar to that of effect handlers [36]: computation \((f\ ())\) is being handled by handler h. We leave for future work the study of handlers in ECPS and of their corresponding logic.
6 Concluding Remarks
To summarize, we have studied program equivalence for a higher-order CPS language with general algebraic effects and general recursion (Sect. 2). Our main contribution is a logic \(\mathcal {F}\) of program properties (Sect. 3) whose induced program equivalence coincides with contextual equivalence (Theorem 1; Sect. 4). Previous work on algebraic effects concentrated on logics that are sound for contextual equivalence, but not complete [35, 38]. Moreover, \(\mathcal {F}\)-logical equivalence also coincides with applicative bisimilarity for our language. We exemplified our results for nondeterminism, probabilistic choice, global store and I/O. A next step would be to consider local effects (e.g. [22, 33, 37, 39]) or normal form bisimulation (e.g. [6]).
References
Abramsky, S.: The lazy \(\lambda \)-calculus. In: Turner, D. (ed.) Research Topics in Functional Programming. Chapter 4, pp. 65–117. Addison Wesley, Boston (1990)
Abramsky, S., Jung, A.: Domain theory. In: Abramsky, S., Gabbay, D.M., Maibaum, T.S.E. (eds.) Handbook of Logic in Computer Science, Chap. 1, vol. 3, pp. 1–168. Oxford University Press, Oxford (1994)
Ahman, D., Plotkin, G.: Refinement types for algebraic effects. In: TYPES (2015)
Biernacki, D., Lenglet, S.: Applicative bisimulations for delimited-control operators. In: Birkedal, L. (ed.) FoSSaCS 2012. LNCS, vol. 7213, pp. 119–134. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28729-9_8
Cartwright, R., Curien, P., Felleisen, M.: Fully abstract semantics for observably sequential languages. Inf. Comput. 111(2), 297–401 (1994)
Dal Lago, U., Gavazzo, F.: Effectful normal form bisimulation. In: Proceedings of ESOP 2019 (2019)
Dal Lago, U., Gavazzo, F., Levy, P.: Effectful applicative bisimilarity: monads, relators, and Howe’s method. In: LICS (2017)
Dal Lago, U., Gavazzo, F., Tanaka, R.: Effectful applicative similarity for call-by-name lambda calculi. In: ICTCS/CILC (2017)
Freyd, P.: Algebraically complete categories. In: Carboni, A., Pedicchio, M.C., Rosolini, G. (eds.) Category Theory. LNM, vol. 1488, pp. 95–104. Springer, Heidelberg (1991). https://doi.org/10.1007/BFb0084215
Goncharov, S., Schröder, L.: A relatively complete generic Hoare logic for order-enriched effects. In: LICS (2013)
Gordon, A.: Operational equivalences for untyped and polymorphic object calculi. In: Gordon, A., Pitts, A. (eds.) Higher Order Operational Techniques in Semantics, pp. 9–54. Cambridge University Press, Cambridge (1998)
Hennessy, M., Milner, R.: Algebraic laws for nondeterminism and concurrency. J. ACM 32(1), 137–161 (1985)
Hoare, C.: An axiomatic basis for computer programming. Commun. ACM 12(10), 576–580 (1969)
Howe, D.: Proving congruence of bisimulation in functional programming languages. Inf. Comput. 124(2), 103–112 (1996)
Hur, C.K., Neis, G., Dreyer, D., Vafeiadis, V.: A logical step forward in parametric bisimulations. Technical report MPI-SWS-2014-003, January 2014
Hyland, M., Levy, P.B., Plotkin, G., Power, J.: Combining algebraic effects with continuations. Theoret. Comput. Sci. 375, 20–40 (2007)
Johann, P., Simpson, A., Voigtländer, J.: A generic operational metatheory for algebraic effects. In: LICS (2010)
Lafont, Y., Reus, B., Streicher, T.: Continuations semantics or expressing implication by negation. Technical report 9321, Ludwig-Maximilians-Universität, München (1993)
Lassen, S.: Relational reasoning about functions and nondeterminism. Ph.D. thesis, University of Aarhus, BRICS, December 1998
Lassen, S.B., Levy, P.B.: Typed normal form bisimulation. In: Duparc, J., Henzinger, T.A. (eds.) CSL 2007. LNCS, vol. 4646, pp. 283–297. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74915-8_23
Matache, C.: Program equivalence for algebraic effects via modalities. Master’s thesis, University of Oxford, September 2018. https://arxiv.org/abs/1902.04645
Melliès, P.-A.: Local states in string diagrams. In: Dowek, G. (ed.) RTA 2014. LNCS, vol. 8560, pp. 334–348. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08918-8_23
Merro, M.: On the observational theory of the CPS-calculus. Acta Inf. 47(2), 111–132 (2010)
Møgelberg, R.E., Staton, S.: Linear usage of state. Log. Meth. Comput. Sci. 10 (2014)
Moggi, E.: Notions of computation and monads. Inf. Comput. 93(1), 55–92 (1991)
Morris, J.: Lambda calculus models of programming languages. Ph.D. thesis, MIT (1969)
Nanevski, A., Morrisett, J., Birkedal, L.: Hoare type theory, polymorphism and separation. J. Funct. Program. 18(5–6), 865–911 (2008)
O’Hearn, P., Reynolds, J., Yang, H.: Local reasoning about programs that alter data structures. In: Fribourg, L. (ed.) CSL 2001. LNCS, vol. 2142, pp. 1–19. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44802-0_1
Pitts, A.: Evaluation logic. In: Birtwistle, G. (ed.) IVth Higher Order Workshop, Banff 1990. Springer, Heidelberg (1991). https://doi.org/10.1007/978-1-4471-3182-3_11
Pitts, A.: Howe’s method for higher-order languages. In: Sangiorgi, D., Rutten, J. (eds.) Advanced Topics in Bisimulation and Coinduction. Chapter 5, pp. 197–232. Cambridge University Press, Cambridge (2011)
Plotkin, G.: LCF considered as a programming language. Theor. Comput. Sci. 5(3), 223–255 (1977)
Plotkin, G., Power, J.: Adequacy for algebraic effects. In: Honsell, F., Miculan, M. (eds.) FoSSaCS 2001. LNCS, vol. 2030, pp. 1–24. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45315-6_1
Plotkin, G., Power, J.: Notions of computation determine monads. In: Nielsen, M., Engberg, U. (eds.) FoSSaCS 2002. LNCS, vol. 2303, pp. 342–356. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45931-6_24
Plotkin, G., Power, J.: Algebraic operations and generic effects. Appl. Categ. Struct. 11(1), 69–94 (2003)
Plotkin, G., Pretnar, M.: A logic for algebraic effects. In: LICS (2008)
Plotkin, G., Pretnar, M.: Handling Algebraic Effects. Log. Methods Comput. Sci. 9(4) (2013)
Power, J.: Indexed Lawvere theories for local state. In: Models, Logics and Higher-Dimensional Categories, pp. 268–282. AMS (2011)
Simpson, A., Voorneveld, N.: Behavioural equivalence via modalities for algebraic effects. In: Ahmed, A. (ed.) ESOP 2018. LNCS, vol. 10801, pp. 300–326. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89884-1_11
Staton, S.: Instances of computational effects. In: Proceedings of LICS 2013 (2013)
Staton, S., Levy, P.B.: Universal properties for impure programming languages. In: Proceedings of POPL 2013 (2013)
Yachi, T., Sumii, E.: A sound and complete bisimulation for contextual equivalence in \(\lambda \)-calculus with call/cc. In: Igarashi, A. (ed.) APLAS 2016. LNCS, vol. 10017, pp. 171–186. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-319-47958-3_10
Yoshida, N., Honda, K., Berger, M.: Logical reasoning for higher-order functions with local state. Log. Methods Comput. Sci. 4(4) (2008)
Acknowledgements
This research was supported by an EPSRC studentship, a Balliol College Jowett scholarship, and the Royal Society. We would like to thank Niels Voorneveld for pointing out example (1), Alex Simpson and Ohad Kammar for useful discussions, and the anonymous reviewers for comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Matache, C., Staton, S. (2019). A Sound and Complete Logic for Algebraic Effects. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_22
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)





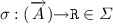 and
and 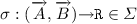 and each
and each 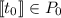 .
. .
.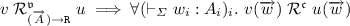 .
.