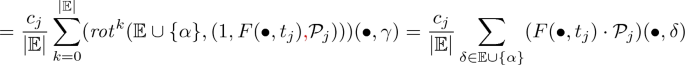Abstract
Unordered data Petri nets (UDPN) are an extension of classical Petri nets with tokens that carry data from an infinite domain and where transitions may check equality and disequality of tokens. UDPN are well-structured, so the coverability and termination problems are decidable, but with higher complexity than for Petri nets. On the other hand, the problem of reachability for UDPN is surprisingly complex, and its decidability status remains open. In this paper, we consider the continuous reachability problem for UDPN, which can be seen as an over-approximation of the reachability problem. Our main result is a characterization of continuous reachability for UDPN and polynomial time algorithm for solving it. This is a consequence of a combinatorial argument, which shows that if continuous reachability holds then there exists a run using only polynomially many data values.
Supported by Polish NCN grant UMO-2016/21/D/ST6/01368, DST Inspire faculty award IFA12-MA-17, and DST/CEFIPRA project EQuaVe.
U. Gupta and P. Shah—Contributed equally to this work.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The theory of Petri nets has been developing since more than 50 years. On one hand, from a theory perspective, Petri nets are interesting due to their deep mathematical structure and despite exhibiting nice properties, like being a well structured transition system [1], we still don’t understand them well. On the other hand, Petri nets are a useful pictorial formalism for modeling and thus found their way to the industry. To connect this theory and practice, it would be desirable to use the developed theory of Petri nets [2,3,4] for the symbolic analysis and verification of Petri nets models. However, we already know that this is difficult in its full generality. It suffices to recall two results that were proved more than 30 years apart. An old but classical result by Lipton [5] shows that even coverability is ExpSpace-hard, while the non-elementary hardness of the reachability relation has just been established this year [6]. Moreover, when we look at Petri nets based formalisms that are needed to model various aspects of industrial systems, we see that they go beyond the expressivity of Petri nets. For instance, colored Petri nets, which are used in modeling workflows [7], allow the tokens to be colored with an infinite set of colors, and introduce a complex formalism to describe dependencies between colors. This makes all verification problems undecidable for this generic model. Given the basic nature and importance of the reachability problem in Petri nets (and its extensions), there have been several efforts to sidestep the complexity-theoretic hardness results. One common approach is to look for easy subclasses (such as bounded nets [8], free-choice nets [9] etc.). The other approach, which we adopt in this work, is to compute over-approximations of the reachability relation.
Continuous Reachability. A natural question regarding the dynamics of a Petri net is to ask what would happen if tokens instead of behaving like discrete units start to behave like a continuous fluid? This simple question led to an elegant theory of so-called continuous Petri nets [10,11,12]. Petri nets with continuous semantics allow markings to be functions from places to nonnegative rational numbers (i.e., in \(\mathbb {Q}^+\)) instead of natural numbers. Moreover, whenever a transition is fired a positive rational coefficient is chosen and both the number of consumed and produced tokens are multiplied with the coefficient. This allows to split tokens into arbitrarily small parts and process them independently. This may occur, e.g., in applications related to hybrid systems where the discrete part is used to control the continuous system [13, 14]. Interestingly, this makes things simpler to analyze. For example reachability under the continuous semantics for Petri nets is \(PTime\)-complete [11]. However, when one wants to analyze extensions of Petri nets, e.g., reset Petri nets with continuous semantics, it turns out that reachability is as hard as reachability in reset Petri nets under the usual semantics i.e. it is undecidableFootnote 1. In this paper we identify an extension of Petri nets with unordered data, for which this is not the case and continuous semantics leads to a substantial reduction in the complexity of the reachability problem.
Unordered Data Petri Nets. The possibility of equipping tokens with some additional information is one of the main lines of research regarding extensions of Petri nets, the best known being Colored Petri nets [15] and various types of timed Petri nets [16, 17]. In [18] authors equipped tokens with data and restricted interactions between data in a way that allow to transfer techniques for well structured transition systems. They identified various classes of nets exhibiting interesting combinatorial properties which led to a number of results [19,20,21,22,23]. Unordered Data Petri Nets (UDPN), are simplest among them: every token carries a single datum like a barcode and transitions may check equality or disequality of data in consumed and produced tokens. UDPN are the only class identified in [18] for which the reachability is still unsolved, although in [20] authors show that the problem is at least Ackermannian-hard (for all other data extensions, reachability is undecidable). A recent attempt to over-approximate the reachability relation for UDPN in [22] considers integer reachability i.e. number of tokens may get negative during the run (also called solution of the state equation). From the above perspective, this paper is an extension of the mentioned line of research.
Our Contribution. Our main contribution is a characterization of continuous reachability in UDPN and a polynomial time algorithm for solving it. Observe that if we find an upper bound on the minimal number of data required by a run between two configurations (if any run exists), then we can reduce continuous reachability in UDPN to continuous reachability in vanilla Petri nets with an exponential blowup and use the already developed characterization from [11]. In Sect. 5 we prove such a bound on the minimal number of required data. The bound is novel and exploits techniques that did not appear previously in the context of data nets. Further, the obtained bounds are lower than bounds on the number of data values required to solve the state equation [22], which is surprising considering that existence of a continuous run requires a solution of a sort of state equation. Precisely, the difference is that we are looking for solutions of the state equation over \(\mathbb {Q}^+\) instead of \(\mathbb {N}\) and in this case we prove better bounds for the number of data required. This also gives us an easy polytime algorithm for finding \(\mathbb {Q}^+\)-solutions of state equations of UDPN (we remark that for Petri nets without data, this appears among standard algebraic techniques [24]).
Finally, with the above bound, we solve continuous reachability in UDPN by adapting the techniques from the non-data setting of [12, 25]. We adapt the characterization of continuous reachability to the data setting and next encode it as system of linear equations with implications. In doing so, however, we face the problem that a naive encoding (representing data explicitly) gives a system of equations of exponential size, giving only an ExpTime-algorithm. To improve the complexity, we use histograms, a combinatorial tool developed in [22], to compress the description of solutions of state equations in UDPNs. However, this may lead to spurious solutions for continuous reachability. To eliminate them, we show that it suffices to first transform the net and then apply the idea of histograms to characterize continuous runs in the modified net. The whole procedure is described in Sect. 7.3 and leads us to our \(PTime\) algorithm for continuous reachability in UDPN. Note that since we easily have \(PTime\) hardness for the problem (even without data), we obtain that the problem of continuous reachability in UDPN is \(PTime\)-complete.
Towards Verification. Over-approximations are useful in verification of Petri nets and their extensions: as explained in [24], for many practical problems, over-approximate solutions are already correct. Further, we can use them as a sub-routine to improve the practical performance of verification algorithms. A remarkable example is the recent work in [25], where the \(PTime\) continuous reachability algorithm for Petri nets from [11] is used as a subroutine to solve the \(ExpSpace\) hard coverability problem in Petri nets, outperforming the best known tools for this problem, such as Petrinizer [26]. Our results can be seen as a first step in the same spirit towards handling practical instances of coverability, but for the extended model of UDPN, where the coverability problem for UDPN is known to be Ackermannian-hard [20].
Omitted proofs and details can be found in the extended version at [27].
2 Preliminaries
We denote integers, non-negative integers, rationals, and reals as \(\mathbb {Z},\mathbb {N},\mathbb {Q},\) and \(\mathbb {R}\), respectively. For a set \(\mathbb {X}\subseteq \mathbb {R}\) denote by \(\mathbb {X}^{+}\), the set of all non-negative elements of \(\mathbb {X}\). We denote by 0, a vector whose entries are all zero. We define in a standard point-wise way operations on vectors i.e. scalar multiplication \(\cdot \), addition \(+\), subtraction −, and vector comparison \(\le \). In this paper, we use functions of the type \(X\rightarrow (Y\rightarrow Z)\), and instead of (f(x))(y), we write f(y, x). For functions f, g where the range of g is a subset of the domain of f, we denote their composition by \(f \circ g\). If \(\pi \) is an injection then by \(\pi ^{-1}\) we mean a partial function such that \(\pi ^{-1}\circ \pi \) is the identity function. Let \(f : X_1 \rightarrow Y\), \(g: X_2 \rightarrow Y\) be two functions with addition and scalar multiplication operations defined on Y. A scalar multiplication of a function is defined as follows \((a\cdot f)(x)=a\cdot f(x)\) for all \(x\in X_1.\) We lift addition operation to functions pointwise, i.e. \(f + g : X_1\cup X_2 \rightarrow Y\) such that

Similarly for subtraction \((f-g)(x) = f(x)+-1\cdot g(x)\), and \(f\le g\) if for all \(x\in X_1\cup X_2, (g-f)(x)\le 0.\)
We use matrices with rows and columns indexed by sets \(\mathbb {S}_1,\mathbb {S}_2\), possibly infinite. For a matrix M, let M(r, c) denote the entry at column c and row r, and \(M(r,\bullet )\), \(M(\bullet ,c)\) denote the row vector indexed by r and column vector indexed by c, respectively. Denote by \( col (M)\), \( row (M)\) the set of indices of nonzero columns and nonzero rows of the matrix M, respectively. Even if we have infinitely many rows or columns, our matrices will have only finitely many nonzero rows and columns, and only this nonzero part will be represented. Following our nonstandard matrix definition we precisely define operations on them, although they are natural. First, a multiplication by a constant number produces a new matrix with row and columns labelled with the same sets \(\mathbb {S}_1, \mathbb {S}_2\) and defined as follows \((a\cdot M)(r,c)=a\cdot (M(r,c))\) for all \((r,c)\in \mathbb {S}_1\times \mathbb {S}_2\). Addition of two matrices is only defined if the sets indexing rows \(\mathbb {S}_1\) and columns \(\mathbb {S}_2\) are the same for both summands \(M_1\) and \(M_2\), \(\forall (r,c)\in \mathbb {S}_1\times \mathbb {S}_2\) the sum \((M_1+M_2)(r,c)=M_1(r,c)+M_2(r,c)\), the subtraction \(M_1-M_2\) is a shorthand for \(M_1+ (-1)\cdot M_2\). Observe that all but finitely many entries in matrices are 0, and therefore when we do computation on matrices we can restrict to rows \( row (M_1)\cup row (M_2)\) and columns \( col (M_1)\cup col (M_2)\). Similarly the comparison for two matrices \(M_1,M_2\) is defined as follows \(M_1 \le M_2\) if \(\forall (r,c)\in ( row (M_1)\cup row (M_2))\times ( col (M_1)\cup col (M_2)) ~ M_1(r,c) \le M_2(r,c)\); relations \(>,\ge ,\le \) are defined analogically. The last operation which we need is matrix multiplication \(M_1\cdot M_2=M_3\), it is only allowed if the set of columns of the first matrix \(M_1\) is the same as the set of rows of the second matrix \(M_2\), the sets of rows and columns of the resulting matrix \(M_3\) are rows of the matrix \(M_1\) and columns of \(M_2\), respectively. \(M_3(r,c)=\sum _{k}M_1(r,k)M_2(k,c)\) where k runs through columns of \(M_1.\) Again, observe that if the row or a column is equal to 0 for all entries then the effect of multiplication is 0, thus we may restrict to \( row (M_1)\) and \( col (M_2)\). Moreover in the sum it suffices to write \(\sum _{k\in col (M_1)}M_1(r,k)M_2(k,c).\)
3 UDPN, Reachability and Its Variants: Our Main Results
Unordered data Petri nets extend the classical model of Petri nets by allowing each token to hold a data value from a countably-infinite domain \(\mathbb {D}\). Our definition is closest to the definition of \(\nu \)-Petri nets from [28]. For simplicity we choose this one instead of using the equivalent but complex one from [18].
Definition 1
Let \(\mathbb {D}\) be a countably infinite set. An unordered data Petri net (UDPN) over domain \(\mathbb {D}\) is a tuple \((P,T,F, Var )\) where P is a finite set of places, T is a finite set of transitions, \( Var \) is a finite set of variables, and \(F:(P \times T) \cup (T \times P) \rightarrow ( Var \rightarrow \mathbb {N})\) is a flow function that assigns each place \(p \in P\) and transition \(t \in T\) a function over variables in Var.
For each transition \(t \in T\) we define functions \(F(\bullet ,t)\) and \(F(t,\bullet )\), \( Var \rightarrow (P \rightarrow \mathbb {N})\) as \(F(\bullet ,t)(p,x) = F(p,t)(x)\) and analogously \(F(t,\bullet )(p,x) = F(t,p)(x)\). Displacement of the transition t is a function \(\varDelta (t): Var \rightarrow (P \rightarrow \mathbb {Z})\) defined as \(\varDelta (t) \overset{\mathrm {def}}{=} F(t,\bullet )- F(\bullet ,t)\).
For \(\mathbb {X}\in \{\mathbb {N}, \mathbb {Z},\mathbb {Q},\mathbb {Q}^+\}\), we define an \(\mathbb {X}\)-marking as a function \(M: \mathbb {D}\rightarrow (P \rightarrow \mathbb {X})\) that is constant 0 on all except finitely many values of \(\mathbb {D}\). Intuitively, \(M(p, \alpha )\) denotes the number of tokens with the data value \(\alpha \) at place p. The fact that it is 0 at all but finitely many data means that the number of tokens in any \(\mathbb {X}\)-marking is finite. We denote the infinite set of all \(\mathbb {X}\)-markings by \(\mathcal {M}_{\mathbb {X}}\).
We define an \(\mathbb {X}\)-step as a triple \((c,t,\pi )\) for a transition \(t \in T\), mode \(\pi \) being an injective map \(\pi : Var \rightarrow \mathbb {D}\), and a scalar constant \(c \in \mathbb {X}^{+}\). An \(\mathbb {X}\)-step \((c,t,\pi )\) is fireable at a \(\mathbb {X}\)-marking \({{\varvec{{i}}}}\) if \({{\varvec{{i}}}}- c \cdot F(\bullet ,t) \circ \pi ^{-1}\in \mathcal {M}_{\mathbb {X}}.\)
The \(\mathbb {X}\)-marking \({{\varvec{{f}}}}\) reached after firing an \(\mathbb {X}\)-step \((c,t,\pi )\) at \({{\varvec{{i}}}}\) is given as \({{\varvec{{f}}}}= {{\varvec{{i}}}}+ c \cdot \varDelta (t) \circ \pi ^{-1}\). We also say that an \(\mathbb {X}\)-step \((c,t,\pi )\) when fired consumes tokens \(c\cdot F(\bullet ,t)\circ \pi ^{-1}\) and produces tokens \(c\cdot F(t,\bullet )\circ \pi ^{-1}\). We define an \(\mathbb {X}\)-run as a sequence of \(\mathbb {X}\)-steps and we can represent it as \(\{(c_i,t_i,\pi _i)\}_{|\rho |}\) where \((c_i,t_i,\pi _i)\) is the \(i^{th}\) \(\mathbb {X}\)-step and \(|\rho |\) is the number of \(\mathbb {X}\)-steps. A run \(\rho = \{(c_i,t_i,\pi _i)\}_{|\rho |}\) is fireable at a \(\mathbb {X}\)-marking \({{\varvec{{i}}}}\) if, \(\forall 1 \le i \le |\rho |\), the step \((c_i, t_i,\pi _i)\) is fireable at \({{\varvec{{i}}}}+ \sum _{j=1}^{i-1}c_i \varDelta (t_j) \circ \pi _j^{-1}\). By \({{\varvec{{i}}}}\xrightarrow []{\rho }_{\mathbb {X}} {{\varvec{{f}}}}\) we denote that \(\rho \) is fireable at \({{\varvec{{i}}}}\) and after firing \(\rho \) at \({{\varvec{{i}}}}\) we reach \(\mathbb {X}\)-marking \({{\varvec{{f}}}}= {{\varvec{{i}}}}+ \sum _{i=1}^{|\rho |} c_i \cdot \varDelta (t_i)\circ \pi _i^{-1}\). We call (the function computed by) the mentioned sum \(\sum _{i=1}^{|\rho |}c_i\varDelta (t_i)\circ \pi _i^{-1}\) as the effect of the run and denote it by \(\varDelta (\rho )\).
We fix some notations for the rest of the paper. We use Greek letters \(\alpha ,\beta ,\gamma \) to denote data values from data domain \(\mathbb {D}\), \(\rho \), \(\sigma \) to denote a run, \(\pi \) to denote a mode and x, y, z to denote the variables. When clear from the context, we may omit \(\mathbb {X}\) from \(\mathbb {X}\)-marking, \(\mathbb {X}\)-run and just write marking, run, etc. Further, we will use letters in bold, e.g., \({\varvec{{m}}}\) to denote markings, where \({{\varvec{{i}}}},{{\varvec{{f}}}}\) will be used for initial and final markings respectively. Further, throughout the paper, unless stated explicitly otherwise, we will refer to a UDPN \(\mathcal {N} = (P,T,F, Var )\), therefore \(P,T,F, Var \) will denote the places, transitions, flow, and variables of this UDPN.
Example 1
An example of a simple UDPN \(\mathcal {N}_1\) is given in Fig. 1. For this example, we have \(P=\{p_1,p_2,p_3,p_4\}\), \(T=\{t\}\), \(Var=\{x,y,z\}\), and the flow relation is given by \(F(p_1,t)=\{y\mapsto 1\}\), \(F(p_2,t)=\{x\mapsto 1\}\), \(F(t,p_3)=\{y\mapsto 2\}\), \(F(t,p_4)=\{x\mapsto 1,z\mapsto 1\}\), and an assignment of 0 to every variable for the remaining of the pairs. Thus, for enabling transition \(p_1\) and \(p_2\) must have one token each with a different data value (since \(x\ne y\)) and after firing two tokens are produced in \(p_3\) with same data value as was consumed from \(p_1\) and two tokens are produced in \(p_4\), one of whom has same data as consumed from \(p_2\).
Definition 2
Given \(\mathbb {X}\)-markings \({{\varvec{{i}}}},{{\varvec{{f}}}}\), we say \({{\varvec{{f}}}}\) is \(\mathbb {X}\)-reachable from \({{\varvec{{i}}}}\) if there exists an \(\mathbb {X}\)-run \(\rho \) s.t., \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {X}} {{\varvec{{f}}}}\).
When \(\mathbb {X}= \mathbb {N}\), \(\mathbb {X}\)-reachability is the classical reachability problem, whose decidability is still unknown, while \(\mathbb {Z}\)-reachability for UDPN is in NP [22].
In this paper we tackle \(\mathbb {Q}\) and \(\mathbb {Q}^+\)-reachability, also called continuous reachability in UDPN.
The first step towards the solution is showing that if a \(\mathbb {Q}^{+}\)-marking \({{\varvec{{f}}}}\) is \(\mathbb {Q}^{+}\)-reachable from a \(\mathbb {Q}^{+}\)-marking \({{\varvec{{i}}}}\), then there exists a \(\mathbb {Q}^{+}\)-run \(\rho \) which uses polynomially many data values and \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {Q}^{+}} {{\varvec{{f}}}}\). We first formalize the set of distinct data values associated with \(\mathbb {X}\)-markings, data values used in \(\mathbb {X}\)-runs and variables associated with a transition.
Definition 3
For \(\mathcal {N} = (P,T,F, Var )\) a UDPN, \(\mathbb {X}\)-marking \({\varvec{{m}}}\), \(t \in T\), and \(\mathbb {X}\)-run \(\rho = \{(c_i,t_i,\pi _i)\}_{|\rho |}\), we define
-
1.
\( vars (t) = \{ x\in Var \mid ~ \exists p \in P ~: F(p,t)(x) \ne 0 \vee F(t,p)(x) \ne 0\}\).
-
2.
\( dval ({\varvec{{m}}}) = \{ \alpha \in \mathbb {D}\mid ~\exists p \in P : {\varvec{{m}}}(p,\alpha ) \ne 0 \}\).
-
3.
\( dval (\rho ) = \{ \alpha \in \mathbb {D}\mid ~ \exists i \le |\rho |~ \exists x \in vars (t_i) : (\pi _i(x) = \alpha ) \}\).
With this we state the first main result of this paper, which provides a bound on witnesses of \(\mathbb {Q},\mathbb {Q}^+\)-reachability, and is proved in Sect. 5.
Theorem 1
For \(\mathbb {X}\in \{\mathbb {Q},\mathbb {Q}^{+}\}\), if an \(\mathbb {X}\)-marking \({{\varvec{{f}}}}\) is \(\mathbb {X}\)-reachable from an initial \(\mathbb {X}\)-marking \({{\varvec{{i}}}}\), then there is an \(\mathbb {X}\)-run \(\rho \) such that \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {X}}{{\varvec{{f}}}}\) and \(| dval (\rho )| \le | dval ({{\varvec{{i}}}})\cup dval ({{\varvec{{f}}}})|+1+\max _{t \in T}(| vars (t)|)\).
Using the above bound, we obtain a polynomial time algorithm for \(\mathbb {Q}\)-reachability, as detailed in Sect. 6.
Theorem 2
Given \(\mathcal {N} = (P,T,F, Var )\) a UDPN and two \(\mathbb {Q}\)-markings i, f, deciding if \({{\varvec{{f}}}}\) is \(\mathbb {Q}\)-reachable from \({{\varvec{{i}}}}\) in \(\mathcal {N}\) is in polynomial time.
Finally, we consider continuous, i.e., \(\mathbb {Q}^+\)-reachability for UDPN. We adapt the techniques used for \(\mathbb {Q}^+\)-reachability of Petri nets without data from [11, 12] to the setting with data, and obtain a characterization of \(\mathbb {Q}^+\)-reachability for UDPN in Sect. 7.1. Finally, in Sect. 7.3, we show how the characterization can be combined with the above bound and compression techniques from [22] to obtain a polynomial sized system of linear equations with implications over \(\mathbb {Q}^+\). To do so, we require a slight transformation of the net which is described in Sect. 7.2. This leads to our headline result, stated below.
Theorem 3
(Continuous reachability for UDPN). Given a UDPN \(\mathcal {N} = (P,T,F, Var )\) and two \(\mathbb {Q}^{+}\)-markings i, f, deciding if \({{\varvec{{f}}}}\) is \(\mathbb {Q}^{+}\)-reachable from \({{\varvec{{i}}}}\) in \(\mathcal {N}\) is in polynomial time.
The rest of this paper is dedicated to proving these theorems. First, we present an equivalent formulation via matrices, which simplifies the technical arguments.
4 Equivalent Formulation via Matrices
From now on, we restrict \(\mathbb {X}\) to a symbol denoting \(\mathbb {Q}\) or \(\mathbb {Q}^+.\) We formulate the definitions presented earlier in terms of matrices, since defining object such as \(\mathbb {X}\)-marking as functions is intuitive to define but difficult to operate upon.
In the following, we abuse the notation and use the same names for objects as well as matrices representing them. We remark that this is safe as all arithmetic operations on objects correspond to matching operations on matrices.
An \(\mathbb {X}\)-marking \({\varvec{{m}}}\) is a \(P \times \mathbb {D}\) matrix M, where \( \forall p \in P,\forall \alpha \in \mathbb {D}, M(p,\alpha ) = {\varvec{{m}}}(p,\alpha )\). As a finite representation, we keep only a \(P\times dval ({\varvec{{m}}})\) matrix of non-zero columns. For a transition \(t \in T\), we represent \(F(t,\bullet ), F(\bullet ,t)\) as \(P \times Var \) matrices. Note that \((t,\bullet )\) is not the position in the matrix, but is part of the name of the matrix; its entry at \((i,j)\in P\times Var \) is given by \(F(t,\bullet )(i,j)\). For a place \(p \in row (F(t,\bullet ))\), the row \(F(t,\bullet )(p,\bullet )\) is a vector in \(\mathbb {N}^{ Var }\), given by an equation \(F(\bullet , t)(p,\bullet )(x)=F(p,t)(x)\) for \(p\in P, t\in T, x\in Var .\) Similarly, \(\varDelta (t)\) is a \(P \times Var \) matrix with \(\varDelta (t)(p,x)=F(t,\bullet )(p,x)-F(\bullet ,t)(p,x)\) for \(t\in T, p\in P, \text { and }x\in Var .\) Although, both \(\varDelta (t)\) and \(F(\bullet ,t)\) are defined as \(P\times Var \) matrices, only the columns for variables in \( vars (t)\) may be non-zero, so often we will iterate only over \( vars (t)\) instead of \( Var \).
Finally, we capture a mode \(\pi : Var \rightarrow \mathbb {D}\) as a \( Var \times \mathbb {D}\) permutation matrix \({\mathcal {P}}\). Although \({\mathcal {P}}\) may not be a square matrix, we abuse notation and call them permutation matrices. \({\mathcal {P}}\) basically represents assignment of variables in \( Var \) to data values just like \(\pi \) does. An entry of 1 represents that the corresponding variable is assigned corresponding data value in mode \(\pi \). Thus, for each mode \(\pi : Var \rightarrow \mathbb {D}\) there is a permutation matrix \({\mathcal {P}}_{\pi }\), such that for all \(x \in Var \), \(\alpha \in \mathbb {D}\), \({\mathcal {P}}_{\pi }(x,\alpha ) = 1\) if \(\pi (x) = \alpha \), and \({\mathcal {P}}_{\pi }(x,\alpha )=0\) otherwise. Formulating a mode as a permutation matrix has the advantage that \(\varDelta (t)\circ \pi ^{-1}\) is captured by \(\varDelta (t) \cdot {\mathcal {P}}_{\pi }\).
Example 2
In the UDPN \(\mathcal {N}_1\) from Example 1, if \(\mathbb {D}=\{red,blue,green,black\}\) then the initial marking \({{\varvec{{i}}}}\) can be represented by the matrix \({{\varvec{{i}}}}\) below and the function \(\varDelta (t)\) by the matrix \(\varDelta (t)\)

If we fire transition t with the assignment \(x=blue, y=green, z=black\), we get the following net depicted below (left), with marking \({{\varvec{{f}}}}\) (below center). The permutation matrix corresponding to the mode of fired transition is given by \({\mathcal {P}}\) matrix on the right. Note that the matrix \({{\varvec{{f}}}}- {{\varvec{{i}}}}\) is indeed the matrix \(\varDelta (t)\cdot {\mathcal {P}}\).

Using the representations developed so far we can represent an \(\mathbb {X}\)-run \(\rho \) as \(\{(c_i,t_i,{\mathcal {P}}_i)\}_{|\rho |}\) where \((c_i, t_i, {\mathcal {P}}_i)\) denotes the \(i^{th}\) \(\mathbb {X}\)-step fired with coefficient \(c_i\) using transition \(t_i\) with a mode corresponding to permutation matrix \({\mathcal {P}}_i\). The sum of the matrices (\(\sum _{i=1}^{|\rho |}c_i \varDelta (t_i)\cdot {\mathcal {P}}_i\)) gives us the effect of the run i.e. \(\varDelta (\rho ) = {{\varvec{{f}}}}- {{\varvec{{i}}}}\) where \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {X}} {{\varvec{{f}}}}\). Effect of an \(\mathbb {X}\)-run \(\rho \) on a data value \(\alpha \) is \(\varDelta (\rho )(\bullet ,\alpha ) \). Also, for an \(\mathbb {X}\)-run \(\rho = \{(c_i,t_i,{\mathcal {P}}_i)\}_{|\rho |}\), define \(k{\rho } = \{(k{c_i},t_i,{\mathcal {P}}_i)\}_{|\rho |}\) where \(k \in \mathbb {X}^{+}\).
5 Bounding Number of Data Values Used in \({\mathbb {Q},\mathbb {Q}^{+}}\)-run
We now prove the first main result of the paper, namely, Theorem 1, which shows a linear upper bound on the number of data values required in a \(\mathbb {Q}^+\)-run and a \(\mathbb {Q}\)-run. Theorem 1 is an immediate consequence of the following lemma, which states that if more than a linearly bounded number of data values are used in a \(\mathbb {Q}\) or \(\mathbb {Q}^+\) run, then there is another such run in which we use at least one less data value.
Lemma 1
Let \(\mathbb {X}\in \{\mathbb {Q},\mathbb {Q}^+\}\). If there exists an \(\mathbb {X}\)-run \(\sigma \) such that \({{\varvec{{i}}}}\xrightarrow {\sigma }_{\mathbb {X}}{{\varvec{{f}}}}\) and \(| dval (\sigma )| > | dval ({{\varvec{{i}}}}) \cup dval ({{\varvec{{f}}}})|+1+\max _{t \in T}(| vars (t)|)\), then there exists an \(\mathbb {X}\)-run \(\rho \) such that \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {X}} {{\varvec{{f}}}}\) and \(| dval (\rho )|\le | dval (\sigma )|-1\).
By repeatedly applying this lemma, Theorem 1 follows immediately. The rest of this section is devoted to proving this lemma. The central idea is to take any \(\mathbb {Q}\) or \(\mathbb {Q}^+\)-run between \({{\varvec{{i}}}}\), \({{\varvec{{f}}}}\) and transform it to use at least one less data value.
5.1 Transformation of an \(\mathbb {X}\)-run
The transformation which we call decrease is defined as a combination of two separate operations on an \(\mathbb {X}\)-run; we name them \( uniformize \) and \( replace \) and denote them by \(\mathcal {U}\) and \(\mathcal {R}\) respectively.
-
\( uniformize \) takes an \(\mathbb {X}\)-step and a non-empty set of data values \({\mathbb {E}}\) as input and produces an \(\mathbb {X}\)-run, such that in the resultant run, the effect of the run for each data value in \({\mathbb {E}}\) is equal.
-
\( replace \) takes an \(\mathbb {X}\)-step, a single data value \(\alpha ,\) and a non-empty set of data values \({\mathbb {E}}\) as input and outputs an \(\mathbb {X}\)-step which doesn’t use data value \(\alpha \).
The intuition behind the decrease operation is that we would like to take two data values \(\alpha \) and \(\beta \) used in the run such that effect on both of them is \(\mathbf 0 \) (they exists as the effect on every data value not present in the initial of final configuration is \(\mathbf 0 \)) and replace usage of \(\alpha \) by \(\beta \). However, such a replacement can only be done if both data are not used together in a single step (indeed, a mode \(\pi \) cannot assign the same data values to two variables). Unfortunately we cannot guarantee the existence of such a \(\beta \) that may replace \(\alpha \) globally. We circumvent this by applying the \( replace \) operation separately for every step, replacing \(\alpha \) with different data values in different steps.
But such a transformation would not preserve the effect of the run. To repair this aspect we uniformize i.e. guarantee that the final effect after replacing \(\alpha \) by other data values is equal for every datum that is used to replace \(\alpha \). As the effect on \(\alpha \) was \(\mathbf 0 \) then if we split it uniformly it adds \(\mathbf 0 \) to effects of data replacing \(\alpha \), which is exactly what we want. We now formalize this intuition below.
The Uniformize Operator. By \(\copyright \) we denote an operator of concatenation of two sequences. Although the data set \(\mathbb {D}\) is unordered, the following definitions require access to an arbitrary but fixed linear order on its elements. The definition of the \( uniformize \) operator needs another operator to act on an \(\mathbb {X}\)-step, which we call \( rotate \) and denote by \( rot \).
Definition 4
For a non-empty finite set of data values \({\mathbb {E}}\subset \mathbb {D}\) and an \(\mathbb {X}\)-step, \(\omega = (c,t,{\mathcal {P}})\), define \( rot ({\mathbb {E}},\omega )= (c,t,{\mathcal {P}}')\) where \({\mathcal {P}}'\) is obtained from \({\mathcal {P}}\) as follows.
-
\(\forall \alpha \in col ({\mathcal {P}}) \setminus {\mathbb {E}}\), \({\mathcal {P}}'(\bullet ,\alpha ) = {\mathcal {P}}(\bullet ,\alpha )\).
-
\(\forall \alpha \in {\mathbb {E}}\), \({\mathcal {P}}'(\bullet ,\alpha ) = {\mathcal {P}}(\bullet ,next_{{\mathbb {E}}}(\alpha ))\), where \(next_{{\mathbb {E}}}(\alpha ) = \min (\{ \beta \in {\mathbb {E}}\mid \beta > \alpha \})\) if \(|\{ \beta \in {\mathbb {E}}\mid \beta> \alpha \}| > 0\) and \(\min ({\mathbb {E}})\) otherwise.
For a fixed set \({\mathbb {E}}\), we can repeatedly apply \( rot ({\mathbb {E}},\bullet )\) operation on an \(\mathbb {X}\)-step, which we denote by \( rot ^k({\mathbb {E}},\omega )\), where k is the number of times we applied the operation (for example: \( rot ^2({\mathbb {E}},\omega )= rot ({\mathbb {E}},( rot ({\mathbb {E}},\omega ))\)).
Definition 5
For a finite and non-empty set of data values \({\mathbb {E}}\subset \mathbb {D}\) and an \(\mathbb {X}\)-step \(\omega = (c,t,{\mathcal {P}})\), we define \( uniformize \) as follows
\(\mathcal {U}({\mathbb {E}},\omega ) = rot ^{0}({\mathbb {E}},\frac{\omega }{|{\mathbb {E}}|})~ \copyright ~ rot ^{1}({\mathbb {E}},\frac{\omega }{|{\mathbb {E}}|}) ~ \copyright ~ rot ^{2}({\mathbb {E}},\frac{\omega }{|{\mathbb {E}}|})~\copyright ~ ... ~\copyright ~ rot ^{|{\mathbb {E}}|-1}({\mathbb {E}},\frac{\omega }{|{\mathbb {E}}|}) \).
An important property of uniformize is its effect on data values.
Lemma 2
For a finite and non-empty set of data values \({{\mathbb {E}}}\subset \mathbb {D}\) and an \(\mathbb {X}\)-step \(\omega = (c,t,{\mathcal {P}})\), \({{\varvec{{i}}}}\xrightarrow {\omega }_{\mathbb {Q}^+} {{\varvec{{f}}}}\), if \({{\varvec{{i}}}}'\xrightarrow {\mathcal {U}({{\mathbb {E}}},\omega )} {{\varvec{{f}}}}'\), then
-
1.
\(\forall \alpha \in dval ( \omega )\backslash {{\mathbb {E}}} \), \( {{\varvec{{f}}}}'(\bullet ,\alpha )-{{\varvec{{i}}}}'(\bullet ,\alpha )={{\varvec{{f}}}}(\bullet ,\alpha )-{{\varvec{{i}}}}(\bullet ,\alpha )\)
-
2.
\(\forall \alpha \in {{\mathbb {E}}},~, {{\varvec{{f}}}}'(\bullet ,\alpha )-{{\varvec{{i}}}}'(\bullet ,\alpha )=\frac{\sum _{\beta \in {{\mathbb {E}}}}({{\varvec{{f}}}}(\bullet ,\beta )-{{\varvec{{i}}}}(\bullet ,\beta ))}{|{\mathbb {E}}|}\).
This lemma tells us the effect of the run on the initial marking is equalized for data values in \({{\mathbb {E}}}\) by the \(\mathcal {U}\) operation, and is unchanged for the other data values.
The Replace Operator. To define the \( replace \) operator it is useful to introduce \(swap_{\alpha ,\beta }({\mathcal {P}})\) which exchanges columns \(\alpha \) and \(\beta \) in the matrix \({\mathcal {P}}\).
Definition 6
For a finite set of data values \({\mathbb {E}}\), an \(\mathbb {X}\)-step \(\omega = (c,t,{\mathcal {P}})\), and \(\alpha \not \in {\mathbb {E}}\) we define \( replace \) as follows
After applying the \( replace \) operation \(\alpha \) is no longer used in the run, which reduces the number of data values used in the run. Observe that \( replace \) can not be always applied to an \(\mathbb {X}\)-step. It requires a zero column labelled with an element from \({\mathbb {E}}\) in the permutation matrix corresponding to the \(\mathbb {X}\)-step.
The Decrease Transformation. Finally, we define the transformation on an \(\mathbb {X}\)-run between two markings which we call \( decrease \) and denote by \( dec \).
Definition 7
For two \(\mathbb {X}\)-markings \({{\varvec{{i}}}}\), \({{\varvec{{f}}}}\), and an \(\mathbb {X}\)-run \(\sigma \) such that \({{\varvec{{i}}}}\xrightarrow {\sigma }_{\mathbb {X}} {{\varvec{{f}}}}\) and \(| dval (\sigma )| > | dval ({{\varvec{{i}}}}) \cup dval ({{\varvec{{f}}}})|+1+\max _{t \in T}(| vars (t)|)\), let \(\{\alpha \} \cup {\mathbb {E}}= dval (\sigma ) \setminus ( dval ({{\varvec{{i}}}}) \cup dval ({{\varvec{{f}}}}))\) and \(\alpha \not \in {\mathbb {E}}\). We define \( decrease \) by, \( dec ({\mathbb {E}},\alpha ,\sigma ) =\)
where \(\sigma (j)\) denotes the \(j^{th}\) \(\mathbb {X}\)-step of \(\sigma \).
Observe that the required size of \( dval (\sigma )\) guarantees existence of a \(\beta \in {\mathbb {E}}\) which can be replaced with \(\alpha \), for every application of the \(\mathcal {R}\) operation. Note that the exchanged data value \(\beta \) could be different for each step. Finally, we can analyze the \( decrease \) transformation and show that if the original run allows for the \( decrease \) transformation (as given in the above definition), then after the application of it, the resulting sequence of transitions is a valid run of the system.
Lemma 3
Let \(\sigma \) be an \(\mathbb {X}\)-run such that \({{\varvec{{i}}}}\xrightarrow {\sigma }_{\mathbb {X}} {{\varvec{{f}}}}\) and \(| dval (\sigma )| > | dval ({{\varvec{{i}}}}) \cup dval ({{\varvec{{f}}}})|+1+\max _{t \in T}(| dval (t)|)\). Let \(\alpha \in dval (\sigma ) \setminus ( dval ({{\varvec{{i}}}}) \cup dval ({{\varvec{{f}}}}))\) and \({\mathbb {E}}= dval (\sigma ) \setminus ( dval ({{\varvec{{i}}}}) \cup dval ({{\varvec{{f}}}}) \cup \{\alpha \})\). Then for \(\rho = dec ({\mathbb {E}}, \alpha , \sigma )\), we obtain \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {X}} {{\varvec{{f}}}}.\)
Proof
Suppose \(\sigma =\sigma _1\sigma _2\ldots \sigma _l\) where each \(\sigma _j=(c_j, t_j, {\mathcal {P}}_j)\), for \(1\le j\le l\) is an \(\mathbb {X}\)-step. Then \(\rho =\rho _1\copyright \ldots \copyright \rho _l\), where each \(\rho _j\) is an \(\mathbb {X}\)-run defined by \(\rho _j=\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}},\sigma _j))\). It will be useful to identify intermediate \(\mathbb {X}\)-markings
We split the proof: first we show that \({{\varvec{{f}}}}={{\varvec{{f}}}}'\) and then \(\rho \) is \(\mathbb {X}\)-fireable from \({{\varvec{{i}}}}.\)
Step 1: Showing that the final markings reached are the same. We prove a stronger statement which implies that \({{\varvec{{f}}}}={{\varvec{{f}}}}'\), namely:
Claim 1
For all \(0\le j\le l\),
-
1.
\({\varvec{{m}}}_j'(\bullet ,\alpha )=\mathbf 0 \)
-
2.
\(\forall \gamma \in \) \( dval ({{\varvec{{i}}}})\cup dval ({{\varvec{{f}}}})\), \({\varvec{{m}}}_j'(\bullet ,\gamma )={\varvec{{m}}}_j(\bullet ,\gamma )\)
-
3.
\(\forall \gamma \in \) \({{\mathbb {E}}}\) \( {\varvec{{m}}}_j'(\bullet ,\gamma )=\frac{1}{|{\mathbb {E}}|}\left( \sum _{\delta \in {{\mathbb {E}}}\cup \{\alpha \}} {\varvec{{m}}}_j(\bullet ,\delta )\right) .\)
The proof is obtained by induction on j. Intuitively, point 1 holds as we shift effects on \(\alpha \) to \(\beta \), point 2 holds as the transformation does not touch \(\gamma \in dval ({{\varvec{{i}}}})\cup dval ({{\varvec{{f}}}}).\) The last and most complicated point follows from the fact that the number of tokens consumed and produced along each segment \(\xrightarrow {\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}},\sigma _j))}\) is the same as for \(\sigma _j\), but uniformized over \({\mathbb {E}}\).
Step 2: Showing that \(\rho \) is an \(\mathbb {X}\)-run. If \(\mathbb {X}=\mathbb {Q}\) then the run \(\rho \) is fireable, as any \(\mathbb {Q}\)-run is fireable, so in this case this step is trivial. The case when \(\mathbb {X}=\mathbb {Q}^+\) is more involved. As we know from Claim 1, each \(m_j'\) is a \(\mathbb {Q}^+\)-marking, so it suffices to prove that for every j, \({\varvec{{m}}}_j'\xrightarrow {\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}},\sigma _j))}_{\mathbb {Q}^{+}}{\varvec{{m}}}_{j+1}'\). Consider a data vector of tokens consumed along the \(\mathbb {Q}^+\)-run \(\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}},\sigma _j))\). If we show that it is smaller than or equal to \({\varvec{{m}}}_j'\) (component-wise), then we can conclude that \(\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}},\sigma _j))\) is indeed \(\mathbb {Q}^+\)-fireable from \({\varvec{{m}}}_j'\). To show this, we examine the consumed tokens for each datum \(\gamma \) separately. There are three cases:
-
(i)
\(\gamma =\alpha \). For this case, every step in \(\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}}, \sigma _j))\) does not make any change on \(\alpha \) so tokens with data value \(\alpha \) are not consumed along the \(\mathbb {Q}^+\)-run \(\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}},\sigma _j))\).
-
(ii)
\(\gamma \in dval ({{\varvec{{i}}}})\cup dval ({{\varvec{{f}}}})\). This is similar to the above case. Consider any data value \(\gamma \in ( dval (\sigma )\backslash {{\mathbb {E}}})\setminus \{\alpha \}\). Since \(\gamma \) does not change on \( rotate \) operation, the \(\mathcal {U}\) operation causes each \(\mathbb {Q}\)-step in \(\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}}, \sigma _j))\) to consume \(\frac{1}{|{\mathbb {E}}|}\) of the tokens with data value \(\gamma \) consumed when \(\sigma _j\) is fired. This is repeated \(|{\mathbb {E}}|\) times and hence the vector of tokens with data value \(\gamma \) consumed along \(\mathcal {U}({{\mathbb {E}}},\mathcal {R}(\alpha ,{\mathbb {E}}, \sigma _j))\) is equal to the vector of tokens with value \(\gamma \) consumed by step \(\sigma _j\). But we know that, it is smaller than \({\varvec{{m}}}_j(\bullet ,\gamma )\) and concluding smaller than \({\varvec{{m}}}_j'(\bullet ,\gamma )\). The last inequality is true as \({\varvec{{m}}}_j(\bullet ,\gamma )={\varvec{{m}}}_j'(\bullet ,\gamma )\) according to Claim 1.
-
(iii)
\(\gamma \in {\mathbb {E}}\). Let \(\omega \) be a triple \((c_j,F(\bullet ,t_j), {\mathcal {P}}_j)\) where \((c_j,t_j, {\mathcal {P}}_j)=\sigma _j.\) \(\omega \) simply describes tokens consumed by \(\sigma _j.\) We slightly overload the notation and treat a triple \(\omega \) like a step, where \(F(\bullet ,t_j)\) represents a transition “_” for which \(F(\bullet ,\_)=F(\bullet ,t_j)\) and \(F(\_,\bullet )\) is a zero matrix. We calculate the vector of consumed tokens with data value \(\gamma \) as follows: \( consumed(\bullet ,\gamma )=\)
$$\frac{1}{|{\mathbb {E}}|}\sum _{k=0}^{|{\mathbb {E}}|-1} \varDelta ( rot ^{k}({\mathbb {E}},\mathcal {R}(\alpha ,{\mathbb {E}},\omega )))(\bullet ,\gamma )= \frac{1}{|{\mathbb {E}}|}\sum _{k=0}^{|{\mathbb {E}}|} \varDelta ( rot ^{k}({{\mathbb {E}}\cup \{\alpha \}},\omega ))(\bullet ,\gamma )$$the first equality is from definition and the second by the \( replace \) operation,
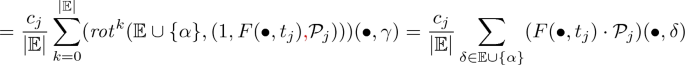
Further, observe that as \(\sigma _j\) can fired in \({\varvec{{m}}}_j\)
$$c_j(F(\bullet ,t_j)\cdot {\mathcal {P}}_j)(\bullet ,\delta )\le {\varvec{{m}}}_j(\bullet ,\delta ) \text { for all }\delta \in \mathbb {D},$$summing up over \(\delta \in {\mathbb {E}}\cup \{\alpha \}\) and multiplying with \(\frac{1}{|{\mathbb {E}}|}\) we get
$$\frac{1}{|{\mathbb {E}}|}c_j\sum _{\delta \in {\mathbb {E}}\cup \{\alpha \}} (F(\bullet ,t_j)\cdot {\mathcal {P}}_j)(\bullet ,\delta ) \le \frac{1}{|{\mathbb {E}}|}\sum _{\delta \in {\mathbb {E}}\cup \{\alpha \}} {\varvec{{m}}}_j(\bullet ,\delta )= {\varvec{{m}}}_j'(\delta ,\gamma ),$$where the last equality comes from Claim 1 point 3. Combining inequalities we get \(consumed(\bullet ,\gamma )\le {\varvec{{m}}}_i'(\bullet ,\gamma )\).
Proof
(of Lemma 1). Now the proof of Lemma 1 (and hence Theorem 1) follow immediately, since we can use the \( decrease \) transformation, to decrease the number of data values required in an \(\mathbb {X}\)-run. We simply take \(\alpha \in dval (\sigma )\setminus ( dval ({{\varvec{{i}}}})\cup dval ({{\varvec{{f}}}}))\) and \({\mathbb {E}}= dval (\sigma )\setminus ( dval ({{\varvec{{i}}}})\cup dval ({{\varvec{{f}}}}))\setminus \{\alpha \}.\) Next, let \(\rho = dec ({{\mathbb {E}}},\alpha ,\sigma ).\) Due to Lemma 3 we know that \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {X}}{{\varvec{{f}}}}\). Moreover, observe that \( dval (\rho )\subseteq dval (\sigma )\). But in addition, \(\alpha \not \in dval (\rho )\) as due to the one of properties of the \( decrease \) operation \(\alpha \) does not participate in the run \(\rho \). So \( dval (\rho )\subset dval (\sigma ).\) Therefore \(| dval (\rho )|\le | dval (\sigma )|-1\).
6 \(\mathbb {Q}\)-reachability is in PTime
We recall the definition of histograms from [22].
Definition 8
A histogram M of order \(q \in \mathbb {Q}\) is a \( Var \times \mathbb {D}\) matrix having non-negative rational entries such that,
-
1.
\(\sum _{\alpha \in col (M)}M(x,\alpha ) = q\) for all \(x \in row (M)\).
-
2.
\(\sum _{x \in row (M)}M(x,\alpha ) \le q\) for all \(\alpha \in col (M)\).
A permutation matrix is a histogram of order 1.
In the following lemma, we state two properties of histograms. We say that a histogram of order a is an [a]-histogram if the histogram has only \(\{0,a\}\) entries.
Lemma 4
Let \(H,H_1,H_2,..,H_n\) be histograms of order \(q,q_1,q_2,...,q_n\) respectively and of same row dimensions then (i) \(\sum _{i=1}^{n}H_i\) is a histogram of order \(\sum _{i}^{n}q_i\), (ii) H can be decomposed as a sum of [\(a_i\)]-histograms such that \(\sum _{i}a_i = q\).
Using histograms we define a representation \(Hist(\rho )\) for an \(\mathbb {X}\)-run \(\rho \), which captures \(\varDelta (\rho )\). From an \(\mathbb {X}\)-run \(\rho = \{(c_j,t_j,{\mathcal {P}}_j)\}_{|\rho |}\) we obtain \(Hist(\rho )\) as follows. For all transitions \(t \in T \), define the set \(I_t = \{ j \in [1..|\rho |]|~ t_j = t \}\). Then calculate the matrix \( H_t = \sum _{i \in I_t} c_i {\mathcal {P}}_i\). Observe that since permutation matrices are histograms and histograms are closed under scalar multiplication and addition, \(H_t\) is a histogram. If \(I_t\) is empty, then \(H_t\) is simply the null matrix. We define \(Hist(\rho )\) as a mapping from T to histograms such that t is mapped to \(H_t\).
Analogous to an \(\mathbb {X}\)-run we can represent \(Hist(\rho )\) simply as \(\{(t_j,H_{t_j})\}\), unlike an \(\mathbb {X}\)-run we don’t indicate the length of the sequence since it is dependent on the net and not the individual run itself.
Proposition 1
Let \(\mathcal {N} = (P,T,F, Var )\) be a UDPN, \({{\varvec{{i}}}},{{\varvec{{f}}}}\) \(\mathbb {X}\)-markings, and \(\sigma \) an \(\mathbb {X}\)-run such that \({{\varvec{{i}}}}\xrightarrow {\sigma }_{\mathbb {X}} {{\varvec{{f}}}}\). Then for each \(t\in T\) there exists \(H_t\) such that:
-
1.
\({{\varvec{{f}}}}-{{\varvec{{i}}}}=\sum _{t\in T} \varDelta (t)\cdot H_t,\)
-
2.
\( col (H_t)\subseteq dval (\sigma )\) for every \(t\in T.\)
A PTime Procedure. We start by observing that from any \(\mathbb {Q}\)-marking \({{\varvec{{i}}}}\), every \(\mathbb {Q}\)-step \((c,t,{\mathcal {P}})\) is fireable and every \(\mathbb {Q}\) run is fireable. This follows from the fact that rationals are closed under addition, thus \({{\varvec{{i}}}}+ c\cdot F(\bullet ,t) \cdot {\mathcal {P}}\) is a marking in \(\mathcal {M}_{\mathbb {Q}}\). Thus if we have to find a \(\mathbb {Q}\)-run \(\rho = \{(c_j,t_j,{\mathcal {P}}_j)\}_{|\rho |}\) between two \(\mathbb {Q}\)-markings, \({{\varvec{{i}}}},{{\varvec{{f}}}}\) it is sufficient to ensure that \({{\varvec{{f}}}}-{{\varvec{{i}}}}= \sum _{j=1}^{|\rho |}c_j\varDelta (t_j)\cdot {\mathcal {P}}_j\). Thus for a \(\mathbb {Q}\)-run all that matters is the difference in markings caused by the \(\mathbb {Q}\)-run which is captured succinctly by \(Hist(\rho ) = \{t_j,H_{t_j}\}\). This brings us to our characterization of \(\mathbb {Q}\)-run.
Lemma 5
Let \(\mathcal {N} = (P,T,F, Var )\) be a UDPN, a marking \({{\varvec{{f}}}}\) is \(\mathbb {Q}\)-reachable from \({{\varvec{{i}}}}\) iff there exists set \({\mathbb {E}}\) of size bounded by \(|{\mathbb {E}}|\le | dval ({{\varvec{{i}}}})\cup dval ({{\varvec{{f}}}})|+1+\max _{t \in T}(| vars (t)|)\) and a histogram \(H_t\) for each \(t \in T\) such that \({{\varvec{{f}}}}- {{\varvec{{i}}}}= \sum _{t\in T} \varDelta (t)\cdot H_t \) and \(\forall t \in T ~ col (H_t)\subseteq {\mathbb {E}}.\)
Using this characterization we can write a system of linear inequalities to encode the condition of Lemma 5. Thus, we obtain our second main result, namely, Theorem 2, with detailed proofs in [27].
7 \(\mathbb {Q}^+\)-reachability is in PTime
Finally, we turn to \(\mathbb {Q}^+\)-reachability for UDPNs and to the proof of Theorem 3. At a high level, the proof is in three steps. We start with a characterization of \(\mathbb {Q}^+\)-reachability in UDPNs. Then we present a polytime reduction of the continuous reachability problem to the same problem but for a special subclass of UDPN, called loop-less nets. Finally, we present how to encode the characterization for loop-less nets into a system of linear equations with implications to obtain a polytime algorithm for continuous reachability in UDPNs.
7.1 Characterizing \(\mathbb {Q}^+\)-reachability
We begin with a definition. For an \(\mathbb {X}\)-run we introduce the notion of the pre and post sets of \(\mathbb {X}-\)run. For an \(\mathbb {X}\)-run, \(\rho = \{(c_i, t_i,{\mathcal {P}}_i)\}_{|\rho |}\) we define \(Pre(\rho ) = \{(p,\alpha ) |~ \exists ~ t_i, \exists ~ x : F(p,t_i)(x) < 0 \wedge {\mathcal {P}}_i(x,\alpha ) = 1\}\). We also define \(Post(\rho ) = \{(p,\alpha ) |~ \exists ~ t_i, \exists ~ x : F(t_i,p)(x) > 0 \wedge {\mathcal {P}}_i(x,\alpha ) = 1\}\). Intuitively, \(Pre(\rho ),Post(\rho )\) denote the set of \((p,\alpha )\) (place, data value) pairs describing tokens that are consumed, produced respectively by the run \(\rho \).
Throughout this section, by a marking we denote a \(\mathbb {Q}^+\)-marking.
Lemma 6
Let \(\mathcal {N}=(P,T,F, Var )\) be an UDPN and \({{\varvec{{i}}}},{{\varvec{{f}}}}\) are markings. For any \(\mathbb {Q}^{+}\)-run \(\sigma \) such that \({{\varvec{{i}}}}\xrightarrow {\sigma }_{\mathbb {Q}^{+}} {{\varvec{{f}}}}\) there exist markings \({{\varvec{{i}}}}'\) and \({{\varvec{{f}}}}'\) (possibly on a different run) such that
-
1.
\({{\varvec{{i}}}}'\) is \(\mathbb {Q}^+\)-reachable from \({{\varvec{{i}}}}\) in at most \(|P|\cdot | dval (\sigma )|\) \(\mathbb {Q}^+\)-steps
-
2.
There is a run \(\sigma '\) such that \( dval (\sigma ')\subseteq dval (\sigma )\) and \({{\varvec{{i}}}}'\xrightarrow {\sigma '}_{\mathbb {Q}}{{\varvec{{f}}}}'\)
-
3.
\({{\varvec{{f}}}}\) is \(\mathbb {Q}^+\)-reachable from \({{\varvec{{f}}}}'\) in at most \(|P|\cdot | dval (\sigma )|\) \(\mathbb {Q}^+\)-steps
-
4.
\(\forall (p,\alpha ) \in Pre(\sigma '), {{\varvec{{i}}}}'(p,\alpha ) > 0\)
-
5.
\(\forall (p,\alpha ) \in Post(\sigma '), {{\varvec{{f}}}}'(p,\alpha ) > 0\)
Remark 1
If in conditions 1 and 3 we drop the requirement on the number of steps then the five conditions still imply continuous reachability.
Note that if there exist markings \({{\varvec{{i}}}}'\) and \({{\varvec{{f}}}}'\) and \(\mathbb {Q}^+\) -runs \(\rho \), \(\rho '\), \(\rho ''\) such that \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {Q}^{+}} {{\varvec{{i}}}}', {{\varvec{{i}}}}' \xrightarrow {\rho '}_{\mathbb {Q}^{+}} {{\varvec{{f}}}}', {{\varvec{{f}}}}' \xrightarrow {\rho ''}_{\mathbb {Q}^{+}} {{\varvec{{f}}}}\) then there is a \(\mathbb {Q}^+\)-run \(\sigma \) such that \({{\varvec{{i}}}}\xrightarrow {\sigma }_{\mathbb {Q}^{+}} {{\varvec{{f}}}}\). The above characterization and its proof are obtained by adapting to the data setting, the techniques developed for continuous reachability in Petri nets (without data) in [11] and [12].
7.2 Transforming UDPN to Loop-less UDPN
For a UDPN \(\mathcal {N}=(P,T,F, Var )\), we construct a UDPN \(\mathcal {N}'\) which is polynomial in the size of \(\mathcal {N}\) and the \(\mathbb {Q}^+\)-reachability problem is equivalent. We define \(PrePlace(t)=\{p \in P | \exists v \in Var \ s.t.\ F(p,t)(v)>0 \}\) and PostPlace(t) \(=\{p \in P| \exists v \in Var \ s.t.\ F(t,p)(v)>0 \}\), where \(t\in T\). The essential property of the transformed UDPN is that for every transition the sets of PrePlace and PostPlace do not intersect. A UDPN \(\mathcal {N}=(P,T,F, Var )\) is said to be loop-less if for all \(t\in T\), \(PrePlace(t) \cap PostPlace(t)=\emptyset .\)
Any UDPN can easily be transformed in polynomial time into a loop-less UDPN such that \(\mathbb {Q}^+\)-reachability is preserved, by doubling the number of places and adding intermediate transitions. Formally, For every net \(\mathcal {N}\) and two markings \({{\varvec{{i}}}},{{\varvec{{f}}}}\) in polynomial time one can construct a loop-less net \(\mathcal {N}'\) and two markings \({{\varvec{{i}}}}',\ {{\varvec{{f}}}}'\) such that \({{\varvec{{i}}}}\xrightarrow {}_{\mathbb {Q}^+}{{\varvec{{f}}}}\) in the net \(\mathcal {N}\) iff \({{\varvec{{i}}}}'\xrightarrow {}_{\mathbb {Q}^+}{{\varvec{{f}}}}'\) in \(\mathcal {N}'.\) Now, the following lemma which describes a property of loop-less nets will be crucial for our reachability algorithm:
Lemma 7
In a loop-less net, for markings \({{\varvec{{i}}}}\), \({{\varvec{{f}}}}\), if there exist a histogram H, and a transition t \(\in \) T such that \({{\varvec{{i}}}}+\varDelta (t)\cdot H={{\varvec{{f}}}}\), then there exist a \(\mathbb {Q}^+\)-run \(\rho \) such that \({{\varvec{{i}}}}\xrightarrow {\rho }_{\mathbb {Q}^+}{{\varvec{{f}}}}\).
7.3 Encoding \(\mathbb {Q}^+\)-reachability as Linear Equations with Implications
Linear equations with implications, as we use them, are defined in [23], but were introduced in [12]. A system of linear equations with implications, also denoted a \(\implies \) system, is a finite set of linear inequalities over the same variables, plus a finite set of implications of the form \(x>0\implies y>0\), where x, y are variables appearing in the linear inequalities.
Lemma 8
[12]. The \(\mathbb {Q}^+\) solvability problem for a \(\implies \) system is in \(PTime\).
We then reduce the \(\mathbb {Q}^+\)-reachability problem to checking the solvability of a system of linear equations with implications, using the characterization established in Lemma 6 in the following lemma.
Lemma 9
\(\mathbb {Q}^+\)-reachability in a UDPN \(\mathcal {N}=(P,T,F, Var )\) between markings \({{\varvec{{i}}}},{{\varvec{{f}}}}\) can be encoded as a set of linear equations with implications in P-time.
Finally, we obtain Theorem 3 as a consequence of Lemmas 8 and 9.
8 Conclusion
In this paper, we provided a polynomial time algorithm for continuous reachability in UDPN, matching the complexity for Petri nets without data. This is in contrast to problems such as discrete coverability, termination, where Petri nets with and without data differ enormously in complexity, and to (discrete) reachability, where decidability is still open. As future work, we aim to implement the continuous reachability algorithm developed here, to build the first tool for discrete coverability in UDPN on the lines of what has been done for Petri nets without data. The main obstacle will be performance evaluation due to lack of benchmarks for UDPNs. Another interesting avenue for future work would be to tackle continuous reachability for Petri nets with ordered data, which would allow us to analyze continuous variants of Timed Petri nets.
Notes
- 1.
This can be seen on the same lines as the proof of undecidability of continuous reachability for Petri nets with zero tests [12].
References
Finkel, A., Schnoebelen, P.: Well-structured transition systems everywhere! Theor. Comput. Sci. 256(1–2), 63–92 (2001)
Rackoff, C.: The covering and boundedness problems for vector addition systems. Theor. Comput. Sci. 6, 223–231 (1978)
Rao Kosaraju, S.: Decidability of reachability in vector addition systems (preliminary version). In: Proceedings of the 14th Annual ACM Symposium on Theory of Computing, San Francisco, California, USA, 5–7 May 1982, pp. 267–281 (1982)
Leroux, J., Schmitz, S.: Demystifying reachability in vector addition systems. In: 30th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2015, Kyoto, Japan, 6–10 July 2015, pp. 56–67 (2015)
Cardoza, E., Lipton, R.J., Meyer, A.R.: Exponential space complete problems for Petri nets and commutative semigroups: preliminary report. In: Proceedings of the 8th Annual ACM Symposium on Theory of Computing, Hershey, Pennsylvania, USA, 3–5 May 1976, pp. 50–54 (1976)
Czerwinski, W., Lasota, S., Lazic, R., Leroux, J., Mazowiecki, F.: The reachability problem for Petri nets is not elementary (extended abstract). CoRR, abs/1809.07115 (2018)
van der Aalst, W.M.P.: The application of Petri nets to workflow management. J. Circ. Syst. Comput. 8(1), 21–66 (1998)
Esparza, J.: Decidability and complexity of Petri net problems — an introduction. In: Reisig, W., Rozenberg, G. (eds.) ACPN 1996. LNCS, vol. 1491, pp. 374–428. Springer, Heidelberg (1998). https://doi.org/10.1007/3-540-65306-6_20
Desel, J., Esparza, J.: Free Choice Petri Nets. Cambridge University Press, New York (1995)
David, R., Alla, H.: Continuous Petri nets. In: Proceedings of the 8th European Workshop on Application and Theory of Petri Nets, Zaragoza, Spain, pp. 275–294 (1987)
Fraca, E., Haddad, S.: Complexity analysis of continuous Petri nets. Fundam. Inform. 137(1), 1–28 (2015)
Blondin, M., Haase, C.: Logics for continuous reachability in Petri nets and vector addition systems with states. In: 32nd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2017, Reykjavik, Iceland, 20–23 June 2017, pp. 1–12 (2017)
David, R., Alla, H.: Petri nets for modeling of dynamic systems: a survey. Automatica 30(2), 175–202 (1994)
Alla, H., David, R.: Continuous and hybrid Petri nets. J. Circ. Syst. Comput. 8, 159–188 (1998)
Jensen, K.: Coloured Petri nets - preface by the section editor. STTT 2(2), 95–97 (1998)
Wang, J.: Timed Petri nets. Timed Petri Nets: Theory and Application. The Kluwer International Series on Discrete Event Dynamic Systems, vol. 9, pp. 63–123. Springer, Boston (1998). https://doi.org/10.1007/978-1-4615-5537-7_4
Abdulla, P.A., Nylén, A.: Timed Petri nets and BQOs. In: Colom, J.-M., Koutny, M. (eds.) ICATPN 2001. LNCS, vol. 2075, pp. 53–70. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45740-2_5
Lazic, R., Newcomb, T.C., Ouaknine, J., Roscoe, A.W., Worrell, J.: Nets with tokens which carry data. Fundam. Inform. 88(3), 251–274 (2008)
Rosa-Velardo, F., de Frutos-Escrig, D.: Forward analysis for Petri nets with name creation. In: Lilius, J., Penczek, W. (eds.) PETRI NETS 2010. LNCS, vol. 6128, pp. 185–205. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13675-7_12
Lazić, R., Totzke, P.: What makes Petri nets harder to verify: stack or data? In: Gibson-Robinson, T., Hopcroft, P., Lazić, R. (eds.) Concurrency, Security, and Puzzles. LNCS, vol. 10160, pp. 144–161. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-51046-0_8
Hofman, P., Lasota, S., Lazić, R., Leroux, J., Schmitz, S., Totzke, P.: Coverability trees for Petri nets with unordered data. In: Jacobs, B., Löding, C. (eds.) FOSSACS 2016. LNCS, vol. 9634, pp. 445–461. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49630-5_26
Hofman, P., Leroux, J., Totzke, P.: Linear combinations of unordered data vectors. In: 32nd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2017, Reykjavik, Iceland, 20–23 June 2017, pp. 1–11 (2017)
Hofman, P., Lasota, S.: Linear equations with ordered data. In: 29th International Conference on Concurrency Theory, CONCUR 2018, Beijing, China, 4–7 September 2018, pp. 24:1–24:17 (2018)
Silva, M., Terue, E., Colom, J.M.: Linear algebraic and linear programming techniques for the analysis of place/transition net systems. In: Reisig, W., Rozenberg, G. (eds.) ACPN 1996. LNCS, vol. 1491, pp. 309–373. Springer, Heidelberg (1998). https://doi.org/10.1007/3-540-65306-6_19
Blondin, M., Finkel, A., Haase, C., Haddad, S.: Approaching the coverability problem continuously. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 480–496. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_28
Esparza, J., Ledesma-Garza, R., Majumdar, R., Meyer, P., Niksic, F.: An SMT-based approach to coverability analysis. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 603–619. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_40
Gupta, U., Shah, P., Akshay, S., Hofman, P.: Continuous reachability for unordered data Petri nets is in PTime. CoRR abs/1902.05604 (2019). arxiv.org/abs/1902.05604
Rosa-Velardo, F., de Frutos-Escrig, D.: Decidability and complexity of Petri nets with unordered data. Theor. Comput. Sci. 412(34), 4439–4451 (2011)
Acknowledgments
We thank the anonymous reviewers for their careful reading and their helpful and insightful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Gupta, U., Shah, P., Akshay, S., Hofman, P. (2019). Continuous Reachability for Unordered Data Petri Nets is in PTime. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)