Abstract
This paper investigates the satisfiability problem for Separation Logic with k record fields, with unrestricted nesting of separating conjunctions and implications, for prenex formulæ with quantifier prefix \(\exists ^*\forall ^*\). In analogy with first-order logic, we call this fragment Bernays-Schönfinkel-Ramsey Separation Logic [\(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\)]. In contrast to existing work in Separation Logic, in which the universe of possible locations is assumed to be infinite, both finite and infinite universes are considered. We show that, unlike in first-order logic, the (in)finite satisfiability problem is undecidable for \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\). Then we define two non-trivial subsets thereof, that are decidable for finite and infinite satisfiability respectively, by controlling the occurrences of universally quantified variables within the scope of separating implications, as well as the polarity of the occurrences of the latter. Beside the theoretical interest, our work has natural applications in program verification, for checking that constraints on the shape of a data-structure are preserved by a sequence of transformations.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Separation Logic [10, 14], or SL, is a logical framework used in program verification to describe properties of the dynamically allocated memory, such as topologies of data structures (lists, trees), (un)reachability between pointers, etc. In a nutshell, given an integer \(k\ge 1\), the logic \(\mathsf {SL}^{\!\scriptstyle {k}}\) is obtained from the first-order theory of a finite partial function \(h: U \rightharpoonup U^k\) called a heap, by adding two substructural connectives: (i) the separating conjunction
 , that asserts a split of the heap into disjoint heaps satisfying
, that asserts a split of the heap into disjoint heaps satisfying
 and
and
 respectively, and (ii) the separating implication or magic wand
respectively, and (ii) the separating implication or magic wand
 , stating that each extension of the heap by a heap satisfying
, stating that each extension of the heap by a heap satisfying
 must satisfy
must satisfy
 . Intuitively, U is the universe of possible of memory locations (cells) and k is the number of record fields in each memory cell.
. Intuitively, U is the universe of possible of memory locations (cells) and k is the number of record fields in each memory cell.
The separating connectives \(*\) and
 allow concise definitions of program semantics, via weakest precondition calculi [10] and easy-to-write specifications of recursive linked data structures (e.g. singly- and doubly-linked lists, trees with linked leaves and parent pointers, etc.), when higher-order inductive definitions are added [14]. Investigating the decidability and complexity of the satisfiability problem for fragments of SL is of theoretical and practical interest. In this paper, we consider prenex SL formulæ with prefix \(\exists ^* \forall ^*\). In analogy with first-order logic with equality and uninterpreted predicates [12], we call this fragment Bernays-Schönfinkel-Ramsey SL [\(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\)].
allow concise definitions of program semantics, via weakest precondition calculi [10] and easy-to-write specifications of recursive linked data structures (e.g. singly- and doubly-linked lists, trees with linked leaves and parent pointers, etc.), when higher-order inductive definitions are added [14]. Investigating the decidability and complexity of the satisfiability problem for fragments of SL is of theoretical and practical interest. In this paper, we consider prenex SL formulæ with prefix \(\exists ^* \forall ^*\). In analogy with first-order logic with equality and uninterpreted predicates [12], we call this fragment Bernays-Schönfinkel-Ramsey SL [\(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\)].
As far as we are aware, all existing work on SL assumes that the universe (set of available locations) is countably infinite. This assumption is not necessarily realistic in practice since the available memory is usually finite, although the bound depends on the hardware and is not known in advance. The finite universe hypothesis is especially useful when dealing with bounded memory issues, for instance checking that the execution of a program satisfies its postcondition, provided that there are sufficiently many available memory cells. In this paper we consider both the finite and infinite satisfiability problems. We show that both problems are undecidable for \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) (unlike in first-order logic) and that they become PSPACE-complete under some additional restrictions, related to the occurrences of the magic wand and universal variables:
-
1.
The infinite satisfiability problem is PSPACE-complete if the positive occurrences of
 (i.e., the occurrences of
(i.e., the occurrences of
 that are in the scope of an even number of negations) contain no universal variables.
that are in the scope of an even number of negations) contain no universal variables. -
2.
The finite satisfiability problem is PSPACE-complete if there is no positive occurrence of
 (i.e.,
(i.e.,
 only occurs in the scope of an odd number of negations).
only occurs in the scope of an odd number of negations).
Reasoning on finite domains is more difficult than on infinite ones, due to possibility of asserting cardinality constraints on unallocated cells, which explains that the latter condition is more restrictive than the former one. Actually, the finite satisfiability problem is undecidable even if there is only one positive occurrence of a
 with no variable within the scope of
with no variable within the scope of
 . These results establish sharp decidability frontiers within \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\).
. These results establish sharp decidability frontiers within \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\).
Undecidability is shown by reduction from BSR first-order formulæ with two monadic function symbols. To establish the decidability results, we first show that every quantifier-free SL formula can be transformed into an equivalent boolean combination of formulæ of some specific patterns, called test formulæ. This result is interesting in itself, since it provides a precise and intuitive characterization of the expressive power of SL: it shows that separating connectives can be confined to a small set of test formulæ. Afterward, we show that such test formulæ can be transformed into first-order formulæ. If the above conditions (1) or (2) are satisfied, then the obtained first-order formulæ are in the BSR class, which ensures decidability. The PSPACE upper-bound relies on a careful analysis of the maximal size of the test formulæ. The analysis reveals that, although the boolean combination of test formulæ is of exponential size, its components (e.g., the conjunctions in its dnf) are of polynomial size and can be enumerated in polynomial space. For space reasons, full details and proofs are given in a technical report [8].
Applications. Besides theoretical interest, our work has natural applications in program verification. Indeed, purely universal SL formulæ are useful to express pre- or post-conditions asserting “local” constraints on the shape of the data structures manipulated by a program. Consider the atomic proposition \(x \mapsto (y_1,\ldots ,y_k)\) which states that the value of the heap at x is the tuple \((y_1, \ldots , y_k)\) and there is no value, other than x, in the domain of h. With this in mind, the following formula describes a well-formed doubly-linked list:
Such constraints could also be expressed by using inductively defined predicates, unfortunately checking satisfiability of SL formulæ, even of very simple fragments with no occurrence of
 in the presence of user-defined inductive predicates is undecidable, unless some rather restrictive conditions are fulfilled [9]. In contrast, checking entailment between two universal formulæ boils down to checking the satisfiability of a \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) formula, which can be done thanks to the decidability results in our paper.
in the presence of user-defined inductive predicates is undecidable, unless some rather restrictive conditions are fulfilled [9]. In contrast, checking entailment between two universal formulæ boils down to checking the satisfiability of a \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) formula, which can be done thanks to the decidability results in our paper.
The separating implication (magic wand) seldom occurs in such shape constraints. However, it is useful to describe the dynamic transformations of the data structures, as in the following Hoare-style axiom, giving the weakest precondition of
 with respect to redirecting the i-th record field of \(\mathsf {x}\) to \(\mathsf {z}\) [10]:
with respect to redirecting the i-th record field of \(\mathsf {x}\) to \(\mathsf {z}\) [10]:

It is easy to check that the precondition is equivalent to the formula
 because, although hoisting universal quantifiers outside of the separating conjunction is unsound in general, this is possible here due to the special form of the left-hand side \(\mathsf {x} \mapsto (y_1,\ldots ,y_{i-1},\mathsf {z},\ldots ,y_k)\) which unambiguously defines a single heap cell. Therefore, checking that
because, although hoisting universal quantifiers outside of the separating conjunction is unsound in general, this is possible here due to the special form of the left-hand side \(\mathsf {x} \mapsto (y_1,\ldots ,y_{i-1},\mathsf {z},\ldots ,y_k)\) which unambiguously defines a single heap cell. Therefore, checking that
 is an invariant of the program statement \(\mathsf {x.i := z}\) amounts to checking that the formula
is an invariant of the program statement \(\mathsf {x.i := z}\) amounts to checking that the formula
 is unsatisfiable. Because the magic wand occurs negated, this formula falls into a decidable class defined in the present paper, for both finite and infinite satisfiability. The complete formalization of this deductive program verification technique and the characterization of the class of programs for which it is applicable is outside the scope of the paper and is left for future work.
is unsatisfiable. Because the magic wand occurs negated, this formula falls into a decidable class defined in the present paper, for both finite and infinite satisfiability. The complete formalization of this deductive program verification technique and the characterization of the class of programs for which it is applicable is outside the scope of the paper and is left for future work.
Related Work. In contrast to first-order logic for which the decision problem has been thoroughly investigated [1], only a few results are known for SL. For instance, the problem is undecidable in general and PSPACE-complete for quantifier-free formulæ [4]. For \(k=1\), the problem is also undecidable, but it is PSPACE-complete if in addition there is only one quantified variable [6] and decidable but nonelementary if there is no magic wand [2]. In particular, we have also studied the prenex form of \(\mathsf {SL}^{\!\scriptstyle {1}}\) [7] and found out that it is decidable and nonelementary, whereas \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {1}})\) is PSPACE-complete. In contrast, in this paper we show that undecidability occurs for \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\), for \(k\ge 2\).
Expressive completeness results exist for quantifier-free \(\mathsf {SL}^{\!\scriptstyle {1}}\) [2, 11] and for \(\mathsf {SL}^{\!\scriptstyle {1}}\) with one and two quantified variables [5, 6]. There, the existence of equivalent boolean combinations of test formulæ is shown implicitly, using a finite enumeration of equivalence classes of models, instead of an effective transformation. Instead, here we present an explicit equivalence-preserving transformation of quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) into boolean combinations of test formulæ, and translate the latter into first-order logic. Further, we extend the expressive completeness result to finite universes, with additional test formulæ asserting cardinality constraints on unallocated cells.
Another translation of quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) into first-order logic with equality has been described in [3]. There, the small model property of quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) [4] is used to bound the number of first-order variables to be considered and the separating connectives are interpreted as first-order quantifiers. The result is an equisatisfiable first-order formula. This translation scheme cannot be, however, directly applied to \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\), which does not have a small model property, being moreover undecidable. Theory-parameterized versions of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) have been shown to be undecidable, e.g. when integer linear arithmetic is used to reason about locations, and claimed to be PSPACE-complete for countably infinite and finite unbounded location sorts, with no relation other than equality [13]. In the present paper, we show that this claim is wrong, and draw a precise chart of decidability for both infinite and finite satisfiability of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\).
2 Preliminaries
Basic Definitions. Let \(\mathbf{\mathbb {Z}}_{\infty } = \mathbf{\mathbb {Z}}\cup \left\{ \infty \right\} \) and \(\mathbf{\mathbb {N}}_{\infty } = \mathbf{\mathbb {N}}\cup \left\{ \infty \right\} \), where for each \(n \in \mathbf{\mathbb {Z}}\) we have \(n + \infty = \infty \) and \(n<\infty \). For a countable set S we denote by \({||{S}||} \in \mathbf{\mathbb {N}}_\infty \) the cardinality of S. Let \(\mathsf {Var}\) be a countable set of variables, denoted as x, y, z and U be a sort. Vectors of variables are denoted by \(\mathbf x\), \(\mathbf y\), etc. A function symbol f has \(\#(f) \ge 0\) arguments of sort U and a sort
 , which is either the boolean sort \(\mathsf {Bool}\) or U. If \(\#(f)=0\), we call f a constant. We use \(\bot \) and \(\top \) for the boolean constants false and true, respectively. First-order (\(\mathsf {FO}\)) terms t and formulæ
, which is either the boolean sort \(\mathsf {Bool}\) or U. If \(\#(f)=0\), we call f a constant. We use \(\bot \) and \(\top \) for the boolean constants false and true, respectively. First-order (\(\mathsf {FO}\)) terms t and formulæ
 are defined by the following grammar:
are defined by the following grammar:

where \(x\in \mathsf {Var}\), f and p are function symbols,
 and
and
 . We write
. We write
 for
for
 ,
,
 for
for
 ,
,
 and
and
 for
for
 . The size of a formula
. The size of a formula
 , denoted as
, denoted as
 , is the number of symbols needed to write it down. Let
, is the number of symbols needed to write it down. Let
 be the set of variables that occur free in
be the set of variables that occur free in
 , i.e. not in the scope of a quantifier. A sentence
, i.e. not in the scope of a quantifier. A sentence
 is a formula where
is a formula where
 .
.
First-order formulæ are interpreted over \(\mathsf {FO}\)-structures (called structures, when no confusion arises) \(\mathcal {S}= (\mathfrak {U},\mathfrak {s},\mathfrak {i})\), where \(\mathfrak {U}\) is a countable set, called the universe, the elements of which are called locations, \(\mathfrak {s}: \mathsf {Var}\rightharpoonup \mathfrak {U}\) is a mapping of variables to locations, called a store and \(\mathfrak {i}\) interprets each function symbol f by a function \(f^\mathfrak {i}: \mathfrak {U}^{\#(f)} \rightarrow \mathfrak {U}\), if
 and \(f^\mathfrak {i}: \mathfrak {U}^{\#(f)} \rightarrow \{\bot ^\mathfrak {i},\top ^\mathfrak {i}\}\) if
and \(f^\mathfrak {i}: \mathfrak {U}^{\#(f)} \rightarrow \{\bot ^\mathfrak {i},\top ^\mathfrak {i}\}\) if
 . A structure \((\mathfrak {U},\mathfrak {s},\mathfrak {i})\) is finite when \({||{\mathfrak {U}}||} \in \mathbf{\mathbb {N}}\) and infinite otherwise. We write
. A structure \((\mathfrak {U},\mathfrak {s},\mathfrak {i})\) is finite when \({||{\mathfrak {U}}||} \in \mathbf{\mathbb {N}}\) and infinite otherwise. We write
 iff
iff
 is true when interpreted in \(\mathcal {S}\). This relation is defined recursively on the structure of
is true when interpreted in \(\mathcal {S}\). This relation is defined recursively on the structure of
 , as usual. When
, as usual. When
 , we say that \(\mathcal {S}\) is a model of
, we say that \(\mathcal {S}\) is a model of
 . A formula is [finitely] satisfiable when it has a [finite] model. We write
. A formula is [finitely] satisfiable when it has a [finite] model. We write
 when
when
 , for every structure \((\mathfrak {U},\mathfrak {s},\mathfrak {i})\).
, for every structure \((\mathfrak {U},\mathfrak {s},\mathfrak {i})\).
The Bernays-Schönfinkel-Ramsey fragment of \(\mathsf {FO}\), denoted by \(\mathsf {BSR}(\mathsf {FO})\), is the set of sentences
 , where
, where
 is a quantifier-free formula in which all function symbols f of arity \(\#(f)>0\) have sort
is a quantifier-free formula in which all function symbols f of arity \(\#(f)>0\) have sort
 .
.
Separation Logic. Let k be a strictly positive integer. The logic \(\mathsf {SL}^{\!\scriptstyle {k}}\) is the set of formulæ generated by the grammar:

where \(x,y,y_1,\ldots ,y_k \in \mathsf {Var}\). The connectives \(*\) and
 are respectively called the separating conjunction and separating implication (magic wand). We write
are respectively called the separating conjunction and separating implication (magic wand). We write
 (\(\multimap \) is called septraction). The size and set of free variables of an \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
(\(\multimap \) is called septraction). The size and set of free variables of an \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 are defined as for first-order formulæ.
are defined as for first-order formulæ.
Given an \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 and a subformula
and a subformula
 of
of
 , we say that
, we say that
 occurs at polarity \(p \in \left\{ -1,0,1 \right\} \) iff one of the following holds: (i)
occurs at polarity \(p \in \left\{ -1,0,1 \right\} \) iff one of the following holds: (i)
 and \(p=1\), (ii)
and \(p=1\), (ii)
 and
and
 occurs at polarity \(-p\) in
occurs at polarity \(-p\) in
 , (iii)
, (iii)
 or
or
 , and
, and
 occurs at polarity p in
occurs at polarity p in
 , for some \(i=1,2\), or (iv)
, for some \(i=1,2\), or (iv)
 and either
and either
 is a subformula of
is a subformula of
 and \(p=0\), or
and \(p=0\), or
 occurs at polarity p in
occurs at polarity p in
 . A polarity of 1, 0 or \(-1\) is also referred to as positive, neutral or negative, respectively. Note that our notion of polarity is slightly different than usual, because the antecedent of a separating implication is of neutral polarity while the antecedent of an implication is usually of negative polarity. This is meant to strengthen upcoming decidability results, see Remark 2.
. A polarity of 1, 0 or \(-1\) is also referred to as positive, neutral or negative, respectively. Note that our notion of polarity is slightly different than usual, because the antecedent of a separating implication is of neutral polarity while the antecedent of an implication is usually of negative polarity. This is meant to strengthen upcoming decidability results, see Remark 2.
\(\mathsf {SL}^{\!\scriptstyle {k}}\) formulæ are interpreted over \(\mathsf {SL}\)-structures \(\mathcal {I}= (\mathfrak {U}, \mathfrak {s}, \mathfrak {h})\), where \(\mathfrak {U}\) and \(\mathfrak {s}\) are as before and \(\mathfrak {h}: \mathfrak {U}\rightharpoonup _{ fin } \mathfrak {U}^k\) is a finite partial mapping of locations to k-tuples of locations, called a heap. As before, a structure \((\mathfrak {U},\mathfrak {s},\mathfrak {h})\) is finite when \({||{\mathfrak {U}}||} \in \mathbf{\mathbb {N}}\) and infinite otherwise. We denote by \(\mathrm {dom}(\mathfrak {h})\) the domain of the heap \(\mathfrak {h}\) and by \({||{\mathfrak {h}}||} \in \mathbf{\mathbb {N}}\) the cardinality of \(\mathrm {dom}(\mathfrak {h})\). Two heaps \(\mathfrak {h}_1\) and \(\mathfrak {h}_2\) are disjoint iff \(\mathrm {dom}(\mathfrak {h}_1) \cap \mathrm {dom}(\mathfrak {h}_2) = \emptyset \), in which case \(\mathfrak {h}_1 \uplus \mathfrak {h}_2\) denotes their union. A heap \(\mathfrak {h}'\) is an extension of \(\mathfrak {h}\) by \(\mathfrak {h}''\) iff \(\mathfrak {h}' = \mathfrak {h}\uplus \mathfrak {h}''\). The relation
 is defined inductively, as follows:
is defined inductively, as follows:

The semantics of equality, boolean and first-order connectives is the usual one. Satisfiability, entailment and equivalence are defined for \(\mathsf {SL}^{\!\scriptstyle {k}}\) as for \(\mathsf {FO}\) formulæ.
The Bernays-Schönfinkel-Ramsey fragment of \(\mathsf {SL}^{\!\scriptstyle {k}}\), denoted by \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\), is the set of sentences
 , where
, where
 is a quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula. Since there is no function symbol of arity greater than zero in \(\mathsf {SL}^{\!\scriptstyle {k}}\), there is no restriction, other than the form of the quantifier prefix defining \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\).
is a quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula. Since there is no function symbol of arity greater than zero in \(\mathsf {SL}^{\!\scriptstyle {k}}\), there is no restriction, other than the form of the quantifier prefix defining \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\).
3 Test Formulæ for \(\mathsf {SL}^{\!\scriptstyle {k}}\)
We define a small set of \(\mathsf {SL}^{\!\scriptstyle {k}}\) patterns of formulæ, possibly parameterized by a positive integer, called test formulæ. These patterns capture properties related to allocation, points-to relations in the heap and cardinality constraints.
Definition 1
The following patterns are called test formulæ:

where \(x,y \in \mathsf {Var}\), \(\mathbf y \in \mathsf {Var}^k\) and \(n \in \mathbf{\mathbb {N}}_\infty \) is a positive integer or \(\infty \).
The semantics of test formulæ is very natural: \(x \hookrightarrow \mathbf y\) means that x points to vector \(\mathbf y\), \(\mathsf {alloc}(x)\) means that x is allocated, and the arithmetic expressions are interpreted as usual, where \({|{h}|}\) and \({|{U}|}\) respectively denote the number of allocated cells and the number of locations (possibly \(\infty \)). Formally:
Proposition 1
Given an \(\mathsf {SL}\)-structure \((\mathfrak {U},\mathfrak {s},\mathfrak {h})\), the following equivalences hold, for all variables \(x, y_1, \ldots , y_k \in \mathsf {Var}\) and integers \(n \in \mathbf{\mathbb {N}}\):
Not all atoms of \(\mathsf {SL}^{\!\scriptstyle {k}}\) are test formulæ, for instance \(x \mapsto \mathbf y\) and \(\mathsf {emp}\) are not test formulæ. However, by Proposition 1, we have the equivalences \(x \mapsto \mathbf y \equiv x \hookrightarrow \mathbf y \wedge \lnot {|{h}|} \ge 2\) and \(\mathsf {emp}\equiv \lnot {|{h}|} \ge 1\). Note that, for any \(n \in \mathbf{\mathbb {N}}\), the test formulæ \({|{U}|}\ge n\) and \({|{h}|}\ge {|{U}|}-n\) are trivially true and false respectively, if the universe is infinite. We write \(t < u\) for \(\lnot (t \ge u)\).
We need to introduce a few notations useful to describe upcoming transformations in a concise and precise way. A literal is a test formula or its negation. Unless stated otherwise, we view a conjunction T of literals as a setFootnote 1 and we use the same symbol to denote both a set and the formula obtained by conjoining the elements of the set. The equivalence relation \(x \approx _T y\) is defined as \(T\,\models \,x \approx y\) and we write \(x \not \approx _T y\) for \(T\,\models \,\lnot x \approx y\). Observe that \(x \not \approx _T y\) is not the complement of \(x \approx _T y\). For a set X of variables, \({|{X}|}_T\) is the number of equivalence classes of \(\approx _T\) in X.
Definition 2
A variable x is allocated in an \(\mathsf {SL}\)-structure \(\mathcal {I}\) iff \(\mathcal {I}\,\models \,\mathsf {alloc}(x)\). For a set of variables \(X \subseteq \mathsf {Var}\), let  and \(\mathsf {nalloc}(X) {\mathop {=}\limits ^{\scriptscriptstyle {\mathsf {def}}}}\bigwedge _{x \in X} \lnot \mathsf {alloc}(x)\). For a set T of literals, let:
and \(\mathsf {nalloc}(X) {\mathop {=}\limits ^{\scriptscriptstyle {\mathsf {def}}}}\bigwedge _{x \in X} \lnot \mathsf {alloc}(x)\). For a set T of literals, let:
We let  be the number of equivalence classes of \(\approx _T\) containing variables allocated in every model of T and
be the number of equivalence classes of \(\approx _T\) containing variables allocated in every model of T and  be the number of equivalence classes of \(\approx _T\) containing variables from X that are not allocated in any model of T. We also let
be the number of equivalence classes of \(\approx _T\) containing variables from X that are not allocated in any model of T. We also let  .
.
Intuitively, \(\mathsf {av}({T})\) [\(\mathsf {nv}({T})\)] is the set of variables that must be [are never] allocated in every [any] model of T, and \(\mathsf {fp}_{X}({T})\) is the footprint of T relative to the set \(X \subseteq \mathsf {Var}\), i.e. the set of formulæ describing allocation and points-to relations over variables from X. For example, if \(T = \{x \approx z, \mathsf {alloc}(x), \lnot \mathsf {alloc}(y), \lnot z \hookrightarrow \mathbf y\}\), then \(\mathsf {av}({T}) = \left\{ x,z \right\} \), \(\mathsf {nv}({T}) = \left\{ y \right\} \), \(\mathsf {fp}_a({T}) = \left\{ \mathsf {alloc}(x),\lnot z \hookrightarrow \mathbf y \right\} \) and \(\mathsf {fp}_{\mathsf {nv}({T})}({T}) = \left\{ \lnot \mathsf {alloc}(y) \right\} \).
3.1 From Test Formulæ to \(\mathsf {FO}\)
The introduction of test formulæ (Definition 1) is motivated by the reduction of the (in)finite satisfiability problem for quantified boolean combinations thereof to the same problem for \(\mathsf {FO}\). The reduction is devised in such a way that the obtained formula is in the BSR class, if possible. Given a quantified boolean combination of test formulæ
 , the \(\mathsf {FO}\) formula
, the \(\mathsf {FO}\) formula
 is defined by induction on the structure of
is defined by induction on the structure of
 :
:

where \(\mathfrak {p}\) is a \((k+1)\)-ary function symbol of sort \(\mathsf {Bool}\) and \(\mathfrak {a}_n,\mathfrak {b}_n\) and \(\mathfrak {c}_n\) are constants of sort \(\mathsf {Bool}\), for all \(n \in \mathbf{\mathbb {N}}\). These function symbols are related by the following axioms, where \(\mathfrak {u}_n, \mathfrak {v}_n\) and \(\mathfrak {w}_n\) are constants of sort U, for all \(n > 0\):

Intuitively, \(\mathfrak {p}\) encodes the heap and \(\mathfrak {a}_n\) (resp. \(\mathfrak {b}_n\)) is true iff there are at least n cells in the domain of the heap (resp. in the universe), namely \(\mathfrak {u}_1, \ldots , \mathfrak {u}_n\) (resp. \(\mathfrak {v}_1, \ldots , \mathfrak {v}_n\)). If \(\mathfrak {c}_n\) is true, then there are at least n locations \(\mathfrak {w}_1, \ldots , \mathfrak {w}_n\) outside of the domain of the heap (free), but the converse does not hold. The \(C_n\) axioms do not state the equivalence of \(\mathfrak {c}_n\) with the existence of at least n free locations, because such an equivalence cannot be expressed in \(\mathsf {BSR}(\mathsf {FO})\)Footnote 2. As a consequence, the transformation preserves sat-equivalence only if the formulæ \({|{h}|}\ge {|{U}|}-n\) occur only at negative polarity (see Lemma 1, Point 2). If the domain is infinite then this problem does not arise since the formulæ \({|{h}|} \ge {|{U}|} - n\) are always false.
Definition 3
For a quantified boolean combination of test formulæ
 , we let
, we let
 be the maximum integer n occurring in a test formula
be the maximum integer n occurring in a test formula
 of the form \({|{h}|}\ge n\), \({|{U}|}\ge n,\) or \({|{h}|}\ge {|{U}|}-n\) from
of the form \({|{h}|}\ge n\), \({|{U}|}\ge n,\) or \({|{h}|}\ge {|{U}|}-n\) from
 and define
and define
 as the set of axioms related to
as the set of axioms related to
 .
.
The relationship between
 and
and
 is stated below.
is stated below.
Lemma 1
Let
 be a quantified boolean combination of test formulæ. The following hold, for any universe \(\mathfrak {U}\) and any store \(\mathfrak {s}\):
be a quantified boolean combination of test formulæ. The following hold, for any universe \(\mathfrak {U}\) and any store \(\mathfrak {s}\):
-
1.
if
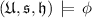 , for a heap \(\mathfrak {h}\), then
, for a heap \(\mathfrak {h}\), then
 , for an interpretation \(\mathfrak {i}\);
, for an interpretation \(\mathfrak {i}\); -
2.
if each test formula \({|{h}|} \ge {|{U}|} - n\) in
 occurs at a negative polarity and
occurs at a negative polarity and
 for an interpretation \(\mathfrak {i}\) such that
for an interpretation \(\mathfrak {i}\) such that
 , then
, then
 , for a heap \(\mathfrak {h}\).
, for a heap \(\mathfrak {h}\).
The translation of \(\mathsf {alloc}(x)\) introduces existential quantifiers depending on x. For instance, \(\forall x ~.~ \mathsf {alloc}(x)\) is translated as \(\forall x \exists y_1 \ldots \exists y_k ~.~ \mathfrak {p}(x,y_1,\ldots ,y_k)\), which lies outside of the \(\mathsf {BSR}(\mathsf {FO})\) fragment. Because upcoming decidability results (Theorem 2) require that
 be in \(\mathsf {BSR}(\mathsf {FO})\), we end this section by delimiting a fragment of \(\mathsf {SL}^{\!\scriptstyle {k}}\) whose translation falls into \(\mathsf {BSR}(\mathsf {FO})\).
be in \(\mathsf {BSR}(\mathsf {FO})\), we end this section by delimiting a fragment of \(\mathsf {SL}^{\!\scriptstyle {k}}\) whose translation falls into \(\mathsf {BSR}(\mathsf {FO})\).
Lemma 2
Given an \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 , where
, where
 is a boolean combination of test formulæ containing no positive occurrence of \(\mathsf {alloc}(z_i)\) for any \(i \in [1,m]\),
is a boolean combination of test formulæ containing no positive occurrence of \(\mathsf {alloc}(z_i)\) for any \(i \in [1,m]\),
 is equivalent (up to transformation into prenex form) to a \(\mathsf {BSR}(\mathsf {FO})\) formula with the same constants and free variables as
is equivalent (up to transformation into prenex form) to a \(\mathsf {BSR}(\mathsf {FO})\) formula with the same constants and free variables as
 .
.
Intuitively, if a formula \(\mathsf {alloc}(x)\) occurs negatively then the quantifiers \(\exists y_1\mathbin {}\dots \mathbin {}\exists y_k\) added when translating \(\mathsf {alloc}(x)\) can be transformed into universal ones by transformation into nnf, and if x is not universal then they may be shifted at the root of the formula since \(y_1,\dots ,y_k\) depend only on x. In both cases, the quantifier prefix \(\exists ^* \forall ^*\) is preserved.
4 From Quantifier-Free \(\mathsf {SL}^{\!\scriptstyle {k}}\) to Test formulæ
This section states the expressive completeness result of the paper, namely that any quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula is equivalent, on both finite and infinite models, to a boolean combination of test formulæ. Starting from a quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 , we define a set
, we define a set
 of conjunctions of test formulæ and their negations, called minterms, such that
of conjunctions of test formulæ and their negations, called minterms, such that
 . Although the number of minterms in
. Although the number of minterms in
 is exponential in the size of
is exponential in the size of
 , checking the membership of a given minterm M in
, checking the membership of a given minterm M in
 can be done in PSPACE. Together with the translation of minterms into \(\mathsf {FO}\) (Sect. 3.1), this fact is used to prove PSPACE membership of the two decidable fragments of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\), defined next (Sect. 5.2).
can be done in PSPACE. Together with the translation of minterms into \(\mathsf {FO}\) (Sect. 3.1), this fact is used to prove PSPACE membership of the two decidable fragments of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\), defined next (Sect. 5.2).
4.1 Minterms
A minterm M is a set (conjunction) of literals containing: exactly one literal \({|{h}|} \ge \mathrm {min}_M\) and one literal \({|{h}|} < \mathrm {max}_M\), where \(\mathrm {min}_M \in \mathbf{\mathbb {N}}\cup \left\{ {|{U}|} - n \mid n \in \mathbf{\mathbb {N}} \right\} \) and \(\mathrm {max}_M \in \mathbf{\mathbb {N}}_{\infty } \cup \left\{ {|{U}|} - n \mid n \in \mathbf{\mathbb {N}} \right\} \), and at most one literal of the form \({|{U}|} \ge n\), respectively \({|{U}|} < n\).
A minterm may be viewed as an abstract description of a heap. The conditions are for technical convenience only and are not restrictive. For instance, tautological test formulæ of the form \({|{h}|} \ge 0\) and/or \({|{h}|} < \infty \) may be added if needed so that the first condition holds. If M contains two literals \(t\ge n_1\) and \(t \ge n_2\) with \(n_1 < n_2\) and \(t \in \{ {|{h}|}, {|{U}|} \}\) then \(t \ge n_1\) is redundant and can be removed – and similarly if M contains literals \({|{h}|} \ge {|{U}|}-n_1\) and \({|{h}|} \ge {|{U}|}-n_2\). Heterogeneous constraints are merged by performing a case split on the value of \({|{U}|}\). For example, if M contains both \({|{h}|} \ge {|{U}|}-4\) and \({|{h}|} \ge 1\), then the first condition prevails if \({|{U}|} \ge 5\) yielding the equivalence disjunction: \({|{h}|} \ge 1 \wedge {|{U}|}<5 \vee {|{h}|} \ge {|{U}|}-4 \wedge {|{U}|}\ge 5\). Thus, in the following, we assume that any conjunction of literals can be transformed into a disjunction of minterms [8].
Definition 4
Given a minterm M, we define the sets:
Thus, \(M = M^e \cup M^u \cup M^a \cup M^p \cup \left\{ {|{h}|} \ge \mathrm {min}_M, {|{h}|} < \mathrm {max}_M \right\} \), for each minterm M. Given a set of variables \(X \subseteq \mathsf {Var}\), a minterm M is (1) E-complete for X iff for all \(x,y \in X\) exactly one of \(x \approx y \in M\), \(\lnot x \approx y \in M\) holds, and (2) A-complete for X iff for each \(x \in X\) exactly one of \(\mathsf {alloc}(x) \in M\), \(\lnot \mathsf {alloc}(x) \in M\) holds.
For a literal \(\ell \), we denote by \(\overline{\ell }\) its complement, i.e.
 and
and
 , where
, where
 is a test formula. Let \(\overline{M}\) be the minterm obtained from M by replacing each literal with its complement. The complement closure of M is
is a test formula. Let \(\overline{M}\) be the minterm obtained from M by replacing each literal with its complement. The complement closure of M is  . Two tuples \(\mathbf y, \mathbf y' \in \mathsf {Var}^k\) are M-distinct if \(y_i \not \approx _M y'_i\), for some \(i \in [1,k]\). Given a minterm M that is E-complete for \(\mathsf {var}({M})\), its points-to closure is \(\mathsf {pc}({M}) {\mathop {=}\limits ^{\scriptscriptstyle {\mathsf {def}}}}\bot \) if there exist literals \(x \hookrightarrow \mathbf y, x' \hookrightarrow \mathbf y' \in M\) such that \(x \approx _M x'\) and \(\mathbf y\), \(\mathbf y'\) are M-distinct, and
. Two tuples \(\mathbf y, \mathbf y' \in \mathsf {Var}^k\) are M-distinct if \(y_i \not \approx _M y'_i\), for some \(i \in [1,k]\). Given a minterm M that is E-complete for \(\mathsf {var}({M})\), its points-to closure is \(\mathsf {pc}({M}) {\mathop {=}\limits ^{\scriptscriptstyle {\mathsf {def}}}}\bot \) if there exist literals \(x \hookrightarrow \mathbf y, x' \hookrightarrow \mathbf y' \in M\) such that \(x \approx _M x'\) and \(\mathbf y\), \(\mathbf y'\) are M-distinct, and  , otherwise. Intuitively, \(\mathsf {pc}({M})\) is \(\bot \) iff M contradicts the fact that the heap is a partial functionFootnote 3. The domain closure of M is
, otherwise. Intuitively, \(\mathsf {pc}({M})\) is \(\bot \) iff M contradicts the fact that the heap is a partial functionFootnote 3. The domain closure of M is  if either \(\mathrm {min}_M = n_1\) and \(\mathrm {max}_M = n_2\) for some \(n_1,n_2 \in \mathbf{\mathbb {Z}}\) such that \(n_1 \ge n_2\), or \(\mathrm {min}_M = {|{U}|} - n_1\) and \(\mathrm {max}_M = {|{U}|} - n_2\), where \(n_2 \ge n_1\); and otherwise:
if either \(\mathrm {min}_M = n_1\) and \(\mathrm {max}_M = n_2\) for some \(n_1,n_2 \in \mathbf{\mathbb {Z}}\) such that \(n_1 \ge n_2\), or \(\mathrm {min}_M = {|{U}|} - n_1\) and \(\mathrm {max}_M = {|{U}|} - n_2\), where \(n_2 \ge n_1\); and otherwise:

where
 is the number of pairwise M-distinct tuples \(\mathbf y\) for which there exists \(\lnot x' \hookrightarrow \mathbf y \in M\) such that \(x \approx _M x'\). Intuitively, \(\mathsf {dc}({M})\) asserts that \(\mathrm {min}_M < \mathrm {max}_M\) and that the domain contains enough elements to allocate all cells. Essentially, given a structure \((\mathfrak {U},\mathfrak {s},\mathfrak {h})\), if \(\mathfrak {h}(x)\) is known to be defined and distinct from n pairwise distinct vectors of locations \(\mathbf v_1, \ldots , \mathbf v_n\), then necessarily at least \(n+1\) vectors must exist. Since there are \({||{\mathfrak {U}}||}^k\) vectors of length k, we must have \({||{\mathfrak {U}}||}^k \ge n+1\), hence \({||{\mathfrak {U}}||} \ge \root k \of {n+1}\). For instance, if \(M = \{ \lnot x \hookrightarrow y_i, \mathsf {alloc}(x), y_i \not \approx y_j \mid i,j \in [1,n], i \not = j \}\), then it is clear that M is unsatisfiable if there are less than n locations, since x cannot be allocated in this case.
is the number of pairwise M-distinct tuples \(\mathbf y\) for which there exists \(\lnot x' \hookrightarrow \mathbf y \in M\) such that \(x \approx _M x'\). Intuitively, \(\mathsf {dc}({M})\) asserts that \(\mathrm {min}_M < \mathrm {max}_M\) and that the domain contains enough elements to allocate all cells. Essentially, given a structure \((\mathfrak {U},\mathfrak {s},\mathfrak {h})\), if \(\mathfrak {h}(x)\) is known to be defined and distinct from n pairwise distinct vectors of locations \(\mathbf v_1, \ldots , \mathbf v_n\), then necessarily at least \(n+1\) vectors must exist. Since there are \({||{\mathfrak {U}}||}^k\) vectors of length k, we must have \({||{\mathfrak {U}}||}^k \ge n+1\), hence \({||{\mathfrak {U}}||} \ge \root k \of {n+1}\). For instance, if \(M = \{ \lnot x \hookrightarrow y_i, \mathsf {alloc}(x), y_i \not \approx y_j \mid i,j \in [1,n], i \not = j \}\), then it is clear that M is unsatisfiable if there are less than n locations, since x cannot be allocated in this case.
Definition 5
A minterm M is footprint-consistentFootnote 4 if for all \(x,x' \in \mathsf {Var}\) and \(\mathbf y, \mathbf y' \in \mathsf {Var}^k\), such that \(x \approx _M x'\) and \(y_i \approx _M y'_i\) for all \(i \in [1,k]\), we have (1) if \(\mathsf {alloc}(x) \in M\) then \(\lnot \mathsf {alloc}(x') \not \in M\), and (2) if \(x \hookrightarrow \mathbf y \in M\) then \(\lnot \mathsf {alloc}(x'), \lnot x' \hookrightarrow \mathbf y' \not \in M\).
We are now ready to define a boolean combination of test formulæ that is equivalent to \(M_1 * M_2\), where \(M_1\) and \(M_2\) are minterms satisfying a number of additional conditions. Let \(\mathsf {npto}({M_1},{M_2})\,{\mathop {=}\limits ^{\scriptscriptstyle {\mathsf {def}}}}\,(M_1 \cap M_2) \cap \{\lnot x \hookrightarrow \mathbf y \mid x \not \in \mathsf {av}({M_1 \cup M_2}), \mathbf y \in \mathsf {Var}^k\}\) be the set of negative points-to literals common to \(M_1\) and \(M_2\), involving left-hand side variables not allocated in either \(M_1\) or \(M_2\).
Lemma 3
Let \(M_1\), \(M_2\) be two footprint-consistent minterms that are and E-complete for \(\mathsf {var}({M_1 \cup M_2})\), with \(\mathsf {cc}({M_1^p}) = \mathsf {cc}({M_2^p})\). Then \(M_1 * M_2 \equiv \mathsf {elim}_*(M_1,M_2)\), where
and
 .
.
Intuitively, if \(M_1\) and \(M_2\) hold separately, then all heap-independent literals from \(M_1 \cup M_2\) must be satisfied (2), the variables allocated in \(M_1\) and \(M_2\) must be pairwise distinct and their footprints, relative to the allocated variables, jointly asserted (3). Moreover, unallocated variables on both sides must not be allocated and common negative points-to literals must be asserted (4). Since the heap satisfying \(\mathsf {elim}_*(M_1,M_2)\) is the disjoint union of the heaps for \(M_1\) and \(M_2\), its bounds are the sum of the bounds on both sides (5) and, moreover, the variables that \(M_2\) never allocates [\(\mathsf {nv}({M_2})\)] may occur allocated in the heap of \(M_1\) and viceversa, thus the constraints
 and
and
 , respectively (6).
, respectively (6).
Next, we show a similar result for the separating implication. For technical convenience, we translate the septraction \(M_1 \multimap M_2\), instead of
 , as an equivalent boolean combination of test formulæ. This is without loss of generality, because
, as an equivalent boolean combination of test formulæ. This is without loss of generality, because
 . Unlike with the case of the separating conjunction (Lemma 3), here the definition of the boolean combination of test formulæ depends on whether the universe is finite or infinite.
. Unlike with the case of the separating conjunction (Lemma 3), here the definition of the boolean combination of test formulæ depends on whether the universe is finite or infinite.
If the complement of some literal \(\ell \in \mathsf {fp}_a({M_1})\) belongs to \(M_2\) then no extension by a heap that satisfies \(\ell \) may satisfy \(\overline{\ell }\). Therefore, as an additional simplifying assumption, we suppose that \(\mathsf {fp}_a({M_1}) \cap \overline{M_2} = \emptyset \), so that \(M_1 \multimap M_2\) is not trivially unsatisfiable. We write
 [
[
 ] if
] if
 has the same truth value as
has the same truth value as
 in all finite [infinite] structures.
in all finite [infinite] structures.
Lemma 4
Let \(M_1\) and \(M_2\) be footprint-consistent minterms that are E-complete for \(\mathsf {var}({M_1 \cup M_2})\), such that: \(M_1\) is A-complete for \(\mathsf {var}({M_1 \cup M_2})\), \(M_2^a \cup M_2^p \subseteq \mathsf {cc}({M_1^a \cup M_1^p})\) and \(\mathsf {fp}_a({M_1}) \cap \overline{M_2} = \emptyset \).
Then,
 , where:
, where:
with
 ,
,
 .
.
A heap satisfies \(M_1 \multimap M_2\) iff it has an extension, by a disjoint heap satisfying \(M_1\), that satisfies \(M_2\). Thus, \(\mathsf {elim}^\dagger _\multimap (M_1,M_2)\) must entail the heap-independent literals of both \(M_1\) and \(M_2\) (7). Next, no variable allocated by \(M_1\) must be allocated by \(\mathsf {elim}^\dagger _\multimap (M_1,M_2)\), otherwise no extension by a heap satisfying \(M_1\) is possible and, moreover, the footprint of \(M_2\) relative to the unallocated variables of \(M_1\) must be asserted (8). The heap’s cardinality constraints depend on the bounds of \(M_1\) and \(M_2\) (9) and, if Y is a set of variables not allocated in the heap, these variables can be allocated in the extension (10). Actually, this is where the finite universe assumption first comes into play. If the universe is infinite, then there are enough locations outside the heap to be assigned to Y. However, if the universe is finite, then it is necessary to ensure that there are at least \(\#_{n}({Y},{M_1})\) free locations to be assigned to Y (10).
4.2 Translating Quantifier-Free \(\mathsf {SL}^{\!\scriptstyle {k}}\) into Minterms
We prove next that each quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula is equivalent to a finite disjunction of minterms:
Lemma 5
Given a quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 , there exist two sets of minterms
, there exist two sets of minterms
 and
and
 such that the following equivalences hold: (1)
such that the following equivalences hold: (1)
 , and (2)
, and (2)
 .
.
The formal definition of
 and
and
 is given in [8] and omitted for the sake of conciseness and readability. Intuitively, these sets are defined by induction on the structure of the formula. For base cases, the following equivalences are used:
is given in [8] and omitted for the sake of conciseness and readability. Intuitively, these sets are defined by induction on the structure of the formula. For base cases, the following equivalences are used:
For formulæ
 or
or
 , the transformation is first applied recursively on
, the transformation is first applied recursively on
 and
and
 , then the obtained formula is transformed into dnf. For formulæ
, then the obtained formula is transformed into dnf. For formulæ
 or
or
 , the transformation is applied on
, the transformation is applied on
 and
and
 , then the following equivalences are used to shift \(*\) and \(\multimap \) innermost in the formula:
, then the following equivalences are used to shift \(*\) and \(\multimap \) innermost in the formula:

Afterwards, the operands of \(*\) and \(\multimap \) are minterms, and the result is obtained using the equivalences in Lemmas 3 and 4, respectively (up to a transformation into dnf). The only difficulty is that these lemmas impose some additional conditions on the minterms (e.g., being E-complete, or A-complete). However, the conditions are easy to enforce by case splitting, as illustrated by the following example:
Example 1
Consider the formula \(x \mapsto x \multimap y \mapsto y\). It is easy to check that \(\mu ^{\scriptscriptstyle {\dagger }}({x \mapsto x}) = \{ M_1 \}\), for \(\dagger \in \left\{ fin , inf \right\} \), where \(M_1 = x \hookrightarrow x \wedge {|{h}|} \ge 1 \wedge {|{h}|} < 2\) and \(\mu ^{\scriptscriptstyle {\dagger }}({y \mapsto y}) = \{ M_2 \}\), where \(M_2 = y \hookrightarrow y \wedge {|{h}|} \ge 1 \wedge {|{h}|} < 2\). To apply Lemma 4, we need to ensure that \(M_1\) and \(M_2\) are E-complete, which may be done by adding either \(x \approx y\) or \(x \not \approx y\) to each minterm. We also have to ensure that \(M_1\) is A-complete, thus for \(z\in \left\{ x,y \right\} \), we add either \(\mathsf {alloc}(z)\) or \(\lnot \mathsf {alloc}(z)\) to \(M_1\). Finally, we must have \(M_2^a \cup M_2^p \subseteq \mathsf {cc}({M_1^a \cup M_1^p})\), thus we add either \(y \hookrightarrow y\) or \(\lnot y \hookrightarrow y\) to \(M_1\). After removing redundancies, we get (among others) the minterms: \(M_1' = x \hookrightarrow x \wedge {|{h}|} \ge 1 \wedge {|{h}|} < 2 \wedge x \approx y\) and \(M'_2= y \hookrightarrow y \wedge {|{h}|} \ge 1 \wedge {|{h}|} < 2 \wedge x \approx y\). Afterwards we compute \(\mathsf {elim}^{\scriptscriptstyle { fin }}_{\multimap }(M_1',M_2') = x \approx y \wedge \lnot \mathsf {alloc}(x) \wedge {|{h}|} \ge 0 \wedge \) \({|{h}|} < 1\). \(\blacksquare \)
As explained in Sect. 3.1, boolean combinations of minterms can only be transformed into sat-equivalent \(\mathsf {BSR}(\mathsf {FO})\) formulæ if there is no positive occurrence of test formulæ \({|{h}|} \ge {|{U}|}-n\) or \(\mathsf {alloc}(x)\) (see the conditions in Lemmas 1 (2) and 2). Consequently, we relate the polarity of these formulæ in some minterm
 with that of a separating implication within
with that of a separating implication within
 . The analysis depends on whether the universe is finite or infinite.
. The analysis depends on whether the universe is finite or infinite.
Lemma 6
For any quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 , the following properties hold:
, the following properties hold:
-
1.
For all
 , we have \(M \cap \{{|{h}|} \ge {|{U}|}-n, {|{h}|} < {|{U}|}-n \mid n \in \mathbf{\mathbb {N}}\} = \emptyset \).
, we have \(M \cap \{{|{h}|} \ge {|{U}|}-n, {|{h}|} < {|{U}|}-n \mid n \in \mathbf{\mathbb {N}}\} = \emptyset \). -
2.
If \({|{h}|} \ge {|{U}|}-n \in M\) [\({|{h}|} < {|{U}|}-n \in M\)] for some minterm
 , then a formula
, then a formula
 occurs at a positive [negative] polarity in
occurs at a positive [negative] polarity in
 .
. -
3.
If \(\mathsf {alloc}(x) \in M\) [\(\lnot \mathsf {alloc}(x) \in M\)] for some minterm
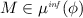 , then a formula
, then a formula
 , such that
, such that
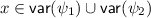 , occurs at a positive [negative] polarity in
, occurs at a positive [negative] polarity in
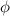 .
. -
4.
If \(M \cap \left\{ \mathsf {alloc}(x),\lnot \mathsf {alloc}(x) \mid x \in \mathsf {Var} \right\} \ne \emptyset \) for some minterm
 , then a formula
, then a formula
 , such that
, such that
 , occurs in
, occurs in
 at some polarity \(p \in \left\{ -1,1 \right\} \). Moreover, \(\mathsf {alloc}(x)\) occurs at a polarity \(-p\), only if \(\mathsf {alloc}(x)\) is in the scope of a
at some polarity \(p \in \left\{ -1,1 \right\} \). Moreover, \(\mathsf {alloc}(x)\) occurs at a polarity \(-p\), only if \(\mathsf {alloc}(x)\) is in the scope of a
 subformula (10) of a formula \(\mathsf {elim}^{\scriptscriptstyle { fin }}_{\multimap }(M_1,M_2)\) used to compute
subformula (10) of a formula \(\mathsf {elim}^{\scriptscriptstyle { fin }}_{\multimap }(M_1,M_2)\) used to compute
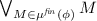 .
.
Given a quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 , the number of minterms occurring in
, the number of minterms occurring in
 [
[
 ] is exponential in the size of
] is exponential in the size of
 , in the worst case. Therefore, an optimal decision procedure cannot generate and store these sets explicitly, but rather must enumerate minterms lazily. We show that (i) the size of the minterms in
, in the worst case. Therefore, an optimal decision procedure cannot generate and store these sets explicitly, but rather must enumerate minterms lazily. We show that (i) the size of the minterms in
 is bounded by a polynomial in the size of
is bounded by a polynomial in the size of
 , and that (ii) the problem “given a minterm M, does M occur in
, and that (ii) the problem “given a minterm M, does M occur in
 [resp. in
[resp. in
 ]?” is in PSPACE. To this aim, we define a measure on a quantifier-free formula
]?” is in PSPACE. To this aim, we define a measure on a quantifier-free formula
 , which bounds the size of the minterms in the sets
, which bounds the size of the minterms in the sets
 and
and
 , inductively on the structure of the formulæ:
, inductively on the structure of the formulæ:

Definition 6
A minterm M is
 by a formula
by a formula
 , if for each literal \(\ell \in M\), the following hold: (i)
, if for each literal \(\ell \in M\), the following hold: (i)
 if \(\ell \in \left\{ {|{h}|} \ge \min _{M_i}, {|{h}|} < \max _{M_i} \right\} \) (ii)
if \(\ell \in \left\{ {|{h}|} \ge \min _{M_i}, {|{h}|} < \max _{M_i} \right\} \) (ii)
 , if \(\ell \in \left\{ {|{U}|} \ge n, {|{U}|} < n \mid n \in \mathbf{\mathbb {N}} \right\} \).
, if \(\ell \in \left\{ {|{U}|} \ge n, {|{U}|} < n \mid n \in \mathbf{\mathbb {N}} \right\} \).
The following lemma provides the desired result:
Lemma 7
Given a quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 , each minterm
, each minterm
 is
is
 by
by
 .
.
The proof goes by a careful analysis of the test formulæ introduced in Lemmas 3 and 4 or created by minterm transformations (see [8] for details). Since
 is polynomially bounded by
is polynomially bounded by
 , this entails that it is possible to check whether
, this entails that it is possible to check whether
 [resp.
[resp.
 ] using space bounded also by a polynomial in
] using space bounded also by a polynomial in
 .
.
Lemma 8
Given a minterm M and an \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula
 , the problems of checking whether
, the problems of checking whether
 and
and
 are in PSPACE.
are in PSPACE.
Remark 1
Observe that the formulæ \(\mathsf {elim}_*(M_1,M_2)\) and
 in Lemmas 3 and 4 are of exponential size, because Y ranges over sets of variables. However these formulæ do not need to be constructed explicitly. To check that
in Lemmas 3 and 4 are of exponential size, because Y ranges over sets of variables. However these formulæ do not need to be constructed explicitly. To check that
 or
or
 , we only have to guess such sets Y. See [8] for details.
, we only have to guess such sets Y. See [8] for details.
5 Bernays-Schönfinkel-Ramsey \(\mathsf {SL}^{\!\scriptstyle {k}}\)
This section gives the results concerning decidability of the (in)finite satisfiability problems within the \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) fragment. \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) is the set of sentences
 , where
, where
 is a quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula, with
is a quantifier-free \(\mathsf {SL}^{\!\scriptstyle {k}}\) formula, with
 , where the existentially quantified variables \(x_1,\ldots ,x_n\) are left free. First, we show that, contrary to \(\mathsf {BSR}(\mathsf {FO})\), the satisfiability of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) is undecidable for \(k\ge 2\). Second, we carve two nontrivial fragments of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\), for which the infinite and finite satisfiability problems are both PSPACE-complete. These fragments are defined based on restrictions of (i) polarities of the occurrences of the separating implication, and (ii) occurrences of universally quantified variables in the scope of separating implications. These results draw a rather precise chart of decidability within the \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) fragment. For \(k=1\), the satisfiability problem of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {1}})\) is in PSPACE [7] (it is undecidable for arbitrary \(\mathsf {SL}^{\!\scriptstyle {1}}\) formulæ [2] and decidable but nonelementary for prenex formulæ [7]).
, where the existentially quantified variables \(x_1,\ldots ,x_n\) are left free. First, we show that, contrary to \(\mathsf {BSR}(\mathsf {FO})\), the satisfiability of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) is undecidable for \(k\ge 2\). Second, we carve two nontrivial fragments of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\), for which the infinite and finite satisfiability problems are both PSPACE-complete. These fragments are defined based on restrictions of (i) polarities of the occurrences of the separating implication, and (ii) occurrences of universally quantified variables in the scope of separating implications. These results draw a rather precise chart of decidability within the \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) fragment. For \(k=1\), the satisfiability problem of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {1}})\) is in PSPACE [7] (it is undecidable for arbitrary \(\mathsf {SL}^{\!\scriptstyle {1}}\) formulæ [2] and decidable but nonelementary for prenex formulæ [7]).
5.1 Undecidability of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\)
Theorem 1
The finite and infinite satisfiability problems are both undecidable for \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\).
We provide a brief sketch of the proof, see [8] for details. We consider the finite satisfiability problem of the \([\forall ,(0),(2)]_=\) fragment of \(\mathsf {FO}\), which consists of sentences of the form
 , where
, where
 is a quantifier-free boolean combination of atomic propositions \(t_1 \approx t_2\), and \(t_1, t_2\) are terms built using two function symbols f and g, of arity one, the variable x and constant c. It is known (see e.g. [1, Theorem 4.1.8]) that finite satisfiability is undecidable for \([\forall ,(0),(2)]_=\). We reduce this problem to \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) satisfiability. The idea is to encode the value of f and g into the heap, in such a way that every element x points to (f(x), g(x)). Given a sentence
is a quantifier-free boolean combination of atomic propositions \(t_1 \approx t_2\), and \(t_1, t_2\) are terms built using two function symbols f and g, of arity one, the variable x and constant c. It is known (see e.g. [1, Theorem 4.1.8]) that finite satisfiability is undecidable for \([\forall ,(0),(2)]_=\). We reduce this problem to \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) satisfiability. The idea is to encode the value of f and g into the heap, in such a way that every element x points to (f(x), g(x)). Given a sentence
 in \([\forall ,(0),(2)]_=\), we proceed by first flattening each term in
in \([\forall ,(0),(2)]_=\), we proceed by first flattening each term in
 consisting of nested applications of f and g. The result is an equivalent sentence
consisting of nested applications of f and g. The result is an equivalent sentence
 , in which the only terms are \(x_i\), c, \(f(x_i)\), \(g(x_i)\), f(c) and g(c), for \(i \in [1,n]\). For example, the formula \(\forall x~.~ f(g(x)) \approx c\) is flattened into \(\forall x_1 \forall x_2~.~ g(x_1) \not \approx x_2 \vee f(x_2) \approx c\). We define the following \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {2}})\) sentences
, in which the only terms are \(x_i\), c, \(f(x_i)\), \(g(x_i)\), f(c) and g(c), for \(i \in [1,n]\). For example, the formula \(\forall x~.~ f(g(x)) \approx c\) is flattened into \(\forall x_1 \forall x_2~.~ g(x_1) \not \approx x_2 \vee f(x_2) \approx c\). We define the following \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {2}})\) sentences
 , for \(\dagger \in \left\{ fin , inf \right\} \):
, for \(\dagger \in \left\{ fin , inf \right\} \):

with
 ,
,
 and
and
 is obtained from
is obtained from
 by replacing each occurrence of c by \(x_c\), each term f(c) [g(c)] by \(y_{c}\) [\(z_c\)] and each term \(f(x_i)\) [\(g(x_i)\)] by \(y_i\) [\(z_i\)]. Intuitively,
by replacing each occurrence of c by \(x_c\), each term f(c) [g(c)] by \(y_{c}\) [\(z_c\)] and each term \(f(x_i)\) [\(g(x_i)\)] by \(y_i\) [\(z_i\)]. Intuitively,
 asserts that the heap is a total function, and
asserts that the heap is a total function, and
 states that every referenced cell is allocatedFootnote 5. It is easy to check that
states that every referenced cell is allocatedFootnote 5. It is easy to check that
 and
and
 are equisatisfiable. The undecidability result still holds for finite satisfiability if a single occurrence of
are equisatisfiable. The undecidability result still holds for finite satisfiability if a single occurrence of
 is allowed, in a (ground) formula \({|{h}|} \ge {|{U}|} - 0\) (see the definition of
is allowed, in a (ground) formula \({|{h}|} \ge {|{U}|} - 0\) (see the definition of
 above).
above).
5.2 Two Decidable Fragments of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\)
The reductions (11) use either positive occurences of \(\mathsf {alloc}(x)\), where x is universally quantified, or test formulæ \({|{h}|} \ge {|{U}|}-n\). We obtain decidable subsets of \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) by eliminating the positive occurrences of both (i) \(\mathsf {alloc}(x)\), with x universally quantified, and (ii) \({|{h}|} \ge {|{U}|}-n\), from
 , where \(\dagger \in \left\{ fin , inf \right\} \) and
, where \(\dagger \in \left\{ fin , inf \right\} \) and
 is any \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) formula. Note that
is any \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\) formula. Note that
 contains no formulæ of the form \({|{h}|} \ge {|{U}|}-n\), which explains why slightly less restrictive conditions are needed for infinite structures.
contains no formulæ of the form \({|{h}|} \ge {|{U}|}-n\), which explains why slightly less restrictive conditions are needed for infinite structures.
Definition 7
Given an integer \(k \ge 1\), we define:
-
1.
\(\mathsf {BSR}^ inf (\mathsf {SL}^{k})\) as the set of sentences
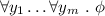 such that for all \(i \in [1,m]\) and all formulæ
such that for all \(i \in [1,m]\) and all formulæ
 occurring at polarity 1 in
occurring at polarity 1 in
 , we have
, we have
 ,
, -
2.
\(\mathsf {BSR}^ fin (\mathsf {SL}^{k})\) as the set of sentences
 such that no formula
such that no formula
 occurs at polarity 1 in
occurs at polarity 1 in
 .
.
Note that
 , for any \(k \ge 1\).
, for any \(k \ge 1\).
Remark 2
Because the polarity of the antecedent of a
 is neutral, Definition 7 imposes no constraint on the occurrences of separating implications at the left of a
is neutral, Definition 7 imposes no constraint on the occurrences of separating implications at the left of a
 Footnote 6.
Footnote 6.
The decidability result of this paper is stated below:
Theorem 2
For any integer \(k\ge 1\) not depending on the input, the infinite satisfiability problem for
 and the finite satisfiability problem for
and the finite satisfiability problem for
 are both PSPACE-complete.
are both PSPACE-complete.
We provide a brief sketch of the proof (all details are available in [8]). In both cases, PSPACE-hardness is an immediate consequence of the fact that the quantifier-free fragment of \(\mathsf {SL}^{\!\scriptstyle {k}}\), without the separating implication, but with the separating conjunction and negation, is PSPACE-hard [4]. For PSPACE-membership, consider a formula
 in
in
 , and its equivalent disjunction of minterms
, and its equivalent disjunction of minterms
 (of exponential size). Lemma 8 gives us an upper bound on the size of test formulæ in
(of exponential size). Lemma 8 gives us an upper bound on the size of test formulæ in
 , hence on the number of constant symbols occurring in
, hence on the number of constant symbols occurring in
 . This, in turns, gives a bound on the cardinality of the model of
. This, in turns, gives a bound on the cardinality of the model of
 . We may thus guess such an interpretation, and check that it is indeed a model of
. We may thus guess such an interpretation, and check that it is indeed a model of
 by enumerating all the minterms in
by enumerating all the minterms in
 (this is feasible in polynomial space thanks to Lemma 8) and translating them on-the-fly into first-order formulæ. The only subtle point is that the model obtained in this way is finite, whereas our aim is to test that the obtained formula has a infinite model. This difficulty can be overcome by adding an axiom ensuring that the domain contains more unallocated elements than the total number of constant symbols and variables in the formula. This is sufficient to prove that the obtained model – although finite – can be extended into an infinite model, obtained by creating infinitely many copies of these elements.
(this is feasible in polynomial space thanks to Lemma 8) and translating them on-the-fly into first-order formulæ. The only subtle point is that the model obtained in this way is finite, whereas our aim is to test that the obtained formula has a infinite model. This difficulty can be overcome by adding an axiom ensuring that the domain contains more unallocated elements than the total number of constant symbols and variables in the formula. This is sufficient to prove that the obtained model – although finite – can be extended into an infinite model, obtained by creating infinitely many copies of these elements.
The proof for
 is similar, but far more involved. The problem is that, if the universe is finite, then \(\mathsf {alloc}(x)\) test formulæ may occur at a positive polarity, even if every
is similar, but far more involved. The problem is that, if the universe is finite, then \(\mathsf {alloc}(x)\) test formulæ may occur at a positive polarity, even if every
 subformula occurs at a negative polarity, due to the positive occurrences of \(\mathsf {alloc}(x)\) within
subformula occurs at a negative polarity, due to the positive occurrences of \(\mathsf {alloc}(x)\) within
 (10) in the definition of \(\mathsf {elim}^{\scriptscriptstyle { fin }}_\multimap (M_1,M_2)\). As previously discussed, positive occurrences of \(\mathsf {alloc}(x)\) hinder the translation into \(\mathsf {BSR}(\mathsf {FO})\), because of the existential quantifiers that may occur in the scope of a universal quantifier. The solution is to distinguish a class of finite structures \((\mathfrak {U},\mathfrak {s},\mathfrak {h})\), the so-called
(10) in the definition of \(\mathsf {elim}^{\scriptscriptstyle { fin }}_\multimap (M_1,M_2)\). As previously discussed, positive occurrences of \(\mathsf {alloc}(x)\) hinder the translation into \(\mathsf {BSR}(\mathsf {FO})\), because of the existential quantifiers that may occur in the scope of a universal quantifier. The solution is to distinguish a class of finite structures \((\mathfrak {U},\mathfrak {s},\mathfrak {h})\), the so-called
 , for some
, for some
 , for which there are locations
, for which there are locations
 , such that every location \(\ell \in \mathfrak {U}\) is either \(\ell _i\) or points to a tuple from the set
, such that every location \(\ell \in \mathfrak {U}\) is either \(\ell _i\) or points to a tuple from the set
 . For such structures, the formulæ \(\mathsf {alloc}(x)\) can be eliminated in a straightforward way because they are equivalent to
. For such structures, the formulæ \(\mathsf {alloc}(x)\) can be eliminated in a straightforward way because they are equivalent to
 . If the structure is not
. If the structure is not
 , then we can show that there exist sufficiently many unallocated cells, so that all the cardinality constraints of the form \({|{h}|} \le {|{U}|}-n\) or \({|{U}|}\ge n\) are always satisfied. This ensures that the truth value of the positive occurrences of \(\mathsf {alloc}(x)\) are irrelevant, because they only occur in formulæ
, then we can show that there exist sufficiently many unallocated cells, so that all the cardinality constraints of the form \({|{h}|} \le {|{U}|}-n\) or \({|{U}|}\ge n\) are always satisfied. This ensures that the truth value of the positive occurrences of \(\mathsf {alloc}(x)\) are irrelevant, because they only occur in formulæ
 that are always true if all test formulæ \({|{h}|} \le {|{U}|}-n\) or \({|{U}|}\ge n\) are true (see the definition of
that are always true if all test formulæ \({|{h}|} \le {|{U}|}-n\) or \({|{U}|}\ge n\) are true (see the definition of
 in Lemma 4).
in Lemma 4).
6 Conclusions and Future Work
We have studied the decidability problem for SL formulæ with quantifier prefix in the language \(\exists ^*\forall ^*\), denoted as \(\mathsf {BSR}(\mathsf {SL}^{\!\scriptstyle {k}})\). Although the fragment was found to be undecidable, we identified two non-trivial subfragments for which the infinite and finite satisfiability are PSPACE-complete. These fragments are defined by restricting the use of universally quantified variables within the scope of separating implications at positive polarity. The universal quantifiers and separating conjunctions are useful to express local constraints on the shape of the data-structure, whereas the separating implications allow one to express dynamic transformations of these data-structures. As a consequence, separating implications usually occur negatively in the formulæ tested for satisfiability, and the decidable classes found in this work are of great practical interest. Future work involves formalizing and implementing an invariant checking algorithm based on the above ideas, and using the techniques for proving decidability (namely the translation of quantifier-free \(\mathsf {SL}(k)\) formulæ into boolean combinations of test formulæ) to solve other logical problems, such as frame inference, abduction and possibly interpolation.
Notes
- 1.
The empty set is thus considered to be true.
- 2.
The converse of \(C_n\): \(\forall x ~.~ (\lnot \mathfrak {c}_n \wedge \forall \mathbf y~.~ \lnot \mathfrak {p}(x, \mathbf y)) \rightarrow \bigvee _{i=1}^{n-1} x \approx \mathfrak {w}_i\) is not in \(\mathsf {BSR}(\mathsf {FO})\).
- 3.
Note that we do not assert the equality \(\mathbf y \approx \mathbf y'\), instead we only check that it is not falsified. This is sufficient for our purpose because in the following we always assume that the considered minterms are E-complete.
- 4.
Footprint-consistency is a necessary, yet not sufficient, condition for satisfiability of minterms. For example, the minterm \(M=\left\{ x \hookrightarrow y,x'\hookrightarrow y',\lnot y\approx y', {|{h}|} < 2 \right\} \) is at the same time footprint-consistent and unsatisfiable.
- 5.
Note that the two definitions of
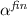 are equivalent. The formula
are equivalent. The formula
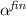 is unsatisfiable on infinite universes, which explains why the definitions of
is unsatisfiable on infinite universes, which explains why the definitions of
 and
and
 differ.
differ. - 6.
The idea is that if a formula \(\mathsf {alloc}(x)\) or \({|{h}|} \ge {|{U}|}-n\) occurs in the antecedent of a
 , then it will be eliminated by the transformation in Lemma 4. In contrast, such test formulæ will not be eliminated if they occur in the subsequent of a
, then it will be eliminated by the transformation in Lemma 4. In contrast, such test formulæ will not be eliminated if they occur in the subsequent of a
 .
.
References
Börger, E., Grädel, E., Gurevich, Y.: The Classical Decision Problem. Perspectives in Mathematical Logic. Springer, Heidelberg (1997)
Brochenin, R., Demri, S., Lozes, E.: On the almighty wand. Inf. Comput. 211, 106–137 (2012)
Calcagno, C., Gardner, P., Hague, M.: From separation logic to first-order logic. In: Sassone, V. (ed.) FoSSaCS 2005. LNCS, vol. 3441, pp. 395–409. Springer, Berlin, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31982-5_25
Calcagno, C., Yang, H., O’Hearn, P.W.: Computability and complexity results for a spatial assertion language for data structures. In: Hariharan, R., Vinay, V., Mukund, M. (eds.) FSTTCS 2001. LNCS, vol. 2245, pp. 108–119. Springer, Berlin, Heidelberg (2001). https://doi.org/10.1007/3-540-45294-X_10
Demri, S., Deters, M.: Expressive completeness of separation logic with two variables and no separating conjunction. In: Henzinger, T.A., Miller, D. (eds.), Joint Meeting of the Twenty-Third EACSL Annual Conference on Computer Science Logic (CSL) and the Twenty-Ninth Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), CSL-LICS 2014, Vienna, Austria, 14–18 July 2014, pp. 37:1–37:10. ACM (2014)
Demri, S., Galmiche, D., Larchey-Wendling, D., Méry, D.: Separation logic with one quantified variable. Theory Comput. Syst. 61(2), 371–461 (2017)
Echenim, M., Iosif, R., Peltier, N.: The complexity of prenex separation logic with one selector. CoRR, abs/1804.03556 (2018)
Echenim, M., Iosif, R., Peltier, N.: On the expressive completeness of Bernays-Schoenfinkel-Ramsey separation logic. ArXiv e-prints (2018)
Iosif, R., Rogalewicz, A., Simacek, J.: The tree width of separation logic with recursive definitions. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 21–38. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_2
Ishtiaq, S.S., O’Hearn, P.W.: BI as an assertion language for mutable data structures. ACM SIGPLAN Not. 36, 14–26 (2001)
Lozes, É.: Expressivité des logiques spatiales. Thèse de doctorat, Laboratoire de l’Informatique du Parallélisme, ENS Lyon, France, November 2004
Ramsey, F.P.: On a problem of formal logic. In: Classic Papers in Combinatorics, pp. 1–24 (1987)
Reynolds, A., Iosif, R., Serban, C.: Reasoning in the Bernays-Schönfinkel-Ramsey fragment of separation logic. In: Bouajjani, A., Monniaux, D. (eds.) VMCAI 2017. LNCS, vol. 10145, pp. 462–482. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-52234-0_25
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: Proceedings of the 17th Annual IEEE Symposium on Logic in Computer Science, LICS 2002, pp. 55–74. IEEE Computer Society (2002)
Acknowledgments
The authors wish to acknowledge the contributions of Stéphane Demri and Étienne Lozes to the insightful discussions during the early stages of this work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Echenim, M., Iosif, R., Peltier, N. (2019). The Bernays-Schönfinkel-Ramsey Class of Separation Logic on Arbitrary Domains. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)





 (i.e., the occurrences of
(i.e., the occurrences of
 that are in the scope of an even number of negations) contain no universal variables.
that are in the scope of an even number of negations) contain no universal variables. (i.e.,
(i.e.,
 only occurs in the scope of an odd number of negations).
only occurs in the scope of an odd number of negations).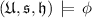 , for a heap
, for a heap  , for an interpretation
, for an interpretation  occurs at a negative polarity and
occurs at a negative polarity and
 for an interpretation
for an interpretation  , then
, then
 , for a heap
, for a heap  , we have
, we have  , then a formula
, then a formula
 occurs at a positive [negative] polarity in
occurs at a positive [negative] polarity in
 .
.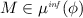 , then a formula
, then a formula
 , such that
, such that
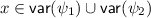 , occurs at a positive [negative] polarity in
, occurs at a positive [negative] polarity in
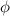 .
. , then a formula
, then a formula
 , such that
, such that
 , occurs in
, occurs in
 at some polarity
at some polarity  subformula (
subformula (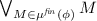 .
.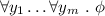 such that for all
such that for all  occurring at polarity 1 in
occurring at polarity 1 in
 , we have
, we have
 ,
, such that no formula
such that no formula
 occurs at polarity 1 in
occurs at polarity 1 in
 .
.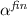 are equivalent. The formula
are equivalent. The formula
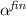 is unsatisfiable on infinite universes, which explains why the definitions of
is unsatisfiable on infinite universes, which explains why the definitions of
 and
and
 differ.
differ. , then it will be eliminated by the transformation in Lemma
, then it will be eliminated by the transformation in Lemma  .
.