Abstract
In this paper, we investigate the complexity of the emptiness problem for Parikh automata equipped with a pushdown stack. Pushdown Parikh automata extend pushdown automata with counters which can only be incremented and an acceptance condition given as a semi-linear set, which we represent as an existential Presburger formula over the final values of the counters. We show that the non-emptiness problem both in the deterministic and non-deterministic cases is NP-c. If the input head can move in a two-way fashion, emptiness gets undecidable, even if the pushdown stack is visibly and the automaton deterministic. We define a restriction, called the single-use restriction, to recover decidability in the presence of two-wayness, when the stack is visibly. This syntactic restriction enforces that any transition which increments at least one dimension is triggered only a bounded number of times per input position. Our main contribution is to show that non-emptiness of two-way visibly Parikh automata which are single-use is NExpTime-c. We finally give applications to decision problems for expressive transducer models from nested words to words, including the equivalence problem.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Parikh automata. Since the classical automata-based approach to model-checking [28], finite automata have been extended in many ways to tackle the automatic verification of more realistic and powerful systems against more expressive specifications. For instance, they have been extended to pushdown systems [3, 26, 30], concurrent systems [5], and systems with counters or specifications with arithmetic constraints have been the focus of many works in verification [7, 11, 15,16,17,18, 23].
Along this line of work, Parikh automata (or \(\mathsf {PA}\)), introduced in [22], are an important instance of automata extension with arithmetic constraints. They are automata on finite words whose transitions are equipped with counter operations. The counters can only be incremented, and do not influence the run (enabling a transition requires no test on counter values), but the acceptance of a run is defined by the membership of the final counter valuations to some semi-linear set S. Expressivity of \(\mathsf {PA}\)s goes beyond regularity, as the language \(L=\{w\mid |w|_a=|w|_b\}\) of words having the same numbers of as and bs is realised by a simple automaton counting the numbers of as and bs in counters \(x_1\) and \(x_2\) respectively, and the accepting condition is given by the linear-set \(\{ (i,i)\mid i\in \mathbb {N}\}\). Semi-linear sets can be defined by formulas in existential Presburger arithmetic, ie first-order formulas with equality and sum predicates over integers, whose free variables are evaluated by the counter values calculated by the run.
A central problem in automata theory is the non-emptiness problem: does the automaton accepts at least one input. Although \(\mathsf {PA}\)s go beyond regular languages, they retain relatively good algorithmic properties. The emptiness problem is decidable, and it is NP-c [12]. The hardness holds even if the semi-linear set is represented as a set of generator vectors. Motivated by applications in transducer theory for well-nested words, we investigate in this article extensions of Parikh automata with a pushdown stack.
First contribution: pushdown Parikh automata. As a first contribution, we study the complexity of the emptiness problem for Parikh automata with a pushdown store. Parikh automata extend finite automata with counter operations and an acceptance condition given as a semi-linear set, pushdown Parikh automata extend pushdown automata in the same way. We show that adding a stack can be done for free with respect to the emptiness problem, which remains, as for stack-free Parikh automata, NP-c. However in this case, we are able to strengthen the lower bound: it remains NP-hard even if there are only two counters, the automaton is deterministic, and the Presburger formula only tests for equality of these two counters. In the stack-free setting, it is necessary to have an unfixed number of counters to get such a lower bound.
Contribution 1
The emptiness problem for pushdown Parikh automata (\(\mathsf {PPA}\)) is NP-c. The lower bound holds even if the automaton is deterministic, has only two counters whose operations are encoded in unary, and they are eventually tested for equality.
Second contribution: adding two-wayness. We investigate the complexity of pushdown Parikh automata when the input head is allowed to move in two directions. It is not difficult to see that in that case emptiness gets undecidable, since, already without counters, one can simulate the intersection of two deterministic pushdown automata, by performing two passes over the input (visiting each input position at most three times). We consider a first restriction on the stack behaviour, which is required to be visibly.
A pushdown stack is called visibly if it is driven by the type of letters it reads, which can be either call symbols, return symbols or internal symbols. Words formed over such a structured alphabet are called nested words, and well-nested words if additionally the call/return structure of the word is well-balanced, such as in the following example:

Automata for nested words, called visibly pushdown automata (or \(\mathsf {VPA}\)), have been introduced in [2]. They are pushdown automata whose stack behaviour is constrained by the input in the following way. Upon reading a call symbol, exactly one symbol is pushed onto the stack. Upon reading a return symbol, exactly one symbol is popped from it. Upon reading an internal symbol, the stack is left unchanged. Hence, the symbol that is pushed while reading a given call symbol is popped while reading its matching return symbol. Consequently, visibly pushdown automata enjoy nice properties, such as closure under Boolean operations and determinisation.
\(\mathsf {VPA}\) have been extended to two-way \(\mathsf {VPA}\) (\(\mathsf {2VPA}\)) [8] with the following stack constraints: in a backward reading mode, the role of the return and call symbols regarding the stack are inverted: when reading a call, exactly one symbol is popped from the stack and when reading a return, one symbol is pushed. It was shown in [8] that adding this visibly condition to two-way pushdown automata allows one to recover decidability for the emptiness problem. However, for Parikh acceptance, this restriction is not sufficient. Indeed, by encoding diophantine equations, we show the following undecidability result:
Contribution 2
The emptiness problem for two-way visibly pushdown Parikh automata (\(\mathsf {2VPPA}\)) is undecidable.
Single-use property. The problem is that by using the combination of two-wayness and a pushdown stack, it is possible to encode polynomially, and even exponentially large counter values, with respect to the length of the input word. We consider therefore the single-use restriction, which appears in several transducer models [6, 8, 10], by which it is possible to keep a linear behaviour for the counters. Informally, a single-use two-way machine bounds the size of the production per input positions. It is syntactically enforced by asking that transitions which strictly increment at least one counter are triggered at most once per input position. Our main result is the decidability of \(\mathsf {2VPPA}\) emptiness under the single-use restriction, with tight complexity.
Contribution 3
(Main). The emptiness problem for two-way single-use visibly pushdown Parikh automata (\(\mathsf {2VPPA_{su}}\)) is NExpTime-c. The hardness holds even if the automaton is deterministic, has only two counters whose operations are encoded in unary, and they are eventually tested for equality.
To prove the upper-bound, we show that two-wayness can be removed from single-use \(\mathsf {2VPPA}\), at the price of one exponential. In other words, single-use \(\mathsf {2VPPA}\) and \(\mathsf {VPPA}\) have the same expressive power, although it can be shown that the former model is exponentially more succinct. The lower bound is obtained by encoding the succinct variant of the subset sum problem, based on a reduction which uses the fact that, by combining the pushdown and two-way features, single-use \(\mathsf {2VPPA}\) can encode doubly-exponential values \(2^{2^n}\) with a polynomial number of states (in n).
Contribution 4
(Applications). As an application, we give an elementary upper-bound (NExpTime) for the equivalence problem of functional single-use two-way visibly pushdown transducers [8], while an ExpTime lower bound was known. This transducer model defines transductions from well-nested words to words and, as shown in [8], they are well-suited to define XML transformations, have the same expressive power as Courcelle’s MSO-transducers [6] (casted to well-nested words), and admit a memory-efficient evaluation algorithm. We also provide two other new results on single-use \(\mathsf {2VPT}\) (not necessarily functional). First, we show that given a positive integer k, it is decidable whether a single-use \(\mathsf {2VPT}\) produces at most k different output words per input (k-valuedness problem). Then, we show the decidability of a typechecking problem: given a single-use \(\mathsf {2VPT}\) T and a finite (stack-free) Parikh automaton P, it is decidable whether the codomain of T has a non-empty intersection with P. This allows for instance to decide whether a single-use \(\mathsf {2VPT}\) produces only well-nested words and thus describes a well-nested words to well-nested words transformation, since the property of a word to be non well-nested is definable, as we show, by a Parikh automaton.
Finite-visit vs single-useness. The single-use property is more general than the more classical finite-visit restriction, used for instance in [9, 19]: it requires to visit any input position a (machine-dependent) constant number of times, while single-useness only bounds the number of visits by producing transitions. Although, consequently to our results, \(\mathsf {2VPPA}\) single-use and finite-visit have the same expressive power, this extra modelling feature is desirable, for instance when using \(\mathsf {2VPPA}\) to test properties of \(\mathsf {2VPT}\): single-use \(\mathsf {2VPT}\) are strictly more expressive than finite-visit ones, and this relaxation is crucial to capture MSO transductions [8]. Moreover, we somehow get it for free: we show that the NExpTime lower bound also holds for finite-visit \(\mathsf {2VPPA}\). Finally, we note that as we deal with single-use machines rather than finite-visit ones, the usual ingredient for going from two-way to one-way consisting of memorizing simply crossing sections of states, is not sufficient to get the result here, since we cannot bound the size of these crossing sections.
Related work. Parikh automata are closely related to reversal-bounded counter machines [18]. In fact, both models have equivalent expressiveness in the nondeterministic case [22]. The difference of expressive power in the deterministic case is due to the fact that counter machines can perform tests on its counters that can influence the run, while counters in Parikh automata only matter at the end of the run. Several extensions of reversal-bounded counter machines were studied, whether they are two-way or equipped with a (visibly) pushdown stack. However, to the best of our knowledge, the combination of the two features has never been studied (see [19] for a survey). It is possible to define a model of single-use reversal-bounded two-way visibly pushdown counter machines, where the single-useness is put on transitions that modify the counters. This model is expressively equivalent to \(\mathsf {2VPPA_{su}}\) in the non-determinstic case, and thanks to our result, has a decidable emptiness problem. The non-emptiness problem for reversal-bounded (one-way) pushdown counter machines for fixed numbers of counters and reversals is known to be in NP [13] and NP-hard [16]. Converting \(\mathsf {PPA}\) into reversal-bounded counter machines would yield an unfixed number of counters. Our NP lower-bound for \(\mathsf {PPA}\) however follows ideas of [16] about encoding, using the stack, integers n with O(log(n)) states and stack symbols.
Two-way (stack-free) reversal-bounded counter machines, even deterministic, are known to have undecidable emptiness problem [19]. Decidability is recovered by taking the finite-visit restriction [19]. Our result on \(\mathsf {2VPPA_{su}}\) entails the decidability of emptiness of two-way reversal-bounded counter machines which are single-use.
Finally, all the decidability results we prove on two-way visibly pushdown transducers were already known in the one-way case [13]. Two-way visibly pushdown transducers, which are strictly more expressive, can also be seen as a model of unranked tree-to-word transducers, modulo tree linearisation. To the best of our knowledge, this is the first model of unranked tree-to-word transducers for which k-valuedness and codomain well-nestedness is shown to be decidable. Another model, introduced in [1], is known to be expressively equivalent to \(\mathsf {2VPT_{su}}\) [8], and in the functional case, has decidable equivalence problem in NExpTime. However, translating \(\mathsf {2VPT_{su}}\) to this model requires an exponential blow-up, yielding a worst complexity for equivalence testing.
Structure. Section 2 introduces the computing models used, the proof of the lower bound for \(\mathsf {2VPPA_{su}}\) is given in Sect. 3 and the upper bound in Sect. 4. Finally, some applications to the main theorem to transducers are given in Sect. 5.
2 Two-Way Visibly Pushdown (Parikh) Automata
In this section, we first recall the definition of two-way visibly pushdown automata and later on extend them to two-way visibly pushdown Parikh automata.
We consider a structured alphabet \(\varSigma \) defined as the disjoint union of call symbols \(\varSigma _c\), return symbols \(\varSigma _r\) and internal symbols \(\varSigma _i\). The set of words over \(\varSigma \) is \(\varSigma ^*\). As usual, \(\epsilon \) denotes the empty word. Amongst nested words, the set of well-nested words \(\varSigma ^*_{\textsf {wn}}\) is defined as the least set such that \(\varSigma _i \cup \{\epsilon \}\) is included into \(\varSigma ^*_{\textsf {wn}}\) and if \(w_1,w_2 \in \varSigma ^*_{\textsf {wn}}\) then both \(w_1w_2\) and \(cw_1r\) (for all \(c \in \varSigma _c\) and \(r \in \varSigma _r\)) belong to \(\varSigma ^*_{\textsf {wn}}\).
When dealing with two-way machines, we assume the structured alphabet \(\varSigma \) to be extended to \(\overline{\varSigma }\) by adding a left and right marker symbols \(\triangleright ,\triangleleft \) in \(\overline{\varSigma }_c\) and \(\overline{\varSigma }_r\) respectively, and we consider words in the language \(\triangleright \varSigma ^* \triangleleft \).
Definition 1
A two way visibly pushdown automaton (\(\mathsf {2VPA}\) for short) A over \(\overline{\varSigma }\) is given by \((Q,q_I,F,\varGamma ,\delta )\) where Q is a finite set of states, \(q_I \in Q\) is the initial state, \(F \subseteq Q\) is a set of final states and \(\varGamma \) is a finite stack alphabet. Given the set \(\mathbb {D}=\{\leftarrow , \rightarrow \}\) of directions, the transition relation \(\delta \) is defined by \(\delta ^{\text {push}} \cup \delta ^{\text {pop}} \cup \delta ^{\text {int}}\) where
-
\(\delta ^{\text {push}} \subseteq ((Q \times \{\rightarrow \} \times \varSigma _c ) \cup (Q \times \{\leftarrow \} \times \varSigma _r)) \times ((Q \times \mathbb {D}) \times \varGamma )\)
-
\(\delta ^{\text {pop}} \subseteq ((Q \times \{\leftarrow \} \times \varSigma _c \times \varGamma ) \cup (Q \times \{\rightarrow \} \times \varSigma _r \times \varGamma )) \times (Q \times \mathbb {D})\)
-
\(\delta ^{\text {int}} \subseteq ((Q \times \mathbb {D}\times \varSigma _i) \times (Q \times \mathbb {D})\)
Additionally, we require that for any states \(q,q'\) and any stack symbol \(\gamma \), if \((q,\leftarrow ,\triangleright ,\gamma ,q',d) \in \delta ^{\text {pop}}\) then \(d=\rightarrow \) and if \((q,\rightarrow ,\triangleleft ,\gamma ,q',d) \in \delta ^{\text {pop}}\) then \(d=\leftarrow \) ensuring that the reading head stays within the bounds of the input word.
Informally, a \(\mathsf {2VPA}\) has a reading head pointing between symbols (and possibly on the left of \(\triangleright \) or the right of \(\triangleleft \)). A configuration of the machine is given by a state, a direction d and a stack content. The next symbol to be read is on the right of the head if \(d=\rightarrow \) and on the left if \(d=\leftarrow \). Note that when reading the left marker from right to left \(\leftarrow \) (resp. the right marker from left to right \(\rightarrow \)), the next direction can only be \(\rightarrow \) (resp. \(\leftarrow \)). The structure of the alphabet induces the behavior of the machine regarding the stack when reading the input word: when reading on the right, a call symbol leads to push one symbol onto the stack while a return symbol pops one symbol from the stack. When reading on the left, a dual behaviour holds. In any direction internal transitions from \(\delta ^{\text {int}}\) read internal symbols and do not affect the stack; hence, at a given position in the input word, the height of the stack is always constant at each visit of that position in the run of the machine. The triggering of a transition leads to the update of the state of the machine, the future direction as well as the stack content. For a direction d, a natural i (\(0 \le i \le |w|\)) and a word w, we denote by
-
\({\text {move}}(d,i)\) the integer \(i-1\) if \(d=\leftarrow \) and \(i+1\) if \(d=\rightarrow \).
-
\({\text {read}}(w,d,i)\) the symbol w(i) if \(d=\leftarrow \) and \(w(i+1)\) if \(d=\rightarrow \).
Note that when switching directions (i.e. when the direction of the first part of the transition is different from the second part), we read twice the same letter. This ensures the good behavior of the stack, as reading a call letter from left to right pushes a stack symbol, we need to pop it if we start moving from right to left.
Formally, a stack \(\sigma \) is a finite word over \(\varGamma \). The empty stack/word over \(\varGamma \) is denoted \(\bot \). For a word w from \(\overline{\varSigma }\) and a \(\mathsf {2VPA}\) \(A=(Q,q_I,F,\varGamma ,\delta )\), a configuration \(\kappa \) of A is a tuple \((q,i,d,\sigma )\) where \(q \in Q\), \(0 \le i \le |w|\), \(d \in \mathbb {D}\) and \(\sigma \) is a stack. A run of A on a word w is a finite sequence \(\rho \) from \(K(\delta K)^*\), where K is the set of all configurations \(\kappa \) (that is a sequence starting and ending with a configuration and alternating between configurations and transitions); a run \(\rho \) is of the form \((q_0,i_0,d_0,\sigma _0) \tau _1 (q_1,i_1,d_1,\sigma _1) \tau _2 \ldots \tau _\ell (q_\ell ,i_\ell ,d_\ell ,\sigma _\ell )\) where for all \(0\le j < \ell \), we have:
-
either \(d_j=\rightarrow \) and \({\text {read}}(w,d_j,i_j) \in \varSigma _c\) or \(d_j=\leftarrow \) and \({\text {read}}(w,d_j,i_j) \in \varSigma _r\), \(\tau _{j+1}=(q_j,d_j,{\text {read}}(w,d_j,i_j),q_{j+1},d_{j+1},\gamma ) \in \delta ^{\text {push}}\), \(i_{j+1}={\text {move}}(i_j,d_j)\) and \(\sigma _{j+1}=\sigma _j\gamma \)
-
either \(d_j=\leftarrow \) and \({\text {read}}(w,d_j,i_j) \in \varSigma _c\) or \(d_j=\rightarrow \) and \({\text {read}}(w,d_j,i_j) \in \varSigma _r\), \(\tau _{j+1}=(q_j,d_j,{\text {read}}(w,d_j,i_j),\gamma ,q_{j+1},d_{j+1}) \in \delta ^{\text {pop}}\), \(i_{j+1}={\text {move}}(i_j,d_j)\) and \(\sigma _{j+1}\gamma =\sigma _j\)
-
\({\text {read}}(w,d_j,i_j)\in \varSigma _i\), \(\tau _{j+1}=(q_j,d_j,{\text {read}}(w,d_j,i_j),q_{j+1},d_{j+1})\in \delta ^{\text {int}}\), \(i_{j+1}=i_j\) and \(\sigma _{j+1}=\sigma _j\).
Note that any configuration is actually a run on the empty word \(\epsilon \). The initial configuration is \((q_I,0,\rightarrow ,\bot )\). A configuration \((q,i,d,\bot )\) is final if \(q \in F\) and i is the last position. A run for the word w is accepting if its first configuration is initial and its last configuration is final. A two-way visibly pushdown automaton A is:
-
deterministic (denoted \(\mathsf {D2VPA}\)) if \(\delta ^{\text {push}}\) (resp. \(\delta ^{\text {pop}}\), \(\delta ^{\text {int}}\)) is a function from \(Q\times \mathbb {D}\times \varSigma \) (resp. \(Q\times \mathbb {D}\times \varSigma \times \varGamma \), \(Q\times \mathbb {D}\times \varSigma \)) to \(Q\times \mathbb {D}\times \varGamma \) (resp. \(Q\times \mathbb {D}\), \(Q\times \mathbb {D}\)).
-
one-way (denoted \(\mathsf {VPA}\)) if all transitions in A have \(\rightarrow \) for direction.
-
finite-visit if for some \(k\ge 0\), any run visits at most k times the same input position.
The size of a \(\mathsf {2VPA}\) is the number of states times the size of the stack alphabet. For A an automaton, we denote by L(A) the language recognized by A.
Lemma 1
([8]). Given a \(\mathsf {2VPA}\) A, deciding if L(A) is empty is ExpTime-complete.
Parikh automata. Parikh automata were introduced in [22]. Informally, they are automata with counters that can only be incremented, and do not act on the transition relation. Acceptance of runs is done by evaluating a Presburger formula whose free variables are set to the counter values. In our setting, a Presburger formula is a positive formula \(\psi (x_1,\ldots ,x_n)=\exists y_1\ldots y_m \varphi (x_1,\ldots ,x_n,y_1,\ldots ,y_m)\) such that \(\varphi \) is a boolean combination of atoms \(s+s'\le t+t'\), for \(s,s',t,t'\in \{0,1,x_1,\ldots ,x_n,y_1,\ldots ,y_m\}\). For a set S and some positive number m, we denote by \(S^m\) the set of all mappings from \([1\ldots m]\) to S. If \((s_1,\ldots ,s_m)\) and \((t_1,\ldots ,t_m)\) are two tuples of \(S^m\) and \(+\) is an binary operation on S, we extend \(+\) to \(S^m\) by considering the operation element-wise, i.e. \((s_1,\ldots ,s_m)+(t_1,\ldots ,t_m)=(s_1+t_1,\ldots ,s_m+t_m)\).
Definition 2
A two-way visibly pushdown Parikh automaton (\(\mathsf {2VPPA}\) for short) is a tuple \(P = (A,\lambda ,\phi )\) where A is a \(\mathsf {2VPA}\) and for some natural \( dim \), \(\lambda \) is a mapping from \(\delta \) to \(\mathbb {N}^ dim \), the set of vectors of length \( dim \) of naturals and \(\phi (x_1, \ldots , x_ dim )\) is a Presburger formula with \( dim \) free variables.
When clear from context, we may omit the free variables from the Presburger formula, and simply note \(\phi \). A run of a \(\mathsf {2VPPA}\) is a run of its underlying \(\mathsf {2VPA}\). We extend canonically the mapping \(\lambda \) to runs. For a run \(\rho \) of the form \((q_0,i_0,d_0,\sigma _0) \tau _1 (q_1,i_1,d_1,\sigma _1) \tau _2 \ldots \tau _\ell (q_\ell ,i_\ell ,d_\ell ,\sigma _\ell )\), we set
We recall that a single configuration c is a run over the empty word \(\epsilon \). For such a run c, we set \(\lambda (c)=0^ dim \). A run \((q_0,i_0,d_0,\sigma _0) \tau _1 (q_1,i_1,d_1,\sigma _1) \tau _2 \ldots \tau _\ell (q_\ell ,i_\ell ,d_\ell ,\sigma _\ell )\) is accepted if \((q_0,i_0,d_0,\sigma _0)\), \((q_\ell ,i_\ell ,d_\ell ,\sigma _\ell )\) are respectively an initial and a final configuration of the underlying automaton and for \(\lambda (\rho ) = (n_1,\ldots , n_ dim )\), \([x_1 \leftarrow n_1,\ldots , x_\ell \leftarrow n_ dim ] \models \phi (x_1, \ldots , x_ dim )\). The language L(P) is the set of words which admit an accepting run. We define the set of values computed by P as \( Val (P)=\{\lambda (\rho )\mid \rho \text { a valid run of the underlying automaton of P}\}\). We define the size of P as the size of A plus the number of symbols in \(\phi \) and \(|\delta |\cdot dim\cdot log(W)\) where W is the maximal value occurring in the codomain of \(\lambda \).
It is deterministic (resp. one-way), denoted \(\mathsf {D2VPPA}\) (resp. \(\mathsf {VPPA}\)) if its underlying automaton is deterministic (resp. one-way). It is known from [4] that \(\mathsf {DPA}\) (i.e. deterministic one-way and stack-free Parikh automata in our setting) are strictly less expressive than their nondeterministic counterpart. As a counter example, they exhibit the language \(L=\{w\mid w_{\#_a(w)}=b\}\), ie all words w such that if n is the number of a in w, the letter at the nth position is a b. Note that even in the two-way case, a deterministic machine recognizing L needs to either have access, during the computation, to the number of a’s, or be able to store, in counters, the position of each b. As the first solution cannot be done since Parikh automata only access their counters at the end of the run, and the second is also impossible since there are only a finite number of counters, this language is also non definable by a \(\mathsf {D2VPPA}\), furthering the separation between deterministic and nondeterministic Parikh automata.
Example 1
As an example, we give a deterministic \(\mathsf {2VPPA}\) P that, given an input \( i^n c^k i^\ell r^k\) with c, i, r in \(\varSigma _c\), \(\varSigma _i\) and \(\varSigma _r\) respectively, accepts if \(k=\ell \) and \(n=k^2\). The \(\mathsf {2VPPA}\) P uses 4 variables \(x_n\), \(x_k\), \(x_\ell \) and y. The first 3 variables are used to count the number of the first block of is, the number of calls and the second block of is respectively. The handling of these 3 variables is straight-forward and can be done in a single pass over the input. The fourth variables y counts the multiplication \(k\cdot \ell \) and doing so is more involved. The part of the underlying \(\mathsf {2VPA}\) of P handling y is given in Fig. 2. On this part, the mapping \(\lambda \) simply increments the counter on transitions going to state 2 (i.e. on reading the letters i from left to right). It makes as many passes on the set of internal symbols in state 2 as there are call symbols, and the state of the stack upon reading \(i^\ell \) for the jth time is \(1^j0^{k-j}\). Finally, the accepting formula \(\phi \) of P is defined by \(x_n=y \wedge x_k=x_\ell \). Note that this widget allows us to compute the set \(\{(k^2,k,k,k^2)\mid k\in \mathbb {N}\}\) which is not semilinear.
A \(\mathsf {2VPPA}\) reading words \(c^k i^\ell r^k\) and making k passes on \(i^\ell \), adding \(k\cdot \ell \) to the variable y. The transitions have two components, the first being the letter read, and the second being the stack operation. There is no stack operation upon reading internal symbols. The variable y is incremented in transitions going to state 2 only.
As we have seen in the previous example, the set \( Val (P)\) is not necessarily semi-linear, even with P a \(\mathsf {D2VPPA}\). We use this fact to encode diophantine equations, and get the following undecidability result:
Theorem 1
The emptiness problem of \(\mathsf {D2VPPA}\) is undecidable.
Single-useness. In order to recover decidability, we adapt to Parikh Automata the notion of single-useness introduced in [8]. Simply put, a \(\mathsf {2VPPA}\) is single-use (denoted \(\mathsf {2VPPA_{su}}\)) if the transitions that affect the variables can only be taken once on any given input position, thus effectively bounding the size of variables linearly with respect to the size of the input. Formally, a state p of a \(\mathsf {2VPPA}\) P is producing if there exists a transition t from p on some symbol and \(\lambda (t)\ne 0^ dim \). A \(\mathsf {2VPPA}\) is single-use if for every input w and every accepting run \(\rho \) over w, there do not exist two different configurations \((p,i,d,\sigma )\) and \((p,i,d,\sigma ')\) with p a producing state, meaning that \(\rho \) does not reach any position in the same direction twice in any given state of P. This property is a syntaxic restriction of the model. However, since this property is regular, it can equivalently be seen as a semantic one. Moreover, deciding the single-useness of a \(\mathsf {2VPPA}\) is ExpTime-c (see [8] for the same result but on transducers). Note that the Parikh automaton given in Example 1 is not single-use, since it passes over the second subword of internal letters i in state 2 as many times as there are call symbols. In the following, we prove that \(\mathsf {2VPPA_{su}}\) have the same expressiveness as \(\mathsf {VPPA}\), while being exponentially more succinct. In particular, this equivalence implies by Parikh’s Theorem [24], semi-linearity of \( Val (P)\) for any \(\mathsf {2VPPA_{su}}\) P.
3 Emptiness Complexity
We show that the non-emptiness problem for \(\mathsf {VPPA}\) is NP-complete. We actually show the upper-bound for the strictly more expressive Pushdown Parikh Automata (\(\mathsf {PPA}\)), i.e. \(\mathsf {VPPA}\) without the visibly restriction. While decidability was known [20, 21], the precise complexity was, to the best of our knowledge, unknown. Let us also remark that the model and the proof are similar to the proof of NP-completeness of k-reversal pushdown systems from [16]. However, it is adapted here to Parikh automata as well as deterministic machines, which was not the case in [16].
Theorem 2
The non-emptiness problem for \(\mathsf {VPPA}\) and \(\mathsf {PPA}\) is NP-complete. The complexity bounds hold even if the automata are deterministic, with a fixed dimension 2, tuples of values in \(\{0,1\}^2\) and with a fixed Presburger formula \(\phi (x_1,x_2) \equiv x_1=x_2\).
From \(\mathsf {2VPPA_{su}}\) to \(\mathsf {VPPA}\) From a two-way visibly pushdown Parikh automaton satisfying the single-useness restriction, one can build an equivalent one-way visibly pushdown Parikh automaton. The construction induces an exponential blow-up, which cannot be avoided, as with most constructions from two-way to one-way machines.
Theorem 3
For any \(\mathsf {2VPPA_{su}}\) A, one can construct a \(\mathsf {VPPA}\) B whose size is at most exponential in the size of A and such that L(A)=L(B). Moreover, the procedure can be done in exponential time.
Proof
(Sketch). The goal is to be able to correctly guess all the transitions exactly taken by a run of the two-way machine at once. More precisely, the one-way machine guesses the behavior of the two-way machine on each well-nested subword of the input, i.e. a set of partial runs over a subword. A partial run is a pair from \(Q\times \{\leftarrow ,\rightarrow \}\). Informally, they describe a maximal subrun over a subword of the input. We call these sets of partial runs profiles, and we define relations C and \(N_{c,r}\) to describe compatible profiles. Formally, the relation \(C\subseteq \mathcal {P}^3\) is the concatenation relation, defined as set of triples \((P,P',P'')\) such that there exists a word \(u=u_1vv'u_2\) where v and \(v'\) are well-nested subwords of u, and a run r on u such that P (resp. \(P'\)) is the profile of v in r (resp. of \(v'\)) and \(P''\) is the profile of \(vv'\) in r. Similarly, the relation \(N_{c,r}\subseteq \mathcal {P}^2\) for c, r call and return letters respectively, is the cr-nesting relation, and defined as the set of pairs \((P,P')\) such that there exists a word \(u=u_1cvru_2\) where v is well-nested, and a run r of A on u such that P is the profile of v in r and \(P'\) is the profile of cvr in r. We prove that these relations are computable in exponential time.
Given these relations, we can compute a \(\mathsf {VPPA}\) B whose runs are bijective to the runs of A. Moreover, we can recover from a run of B which transitions are effectively taken at each positions by its bijective run of A. Then, the increment function simply does all the increments done by the run at a given position at once. Since the operation is the addition on integers, it is commutative and the variables are updated in the same way they were by the run of A. Note that we only recover which transitions are taken, and not how many times they are taken, which can depend on the size of the input. However, since A is single-use, we only have to add each non zero transition once, which gives the result.
As a direct corollary of Theorems 3 and 2, we get the following.
Corollary 1
The emptiness of \(\mathsf {2VPPA_{su}}\) can be decided in NExpTime.
4 NExpTime-Hardness
In this section, we show that the problem of deciding whether the language of a \(\mathsf {2VPPA_{su}}\) is non-empty is hard for NExpTime. Moreover, we show that this hardness does not depend on the fact that we have taken existential Presburger formulas, nor on the vector dimensions, and nor on the fact that the values in the tuples are encoded in binary.
Theorem 4
The non-emptiness problem for \(\mathsf {2VPPA_{su}}\) is NExpTime-hard. The result holds even if the automaton is deterministic, of dimension 2, with counter updates in \(\{0,1\}\), the Presburger formula is \(\phi (x_1,x_2)\equiv x_1=x_2\), and it is finite-visit.
Succinct Subset Sum Problem. We reduce to the succinct subset sum problem (SSSP), which is NExpTime-hard [16]. Let us define SSSP. Let \(m,k\ge 1\), \(X = \{ x_1,\dots ,x_k\}\) and \(Y = \{ y_1,\dots ,y_m\}\) be sets of Boolean variables. Let \(\theta \) be a Boolean formula over \(X\cup Y\). Any word \(v\in \{0,1\}^{k+m}\) naturally defines a valuation of \(X\cup Y\) (the first bit of v is the value of \(x_1\), etc.). We denote by \(\theta [v]\in \{0,1\}\) the truth value of \(\theta \) under the valuation v. The formula \(\theta \) defines \(2^k\) non-negative integers \(a_1,\dots ,a_{2^k}\) each with \(2^m\) bits, as follows:
where \(b_i\) is the binary encoding over k bits of i, and \(d_1,\dots ,d_{2^m}\) is the lexicographic enumeration of \(\{0,1\}^m\), starting from \(0^m\). Note that for all \(i\in \{1,\dots ,2^k\}\), \(a_i\in \{0,\dots ,2^{2^{m}}-1\}\). The Succinct Subset Sum Problem asks, given X, Y and \(\theta \), whether there exists \(J\subseteq \{1,\dots ,2^k-1\}\) such that \(\sum _{j\in J} a_j = a_{2^k}\).
Overview of the construction and encoding the values \(a_i\). Given an instance of SSSP \(\mathcal {I}\), our goal is to construct a \(\mathsf {D2VPPA_{su}}\) \(\mathcal {P} = (C,\rho ,\phi )\) of dimension 2 such that \(|\mathcal {P}|\) is polynomial in \(|\theta | + k + m\) and \(\mathcal {L}(\mathcal {P})\ne \varnothing \) iff \(\mathcal {I}\) has a solution.
The main idea is to ensure that \(\mathcal {L}(C) = \{ X_1e_{1}\dots X_{2^k-1}e_{2^k-1}\#e_{2^k}\mid X_i\in \{0,1\}\}\) where the \(X_i\) are internal symbols which are used to encode a subset \(J\subseteq \{1,\dots ,2^k-1\}\), and each \(e_{i}\) is an encoding of \(a_i\), defined later, over some alphabet containing the symbol \(\mathbb {1}\), and such that the number of occurrences of \(\mathbb {1}\) in \(e_{i}\) is \(a_i\). In other words, \(e_{i}\) somehow encodes \(a_i\) in unary. For the vector part, the machine \(\mathcal {P}\), when running over \(X_ie_i\), updates its dimensions depending on two cases: (1) if \(X_i = 1\) (“put value \(a_i\) in J”), then any transition reading \(\mathbb {1}\) has weight (1, 0) and any other transition has weight (0, 0), (2) if \(X_i = 0\), then every transition has weight (0, 0). So, if \(X_i = 1\), the value in the first dimension after processing \(X_ie_i\) has been incremented by \(a_i\). Similarly, when processing \(\#e_{2^k}\), any transition reading \(\mathbb {1}\) increments the 2nd dimension by 1, so that after processing \(\#e_{2^k}\), this dimension has value \(a_{2^k}\). The formula \(\phi (x_1,x_2)\) then only requires equality of \(x_1\) and \(x_2\), i.e. \(\phi (x_1,x_2) \equiv x_1=x_2\).
We now explain how to encode \(a_i\) by a well-nested word \(e_{i}\). Due to the finite-visit restriction, every incremental transition can be triggered at most once for each input position. Since the value \(a_i\) is possibly doubly exponential in m and we are allowed to have a polynomial number of transitions (in \(|\theta |+k+m\)), necessarily \(e_{i}\) must be of doubly exponential length. The main idea is to use the stack and the two-wayness to recognise with a polynomial number of states well-nested words which are of doubly exponential length. We need a series of intermediate lemmas to achieve this idea. We start with a useful result about intersection of finite automata, here reversible finite automata (deterministic and backward deterministic). Let \(\varSigma = \{ 1,\dots ,m\}\) and let us define recursively the sequence of words \((u_i)_{0\le i\le m}\in \varSigma ^*\) as follows: \(u_0 = 1\), \(u_i = u_{i-1} i u_{i-1}\) for \(1\le i<m\) and \(u_m = u_{m-1} m u_{m-1} m\).
Lemma 2
The word \(u_m\) has length \(2^m\), and there exist m reversible finite automata \(A_0,\dots ,A_m\) (Fig. 3) such that (i) each \(A_i\) has O(1) states, and (ii) \(\bigcap _{i=1}^m L(A_i) = \{ u_m \}\).
Encoding of the values \(a_i\). The idea is to define a well-nested word \(e_{i}\) over an alphabet of call symbols \(\varSigma _c = \{ c_1,\dots ,c_m\}\), an alphabet of return symbols \(\varSigma _r = \{ r_1,\dots ,r_m\}\) and an alphabet of internal symbols  . The number of occurrences of \(\mathbb {1}\) in \(e_{i}\) will be exactly \(a_i\), i.e. \(\#_\mathbb {1}(e_{i}) = a_i\) and hence, the Parikh automaton will just have to count the number of \(\mathbb {1}\) occurrences. Let us remind the reader that \(a_i\) is actually given by \(\theta \), and therefore, the automaton \(\mathcal {P}\) will somehow have to evaluate \(\theta \) for valuations of its variables that will be contained in \(e_{i}\). Let us now define the words \(e_{i}\). For that, we call a binary tree either an internal symbol
. The number of occurrences of \(\mathbb {1}\) in \(e_{i}\) will be exactly \(a_i\), i.e. \(\#_\mathbb {1}(e_{i}) = a_i\) and hence, the Parikh automaton will just have to count the number of \(\mathbb {1}\) occurrences. Let us remind the reader that \(a_i\) is actually given by \(\theta \), and therefore, the automaton \(\mathcal {P}\) will somehow have to evaluate \(\theta \) for valuations of its variables that will be contained in \(e_{i}\). Let us now define the words \(e_{i}\). For that, we call a binary tree either an internal symbol  , or a well-nested word of the form \(c_j t_1 t_2 r_j\) where \(t_1,t_2\) are themselves binary trees. For a well-nested word of the form cwr, a root-to-leaf branch \(\pi \) is a sequence of calls \(x_1\dots x_n\) such that \(cwr = x_1 w_1 x_2 w_2 \dots x_n w_n r_n w'_n r_{n-1} w'_{n-1}\dots r_2 w'_2 r_1\) where \(x_1=c\), \(r_1=r\) and for some \(w_i,w'_i\) well-nested words such that \(w_n\) contains only internal symbols. The height of a binary tree t is the maximal length of a root-to-leaf branch, and it is complete if all root-to-leaf branches have the same length. Note that the number of internal symbols of a complete binary tree of height n is \(2^n\).
, or a well-nested word of the form \(c_j t_1 t_2 r_j\) where \(t_1,t_2\) are themselves binary trees. For a well-nested word of the form cwr, a root-to-leaf branch \(\pi \) is a sequence of calls \(x_1\dots x_n\) such that \(cwr = x_1 w_1 x_2 w_2 \dots x_n w_n r_n w'_n r_{n-1} w'_{n-1}\dots r_2 w'_2 r_1\) where \(x_1=c\), \(r_1=r\) and for some \(w_i,w'_i\) well-nested words such that \(w_n\) contains only internal symbols. The height of a binary tree t is the maximal length of a root-to-leaf branch, and it is complete if all root-to-leaf branches have the same length. Note that the number of internal symbols of a complete binary tree of height n is \(2^n\).
Then, \(e_{i}\) is the well-nested word defined by \(e_i = c_{j_1} b_i d_1 t_1 c_{j_2} b_i d_2 t_2 \dots c_{j_{2^m}} b_i d_{2^m} t_{2^m} r_{j_{2^m}}\dots r_{j_1}\) where
-
1.
the words \(t_i\) are binary trees
-
2.
every root-to-leaf branch \(\pi = c_{i_1}\dots c_{i_\ell }\) of \(e_{i}\) satisfies \(i_1\dots i_\ell = u_m\)
-
3.
\(b_i \in \{0,1\}^k\) and \(d_1,\dots ,d_{2^m}\) is a lexicographic enumeration of \(\{0,1\}^m\) (starting from \(0^m\))
-
4.
for all j, all internal symbols occurring in \(t_j\) are \(\mathbb {1}\) if \(\theta [b_id_j]=1\),
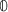 otherwise.
otherwise.
Our goal is now to prove that \(e_{i}\) is a correct encoding of \(a_i\).
Lemma 3
For all \(i\in \{1,\dots ,2^k\}\), \(\#_\mathbb {1}(e_{i}) = a_i\), where \(\#_\mathbb {1}(e_i)\) denotes the number of occurrences of \(\mathbb {1}\) in \(e_i\).
Proof
By Condition 2, every root-to-leaf branch of \(e_{i}\) has length \(2^m\). Therefore, for all \(j\in \{1,\dots ,2^m\}\), every root-to-leaf branch in \(t_j\) has length \(2^{m}-j\). In particular, \(t_{2^m}\) does not contain any call symbol. Hence all the trees \(t_j\) are complete binary trees of height \(2^{m}-j\). So, every \(t_j\) has \(2^{2^m-j}\) internal symbols and by Condition 4, we get \(\#_\mathbb {1}(t_j) = \theta [b_id_j].2^{2^m-j}\). Therefore, \( \#_\mathbb {1}(e_i) = \sum _{j=1}^{2^m} \#_\mathbb {1}(t_j) = \sum _{j=1}^{2^m} \theta [b_id_j].2^{2^m-j} = a_i \).
Note that Condition 3 was not used in the previous proof, but it will be useful to define a succinct \(\mathsf {D2VPA}\) recognising \(e_i\). The key result is the following. It states the existence of a succinct \(\mathsf {D2VPA}\) which recognises exactly the candidate solutions to SSSP.
Lemma 4
One can construct a \(\mathsf {D2VPA}\) \(\mathcal {B}\) such that \(\mathcal {B}\) has polynomially many states in \(|\theta |+k+m\) and \( L(\mathcal {B}) = \{ X_1e_1\dots X_{2^k-1}e_{2^k-1}\#e_{2^k}\mid X_i\in \{0,1\}\} \).
Proof
(Sketch). First, we show the existence of a \(\mathsf {D2VPA}\) \(\mathcal {A}\) with polynomially many states in \(|\theta |+k+m\) such that \(L(\mathcal {A}) = \{ e_i\mid i\in \{1,\dots ,2^k\}\}\) (Proposition ?? in Appendix). The main idea is to construct succinct \(\mathsf {D2VPA}\) which check each of the conditions 1 to 4 of the definition of the encoding independently, and then to take their intersection (by running the first, then the second, etc.). Condition 1 is easy to check. For condition 2, we rely on Lemma 2, and run sequentially the automata \(A_i\) (in m passes) to check independently that for all i, each root-to-leaf branch has a sequence of indices that belongs to \(A_i\). Thanks to the reversibility of \(A_i\), it is possible when going upward in the tree, to recover the previous state of \(A_i\). For condition 3, we rely on the two-wayness to check that a sequence of m bits is a successor of another sequence succinctly, by doing O(m) passes over the two successor vectors. The stack is not necessary there. For condition 4, we rely on the existence of a succinct 2DFA which accepts all the valuations that satisfy a given Boolean formula.
We can finally construct the \(\mathsf {D2VPPA_{su}}\) \(\mathcal {P} = (\mathcal {C},\rho ,\phi )\) of dimension 2 whose language is non-empty iff the SSSP instance \(\mathcal {I}\) has a solution. The automaton \(\mathcal {C}\) performs a first pass on the whole word by running the automaton \(\mathcal {B}\) of Lemma 4, to check that the input is of the form \(X_1e_1\dots X_{2^k-1}e_{2^k-1}\#e_{2^k}\). During this pass, no vector dimension is incremented. During a second pass, \(\mathcal {C}\), when reading some \(X_i = 1\), it goes to some state \(q_1\) from which it increments the 1st dimension whenever \(\mathbb {1}\) is read (all other transitions have value (0, 0)). When reading some \(X_{i+1}\), it stays in \(q_1\) if \(X_{i+1}=1\) or to \(q_0\) otherwise, from which no transition touches the counters. When reading \(\#\), it goes to a state from which it increments only the 2nd dimension on reading \(\mathbb {1}\). Note that this automaton is single-use: any symbol \(\mathbb {1}\) occurring in the whole input word is counted at most once. It is even finite-visit (each position is visited \(O(m+k+|\theta |)\) times). Finally, one only needs to check whether the first dimension equals the second one, using a formula \(\phi (x_1,x_2)\equiv x_1=x_2\). Note that the following lemma proves Theorem 4, since SSSP is NExpTime-c.
Lemma 5
Given an instance \(X,Y,\theta \) of SSSP, one can construct a \(\mathsf {D2VPPA_{su}}\) \(\mathcal {P}\) of polynomial size in \(|\theta |+|X|+|Y|\) such that \(L(\mathcal {P})\ne \varnothing \) iff SSSP has a solution.
5 Applications to Decision Problems for Nested Word Transducers
In this section, we give two applications of \(\mathsf {2VPPA}\), namely on decision problems for two-way visibly pushdown transducers (\(\mathsf {2VPT}\)). \(\mathsf {2VPT}\) were introduced in [8] as a model to define transductions from well-nested words to words, or, modulo tree linearisation, from tree to words. It was shown that they can express, even in their deterministic and single-use version, all functions from well-nested words to words definable in MSOT, in the sense of Courcelle [6], while having decidable equivalence problem. No upper bound was provided however. Using \(\mathsf {2VPPA}\), we show that the equivalence of \(\mathsf {2VPT_{su}}\) defining functions can be tested in NExpTime. We also consider other standard problems from transducer theory and show, again using \(\mathsf {2VPPA}\), their decidability. First, let us define formally \(\mathsf {2VPT}\).
A two-way visibly pushdown transducer (\(\mathsf {2VPT}\) for short) is a pair \((A,\mu )\) where A is a \(\mathsf {2VPA}\) and \(\mu \) is a morphism from the sequences of transitions \(\delta ^*\) to some output alphabet \(\varGamma ^*\). A run of a \(\mathsf {2VPT}\) is a run of its underlying \(\mathsf {2VPA}\). The output of a run \(\rho \) of the form \((q_0,i_0,d_0,\sigma _0) \tau _1 (q_1,i_1,d_1,\sigma _1) \tau _2 \ldots \tau _\ell (q_\ell ,i_\ell ,d_\ell ,\sigma _\ell )\) is \(\mu (\tau _1...\tau _\ell )\). A run is accepted if it is accepted by its underlying automaton. The transduction defined by a \(\mathsf {2VPT}\) is the set of pairs (u, v) such that v is the output of some accepting run on u. A state p of a \(\mathsf {2VPT}\) is producing if there exists a transition \(\tau \) such that p is the first component of \(\tau \) and \(\mu (\tau )\ne \epsilon \). Similarly to Parikh automata, a \(\mathsf {2VPT}\) T is single-use (denoted \(\mathsf {2VPT_{su}}\)) if for any valid run of T, we do not reach the same position twice in the same producing state. It is deterministic, denoted \(\mathsf {D2VPT}\), if its underlying automaton is deterministic.
Deciding the k-valuedness and equivalence problems. For any positive integer k, we say that a transducer is k-valued if all input word have at most k different outputs. In particular, it is 1-valued if it defines a (partial) function, and also called functional in that case.
Theorem 5
Let T be a \(\mathsf {2VPT_{su}}\), and k an integer. Then the k-valuedness of T can be decided in NExpTime. It is also ExpTime-hard.
The theorem is proved by reducing the k-valuedness of T to the emptiness of a \(\mathsf {2VPPA_{su}}\) \(\mathcal {P}\) that guesses \(k+1\) runs of T that produce \(k+1\) different outputs. To ensure that the output are different, during each run \(\mathcal {P}\) guesses, and stores in counters, k output positions and the letters produced at these positions. The formula of \(\mathcal {P}\) at the end simply checks, for each pairs of runs, that the same positions were guessed by both runs, and that the letters were different, ensuring that the guessed runs have different output pairwise. As two functional transducers are equivalent if they have the same domain and their union is 1-valued, we get the following corollary.
Corollary 2
The equivalence of two functional \(\mathsf {2VPT_{su}}\) T and \(T'\) can be decided in NExpTime. It is also ExpTime-hard.
The NexpTime complexity of equivalence of tree to string transducers was already established for Streaming Tree to string transducers (STST), introduced in [1]. However, the conversion between the \(\mathsf {2VPT_{su}}\) and STST yields an exponential blow-up.
We can generalize Corollary 2 to strictly k-valued transducers. We say that a transducer T is strictly k-valued if each input word in the domain of T has exactly k different images. Then similarly to the previous corollary, two strictly k-valued transducers are equivalent if, and only if, they have same domain and their union is k-valued.
Corollary 3
The equivalence of two strictly k-valued \(\mathsf {2VPT_{su}}\) T and \(T'\) can be decided in NExpTime. It is also ExpTime-hard.
Strict k-valuedness is however an undecidable property (this can be shown by using the Post correspondence problem), even for \(k=2\). Deciding the equivalence problem for k-valued \(\mathsf {2VPT_{su}}\) (which are not necessarily strictly k-valued) is open already in the stack-less case, and a (very) particular case has been solved in [14].
Type-checking against Parikh properties. Given a \(\mathsf {2VPT}\) T, it might be desirable to check some properties of the output words it produces, i.e., for a language L, whether the codomain of T is included in L. Formally, the type-checking problem asks, given a transducer T and a language L, whether \(T(\varSigma ^*)\subseteq L\). Unfortunately, this problem is undecidable when L is given by a visibly pushdown automaton (and T is a \(\mathsf {VPT}\)) [13]. Nevertheless, we show that the type-checking problem is decidable when T is a \(\mathsf {2VPT_{su}} \) and L is the complement of the language given by a (stack-less) Parikh Automaton. As a consequence, we are able to decide whether a \(\mathsf {2VPT_{su}}\) T produces only well-nested words, i.e. if the output alphabet of T is structured and for every input word u and any \(v\in T(u)\), v is a well-nested word.
Theorem 6
Let T be a \(\mathsf {2VPT_{su}}\) and P be a (stack-free) Parikh Automaton over the output alphabet of T. Then we can decide whether \(T(\varSigma ^*)\cap L(P)=\emptyset \) in NExpTime. It is also ExpTime-hard.
This is done by constructing a \(\mathsf {2VPPA_{su}}\) \(P'\) which simulates T, and instead of producing letters, simulates P on the output of T. A word w on a structured alphabet \(\varSigma \) is not well-nested if either \(|w|_c\ne |w|_r\), i.e. the number of call letters is not equal to the number of return letters, or if there exists a prefix u of w such that \(|u|_c < |u|_r\). As this can be checked by a (non-deterministic) Parikh automata, we get the following corollary.
Corollary 4
Let T be a \(\mathsf {2VPT_{su}}\) whose output alphabet is structured. It can be decided in CoNExpTime whether T only produces well-nested words.
References
Alur, R., D’Antoni, L.: Streaming tree transducers. In: Czumaj, A., Mehlhorn, K., Pitts, A., Wattenhofer, R. (eds.) ICALP 2012. LNCS, vol. 7392, pp. 42–53. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31585-5_8
Alur, R., Madhusudan, P.: Adding nesting structure to words. J. ACM 56(3), 16:1–16:43 (2009)
Burkart, O., Steffen, B.: Model checking the full modal mu-calculus for infinite sequential processes. In: Degano, P., Gorrieri, R., Marchetti-Spaccamela, A. (eds.) ICALP 1997. LNCS, vol. 1256, pp. 419–429. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63165-8_198
Cadilhac, M., Finkel, A., McKenzie, P.: On the expressiveness of Parikh automata and related models. In: Proceedings of the Third Workshop on Non-Classical Models for Automata and Applications - NCMA 2011, Milan, Italy, 18 July–19 July 2011, pp. 103–119 (2011)
Clarke, E.M., Emerson, E.A., Sistla, A.P.: Automatic verification of finite state concurrent systems using temporal logic specifications. In: Conference Record of the Tenth Annual ACM Symposium on Principles of Programming Languages, pp. 117–126. ACM, January 1983
Courcelle, B., Engelfriet, J.: Graph Structure and Monadic Second-Order Logic - A Language-Theoretic Approach. Encyclopedia of Mathematics and its Applications, vol. 138. Cambridge University Press (2012). http://www.cambridge.org/fr/knowledge/isbn/item5758776/?site_locale=fr_FR
Dang, Z., Ibarra, O.H., Bultan, T., Kemmerer, R.A., Su, J.: Binary reachability analysis of discrete pushdown timed automata. In: Emerson, E.A., Sistla, A.P. (eds.) CAV 2000. LNCS, vol. 1855, pp. 69–84. Springer, Heidelberg (2000). https://doi.org/10.1007/10722167_9
Dartois, L., Filiot, E., Reynier, P.-A., Talbot, J.-M.: Two-way visibly pushdown automata and transducers. In: Proceedings of the 31st Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2016, New York, NY, USA, 5–8 July 2016, pp. 217–226 (2016). https://doi.org/10.1145/2933575.2935315
Engelfriet, J., Hoogeboom, H.J.: MSO definable string transductions and two-way finite-state transducers. ACM Trans. Comput. Logic 2(2), 216–254 (2001)
Engelfriet, J., Maneth, S.: Macro tree transducers, attribute grammars, and MSO definable tree translations. Inf. Comput. 154(1), 34–91 (1999). https://doi.org/10.1006/inco.1999.2807. http://www.sciencedirect.com/science/article/pii/S0890540199928079
Esparza, J., Ganty, P.: Complexity of pattern-based verification for multithreaded programs. ACM SIGPLAN Not. - POPL 2011 46(1), 499–510 (2011). https://doi.org/10.1145/1925844.1926443
Figueira, D., Libkin, L.: Path logics for querying graphs: combining expressiveness and efficiency. In: 30th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2015, Kyoto, Japan, 6–10 July 2015, pp. 329–340 (2015). https://doi.org/10.1109/LICS.2015.39
Filiot, E., Raskin, J.-F., Reynier, P.-A., Servais, F., Talbot, J.-M.: Properties of visibly pushdown transducers. In: Hliněný, P., Kučera, A. (eds.) MFCS 2010. LNCS, vol. 6281, pp. 355–367. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15155-2_32
Gallot, P., Muscholl, A., Puppis, G., Salvati, S.: On the decomposition of finite-valued streaming string transducers. In: STACS 2017. LIPIcs, vol. 66, pp. 34:1–34:14 (2017). https://doi.org/10.4230/LIPIcs.STACS.2017.34. http://drops.dagstuhl.de/opus/volltexte/2017/6999
Haase, C.: On the complexity of model checking counter automata. Ph.D. thesis, University of Oxford, UK (2012). http://ora.ox.ac.uk/objects/uuid:f43bf043-de93-4b5c-826f-88f1bd4c191d
Hague, M., Lin, A.W.: Model checking recursive programs with numeric data types. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 743–759. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_60
Hague, M., Lin, A.W.: Synchronisation- and reversal-bounded analysis of multithreaded programs with counters. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 260–276. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31424-7_22
Ibarra, O.H.: Reversal-bounded multicounter machines and their decision problems. J. ACM 25(1), 116–133 (1978). http://doi.acm.org/10.1145/322047.322058
Ibarra, O.H.: Automata with reversal-bounded counters: a survey. In: Jürgensen, H., Karhumäki, J., Okhotin, A. (eds.) DCFS 2014. LNCS, vol. 8614, pp. 5–22. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-09704-6_2
Karianto, W.: Parikh automata with pushdown stack. Technical report (2004)
Klaedtke, F.: Parikh automata and monadic second-order logics with linear cardinality constraints. Technical report, 30 July 2002
Klaedtke, F., Rueß, H.: Monadic second-order logics with cardinalities. In: Baeten, J.C.M., Lenstra, J.K., Parrow, J., Woeginger, G.J. (eds.) ICALP 2003. LNCS, vol. 2719, pp. 681–696. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-45061-0_54. http://dl.acm.org/citation.cfm?id=1759210.1759277
König, B., Esparza, J.: Verification of graph transformation systems with context-free specifications. In: Ehrig, H., Rensink, A., Rozenberg, G., Schürr, A. (eds.) ICGT 2010. LNCS, vol. 6372, pp. 107–122. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15928-2_8
Parikh, R.J.: On context-free languages. J. ACM 13(4), 570–581 (1966). https://doi.org/10.1145/321356.321364
Scarpellini, B.: Complexity of subcases of Presburger arithmetic. Trans. Am. Math. Soc. 284(1), 203–218 (1984)
Schwoon, S.: Model checking pushdown systems. Ph.D. thesis, Technical University Munich, Germany (2002). http://tumb1.biblio.tu-muenchen.de/publ/diss/in/2002/schwoon.html
Shepherdson, J.C.: The reduction of two-way automata to one-way automata. IBM J. Res. Dev. 3(2), 198–200 (1959)
Vardi, M.Y., Wolper, P.: An automata-theoretic approach to automatic program verification (preliminary report). In: LICS, pp. 332–344. IEEE Computer Society (1986)
Verma, K.N., Seidl, H., Schwentick, T.: On the complexity of equational horn clauses. In: Nieuwenhuis, R. (ed.) CADE 2005. LNCS (LNAI), vol. 3632, pp. 337–352. Springer, Heidelberg (2005). https://doi.org/10.1007/11532231_25
Walukiewicz, I.: Pushdown processes: games and model-checking. Inf. Comput. 164(2), 234–263 (2001). https://doi.org/10.1006/inco.2000.2894. http://www.sciencedirect.com/science/article/pii/S0890540100928943
Acknowledgements
This work was supported by the Belgian FNRS CDR project Flare (J013116), the ARC project Transform (Fédération Wallonie Bruxelles) and by the ANR Project DELTA, ANR-16-CE40-0007. Emmanuel Filiot is an FNRS research associate (Chercheur Qualifié).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Dartois, L., Filiot, E., Talbot, JM. (2019). Two-Way Parikh Automata with a Visibly Pushdown Stack. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)








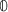 otherwise.
otherwise.