Rewriting Abstract Structures: Materialization Explained Categorically

Abstract

The paper develops an abstract (over-approximating) semantics for double-pushout rewriting of graphs and graph-like objects. The focus is on the so-called materialization of left-hand sides from abstract graphs, a central concept in previous work. The first contribution is an accessible, general explanation of how materializations arise from universal properties and categorical constructions, in particular partial map classifiers, in a topos. Second, we introduce an extension by enriching objects with annotations and give a precise characterization of strongest post-conditions, which are effectively computable under certain assumptions.

T. Heindel—Partially supported by AFOSR.

1 Introduction

Abstract interpretation [12] is a fundamental static analysis technique that applies not only to conventional programs but also to general infinite-state systems. Shape analysis [30], a specific instance of abstract interpretation, pioneered an approach for analyzing pointer structures that keeps track of information about the “heap topology”, e.g., out-degrees or existence of certain paths. One central idea of shape analysis is materialization, which arises as companion operation to summarizing distinct objects that share relevant properties. Materialization, a.k.a. partial concretization, is also fundamental in verification approaches based on separation logic [5, 6, 24], where it is also known as rearrangement [26], a special case of frame inference. Shape analysis—construed in a wide sense—has been adapted to graph transformation [29], a general purpose modelling language for systems with dynamically evolving topology, such as network protocols and cyber-physical systems. Motivated by earlier work of shape analysis for graph transformation [1, 2, 4, 27, 28, 31], we want to put the materialization operation on a new footing, widening the scope of shape analysis.

A natural abstraction mechanism for transition systems with graphs as states “summarizes” all graphs over a specific shape graph. Thus a single graph is used as abstraction for all graphs that can be mapped homomorphically into it. Further annotations on shape graphs, such as cardinalities of preimages of its nodes and general first-order formulas, enable fine-tuning of the granularity of abstractions. While these natural abstraction principles have been successfully applied in previous work [1, 2, 4, 27, 28, 31], their companion materialization constructions are notoriously difficult to develop, hard to understand, and are redrawn from scratch for every single setting. Thus, we set out to explain materializations based on mathematical principles, namely universal properties (in the sense of category theory). In particular, partial map classifiers in the topos of graphs (and its slice categories) cover the purely structural aspects of materializations; this is related to final pullback complements [13], a fundamental construction of graph rewriting [7, 25]. Annotations of shape graphs are treated orthogonally via op-fibrations.

The first milestones of a general framework for shape analysis of graph transformation and more generally rewriting of objects in a topos are the following:

A rewriting formalism for graph abstractions that lifts the rule-based rewriting from single graphs to abstract graphs; it is developed for (abstract) objects in a topos.

We characterize the materialization operation for abstract objects in a topos in terms of partial map classifiers, giving a sound and complete description of all occurrences of right-hand sides of rules obtained by rewriting an abstract object.    $\rightarrow$ Sect. 3

We decorate abstract objects with annotations from an ordered monoid and extend abstract rewriting to abstract objects with annotations. For the specific case of graphs, we consider global annotations (counting the nodes and edges in a graph), local annotations (constraining the degree of a node), and path annotations (constraining the existence of paths between certain nodes).    $\rightarrow$ Sect. 4

We show that abstract rewriting with annotations is sound and, with additional assumptions, complete. Finally, we derive strongest post-conditions for the case of graph rewriting with annotations.    $\rightarrow$ Sect. 5

Related work: The idea of shape graphs together with shape constraints was pioneered in [30] where the constraints are specified in a three-valued logic. A similar approach was proposed in [31], using first-order formulas as constraints. In partner abstraction [3, 4], cluster abstraction [1, 2], and neighbourhood abstraction [28] nodes are clustered according to local criteria, such as their neighbourhood and the resulting graph structures are enriched with counting constraints, similar to our constraints. The idea of counting multiplicities of nodes and edges is also found in canonical graph shapes [27]. The uniform treatment of monoid annotations was introduced in previous work [9, 10, 20], in the context of type systems and with the aim of studying decidability and closure properties, but not for abstract rewriting.

2 Preliminaries

This paper presupposes familiarity with category theory and the topos structure of graphs. Some concepts (in particular elementary topoi, subobject and partial map classifiers, and slice categories) are defined in the full version of this paper [8], which also contains all the proofs.

The rewriting formalism for graphs and graph-like structures that we use throughout the paper is the double-pushout (DPO) approach [11]. Although it was originally introduced for graphs [16], it is well-defined in any category ${\mathbf {C}}$. However, certain standard results for graph rewriting require that the category ${\mathbf {C}}$ has “good” properties. The category of graphs is an elementary topos—an extremely rich categorical structure—but weaker conditions on ${\mathbf {C}}$, for instance adhesivity, have been studied [14, 15, 21].

Definition 1

(Double-pushout rewriting). A production in ${\mathbf {C}}$ is a span of monos in ${\mathbf {C}}$; the objects L and R are called left- and right-hand side, respectively. A match of a production to an object X of ${\mathbf {C}}$ is a mono in ${\mathbf {C}}$. The production p rewrites X to Y at $m_L$ (resp. the match $m_L$ to the co-match $m_R :R\rightarrow Y$) if the production and the match (and the co-match) extend to a diagram in ${\mathbf {C}}$, shown to the right, such that both squares are pushouts.

In this case, we write (resp. ). We also write if there exists an object Y such that and if the specific match $m_L$ is not relevant.

Given a production p and a match $m_L$, if there exist arrows $X \leftarrow C$ and $C \leftarrow I$ that make the left-hand square of the diagram in Definition 1 a pushout square, then the gluing condition is satisfied.

If ${\mathbf {C}}$ is an adhesive category (and thus also if it is a topos [22]) and the production consists of monos, then all remaining arrows of double-pushout diagrams of rewriting are monos [21] and the result of rewriting—be it the object Y or the co-match $m_R$—is unique (up to a canonical isomorphism).

2.1 Subobject Classifiers and Partial Map Classifiers of Graphs

A standard category for graph rewriting that is also a topos is the category of edge-labelled, directed graphs that we shall use in examples, as recalled in the next definition. Note that due to the generality of the categorical framework, our results also hold for various other forms of graphs, such as node-labelled graphs, hypergraphs, graphs with scopes or graphs with second-order edges.

Definition 2

(Category of graphs). Let $\varLambda$ be a fixed set of edge labels. A $(\varLambda$-labelled) graph is a tuple where $V_G$ is a finite set of nodes, $E_G$ is a finite set of edges, are the source and target mappings and is the labelling function. Let G, H be two $\varLambda$-labelled graphs. A graph morphism $\varphi :G\rightarrow H$ consists of two functions $\varphi _V:V_G\rightarrow V_{H}$, $\varphi _E:E_G\rightarrow E_{H}$, such that for each edge $e\in E_G$ we have , and . If $\varphi _V,\varphi _E$ are both bijective, $\varphi$ is an isomorphism. The category having ($\varLambda$-labelled) graphs as objects and graph morphisms as arrows is denoted by ${\mathbf {Graph}}$.

We shall often write $\varphi$ instead of $\varphi _V$ or $\varphi _E$ to avoid clutter. The graph morphisms in our diagrams will be indicated by black and white nodes and thick edges. In the category ${\mathbf {Graph}}$, where the objects are labelled graphs over the label alphabet $\varLambda$, the subobject classifier $\mathtt {true}$ is displayed to the right where every $\varLambda$-labelled edge represents several edges, one for each $\lambda \in \varLambda$.

The subobject classifier from the terminal object $\mathbf {1}$ to $\varOmega$ allows us to single out a subgraph X of a graph Y, by mapping Y to $\varOmega$ in such a way that all elements of X are mapped to the image of $\mathtt {true}$.

Given arrows $\alpha ,m$ as in the diagram in Definition 3, we can construct the most general pullback, called final pullback complement [7, 13].

Definition 3

(Final pullback complement). A pair of arrows is a final pullback complement (FPBC) of another pair if

Final pullback complements and subobject classifiers are closely related to partial map classifiers (see [13, Corollary 4.6]): a category has FPBCs (over monos) and a subobject classifier if and only if it has a partial map classifier. These exist in all elementary topoi.

Proposition 4

(Final pullback complements, subobject and partial map classifiers). Let ${\mathbf {C}}$ be a category with finite limits. Then the following are equivalent:

• (1) ${\mathbf {C}}$ has a subobject classifier $\mathtt {true} :\mathbf {1} \rightarrowtail \varOmega$ and final pullback complements for each pair of arrows with m mono;

• (2) ${\mathbf {C}}$ has a partial map classifier .

2.2 Languages

The main theme of the paper is “simultaneous” rewriting of entire sets of objects of a category by means of rewriting a single abstract object that represents a collection of structures—the language of the abstract object. The simplest example of an abstract structure is a plain object of a category to which we associate the language of objects that can be mapped to it; the formal definition is as follows (see also [10]).

Definition 5

(Language of an object). Let A be an object of a category ${\mathbf {C}}$. Given another object X, we write $X\dashrightarrow A$ whenever there exists an arrow from X to A. We define the language¹ of A, denoted by $\mathcal {L}(A)$, as $\mathcal {L}(A) = \{X \in {\mathbf {C}}\mid X\dashrightarrow A \}$.

Whenever $X \in \mathcal {L}(A)$ holds, we will say that X is abstracted by A, and A is called the abstract object. In the following we will also need to characterize a class of (co-)matches which are represented by a given (co-)match (which is a mono).

Definition 6

(Language of a mono). Let be a mono in ${\mathbf {C}}$. The language of $\varphi$ is the set of monos m with source L that factor $\varphi$ such that the square on the right is a pullback:

Intuitively, for any arrow we have $X\in \mathcal {L}(A)$ and X has a distinguished subobject L which corresponds precisely to the subobject . In fact $\psi$ restricts and co-restricts to an isomorphism between the images of L in X and A. For graphs, no nodes or edges in X outside of L are mapped by $\psi$ into the image of L in A.

3 Materialization

Given a production , an abstract object A, and a (possibly non-monic) arrow $\varphi :L\rightarrow A$, we want to transform the abstract object A in order to characterize all successors of objects in $\mathcal {L}(A)$, i.e., those obtained by rewriting via p at a match compatible with $\varphi$. (Note that $\varphi$ is not required to be monic, because a monic image of the left-hand side of p in an object of $\mathcal {L}(A)$ could be mapped non-injectively to A.) Roughly, we want to lift DPO rewriting to the level of abstract objects.

For this, it is necessary to use the materialization construction, defined categorically in Sect. 3.1, that enables us to concretize an instance of a left-hand side in a given abstract object. This construction is refined in Sect. 3.2 where we restrict to materializations that satisfy the gluing condition and can thus be rewritten via p. Finally in Sect. 3.3 we present the main result about materializations showing that we can fully characterize the co-matches obtained by rewriting.

3.1 Materialization Category and Existence of Materialization

From now on we assume ${\mathbf {C}}$ to be an elementary topos. We will now define the materialization, which, given an arrow $\varphi :L\rightarrow A$, characterizes all objects X, abstracted over A, which contain a (monic) occurrence of the left-hand side compatible with $\varphi$.

Definition 7

(Materialization). Let $\varphi :L\rightarrow A$ be an arrow in ${\mathbf {C}}$. The materialization category for $\varphi$, denoted , has as

If has a terminal object it is denoted by and is called the materialization of $\varphi$.

Sometimes we will also call the object the materialization of $\varphi$, omitting the arrows.

Since we are working in a topos by assumption, the slice category over A provides us with a convenient setting to construct materializations. Note in particular that in the diagram in Definition 7 above, the span is a partial map from X to L in the slice category over A. Hence the materialization corresponds to the partial map classifier for L in this slice category.

Proposition 8

(Existence of materialization). Let $\varphi :L \rightarrow ~A$ be an arrow in ${\mathbf {C}}$, and let $\eta _\varphi :\varphi \rightarrow F(\varphi )$, with $F(\varphi ) :\bar{A} \rightarrow A$, be the partial map classifier of $\varphi$ in the slice category ${\mathbf {C}}\!\downarrow \! A$ (which also is a topos).² Then is the materialization of $\varphi$, hence .

As a direct consequence of Propositions 4 and 8 (and the fact that final pullback complements in the slice category correspond to those in the base category [25]), the terminal object of the materialization category can be constructed for each arrow of a topos by taking final pullback complements.

Corollary 9

(Construction of the materialization). Let $\varphi :L \rightarrow A$ be an arrow of ${\mathbf {C}}$ and let $\mathtt {true}_A :A \rightarrowtail A \times \varOmega$ be the subobject classifier (in the slice category ${\mathbf {C}}\downarrow A$) from $\textit{id}_A :A \rightarrow A$ to the projection $\pi _1 :A \times \varOmega \rightarrow A$.

Then the terminal object in the materialization category consists of the arrows $\eta _\varphi$ and $\psi = \pi _1\circ \chi _{\eta _\varphi }$, where is the final pullback complement of .

Example 10

We construct the materialization for the following morphism $\varphi :L \rightarrow A$ of graphs with a single (omitted) label:

In particular, the materialization is obtained as a final pullback complement as depicted to the right (compare with the corresponding diagram in Corollary 9). Note that edges which are not in the image of $\eta _\varphi$ resp. $\mathtt {true}_A$ are dashed.

This construction corresponds to the usual intuition behind materialization: the left-hand side and the edges that are attached to it are “pulled out” of the given abstract graph.

We can summarize the result of our constructions in the following proposition:

Proposition 11

(Language of the materialization). Let $\varphi :L\rightarrow A$ be an arrow in ${\mathbf {C}}$ and let be the corresponding materialization. Then we have

3.2 Characterizing the Language of Rewritable Objects

A match obtained through the materialization of the left-hand side of a production from a given object may not allow a DPO rewriting step because of the gluing condition. We illustrate this problem with an example.

Example 12

Consider the materialization from Example 10 and the production shown in the diagram to the right. It is easy to see that the pushout complement of morphisms does not exist.

Nevertheless there exist factorizations abstracted by that could be rewritten using the production.

In order to take the existence of pushout complements into account, we consider a subcategory of the materialization category.

Definition 13

(Materialization subcategory of rewritable objects). Let $\varphi :L\rightarrow A$ be an arrow of ${\mathbf {C}}$ and let be a mono (corresponding to the left leg of a production). The materialization subcategory of rewritable objects for $\varphi$ and $\varphi _L$, denoted , is the full subcategory of containing as objects all factorizations of $\varphi$, where m is a mono and has a pushout complement.

Its terminal element, if it exists, is denoted by and is called the rewritable materialization.

We show that this subcategory of the materialization category has a terminal object.

Proposition 14

(Construction of the rewritable materialization). Let $\varphi :L\rightarrow A$ be an arrow and let be a mono of ${\mathbf {C}}$. Then the rewritable materialization of $\varphi$ w.r.t. $\varphi _L$ exists and can be constructed as the following factorization of $\varphi$. In the left diagram, F is obtained as the final pullback complement of , where is the materialization of $\varphi$ (Definition 7). Next in the right diagram is the pushout of the span and $\alpha$ is the resulting mediating arrow.

Example 15

We come back to the running example (Example 12) and, as in Proposition 14, determine the final pullback complement of (see diagram below left) and obtain by taking the pushout over (see diagram below right).

It remains to be shown that represents every factorization which can be rewritten. As before we obtain a characterization of the rewritable objects, including the match, as the language of an arrow.

Proposition 16

(Language of the rewritable materialization). Assume there is a production and let be the match for the rewritable materialization for $\varphi$ and $\varphi _L$. Then we have

3.3 Rewriting Materializations

In the next step we will now rewrite the rewritable materialization with the match , resulting in a co-match . In particular, we will show that this co-match represents all co-matches that can be obtained by rewriting an object X of $\mathcal {L}(A)$ at a match compatible with $\varphi$. We first start with an example.

Example 17

We can rewrite the materialization as follows:

Proposition 18

(Rewriting abstract matches). Let a match and a production be given. Assume that $\tilde{A}$ is rewritten along the match $n_L$, i.e., . Then

If we combine Propositions 16 and 18, we obtain the following corollary that characterizes the co-matches obtained from rewriting a match compatible with $\varphi :L\rightarrow A$.

Corollary 19

(Co-match language of the rewritable materialization). Let $\varphi :L\rightarrow A$ and a production be given. Assume that is obtained as the rewritable materialization of $\varphi$ and $\varphi _L$ with match (see Proposition 14). Furthermore let . Then

This result does not yet enable us to construct post-conditions for languages of objects. The set of co-matches can be fully characterized as the language of a mono, which can only be achieved by fixing the right-hand side R and thus ensuring that exactly one occurrence of R is represented. However, as soon as we forget about the co-match, this effect is gone and can only be retrieved by adding annotations, which will be introduced next.

4 Annotated Objects

We now endow objects with annotations, thus making object languages more expressive. In particular we will use ordered monoids in order to annotate objects. Similar annotations have already been studied in [20] in the context of type systems and in [10] with the aim of studying decidability and closure properties, but not for abstract rewriting.

Definition 20

(Ordered monoid). An ordered monoid $(\mathcal {M},+,\le )$ consists of a set $\mathcal {M}$, a partial order $\le$ and a binary operation $+$ such that $(\mathcal {M},+)$ is a monoid with unit 0 (which is the bottom element wrt. $\le$) and the partial order is compatible with the monoid operation. In particular $a\le b$ implies $a+c\le b+c$ and $c+a\le c+b$ for all $a,b,c\in \mathcal {M}$. An ordered monoid is commutative if $+$ is commutative.

A tuple $(\mathcal {M},+,-,\le )$, where $(\mathcal {M},+,\le )$ is an ordered monoid and − is a binary operation on $\mathcal {M}$, is called an ordered monoid with subtraction.

We say that subtraction is well-behaved whenever for all $a,b\in \mathcal {M}$ it holds that $a-a = 0$ and $(a-b)+b = a$ whenever $b\le a$.

For now subtraction is just any operation, without specific requirements. Later we will concentrate on specific subtraction operations and demand that they are well-behaved.

In the following we will consider only commutative monoids.

Definition 21

(Monotone maps and homomorphisms). Let $\mathcal {M}_1$, $\mathcal {M}_2$ be two ordered monoids. A map $h:\mathcal {M}_1\rightarrow \mathcal {M}_2$ is called monotone if $a\le b$ implies $h(a)\le h(b)$ for all $a,b\in \mathcal {M}_1$. The category of ordered monoids with subtraction and monotone maps is called ${\mathbf {Mon}}$.

A monotone map h is called a homomorphism if $h(0)=0$ and $h(a+b)= h(a)+h(b)$. If $\mathcal {M}_1,\mathcal {M}_2$ are ordered monoids with subtraction, we say that h preserves subtraction if $h(a-b) = h(a)-h(b)$.

Example 22

Let $n \in \mathbb {N}\backslash \{0\}$ and take $\mathcal {M}_n = \{0,1,\dots ,n,*\}$ (zero, one, $\dots$, n, many) with $0 \le 1 \le \dots \le n\le *$ and addition as (commutative) monoid operation with the proviso that $a+b=*$ if the sum is larger than n. In addition $a+* = *$ for all $a\in \mathcal {M}_n$. Subtraction is truncated subtraction where $a-b = 0$ if $a \le b$. Furthermore $*-a = *$ for all $a\in \mathbb {N}$. It is easy to see that subtraction is well-behaved.

Given a set S and an ordered monoid (with subtraction) $\mathcal {M}$, it is easy to check that also $\mathcal {M}^S$ is an ordered monoid (with subtraction), where the elements are functions from S to $\mathcal {M}$ and the partial order, the monoidal operation and the subtraction are taken pointwise.

The following path monoid is useful if we want to annotate a graph with information over which paths are present. Note that due to the possible fusion of nodes and edges caused by the abstraction, a path in the abstract graph does not necessarily imply the existence of a corresponding path in a concrete graph. Hence annotations based on such a monoid, which provide information about the existence of paths, can yield useful additional information.

Example 23

Given a graph G, we denote by $E_G^+\subseteq V_G\times V_G$ the transitive closure of the edge relation . The path monoid $\mathcal {P}_G$ of G has the carrier set $\mathcal {P}(E_G^+)$. The partial order is simply inclusion and the monoid operation is defined as follows: given $P_0,P_1\in \mathcal {P}_G$, we have

$$\begin{aligned} P_0+P_1= & {} \{(v_0,v_n)\mid \exists v_1,\dots ,v_{n-1} :(v_i,v_{i+1})\in P_{j_i}, \\&\qquad \qquad \qquad {j_0 \in \{0,1\}}, j_{i+1} = 1-j_i, i\in \{0,\dots ,n-1\} {\text { and } n \in \mathbb {N}}\}. \end{aligned}$$

That is, new paths can be formed by concatenating alternating path fragments from $P_0,P_1$. It is obvious to see that $+$ is commutative and one can also show associativity. $P=\emptyset$ is the unit. Subtraction simply returns the first parameter: $P_0-P_1 = P_0$.

We will now formally define annotations for objects via a functor from a given category to ${\mathbf {Mon}}$.

Definition 24

(Annotations for objects). Given a category ${\mathbf {C}}$ and a functor $\mathcal {A} :{\mathbf {C}}\rightarrow {\mathbf {Mon}}$, an annotation based on ${\mathcal {A}}$ for an object $X \in {\mathbf {C}}$ is an element $a \in \mathcal {A}(X)$. We write $\mathcal {A}_\varphi$, instead of $\mathcal {A}(\varphi )$, for the action of functor $\mathcal {A}$ on a ${\mathbf {C}}$-arrow $\varphi$. We assume that for each object X there is a standard annotation based on $\mathcal {A}$ that we denote by $s_X$, thus $s_X \in \mathcal {A}(X)$.

It can be shown quite straightforwardly that the forgetful functor mapping an annotated object X[a], with $a \in \mathcal {A}(X)$, to X is an op-fibration (or co-fibration [19]), arising via the Grothendieck construction.

Our first example is an annotation of graphs with global multiplicities, counting nodes and edges, where the action of the functor is to sum up those multiplicities.

Example 25

Given $n\in \mathbb {N}\backslash \{0\}$, we define the functor $\mathcal {B}^n:{\mathbf {Graph}}\rightarrow {\mathbf {Mon}}$: For every graph G, $\mathcal {B}^n(G) = \mathcal {M}_n^{V_G\cup E_G}$. For every graph morphism $\varphi :G \rightarrow H$ and $a \in \mathcal {B}^n(G)$, we have $\mathcal {B}^n_{\varphi }(a) \in \mathcal {M}_n^{V_{H} \cup E_{H}}$ with:

$$ \mathcal {B}^n_{\varphi }(a)(y) = \sum \limits _{\varphi (x)=y}^{} a(x), \quad \textit{where } x \in (V_G \cup E_G) \textit{ and } y \in (V_{H} \cup E_{H}). $$

Therefore an annotation based on a functor $\mathcal {B}^n$ associates every item of a graph with a number (or the top value $*$). We will call such annotations multiplicities. Furthermore the action of the functor on a morphism transforms a multiplicity by summing up (in $\mathcal {M}_n$) the values of all items of the source graph that are mapped to the same item of the target graph.

For a graph G, its standard multiplicity $s_G \in \mathcal {B}^n(G)$ is defined as the function which maps every node and edge of G to 1.

As another example we consider local annotations which record the out-degree of a node and where the action of the functor is to take the supremum instead of the sum.

Example 26

Given $n\in \mathbb {N}\backslash \{0\}$, we define the functor $\mathcal {S}^n:{\mathbf {Graph}}\rightarrow {\mathbf {Mon}}$ as follows: For every graph G, $\mathcal {S}^n(G) = \mathcal {M}_n^{V_G}$. For every graph morphism $\varphi :G \rightarrow H$ and $a \in \mathcal {S}^n(G)$, we have $\mathcal {S}^n_{\varphi }(a) \in \mathcal {M}_n^{V_{H}}$ with:

$$ \mathcal {S}^n_{\varphi }(a)(w) = \bigvee \limits _{\varphi (v)=w}^{} a(v), \quad \textit{where } v \in V_G \textit{ and } w \in V_{H}. $$

For a graph G, its standard annotation $s_G \in \mathcal {S}^n(G)$ is defined as the function which maps every node of G to its out-degree (or $*$ if the out-degree is larger than n).

Finally, we consider annotations based on the path monoid (see Example 23).

Example 27

We define the functor $\mathcal {T}:{\mathbf {Graph}}\rightarrow {\mathbf {Mon}}$ as follows: For every graph G, $\mathcal {T}(G) = \mathcal {P}_G$. For every graph morphism $\varphi :G \rightarrow H$ and $P \in \mathcal {T}(G)$, we have $\mathcal {T}_{\varphi }(P) \in \mathcal {P}_{H}$ with:

$$ \mathcal {T}_{\varphi }(P) = \{(\varphi (v),\varphi (w))\mid (v,w)\in P\}. $$

For a graph G, its standard annotation $s_G \in \mathcal {T}(G)$ is the transitive closure of the edge relation, i.e., $s_G = E_G^+$.

In the following we will consider only annotations satisfying certain properties in order to achieve soundness and completeness.

Definition 28

(Properties of annotations). Let $\mathcal {A}:{\mathbf {C}}\rightarrow {\mathbf {Mon}}$ be an annotation functor, together with standard annotations. In this setting we say that

• the homomorphism property holds if whenever $\varphi$ is a mono, then $\mathcal {A}_\varphi$ is a monoid homomorphism, preserving also subtraction.

• the adjunction property holds if whenever is a mono, then

  • $\mathcal {A}_\varphi :\mathcal {A}(A)\rightarrow \mathcal {A}(B)$ has a right adjoint $red _\varphi :\mathcal {A}(B)\rightarrow \mathcal {A}(A)$, i.e., $red _\varphi$ is monotone and satisfies $a \le red _\varphi (\mathcal {A}_\varphi (a))$ for $a\in \mathcal {A}(A)$ and $\mathcal {A}_\varphi ( red _\varphi (b))\le b$ for $b\in \mathcal {A}(B)$.³

  • $red _\varphi$ is a monoid homomorphism that preserves subtraction.

  • it holds that $red _\varphi (s_B) = s_A$, where $s_A,s_B$ are standard annotations.

Furthermore, assuming that $\mathcal {A}_\varphi$ has a right adjoint $red _\varphi$, we say that

• the pushout property holds, whenever for each pushout as shown in the diagram to the right, with all arrows monos where $\eta = \psi _1 \circ \varphi _1 = \psi _2 \circ \varphi _2$, it holds that for every $d\in \mathcal {A}(D)$:

  $$ d = \mathcal {A}_{\psi _1}( red _{\psi _1}(d)) + (\mathcal {A}_{\psi _2}( red _{\psi _2}(d)) - \mathcal {A}_{\eta }( red _{\eta }(d))). $$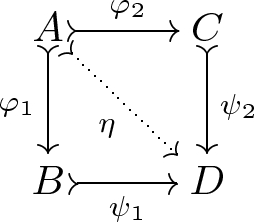

  

  We say that the pushout property for standard annotations holds if we replace d by $s_D$, $red _\eta (d)$ by $s_A$, $red _{\psi _1}(d)$ by $s_B$ and $red _{\psi _2}(d)$ by $s_C$.

• the Beck-Chevalley property holds if whenever the square shown to the right is a pullback with $\varphi _1$, $\psi _2$ mono, then it holds for every $b\in \mathcal {A}(B)$ that

  $$ \mathcal {A}_{\varphi _2}( red _{\varphi _1}(b)) = red _{\psi _2}(\mathcal {A}_{\psi _1}(b)). $$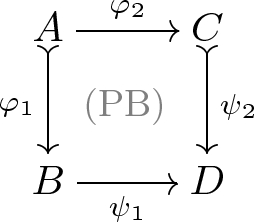

  

Note that the annotation functor from Example 25 satisfies all properties above, whereas the functors from Examples 26 and 27 satisfy both the homomorphism property and the pushout property for standard annotations, but do not satisfy all the remaining requirements [8].

We will now introduce a more flexible notion of language, by equipping the abstract objects with two annotations, establishing lower and upper bounds.

Definition 29

(Doubly annotated object). Given a topos ${\mathbf {C}}$ and a functor $\mathcal {A}:{\mathbf {C}}\rightarrow \mathbf {Mon}$, a doubly annotated object $A[a_1,a_2]$ is an object A of ${\mathbf {C}}$ with two annotations $a_1,a_2\in \mathcal {A}(A)$.An arrow $\varphi :A[a_1,a_2]\rightarrow B[b_1,b_2]$, also called a legal arrow, is a ${\mathbf {C}}$-arrow $\varphi :A\rightarrow B$ such that $\mathcal {A}_\varphi (a_1)\ge b_1$ and $\mathcal {A}_\varphi (a_2) \le b_2$.

The language of a doubly annotated object $A[a_1,a_2]$ (also called the language of objects which are abstracted by $A[a_1,a_2]$) is defined as follows:

Note that legal arrows are closed under composition [9]. Examples of doubly annotated objects are given in Example 36 for global annotations from Example 25 (providing upper and lower bounds for the number of nodes resp. edges in the preimage of a given element). Graph elements without annotation are annotated by $[0,*]$ by default.

Definition 30

(Isomorphism property). An annotation functor $\mathcal {A}:{\mathbf {C}}\rightarrow \mathbf {Mon}$, together with standard annotations, satisfies the isomorphism property if the following holds: whenever $\varphi :X[s_X,s_X]\rightarrow Y[s_Y,s_Y]$ is legal, then $\varphi$ is an isomorphism, i.e., $\mathcal {L}(Y[s_Y,s_Y])$ contains only Y itself (and objects isomorphic to Y).

5 Abstract Rewriting of Annotated Objects

We will now show how to actually rewrite annotated objects. The challenge is both to find suitable annotations for the materialization and to “rewrite” the annotations.

5.1 Abstract Rewriting and Soundness

We first describe how the annotated rewritable materialization is constructed and then we investigate its properties.

Definition 31

(Construction of annotated rewritable materialization). Let be a production and let $A[a_1,a_2]$ be a doubly annotated object. Furthermore let $\varphi :L\rightarrow A$ be an arrow.

We first construct the factorization , obtaining the rewritable materialization from Definition 13. Next, let M contain all maximal⁴ elements of the set

Then the doubly annotated objects with $(a'_1,a'_2)\in M$ are the annotated rewritable materializations for $A[a_1,a_2]$, $\varphi$ and $\varphi _L$.

Note that in general there can be several such materializations, differing by the annotations only, or possibly none. The definition of M ensures that the upper bound $a'_2$ of the materialization covers the annotations arising from the left-hand side. We cannot use a corresponding condition for the lower bound, since the materialization might contain additional structures, hence the arrow $n_L$ is only “semi-legal”. A more symmetric condition will be studied in Sect. 5.2.

Proposition 32

(Annotated rewritable materialization is terminal). Given a production , let be the match of L in an object X such that , i.e., X can be rewritten. Assume that X is abstracted by $A[a_1,a_2]$, witnessed by $\psi$. Let $\varphi = \psi \circ m_L$ and let the the corresponding rewritable materialization. Then there exists an arrow $\zeta _A$ and a pair of annotations $(a'_1,a'_2)\in M$ for (as described in Definition 31) such that the diagram below commutes and the square is a pullback in the underlying category. Furthermore the triangle consists of legal arrows. This means in particular that $\zeta _A$ is legal.

Having performed the materialization, we will now show how to rewrite annotated objects. Note that we cannot simply take pushouts in the category of annotated objects and legal arrows, since this would result in taking the supremum of annotations, when instead we need the sum (subtracting the annotation of the interface I, analogous to the inclusion-exclusion principle).

Definition 33

(Abstract rewriting step $\leadsto$). Let be a production and let $A[a_1,a_2]$ be an annotated abstract object. Furthermore let $\varphi :L\rightarrow A$ be a match of a left-hand side, let be the match obtained via materialization and let $(a'_1,a'_2)\in M$ (as in Definition 31).

Then $A[a_1,a_2]$ can be transformed to $B[b_1,b_2]$ via p if there are arrows such that the two squares below are pushouts in the base category and $b_1,b_2$ are defined as:

where $c_1,c_2$ are maximal annotations such that:

In this case we write and say that $A[a_1,a_2]$ makes an abstract rewriting step to $B[b_1,b_2]$.

We will now show soundness of abstract rewriting, i.e., whenever an object X is abstracted by $A[a_1,a_2]$ and X is rewritten to Y, then there exists an abstract rewriting step from $A[a_1,a_2]$ to $B[b_1,b_2]$ such that Y is abstracted by $B[b_1,b_2]$.

Assumption: In the following we will require that the homomorphism property as well as the pushout property for standard annotations hold (cf. Definition 28).

Proposition 34

(Soundness for $\leadsto$). Relation $\leadsto$ is sound in the following sense: Let $X\in \mathcal {L}(A[a_1,a_2])$ (witnessed via a legal arrow $\psi :X[s_X,s_X]\rightarrow A[a_1,a_2]$) where . Then there exists an abstract rewriting step such that $Y\in \mathcal {L}(B[b_1,b_2])$.

5.2 Completeness

The conditions on the annotations that we imposed so far are too weak to guarantee completeness, that is the fact that every object represented by $B[b_1,b_2]$ can be obtained by rewriting an object represented by $A[a_1,a_2]$. This can be clearly seen by the fact that the requirements hold also for the singleton monoid and, as discussed before, the graph structure of B is insufficient to characterize the successor objects or graphs.

Hence we will now strengthen our requirements in order to obtain completeness.

Assumption: In addition to the assumptions of Sect. 5.1, we will need that subtraction is well-behaved and that the adjunction property, the pushout property, the Beck-Chevalley property (Definition 28) and the isomorphism property (Definition 30) hold.

The global annotations from Example 25 satisfy all these properties. In particular, given an injective graph morphism the right adjoint $red _\varphi : \mathcal {M}_n^{V_H\cup E_H} \rightarrow \mathcal {M}_n^{V_G\cup E_G}$ to $\mathcal {B}^n_\varphi$ is defined as follows: given an annotation $b\in \mathcal {M}_n^{V_H\cup E_H}$, $red _\varphi (b)(x) = b(\varphi (x))$, i.e., $red _\varphi$ simply provides a form of reindexing.

We will now modify the abstract rewriting relation and allow only those abstract annotations for the materialization that reduce to the standard annotation of the left-hand side.

Definition 35

(Abstract rewriting step $\hookrightarrow$). Given $\varphi :L\rightarrow A$, assume that $B[b_1,b_2]$ is constructed from $A[a_1,a_2]$ via the construction described in Definitions 31 and 33, with the modification that the set of annotations from which the set of maximal annotations M of the materialization are taken, is replaced by:

In this case we write .

Due to the adjunction property we have $\mathcal {A}_{n_L}(s_L) = \mathcal {A}_{n_L}( red _{n_L}(a'_2)) \le a'_2$ and hence the set M of annotations of Definition 35 is a subset of the corresponding set of Definition 33.

Example 36

We give a small example of an abstract rewriting step (a more extensive, worked example can be found in the full version [8]). Elements without annotation are annotated by $[0,*]$ by default and those with annotation [0, 0] are omitted. Furthermore elements in the image of the match and co-match are annotated by the standard annotation [1, 1] to specify the concrete occurrence of the left-hand and right-hand side.

The variant of abstract rewriting introduced in Definition 35 can still be proven to be sound, assuming the extra requirements stated above.

Proposition 37

(Soundness for $\hookrightarrow$). Relation $\hookrightarrow$ is sound in the sense of Proposition 34.

Using the assumptions we can now show completeness.

Proposition 38

(Completeness for $\hookrightarrow$). If and $Y\in \mathcal {L}(B[b_1,b_2])$, then there exists $X\in \mathcal {L}(A[a_1,a_2])$ (witnessed via a legal arrow $\psi :X[s_X,s_X]\rightarrow A[a_1,a_2]$) such that and $\varphi = \psi \circ m_L$.

Finally, we can show that annotated graphs of this kind are expressive enough to construct a strongest post-condition. If we would allow several annotations for objects, as in [9], we could represent the language with a single (multiply) annotated object.

Corollary 39

(Strongest post-condition). Let $A[a_1,a_2]$ be an annotated object and let $\varphi :L\rightarrow A$. We obtain (several) abstract rewriting steps , where we always obtain the same object B. (B is dependent on $\varphi$, but not on the annotation.) Now let . Then

6 Conclusion

We have described a rewriting framework for abstract graphs that also applies to objects in any topos, based on existing work for graphs [1, 2, 4, 27, 28, 31]. In particular, we have given a blueprint for materialization in terms of the universal property of partial map classifiers. This is a first theoretical milestone towards shape analysis as a general static analysis method for rule-based systems with graph-like objects as states. Soundness and completeness results for the rewriting of abstract objects with annotations in an ordered monoid provide an effective verification method for the special case of graphs We plan to implement the materialization construction and the computation of rewriting steps of abstract graphs in a prototype tool.

The extension of annotations with logical formulas is the natural next step, which will lead to a more flexible and versatile specification language, as described in previous work [30, 31]. The logic can possibly be developed in full generality using the framework of nested application conditions [18, 23] that applies to objects in adhesive categories. This logical approach might even reduce the proof obligations for annotation functors. Another topic for future work is the integration of widening or similar approximation techniques, which collapse abstract objects and ideally lead to finite abstract transition systems that (over-)approximate the typically infinite transitions systems of graph transformation systems.