Abstract
We offer a graphical interpretation of unfairness in a dataset as the presence of an unfair causal effect of the sensitive attribute in the causal Bayesian network representing the data-generation mechanism. We use this viewpoint to revisit the recent debate surrounding the COMPAS pretrial risk assessment tool and, more generally, to point out that fairness evaluation on a model requires careful considerations on the patterns of unfairness underlying the training data. We show that causal Bayesian networks provide us with a powerful tool to measure unfairness in a dataset and to design fair models in complex unfairness scenarios.
You have full access to this open access chapter, Download chapter PDF
1 Introduction
Machine learning is increasingly used in a wide range of decision-making scenarios that have serious implications for individuals and society, including financial lending [10, 35], hiring [8, 27], online advertising [26, 40], pretrial and immigration detention [5, 42], child maltreatment screening [13, 46], health care [18, 31], and social services [1, 22]. Whilst this has the potential to overcome undesirable aspects of human decision-making, there is concern that biases in the data and model inaccuracies can lead to decisions that treat historically discriminated groups unfavourably. The research community has therefore started to investigate how to ensure that learned models do not take decisions that are unfair with respect to sensitive attributes (e.g. race or gender).
This effort has led to the emergence of a rich set of fairness definitions [12, 15, 20, 23, 37] providing researchers and practitioners with criteria to evaluate existing systems or to design new ones. Many such definitions have been found to be mathematically incompatible [7, 12, 14, 15, 29], and this has been viewed as representing an unavoidable trade-off establishing fundamental limits on fair machine learning, or as an indication that certain definitions do not map on to social or legal understandings of fairness [16].
Most fairness definitions focus on the relationship between the model output and the sensitive attribute. However, deciding which relationship is appropriate for the model under consideration requires careful considerations about the patterns of unfairness underlying the training data. Therefore, the choice of a fairness definition always needs to consider the dataset used to train the model. In this manuscript, we use the framework causal Bayesian network draw attention to this point, by visually describing unfairness in a dataset as the presence of an unfair causal effect of the sensitive attribute in the data-generation mechanism. We then use this viewpoint to raise concern on the fairness debate surrounding the COMPAS pretrial risk assessment tool. Finally, we show that causal Bayesian networks offer a powerful tool for representing, reasoning about, and dealing with complex unfairness scenarios.
2 A Graphical View of (Un)fairness
Consider a dataset \(\varDelta =\{a^n,x^n,y^n\}_{n=1}^N\), corresponding to N individuals, where \(a^n\) indicates a sensitive attribute, and \(x^n\) a set of observations that can be used (together with \(a^n\)) to form a prediction \(\hat{y}^n\) of outcome \(y^n\). We assume a binary setting \(a^n,y^n,\hat{y}^n\in \{0,1\}\) (unless otherwise specified), and indicate with \(A,\mathcal{X}\), Y, and \(\hat{Y}\) the (set of) random variablesFootnote 1 corresponding to \(a^n,x^n,y^n\), and \(\hat{y}^n\).
In this section we show at a high-level that a correct use of fairness definitions concerned with statistical properties of \(\hat{Y}\) with respect to A requires an understanding of the patterns of unfairness underlying \(\varDelta \), and therefore of the relationships among A, \(\mathcal{X}\) and Y. More specifically we show that:
-
(i)
Using the framework of causal Bayesian networks (CBNs), unfairness in \(\varDelta \) can be viewed as the presence of an unfair causal path from A to \(\mathcal{X}\) or Y.
-
(ii)
In order to determine which properties \(\hat{Y}\) should possess to be fair, it is necessary to question and understand unfairness in \(\varDelta \).

Assume a dataset \(\varDelta =\{a^n,x^n=\{q^n,d^n\},y^n\}_{n=1}^N\) corresponding to a college admission scenario in which applicants are admitted based on qualifications Q, choice of department D, and gender A; and in which female applicants apply more often to certain departments. This scenario can be represented by the CBN on the left (see Appendix A for an overview of BNs, and Sect. 3 for a detailed treatment of CBNs). The causal path \(A\rightarrow Y\) represents direct influence of gender A on admission Y, capturing the fact that two individuals with the same qualifications and applying to the same department can be treated differently depending on their gender. The indirect causal path \(A\rightarrow D \rightarrow Y\) represents influence of A on Y through D, capturing the fact that female applicants more often apply to certain departments. Whilst the direct influence \(A\rightarrow Y\) is certainly an unfair one, the paths \(A\rightarrow D\) and \(D\rightarrow Y\), and therefore \(A\rightarrow D \rightarrow Y\), could either be considered as fair or as unfair. For example, rejecting women more often due to department choice could be considered fair with respect to college responsibility. However, this could be considered unfair with respect to societal responsibility if the departmental differences were a result of systemic historical or cultural factors (e.g. if female applicants apply to specific departments at lower rates because of overt or covert societal discouragement). Finally, if the college were to lower the admission rates for departments chosen more often by women, then the path \(D \rightarrow Y\) would be unfair.
Deciding whether a path is fair or unfair requires careful ethical and sociological considerations and/or might not be possible from a dataset alone. Nevertheless, this example illustrates that we can view unfairness in a dataset as the presence of an unfair causal path from the sensitive attribute A to \(\mathcal{X}\) or Y.
Different (un)fair path labeling requires \(\hat{Y}\) to have different characteristics in order to be fair. In the case in which the causal paths from A to Y are all unfair (e.g. if \(A\rightarrow D \rightarrow Y\) is considered unfair), a \(\hat{Y}\) that is statistically independent of A (denoted with  ) would not contain any of the unfair influence of A on Y. In such a case, \(\hat{Y}\) is said to satisfy demographic parity.
) would not contain any of the unfair influence of A on Y. In such a case, \(\hat{Y}\) is said to satisfy demographic parity.
Demographic Parity (DP). \(\hat{Y}\) satisfies demographic parity if  , i.e. \(p(\hat{Y}=1|A=0)=p(\hat{Y}=1|A=1)\), where e.g. \(p(\hat{Y}=1|A=0)\) can be estimated as
, i.e. \(p(\hat{Y}=1|A=0)=p(\hat{Y}=1|A=1)\), where e.g. \(p(\hat{Y}=1|A=0)\) can be estimated as
with \(\mathbb {1}_{\hat{y}^n = 1, a^n=0}=1\) if \(\hat{y}^n = 1\) and \(a^n=0\) (and zero otherwise), and where \(N_0\) is the number of individuals with \(a^n=0\). Notice that many classifiers, rather than a binary prediction \(\hat{y}^n\in \{0,1\}\), output a degree of belief that the individual belongs to class 1, \(r^n\), also called score. This could correspond to the probability of class 1, \(r^n=p(y^n = 1 | a^n, x^{n})\), as in the case of logistic regression. To obtain the prediction \(\hat{y}^n\in \{0,1\}\) from \(r^n\), it is common to use a threshold \(\theta \), i.e. \(\hat{y}^n=\mathbb {1}_{r^n>\theta }\). In this case, we can rewrite the estimate for \(p(\hat{Y}=1|A=0)\) as
Notice that  implies
implies  for all values of \(\theta \).
for all values of \(\theta \).
In the case in which the causal paths from A to Y are all fair (e.g. if \(A\rightarrow Y\) is absent and \(A\rightarrow D\rightarrow Y\) is considered fair), a \(\hat{Y}\) such that  or
or  would be allowed to contain such a fair influence, but the (dis)agreement between Y and \(\hat{Y}\) would not be allowed to depend on A. In these cases, \(\hat{Y}\) is said to satisfy equal false positive/false negative rates and calibration respectively.
would be allowed to contain such a fair influence, but the (dis)agreement between Y and \(\hat{Y}\) would not be allowed to depend on A. In these cases, \(\hat{Y}\) is said to satisfy equal false positive/false negative rates and calibration respectively.
Equal False Positive and Negative Rates (EFPRs/EFNRs). \(\hat{Y}\) satisfies EFPRs and EFNRs if  , i.e. (EFPRs) \(p(\hat{Y}=1|Y=0,A=0)=p(\hat{Y}=1|Y=0,A=1)\) and (EFNRs) \(p(\hat{Y}=0|Y=1,A=0)=p(\hat{Y}=0|Y=1,A=1)\).
, i.e. (EFPRs) \(p(\hat{Y}=1|Y=0,A=0)=p(\hat{Y}=1|Y=0,A=1)\) and (EFNRs) \(p(\hat{Y}=0|Y=1,A=0)=p(\hat{Y}=0|Y=1,A=1)\).
Calibration. \(\hat{Y}\) satisfies calibration if  . In the case of score output R, this condition is often instead called predictive parity at threshold \(\theta \), \(p(Y=1|R>\theta ,A=0)=p(Y=1|R>\theta ,A=1)\), and calibration defined as requiring
. In the case of score output R, this condition is often instead called predictive parity at threshold \(\theta \), \(p(Y=1|R>\theta ,A=0)=p(Y=1|R>\theta ,A=1)\), and calibration defined as requiring  .
.
In the case in which at least one causal path from A to Y is unfair (e.g. if \(A\rightarrow Y\) is present), EFPRs/EFNRs and calibration are inappropriate criteria, as they would not require the unfair influence of A on Y to be absent from \(\hat{Y}\) (e.g. a perfect model (\(\hat{Y} = Y\)) would automatically satisfy EFPRs/EFNRs and calibration, but would contain the unfair influence). This observation is particularly relevant to the recent debate surrounding the correctional offender management profiling for alternative sanctions (COMPAS) pretrial risk assessment tool. We revisit this debate in the next section.
2.1 The COMPAS Debate
Over the past few years, numerous state and local governments around the United States have sought to reform their pretrial court systems with the aim of reducing unprecedented levels of incarceration, and specifically the population of low-income defendants and racial minorities in America’s prisons and jails [2, 24, 30]. As part of this effort, quantitative tools for determining a person’s likelihood for reoffending or failure to appear, called risk assessment instruments (RAIs), were introduced to replace previous systems driven largely by opaque discretionary decisions and money bail [6, 25]. However, the expansion of pretrial RAIs has unearthed new concerns of racial discrimination which would nullify the purported benefits of these systems and adversely impact defendants’ civil liberties.
An intense ongoing debate, in which the research community has also been heavily involved, was triggered by an exposé from investigative journalists at ProPublica [5] on the COMPAS pretrial RAI developed by Equivant (formerly Northpointe) and deployed in Broward County in Florida. The COMPAS general recidivism risk scale (GRRS) and violent recidivism risk scale (VRRS), the focus of ProPublica’s investigation, sought to leverage machine learning techniques to improve the predictive accuracy of recidivism compared to older RAIs such as the level of service inventory-revised [3] which were primarily based on theories and techniques from a sub-field of psychology known as the psychology of criminal conduct [4, 9]Footnote 2.
Number of black and white defendants in each of two aggregate risk categories [14]. The overall recidivism rate for black defendants is higher than for white defendants (52% vs. 39%), i.e.  . Within each risk category, the proportion of defendants who reoffend is approximately the same regardless of race, i.e.
. Within each risk category, the proportion of defendants who reoffend is approximately the same regardless of race, i.e.  . Black defendants are more likely to be classified as medium or high risk (58% vs. 33%) i.e.
. Black defendants are more likely to be classified as medium or high risk (58% vs. 33%) i.e.  . Among individuals who did not reoffend, black defendants are more likely to be classified as medium or high risk than white defendants (44.9% to 23.5%). Among individuals who did reoffend, white defendant are more likely to be classified as low risk than black defendants (47.7% vs 28%), i.e.
. Among individuals who did not reoffend, black defendants are more likely to be classified as medium or high risk than white defendants (44.9% to 23.5%). Among individuals who did reoffend, white defendant are more likely to be classified as low risk than black defendants (47.7% vs 28%), i.e.  .
.
ProPublica’s criticism of COMPAS centered on two concerns. First, the authors argued that the distribution of the risk score \(R\in \{1,\ldots ,10\}\) exhibited discriminatory patterns, as black defendants displayed a fairly uniform distribution across each value, while white defendants exhibited a right skewed distribution, suggesting that the COMPAS recidivism risk scores disproportionately rated white defendants as lower risk than black defendants. Second, the authors claimed that the GRRS and VRRS did not satisfy EFPRs and EFNRs, as \(\text {FPRs}\,=\,44.9\%\) and \(\text {FNRs}\,=\,28.0\%\) for black defendants, whilst \(\text {FPRs}\,=\,23.5\%\) and \(\text {FNRs}\,=\,47.7\%\) for white defendants (see Fig. 1). This evidence led ProPublica to conclude that COMPAS had a disparate impact on black defendants, leading to public outcry over potential biases in RAIs and machine learning writ large.
In response, Equivant published a technical report [19] refuting the claims of bias made by ProPublica and concluded that COMPAS is sufficiently calibrated, in the sense that it satisfies predictive parity at key thresholds. Subsequent analyses [12, 15, 29] confirmed Equivant’s claims of calibration, but also demonstrated the incompatibility of EFPRs/EFNRs and calibration due to differences in base rates across groups ( ) (see Appendix B). Moreover, the studies suggested that attempting to satisfy these competing forms of fairness force unavoidable trade-offs between criminal justice reformers’ purported goals of racial equity and public safety.
) (see Appendix B). Moreover, the studies suggested that attempting to satisfy these competing forms of fairness force unavoidable trade-offs between criminal justice reformers’ purported goals of racial equity and public safety.
As explained in Sect. 2,  is an appropriate fairness criterion when influence from A is considered unfair, whilst EFPRs/EFNRs and calibration, by requiring the rate of (dis)agreement between Y and \(\hat{Y}\) to be the same for black and white defendants (and therefore by not being concerned with dependence of Y on A), are appropriate when influence from A is considered fair. Therefore, if dependence of Y on A includes influence of A in Y through an unfair causal path, both EFPRs/EFNRs and calibration would be inadequate, and the fact that they cannot be satisfied at the same time irrelevant.
is an appropriate fairness criterion when influence from A is considered unfair, whilst EFPRs/EFNRs and calibration, by requiring the rate of (dis)agreement between Y and \(\hat{Y}\) to be the same for black and white defendants (and therefore by not being concerned with dependence of Y on A), are appropriate when influence from A is considered fair. Therefore, if dependence of Y on A includes influence of A in Y through an unfair causal path, both EFPRs/EFNRs and calibration would be inadequate, and the fact that they cannot be satisfied at the same time irrelevant.
As previous research has shown [28, 34, 43], modern policing tactics center around targeting a small number of neighborhoods—often disproportionately populated by non-white and low income residents—with recurring patrols and stops. This uneven distribution of police attention, as well as other factors such as funding for pretrial services [30, 45], means that differences in base rates between racial groups are not reflective of ground truth rates. We can rephrase these findings as indicating the presence of a direct path \(A\rightarrow Y\) (through unobserved neighborhood) in the CBN representing the data-generation mechanism (Fig. 2). Such tactics also imply an influence of A on Y through the set of variables \({\mathcal F}\) containing number of prior arrests. In addition, the influence of A on Y through \(A\rightarrow Y\) and \(A \rightarrow {\mathcal F} \rightarrow Y\) could be more prominent or contain more unfairness due to racial discrimination.
These observations indicate that EFPRs/EFNRs and calibration are inappropriate criteria for this case, and more generally that the current fairness debate surrounding COMPAS gives insufficient consideration to the patterns of unfairness underlying the data. Our analysis formalizes the concerns raised by social scientists and legal scholars on mismeasurement and unrepresentative data in the US criminal justice system. Multiple studies [21, 33, 36, 45] have argued that the core premise of RAIs, to assess the likelihood a defendant reoffends, is impossible to measure and that the empirical proxy used (e.g. arrest or conviction) introduces embedded biases and norms which render existing fairness tests unreliable.
This section used the CBN framework to describe at a high-level different patterns of unfairness that can underlie a dataset and to point out issues with current deployment of fairness definitions. In the remainder of the manuscript, we use this framework more extensively to further advance our analysis on fairness. Before doing that, we give some background on CBNs [17, 38, 39, 41, 44], assuming that all variables except A are continuous.
3 Causal Bayesian Networks
A Bayesian network is a directed acyclic graph where nodes and edges represent random variables and statistical dependencies. Each node \(X_i\) in the graph is associated with the conditional distribution \(p(X_i|\text {pa}(X_i))\), where \(\text {pa}(X_i)\) is the set of parents of \(X_i\). The joint distribution of all nodes, \(p(X_1, \ldots , X_I)\), is given by the product of all conditional distributions, i.e. \(p(X_1,\ldots ,X_I)=\prod _{i=1}^Ip(X_i|\text {pa}(X_i))\) (see Appendix A for more details on Bayesian networks).
When equipped with causal semantic, namely when representing the data-generation mechanism, Bayesian networks can be used to visually express causal relationships. More specifically, CBNs enable us to give a graphical definition of causes and causal effects: if there exists a directed path from A to Y, then A is a potential cause of Y. Directed paths are also called causal paths.
The causal effect of A on Y can be seen as the information traveling from A to Y through causal paths, or as the conditional distribution of Y given A restricted to causal paths. This implies that, to compute the causal effect, we need to disregard the information that travels along non-causal paths, which occurs if such paths are open. Since paths with an arrow emerging from A are either causal or closed (blocked) by a collider, the problematic paths are only those with an arrow pointing into A, called back-door paths, which are open if they do not contain a collider.
An example of an open back-door path is given by \(A\leftarrow C \rightarrow Y\) in the CBN \(\mathcal{G}\) of Fig. 3(a): the variable C is said to be a confounder for the effect of A on Y, as it confounds the causal effect with non-causal information. To understand this, assume that A represents hours of exercise in a week, Y cardiac health, and C age: observing cardiac health conditioning on exercise level from p(Y|A) does not enable us to understand the effect of exercise on cardiac health, since p(Y|A) includes the dependence between A and Y induced by age.
Each parent-child relationship in a CBN represents an autonomous mechanism, and therefore it is conceivable to change one such a relationship without changing the others. This enables us to express the causal effect of \(A=a\) on Y as the conditional distribution \(p_{\rightarrow A=a}(Y|A=a)\) on the modified CBN \(\mathcal{G}_{\rightarrow A=a}\) of Fig. 3(b), resulting from replacing p(A|C) with a Dirac delta distribution \(\delta _{A=a}\) (thereby removing the link from C to A) and leaving the remaining conditional distributions p(Y|A, C) and p(C) unaltered – this process is called intervention on A. The distribution \(p_{\rightarrow A=a}(Y|A=a)\) can be estimated as \(p_{\rightarrow A=a}(Y|A=a) = \int _C p_{\rightarrow A=a}(Y|A=a,C)p_{\rightarrow A=a}(C|A=a) = \int _C p(Y|A=a,C)p(C)\). This is a special case of the following back-door adjustment formula.
Back-Door Adjustment. If a set of variables \(\mathcal{C}\) satisfies the back-door criterion relative to \(\{A, Y\}\), the causal effect of A on Y is given by \(p_{\rightarrow A}(Y|A)=\int _\mathcal{C} p(Y|A,\mathcal{C})p(\mathcal{C})\). \(\mathcal{C}\) satisfies the back-door criterion if (a) no node in \(\mathcal{C}\) is a descendant of A and (b) \(\mathcal{C}\) blocks every back-door path from A to Y.
The equality \(p_{\rightarrow A=a}(Y|A=a,\mathcal{C}) = p(Y|A=a,\mathcal{C})\) follows from the fact that \(\mathcal{G}_{A \rightarrow }\), obtained by removing from \(\mathcal{G}\) all links emerging from A, retains all (and only) the back-door paths from A to Y. As \(\mathcal{C}\) blocks all such paths,  in \(\mathcal{G}_{A \rightarrow }\). This means that there is no non-causal information traveling from A to Y when conditioning on \(\mathcal{C}\) and therefore conditioning on A coincides with intervening.
in \(\mathcal{G}_{A \rightarrow }\). This means that there is no non-causal information traveling from A to Y when conditioning on \(\mathcal{C}\) and therefore conditioning on A coincides with intervening.
Conditioning on C to block an open back-door path may open a closed path on which C is a collider. For example, in the CBN of Fig. 4(a), conditioning on C closes the paths \(A\leftarrow C\leftarrow X \rightarrow Y\) and \(A\leftarrow C\rightarrow Y\), but opens the path \(A\leftarrow E\rightarrow C\leftarrow X \rightarrow Y\) (additional conditioning on X would close \(A\leftarrow E\rightarrow C\leftarrow X \rightarrow Y\)).
The back-door criterion can also be derived from the rules of do-calculus [38, 39], which indicate whether and how \(p_{\rightarrow A}(Y|A)\) can be estimated using observations from \(\mathcal{G}\): for many graph structures with unobserved confounders the only way to compute causal effects is by collecting observations directly from \(\mathcal{G}_{\rightarrow A}\) – in this case the effect is said to be non-identifiable.
Potential Outcome Viewpoint. Let \(Y_{A=a}\) be the random variable with distribution \(p(Y_{A=a}) = p_{\rightarrow A=a}(Y|A=a)\). \(Y_{A=a}\) is called potential outcome and, when not ambiguous, we will refer to it with the shorthand \(Y_a\). The relation between \(Y_{a}\) and all the variables in \(\mathcal{G}\) other than Y can be expressed by the graph obtained by removing from \(\mathcal{G}\) all the links emerging from A, and by replacing Y with \(Y_{a}\). If \(Y_{a}\) is independent on A in this graph, thenFootnote 3 \(p(Y_a)=p(Y_a|A=a)=p(Y|A=a)\). If \(Y_{a}\) is independent of A in this graph when conditioning on \(\mathcal{C}\), then
i.e. we retrieve the back-door adjustment formula.
In the remainder of the section we show that, by performing different interventions on A along different causal paths, it is possible to isolate the contribution of the causal effect of A on Y along a group of paths.
Direct and Indirect Effect
Consider the CBN of Fig. 4(b), containing the direct path \(A\rightarrow Y\) and one indirect causal path through the variable M. Let \(Y_{a}(M_{\bar{a}})\) be the random variable with distribution equal to the conditional distribution of Y given A restricted to causal paths, with \(A=a\) along \(A\rightarrow Y\) and \(A=\bar{a}\) along \(A\rightarrow M\rightarrow Y\). The average direct effect (ADE) of \(A=a\) with respect to \(A=\bar{a}\), defined as
where e.g. \(\langle Y_{a} \rangle _{p(Y_{a})}=\int _{Y_{a}} Y_{a}p(Y_{a})\), measures the difference in flow of causal information from A to Y between the case in which \(A=a\) along \(A\rightarrow Y\) and \(A=\bar{a}\) along \(A\rightarrow M\rightarrow Y\) and the case in which \(A=\bar{a}\) along both paths.
Analogously, the average indirect effect (AIE) of \(A=a\) with respect to \(A=\bar{a}\), is defined as \(\text {AIE}_{\bar{a} a } =\langle Y_{\bar{a}}(M_a) \rangle _{p(Y_{\bar{a}}(M_a))} - \langle Y_{\bar{a}} \rangle _{p(Y_{\bar{a}})}\).
The difference \(\text {ADE}_{\bar{a} a } - \text {AIE}_{a \bar{a} }\) gives the average total effect (ATE) \(\text {ATE}_{\bar{a} a} = \langle Y_{a} \rangle _{p(Y_{a})} - \langle Y_{\bar{a}} \rangle _{p(Y_{\bar{a}})}\)Footnote 4.
Top: CBN with the direct path from A to Y and the indirect paths passing through M highlighted in red. Bottom: CBN corresponding to (1). (Color figure online)
Path-Specific Effect
To estimate the effect along a specific group of causal paths, we can generalize the formulas for the ADE and AIE by replacing the variable in the first term with the one resulting from performing the intervention \(A=a\) along the group of interest and \(A=\bar{a}\) along the remaining causal paths. For example, consider the CBN of Fig. 5 (top) and assume that we are interested in isolating the effect of A on Y along the direct path \(A\rightarrow Y\) and the paths passing through M, \(A\rightarrow M \rightarrow ,\ldots ,\rightarrow Y\), namely along the red links. The path-specific effect (PSE) of \(A=a\) with respect to \(A=\bar{a}\) for this group of paths is defined as
where \(p(Y_a(M_a, L_{\bar{a}} (M_a)))\) is given by
In the simple case in which the CBN corresponds to a linear model, e.g.
where \(\epsilon _c\), \(\epsilon _m\), \(\epsilon _l\) and \(\epsilon _y\) are unobserved independent zero-mean Gaussian variables, we can compute \(\langle Y_{\bar{a}} \rangle \) by expressing Y as a function of \(A=\bar{a}\) and the Gaussian variables, by recursive substitutions in C, M and L, i.e.
and then take the mean, obtaining \(\langle Y_{\bar{a}} \rangle =\theta ^y+\theta ^y_{a}\bar{a}+\theta ^y_{m}(\theta ^m+\theta ^m_{a}\bar{a})+\theta ^y_{l}(\theta ^l+\theta ^l_{a}\bar{a}+\theta ^l_{m}(\theta ^m+\theta ^m_{a}\bar{a}))\). Analogously
For \(a=1\) and \(\bar{a} = 0\), this gives
The same conclusion could have been obtained by looking at the graph annotated with path coefficients (Fig. 5 (bottom)). The PSE is obtained by summing over the three causal paths of interest (\(A\rightarrow Y\), \(A\rightarrow M \rightarrow Y\), and \(A\rightarrow M \rightarrow L \rightarrow Y\)) the product of all coefficients in each path.
Notice that \(\text {AIE}_{\bar{a} a}\), given by

coincides with \(\text {AIE}^a_{\bar{a} a}\), given by

Effect of Treatment on Treated. Consider the conditional distribution \(p(Y_{a}|A=\bar{a})\). This distribution measures the information travelling from A to Y along all open paths, when A is set to a along causal paths and to \(\bar{a}\) along non-causal paths. The effect of treatment on treated (ETT) of \(A=a\) with respect to \(A=\bar{a}\) is defined as \(\text {ETT}_{\bar{a} a} = \langle Y_{a} \rangle _{p(Y_{a}|A=\bar{a})}- \langle Y_{\bar{a}} \rangle _{p(Y_{\bar{a}}|A=\bar{a})} = \langle Y_{a} \rangle _{p(Y_{a}|A=\bar{a})} - \langle Y \rangle _{p(Y|A=\bar{a})}\). As the PSE, the ETT measures difference in flow of information from A to Y when A takes different values along different paths. However, the PSE considers only causal paths and different values for A along different causal paths, whilst the ETT considers all open paths and different values for A along causal and non-causal paths respectively. Similarly to \(\text {ATE}_{\bar{a} a}\), \(\text {ETT}_{\bar{a} a}\) for the CBN of Fig. 4(b) can be expressed as
Notice that, if we define difference in flow of non-causal (along the open back-door paths) information from A to Y when \(A=a\) with respect to when \(A=\bar{a}\) as \(\text {NCI}_{\bar{a} a} = \langle Y_{\bar{a}} \rangle _{p(Y_{\bar{a}}|A=a)} - \langle Y \rangle _{p(Y|A=\bar{a})}\), we obtain
4 Fairness Considerations Using CBNs
Equipped with the background on CBNs from Sect. 3, in this section we further investigate unfairness in a dataset \(\varDelta =\{a^n, x^n, y^n\}_{n=1}^N\), discuss issues that might arise when building a decision system from it, and show how to measure and deal with unfairness in complex scenarios, revisiting and extending material from [11, 32, 47].
4.1 Back-Door Paths from A to Y
In Sect. 2 we have introduced a graphical interpretation of unfairness in a dataset \(\varDelta \) as the presence of an unfair causal path from A to \(\mathcal{X}\) or Y. More specifically, we have shown through a college admission example that unfairness can be due to an unfair link emerging (a) from A or (b) from a subsequent variable in a causal path from A to Y (e.g. \(D\rightarrow Y\) in the example). Our discussion did not mention paths from A to Y with an arrow pointing into A, namely back-door paths. This is because such paths are not problematic.

To understand this, consider the hiring scenario described by the CBN on the left, where A represents religious belief and E educational background of the applicant, which influences religious participation (\(E\rightarrow A\)). Whilst  due to the open back-door path from A to Y, the hiring decision Y is only based on E.
due to the open back-door path from A to Y, the hiring decision Y is only based on E.
4.2 Opening Closed Unfair Paths from A to Y
In Sect. 2, we have seen that, in order to reason about fairness of \(\hat{Y}\), it is necessary to question and understand unfairness in \(\varDelta \). In this section, we warn that another crucial element needs to be considered in the fairness discussion around \(\hat{Y}\), namely
-
(i)
The subset of variables used to form \(\hat{Y}\) could project into \(\hat{Y}\) unfair patterns in \(\mathcal{X}\) that do not concern Y.
This could happen, for example, if a closed unfair path from A to Y is opened when conditioning on the variables used to form \(\hat{Y}\).
As an example, assume the CBN in Fig. 6 representing the data-generation mechanism underlying a music degree scenario, where A corresponds to gender, M to music aptitude (unobserved, i.e. \(M\notin \varDelta \)), X to the score obtained from an ability test taken at the beginning of the degree, and Y to the score obtained from an ability test taken at the end of the degree. Individuals with higher music aptitude M are more likely to obtain higher initial and final scores (\(M\rightarrow X\), \(M\rightarrow Y\)). Due to discrimination occurring at the initial testing, women are assigned a lower initial score than men for the same aptitude level (\(A \rightarrow X\)). The only path from A to Y, \(A\rightarrow X \leftarrow M \rightarrow Y\), is closed as X is a collider on this path. Therefore the unfair influence of A on X does not reach Y ( ). Nevertheless, as
). Nevertheless, as  , a prediction \(\hat{Y}\) based on the initial score X only would contain the unfair influence of A on X. For example, assume the following linear model: \(Y=\gamma M, X =\alpha A + \beta M\), with \(\langle A^2 \rangle _{p(A)}=1\) and \(\langle M^2 \rangle _{p(M)}=1\). A linear predictor of the form \(\hat{Y} = \theta _X X\) minimizing \(\langle (Y-\hat{Y})^2 \rangle _{p(A)p(M)}\) would have parameters \(\theta _X=\gamma \beta /(\alpha ^2+\beta ^2)\), giving \(\hat{Y} = \gamma \beta (\alpha A + \beta M)/(\alpha ^2+\beta ^2)\), i.e.
, a prediction \(\hat{Y}\) based on the initial score X only would contain the unfair influence of A on X. For example, assume the following linear model: \(Y=\gamma M, X =\alpha A + \beta M\), with \(\langle A^2 \rangle _{p(A)}=1\) and \(\langle M^2 \rangle _{p(M)}=1\). A linear predictor of the form \(\hat{Y} = \theta _X X\) minimizing \(\langle (Y-\hat{Y})^2 \rangle _{p(A)p(M)}\) would have parameters \(\theta _X=\gamma \beta /(\alpha ^2+\beta ^2)\), giving \(\hat{Y} = \gamma \beta (\alpha A + \beta M)/(\alpha ^2+\beta ^2)\), i.e.  . Therefore, this predictor would be using the sensitive attribute to form a decision, although implicitly rather than explicitly. Instead, a predictor explicitly using the sensitive attribute, \(\hat{Y} = \theta _X X + \theta _A A\), would have parameters
. Therefore, this predictor would be using the sensitive attribute to form a decision, although implicitly rather than explicitly. Instead, a predictor explicitly using the sensitive attribute, \(\hat{Y} = \theta _X X + \theta _A A\), would have parameters
i.e. \(\hat{Y} = \gamma M\). Therefore, this predictor would be fair. From the CBN we can see that the explicit use of A can be of help in retrieving M. Indeed, since  , using A in addition to X can give information about M. In general (e.g. in a non-linear setting) it is not guaranteed that using A would ensure
, using A in addition to X can give information about M. In general (e.g. in a non-linear setting) it is not guaranteed that using A would ensure  . Nevertheless, this example shows how explicit use of the sensitive attribute in a model can ensure fairness rather than lead to unfairness.
. Nevertheless, this example shows how explicit use of the sensitive attribute in a model can ensure fairness rather than lead to unfairness.
This observation is relevant to one of the simplest fairness definitions, motivated by legal requirements, called fairness through unawareness, which states that \(\hat{Y}\) is fair as long as it does not make explicit use of the sensitive attribute A. Whilst this fairness criterion is often indicated as problematic because some of the variables used to form \(\hat{Y}\) could be a proxy for A (such as neighborhood for race), the example above shows a more subtle issue with it.
4.3 Path-Specific Population-Level Unfairness
In this section, we show that the path-specific effect introduced in Sect. 3 can be used to quantify unfairness in \(\varDelta \) in complex scenarios.
Consider the college admission example discussed in Sect. 2 (Fig. 7). In the case in which the path \(A\rightarrow D\), and therefore \(A\rightarrow D\rightarrow Y\), is considered unfair, unfairness overall population can be quantified with \(\langle Y \rangle _{p(Y|a)}-\langle Y \rangle _{p(Y|{\bar{a}})}\) (coinciding with \(\text {ATE}_{\bar{a} a} = \langle Y_{a} \rangle _{p(Y_{a})}-\langle Y_{\bar{a}} \rangle _{p(Y_{\bar{a}})}\)) where, for example, \(A=a\) and \(A=\bar{a}\) indicate female and male applicants respectively.
In the more complex case in which the path \(A \rightarrow D\rightarrow Y\) is considered fair, unfairness can instead be quantified with the path-specific effect along the direct path \(A\rightarrow Y\), \(\text {PSE}_{\bar{a} a}\), given by
Notice that computing \(p(Y_{a}(D_{\bar{a}}))\) requires knowledge of the CBN. If the CBN structure is not known or estimating its conditional distributions is challenging, the resulting estimate could be imprecise.
Path-Specific Individual-Level Unfairness
In the college admission example of Fig. 7 in which the path \(A \rightarrow D\rightarrow Y\) is considered fair, rather than measuring unfairness overall population, we might want to know e.g. whether a rejected female applicant \(\{a^n=a=1, q^n, d^n, y^n=0\}\) was treated unfairly. We can answer this question by estimating whether the applicant would have been admitted had she been male (\(A=\bar{a}=0\)) along the direct path \(A\rightarrow Y\) from \(p(Y_{\bar{a}}(D_a)|A=a, Q=q^n, D=d^n)\) (notice that the outcome in the actual world, \(y^n\), corresponds to \(p(Y_{a}(D_a)|A=a, Q=q^n, D=d^n)=\mathbb {1}_{Y_{a}(D_a)=y^n}\)).
To understand how this can be achieved, consider the following linear model associated to a CBN with the same structure as the one in Fig. 7

The relationships between A, Q, D, Y and \(Y_{\bar{a}}(D_a)\) in this model can be inferred from the twin Bayesian network [38] on the left resulting from the intervention \(A=a\) along \(A\rightarrow D\) and \(A=\bar{a}\) along \(A\rightarrow Y\): in addition to A, Q, D, Y, the network contains the variables \(Q^*\), \(D_a\) and \(Y_{\bar{a}}(D_a)\) corresponding to the counterfactual world in which \(A=\bar{a}\) along \(A\rightarrow Y\). The two groups of variables are connected through \(\epsilon _d, \epsilon _q, \epsilon _y\), indicating that the factual and counterfactual worlds share the same unobserved randomness. From this network, we can deduce that  Footnote 5, and therefore that we can express \(p(Y_{\bar{a}}(D_a)|A=a, Q=q^n, D=d^n)\) as
Footnote 5, and therefore that we can express \(p(Y_{\bar{a}}(D_a)|A=a, Q=q^n, D=d^n)\) as

As \(\epsilon ^n_q=q^n-\theta ^q\), \(\epsilon ^n_d = d^n-\theta ^d-\theta ^d_a\), we obtainFootnote 6 \(\langle Y_{\bar{a}}(D_a) \rangle _{p(Y_{\bar{a}}(D_a)|A=a, Q=q^n, D=d^n)}=\theta ^y+\theta ^y_{q}q^n+\theta ^y_{d}d^n\).
Equation (4) suggests that, in more complex scenarios (e.g. in which the variables are non-linearly related), we can obtain a Monte-Carlo estimate of \(p(Y_{\bar{a}}(D_a)|a,q^n, d^n)\) by sampling \(\epsilon _q\) and \(\epsilon _d\) from \(p(\epsilon _q, \epsilon _d|a, q^n, d^n)\).
In [11], we used this approach to introduce a prediction system such that the two distributions \(p(\hat{Y}_{\bar{a}}(D_a)|A=a, Q=q^n, D=d^n)\) and \(p(\hat{Y}_{a}(D_a)|A=a, Q=q^n, D=d^n)\) coincide – we called this property path-specific counterfactual fairness.
5 Conclusions
We used causal Bayesian networks to provide a graphical interpretation of unfairness in a dataset as the presence of an unfair causal effect of a sensitive attribute. We used this viewpoint to revisit the recent debate surrounding the COMPAS pretrial risk assessment tool and, more generally, to point out that fairness evaluation on a model requires careful considerations on the patterns of unfairness underlying the training data. We then showed that causal Bayesian networks provide us with a powerful tool to measure unfairness in a dataset and to design fair models in complex unfairness scenarios.
Our discussion did not cover difficulties in making reasonable assumptions on the structure of the causal Bayesian network underlying a dataset, nor on the estimations of the associated conditional distributions or of other quantities of interest. These are obstacles that need to be carefully considered to avoid improper usage of this framework.
Notes
- 1.
Throughout the paper, we use capital and small letters for random variables and their values, and calligraphic capital letters for sets of variables.
- 2.
While the exact methodology underlying GRRS and VRRS is proprietary, publicly available reports suggest that the process begins with a defendant being administered a 137 point assessment during intake. This is used to create a series of dynamic risk factor scales such as the criminal involvement scale and history of violence scale. In addition, COMPAS also includes static attributes such as the defendant’s age and prior police contact (number of prior arrests). The raw COMPAS scores are transformed into decile values by ranking and calibration with a normative group to ensure an equal proportion of scores within each scale value. Lastly, to aid practitioner interpretation, the scores are grouped into three risk categories. The scale values are displayed to court officials as either Low (1–4), Medium (5–7), and High (8–10) risk.
- 3.
The equality \(p(Y_a|A=a)=p(Y|A=a)\) is called consistency.
- 4.
Often the AIE of \(A=a\) with respect to \(A=\bar{a}\) is defined as \(\text {AIE}^a_{\bar{a} a} = \langle Y_{a} \rangle _{p(Y_{a})} - \langle Y_{a}(M_{\bar{a}}) \rangle _{p(Y_{a}(M_{\bar{a}}))}= -\text {AIE}_{a \bar{a} }\), which differs in setting A to a rather than to \(\bar{a}\) along \(A\rightarrow Y\). In the linear case, the two definitions coincide (see Eqs. (2) and (3)). Similarly the ADE can be defined as \(\text {ADE}^a_{\bar{a} a} = \langle Y_{a} \rangle _{p(Y_{a})} - \langle Y_{\bar{a}}(M_a) \rangle _{p(Y_{\bar{a}}(M_a))}= -\text {ADE}_{a \bar{a} }\).
- 5.
Notice that
 , but
, but  .
. - 6.
Notice that
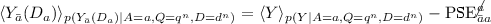 . Indeed \(\langle Y \rangle _{p(Y|A=a, Q=q^n, D=d^n)}=\theta ^y+\theta ^y_{a}+\theta ^y_{q}q^n+\theta ^y_{d}d^n\) and \(\text {PSE}_{\bar{a} a}=\theta ^y_a\). This equivalence does not hold in the non-linear setting.
. Indeed \(\langle Y \rangle _{p(Y|A=a, Q=q^n, D=d^n)}=\theta ^y+\theta ^y_{a}+\theta ^y_{q}q^n+\theta ^y_{d}d^n\) and \(\text {PSE}_{\bar{a} a}=\theta ^y_a\). This equivalence does not hold in the non-linear setting.
References
AI Now Institute. Litigating Algorithms: Challenging Government Use of Algorithmic Decision Systems (2018)
Alexander, M.: The New Jim Crow: Mass Incarceration in the Age of Colorblindness. The New Press, New York (2012)
Andrews, D.A., Bonta, J.: Level of Service Inventory - Revised. Multi-Health Systems, Toronto (2000)
Andrews, D.A., Bonta, J., Wormith, J.S.: The recent past and near future of risk and/or need assessment. Crime Delinq. 52(1), 7–27 (2006)
Angwin, J., Larson, J., Mattu, S., Kirchner, L.: Machine Bias: there’s software used across the country to predict future criminals. And it’s biased against blacks, May 2016. https://www.propublica.org/article/machine-bias-risk-assessments-in-criminal-sentencing
Arnold, D., Dobbie, W., Yang, C.S.: Racial bias in bail decisions. Q. J. Econ. 133, 1885–1932 (2018)
Berk, R., Heidari, H., Jabbari, S., Kearns, M., Roth, A.: Fairness in criminal justice AQ3 risk assessments: the state of the art. Sociol. Methods Res. (2018)
Bogen, M., Rieke, A.: Help wanted: an examination of hiring algorithms, equity, and bias. Technical report, Upturn (2018)
Brennan, T., Dieterich, W., Ehret, B.: Evaluating the predictive validity of the COMPAS risk and needs assessment system. Crim. Justice Behav. 36(1), 21–40 (2009)
Byanjankar, A., Heikkilä, M., Mezei, J.: Predicting credit risk in peer-to-peer lending: a neural network approach. In: IEEE Symposium Series on Computational Intelligence, pp. 719–725 (2015)
Chiappa, S.: Path-specific counterfactual fairness. In: Thirty-Third AAAI Conference on Artificial Intelligence (2019)
Chouldechova, A.: Fair prediction with disparate impact: a study of bias in recidivism prediction instruments. Big Data 5(2), 153–163 (2017)
Chouldechova, A., Putnam-Hornstein, E., Benavides-Prado, D., Fialko, O., Vaithianathan, R.: A case study of algorithm-assisted decision making in child maltreatment hotline screening decisions. Proc. Mach. Learn. Res. 81, 134–148 (2018)
Corbett-Davies, S., Pierson, E., Feller, A., Goel, S., Huq, A.: A computer program used for bail and sentencing decisions was labeled biased against blacks. It’s actually not that clear, October 2016. https://www.washingtonpost.com/news/monkey-cage/wp/2016/10/17/can-an-algorithm-be-racist-our-analysis-is-more-cautious-than-propublicas/?utm_term=.8c6e8c1cfbdf
Corbett-Davies, S., Pierson, E., Feller, A., Goel, S., Huq, A.: Algorithmic decision making and the cost of fairness. In: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 797–806 (2017)
Corbett-Davies, S., Goel, S.: The measure and mismeasure of fairness: a critical review of fair machine learning. CoRR, abs/1808.00023 (2018)
Dawid, P.: Fundamentals of statistical causality. Technical report, University College London (2007)
De Fauw, J., et al.: Clinically applicable deep learning for diagnosis and referral in retinal disease. Nat. Med. 24(9), 1342–1350 (2018)
Dieterich, W., Mendoza, C., Brennan, T.: COMPAS risk scales: demonstrating accuracy equity and predictive parity (2016)
Dwork, C., Hardt, M., Pitassi, T., Reingold, O., Zemel, R.: Fairness through awareness. In: Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, pp. 214–226 (2012)
Eckhouse, L., Lum, K., Conti-Cook, C., Ciccolini, J.: Layers of bias: a unified approach for understanding problems with risk assessment. Crim. Justice Behav. 46, 185–209 (2018)
Eubanks, V.: Automating Inequality: How High-Tech Tools Profile, Police, and Punish the Poor. St. Martin’s Press, New York (2018)
Feldman, M., Friedler, S.A., Moeller, J., Scheidegger, C., Venkatasubramanian, S.: Certifying and removing disparate impact. In: Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 259–268 (2015)
Flores, A.W., Bechtel, K., Lowenkamp, C.T.: False positives, false negatives, and false analyses: a rejoinder to “Machine Bias: there’s software used across the country to predict future criminals. And it’s biased against blacks”. Fed. Probat. 80(2), 38–46 (2016)
Harvard Law School. Note: Bail reform and risk assessment: The cautionary tale of federal sentencing. Harvard Law Rev. 131(4), 1125–1146 (2018)
He, X., et al.: Practical lessons from predicting clicks on ads at Facebook. In: Proceedings of the Eighth International Workshop on Data Mining for Online Advertising, pp. 1–9 (2014)
Hoffman, M., Kahn, L.B., Li, D.: Discretion in hiring. Q. J. Econ. 133(2), 765–800 (2018)
Isaac, W.S.: Hope, hype, and fear: the promise and potential pitfalls of artificial intelligence in criminal justice. Ohio State J. Crim. Law 15(2), 543–558 (2017)
Kleinberg, J., Mullainathan, S., Raghavan, M.: Inherent trade-offs in the fair determination of risk scores. In: 8th Innovations in Theoretical Computer Science Conference, pp. 43:1–43:23 (2016)
Koepke, J.L., Robinson, D.G.: Danger ahead: risk assessment and the future of bail reform. Wash. Law Rev. 93, 1725–1807 (2017)
Kourou, K., Exarchos, T.P., Exarchos, K.P., Karamouzis, M.V., Fotiadis, D.I.: Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 13, 8–17 (2015)
Kusner, M.J., Loftus, J.R., Russell, C., Silva, R.: Counterfactual fairness. In: Advances in Neural Information Processing Systems 30, pp. 4069–4079 (2017)
Lum, K.: Limitations of mitigating judicial bias with machine learning. Nat. Hum. Behav. 1(7), 1 (2017)
Lum, K., Isaac, W.: To predict and serve? Significance 13(5), 14–19 (2016)
Malekipirbazari, M., Aksakalli, V.: Risk assessment in social lending via random forests. Expert Syst. Appl. 42(10), 4621–4631 (2015)
Mayson, S.G.: Bias in, bias out. Yale Law Sch. J. 128 (2019)
Mitchell, S., Potash, E., Barocas, S.: Prediction-based decisions and fairness: a catalogue of choices, assumptions, and definitions (2018)
Pearl, J.: Causality: Models, Reasoning, and Inference. Cambridge University Press, Cambridge (2000)
Pearl, J., Glymour, M., Jewell, N.P.: Causal Inference in Statistics: A Primer. Wiley, Hoboken (2016)
Perlich, C., Dalessandro, B., Raeder, T., Stitelman, O., Provost, F.: Machine learning for targeted display advertising: transfer learning in action. Mach. Learn. 95(1), 103–127 (2014)
Peters, J., Janzing, D., Schölkopf, B.: Elements of Causal Inference: Foundations and Learning Algorithms. MIT Press, Cambridge (2017)
Rosenberg, M., Levinson, R.: Trump’s catch-and-detain policy snares many who call the U.S. home, June 2018. https://www.reuters.com/investigates/special-report/usa-immigration-court
Selbst, A.D.: Disparate impact in big data policing. Georgia Law Rev. 52, 109–195 (2017)
Spirtes, P., et al.: Causation, Prediction, and Search. MIT Press, Cambridge (2000)
Stevenson, M.T.: Assessing risk assessment in action. Minnesota Law Rev. 103, 303 (2017)
Vaithianathan, R., Maloney, T., Putnam-Hornstein, E., Jiang, N.: Children in the public benefit system at risk of maltreatment: identification via predictive modeling. Am. J. Prev. Med. 45(3), 354–359 (2013)
Zhang, J., Bareinboim, E.: Fairness in decision-making - the causal explanation formula. In: Proceedings of the 32nd AAAI Conference on Artificial Intelligence (2018)
Acknowledgements
The authors would like to thank Ray Jiang, Christina Heinze-Deml, Tom Stepleton, Tom Everitt, and Shira Mitchell for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A Bayesian Networks
A graph is a collection of nodes and links connecting pairs of nodes. The links may be directed or undirected, giving rise to directed or undirected graphs respectively.
A path from node \(X_i\) to node \(X_j\) is a sequence of linked nodes starting at \(X_i\) and ending at \(X_j\). A directed path is a path whose links are directed and pointing from preceding towards following nodes in the sequence.
A directed acyclic graph (DAG) is a directed graph with no directed paths starting and ending at the same node. For example, the directed graph in Fig. 8(a) is acyclic. The addition of a link from \(X_4\) to \(X_1\) makes the graph cyclic (Fig. 8(b)). A node \(X_i\) with a directed link to \(X_j\) is called parent of \(X_j\). In this case, \(X_j\) is called child of \(X_i\).
A node is a collider on a path if it has (at least) two parents on that path. Notice that a node can be a collider on a path and a non-collider on another path. For example, in Fig. 8(a) \(X_3\) is a collider on the path \(X_1 \rightarrow X_3 \leftarrow X_2\) and a non-collider on the path \(X_2\rightarrow X_3\rightarrow X_4\).
A node \(X_i\) is an ancestor of a node \(X_j\) if there exists a directed path from \(X_i\) to \(X_j\). In this case, \(X_j\) is a descendant of \(X_i\).
A Bayesian network is a DAG in which nodes represent random variables and links express statistical relationships between the variables. Each node \(X_i\) in the graph is associated with the conditional distribution \(p(X_i|\text {pa}(X_i))\), where \(\text {pa}(X_i)\) is the set of parents of \(X_i\). The joint distribution of all nodes, \(p(X_1,\ldots ,X_I)\), is given by the product of all conditional distributions, i.e. \(p(X_1,\ldots ,X_I)=\prod _{i=1}^Ip(X_i|\text {pa}(X_i))\).
In a Bayesian network, the sets of variables \(\mathcal{X}\) and \(\mathcal{Y}\) are statistically independent given \(\mathcal{Z}\) ( ) if all paths from any element of \(\mathcal{X}\) to any element of \(\mathcal{Y}\) are closed (or blocked). A path is closed if at least one of the following conditions is satisfied:
) if all paths from any element of \(\mathcal{X}\) to any element of \(\mathcal{Y}\) are closed (or blocked). A path is closed if at least one of the following conditions is satisfied:
-
(a)
There is a non-collider on the path which belongs to the conditioning set \(\mathcal{Z}\).
-
(b)
There is a collider on the path such that neither the collider nor any of its descendants belong to the conditioning set \(\mathcal{Z}\).
Appendix B EFPRs/EFNRs and Calibration
Assume that EFPRs/EFNRs are satisfied, i.e. \(p(\hat{Y} = 1 |A=0, Y=1)=p(\hat{Y} =1|A=1, Y=1)\equiv p_{\hat{Y}_1|Y_1}\) and \(p(\hat{Y} = 1 |A=0, Y=0)=p(\hat{Y} =1|A=1, Y=0)\equiv p_{\hat{Y}_1|Y_0}\). From
we see that, to also satisfy \(p(Y = 1 |A=0, \hat{Y}=1) = p(Y = 1 |A=1, \hat{Y}=1)\), we need  , i.e. \(p_{Y_1|A_0} = p_{Y_1|A_1}\).
, i.e. \(p_{Y_1|A_0} = p_{Y_1|A_1}\).
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this chapter
Cite this chapter
Chiappa, S., Isaac, W.S. (2019). A Causal Bayesian Networks Viewpoint on Fairness. In: Kosta, E., Pierson, J., Slamanig, D., Fischer-Hübner, S., Krenn, S. (eds) Privacy and Identity Management. Fairness, Accountability, and Transparency in the Age of Big Data. Privacy and Identity 2018. IFIP Advances in Information and Communication Technology(), vol 547. Springer, Cham. https://doi.org/10.1007/978-3-030-16744-8_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-16744-8_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-16743-1
Online ISBN: 978-3-030-16744-8
eBook Packages: Computer ScienceComputer Science (R0)









 , but
, but  .
.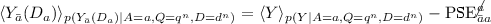 . Indeed
. Indeed 
