Abstract
Since the first scanning laser ophthalmoscope (SLO) was introduced in the early 1980s, this imaging technique has been adapted and optimized for various clinical applications based on different contrast mechanism. Reflectance imaging, where the back scattered light is detected, is widely used for eye tracking and as reference image for OCT applications. But also the reflectance modality itself has several important diagnostic applications: laser scanning tomography (SLT), imaging with different laser wavelengths (Multicolor contrast) and others. Fluorescence imaging channels with different excitation wavelengths were introduced to SLOs for angiography, i.e. for the visualization of the vascular system after intravenously injecting an appropriate dye, as well as for autofluorescence imaging of endogenous fluorophores within the retina.
This chapter gives an introduction to the history of SLO technology and a general overview on its clinical applications. In the following sections the focus is directed on one distinct clinical application for each of the major imaging modalities: reflectance, angiography and autofluorescence. First, the assessment of the optic nerve head for glaucoma diagnostic by means of laser scanning tomography is presented, before in the third section the clinical aspect of wide field SLO angiography is discussed. Finally, an introduction to quantitative autofluorescence (qAF) is given, a new research tool, which is used to measure the accumulation of lipofuscin within the retinal pigment epithelium (RPE) for normal subjects and for patients with macular dystrophies.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- Ophthalmoscopy
- Scanning laser ophthalmoscopy (SLO)
- Confocal scanning laser ophthalmoscope (cSLO)
- Resolution
- Cone imaging
- Scanning laser tomography (SLT)
- Optic nerve head topography
- Glaucoma diagnostics
- Wide field angiography
- Ultra wide field imaging
- Indocyanine green angiography (ICGA)
- Lipofuscin
- Autofluorescence (AF)
- Quantitative autofluorescence (qAF)
1 Introduction and Technology
1.1 History
20 years after Theodore Maiman announced in New York in a press conference the invention of the laser [1], the first laser scanning ophthalmoscope, was demonstrated in a paper by Webb, Hughes and Pomerantzeff [2]. They named their instrument “flying spot TV ophthalmoscope” since firstly, they used a scanned beam of an ArKr-laser (resp. HeNe-laser for the red wavelength range) to generate a fast “flying” laser spot on the subjects retina and secondly, the amplified output voltage of the photomultiplier, which was used to detect the back-scattered light from the retina, was directly connected to the input channel of a television tube monitor. The optical set-up of this device is reprinted in Fig. 2.1. The expanded beam of a gas laser is scanned by horizontal and vertical scanning mirrors and deflected by a half-silver coated turning mirror (TM); all components are positioned in conjugate planes to the entrance pupil of the eye. The backscattered light is coupled by the partially transmitting turning mirror into the detection arm with several spatial filters to avoid artifacts from reflections at the final lens and at the cornea.
Adapted from reference [2]: Optical set-up of the Boston “Flying Spot TV Ophthalmoscope” (upper part) and block diagram of electronics (lower part)
In the following years Robert Webb and his team, but also the Heidelberg group of Josef Bille continuously improved and refined the performance of the then re-baptized Scanning Laser Ophthalmoscope (SLO) [3, 4], including the use of frame grabber boards allowing for conversion to digital images. Image contrast was drastically improved by confocal detection eliminating scattered light originating from outside the focal volume [5, 6]. Laser Scanning Tomography (SLT) was introduced, were a stack of 2D SLO images was acquired with each frame positioned at a different, equally spaced focal plane and from the 3D data stack a tomography image was calculated. (see [7, 8] and Sect. 2.2.2 for details).
Together with ophthalmologists the technical groups started to evaluate the clinical value of the new imaging technique in first clinical studies [9]. A perimeter was integrated into the SLO in order to determine scotoma maps of patients [10, 11], and a study on macular holes and other macular disease was accomplished at the department of ophthalmology in San Diego in cooperation with the Heidelberg team [6].
Already in 1989 Josef Bille at al. proposed and demonstrated the use of adaptive optics in order to improve the axial resolution of the confocal SLO [12].
1.2 Modern Confocal SLO
In Fig. 2.2 a set-up of an SLO is represented, which is reduced for simplicity to its key components, which are integral parts of every SLO system. The emission of a laser diode is collimated by a lens (CL) and the beam passes through an out-coupling beam splitter (BSP) before it enters the XY-scanning unit (XY). The scanning unit deflects the laser beam in two dimensions and thus generates the raster pattern on the retina. The scan pupil in the plane of XY is relayed by imaging optics onto the entrance pupil of the examined eye (L1, L2). The anterior segment of the eye (cornea and lens) focuses the laser beam onto the retina. The optics must be adjustable in order to provide compensation for myopic resp. hyperopic eyes . Contrary to Fig. 2.1, the signal light (backscattered light or emitted fluorescence) travels the same optical path back and is “descanned” to a stationary beam. It is separated from the incident laser beam by means of the beam splitter (BSP) and deflected into the detection arm of the system. The signal light is then focused by a lens (FL) onto a pinhole (PH), which serves as confocal aperture and is located at a plane conjugate to the retina and to the emitting laser diode. The light is finally detected (APD) and converted to an electrical signal, which is then amplified, digitized and transferred to the computer, where the digital image is reconstructed, preprocessed and displayed on the monitor. Usually the synchronization signals frame, line, and pixel clock are derived from the scanning system , where on one hand the line clock of the fast scanning direction (here horizontal X-axis) is divided into an equally spaced pixel clock and on the other hand the frame clock is generated to trigger the scan ramp of the slower scan axis (here vertical Y-axis). Due to the confocal set-up, back-scattered light, which originates from structures anterior and posterior to the focal plane, is blocked efficiently by the pinhole aperture (PH). For fluorescence imaging a barrier filter needs to be inserted in the detection arm (typically between BSP and FL, not shown in Fig. 2.2) in order to block the reflected excitation light.
basic set-up of a SLO. The core components are: a laser (here laser diode LD), an XY scanning unit (defining the scan pupil), optics to relay the scan pupil onto the entrance pupil of the eye, a beam splitter (BSP) to separate the backscattered signal from the incident laser path, the pinhole (PH), and a high sensitivity avalanche photodiode detector (APD). The green dotted arrow indicates the scan sweep. An out of focus beam is also shown (yellow interrupted line) to illustrate the strong attenuation of such beam at the pinhole
1.3 SLO Core Components
In the following the technology of core components is discussed:
1.3.1 Laser Source
The early SLOs incorporated gas lasers with their superior beam profile and their stable, continuous wave (cw) laser emission. For reflectance imaging usually the red HeNe laser line (helium neon laser) was used, whereas for fluorescence applications the turquoise 488 nm laser line of the Argon laser (Ar+ laser) became very popular. This wavelength matches almost perfectly the absorption maximum of sodium fluorescein, a standard dye, which was used in clinics already since the 1960s for fluorescein angiography (FA) with fundus cameras [13].
The Heidelberg Retina Tomograph (HRT) was the first SLO, which used instead of a bulky and little efficient gas laser a compact and less expensive red laser diode at 670 nm. Whereas in the red and near infrared wavelength range these laser diodes were available already in the early 1990s, for the fluorescein angiography the replacement of the gas lasers took more time. In Fig. 2.3 three generations of blue lasers emitting at 488 nm, which were used in Heidelberg Retina Angiography systems (HRA) , are displayed.
laser devices emitting at 488 nm for FA and AF imaging in Heidelberg Engineering systems: (a) Ar+ laser from Uniphase Inc. used in the HRA “classic”, (b) “Sapphire” laser, an optically pumped solid state laser (OPSL) from Coherent Inc. (HRA2 and early Spectralis) and (c) a laser diode in a TO56 (Ø5.6mm) package (Spectralis)
1.3.2 Scan Unit
The biggest challenge of a fast 2D scanning system is the high line rate of 8 kHz or more, which is required for the fast scanning direction. In the following it is assumed, that the fast scan axis of the 2D scan pattern is the horizontal X-direction, and the slow axis refers to the vertical Y-scan. Such a fast line scan rate is required in order to achieve frame rates of >15 Hz while maintaining still a sufficient high density for square pixels, i.e. pixels with same separation in X- and Y-direction. In addition to the high speed, also the optical scan angle and the size of the scan pupil, i.e. the mirror size, are crucial parameters, which need to be carefully balanced. A lower primary scan angle can be compensated by appropriate magnification optics, which will, however, at the same time reduce the diameter of the pupil area defining the solid angle under which back scattering or fluorescence emission can be detected.
These demanding specifications can be met by resonant scanners, where the mirror is mounted on a beryllium torsion bar with a counter weight at the other end. The total system of mirror , torsion bar and counter weight has an intrinsic resonance frequency with high Q-value of half the line rate and is excited by a phase locked loop (PLL) circuit to the fast sinusoidal scanner oscillation.
A common alternative to resonant scanners are polygon scanners, where a polygon-shaped mirror is rotated by means of a fast DC motor at up to 60,000 rpm. For a polygon mirror with eight mirror facets, this would correspond to a line frequency of 8 kHz. Again , the size of the scan pupil and the required scan angle limit the number of facets and therefore also the scan rate.
For the slow axis (vertical direction) in general galvanometric scanners are used, which are usually controlled in a closed loop with a saw-tooth ramp.
1.3.3 Beam Splitter
Different beam splitter optics (plates or cubes) have been used for separating the back scattered signal light from the incident laser beam path. For fluorescence systems (angiography and autofluorescence) the use of dichroic mirrors is the optimum choice. The dielectric coating of these mirrors is usually designed in a way that the beam splitter plate has a high transmission for the excitation laser wavelength , but shows a strong reflectivity for the “red-shifted” fluorescence emission.
For reflectance imaging, a splitting ratio of 20:80 is usually a good choice: a transmission of 20% is in many cases sufficient, since the maximum laser power, which can be applied to the eye, is limited anyway by laser safety requirements. On the other hand, it is of course desirable to couple as much as possible of the back scattered signal light into the detection branch.
Another option is the use of a polarizing beam splitter: the laser beam is p-polarized and therefore passes through the polarizing beam splitter to a very high percentage. After the beam splitter, a quarter wave plate is inserted, which rotates the polarization due to the double pass (out-going and back scattering beams) by 90° in a way, that the signal light is now s-polarized and thus reflected by the polarizing beam splitter into the detection unit. It is important to note, that the birefringent structures within the eye (e.g. cornea, retinal nerve fiber layer) can cause an inhomogeneous illumination of the image, since the combined action of the quarter wave plate and the birefringent tissue will lead to an imperfect 90° rotation of the polarization.
1.3.4 Imaging Optics
Optics are required to relay the scan pupil to the entrance pupil of the eye. In many cases a telecentric 4f design is chosen, as shown schematically in Fig. 2.2. The advantage of such a design is, that by adjusting the distance between the two lens groups (L1 and L2), the convergence or divergence of the laser beam at the scan pupil can be adjusted to correct for the refraction error of the eye, without changing the magnification of the scan angle at the entrance pupil.
By using lens groups with different effective focal lengths, the primary scan angle can be magnified or reduced and the beam diameter at the eye pupil is correspondingly decreased resp. increased . Especially for the design of wide field imaging optics, it is important, to integrate the lens data of wide field model eye into the optics design file in order to achieve over the complete scan field a sharp fundus image.
1.3.5 Detectors
Whereas in early SLO systems photomultiplier tubes (PMT) were used because of their at that time unique sensitivity, nowadays semiconductor based detectors as avalanche photodiodes (APD) and silicon photomultiplier (SiPM) are the first choice.
APDs consist of a semiconductor p-n junction, where the incident photons create free electrons in the absorption zone. These carriers are sucked to the multiplication zone , where a high reverse voltage leads to their avalanche-like multiplication due to impact ionization. Typically a gain of more than 100 can be achieved, and this gain is proportional to the applied reverse voltage.
APDs can be operated as well in the Geiger mode for single photon counting. In these single photon avalanche photodiodes (SAPD) the applied reverse voltage is above the breakdown voltage, and an initial charge carrier created by a single photon is extremely multiplied up to currents in the range of a milliampere. The leading edge of this current is used to trigger a photon counter. During the high current, the bias voltage drops below breakdown voltage and the device is blind for the detection of new photons. This effect limits the maximum count rate of the SAPDs.
Silicon photomultipliers (SiPM) consist of an array of APDs operated in the Geiger mode . The dimension of such an array is typically in the order of a few millimeters. The dimension of each single SAPD cell is in the range of 10 … 100 μm, i.e. the array typically consists of several 1000 elements. The output channels of the individual cells are connected in one common parallel read-out element. Although each element is operated in the digital Geiger mode , the combined output of the complete device yields an analogue output, which is proportional to the incident photon flux until the saturation level is reached.
1.4 Resolution of the SLO
1.4.1 Limitations and Numerical Aperture (NA) of the Eye
The optical resolution of the scanning laser ophthalmoscope is limited by the anatomy of the human eye itself. As in any conventional light microscope the minimum spot size of the focused laser in the object plane is limited by diffraction.
The numerical aperture NA of an optical system characterizes the range of angles (half cone angle θ, i.e. measured against optical axis) over which the system can accept or emit light. It also is a measure of the optical resolution in a diffraction limited system. For the human eye it is defined by:
where n = 1.336 is the refractive index of the vitreous, D the pupil diameter, f p the posterior focal length of the emmetropic eye (f p = 22.3 mm), and f eye the anterior focal length , which determines the lateral scaling parameters of the retina. The error due to the small angle approximation in Eq. (2.1) is less than 1.25%.
For undilated pupils the maximum NAeye is about 0.09 (D = 3 mm) and it can be increased by a factor of 2–3 by dilating the pupil with a drug to D = 6 − 8 mm. However, due to the limited optical quality of the eye and due to the strong increase of the optical aberrations in the periphery, the distortions of the wave front in contrary result in a larger focal volume on the retina and thus decrease the optical resolution compared to undilated pupils [14, 15]. In order to exploit the full diffraction limited resolution for dilated pupils, an adaptive optical (AO) element must be used to compensate the distortions of the optical wave front of the individual eye. With this concept, the lateral resolution can be increased by a factor of 2–3 and the axial resolution even by a factor of 4–9 compared to undilated pupils (see also Chaps. 16–18). The following considerations are only valid for eyes without optical aberrations, i.e. either for undilated eyes with sufficient optical quality, or for dilated pupils with AO compensation.
In order to calculate the lateral and axial extension of the focus spot, the light propagation integral of the pupil function needs to be solved. In the following the results for two different approaches are summarized: Fraunhofer diffraction at a circular aperture and propagation of a Gaussian beam.
1.4.2 Fraunhofer Diffraction at a Circular Aperture
Fraunhofer diffraction assumes an incident plane wave (e.g. a collimated laser beam) with constant amplitude over the complete, circular aperture with diameter D. The latter assumption is usually only a rough approximation, since the laser profile typically is not flat. The radially symmetric intensity distribution I(r,z) in the focal volume can be separated in one expression I(r,z = 0) describing the lateral intensity in the focal plane and a second term I(r = 0,z) describing the axial distribution for r = 0 as a function of axial distance z [16, 17]:
and
with J 1 in the upper equation referring to the first order Bessel function . The first minimum of this radial symmetric distribution is at:
r min represents the radius of the so-called Airy disk. Under the assumption, that two structures can be separated, when the maximum of the first structure coincides with the minimum of the second structure (Rayleigh criterion), one obtains for the lateral resolution δxRC:
In a similar way from the distribution I(r = 0, z) a value δzFWHM for the full width at half maximum can be derived [17]:
For small numerical apertures with NA eye < 0.5 this yields:
1.4.3 Beam Waist for Propagating Gaussian Beam
The propagation theory of Gaussian beams is described in literature and in optics textbooks [18, 19]. It assumes a Gaussian intensity profile, which is the case for many lasers (TEM00 Mode) and also for the output of single mode fibers. However, it normally does not consider the truncation of the Gaussian beam at the finite aperture, which results in a broadening of the focus distribution. The propagation of the non-truncated beam is described by the beam waist ω(z), which gives the beam radius (intensity drop to 1/e2) as function of the axial position z. The beam waist in the focus plane is denoted ω 0, the Rayleigh length zr refers to the z-distance, where the cross section radius is increased by a factor of √2, i.e. the area is doubled.
with
and
Dickson [19] investigated the influence of truncation of the Gaussian beam by a circular aperture, which depends on the ratio of the truncating circular aperture with radius r A and the Gaussian beam waist in the pupil plane ω p:
-
for r A ≥ 2 · ω p the truncation effect is negligible.
-
for r A = ω p, the truncation will result in an increase of the focus waist of ≈50%.
-
for r A ≪ ω p, the focus waist will approximate the result of the Fraunhofer diffraction pattern.
For SLO examination on an undilated eye the limiting aperture is usually the iris (2–3 mm diameter), which is often in the order of the beam diameter of the laser beam (r A ≈ ω p), thus a truncation factor of ×1.5 is in many applications justified.
1.4.4 Resolution Improvement Due to Confocal Detection
In order to determine the influence of the confocal aperture on the lateral and axial resolution, the illumination point spread function (PSF, i.e. the 3D intensity distribution of an ideal point source imaged onto the sample) needs to be multiplied with the detection point spread function defined by the image of a point source emitter within the sample onto the pinhole aperture. Thus, in theory the confocal detection could improve the resolution by a factor of 1/√2, however, this enhancement is only achieved when the pinhole size is much smaller than the Airy disk diameter projected into the pinhole plane. Usually, for intensity reasons , this is not the case in commercially available cSLOs.
In Table 2.1 some values for typical focus spot parameters are summarized for different assumptions, wavelengths and pupil diameters:
1.5 Example for High Resolution SLO Image
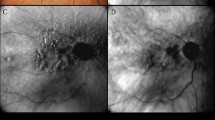
The following SLO image was acquired with a Spectralis using a high magnification objective (HMO) on a healthy subject. The HMO reduces the optical scan angle by a factor of 2 and in addition the digital pixel density is doubled in both scan directions. This results in a 16× higher pixel density compared to the standard 30° HR scan image (see Fig. 2.4). The laser wavelength was 815 nm and in order to avoid additional aberrations, the pupil was not dilated. The measurement was taken at an eccentricity of about 10°. The diameter of the cone cells (inner segments) varies between ≈2 μm and 7 μm with eccentricity increasing from 0° to 5° [20]. Further in the periphery a slow further increase to about 8 μm is reported. The images clearly demonstrate, that structures as small as 6–8 μm can be imaged in the retina, without the use of adaptive optics.
(a) High resolution SLO image on a healthy subject at an eccentricity of 10°. The size of the image is 8° × 8° corresponding to about 2.3 mm × 2.3 mm. (b) Detail of the fundus image clearly displaying the cone pattern, without the use of adaptive optics. (c) For orientation: 30° image of the same eye
2 Laser Scanning Tomography
Gerhard Zinser and his team developed in 1991 the Heidelberg Retina Tomograph (HRT) , a commercial SLO, which was from the beginning dedicated for the diagnosis of glaucoma by assessing the morphology of the optical nerve head.
Together with his partner, Christoph Schoess, he founded Heidelberg Engineering and the HRT was the first product of the company. Both were before employees with Heidelberg Instruments, were Gerhard Zinser led the R&D department for laser scanning ophthalmology and built already in the late 1980s a series of prototypes of a confocal SLO, which was named Heidelberg Laser Tomographic Scanner (LTS) . In 1998 (HRTII) and in 2005 (HRT3) the next generations of the HRT with improvements in the data acquisition work flow as well as in the analysis software were released (see Fig. 2.5).
2.1 HRTII/HRT3 Acquisition Work Flow
For laser scanning tomography a set of 2D SLO frames at equally spaced focal positions is acquired. Therefore, between two frames of a series, the focus of the laser is shifted by means of a motorized telescope within the camera head. For the HRTII/HRT3 the data acquisition work flow is as follows:
First the patient is positioned and fixates with the examined eye on a fixation target presented at about 12° nasally , such that the optic nerve head (ONH) appears centered within the 15° × 15° scan field.
The user then aligns the camera head in three dimensions, in order to make sure, that the scan pupil, i.e. the pivot point of the scanning laser beam, coincides exactly with the entrance pupil of the eye. The SLO image is displayed on the monitor and the brightness of the image, i.e. the detector sensitivity, is adjusted automatically (auto-brightness) to make sure, that the signal falls over the complete z-scan within the linear range of the detector and no saturation effects corrupt the data. Once the camera is properly aligned, the acquire button is pressed and the acquisition of three consecutive z-scans is started. The first series consists of a stack of 64 images with a focal plane distance of 62.5 μm, i.e. covering an overall z-range of 4 mm in the eye. From this first series, the required z-scan depth for the two consecutive z-scan is calculated (depending on the ONH geometry 2–4 mm), in order to avoid unnecessary long acquisition time. Finally an automatic quality control check is performed, and if o.k. the series are saved on the computer.
2.2 HRTII/HRT3 Data Processing
Each of the three acquired series is corrected for eye movements during the z-scan by laterally matching and shifting each image with respect to the previous image within the scan.
On the basis of the corrected data set a topography and a reflectance image is calculated for the three series. In Fig. 2.6 the working principle of the computation algorithm is displayed. For each lateral pixel (xy-position), the z-profile is analyzed and the xy-values for the reflectance (mean brightness) and topography (surface height of the retina) images are calculated corresponding to the equations in Fig. 2.6. On the basis of the three sets of images finally a mean tomography and a mean reflectance image is calculated (see Fig. 2.7). For better visualization, the topography of the ONH can be displayed also as a 3D surface, as shown in Fig. 2.8.
2.3 Contour Line, Reference Plane and Stereometric Parameters
After data acquisition and calculation of the reflection and topography images, a contour line around the optic disk needs to be defined, similar as it is the case in cup/disk ratio measurements on fundus images. The contour line is used to calculate stereometric parameters as the rim area, rim volume, cup shape measure and others, which describe the shape of the ONH. In addition, these parameters can be combined by means of several discriminant functions, which have been proven in clinical studies to have a high sensitivity and specificity for glaucoma detection [21,22,23,24].
The ONH contour needs to be manually defined by the physician and some experience is required to correctly place the line around the optic disk. However, it has been shown in a clinical study [25], that the variability between contour lines drawn by different physicians has only little effect on the parameter data. In addition, the contour line needs to be defined only once for the baseline data and then is automatically transferred to the new image data acquired during follow-up examinations.
The reference plane is calculated on the basis of the defined contour line: the plane is parallel to the peripapillary retinal surface and it is set 50 μm below the retinal surface height at the papillomacular bundle, which is located in the 350–356° section (temporal) of the contour line. The reference line is used to separate between rim and cup area resp. volume. Structures inside the contour line are defined either as neuroretinal rim, if their surface height (maximum of the z-profile) lies above, or as cup, if their surface height lies below the reference plane (Fig. 2.9). This definition of the reference plane allows for objectively comparing follow-up exams to the baseline data.
2.4 Analysis of HRT Optic Nerve Head (ONH) Data
2.4.1 ONH Classification Based on Moorfields Regression Analysis
In 1998 Wollstein et al. from the Moorfields hospital in London proposed a linear regression analysis based on the rim to disc area ratios for the ONH [26]. They imaged in a cross-sectional study 80 normal subjects and calculated from the linear regression curves different confidence intervals (CI) for normal subjects. The data was analyzed for the global ONH as well as separately for six different sectors (see Fig. 2.10). This approach was implemented with an extended reference database in the HRT software, in order to classify acquired ONH data as follows: “within normal limits” for subjects with a rim-disc area ratio within the 99% CI (globally and in all six sectors), “borderline” for subjects, where at least one of the seven parameters was outside the 99% CI but still within the 99.9% CI, and “outside normal limits”, when the rim-disc area ratio for at least one of the seven parameters was outside the 99.9% CI of the reference database. Examples for such a classification are shown in Figs. 2.10 and 2.11.
2.4.2 Follow-Up and Progression Analysis
In order to differentiate between a progressing glaucomatous and a stable ONH, follow-up examinations acquired at later time points are compared with the original baseline data. Therefore, first the follow-up images are matched to the baseline images, in order to compensate for head tilts, accommodation differences and other external influences and in a second step the baseline contour line is transferred to the new images to enable the calculation of all the follow-up stereometric parameters.
One possibility to visualize the temporal development is to plot the stereo-metric parameters versus time, with the date of the baseline examination as origin of the time axis. Since the absolute changes and also the sign of the changes vary for different parameters, the temporal change of each stereometric parameter is normalized to the difference of this parameter averaged over a healthy group and over a group of glaucoma patients.
Another possibility to visualize the changes in a time series of ONH topography images was proposed by Chauhan et al. [27]. They assessed by means of statistical methods the significance of changes of clustered super-pixels in the topography images and visualized these changes by colored overlays: red indicating a decrease of surface height (i.e. increase of excavation) and green indicating an increase of surface height.
2.5 Summary SLT for Glaucoma Diagnostics
Laser scanning tomography was for several years the gold standard for diagnosis and monitoring the progression of glaucoma by assessing the morphology of the optical nerve head. Numerous clinical studies, which have been published in peer-reviewed journals, have shown, that the HRT enables reproducible measurements of the morphology of the optic nerve head [7, 28], has a very high sensitivity and specificity for discriminating patients with early glaucoma from normal subjects [26, 29] and that the success of therapeutic intervention can be reliably assessed by documenting the stagnancy resp. the progression of the disease [27, 30, 31].
Only with the availability of spectral domain OCT systems (see Chap. 3), which provided on one hand a much better axial resolution compared to the confocal SLO and on the other hand a much shorter acquisition time and higher spatial accuracy compared to the previous commercially available time domain OCT device, the demand for laser scanning tomography technology slowly decreased. However, since glaucoma is a slowly progressing disease, where the progression needs to be monitored carefully over years and presently acquired data needs to be compared with baseline and follow-up data acquired years ago, the HRT is still a valuable instrument used on a daily base in clinical practices for monitoring and managing glaucoma patients.
3 Widefield Indocyanine Green Angiography (ICGA)
The advent of widefield imaging has for the first time offered the chance to investigate both, the central and the peripheral retina, in a single examination. A wide visualization of the retinal periphery is necessary for the screening, diagnosis, monitoring, and treatment of many diseases. Early diagnosis of peripheral retinal or choroidal disease could reduce a potential vision loss.
Fluorescein angiography (FA) and indocyanine green angiography (ICGA ) are two imaging modalities that use a water-soluble dye to visualize retinal and choroidal vasculature [32].
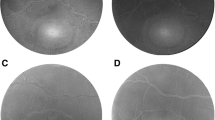
Simultaneous widefield fluorescein and indocyanine green angiography with confocal scanning laser ophthalmoscope can be performed to explore areas of peripheral chorioretinal non-perfusion and neovascularization beyond the range of conventional fundus cameras. Several add-on lenses for confocal SLOs can be used to obtain different fields of view (see Fig. 2.12).
Indocyanine green angiography images of a patient with retinal vein occlusion. From the left to the right: 30° field of view with standard Spectralis objective, 55° WFO, 60° with Ocular Lee-Mainster SLO lens, 102° UWF, 120° on horizontal axis and 80° on vertical axis with Optos imaging system, and 150° with the Ocular Staurenghi contact lens in combination with Spectralis
Using widefield angiography important clinical observations have been made under several conditions. One important application of widefield angiography is in patients with diabetic retinopathy. Several studies have demonstrated the association between peripheral retinal non-perfusion and the occurrence of neovascularization and diabetic macular edema [33,34,35]. The Diabetic Retinopathy Study introduced imaging of diabetic retinopathy in the retinal periphery by obtaining 7-standard fields . By combining these 30-degree images, a montage visualizes about 75° of the retina [36]. Ultra widefield fluorescein angiography images captured 3.9 times more area of retinal non-perfusion, 1.9 times more neovascularization and 3.2 times more retinal surface area than what is seen within the ETDRS standard 7-fields overlay [34] (Fig. 2.13).
Another important use of widefield fluorescein angiography in diabetic retinopathy is the evaluation of peripheral retinal areas of non-perfusion or neovascularization to perform a target laser photocoagulation (Fig. 2.14). This treatment is useful to reduce the vascular endothelial growth factor production and to increase oxygen diffusion from the choroid [37, 38]. Widefield fluorescein angiography allows for treating specific areas of retinal non-perfusion while using less energy and sparing relatively better perfused tissue from laser-induced tissue scarring.
Also in patients with retinal vein occlusion, ultra widefield angiography may be a powerful tool to identify therapeutic target areas for photocoagulation, allowing for efficient treatment of ischemic retina, and for potentially minimizing collateral destruction of adjacent viable perfused retina [39].
Widefield angiography is also used in patients with uveitis. The diagnosis and management of uveitis is challenging. Accurate diagnosis, definitions of activity and response to treatment are typically defined by clinical and angiographic appearance [40]. Some features of posterior uveitis, such as perivascular sheathing , peripheral capillary non-perfusion , venous staining or leakage, cystoid macular edema, and disc edema, could be detected by widefield angiography [41]. This technique allows for detecting images of both central and peripheral retina simultaneously giving more precise details then montage reconstruction.
Intraocular choroidal tumors are better visualized using wide field angiography. Differential diagnosis is supported by using multimodal imaging approach. Abnormal choroidal vessel or intrinsic vessels as in hemangioma or in melanoma are better seen in widefield angiography allowing for a more precise diagnosis.
Imaging the peripheral retina has significantly improved over the past years. Widefield angiographic technology has become an important clinical tool with regards to early diagnosis, treatment and monitoring of most sight-threatening retinal and choroidal diseases.
4 Quantitative Autofluorescence of the Retina
Confocal scanning laser ophthalmoscopy has been the imaging system of choice for auto-fluorescence (AF) imaging because of its high sensitivity and its image averaging capabilities that are required to record the fundus AF with acceptable signal/noise ratios using safe retinal exposures. The first clinical AF imaging systems were introduced in the mid-1990s [42, 43] using an excitation wavelength of 488 nm. Subsequent developments and the introduction of several commercial imaging platforms have further broadened the field and allowed AF imaging to become an important imaging modality for clinical diagnosis [44].
4.1 Origin and Spectral Characteristics of Fundus Auto-Fluorescence (AF)
The fluorophore responsible for AF of the fundus is principally lipofuscin residing in the retinal pigment epithelium [45]. Lipofuscin is a byproduct of the visual cycle. The tips of the outer segments of photoreceptor are damaged by photo-oxidation and are phagocytosed on a daily basis. These materials contain poly-saturated fatty acids and byproducts of the visual cycle that are partially digested in the RPE. A small fraction is chemically incompatible for degradation and accumulates in lysosomes of the RPE as lipofuscin , a mixture of various fluorophores. Chemically some of these compounds have been identified and synthetized as bisretinoids [46, 47].
In-vivo spectrophotometric and imaging studies of AF have shown that the fluorescence can be excited from 430 nm to about 600 nm [45, 48, 49]. In healthy subjects, the excitation spectrum is maximum around 500 nm with a shift towards longer wavelengths with increasing age (Fig. 2.15). The fluorescence is emitted over a broad spectral band extending from the excitation wavelength to about 800 nm, with a maximum shifting from 600 nm to 660 nm as the excitation wavelength is changed from 430 nm to 600 nm, respectively. This “red-shift” occurs for excitations at the long wavelength end of the absorption spectrum of some fluorophore in viscous or polar environment [50]. The emission spectra in healthy subjects shift slightly towards shorter wavelengths with increasing age, a trend that is accentuated in AMD [51]. This could be the result of oxidation of lipofuscin and/or due to a fluorescence contribution of Bruch’s membrane deposit.
Average excitation spectra (left) and emission spectra (right) of fundus auto-fluorescence: Blue spectra: group of young healthy subjects (n = 26; 15–28 years), and Red spectra: group of old healthy subjects (54–67 years). The excitation spectra represent the emission at 620 nm plotted against the respective excitation wavelength (430, 470, 510, 550 nm). The error bars are the 95% Confidence Intervals. All spectra were corrected to account for the absorption of the ocular media. Interrupted lines (left panel) are uncorrected (as measured outside of the eye)
4.2 Quantitative Auto-Fluorescence (AF) Imaging
Quantitative measurements of fundus AF from images acquired with SLO would be possible if one also measured the laser power, and recorded the sensitivity and zero value after acquiring each image. Grey levels in the image and the gain versus sensitivity calibration then allow quantification of AF levels. However this was judged not practical because these measurements are not necessarily easy to perform. Instead, a fluorescent standard was incorporated as a reference in a Spectralis SLO path (Heidelberg Engineering. Heidelberg. Germany). The reference is located in a plane conjugate to the retina, so that it is always in focus with the fundus image (Fig. 2.16). Average grey levels of the reference allow accounting for the effect of variation in laser power and detector gain [52].
Successful acquisition of images for quantifying fundus AF depends in large part on the skills of the operator, and a dedicated operator is highly recommended. Detailed protocols for acquiring optimal AF images have been published [53] including special protocols used in quantitative work [54]. In essence, the fundus of the dilated test eye (>6 mm diameter) is first illuminated with 488 nm light for a 20–30 s long period to reduce AF attenuation by photo-pigment absorption (bleaching). Focus and camera alignment are optimized during that period. Critical uniformity AF signal over the whole field is attained by fine axial adjustment of the camera position. The sensitivity is adjusted to avoid non-linear effects for both the fundus and the internal reference (see later). After final alignment a ‘video’ of 9 or 12 frames is acquired. After rejection of low quality frames (eye-movement, iris obstruction), the remaining frames are aligned and averaged and saved in the “non-normalized” mode (no histogram stretching) to create the AF image for analysis.
The AF is then quantified as qAF by comparing the grey levels (GL) of every pixel of the fundus image with the mean GL measured at of the internal reference, accounting for the zero-signal (no light):
RCF is the ‘Reference Calibration Factor’ obtained from calibration of the internal reference with a Master fluorescent target . The (M em/M)2 term accounts for differences in magnification between the test eye and an emmetropic eye (Fig. 2.17).
The magnification correction factor (Mem/M)2 is a function of refractive error and of radius of curvature of the cornea. The factors were computed on the basis of Gullstrand eye model (No. 2) and the optical characteristics of the Spectralis. The cloud of grey points represents the distribution of magnification correction factors and refractive errors for the healthy subjects. The average magnification factor was 1.06 and the 95% confidence interval was 0.87–1.25
The last term of the Eq. (2.9) accounts for the absorption of the excitation light and the fluorescence emission by the ocular media. We have used the algorithm of van de Kraats and van Norren [55] to estimate the average optical density of the ocular media at a given age. In order to eliminate some unknown terms, this density was expressed relative to the media density at age 20 years [56]. Thus, qAF reflects fundus AF relative to that which would be measured through the media of a 20-year-old emmetropic eye with average ocular dimensions.
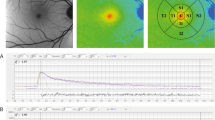
After acquiring mean GL’s from the internal reference and zero-strip (or the info panel), all pixels’ GL of the image are converted into qAF by applying Eq. (2.9). The resulting qAF image is analyzed with dedicated software. The same program was duplicated in the Heidelberg version of its qAF software. Mean qAF’s are then computed at eight standard locations in the fundus (Fig. 2.18). To obtain a single qAF metric for an eye, we generally average the qAF of segments of the middle ring. This average, qAF 8, minimizes the variation of the natural distribution of AF at the posterior pole; it is highest in the supero-temporal quadrant and lowest in the infero-nasal quadrant [57, 58].
The standard sampling areas are eight segments organized in an annulus around the fovea. The inner and outer radii of this ring are 0.58 × FD and 0.78 × FD, respectively, where FD is the horizontal distance between the edge of the disc and the foveal center. The histogram for each segment is fitted with two Gaussians allowing for the separation of fundus pixels (red) and in some cases pixels from vessels (blue). The green bracket shows the range , over which GLs are integrated to yield a mean value for that segment. The GL for the optic disk is also calculated and serves as criterion to define ‘atrophy’ when analyzing retinal degenerations
A critical condition for the validity of Eq. (2.9) is that the exposure of the detector is in the linear range of the GL versus light exposure characteristics (Fig. 2.19). Non-linear behavior occurs at high GL’s because noise may cause some of the exposures to correspond to GL > 255. This ‘saturation’ can be avoided by limiting the GL’s to those indicated by curve A (the software produces pixel-size colored flashes when this occurs). Similarly, at low GL many of the GL may in fact correspond to GL < 0 (non-linearity not shown). Keeping the sensitivities higher than that shown by curve B (71) will prevent this error and insure that GL(Reference)-GL(Zero) remains above about 20. Finally, at sensitivities higher than about 91 (line C) the detector’s gain becomes extremely variable and unstable.
Variation of the fundus grey levels (GL, corrected for zero level) as a function of the fluorescence intensity measured outside the eye (last two terms of Eq. 2.1 account for intraocular parameters). The blue points represent the actual operation points for GL’s in the fundus image at about 8° from the fovea for a population of healthy eyes [58] and those with retinal dystrophies [59, 60]. Similarly grey points correspond to the levels at the fovea. Curves of constant sensitivity indicate non-linearity at high GL
4.3 Research Studies
qAF methodology has been used for normative studies [58, 61], and in investigations of patients affected by Best vitelliform macular dystrophy [60], recessive Stargardt disease [59], Bull’s eye maculopathy [62], Retinitis Pigmentosa [63], and Age related macular degeneration [64]. Additionally, studies of subjects with a monoallelic ABCA4 mutation were also reported [61, 65]. The method appears robust when the image quality is good particularly in terms of uniformity. In different studies, repeatability for two sessions on the same day varied from ±6% to 10% (95%CI) and concordance between eyes was ±13–20%. These studies have demonstrated that quantification of AF with this standardized approach can aid in assessing whether specific fundus areas in pathological conditions have normal or abnormal AF levels, in providing valuable genotype-phenotype correlations and in studying the natural history of disease progression in contrast to normal aging. However, long-term repeatability will have to be systematically investigated before longitudinal studies are undertaken.
5 Summary and Conclusion
The scanning laser ophthalmoscope has, since its invention in 1980, undergone numerous improvements and has evolved in a sophisticated and versatile imaging modality. Today, SLO imaging is a very established tool in clinical routine. Two examples, the scanning laser tomography for glaucoma diagnostics (Sect. 2.2), as well as the wide field SLO angiography and its importance for the assessment of various retinal and choroidal diseases (Sect. 2.3), have been discussed in detail. But also other SLO applications as multicolor imaging [66] and autofluorescence imaging [67] are successfully used in clinical routine for the diagnoses and progression control of various diseases as e.g. age-related macular degeneration (AMD) and hereditary macular dystrophies.
Furthermore, in many devices SLO technology is used to provide a reference image in order to actively track eye movements and thus stabilize the area of interest for other examination technologies as optical coherence tomography (OCT) (Chap. 3), OCT angiography (Chap. 6), fluorescence lifetime imaging ophthalmoscopy (FLIO, Chap. 10) and microperimetry [68].
Finally, SLO autofluorescence imaging is a very active field of research, since it visualize the distribution of intrinsic fluorophores (mainly lipofuscin components), which play an important role in the visual cycle (renewal) of photoreceptors. Therefore, the quantification of the intrinsic fluorescence as described in Sect. 2.4 can provide a better understanding of the natural history of diseases and their pathological mechanisms.
References
Maiman T. Speech by Dr. Theodore H. Maiman, Hughes Aircraft Company. 1960. at a Press Conference at the Hotel Delmonico, New York.
Webb RH, Hughes GW, Pomerantzeff O. Flying spot TV ophthalmoscope. Appl Optics. 1980;19(17):2991–7.
Webb RH, Hughes GW. Scanning laser ophthalmoscope. IEEE Trans Biomed Eng. 1981;28(7):488–92.
Plesch A, Klingbeil U, Bille J. Digital laser scanning fundus camera. Appl Optics. 1987;26(8):1480–6.
Webb RH, Hughes GW, Delori FC. Confocal scanning laser ophthalmoscope. Appl Optics. 1987;26(8):1492–9.
Bartsch D-U, et al. Confocal laser tomographic analysis of the retina in eyes with macular hole formation and other focal macular diseases. Am J Ophthalmol. 1989;108(3):277–87.
Kruse FE, et al. Reproducibility of topographic measurements of the optic nerve head with laser tomographic scanning. Ophthalmology. 1989;96(9):1320–4.
Zinser G, et al. Confocal laser tomographic scanning of the eye. In: 33rd Annual Technical Symposium. Bellingham, WA: SPIE; 1989.
Mainster MA, et al. Scanning laser ophthalmoscopy: clinical applications. Ophthalmology. 1982;89(7):852–7.
Timberlake GT, et al. Retinal localization of scotomata by scanning laser ophthalmoscopy. Invest Ophthalmol Vis Sci. 1982;22(1):91–7.
Rohrschneider K, et al. Static fundus perimetry using the scanning laser ophthalmoscope with an automated threshold strategy. Graefes Arch Clin Exp Ophthalmol. 1995;233(12):743–9.
Dreher AW, Bille JF, Weinreb RN. Active optical depth resolution improvement of the laser tomographicscanner. Appl Optics. 1989;28(4):804–8.
Gass JDM, et al. A combined technique of fluorescein funduscopy and angiography of the eye. Arch Ophthalmol. 1967;78(4):455–61.
Liang J, et al. Objective measurement of wave aberrations of the human eye with the use of a Hartmann–Shack wave-front sensor. J Opt Soc Am A. 1994;11(7):1949–57.
Liang J, Williams DR. Aberrations and retinal image quality of the normal human eye. J Opt Soc Am A. 1997;14(11):2873–83.
Niedrig H. Bergmann-Schaefer: Lehrbuch der Experimentalphysik. Optik. 1993;3:9.
McConnell G, Amos W, Wilson T. Confocal microscopy. In: Handbook of comprehensive biophysics. Amsterdam: Elsevier; 2011.
Marshall GF, Stutz GE. Handbook of optical and laser scanning. Boca Raton, FL: CRC Press; 2004.
Dickson LD. Characteristics of a propagating gaussian beam. Appl Optics. 1970;9(8):1854–61.
Scoles D, et al. In vivo imaging of human cone photoreceptor inner segments. Invest Ophthalmol Vis Sci. 2014;55(7):4244–51.
Iester M, Mikelberg FS, Drance SM. The effect of optic disc size on diagnostic precision with the heidelberg retina tomograph. Ophthalmology. 1997;104(3):545–8.
Vihanninjoki K, et al. Search for an optimal combination of structural and functional parameters for the diagnosis of glaucoma. Graefes Arch Clin Exp Ophthalmol. 2000;238(6):477–81.
Ferreras A, et al. Discriminating between normal and glaucoma-damaged eyes with the heidelberg retina tomograph 3. Ophthalmology. 2008;115(5):775–781.e2.
Iester M, et al. Comparison between discriminant analysis models and “glaucoma probability score” for the detection of glaucomatous optic nerve head changes. J Glaucoma. 2008;17(7):535–40.
Miglior S, et al. Intraobserver and interobserver reproducibility in the evaluation of optic disc stereometric parameters by Heidelberg Retina Tomograph. Ophthalmology. 2002;109(6):1072–7.
Wollstein G, Garway-Heath DF, Hitchings RA. Identification of early glaucoma cases with the scanning laser ophthalmoscope. Ophthalmology. 1998;105(8):1557–63.
Chauhan BC, et al. Technique for detecting serial topographic changes in the optic disc and peripapillary retina using scanning laser tomography. Invest Ophthalmol Vis Sci. 2000;41(3):775–82.
Mikelberg FS, Wijsman K, Schulzer M. Reproducibility of topographic parameters obtained with the heidelberg retina tomograph. J Glaucoma. 1993;2:101.
Zangwill LM, et al. Discriminating between normal and glaucomatous eyes using the heidelberg retina tomograph, GDx nerve fiber analyzer, and optical coherence tomograph. Arch Ophthalmol. 2001;119(7):985–93.
Chauhan BC, et al. Optic disc and visual field changes in a prospective longitudinal study of patients with glaucoma: comparison of scanning laser tomography with conventional perimetry and optic disc photography. Arch Ophthalmol. 2001;119(10):1492.
Chauhan BC, Nicolela MT, Artes PH. Incidence and rates of visual field progression after longitudinally measured optic disc change in glaucoma. Ophthalmology. 2009;116(11):2110–8.
Flower RW, Hochheimer BF. A clinical technique and apparatus for simultaneous angiography of the separate retinal and choroidal circulations. Invest Ophthalmol Vis Sci. 1973;12(4):248–61.
Patel RD, et al. Characterization of ischemic index using ultra-widefield fluorescein angiography in patients with focal and diffuse recalcitrant diabetic macular edema. Am J Ophthalmol. 2013;155(6):1038–1044.e2.
Wessel MM, et al. Peripheral retinal ischaemia, as evaluated by ultra-widefield fluorescein angiography, is associated with diabetic macular oedema. Br J Ophthalmol. 2012;96(5):694–8.
Kimble JA, Brandt BM, McGwin G Jr. Clinical examination accurately locates capillary nonperfusion in diabetic retinopathy. Am J Ophthalmol. 2005;139(3):555–7.
Group, E.T.D.R.S.R. Early treatment diabetic retinopathy study design and baseline patient characteristics: ETDRS report number 7. Ophthalmology. 1991;98(5):741–56.
Stefánsson E. The therapeutic effects of retinal laser treatment and vitrectomy. A theory based on oxygen and vascular physiology. Acta Ophthalmol Scand. 2001;79(5):435–40.
Spranger J, et al. Release of the angiogenesis inhibitor angiostatin in patients with proliferative diabetic retinopathy: association with retinal photocoagulation. Diabetologia. 2000;43(11):1404–7.
Prasad PS, et al. Ultra wide-field angiographic characteristics of branch retinal and hemicentral retinal vein occlusion. Ophthalmology. 2010;117(4):780–4.
Jabs DA, et al. Standardization of uveitis nomenclature for reporting clinical data. Results of the First International Workshop. Am J Ophthalmol. 2005;140(3):509–16.
Reeves GM, et al. Use of Staurenghi lens angiography in the management of posterior uveitis. Acta Ophthalmol. 2013;91(1):48–51.
von Rückmann A, Fitzke FW, Bird AC. Distribution of fundus autofluorescence with a scanning laser ophthalmoscope. Br J Ophthalmol. 1995;119:543–62.
Solbach U, et al. Imaging of retinal autofluorescence in patients with age-related macular degeneration. Retina. 1997;17(5):385–9.
Lois N, Forrester JV, editors. Fundus autofluorescence. 2nd ed. Philadelphia, PA: Wolters Kluewer; 2016.
Delori FC, et al. In vivo fluorescence of the ocular fundus exhibits retinal pigment epithelium lipofuscin characteristics. Invest Ophthalmol Vis Sci. 1995;36:718–29.
Sparrow JR, et al. A2E, a byproduct of the visual cycle. Vision Res. 2003;43(28):2983–90.
Sparrow JR, et al. The bisretinoids of retinal pigment epithelium. Prog Retin Eye Res. 2012;31(2):121–35.
Morgan JI, et al. Light-induced retinal changes observed with high-resolution autofluorescence imaging of the retinal pigment epithelium. Invest Ophthalmol Vis Sci. 2008;49(8):3715–29.
Spaide RF. Fundus autofluorescence and age-related macular degeneration. Ophthalmology. 2003;110(2):392–9.
Lakowicz JR. Principles of fluorescence spectroscopy. 2nd ed. New York, NY: Kluwer Academic. Plenum Publishers; 1999.
Arend OA, et al. In-vivo fundus-fluoreszenz-messungen bei patienten mit alterabhangiger makulardegeneration. Ophthalmologie. 1995;92:647–53.
Delori F, et al. Quantitative measurements of autofluorescence with the scanning laser ophthalmoscope. Invest Ophthalmol Vis Sci. 2011;52(13):9379–90.
Schmitz-Valckenberg S, et al. How to obtain the optimal fundus autofluorescence image with the confocal scanning laser ophthalmoscope. In: Holz F, et al., editors. Atlas of fundus autofluorescence imaging. Berlin; New York, NY: Springer; 2007. p. 37–47.
Delori FC, Duncker T, Sparrow JR. Quantitative autofluorescence: the measurement of fundus autofluorescence levels. In: Lois N, Forrester JV, editors. Fundus autofluorescence. Philadelphia, PA: Wolters Kluewer; 2016.
van de Kraats J, van Norren D. Optical density of the aging human ocular media in the visible and the UV. J Opt Soc Am A Opt Image Sci Vis. 2007;24(7):1842–57.
Delori FC. et al. Supplementary material. Quantitative measurements of autofluorescence with the scanning laser ophthalmoscope; 2011. http://www.iovs.org/lookup/suppl/doi:10.1167/iovs.11-8319/-/DCSupplemental.
Delori FC, Goger DG, Dorey CK. Age-related accumulation and spatial distribution of lipofuscin in RPE of normal subjects. Invest Ophthalmol Vis Sci. 2001;42(8):1855–66.
Greenberg JP, et al. Quantitative fundus autofluorescence in healthy eyes. Invest Ophthalmol Vis Sci. 2013;54(8):5684–93.
Burke TR, et al. Quantitative fundus autofluorescence in recessive stargardt disease. Invest Ophthalmol Vis Sci. 2014;55:2841.
Duncker T, et al. Quantitative fundus autofluorescence and optical coherence tomography in best vitelliform macular dystrophy. Invest Ophthalmol Vis Sci. 2014;55(3):1471–82.
Muller PL, et al. Monoallelic ABCA4 mutations appear insufficient to cause retinopathy: a quantitative autofluorescence study. Invest Ophthalmol Vis Sci. 2015;56(13):8179–86.
Duncker T, et al. Quantitative fundus autofluorescence distinguishes ABCA4-associated and non-ABCA4-associated bull’s-eye maculopathy. Ophthalmology. 2015;122(2):345–55.
Schuerch K, et al. Quantifying fundus autofluorescence in patients with retinitis pigmentosa. Invest Ophthalmol Vis Sci. 2017;58(3):1843–55.
Gliem M, et al. Quantitative fundus autofluorescence in early and intermediate age-related macular degeneration. JAMA Ophthalmol. 2016;134(7):817–24.
Duncker T, et al. Quantitative fundus autofluorescence and optical coherence tomography in ABCA4 carriers. Invest Ophthalmol Vis Sci. 2015;56(12):7274–85.
Tan AC, et al. Clinical application of multicolor imaging technology. Ophthalmologica. 2016;236(1):8–18.
Schmitz-Valckenberg S, et al. Fundus autofluorescence imaging: review and perspectives. Retina. 2008;28(3):385–409.
Varano M, Scassa C. Scanning laser ophthalmoscope microperimetry. Semin Ophthalmol. 1998;13(4):203–9.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Fischer, J., Otto, T., Delori, F., Pace, L., Staurenghi, G. (2019). Scanning Laser Ophthalmoscopy (SLO). In: Bille, J. (eds) High Resolution Imaging in Microscopy and Ophthalmology. Springer, Cham. https://doi.org/10.1007/978-3-030-16638-0_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-16638-0_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-16637-3
Online ISBN: 978-3-030-16638-0
eBook Packages: MedicineMedicine (R0)