Aquaponics Systems Modelling

Abstract

Mathematical models can take very different forms and very different levels of complexity. A systematic way to postulate, calibrate and validate, as provided by systems theory, can therefore be very helpful. In this chapter, dynamic systems modelling of aquaponic (AP) systems, from a systems theoretical perspective, is considered and demonstrated to each of the subsystems of the AP system, such as fish tanks, anaerobic digester and hydroponic (HP) greenhouse. It further shows the links between the subsystems, so that in principle a complete AP systems model can be built and integrated into daily practice with respect to management and control of AP systems. The main challenge is to choose an appropriate model complexity that meets the experimental data for estimation of parameters and states and allows us to answer questions related to the modelling objective, such as simulation, experiment design, prediction and control.

1 Introduction

In general, mathematical models can take very different forms depending on the system under study, which may range from social, economic and environmental to mechanical and electrical systems. Typically, the internal mechanisms of social, economic or environmental systems are not very well known or understood and often only small data sets are available, while the prior knowledge of mechanical and electrical systems is at a high level, and experiments can easily be done. Apart from this, the model form also strongly depends on the final objective of the modelling procedure. For instance, a model for process design or simulation should contain much more detail than a model used for studying different long-term scenarios.

In particular, for a wide range of applications (e.g. Keesman 2011), models are developed to:

• Obtain or enlarge insight in different phenomena, for example, recovering physical or economic relationships.

• Analyse process behaviour using simulation tools, for example, process training of operators or weather forecasts.

• Estimate state variables that cannot be easily measured in real time on the basis of available measurements, for instance, online process information.

• Control, for instance, in the internal model control or model-based predictive control concept or to manage processes.

A critical step in the modelling of any system is to find a mathematical model which adequately describes the actual situation or state. Firstly, the system boundaries and the system variables have to be specified. Then relationships between these variables have to be specified on the basis of prior knowledge, and assumptions about the uncertainties in the model have to be made. Combining this information defines the model structure. Still the model may contain some unknown or incompletely known coefficients, the model parameters, which in case of time-varying behaviour define an additional set of system variables. For a general introduction to mathematical modelling we refer to, for instance, Sinha and Kuszta (1983), Willems and Polderman (1998) and Zeigler et al. (2000).

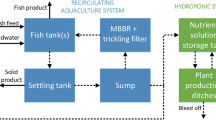
In this chapter, the modelling of an aquaponic (food) production (AP) system will be described. Figure 11.1 shows a typical example of an AP system, i.e. the so-called decoupled three-loop aquaponic system. As a result of basic principles modelling, using conservation laws and constitutive relationships, mathematical models of all kinds of AP systems are usually represented as a set of ordinary or partial differential equations. These mathematical models are commonly used for design, estimation and control. In each of these specific modelling objectives, we distinguish between analysis and synthesis.

Fig. 11.1

Decoupled, three-loop aquaponic system with RAS, hydroponic and remineralization subsystems. (Goddek, 2017)

The outline of the chapter is as follows. In Sect. 11.1 some background on mathematical systems modelling is presented. Sections 11.2, 11.3, 11.4 and 11.5 describe the modelling of a recirculating aquaculture system (RAS), anaerobic digestion, hydroponic (HP) greenhouse and a multi-loop AP system, respectively. In Sect. 11.6 modelling tools are introduced and illustrated with some examples. The chapter concludes with a Discussion and Conclusions section.

2 Background

Many definitions of a system are available, ranging from loose descriptions to strict mathematical formulations. In what follows, a system is considered to be an object in which different variables interact at all kinds of time and space scales and that produces observable signals. These types of systems are also called open systems. A graphical representation of a general open system (S) with vector-valued input and output signals is represented in Fig. 11.2. Thus, multiple inputs or outputs are combined in one single arrow. So, the system variables may be scalars or vectors. In addition, they can be continuous or discrete functions of time. It is important to stress that the arrows in Fig. 11.2 represent signal flows and thus not necessarily physical flows.

Fig. 11.2

General open system representation

It is also possible to connect systems into a network, as in an AP system, with parallel, feedback and feedforward paths. Figure 11.3 presents an example of such a network.

Fig. 11.3

Open system network representation

For controller/management analysis and synthesis, it is often convenient to connect the system (S) to the controller or management strategy (C), as in Fig. 11.4. Most often the input to the controller or management strategy is the external steering signal of the controlled system, and the output of the system is the observed system’s behaviour.

Fig. 11.4

Controlled system

Finally, to emphasize the incorporation of a mathematical model (M) into the controller structure or management strategy, the following model-based controlled system representation is introduced (Fig. 11.5).

Fig. 11.5

Model-based controlled system

For now, it suffices to present the block diagram representation. In subsequent sections, the modelling of AP systems will be worked out in more detail.

In systems theory the basic structure of a mathematical model (M) is schematically represented as in Fig. 11.6. In Fig. 11.6, x is the so-called state of the system, u the control input, y the output, w the disturbance input and v the output noise. In general, each of these variables is vector-valued.

Fig. 11.6

Basic structure of mathematical model (M)

In continuous time, the following set of equations describes a general dynamic model (M), with parameter vector p, in what is called state-space form:

$$ {\displaystyle \begin{array}{l}\frac{dx(t)}{dt}=f\left(t,x(t),u(t),w(t);p\right),\kern2em x(0)={x}_0\\ {}y(t)=g\left(t,x(t),u(t);p\right)+v(t),\kern2em t\in {\Re}^{+}\end{array}} $$

(11.1)

where the first equation describes the nonlinear and time-varying dynamics of the system in terms of state variables (x) and the second one expresses the algebraic relationship between u, x and y. This state-space model representation has been a starting point for many software implementations for design, control and estimation. In what follows, however, only deterministic models, thus without the stochastic vectors v and w, are considered. Let us illustrate this theory on a fish tank system.

Example: Fish Tank System

Consider the following fish tank, which is a typical example of the general system presented in Fig. 11.7.

Fig. 11.7

Fish tank with volume-controlled flow using level controller (LC)

Let us start with specifying our prior knowledge of the internal system mechanisms. The following mass balance can be defined in terms of the volume of the storage tank (V), also called the state of the system, inflows u(t) and outflows y(t):

$$ \frac{dV(t)}{dt}=u(t)-y(t) $$

(11.2)

Suppose there is a level controller (LC) that keeps the outflow proportional to the volume in the tank. This can be enforced by implementing the following proportional control law,

$$ Y(t)= KV(t) $$

(11.3)

with K a real, positive constant. Hence, after substituting Eq. (11.3) into (11.2), we obtain the following differential equation

$$ \frac{dV(t)}{dt}+ KV(t)=u(t) $$

(11.4)

For this specific linear differential equation with constant coefficients, an analytical solution exists and is given by

$$ y(t)=y(0){e}^{- Kt}+{\int}_0^t{Ke}^{-K\left(t-s\right)}u(s) ds $$

(11.5)

under the assumption that u(t) = 0 for t < 0. From this example it is clear that applying first principles – mass conservation in this case – directly leads to an ordinary differential equation. In state-space format, the model can be represented as

$$ {\displaystyle \begin{array}{l}\frac{dx(t)}{dt}=- Kx(t)+u(t)\\ {}y(t)= Kx(t)\end{array}} $$

(11.6)

With x volume, u flow input and K controller gain. Thus, in terms of the general state-space Eq. (11.1), f(t, x(t), u(t); p) ≡  − Kx(t) + u(t) and g(t, x(t), u(t); p) ≡ Kx(t).

For two volume-controlled fish tanks in series with volume V ₁ and V ₂, and controller gain K ₁ and K ₂, respectively, two mass balances can be formulated, i.e.

$$ {\displaystyle \begin{array}{l}\frac{dV_1(t)}{dt}=-{K}_1{V}_1(t)+u(t)\\ {}\frac{dV_2(t)}{dt}={K}_1{V}_1(t)-{K}_2{V}_2(t)\end{array}} $$

(11.7)

In vector-matrix form, and for physical outflow y(t), we can write:

$$ {\displaystyle \begin{array}{c}\frac{d}{dt}\left[\begin{array}{l}{V}_1(t)\\ {}{V}_2(t)\end{array}\right]=\left[\begin{array}{cc}-{K}_1& 0\\ {}{K}_1& -{K}_2\end{array}\right]\left[\begin{array}{l}{V}_1(t)\\ {}{V}_2(t)\end{array}\right]+\left[\begin{array}{l}1\\ {}0\end{array}\right]u(t)\\ {}\kern-8.25em y(t)={K}_2{V}_2(t)\end{array}} $$

(11.8)

And thus, with x ₁ = V ₁,x ₂ = V ₂: $f\left(t,x(t),u(t);p\right)\equiv \left[\begin{array}{l}-{K}_1{x}_1(t)+u(t)\\ {}{K}_1{x}_1(t)-{K}_2{x}_2(t)\end{array}\right]$ and g(t, x(t), u(t); p) ≡ K ₂x ₂(t).

In the next sections, each of the subsystems of the AP system (Fig. 11.1) will be described in more detail.

3 RAS Modelling

Global fish aquaculture reached 50 million tons in 2014 (FAO 2016). Given the growing human population, there is a growing demand for fish proteins. Sustainable growth of aquaculture requires novel (bio)technologies such as recirculating aquaculture systems (RAS). RAS have a low water consumption (Orellana 2014) and allow for a recycling of excretory products (Waller et al. 2015). RAS provide suitable living conditions for fish, as a result of a multistep water treatment, such as particle separation, nitrification (biofiltration), gas exchange and temperature control. Dissolved and particulate excretory products can be transferred to secondary treatment such as plant (Waller et al. 2015) or algae production in integrated aqua-agriculture (IAAC) systems. IAAC systems are sustainable alternatives to conventional aquaculture systems and in particular are a promising expansion to RAS. In RAS it would be necessary to circulate the process water which has special implications for the process technology in both, the RAS and the algae/plant system. To combine RAS and algae/plant system, a deep understanding of the interaction between fish and water treatment is prerequisite and can be derived from dynamic modelling. The metabolism in fish follows a daily pattern which is well represented by the gastric evacuation rate (Richie et al. 2004). Particle separation, biofiltration and gas exchange are subjected to the same pattern. For design purposes the characterization of the basic components of a RAS treatment system should be investigated through simulation models. These simulation models are highly complex. Available numerical models for RAS capture only a small part of the complexity and consider only a part of the components with corresponding mechanisms. Hence, in this chapter, only a small part of a dynamic RAS model will be presented, i.e. nitrification-based biofiltration. The conversion of toxic ammonia into nitrate is a central process in the water treatment process in RAS. In the following, the dynamic modelling of the mass balance of ammonia excretion of fish and the conversion of ammonia into nitrate will be demonstrated as well as the transfer of the nutrient into an aquaponic system. With this it is possible not only to engineer a RAS but also to integrate fish production into an IAAC system based on valid parameters.

3.1 Dynamic Model of Nitrification-Based Biofiltration in RAS

The model is subdivided into a fish model for European seabass, Dicentrarchus labrax, a model describing the time- dependenting excretion of ammonia, and a nitrification model (Fig. 11.8). The fish excretion pattern is introduced into the model through the input vector u (Eq. 11.15), similar to the approach used by Wik et al. (2009). The complexity of the fish model is kept low to be able to explain its method of implementation. Nonetheless, a short introduction into modelling fish is presented in Sect. 11.3.2. Four basic aspects important to describe the nutrient flow in RAS (Badiola et al. 2012) are:

• 1. The flow Q, which is the total process water flow per unit time through the RAS, determines the mass transfer of all dissolved and particulate matter, including ammonia and nitrate.

• 2. The excretion of the fish input ammonia to the RAS process water and is depicted by the product of matrix B and vector u (Eq. 11.15).

• 3. The ammonia conversion into nitrate, taking place in the nitrification, is depicted in the nitrification vector n (Eq. 11.15).

• 4. The nutrient transfer from the RAS to a connected HP system is depicted in vector u (Eq. 11.15). Other important aspects of the RAS process chain such as solid removal, dissolved oxygen concentration and carbon dioxide concentration are not considered here. Hints for modelling these can be found in Sects. 3.1.1 and 3.2.2 of this book.

Fig. 11.8

RAS setup with fish tank, pump, nitrification reactor and water transfer to hydroponic system

3.2 Fish

A variety of models in the scientific literature predict growth and feed intake of different aquatic species. The models describe growth as weight gain per day, as percentage growth increment or as specific growth rate based on an exponential growth model. Models are often valid for specific life stages. Feed consumption, biomass and gender are influencing the model output as well as the environmental conditions such as temperature, oxygen level and nutrient concentration (Lugert et al. 2014). Careful research is needed to identify the correct model used for the specific application. Commercial RAS that consists of several cohorts of fish in different life stages require the modelling to incorporate cohorts into the model (Fig. 8.6) (Halamachi and Simon 2005). The excretory mass flow for the European seabass (Dicentrarchus labrax) can be estimated with algorithms published by Lupatsch and Kissil (1998).

Here the net nitrogen mass flow into the process water is estimated from the feed composition (protein content), the amount of given feed and the nitrogen retained in body tissues through the growth (weight increment) of fish. The faecal nitrogen losses are not included in the model, but excretion rate is corrected assuming a share of 0.25 and 0.75 of nitrogen excretion for faecal loss and ammonia excretion, respectively. The nitrogen input through the feeding of fish is estimated from the protein content and the average relative nitrogen content of proteins which is assumed to be 0.16. The protein content of seabass tissue is reported at around 0.17 g proteins g⁻¹ seabass (Lupatsch et al. 2003). For a fish gaining body weight by consuming a given amount of feed, the nitrogen excretion (X_N,excreted, g) can be calculated from Eq. (11.9). It is assumed that the feed (X_feed) contains 0.5 g protein g⁻¹ fish. It is further assumed that the feed conversion rate equals 1, i.e. 1 g of feed consumption is resulting in 1 g of body weight increase (Fig. 11.9):

Fig. 11.9

Representation of the mass flows (Sankey chart) of feed ingredients and excretory products for a fish consuming 1000 g of feed assuming an FCR of 1

$$ {X}_{N,\mathrm{excreted}}={X}_{\mathrm{feed}}\ast 0.16\ast 0.75\ast \left(0.5-0.17\right) $$

(11.9)

Dissolved ammonia excreted via the gills of fish follows similar daily pattern as the gastric evacuation rate (GER). GER is described for cold water and warm water fish by He and Wurtsbaugh (1993) and Richie et al. (2004), respectively. The excretory pattern can be well simulated with a sine function. The ammonia excretion can be calculated from Eq. (11.10):

$$ {X}_{{\mathrm{NH}}_x-N,\mathrm{excreted}}={X}_{N,\mathrm{excreted}}\;\left[g\right]\ast \left(\sin \left(\frac{2\pi }{1440}\right)+1\right) $$

(11.10)

3.3 RAS

A variety of models describing RAS having different levels of complexity can be found in the literature. Very complex models are available for specific aspects, such as the interaction of soluble gases and alkalinity (Colt 2013) or the description of the microbial community (Henze et al. 2002). More practical models for the mass balance of RAS are published by Sánchez-Romero et al. (2016), Pagand et al. (2000), Wik et al. (2009) and Weatherley et al. (1993). All models provide information on excretory mass flows and/or nutrient flows in dependence of time and location in the process chain. Such models provide a base for the simulation of the coupling of RAS and HP. The most important dissolved matter in RAS modelling is total ammonia nitrogen (TAN). Besides TAN the chemical (COD) and biological (BOD) oxygen demand, the total suspended solids (TSS) and dissolved oxygen concentration need to be considered. However, different notations in the scientific literature make it sometimes hard to read, to convert and to implement the information into models. In the following, notations as recommended by Corominas et al. (2010) will be used. TAN will be rewritten as X_NHx-N and nitrate nitrogen will be expressed as X_NO3-N.

3.4 Model Example

The model as it is described in the following is only valid for the RAS presented in Fig. 11.8. Other possible process chains for RAS are discussed in Sect. 11.3 of this chapter. For the mathematical depiction of physical systems, the following assumptions were made:

• (a) Density of water is assumed to be constant.

• (b) Tank and reactor are assumed to be well mixed.

• (c) Tank and reactor volume are assumed to be constant.

• (d) Process water flow is always greater than zero.

The assumption of a well-mixed tank and reactor leads to a mass balance equation for continuous stirred-tank reactor (CSTR) as described by Drayer and Howard (2014) in Eq. (11.11). It must be mentioned that diffusive processes can usually be neglected in RAS calculations because of a typically high process water flow rate. For a multi-tank RAS, the following holds:

$$ {\displaystyle \begin{array}{c}\mathrm{Accumulation}=\mathrm{Inflow}\hbox{--} \mathrm{outflow}+\mathrm{generation}\hbox{--} \mathrm{reduction}\\ {}{V}_i{\dot{x}}_i={Q}_{\mathrm{in}}{x}_{i,\mathrm{in}}-{Q}_{\mathrm{out}}{x}_{i,\mathrm{out}}+{x}_{i,\mathrm{gen}}-{x}_{i,\mathrm{red}}\\ {}j=\left\{\begin{array}{cc}n,& i=1\\ {}i-1,& i\ne 1\end{array}\right.\end{array}} $$

(11.11)

In the above given equation n represents the number of tanks in the System, ${\dot{x}}_i$ is the change of concentration of a given substrate x in a volume given by V _i.. The process water flow into the tank or reactor is represented by Q _in. V _i is the volume of the component where the process water flow Q _in is entering in. The process water flow Q _in came from a component having the volume V _j.

The conversion of X_NHx-N into X_NO3-N in nitrifying biofilters takes place on the surface area A [m²] available on the bio-carriers in the nitrification reactor (Rusten 2006). The available bioactive surface in the nitrification is calculated by multiplying the volume of the reactor with the volume-specific active surface of the bio-carriers A_S [m²· m⁻³]. The total bioactive surface is calculated (Eq. 11.12) from the relative filling f_bc of the nitrification reactor which usually is 0.6 (for details, see Rusten 2006).

$$ \mathrm{A}={\mathrm{V}}_{\mathrm{nitrification}}\ast {\mathrm{A}}_{\mathrm{S}}\ast {\mathrm{f}}_{\mathrm{bc}} $$

(11.12)

The total daily TAN microbial conversion μ_max [g d⁻¹] (nitrification) was calculated by multiplying the specific TAN conversion (nitrification) rate, NHx_{conversion-rate} [g m⁻² d⁻¹], with the total active surface area, A [m²], of the bio-carriers. Values for TAN conversion in different types of nitrifying biofilters can be found in literature. For moving bed biofilm reactors (MBBR), values are reported by Rusten (2006). This rate is valid for certain process conditions, and it is assumed that the bacteria biofilm is fully developed over the whole.

$$ {\upmu}_{\mathrm{mm}}={\mathrm{A}}^{\ast }{\mathrm{NHx}}_{\mathrm{Conversion}-\mathrm{rate}} $$

(11.13)

The total mass of NH_x converted into NO₃-N can subsequently be calculated with a Monod kinetic (Eq. 11.14). For this the NH_x-N concentration, X_NHx-N,2 [g · l⁻¹], in the volume of the nitrification reactor (MBBR) V ₂, is needed.

$$ {\displaystyle \begin{array}{l}\frac{d}{dt}{X}_{{\mathrm{N}\mathrm{H}}_x-\mathrm{N},2}=-{\upmu}_{\mathrm{max}}\ast \left(\frac{X_{{\mathrm{N}\mathrm{H}}_x-\mathrm{N},2}}{K_s+{X}_{{\mathrm{N}\mathrm{H}}_x-\mathrm{N},2}}\right)\ast \frac{1}{V_2}\kern1em \mathrm{with}\kern1em {\mathrm{K}}_{\mathrm{s}}=\frac{\upmu_{\mathrm{max}}}{2}\\ {}\frac{d}{dt}{X}_{\mathrm{N}{0}_{\mathrm{s}}-\mathrm{N},2}=+{\upmu}_{\mathrm{max}}\ast \left(\frac{X_{{\mathrm{N}\mathrm{H}}_x-\mathrm{N},2}}{K_s+{X}_{{\mathrm{N}\mathrm{H}}_x-\mathrm{N},2}}\right)\ast \frac{1}{V_2}\kern1em \mathrm{with}\kern1em {\mathrm{K}}_{\mathrm{s}}=\frac{\upmu_{\mathrm{max}}}{2}\end{array}} $$

(11.14)

Given Eqs. (11.9, 11.10, 11.11, 11.12, 11.13 and 11.14), the following state-space model (combining fish-nitrification) results

$$ {\displaystyle \begin{array}{l}\kern8em \frac{dx(t)}{dt}={\boldsymbol{A}}^{\ast}\boldsymbol{X}+{\boldsymbol{B}}^{\ast}\boldsymbol{u}+\boldsymbol{n}\\ {}\boldsymbol{X}=\left[\begin{array}{l}{X}_{{\mathrm{NH}}_x-\mathrm{N},1}\\ {}{X}_{{\mathrm{NH}}_x-\mathrm{N},2}\\ {}{X}_{{\mathrm{NO}}_3-\mathrm{N},1}\\ {}{X}_{{\mathrm{NO}}_3-\mathrm{N},2}\end{array}\right]\kern1em \boldsymbol{u}=\left[\begin{array}{c}{X}_{{\mathrm{NH}}_x-\mathrm{N},\mathrm{excreted}}\\ {}\mathbf{0}\\ {}{{\boldsymbol{Q}}_{\mathbf{Exc}}}^{\ast }{X}_{{\mathrm{NH}}_x-\mathrm{N},\mathrm{hydroponics}}\\ {}\mathbf{0}\end{array}\right]\kern1em \boldsymbol{n}=\left[\begin{array}{c}\mathbf{0}\\ {}-\frac{\upmu_{\mathbf{max}}\ast {\left[\boldsymbol{X}\right]}_2}{{\boldsymbol{K}}_{\boldsymbol{s}}+{\left[\boldsymbol{X}\right]}_2}\ast \frac{1}{{\boldsymbol{V}}_2}\\ {}\mathbf{0}\\ {}+\frac{\upmu_{\boldsymbol{max}}\ast {\left[\boldsymbol{X}\right]}_2}{{\boldsymbol{K}}_{\boldsymbol{s}}+{\left[\boldsymbol{X}\right]}_2}\ast \frac{1}{{\boldsymbol{V}}_2}\end{array}\right]\\ {}A=\left[\begin{array}{cccc}-\frac{Q}{V_1}-\frac{Q_{\mathrm{Exc}}}{V_1}& \frac{Q}{V_1}& 0& 0\\ {}\frac{Q}{V_2}& -\frac{Q}{V_2}& 0& 0\\ {}0& 0& -\frac{Q}{V_1}-\frac{Q_{\mathrm{Exc}}}{V_1}& \frac{Q}{V_1}\\ {}0& 0& \frac{Q}{V_2}& -\frac{Q}{V_1}\end{array}\right]\\ {}\times B=\left[\begin{array}{cccc}\frac{1}{V_1}& 0& 0& 0\\ {}0& \frac{1}{V_2}& 0& 0\\ {}0& 0& \frac{1}{V_1}& 0\\ {}0& 0& 0& \frac{1}{V_2}\end{array}\right]\end{array}} $$

(11.15)

Example

In this example, a theoretical RAS with V_reactor = 1300 l and V_tank = 6000 l is simulated.

All simulations had a daily feed input of 2000 g/day with 500 g protein/kg feed (Eq. 11.8). The daily TAN excretion was assumed to be a sine curve (Eq. 11.9). Active surface of the bio-carriers A_S is 300 [m² m⁻³], and the relative filling of the reactor f_bc is 0.6. Specific TAN conversion rate, NHx_{conversion-rate}, is 1.2 [g m^{−2 −}d], and the biofilm is supposed to be fully developed (Eqs. 11.11 and 11.12). The state-space representation (Eq. 11.14) was implemented in MATLAB Simulink. The Example showcases the importance of mass flow for nutrient concentrations in coupled systems (Fig. 11.10 and 11.11).

Fig. 11.10

Simulation of TAN (X_NHx-N,1) in [mg/l] over 2 days = 2880 min with Q = 300 l/min (blue) and Q = 200 l/min (orange)

4 Modelling Anaerobic Digestion

Anaerobic digestion (AD) of organic material is a process that involves the sequential steps of hydrolysis, acidogenesis, acetogenesis and methanogenesis (Batstone et al. 2002). The anaerobic digestion of a mixture of proteins, carbohydrates and lipids is visualized in Figure 11.11. Most often, hydrolysis is considered as the rate-limiting step in the anaerobic digestion of complex organic matter (Pavlostathis and Giraldo-Gomez 1991). Thus, increasing the hydrolysis reaction rate will most likely lead to a higher anaerobic digestion reaction rate. However, increasing the reaction rates needs further understanding of the related process. Further understanding can be obtained via experimentation and/or mathematical modelling. As there are many factors influencing, for instance, the hydrolysis process, such as ammonia concentration; temperature; substrate composition; particle size; pH; intermediates; degree of hydrolysis; i.e. the potential of hydrolysable content; and residence time, it is almost impossible to evaluate the total effect of the factors on the hydrolysis reaction rate through experimentation. Mathematical modelling could therefore be an alternative, but as a result of all the uncertainties in model formulation, rate coefficients and initial conditions, no unique answers can be expected. But, a mathematical modelling framework would allow sensitivity and uncertainty analyses to facilitate the modelling process. As mentioned before, hydrolysis is just one of the steps in anaerobic digestion. Consequently, understanding and optimization of the full anaerobic digestion process needs connections from hydrolysis to the other processes taking place during anaerobic digestion and interactions between all these steps.

Fig. 11.11

Simulation of nitrate-N (X_NO3-N,1) in [mg/l] over 50 days = 72,000 min with Q_Exc = 300 l/day (yellow), Q_Exc = 480 l/day (orange) and Q_Exc = 600 l/day (blue)

The well-known and widely used ADM1 (anaerobic digestion model #1) is a structured model including disintegration and hydrolysis, acidogenesis, acetogenesis and methanogenesis steps. Disintegration and hydrolysis are two extracellular steps. In the disintegration step, composite particulate substrates are converted into inert material, particulate carbohydrates, protein and lipids. Subsequently, the enzymatic hydrolysis step decomposes particulate carbohydrates, protein and lipids to monosaccharides, amino acids and long-chain fatty acids (LCFA), respectively (Batstone et al. 2002) (see Fig. 11.12).

Fig. 11.12

A simplified scheme for the anaerobic digestion of complex particulate organic matter. (based on El-Mashad 2003)

ADM1 is a mathematical model that describes the biological processes and physicochemical processes of anaerobic digestion as a set of differential and algebraic equations (DAE). The model contains 26 dynamic state variables in terms of concentrations, 19 biochemical kinetic processes, 3 gas-liquid transfer kinetic processes and 8 implicit algebraic variables for each process unit. As an alternative, Galí et al. (2009) described the anaerobic process as a set of differential equations with 32 dynamic state variables in terms of concentrations and an additional 6 acid-base kinetic processes per process unit. For an overview of the modelling of anaerobic digestion processes, we refer to Ficara et al. (2012). However, in what follows and for some first insights into the AD process, we will present a simple nutrient-balance model of AD in a sequencing batch reactor (SBR).

4.1 Nutrient Mineralization

The nutrient mineralization can be calculated using the following equation (Delaide et al. 2018):

$$ \mathrm{NR}=100\%\times \left(\frac{{\mathrm{DN}}_{\mathrm{out}}-{\mathrm{DN}}_{\mathrm{in}}}{{\mathrm{TN}}_{\mathrm{in}}-{\mathrm{DN}}_{\mathrm{in}}}\right) $$

(11.15a)

where NR is the nutrient recovery at the end of the experiment in percent, DN_out is the total mass of dissolved nutrient in the outflow, DN_in is the total mass of dissolved nutrient in the inflow and TN_in is the total mass of dissolved plus undissolved nutrients in the inflow (see also Fig. 11.13).

Fig. 11.13

Overall reactor scheme for determining the mineralization potential, where DN are the dissolved nutrients in the water, UN the undissolved nutrients in the sludge (i.e. TN-DN) and TN the total nutrients

4.2 Organic Reduction

The organic reduction performance of the reactor can be calculated using the following equation:

$$ {\eta}_{\mathrm{OM}}=1-\frac{\varDelta \mathrm{OM}+{T}_{\mathrm{OM}\kern0.5em \mathrm{out}}}{T_{\mathrm{OM}\kern0.5em \mathrm{in}}} $$

(11.15b)

where ΔOM is the organic matter (i.e. COD, TS, TSS, etc.) inside the reactor at the end of the experiment minus the one at the beginning of the experiment, T_{OM out} is the total OM outflow and T_{OM in} is the total OM inflow (see also Fig. 11.14).

Fig. 11.14

Overall reactor scheme for determining the organic material reduction potential, where T_OM is the total organic matter and ΔOM the change of organic matter inside the reactor

5 HP Greenhouse Modelling

The crop water use and nutrient uptake is a central subsystem of aquaponics. The HP part is complex, as pure uptake of water and dissolved nutrients do not simply follow a rather simple linear relationship as, e.g. fish growth. To create a full-functional model, a complete greenhouse simulator is needed. This involves sub-model systems of greenhouse physics including climate controllers and crop biology covering interactive processes with biological and physical stressors.

However, from the HP point of view, greenhouse climate is the main driver for the complete aquaponic system, including, next to the nutrient balances, feedback loops of heat produced by the fish and additional CO₂ supplied to the plants as reported by Körner et al. (2017) (Fig. 11.15).

Fig. 11.15

Additional symbiotic behaviour of an aquaponic system

In this model, the fish culture produces heat through metabolic processes. The amount of heat produced by the fish is directly calculated from oxygen consumption that is a function of temperature and a constant for heat production for one unit oxygen consumed (i.e. 13608 J g⁻¹ fish). Heat from breakdown of organic matter (Q_bio), e.g. faeces and feed remain, is also contributing to the heat balance. Energy supply to the water system can then be calculated by heat production through the fish calculated from an average oxygen consumption rate (f_O2,Twb). Additional heat production can then be calculated by biological breakdown of faeces (Fig. 11.16).

Fig. 11.16

Aquaculture system implemented in the greenhouse with humidity, temperature and CO2 concentrations of the air (RH_air T_air, CO_2,air), heat from (Q) fish environment (fish), biological breakdown (bio) and heat fluxes (ɸ), taken from Körner et al. (2017)

CO₂ production from the aquatic subsystem (${d}_{CO_2}$, g h⁻¹ ), i.e. delivery to the aerial environment (d, g h⁻¹), can be calculated for the given water temperature (T_H2O, K) from oxygen delivery to the system ( ${d}_{O_2},$ g h⁻¹) at water base temperature (T_H2O,b, K) and the Q₁₀ value of fish respiration (Q_10,R). The following relationships are used:

$$ {\displaystyle \begin{array}{c}{d}_{O_2}={\mathrm{f}}_{\mathrm{f}\mathrm{ish}}\ {\mathrm{f}}_{{\mathrm{O}}_2}\ {\mathrm{w}}_{{\mathrm{O}}_2}\\ {}{d}_{CO_2}=\frac{\left[{\mathrm{CO}}_2\right]}{\left[{\mathrm{O}}_2\right]}{d}_{O_2}\ {{\mathrm{Q}}_{10,\mathrm{R}}}^{\left({\mathrm{T}}_{\mathrm{H}2\mathrm{O}}-{\mathrm{T}}_{\mathrm{H}2\mathrm{O},\mathrm{b}}\right)/10}\end{array}} $$

(11.16)

with feed amount for the fish (f_fish, g h⁻¹), oxygen consumption rate at base temperature (f_O2, kg [O₂] kg⁻¹ [feed]), fraction of feed loss w_O2 (⁻) and mass balance of O₂/CO₂ (⁻).

To calculate the basis of aquaponics, i.e. the process flow (indicated with arrows, →) greenhouse macroclimate → microclimate → evapotranspiration → nutrients uptake, various greenhouse simulators that were developed in the past can be used and combined with aquaculture to an aquaponic system. All greenhouse models include a crop growth model. The model quality, however, can vary a lot from simple empirical regression models, e.g. Boote and Jones (1987), via deterministic models, e.g. Heuvelink (1996), to functional structural plant models (FSPM), e.g. Buck-Sorlin et al. (2011). As current crop growth and development models are inaccurate and have limited predictive power (Poorter et al. 2013), models are occasionally employed in crop management, but then mainly for planning issues in greenhouse simulators, e.g. Vanthoor (2011) and Körner and Hansen (2011). Prediction accuracy is jeopardized by many sources of uncertainty, such as modelling errors, variability between plants, variability between greenhouses and uncertain external climate conditions. As for predictions, accuracy also varies strongly per situation. However, online feeding of sensor information into the plant model can make plant model predictions considerably more reliable and useful to the grower.

Greenhouse simulators were developed in and for several places, e.g. the Virtual Grower (Frantz et al. 2010), KASPRO (De Zwart 1996), Greenergy Energy Audit Tool (Körner et al. 2008), The Virtual Greenhouse (Körner and Hansen 2011), The Adaptive Greenhouse (Vanthoor 2011), Hortex (Rath 1992, 2011) and the integrated aquaponic greenhouse model (Goddek and Körner 2019). At a research level, some models (i.e. simulation models in combination with certain greenhouse technologies) have been developed that potentially can be used to optimize investments and structural modifications to the production unit and production process. However, most systems entail closed software environments that can only be used by the developers, and many of them only exist in a research mode and lack further development and acceptance from the industry. However, there is yet no common basis for model sharing and collaborative model development. As a result, most modellers and modelling teams work in isolation developing their own models and codes. A shortcoming of that procedure is that greenhouse simulation models are developed in parallel in disparate research environments, which fail in cooperative growth and development.

All HP greenhouse model simulators are a compilation of sub-models that depend on the aim to integrate the interaction of plants and greenhouse equipment. The general two-part differentiation in greenhouse models and also in control and planning is the shoot and the root environment. Rather complicated and differentiated model approaches have been done for the greenhouse climate (Bot 1993; de Zwart 1996), and greenhouse crop growth has been intensively modelled in the 1990s for the main greenhouse crops such as tomatoes (Heuvelink 1996), cucumber (Marcelis 1994) and lettuce (Liebig and Alscher 1993). However, in order to calculate the water and nutrient uptake of crops, the microclimate, i.e. the climate close to and on the plant organs, needs to be known (Challa and Bakker 1999). This is an ongoing issue in greenhouse modelling, as microclimate variables, such as the central leaf temperature, are highly variable and dependent on many parameters and variables. One version of a leaf temperature model used in a crop canopy for crop temperature (T_c) integrated over vertical layers (z) by Körner et al. (2007) integrating absorbed irradiative net fluxes (R_n,a, Wm⁻²), boundary layer and stomata resistances (r_b and r_s, respectively, sm⁻¹) and vapour pressure deficit at the leaf surface (VPD_s, Pa) in the canopy is shown here, i.e.

$$ {\mathrm{T}}_{\mathrm{c}}\left(\mathrm{z}\right)-{\mathrm{T}}_{\mathrm{a}}=\frac{\frac{1}{\uprho_{\mathrm{a}}{\mathrm{c}}_{\mathrm{p}}}\left({\mathrm{r}}_{\mathrm{b}}\left(\mathrm{z}\right)+{\mathrm{r}}_{\mathrm{s}}\left(\mathrm{z}\right)\right){\mathrm{R}}_{\mathrm{n},\mathrm{a}}\left(\mathrm{z}\right)-\frac{1}{\upgamma}{\mathrm{VPD}}_{\mathrm{s}}\left(\mathrm{z}\right)}{1+\frac{\updelta}{\upgamma}+\frac{{\mathrm{r}}_{\mathrm{s}}\left(\mathrm{z}\right)}{{\mathrm{r}}_{\mathrm{b}}\left(\mathrm{z}\right)}+\frac{1}{\uprho_{\mathrm{a}}{\mathrm{c}}_{\mathrm{p}}/4{{\upsigma \mathrm{T}}_a}^3}\left({\mathrm{r}}_{\mathrm{b}}\left(\mathrm{z}\right)+{\mathrm{r}}_{\mathrm{s}}\left(\mathrm{z}\right)\right)} $$

(11.17)

with greenhouse air temperature (T_a, K), vapour pressure air density (ρ_a, g m⁻²), Stefan-Boltzmann constant (σ, Wm⁻² K⁻⁴), specific heat capacity of the air (c_p, J g⁻¹ K⁻¹), the psychrometric constant (γ, Pa K⁻¹) and the slope between saturated vapour pressure and greenhouse air temperature (δ, Pa K⁻¹).

Leaf temperature is the central part of the microclimate model, it has feedback loops to several input variables and especially stomata resistance (often also used as its reciprocal, the conductance), and the calculation needs several simulation steps for equilibrium. For HP, as part of the aquaponic system, however, modelling water and nutrient fluxes is most important. All water and nutrient balances in a closed multi-loop system are controlled based on the evapotranspiration rate of the crop ET_c (Chap. 8). Commonly ET_c is calculated as latent heat of evaporation, i.e. in energy terms (λE, Wm⁻²), and can be in accordance to leaf temperature expressed in different canopy layers z

$$ \uplambda \mathrm{E}\left(\mathrm{z}\right)=\left(\frac{\frac{\updelta}{\upgamma}{\mathrm{R}}_{\mathrm{n},\mathrm{a}}\left(\mathrm{z}\right)+\frac{\uprho_{\mathrm{a}}{\mathrm{c}}_{\mathrm{p}}}{\upgamma}\left(\frac{1}{{\mathrm{r}}_{\mathrm{b}}\left(\mathrm{z}\right)}+\frac{1}{\uprho_{\mathrm{a}}{\mathrm{c}}_{\mathrm{p}}/4{{\upsigma \mathrm{T}}_{\mathrm{a}}}^3}\right){\mathrm{VPD}}_{\mathrm{s}}\left(\mathrm{z}\right)}{1+\frac{\updelta}{\upgamma}+\frac{{\mathrm{r}}_{\mathrm{s}}\left(\mathrm{z}\right)}{{\mathrm{r}}_{\mathrm{b}}\left(\mathrm{z}\right)}+\frac{1}{\uprho_{\mathrm{a}}{\mathrm{c}}_{\mathrm{p}}/4{{\upsigma \mathrm{T}}_{\mathrm{a}}}^3}\left({\mathrm{r}}_{\mathrm{s}}\left(\mathrm{z}\right)+{\mathrm{r}}_{\mathrm{b}}\left(\mathrm{z}\right)\right)}\right) $$

(11.18)

To calculate ET_c (L m^-2), λE needs to be multiplied with the constant L_w (heat of vaporization of water; 2454·103 J kg⁻¹) and the specific weight of water (9.789 kN·m³ at 20 °C).

Equation (11.18), however, only calculates the water flux through the crop, while the easiest way to estimate nutrient uptake is the assumption that nutrients are taken up/absorbed as dissolved in irrigation water and assuming that no element specific chemical, biological or physical resistances exist. In reality uptake of nutrients is a highly complicated matter. Consequently, to maintain equilibrium, all nutrients taken up by the crop as contained in the nutrient solution need to be added back to the hydroponics system (see Chap. 8). However, Eq. (11.18) only calculates the potential ETc, while too high potential levels can result in a higher transpiration than plants can handle, and then potential water loss may exceed water uptake. For that, the simple assumption of nutrient uptake is not satisfying. As described in Chap. 10, the different nutrients can have different states and change states with, e.g. pH, while the plant availability strongly depends on pH and the relation of nutrients to each other. In addition, the microbiome in the root zone plays an important role, which is not implemented in models yet. Some models, however, differentiate between phloem and xylem pathways. The vast amount of nutrients, however, is not modelled in detail for aquaponics nutrient balancing and sizing of systems, while the easiest way to estimate nutrient uptake is the assumption that nutrients are taken up/absorbed as dissolved in irrigation water and apply the above explained ETc calculation approach.

For control purposes the greenhouse is typically considered as a black box, where outside climate conditions determine the disturbance inputs, CO₂ supply, heating and ventilation are the control inputs, and the greenhouse macro- and microclimate define the output of the system (Fig. 11.17).

Fig. 11.17

Input-output system of a greenhouse

To control the greenhouse, the actions are directed to minimize the fast impacts of the disturbances, i.e. being ahead of expected changes by smart control. For that, control actions such as feedback and feedforward are used (Chap. 8). The best control, however, can be achieved when using a complete greenhouse model and combine it with weather forecast (Körner and Van Straten, 2008) attaining a model-based optimal greenhouse climate control, as worked out by Van Ooteghem (2007).

6 Multi-loop Aquaponic Modelling

Traditional aquaponic designs comprise of aquaculture and hydroponic units involving recirculating water between both subsystems (Körner et al. 2017; Graber and Junge 2009). In such one-loop aquaponic systems, it is necessary to make trade-offs between the conditions of both subsystems in terms of pH, temperature and nutrient concentrations, as fish and plants share one ecosystem (Goddek et al. 2015). By contrast, decoupled double-loop aquaponic systems separate the RAS and hydroponic units from one another, creating detached ecosystems with inherent advantages for both plants and fish. Recently, there has been an increased interest in closing the loop in terms of nutrients as well as increasing the input-output efficiency. For that reason, remineralization (Goddek 2017; Emerenciano et al. 2017; Goddek et al. 2018; Yogev et al. 2016) and desalination loops (Goddek and Keesman 2018) have been incorporated into the overall system design. Such systems are called decoupled multi-loop aquaponic system (Goddek et al. 2016).

Sizing the respective subsystems is fundamental of having a functioning check-and-balance system. For sizing one-loop systems, a simple rule of thumb is generally used, determining the hydroponic cultivation area based on the daily feed input to the RAS (Knaus and Palm 2017; Licamele 2009). The higher degree of complexity of multi-loop systems does not allow this approach anymore, as it comes with inherent risks for making false assumptions for each subsystem. There is a growing body of literature that examines mass balances for aquaponic systems (Körner et al. 2017; Goddek et al. 2016; Reyes Lastiri et al. 2016; Karimanzira et al. 2016). While some research has been carried out in developing numerical models for one- and multi-loop aquaponic systems, no single study exists that integrates a multi-loop aquaponic model with a complemented full-scale deterministic greenhouse model. This is particularly relevant for sizing the system, since plant growth and nutrient uptake are location dependent with crop transpiration as major driver. In concrete terms, this means that the climate within a greenhouse – which is highly dependent on the external weather conditions – has a high impact on plant growth given environmental factors such as relative humidity (RH), light irradiation, temperature, carbon dioxide (CO₂) levels, etc. that were incorporated in greenhouse microclimate modelling (Körner et al. 2007; Janka et al. 2018).

7 Modelling Tools

In aquaponics, flow charts or stock and flow diagrams (SFD) and causal loop diagrams (CLDs) are commonly used to illustrate the functionality of the aquaponic system. In the following, flow chart and CLDs will be described.

7.1 Flow Charts

To get a systemic understanding of the aquaponics, flow charts with the most important components of the aquaponics are a good tool to show how material flows in the system. This can help, for example, in finding missing components and unbalanced flows and mainly influencing determinants of the subprocesses. Figure 11.18 shows a simple flow chart in aquaponics. In the flow chart, fish food and water are added to the fish tank, where the feed is taken by the fish for growth, the water is enriched with the fish waste and the nutrient-enriched water is added to the hydroponics system to produce plant biomass. From the flow chart, a CLD shown in Fig. 11.19 can be easily constructed.

Fig. 11.18

Example of a flow chart in aquaponics (only RAS and HP exchange)

Fig. 11.19

Causal loop diagram (CLD) illustrating examples of a reinforcing and a balanced loop within aquaponic systems. The reinforcing loop (R) is one in which an action produces a result which influences more of the same action and consequently resulting in growth or decline, where as a balancing loop (B) attempts to bring things to a desired state and keep them there (e.g. temperature regulation in the house)

7.2 Causal Loop Diagrams

Causal loop diagrams (CLDs) are a tool to show the feedback structure of a system (Sterman 2000). These diagrams can create a foundation for understanding complex systems by visualizing the interconnection of different variables within a system. When drawing a CLD, variables are pictured as nodes. These nodes are connected by edges, which form a connection between two variables accordingly. Figure 11.19 shows that such edges can be marked as either positive or negative. This depends on the relation of the variables to one another. When both variables change into the same direction, then one can speak of a positive causal link. A negative causal link thus causes a change in opposite directions. When connecting two nodes from both sides, one creates a closed cycle that can have two characteristics: (1) a reinforcing loop that describes a causal relationship, creating exponential growth or collapse within the loop or (2) a balancing loop in which the causal influences keep the system in an equilibrium. Figure 11.19 shows an example of both types of loops.

Let us illustrate this (Fig. 11.20) for the flow chart of Fig. 11.18.

Fig. 11.20

Example CLD for RAS and HP exchange

It is obvious that CLD and SFD are very useful for system understanding, when the model does not require numerical accuracy. If numerical accuracy is required, the process should be studied further with a system dynamic tool diagram (SDTD) and modelled in dynamic system simulation software. For example, the CLD in Fig. 11.20 can be augmented with differential equations to a SDTD (Fig. 11.21).

Fig. 11.21

Example SDTD for RAS and HP exchange

From the SDTD, we can now see how the differential equations for the nutrients balance in the tank look like. We know that the nutrient flow out of the fish tank (M _xfout) must be the water flow (Q _fout) times the concentration in the out stream (C _xf):

$$ {M}_{xf out}=={C}_{xf}\ {Q}_{fout} $$

Assuming a stirred tank gives the nutrient concentration of the fink tank to:

$$ {C}_{\mathrm{xf}}={M}_{\mathrm{xf}}/{V}_f $$

The differential equations of the RAS part can be derived to:

$$ {\displaystyle \begin{array}{c}{dV}_f/ dt={Q}_{\mathrm{fin}}-{Q}_{\mathrm{fout}}\\ {}{dM}_{\mathrm{xf}}/ dt={M}_{\mathrm{xf}\mathrm{in}}-{M}_{\mathrm{xf}\mathrm{out}},\end{array}} $$

and for the concentration

$$ dc/ dt=\left({Q}_{\mathrm{fin}}{C}_{\mathrm{xf}\mathrm{in}}-{Q}_{\mathrm{fou}t}{C}_{\mathrm{xf}}\right)/{V}_f $$

7.3 Software

In addition to basic computer languages, such as Fortran, C++ and Python, for fast computation and fully user-specific implementation, all kinds of advanced software tools are available. These advanced software tools offer a variety of environments, concepts and options. We can model state variables, differential equations, connections and loops. In addition, we can use the model for simulations, stability analysis, optimization and control.

The main reasons for modelling of a system are to understand and control it. Therefore, the model helps to predict the system dynamics or behaviour. The software applications could allow us to do three consequent tasks: (a) the modelling itself, (b) the simulations of the model(s) and (c) optimization of the model and/or simulation.

Mathematica software is for functional analysis of mathematically described problems (Wolfram 1991). The concept is based on the LISP approach (McCarthy and Levin 1965.), a very effective functional programming language. The syntax is reasonably simple, and this software is popular in mathematics, physics and systems biology. Especially, the Ndsolve module helps to solve ordinary differential equations, plot the solution and find specific values.

Very similar tools for solving ODEs are offered by the Maple. This software is very powerful; between its features belong boundary problems solution, exact solutions and mathematical approximations. Copasi (complex pathway simulator) is a software tool for simulation and analysis of biochemical networks via ordinary differential equations.

SageMath is a free open-source mathematics software system. The software is Python-based and facilitates the simulation of ODE models. Data2Dynamics software is a collection of numerical methods for quantitative dynamic modelling and is a comprehensive model and data description language. The software allows the analysis of noise, calibration and uncertainty predictions and has libraries of biological models.

Probably the best simulation language is Simula (probably not in use anymore) and Simula 67, considered at the beginning as a package for Algol 60. These were the first fully object-oriented languages, introducing classes, inheritance, subclasses, garbage collector and others. In the beginning of the twenty-first century, the creators Ole-Johan Dahl and Kristen Nygaard were awarded the IEEE John von Neumann Medal and the A. M. Turing Award (Dahl and Nygaard 1966).

The idea behind Simula was that objects have life; they start to exist, do their being and cease. The objects are defined as general classes (template code), and each instance of such object has a ‘life’ in the simulation. The language was quite difficult to learn. However, it offered the possibility to model processes object by object and run simulation of their lives. The simulation runs on the basis of discrete events, and it is possible to simulate objects in co-routine. More tasks can start, run, detach, resume and complete in overlapping time periods in quasiparallel processes. Today’s hardware allows us modelling and simulation in fully parallel threads. However, many of the Simula concepts were already used for development of other languages, namely, Java, C/C++/C# and persistent objects libraries like DOL (Soukup and Machacek 2014). Current successor of Simula is BETA, extending and featuring the possibilities of inheritance in concepts of nested (sub)classes (with nested local time) and patterns (Madsen et al. 1993).

It is always an option to use any of the object-oriented languages and specific libraries and program all the necessary code for a specific model. On the other hand, already existing graphical programming environments allow to design and link the structure of the modelled system from libraries of objects (signal generator, sum, integrator, etc.), parametrize them and run the simulation in virtual time.

Another popular software for simulation is MathWorks Simulink, describing itself as a model-based design tool. The environment allows to combine and parametrize predefined blocks (from wide range of libraries) and diagrams into subsystems. The programming is done using graphical blocks and their connections into functional parts with feedback loops. The environment is widely used for control, automation and signal processing. Another possibility is to integrate own code from MathWorks Matlab language or use various toolboxes (Jablonsky et al. 2016). One of them, SensSB, is focused on the sensitivity analysis and allows to import other models using the Systems Biology Markup Language. For just the visualization of existing models in Simulink, it is also possible to use the very quick models viewer DiffPlug. PottersWheel supports the modelling of time-dependent dynamic systems, parameter calibration, analysis and prediction. Interesting tool is the experimental design for model verification.

For the modelling and analysis of system dynamics, similar strategy is used by the Stella Architect isee software application, where the model is composed of blocks, which are connected by relations. Stella allows modelling and simulation of very different types of applications, ranging from medical needs through building construction to the airplanes. Stella is sometimes marketed as iThink software. Powersim software was designed originally for economic purposes. However, it developed into more sophisticated tool, including electronic, solar power or drug treatment simulations. The former developer of Powersim is currently producing a similar software for more complex tasks Dynaplan Smia. Vensim is a system for modelling big data relationships of real systems. The power of Vensim is that it allows causal tracking, sensitivity analysis, calibration and intensive simulation. However, the software is also capable of dealing with wide range of simple and complex real systems (Hassan et al. 2016). True-World system dynamics software facilitates complex multibody dynamic simulations in discrete and continuous time. The modelling basically starts from balances.

Completely different approaches to modelling and simulation are cellular automata or agent-based modelling approaches, popularized by Stephen Wolfram (Wolfram 1991) as a new kind of science. The approach is sometimes also called the game of life. The modelling is implemented via interactions of autonomous individuals (Macal and North 2005). The simulations show emergent behaviour and therefore are very popular in systems biology for population dynamics. A simple tool for basic (and advanced, as well) agent-based modelling and simulation is the NetLogo software, where simple descriptions and parametrization create powerful models. The software allows visualization of the time development and noise induction (Stys et al. 2015). The application is written in Java, which sometimes limits the available memory. Probably the biggest effort in the multi-agent modelling was done by development of Wolfram software, which is the continuation of popular Mathematica, with extended tools for modelling and simulation. It has put Simulink-like modelling in a more attractive suit and also creates possibilities of agent-based modelling and much more tools for other mathematical disciplines (multivariate statistics, data mining, global optimization).

AnyLogic is very interesting software for problems of flow – information, money, traffic, logistic and mining. The simulation solves the problem of optimal flow in the designed system with minimal effort and maximal efficiency. The used concepts are system dynamics and agent-based and discrete-event modelling. It also offers hybrids between different modelling concepts. The software is useful, for example, in the epidemic spread simulations (Emrich et al. 2007).

Another agent-based modelling tool is Insight Maker, for simulation of population interacting in geographic or network space. The software supports graphical model construction, usage of multiple paradigms, embedded scripting and optimization toolset (Fortmann-Roe 2014).

For the modelling itself, description of the state variables, solution of the ODEs, parametrization and time dependency analysis, the first group of software, from Mathematica to Matlab, could be used without hesitation. They represent powerful tools for the modelling purposes. In case of more complex analysis, such as related to big data, simulation, noise induction, optimization, sensitivity and stochastics, more advanced tools are required, with object-oriented approach, involving also higher induction in the programming languages syntax.

8 Discussion and Conclusions

Aquaponics are complex technical and biological systems. For example, possible explanations for fish not growing properly can be small food rations, adverse water quality, technical problems causing stress, etc. Due to the inherently slow biology, scientific investigations of the validity of these explanations would be tedious and require several experimental trials to get all important factors and their interactions, demanding a lot of facilities, expertise, research time and financial assets. Therefore, the issue of modelling aquaponic systems was addressed in this chapter. In aquaponics, modelling is required for different objectives: (i) insight/understanding, (ii) analysis, (iii) estimation and (iv) management and control. For all these objectives, appropriate models are required. For example, to achieve objectives (ii) and (iii), an empirical approach can be utilized which uses statistical models to analyse data from previous experimental trials with the objective of extracting as much information as possible without conducting new experiments. Statistical models can reveal the most important factors affecting fish and crop production in the aquaponic systems. Future experiments could concentrate on these factors, thus making the utilization of costly research assets more effective.

The complexity of aquaponic systems, due to their feedback character and the interactions between RAS and hydroponic system, water treatment and fish growth, implies that in order to fulfil objectives (i) and (iv), i.e. to understand or optimize a plant (configuration, size, fish, feed, flows, etc.) with respect to cost, stability, robustness and water quality, non-trivial theoretical models of most of the system components described in this chapter are required. The advantage of these theoretical models presented over statistical models is their stronger ability to analyse the process underlying the aquaponics and the possibility to model the time aspect (dynamics). Statistical models just confirm or refute a hypothesis and to what extent variables covary but give no evidence of the underlying processes. On the other hand, theoretical models allow us to simulate the processes according to a hypothesis, compare simulated with observed data, evaluate both the hypothesis and the model and make adaptions. The validity of statistical models may not be beyond the operational range they were trained for, whereas theoretical models can be defined and used for a wide range of environments, provided that the models are validated for these ranges before application. For example, the multiple regression model used to assess relationships between fish growth with Oreochromis niloticus as fish species and environmental variables in an aquaponics facility in Germany cannot be easily applied to Spain with Cyprinus carpio, whereas a theoretical model describing the underlying processes (e.g. fish behaviour, aquaculture, freshwater ecology) as mathematical equations can be adjusted relatively easily because the fish and ecological process underlying that model are basically the same for the two sites.

Nevertheless, theoretical models also require some parameters such as reaction constants and substance settling velocity in settling tank to be determined. This is achieved commonly based on empirical study of one facility or very few facilities or in most cases from previously published studies (secondary sources). Studies based on secondary sources have limitations imposed by the given structure and amount of the available data, which is not existent when the data come from an experimental setup designed ad hoc for the study. However, estimating model parameters using experimental data from one aquaponics facility only can have problems regarding generalizability and replication of the results due to particular conditions present in the study. The data scarcity sometimes imposes strong restrictions to models that limit their practicality. The development of studies for parameter estimation with primary data that use a larger number of aquaponics facilities than earlier studies does help to overcome the present limitations and provide better and reliable results. This, however, is not an easy challenge for aquaponics researchers.

Simulation of aquaponics with the mathematical models under a wide range of management conditions will improve the understanding of aquaponics, verify different aquaponics configurations and point the way to the most promising strategies for improving aquaponics facilities. Again, this can lead to a more efficient way of conducting experiments.

Some modelling tools were also presented in this chapter. Traditionally, stock and flow diagrams (SFD) have been used for understanding processes as support tools for quantitative analysis. They are used to comprehend the flow and fluxes of quantities but lack the ability to illustrate the information associated to the flow and fluxes. Causal loop diagram (CLD) can be used to transfer complex SFD system into understandable simplified feedback structures. Together, the SFDs and the CLDs fully define the differential equation system. If only a simple qualitative understanding of the system is required, then CLD and SFD may be enough, but if the answer requires a numerical accuracy, then the problem can be investigated further with system dynamic tool diagrams (SDTD) and subsequently be modelled in a software tool for numerical simulation.