Skip to main content
SpringerLink
Log in

The Static Magnetic Field

  • Chapter
  • First Online:
Engineering Electromagnetics

Abstract

After discussing the static electric field and steady currents, we are now ready to take another significant step in the study of electromagnetics, the study of the static magnetic field. But what exactly is a magnetic field? This question will be answered gradually, but, for a simple description, we may say it is a new type of force field in the same sense that the electric field is a force field. Take, for example, a magnet. It attracts or repels other magnets and generates a “magnetic field” around itself. The permanent magnet generates a static (time-independent) magnetic field. A direct current can also generate a static magnetic field. How do we know that? As with many other aspects of electromagnetics, we know by experiment.

“There’s a South Pole,” said Christopher Robin, “and I expect there’s an East Pole and a West Pole, though people don’t like talking about them.”

Winnie-The-Pooh

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
eBook
USD 16.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 89.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 109.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    Hans Christian Oersted (1777–1851), Danish scientist and professor of physics. He tried for many years to establish the link between electricity and magnetism, a link that was suspected to exist by him and many other scientists of the same period. He finally managed to do so in his now famous experiment of 1819 in which he showed that a current in a wire affects a magnetic needle (compass needle). He disclosed his experiments, all made in the presence of distinguished witnesses, in 1820. Oersted was very careful to ensure that what he saw was, in fact, a magnetic phenomenon by repeating the experiments many times and with various “needles,” in addition to the magnetic needle (to show that the effect does not exist in conducting materials such as copper or insulating materials such as glass—only in magnetized materials). Intervening materials between the wire and needle were also tested. As was the custom of the day, his work was written and communicated in Latin in a pamphlet titled: “Experimenta circa efficaciam, conflictus eletrici in acum magneticam.”

  2. 2.

    See the footnote on page 337.

  3. 3.

    Hendrik Antoon Lorentz (1853–1928). Dutch physicist who is best known for his work on the effects of magnetism on radiation. For this he received the Nobel Prize in 1902. In his attempt to explain electricity, magnetism, and light, he arrived at the Lorentz transformation, which helped Albert Einstein in formulating his theory of relativity.

  4. 4.

    Jean-Baptiste Biot (1774–1862) was a professor of physics and astronomy. Among other topics, he worked on optics and the theory of light. Félix Savart (1791–1841) was a physician by training but later became professor of physics. This law is attributed to Biot and Savart because they were the first to present quantitative results for the force of a current on a magnet (in fact quantifying Oersted’s discovery). The experiments mentioned here are described in detail in James Clerk Maxwell’s Treatise on Electricity and Magnetism (Part IV, Chapter II), as Ampère’s experiments. The law was presented in 1820, about a year after the landmark experiment by Oersted established the link between current and the magnetic field.

  5. 5.

    Ampère’s law is named after André-Marie Ampère (see footnote on page 337). Ampère derived this law from study of the solenoidal (circular) nature of the magnetic field of straight wires.

  6. 6.

    After Nicola Tesla (1856–1943). Tesla is well known for his invention of AC electric machines and development of the multiphase system of AC power. This happened in the early 1880s, followed by a number of other important engineering designs, including the installation of the first, large-scale AC power generation and distribution system at Niagara Falls (approx. 12 MW), in 1895. His induction motor became a staple of AC power systems, but his patents (about 500 in all) include transformers, generators, and systems for transmission of power. Tesla also had designs of grandiose scale, including “worldwide aerial transmission of power,” high-frequency, high-voltage generators and many others. Tesla was always somewhat of a “magician” and liked to keep his audience guessing, but later in his life, he became more of an eccentric and a recluse. Although some of his designs were more dreams than engineering, he is considered by many as the greatest inventor in electrical engineering. His statement regarding his student pay that there are “too many days after the first of the month” is even more familiar than his inventions, even to those that never heard it.

  7. 7.

    The search for monopoles (single magnetic poles) is still continuing in basic physics research. No evidence of their existence has ever been found either on macroscopic or microscopic levels.

  8. 8.

    The magnetic vector potential was considered by James Clerk Maxwell to be a fundamental quantity from which the magnetic flux density was derived. He called it the “Electrokinetic Momentum.” In fact, Maxwell used the scalar and vector potentials to define fields. The fields as we use them today were introduced as fundamental quantities by Oliver Heaviside and Heinrich Hertz. Oliver Heaviside, in particular, had some harsh words about potential functions. He considered the magnetic vector potential an “absurdity” and “Maxwell’s monster,” which should be “murdered.” Harsh words, but then Heaviside had harsh words for many people and subjects. Although we use Heaviside’s form of electromagnetics in using field variables, we also make considerable use of potential functions. The guiding rule for us is simplicity and convenience.

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, University of Akron, Akron, OH, USA

    Nathan Ida

Authors
  1. Nathan Ida
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nathan Ida .

Problems

Problems

Note: In the problems that follow, all materials and spaces have permeability μ0 = 4π × 10− 7 [H/m] unless otherwise specified.

8.1.1 The Biot–Savart Law

  1. 8.1

    Magnetic Flux Density Due to Filamentary Currents. A current I [A] flows in a conductor shaped as an equilateral triangle (Figure 8.25). Calculate the magnetic flux density:

    1. (a)

      At the center of gravity of the triangle (where the three normals to the sides meet).

    2. (b)

      At a vertex of the triangle.

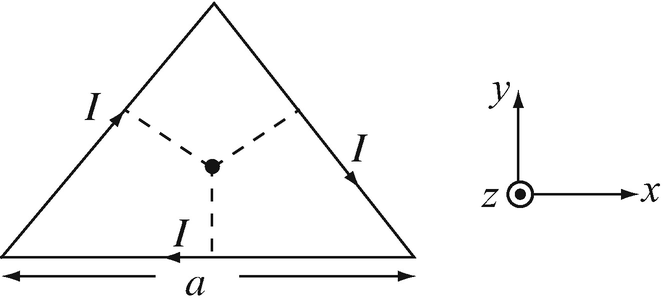
    figure 25

    Figure 8.25

  2. 8.2

    Magnetic Flux Density of Semi-infinite Segments. An infinitely long wire carrying a current I [A] is bent as shown in Figure 8.26. Find the magnetic flux density at points P1 and P2. (P2 is at the center of the horizontal wire, at a distance d [m] from the bend.)

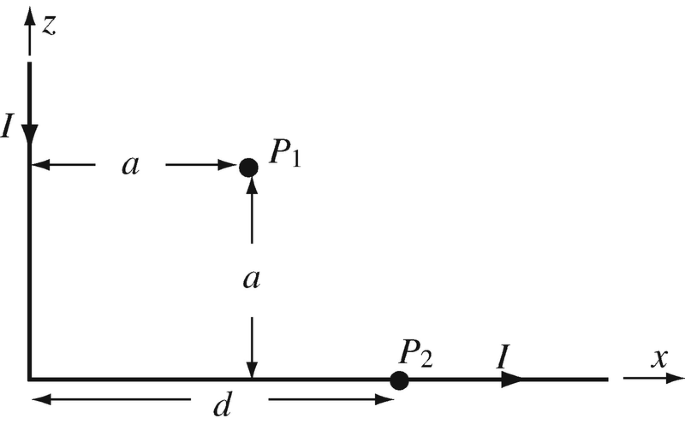
    figure 26

    Figure 8.26

  3. 8.3

    Magnetic Flux Density of Circular and Hexahedral Loops. In an application it is required to produce a flux density B0 [T] at the center of a wire loop of radius R [m], carrying a current IL [A]. To simplify the laying of the wire, the loop is replaced with a hexagon circumscribed in the loop as shown in Figure 8.27. The hexagonal wire carries a current IH [A]. Calculate the ratio IH/IL so that the hexagonal wire produces the same flux density B0 [T] at P as the circular loop.

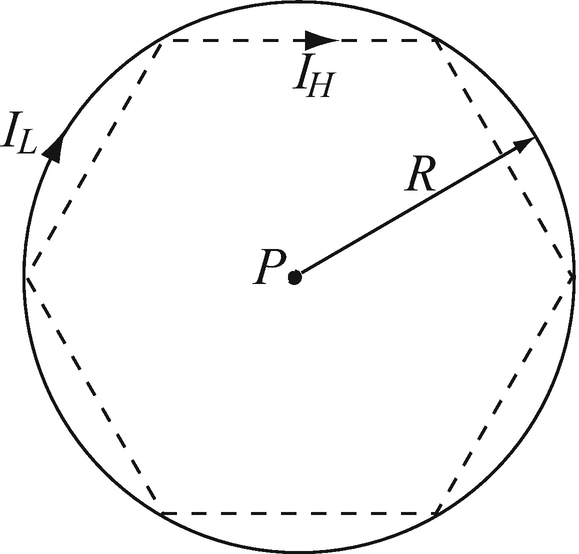
    figure 27

    Figure 8.27

  4. 8.4

    Magnetic Flux Density of Polygonal Loop. Show that the magnetic flux density at the center of a loop of wire carrying a current I [A] and shaped like a regular plane polygon of 2n sides, the distance between parallel sides being 2a [m], is B = (μ0nI/πa)sin(180°/2n) [T].

  5. 8.5

    Application: Magnetic Field of Moving Charges. A thin insulating disk of outer radius b has a uniform charge density ρs [C/m2] distributed over the surface between r = a [m] and r = b [m]. The charges are bound and cannot move from their location. If the disk is rotating at an angular velocity ω, calculate the magnetic field intensity at the center of the disk (Figure 8.28). Note. The first experiment to show the equivalency between moving charges and magnetic field was produced by Henry A. Rowland (1849–1901) in 1875. He showed that a charge placed on a disk (rotating at 3,660 rpm) produced a magnetic field exactly like that of a closed-loop current.

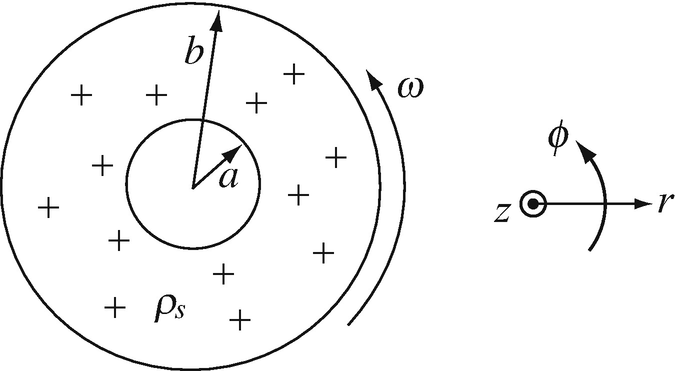
    figure 28

    Figure 8.28

  6. 8.6

    Magnetic Flux Density of a Loop. The rectangular wire loop in Figure 8.29 carries a current I [A] as shown.

    1. (a)

      Calculate the magnetic flux density (magnitude and direction) at a point h [m] high above the center of the loop (see Figure 8.29).

    2. (b)

      Show that as the ratio b/a or a/b tends to zero, the flux density in (a) tends to zero.

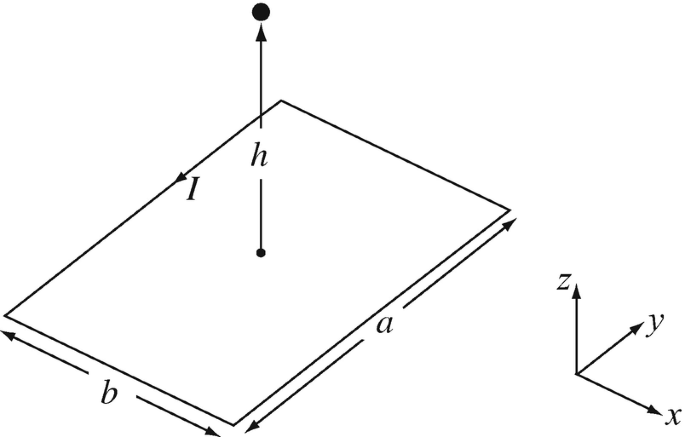
      figure 29

      Figure 8.29

  7. 8.7

    Application: Magnetic Flux Density of a Spiral Coil. A wire is bent to form a flat spiral coil and carries a current I [A]. Calculate the flux density at a point h [m] high above the center of the spiral (Figure 8.30). The coil radius is a [m]. The spiral has N uniformly distributed turns. Assume each turn is a perfect circle.

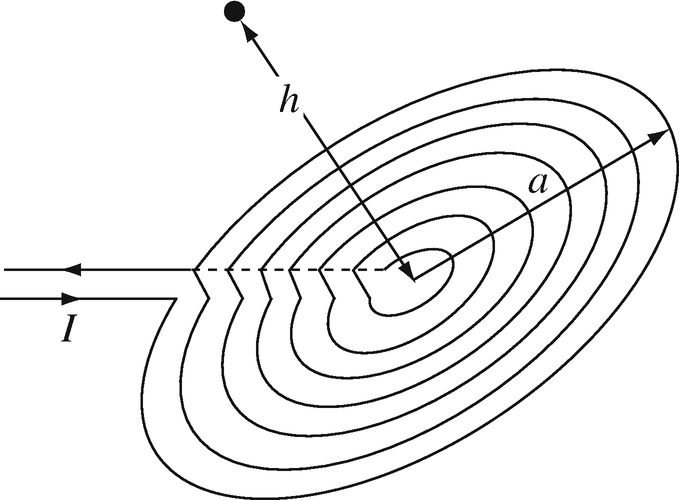
    figure 30

    Figure 8.30

  8. 8.8

    Application: Magnetic Fields of Planar Structures. A semiconductor material is made as shown in Figure 8.31. The long ends of the piece are connected to a voltage source. This causes electrons to move toward the positive connection and holes toward the negative connection. Holes and electrons move at the same velocity v [m/s] and have the same charge magnitude q [C] each. The hole and electron densities are equal to ρ holes/m3 and ρ electrons/m3, respectively:

    1. (a)

      Set up the integrals needed to calculate the magnetic flux density at a height h [m] above the center of the piece (see Figure 8.31). Do not evaluate the integrals.

    2. (b)

      Optional: Evaluate the integrals in (a) for the following data: a = 0.02 m, b = 0.05 m, d = 0.5 m, h = 0.1 m, ρ = 1020 (holes or electrons/m3), v = 1 m/s, q = 1.6 × 10−19 C. Note. The integration is very tedious. You may wish to perform the integration numerically.

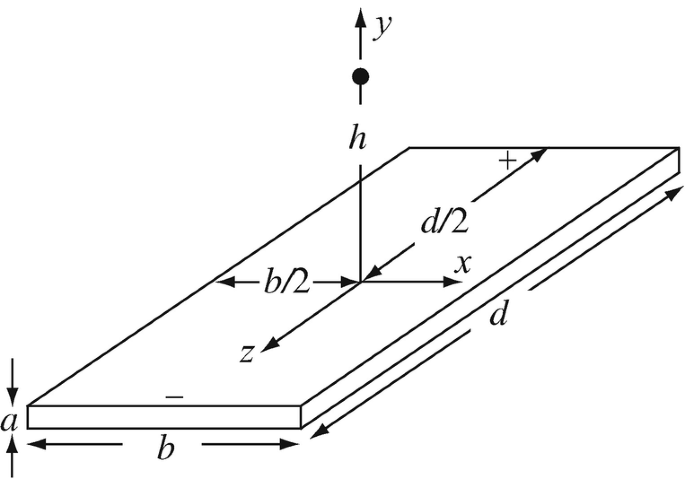
      figure 31

      Figure 8.31

8.1.2 Ampère’s Law

  1. 8.9

    Magnetic Flux Density of Thick Conductors. Two, infinitely long cylindrical conductors of radius a [m] carry a current I [A] each. One conductor coincides with the y axis, whereas the second is parallel to the z axis, in the x−z plane, at a distance d [m] from the origin as shown in Figure 8.32. The currents are in the positive y direction in the first conductor and in the positive z direction in the second conductor. Calculate the magnetic flux density (magnitude and direction) at all points on the z axis.

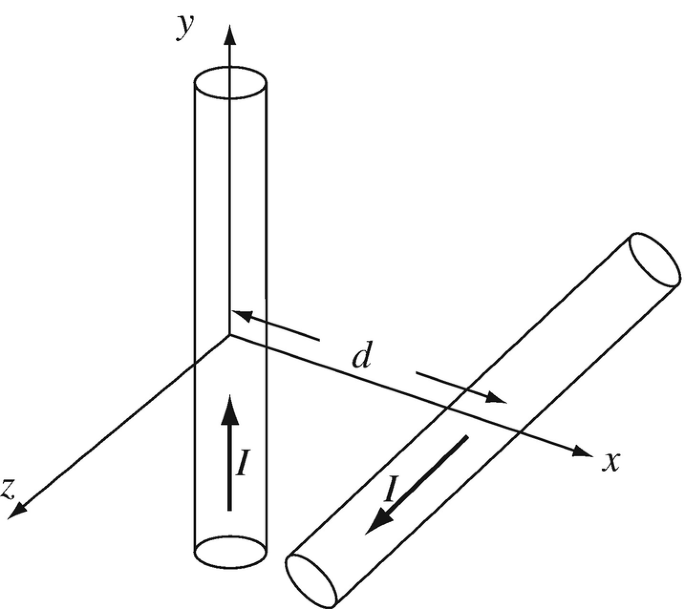
    figure 32

    Figure 8.32

  2. 8.10

    Magnetic Flux Density of Thick Conductors. Two infinitely long cylinders, one of radius a [m] and one of radius b [m], are separated as shown in Figure 8.33. One cylinder is directed parallel to the z axis, in the x−z plane, the other parallel to the y axis, in the x−y plane. A current density J [A/m2] flows in each, directed in the positive y and z directions as shown. Calculate the magnetic flux density at a general point P(x,y,z) outside the cylinders.

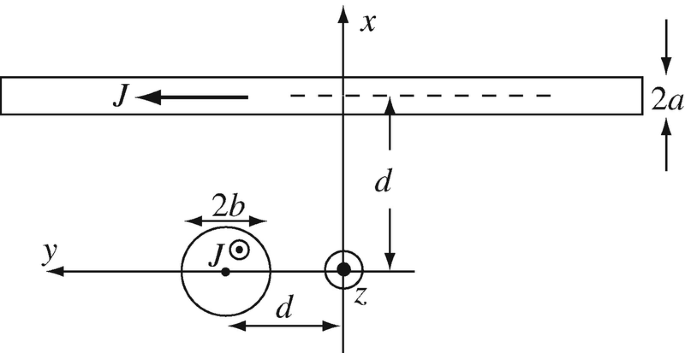
    figure 33

    Figure 8.33

  3. 8.11

    Application: Magnetic Flux Density Due to Power Lines. A high-voltage transmission line operates at 750 kV and 2,000 A maximum. The towers used to support the lines are h = 20 m high and the lines are separated a distance 2a = 6 m (Figure 8.34). Calculate:

    1. (a)

      The magnetic flux density anywhere at ground level.

    2. (b)

      The magnetic flux density (magnitude and direction) at ground level, midway between the two wires.

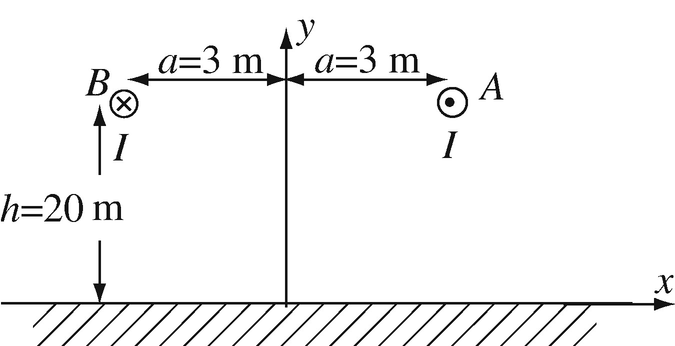
      figure 34

      Figure 8.34

8.1.3 Ampère’s Law, Superposition

  1. 8.12

    Magnetic Flux Density Due to Current Distribution Two long copper strips on a printed circuit board are shown in cross section. The strips are long and their thickness t is negligible. A current flows in strip (1) into the page and returns (out of the page) in strip (2) as shown in Figure 8.35. The current is uniformly distributed in the cross-section of each strip. Calculate the magnetic flux density at point P (direction and magnitude). P is midway between the edges of the strips.

    figure 35

    Figure 8.35

  2. 8.13

    Magnetic Flux Density Due to Volume Distribution of Currents. A very long, L-shaped conductor with dimensions shown in cross section in Figure 8.36 carries a total current I [A]. The current is in the positive z direction (out of the paper) and is uniformly distributed in the cross-section:

    1. (a)

      Set up the integrals needed to calculate the magnetic flux density (magnitude and direction) at point P(a,a).

    2. (b)

      Optional: Evaluate the integrals in (a) for the following data: a = 0.05 m, b = 0.025 m, I = 100 A. Note. The integration is very tedious. You may wish to perform the integration numerically.

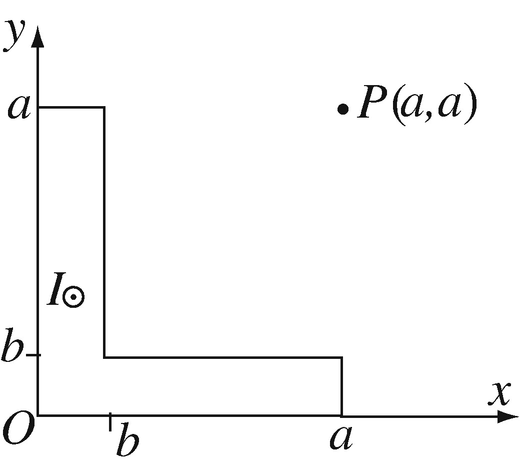
      figure 36

      Figure 8.36

  3. 8.14

    Magnetic Field of a Current Sheet. A thin layer of wires forms an infinite sheet of current. There are N wires per meter and each wire carries a current I [A] as shown in Figure 8.37. Calculate the magnitude and direction of the magnetic flux density everywhere in space.

    figure 37

    Figure 8.37

  4. 8.15

    Application: Magnetic Field of Thin and Thick Conductors. An infinitely long thin wire is placed at the center of a hollow, infinitely long cylindrical conductor as shown in Figure 8.38. The conductor carries a current density J [A/m2] and the wire carries a current I [A]. The direction of J is out of the page. Find the magnetic flux density for the regions 0 < r < r1, r1 < r < r2, r > r2 for the following conditions: (a) I = 0. (b) I in the direction of J. (c) I in the direction opposing J.

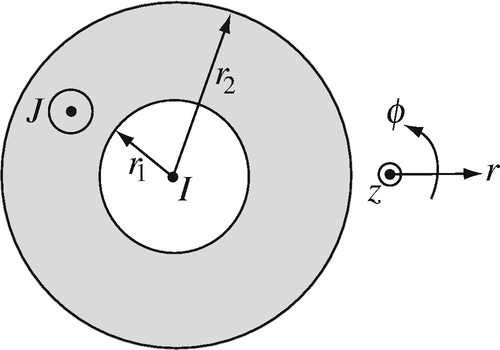
    figure 38

    Figure 8.38

  5. 8.16

    Magnetic Flux Density Due to Rotating Surface Charge Density. A long conducting cylinder of radius b [m] contains a uniformly distributed surface charge density ρs [C/m2] on its outer surface. The cylinder spins at an angular velocity ω [rad/s] around its axis (Figure 8.39). Calculate the magnetic field intensity everywhere.

    figure 39

    Figure 8.39

  6. 8.17

    Superposition of Magnetic Flux Densities Due to Thick Conductors. A hollow, infinitely long cylindrical conductor has an outer radius b [m] and an inner radius a [m]. An offset solid cylinder of radius c [m] is located inside the large cylinder as shown in Figure 8.40. The two cylinders are parallel and their centers are offset by a distance d [m]. Assuming that the current density in each cylinder is J [A/m2] and is uniform, calculate the magnetic flux density at point A (outside the larger cylinder). The current in the larger cylinder is out of the page, and in the smaller cylinder, it is into the page.

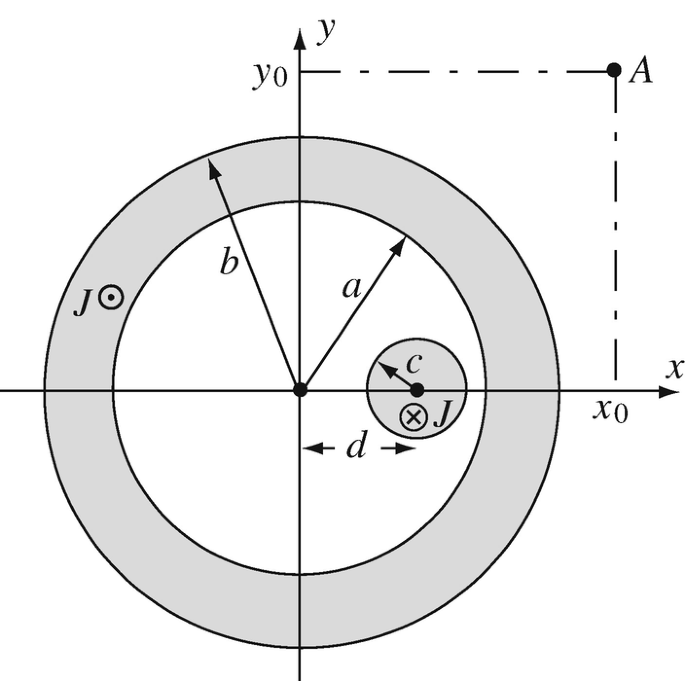
    figure 40

    Figure 8.40

  7. 8.18

    Application: Magnetic Field in a Coaxial Cable. Given a very long (infinite) thin wire with current I [A] and a very long (infinite) cylindrical tube of thickness r2 – r1 with uniform current density J1 [A/m2] as shown in Figure 8.41, find:(a) B for 0 < r < r1, (b) B for r2 < r < ∞.

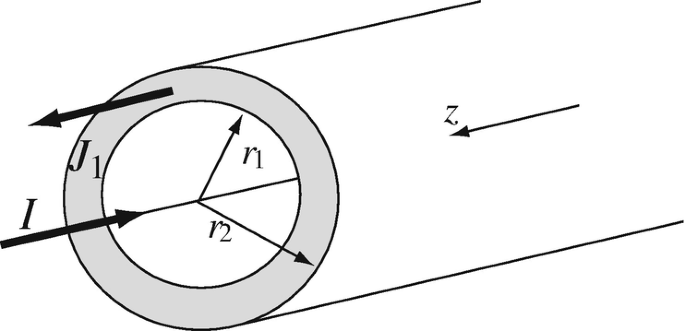
    figure 41

    Figure 8.41

  8. 8.19

    Magnetic Field in Coaxial Solenoids. A long solenoid (a single layer of very thin wire turns) of radius r1 [m] is placed inside a second long solenoid of radius r2 [m]. The currents in the solenoids are equal but in opposite directions, as shown in Figure 8.42a in axial cross section and in Figure 8.42b in radial cross-section, and each solenoid has n turns per meter length:

    1. (a)

      Calculate the magnetic flux density for 0 < r < r1, r1 < r < r2 and r > r2.

    2. (b)

      Repeat (a), if the current in the inner solenoid is reversed.

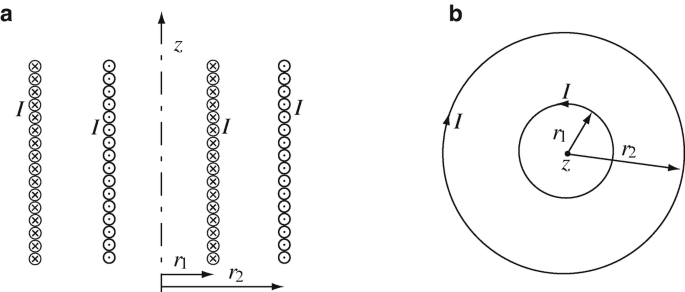
      figure 42

      Figure 8.42

  9. 8.20

    Superposition of Solutions in Solid Conductors. A very long (infinite) tubular conductor has radius b [m] and an offset hole of radius c as shown in Figure 8.43. The center of the hole is offset a distance d [m] from the center of the conductor. If the current density in the conductor flows out of the paper, is uniform in the conductor’s cross-section (shaded area) and equals J [A/m2], calculate the magnetic field intensity at A.

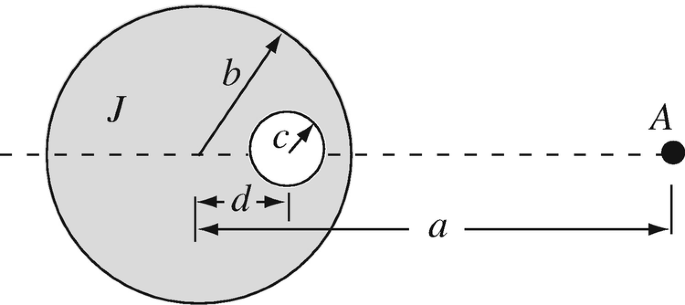
    figure 43

    Figure 8.43

  10. 8.21

    Application: Magnetic Flux Density Due to a Cable. Three very long cylindrical, solid conductors are arranged on a line as shown. The center conductor has radius 2a [m] and carries a current I [A] flowing into the page. The two outer conductors have radius a [m] and each carries a current I/2 [A] out of the page. They form a cable so that a current I [A] flows in one direction in the center conductor and returns (in the opposite direction) in the outer two conductors (Figure 8.44). Find the magnetic flux density (magnitude and direction) at points A, B, C and D.

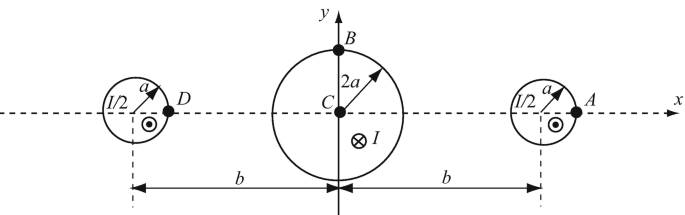
    figure 44

    Figure 8.44

8.1.4 Biot–Savart Law, Magnetic Vector Potential

  1. 8.22

    Magnetic Vector Potential of Current Segment. A very long (but not infinite) straight wire carries a current I [A] and is located in air:

    1. (a)

      Calculate the magnetic vector potential at a distance a [m] from the center of the wire. Assume for simplicity that the wire extends from − L [m] to + L [m] and that L ≫ a.

    2. (b)

      From the result in (a), what must be the magnetic vector potential for an infinitely long current-carrying wire?

  2. 8.23

    Magnetic Vector Potential of Loops. A circular loop and a square loop are given as shown in Figure 8.45:

    1. (a)

      Find the ratio between the magnetic flux densities at the center of the two loops.

    2. (b)

      What is the magnetic vector potential at the center of each loop? Hint. Use Cartesian rather than cylindrical coordinates for the integration for both loops.

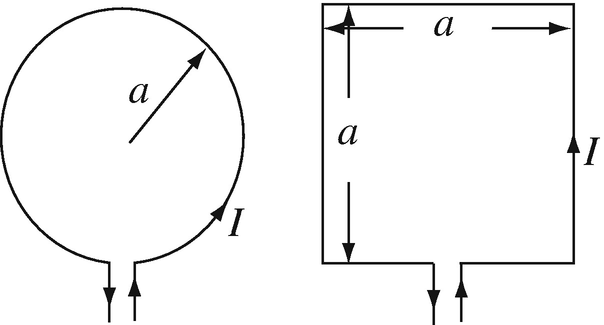
      figure 45

      Figure 8.45

  3. 8.24

    Application: Magnetic Flux. A straight wire carries a current I = 1 A. A square loop is placed flat in the plane of the wire as shown in Figure 8.46. Calculate:

    1. (a)

      The flux, using the magnetic flux density.

    2. (b)

      The flux, using the magnetic vector potential. (Hint. Use the result of Problem 8.22. Compare the results in (a) and (b).)

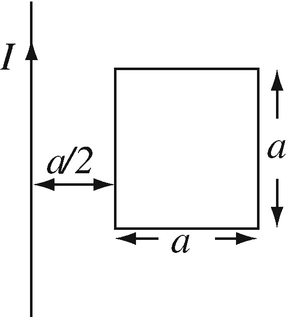
      figure 46

      Figure 8.46

  4. 8.25

    Magnetic Flux. A straight, infinitely long wire carries a current I = 10 A and passes either above or next to a loop of radius a = 0.1 m as shown in Figure 8.47:

    1. (a)

      If the wire passes as in Figure 8.47a, show from symmetry considerations that the total flux through the loop is zero, regardless of how close the loop and the wire are.

    2. (b)

      If the loop is moved sideways as in Figure 8.47b, calculate the total flux through the loop. Assume the loop and wire are in the same plane.

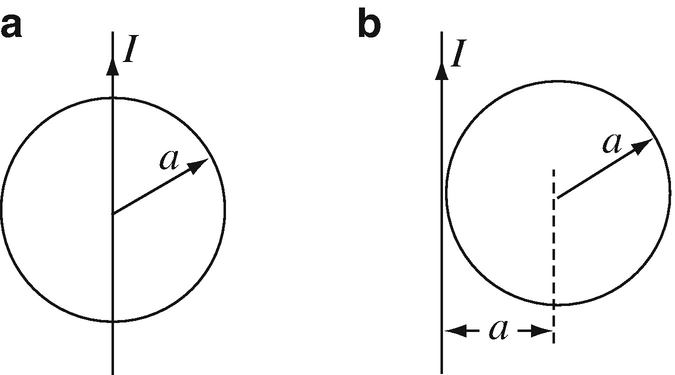
    figure 47

    Figure 8.47

8.1.5 Magnetic Scalar Potential

  1. 8.26

    Magnetic Scalar Potential Between the Poles of a Permanent Magnet. The magnetic flux density between the poles of a large magnet is 0.1 T and is uniform everywhere between the poles in Figure 8.48. Calculate the magnetic scalar potential difference between the poles.

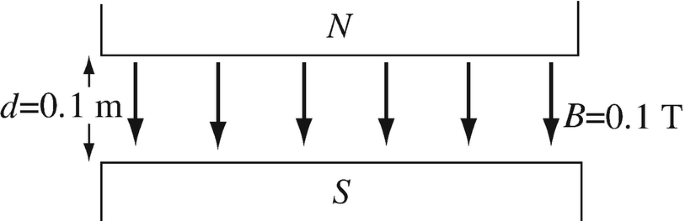
    figure 48

    Figure 8.48

  2. 8.27

    Magnetic Scalar Potential Between the Poles of a Permanent Magnet. The magnetic scalar potential difference between the poles of a magnet is 100 A (Figure 8.49). Calculate the magnetic field intensity if the space between the poles is air and the magnetic field intensity is uniform.

    figure 49

    Figure 8.49

Rights and permissions

Reprints and permissions

Copyright information

© 2021 Springer Nature Switzerland AG

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Ida, N. (2021). The Static Magnetic Field. In: Engineering Electromagnetics. Springer, Cham. https://doi.org/10.1007/978-3-030-15557-5_8

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-15557-5_8

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-15556-8

  • Online ISBN: 978-3-030-15557-5

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics

Search

Navigation