Vector Algebra

Abstract

Vector algebra is the algebra of vectors: a set of mathematical rules that allows meaningful and useful operations in the study of electromagnetics. We will define vectors and the necessary operations shortly, but, for now, it is useful to remember the following axiom which will be followed throughout this book: Nothing will be defined, no quantity or operation will be used, unless it has some utility either in explaining the observed physical quantities or otherwise simplifies the discussion of a topic. This is important because, as we increase our understanding of the subject, topics may seem to be disconnected, particularly in this and the following chapter. The discussion of vector algebra and vector calculus will be developed separately from the ideas of the electromagnetic field but for the purpose of describing the electromagnetic field. It is also implicit in this statement that by doing so, we should be able to simplify the discussion of electromagnetics and, necessarily, better understand the physical properties of fields.

The vector analysis I use may be described either as a convenient and systematic abbreviation of Cartesian analysis… In this form it is not more difficult, but easier to work than Cartesians. Of course, you have to learn it. Initially, unfamiliarity may make it difficult…

—Oliver Heaviside (1850–1925), a self-taught mathematician and electrical engineer in his introduction to Vector Analysis, originally published in 1893 (Electromagnetic Theory, Chelsea Publishing Co., N.Y., 1971, Vol. 1, p. 135).

Problems

1.1.1 Vectors and Scalars

• 1.1 Two points P₁(1,0,1) and P₂(6,–3,0) are given. Calculate:

  • (a) The scalar components of the vector pointing from P₁ to P₂.

  • (b) The scalar components of the vector pointing from the origin to P₁.

  • (c) The magnitude of the vector pointing from P₁ to P₂.

• 1.2 A ship is sailing in a north–east direction at a speed of 50 km/h. The destination of the ship is 3,000 km directly east of the starting point. Note that speed is the absolute value of velocity:

  • (a) What is the velocity vector of the ship?

  • (b) How long does it take the ship to reach its destination?

  • (c) What is the total distance traveled from the starting point to its destination?

1.1.2 Addition and Subtraction of Vectors

• 1.3 An aircraft flies from London to New York at a speed of 800 km/h. Assume New York is straight west of London at a distance of 5,000 km. Use a Cartesian system of coordinates, centered in London, with New York in the negative x direction. At the altitude the airplane flies, there is a wind, blowing horizontally from north to south (negative y direction) at a speed of 100 km/h:

  • (a) What must be the direction of flight if the airplane is to arrive in New York?

  • (b) What is the speed in the London–New York direction?

  • (c) How long does it take to cover the distance from London to New York?

• 1.4 Vectors A and B are given: $\mathbf{A}=\hat{\mathbf{x}}5+\hat{\mathbf{y}}3-\hat{\mathbf{z}}1$ and $\mathbf{B}=-\hat{\mathbf{x}}3+\hat{\mathbf{y}}5-\hat{\mathbf{z}}2$. Calculate:

  • (a) ∣A∣.

  • (b) A + B.

  • (c) A – B.

  • (d) B – A.

  • (e) Unit vector in the direction of B – A.

1.1.3 Sums and Scaling of Vectors

• 1.5 Three vectors are given as: $\mathbf{A}=\hat{\mathbf{x}}3+\hat{\mathbf{y}}1+\hat{\mathbf{z}}3,\mathbf{B}=-\hat{\mathbf{x}}3+\hat{\mathbf{y}}3+\hat{\mathbf{z}}3$ and $\mathbf{C}=\hat{\mathbf{x}}-\hat{\mathbf{y}}2+\hat{\mathbf{z}}2$:

  • (a) Calculate the sums A + B + C, A + B – C, A – B – C, A – B + C, A + (B – C), and (A + B) – C using one of the geometric methods.

  • (b) Calculate the same sums using direct summation of the vectors.

  • (c) Comment on the two methods in terms of ease of solution and physical interpretation of results.

• 1.6 A geostationary satellite is located at a distance of 35,786 km above the equator. At that position it is stationary above a fixed point on the planet (i.e. it appears motionless when viewed from Earth). To force the satellite to re-enter the atmosphere a rocket is fired in the direction of motion of the satellite reducing its speed by 1,000 km/h. If the radius of the planet is 6378 km and the time for one rotation is exactly 24 h find:

  • (a) The velocity vectors before and after the rocket is fired.

  • (b) The scaling factor for the velocity produced by this action.

• 1.7 A particle moves with a velocity $\mathbf{v}=\hat{\mathbf{x}}300+\hat{\mathbf{y}}50-\hat{\mathbf{z}}100$ [m/s]. Now the velocity is reduced by a factor of 2:

  • (a) Calculate the direction of motion of the particle.

  • (b) What is the speed of the particle?

• 1.8 Given a quadrilateral a, b, c, d that has no parallel sides, show, using vector algebra, that the midpoints of its four sides, marked as A, B, C, D in Figure 1.33 form the vertices of a parallelogram, that is that AB is parallel to DC and AD is parallel to BC.

  

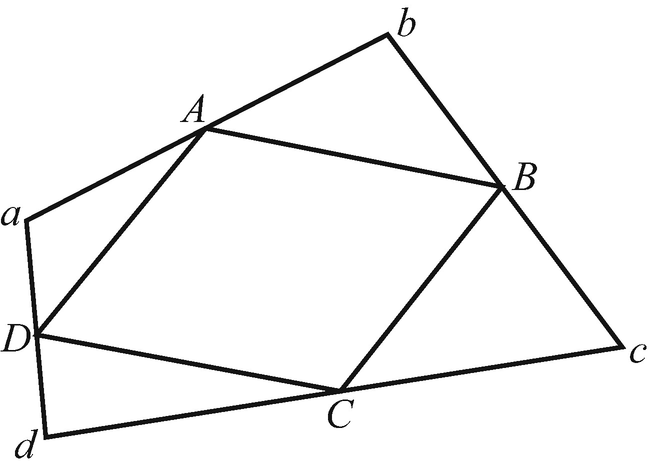
  Figure 1.33

1.1.4 Scalar and Vector Products

• 1.9 Calculate the unit vector normal to the plane 3x + 4y + z = 0.

• 1.10 Two vectors ${\mathbf{v}}_1=\hat{\mathbf{x}}3+\hat{\mathbf{y}}1-\hat{\mathbf{z}}2$ [m/s] and ${\mathbf{v}}_2=-\hat{\mathbf{x}}2+\hat{\mathbf{y}}3$ [m/s] describe the velocities of two objects in space:

  • (a) Calculate the angle between the trajectories of the two objects.

  • (b) If the ground coincides with the x–y plane, calculate the ground velocities of each object.

  • (c) What is the angle between the ground velocities?

• 1.11 Find a unit vector normal to the following planes, at the given point:

  • (a) z = −x – y, at point P(0,0,0).

  • (b) 4x – 3y + z + 5 = 0, at point P(0,0,–5).

  • (c) z = ax + by, at point P(0,0,0).

• 1.12 A force is given as $\mathbf{F}=\hat{\mathbf{x}}a/x\left[\mathrm{N}\right]$ where a is a given constant and x is a variable. Calculate the vector component of F in the direction of the vector $\mathbf{A}=\hat{\mathbf{x}}3+\hat{\mathbf{y}}1-\hat{\mathbf{z}}2$.

• 1.13 Write a formula for calculation of the area of a general triangle defined by its three vertex points: P₁(x₁,y₁,z₁), P₂(x₂,y₂,z₂) and P₃(x₃,y₃,z₃).

• 1.14 Show using vector algebra that the law of sines holds in the triangle in Figure 1.34, where A, B, and C are the lengths of the corresponding sides; that is, show that the following is correct:

  

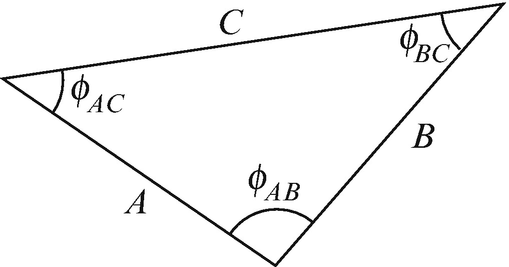
  Figure 1.34

  $$ \frac{A}{\sin {\phi}_{BC}}=\frac{B}{\sin {\phi}_{AC}}=\frac{C}{\sin {\phi}_{AB}}. $$

• 1.15 Given the general triangle in Figure 1.34 with sides of length A, B, C, show using vector algebra that the cosines of the angles ϕ_AB, ϕ_AC, ϕ_BC are:

  $$ \cos {\phi}_{AB}=\frac{A^2+{B}^2-{C}^2}{2 AB},\cos {\phi}_{AC}=\frac{A^2+{C}^2-{B}^2}{2 AC},\cos {\phi}_{BC}=\frac{B^2+{C}^2-{A}^2}{2 BC}, $$

• 1.16 A vector is given as $\mathbf{A}=\hat{\mathbf{x}}3+\hat{\mathbf{y}}1-\hat{\mathbf{z}}2$:

  • (a) Find the angle between A and the positive z axis.

  • (b) Find a vector perpendicular to A and a unit vector in the direction of the positive z axis.

• 1.17 A force is given as $\mathbf{F}=\hat{\mathbf{x}}1+\hat{\mathbf{y}}5-\hat{\mathbf{z}}1\left[\mathrm{N}\right]$. Calculate the magnitude of the force in the direction of the vector $\mathbf{A}=-\hat{\mathbf{x}}3+\hat{\mathbf{y}}2-\hat{\mathbf{z}}2$.

• 1.18 Three vertices of a parallelogram are given as P₁(7,3,1), P₂(2,1,0), and P₃(2,2,5):

  • (a) Find the area of a parallelogram with these vertices.

  • (b) Is the answer in (a) unique: that is, is there only one parallelogram that can be defined by these points? If not, what are the other possible solutions?

• 1.19 A plane through the origin of the system of coordinates is defined by two points: P₁(1,2,−1) and P₂(5,3,2). Find the equation of the plane.

1.1.5 Multiple Products

• 1.20 Three vectors are given as $\mathbf{A}=\hat{\mathbf{x}}3-\hat{\mathbf{y}}x-\hat{\mathbf{z}}2x$, $\mathbf{B}=-\hat{\mathbf{x}}2x+\hat{\mathbf{y}}5$, $\mathbf{C}=\hat{\mathbf{y}}3{x}^2+\hat{\mathbf{z}}y$:

  • (a) Calculate the product A ċ (B × C).

  • (b) Calculate the product B × (A × C).

  • (c) Calculate the product (A × B) ċ C.

• 1.21 To define the volume of a parallelepiped, we need to define a corner of the parallelepiped and three vectors emanating from this point (see Exercise 1.11). Four corners of a parallelepiped are known as P₁(0,0,0), P₂(a,0,1), P₃(a,2,c), and P₄(1,b,1):

  • (a) Show that there are six vectors that can be defined using these nodes, but only three vectors, emanating from a node, are necessary to define a parallelepiped.

  • (b) Show that there are four possible parallelepipeds that can be defined using these four nodes, depending on which node is taken as the root node.

  • (c) Calculate the volumes of the four parallelepipeds.

• 1.22 Which of the following vector products yield zero and why? A, B, and C are vectors and C = A × B.

  • (a) A × (A × B).     (e) B × (A × B).

  • (b) A × (B × B).     (f) (A × A) × B.

  • (c) C × C.        (g) A × C.

  • (d) (A × B) × C.     (h) (C × A) × B.

• 1.23 Which of the following products are properly defined and which are not? Explain why. (a and b are scalars, A, B, and C are vectors.)

  • (a) abA × C.      (d) (A × B) ċ A.

  • (b) A × C × B.     (e) aB ċ C.

  • (c) B ċ C × A.      (f) (aB × bA).

• 1.24 Which of the following products are meaningful? Explain. A, B, C are vectors and C = B × A; c is a scalar.

  • (a) A ċ (B × C).     (e) (A ċ B) ċ C.

  • (b) cA ċ (A × B).     (f) A ċ (C × B).

  • (c) C ċ C.       (g) A ċ (A × C).

  • (d) (A ċ B) × (A × B).  (h) A ċ (A × A).

• 1.25 Vectors $\mathbf{A}=\hat{\mathbf{x}}1+\hat{\mathbf{y}}1+\hat{\mathbf{z}}2$, $\mathbf{B}=\hat{\mathbf{x}}2+\hat{\mathbf{y}}1+\hat{\mathbf{z}}2$, and $\mathbf{C}=\hat{\mathbf{x}}1-\hat{\mathbf{y}}2+\hat{\mathbf{z}}3$ are given. Find the height of the parallelepiped defined by the three vectors:

  • (a) If A and B form the base.

  • (b) If A and C form the base.

  • (c) If B and C form the base.

1.1.6 Scalar and Vector Fields

• 1.26 A pressure field is given as P = x(x – 1)(y – 2) + 1:

  • (a) Sketch the scalar field in the domain 0 < x,y < 1.

  • (b) Find the point(s) at which the slope of the field is zero.

• 1.27 Sketch the scalar fields

  $$ A=x+y,\kern1em B=x-y,\kern1em c=\frac{x+y}{\sqrt{x^2+{y}^2}}. $$

• 1.28 Sketch the vector fields

  $$ \mathbf{A}=\hat{\mathbf{x}}y+\hat{\mathbf{y}}x,\kern1em \mathbf{B}=\hat{\mathbf{x}}y-\hat{\mathbf{y}}x,\kern1em \mathbf{C}=\frac{\hat{\mathbf{x}}x+\hat{\mathbf{y}}y}{\sqrt{x^2+{y}^2}}. $$

1.1.7 Systems of Coordinates

• 1.29 Three points are given in Cartesian coordinates: P₁(1,1,1), P₂(1,1,0), and P₃(0,1,1):

  • (a) Find the points P₁, P₂, and P₃ in cylindrical and spherical coordinates.

  • (b) Find the equation of a plane through these three points in Cartesian coordinates.

  • (c) Find the equation of the plane in cylindrical coordinates.

  • (d) Find the equation of the plane in spherical coordinates.

• 1.30 Write the equation of a sphere of radius a:

  • (a) In Cartesian coordinates.

  • (b) In cylindrical coordinates.

  • (c) In spherical coordinates.

• 1.31 A sphere of radius a is given. Choose any point on the sphere. Describe this point:

  • (a) In spherical coordinates.

  • (b) In Cartesian coordinates.

  • (c) In cylindrical coordinates.

• 1.32 Two points are given in cylindrical coordinates as P₁(3,π/6,−1) and P₂(−2,0,2).

  • (a) Write the vector connecting P₁(tail) to P₂(head) in cylindrical coordinates.

  • (b) Write the vector connecting P₂(tail) to P₁(head) in spherical coordinates.

  • (c) Find the length of the vectors in (a) and (b).

• 1.33 Two points are given in spherical coordinates as P₁(0,36°,−72°) and P₂(5,−120°,45°).

  • (a) The magnitude of the vector connecting P₁(tail) to P₂(head).

  • (b) The unit vector in the direction of the vector in (a) in cylindrical coordinates.

  • (c) The unit vector in the direction of the vector in (a) in spherical coordinates.

• 1.34 Transform the vector $\mathbf{A}=\hat{\mathbf{x}}2-\hat{\mathbf{y}}5+\hat{\mathbf{z}}3$ into spherical coordinates at (x = −2, y = 3, z = 1). That is, find the general transformation of the vector and then substitute the coordinates of the point to obtain the transformation at the specific point.

• 1.35 Vector $\mathbf{A}=\hat{\mathbf{r}}3\cos \phi -\hat{\boldsymbol{\upphi}}2{r}^{1/2}+\hat{\mathbf{z}} r\phi$ is given:

  • (a) Transform the vector to Cartesian coordinates.

  • (b) Find the scalar components of the vector in spherical coordinates.

1.1.8 Position Vectors

• 1.36 Points P₁(x₁,y₁,z₁) and P₂(x₂,y₂,z₂) are given:

  • (a) Calculate the position vector r₁ of point P₁.

  • (b) Calculate the position vector r₂ of P₂.

  • (c) Calculate the vector R connecting P₂(tail) to P₁(head).

  • (d) Show that the vector R can be written as R = r₁ – r₂.

• 1.37 Two points on a sphere of radius 3 are given as P₁(3,0°,30°) and P₂(3,45°,45°):

  • (a) Find the position vectors P₁ and P₂ pointing to P₁ and P₂ respectively.

  • (b) Find the vector connecting P₁(tail) to P₂(head).

  • (c) Using the vectors in (a) write the vector P₁P₂ (P₁ tail, to P₂ head) in cylindrical and Cartesian coordinates.

• 1.38 Given the position vectors $\mathbf{A}=\hat{\mathbf{x}}{A}_x+\hat{\mathbf{y}}{A}_y+\hat{\mathbf{z}}{A}_z$ and $\mathbf{B}=\hat{\mathbf{x}}{B}_x+\hat{\mathbf{y}}{B}_y+\hat{\mathbf{z}}{B}_z$, find the equation of the plane they form.