Keywords

1 Introduction

At the heart of research in mathematics education is a desire that all students become competent and confident in mathematics. Unfortunately, this does not describe a multitude of students in educational settings around the world (Mullis, Martin, Foy, & Arora, 2012; Topper, 2011). In particular, females’ success in mathematics is often hampered by negative gender stereotypes (Good, Rattan, & Dweck, 2012). This research focuses on differences by gender in a common undergraduate mathematics course, introductory statistics.

Students’ beliefs about themselves as learners of mathematics play a key role in their mastery of mathematics (Nurmi, Hannula, Maijala, & Pehkonen, 2003; Schoenfeld, 1992). Dweck’s (1999) seminal research on the role of students’ implicit theories of intelligence, also referred to as mind-sets, examines students’ beliefs about knowledge acquisition. Dweck (2006) identified two implicit theories of knowledge: incremental and entity. Incremental theorists, also referred to as individuals with growth mind-sets, believe that intelligence is malleable and can be increased with effort (Bruning, Schraw, & Norby, 2011). Entity theorists view intelligence as unchangeable and are referred to as having fixed mind-sets (Dweck & Leggett, 1988). Effort cannot influence intelligence in an entity mind-set since intelligence is fixed. These mind-sets play an important role in academic persistence and achievement, both of which are important for college success (Good et al., 2012). Research has shown that mind-sets can be altered and that targets of stereotype threat decrease achievement gaps with mind-set training (Aronson, Fried, & Good, 2002).

This research is a continuation of a previous study on the role of mind-set training in introductory statistics college courses which noted that students who received mind-set training decreased in effort expended to learn statistics at a statistically significant greater rate while demonstrating less mastery of statistical content (Zonnefeld, 2015). One limitation of the previous research was a change in instructors and number of course credits and requirements between the control group and treatment group.

This follow-up research expands Dweck’s important body of research by focusing on the differences within each treatment group by gender. All students completed both a pre-test and post-test which examined attitudes towards statistics and mastery of statistics. Students in the treatment group received training in incremental theories of intelligence throughout the semester during which they were enrolled in introductory statistics. Effects of incremental mind-set training were examined regarding student attitudes toward statistics and student mastery of statistical content by gender in both the control and treatment groups. Two research questions guide this research:

  1. 1.

    What differences exist by gender in the change in students’ attitudes toward statistics for students who received training in an incremental mind-set and those who did not when controlling for initial attitudes?

  2. 2.

    What differences exist by gender in mastery of statistics for students who received training in an incremental mind-set and for those who did not when controlling for initial mastery?

Research on implicit theories of knowledge has grown rapidly in recent decades. Unfortunately, only a handful of studies have examined creating a growth mind-set in the mathematics classroom (Kim & Kellert, 2010). This research answers the call from Dweck (2008) to “study ways in which the education environment can teach and support a growth mind-set over time” (p. 2). Shores and Smith (2010) have also called for future research, specifically in mathematics education, to focus on developing strategies to improve students’ implicit theories of knowledge with the goal of helping students develop methods to cope with failure. This research heeds the call by examining the role of mind-set training by gender in introductory statistics courses.

According to the Organisation for Economic Co-operation and Development, college graduation rates vary from 22 to 60% worldwide (Weston, 2014). Pang (2010) suggested that improving students’ experiences in mathematics courses will increase the perseverance of many aspiring college graduates. Statistics is a unique mathematics course that is required for many undergraduate students and the number of students who take statistics continues to grow (Onwuegbuzie & Wilson, 2003). Unfortunately, many of the students enrolled in statistics would not choose to take the course if it were not a program requirement (Cook, 2010). Subsequently, statistics becomes a ‘problem subject’ for many students (Onwuegbuzie & Wilson, 2003). An examination of possible methods to support students is valuable and timely.

Recent decades “have seen an extraordinary level of activity focused on how students learn statistics” (Aliaga et al., 2005, p. 8). Unfortunately, given the growth of research in both implicit theories of intelligence and statistics education, a paucity of research exists connecting mind-sets, attitudes, and achievement in statistics courses. Results of this study add to the knowledge base of implicit theories of knowledge and support continuous improvement in undergraduate statistics pedagogy.

One limitation to the generalisability of this study is the statistics curriculum implemented by the college. All course sections used a reform-based statistics curriculum which was under development. The curriculum utilised simulation-based methods which introduced inference earlier in the semester (Tintle et al., 2016). This curriculum was in its final stages of development and was not expected to be a factor in the study.

The quasi-experimental design of this study was a limitation since it only allowed for conclusions of association, not causation. A delimitation of the sample was that it was comprised of students from one college who enrolled in a specific statistics course. This also limits the generalisability of the findings.

An additional limitation of this research was the role of the environment. There is evidence that the educator affects the learning, attitude, and even mind-set of students in their class (Cutts, 2008; Dweck, 2008). The professors for the treatment classes were debriefed on the study, theories of intelligence, and the role of the teacher in fostering incremental mind-sets in an effort to create a supportive classroom environment. Unfortunately, different instructors were used for the control and treatment groups. Additionally, the number of credits increased from 3-credits to 4-credits from the control to the treatment semester.

The remainder of this paper is organised as follows. Section two reviews relevant research followed by section three which outlines the methodology utilised. Section four shares the results of the study and statistical analysis followed by conclusions in section five.

2 Relevant Literature

A review of relevant literature begins with current research on undergraduate statistics. This is followed by theoretical foundations, cognitive learning theory, and closes with gender stereotypes.

2.1 Undergraduate Statistics Courses

A common roadblock on many students’ path to graduation is successfully completing a college-level mathematics course (Topper, 2011); this is a momentum point that is “very strongly correlated with postsecondary achievement” (Leinbach & Jenkins, 2008, p. 20). Introductory mathematics courses have earned the title ‘gatekeeper to achieving a college degree’ with Bryk and Treisman (2010) arguing that “math should be a gateway, not a gatekeeper, to a successful college education” (p. 1).

A commonly required mathematics course in many undergraduate programs is introductory statistics (Ruggeri, 2011). Statistics is a unique mathematics course that combines quantitative skills with analysis. As a result of the need for analytical skills in a diverse set of professions, the number of students required to take statistics has rapidly increased in the past half century making statistics the most common subject across disciplines (Ruggeri, 2011). Statistics has morphed from a course taught to “a narrow group of future scientists in agriculture and biology, to a family of courses, taught to students at many levels, from pre-high school to post-baccalaureate, with very diverse interests and goals” (Aliaga et al., 2005, p. 7).

As a mathematics course, statistics creates an obstacle for undergraduates, as many students experience anxiety and negative attitudes toward the subject (Evans, 2007; Ruggeri, 2011; Ruggeri, Dempster, Hanna, 2008a; Ruggeri et al., 2008b). As student diversity has increased in introductory statistics courses, so have the demands. “Today’s teachers face challenges of motivation and exposition that are substantially greater than those of half a century ago” (Aliaga et al., 2005, p. 7). With the increase in diversity of undergraduate majors, students may not see the relevance of statistics in their lives, contributing to a struggle for motivation (Kim & Kellert, 2010).

One response to poor performance in introductory mathematics courses and low undergraduate retention rates is increasing the academic entrance requirements for students; however, ability is not the sole predictor of success (Lucio, Rapp-Paglicci, & Rowe, 2011). Educators recognise that students of similar abilities often achieve at vastly different levels (Boese, Stewart, Perry, & Hamm, 2013).

Cognitive learning theory may give insight into the disparity seen between students’ achievements and their ability levels. While promising research has been conducted on mathematical mind-sets concerning students’ belief in their ability to learn mathematics, no research is available on the impact of training in incremental theories of intelligence on their achievement and attitudes in introductory statistics courses. The next section will outline theoretical foundations for the research.

2.2 Theoretical Foundations

While there is not a clear consensus regarding the theoretical frameworks to conceptualise affect in mathematics education (Hannula, 2004), I chose to use DeBellis and Goldin’s (1997) framework of four concepts in affect research: emotions, attitudes, beliefs, and values as it encompassed the aspects that best fit my research questions and the instruments chosen.

Beliefs are an important concept in affect. An examination of a student’s epistemological beliefs regarding mathematical knowledge and its acquisition can reveal important keys to student affect and achievement since beliefs “act as a filter” influencing all thoughts and actions (Nurmi et al., 2003, p. 454). Schommer (1990) suggested that student’s beliefs regarding knowledge are complex and vary on four dimensions: simple knowledge, certain knowledge, fixed ability, and quick learning. See Fig. 9.1 for descriptions of each.

Fig. 9.1
figure 1

Schommer’s (1990) framework of beliefs regarding knowledge

Full size image

Implicit theories of knowledge focuses on the third and fourth dimensions of fixed ability and quick learning. The next section discusses cognitive learning theory in detail.

2.3 Cognitive Learning Theory

Cognitive learning theory focuses on metacognition, the effects of underlying thought processes on the learner. Students do more than gain knowledge and master skills while learning; they simultaneously build beliefs about their ability to be successful learners (Boekaerts, Otten, & Voeten, 2003). This section starts with an examination of the role of attitudes in statistics education, followed by attribution theory and closes with mind-set theory.

2.3.1 Attitudes

Student attitudes play an important factor in academic achievement creating a challenge for professors as anxiety and negative attitudes towards statistics are common (Chiesi & Primi, 2010; Evans, 2007; Kesici, Baloğlu, & Deniz, 2011; McGrath, 2014; Onwuegbuzie & Wilson, 2003; Ruggeri et al., 2008a, 2008b). Chiesi and Primi (2010) examined undergraduate students enrolled in introductory statistics both before and after the semester using the Student Attitudes Towards Statistics—36© (SATS) instrument finding that attitudes at the beginning of the semester were related to achievement at the end of the course. An additional relationship indicated that students’ attitudes at the beginning of the semester were directly related to their mathematical knowledge. This creates a challenge for many instructors since students enter introductory statistics with a wide variety of mathematical backgrounds. Evans (2007) found similar correlations between attitudes and achievement in statistics classes while Bandalos, Yates, and Thorndike-Christ (1995) observed a negative relationship between students’ efficacy and their anxiety about statistics.

It is clear that attitudes impact students’ achievement in statistics. Unfortunately, Evans (2007) found no methods in his research for instructors to help improve student attitudes. More research is necessary to understand and address the issues of statistics anxiety and negative attitudes toward statistics (Ruggeri et al., 2008a, b).

2.3.2 Attribution Theory

Bernard Weiner contributed a key advance in metacognition through attribution theory. Attributions are an important aspect of cognitive learning theory that can have both positive and negative influences on students. Attribution theory was proposed by Weiner (1985) in the mid-eighties and since then, has been promoted by educators and educational psychologists as an effective method to improve achievement and motivation for students with academic difficulties (Banks & Woolfson, 2008; Robertson, 2000). Attributions are classified along three dimensions: locus, stability, and controllability (Banks & Woolfson, 2008; Boekaerts et al., 2003). Locus refers to the location of the cause as internal or external to the student (Shores & Smith, 2010). Stability is a belief about the possibility of change for the cause and controllability refers to the ability to affect future outcomes (Syed, 2013).

When students fall behind academically, it is important for teachers to understand what is causing their struggle (Shores & Smith, 2010). Of particular concern are failure attributions that are stable and beyond a student’s control (Hall, Hladkyj, Perry, & Ruthig, 2004; Shores & Smith, 2010). Attributions occur frequently in mathematics. Boekaerts et al. (2003) found evidence in their work with 113 middle school students in the Netherlands that attribution patterns are different in mathematics than the subjects of native language and history. Students attribute success in mathematics to effort, but failure to ability (Boekaerts et al., 2003). Effort is an important causal attribution since it is closely tied to a growth mind-set. Students will use effort attributions only if they believe that their intelligence can be improved. This concurs with research from Harari and Covington (1981) who found that students who used effort attributions persisted longer in tasks following a failure.

Connections between attributions and self-efficacy have also been observed. Students who believed they were lower achievers, regardless of their teacher’s perception of ability, displayed more maladaptive attributions (Banks & Woolfson, 2008). This finding points to the importance of attributions not only to low-achievers, but also for students who perceive themselves as low-achievers. Attribution theory is a foundation for mind-set theory and continues to play an important role in students’ behaviours.

2.3.3 Mind-Set Theory

Mind-set theory expands upon the foundation built by Weiner (1985) in attribution theory to a more comprehensive approach as it not only looks back explaining reasons for success or failure, but also looks forward to include goals (Dweck, 1999). An impetus for the introduction of mind-set theory is new research in cognitive neuroscience. Research in recent decades has revealed how the brain functions and that its ability to grow and increase in intelligence is much greater than was previously assumed (Cutts, 2008; Dweck, 2010; Good, Aronson, & Inzlicht, 2003). Knowledge about the increased neuroplasticity of the brain has powerful effects for individuals.

Mind-sets are metacognitive processes that an individual holds concerning beliefs about their cognitive abilities (Burns & Isbell, 2007; Mangels, Butterfield, Lamb, & Dweck, 2006). Anderson (1995) referred to mind-sets as knowledge structures that influence affective reactions and behaviours. It should be noted that mind-sets are domain specific (Dweck & Leggett, 1988) and affect motivation, goal setting, and persistence. In a typical population, approximately forty percent of individuals identify with the entity mind-set and forty percent relate to the incremental mind-set with the remaining twenty percent of individuals not consistent enough in their responses to be classified as holding either theory (Dweck, 2008).

Entity theorists hold fixed mind-sets and see their environments and abilities as set with little that can be done to alter them (Dweck & Leggett, 1988). They believe that an examination of their current abilities predicts their future capacity (Dweck, 1999). Students with a fixed mind-set feel smart with easy, low-effort successes, outperforming other students (Dweck, 1999). The self-imposed rule to look smart prohibits entity theorists from seeking remediation when necessary. Students’ theory of intelligence affects their behaviours with students holding entity mind-sets responding differently to failure (Burns & Isbell, 2007). Entity mind-sets are in contrast to the incremental mind-sets held by other students.

Incremental theorists hold a growth mind-set and believe that intelligence can be developed. They do not fear challenges or failure, but feel smart when they are fully engaged, stretching themselves, and putting their skills to use (Dweck, 1999). Incremental theorists thrive when they are growing and learning.

Evidence is mounting regarding the role that students’ mind-sets play in learning mathematics. Research has shown that students with fixed mind-sets towards mathematics and science ability “are at a significant disadvantage compared to students who believe that their abilities can be developed” (Dweck, 2008, p. 1). In a study of seventh-grade students, teachers, who were blind to treatment, chose three times as many students in the growth treatment group as showing marked improvement in their motivation compared to those in the control group (Blackwell, Trzesniewski, & Dweck, 2007). One of the largest areas of difference between the entity and incremental mind-sets is in students’ goal setting.

Theory of intelligence is a reliable predictor of student’s goal orientation (Dweck & Leggett, 1988; Heyman & Dweck, 1998). Individuals that hold entity mind-sets tend toward performance goals, while individuals with incremental mind-sets favour mastery goals. Performance goals focus on demonstrating an individual’s competence. Mastery goals focus on mastering a skill. An individual with this mastery goal will not see failing as a failure, but as a learning experience.

Goal orientation also affects individuals’ views of effort. Dweck and Leggett (1988) found evidence that students with performance goals viewed effort and ability as inversely related. It is this irony that can be paralysing to students with performance goals. When they most need to exert extra effort, they draw back in a defensive response fearing that investing effort reveals their ability as deficient. In contrast to this, mastery goals provide an inoculation to failure in many students since failure is not alarming, but rather, an opportunity to learn (Dweck & Leggett, 1988). Mastery goals are associated with students who seek out challenging tasks, increase motivation, and strive under failure (Grant & Dweck, 2003).

Fortunately, there is evidence that mind-sets are dynamic and that individuals’ tendencies change as they grow and develop with training in an incremental mind-sets showing good potential in many studies (Anderson, 1995; Donohoe, Topping, & Hannah, 2012; Kim & Kellert, 2010). Training has also been linked to increased resiliency and academic performance in students (Donohoe et al., 2012).

While a majority of mind-set research discusses implicit theories of intelligence in a favourable light, there are also criticisms. Donohoe et al. (2012) questioned if it is possible to make a large difference in mind-set with only brief interventions. They, along with Blackwell et al. (2007), raised concerns about the longevity of the positive effects of implicit theory interventions. Some conflicting evidence has also arisen regarding the connection between mind-set and academic achievement (Blackwell et al., 2007). Furnham, Chamorro-Premuzic, and McDougall (2002) found evidence in a British study of college students that students’ mind-sets were not related to achievement, but to their personality. The closing section of the literature review will examine research regarding gender stereotypes in mathematics.

2.4 Gender Stereotypes

The mathematics community has historically utilised a talent-driven approach to mathematics, emphasising that mathematics ability is innate (Clinkenbeard, 2015; Good et al., 2012; Leslie, Cimpian, Meyer, & Freeland, 2015). Alongside this emphasis is a persistent stereotype that males are more capable of mathematical thinking and quantitative reasoning than females (Dweck, 2008; Good et al., 2012; Steel & Aronson, 1995). At their heart, stereotypes represent entity mind-set beliefs. They are erroneous knowledge structures that apply fixed abilities to certain groups of people (Anderson, 1995; Dweck, 2008). Aronson et al. (2002) found that stereotype targets behave similar to entity theorists when their gender is made salient by choosing easier, success-assuring tasks.

The combination in mathematics of a talent-driven approach and gender stereotypes creates ideal conditions for stereotype threat. Stereotype threat is a burden that an individual feels to confirm cultural stereotypes which limit his or her academic abilities and achievement (Aronson et al., 2002; Grant & Dweck, 2003) and may provide important insight into why females have been historically under-represented in mathematics fields (Dweck, 2008). “A key factor driving students’ intent to pursue math should be their personal sense that they belong in mathematics” (Good et al., 2012, p. 700). Women who identify with groups that have negative mathematical stereotypes may face obstacles. Aronson and colleagues (2002) claimed that a perceived stereotype could be strong enough to sway a student’s implicit beliefs of intelligence. Students must first “be convinced that anyone can learn mathematics” or they have already crippled themselves by identifying with a ‘have-not’ group” (Clinkenbeard, 2015, p. 28).

Fortunately, there is evidence that training in incremental mind-sets can help females counter the negative effects of stereotypes. Good et al. (2003) conducted a study in which college students mentored seventh-grade students who were at-risk of stereotype threat. Students were divided into four groups. The first group received mentoring that encouraged a growth mind-set, the second group received mentoring concerning the transition to middle school, and the third group received both the growth mind-set and transition mentoring. The final group received an anti-drug message and served as a control for the experiment. At the end of the school year, females trained in the incremental mind-set received significantly higher scores on a standardised maths test (Good et al., 2003). Additionally, females showed greater gains than males and decreased the achievement gap. This finding supports Dweck’s (2008) conclusion that females with growth mind-sets are less at risk of negative effects from stereotypes.

This review has examined literature regarding undergraduate statistics, theoretical foundations supporting the research, cognitive learning theory and the impact of gender stereotypes on female’s mathematics achievement. The next section will examine the methods used to conduct the research.

3 Method

3.1 Population and Sample

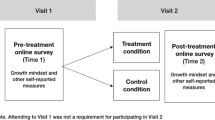
The population for this study was undergraduate students at a small, faith-based, liberal arts university located in the United States. This study made use of a pre-test/post-test design. The research was quasi-experimental since a treatment was applied, but the sample was not randomly selected. The sample consisted of students who enrolled in introductory statistics in the semesters under examination and completed all aspects of the research.

The treatment group consisted of 121 students enrolled in introductory statistics courses during the experiment with a gender breakdown of 47.8% female and 52.2% male. The response rate was 52.9% resulting in 64 students who completed pre-test and post-test assessments in the four introductory statistics classes between August 2014 and May 2015.

The control group consisted of 234 students who enrolled in introductory statistics during August 2013 to May 2014. The response rate was 47.4% resulting in 111 students who completed pre-test and post-test assessments. The gender distribution in the control group was similar to the treatment group with 52.3% female and 47.7% male.

3.2 Instrumentation

Two instruments were used to assess each student’s attitude toward statistics and mastery of statistical knowledge: The Student Attitudes Towards Statistics—36© (SATS) and the Comprehensive Assessment of Outcomes in a first Statistics course (CAOS). Both instruments were implemented at the beginning and the end of the course. Since both instruments were pre-existing with established reliability and validity, a pilot study was not conducted.

The SATS© (Schau, 2003) instrument was selected to assess each student’s attitude since it has been widely used in statistics education research (Bond, Perkins, & Ramirez, 2012; Chiesi & Primi, 2010; Coetzee & van der Merwe, 2010; Harpe, Phipps, & Alowayesh, 2012; Swanson, Vander Stoep, & Tintle, 2014). The 36-item online SATS© tool provided a valid representation of students’ attitudes regarding statistics. Each item required a response on a seven-point Likert scale. Responses were grouped into six components of attitude: affect, cognitive competence, value, difficulty, interest, and effort. Internal consistency for all components of the SATS© (.66 < α < .85) was established (delMas, Garfield, Ooms, & Chance, 2007). See Fig. 9.2 for sample questions.

Fig. 9.2
figure 2

Examples of SATS© component questions. The asterisk (*) represents a reversed scored item

Full size image

The CAOS (delMas et al., 2007) measures mastery of statistical concepts and has been implemented widely in statistical education research (Hannigan, Gill, & Leavy, 2013; Slauson, 2008; Tintle, Vander Stoep, Holmes, Quisenberry, & Swanson, 2011; Tintle, Rogers, Chance, Cobb, Rossman, Roy, . . . & Vander Stoep 2014; Zieffler, 2007). The 40-item instrument was administered online to assess students’ mastery of statistics at both the beginning and at the end of each semester. Internal consistency for all components of the CAOS (α < .77) was established by Nolan, Beran, and Hecker (2012).

3.3 Growth Mind-Set Treatments

The incremental mind-set treatment was given to all students in the four introductory statistics classes between August 2014 and May 2015 which comprised the treatment group. The training was designed using materials and findings from successful interventions in the review of literature. The treatment consisted of four incremental mind-set-training sessions throughout each semester. The goal of the sessions was to help students understand how the brain functions biologically with a focus on the malleability of intelligence. In this study, each of the four 15-minute training sessions was implemented approximately three weeks apart. Each session occurred during class time and was led by the researcher to ensure consistency. Verbal permission to conduct the trainings was granted by the professors responsible for teaching each of the introductory statistics courses.

A number of approaches have successfully been employed to alter students’ mental constructs. Both attribution training and mind-set training have employed the use of videos (Boese et al., 2013), reading activities (Kim & Kellert, 2010), writing activities (Aronson et al., 2002; Hall et al., 2004), and computer-assisted instruction (Donohoe et al., 2012). In his study of attribution training, Robertson (2000, p. 118) found that no single medium was more effective than others. Given this finding, multiple approaches were implemented in an effort to differentiate the treatment delivery and connect with a variety of students in different methods.

The design of the sessions was adapted from the research of Berkeley, Mstropieri, and Scruggs (2011), Boese and colleagues (2013), Burk (2011), Cutts (2008), Hall and colleagues (2004), and Sriram (2010) implementing combinations of a brief video, article, presentation, or activity which introduced concepts in incremental theory including mind-sets, the physiology of the brain, response to feedback, goals, and the role of effort. Following the success that Robertson (2000) found when combining strategy instruction with reattribution training, students were also given guidance in the sessions on successful techniques for mastering statistics. Dweck supported this approach with the rationale that telling a student to try harder is not enough without providing strategies to do so (Sparks, 2013). Pinxten et al. (2014) concur stating that “domain-specific interventions are more effective” than general interventions (p. 170). Students in the treatment were given guidance throughout each semester on how to respond to challenges and negative feedback in the course. They were also directed to resources to help improve their mastery of statistics including online material and tutoring that was available on campus, free of charge.

A consolidation activity closed each treatment to help students personalise the new information they received (Hall et al., 2004). The consolidation took the form of a small group discussion or an individual writing task. See Fig. 9.3 for the focus of each of the sessions.

Fig. 9.3
figure 3

Treatment outline. An outline of each incremental mind-set training session

Full size image

3.4 Data Collection

The SATS© and CAOS instruments were administered online, outside of class during the first week of class and again during the last week of class for the semester. The CAOS assessments had been regular requirements of introductory statistics classes for the institution since the fall of 2011 in conjunction with a grant for the National Science Foundation. Similarly, the SATS© assessments had been regularly assessed since fall of 2013 in conjunction with the same grant.

Students who completed, at the minimum, the initial opt-out screen of all pre-assessments received credit for a daily assignment. Similarly, students who completed, at the minimum, the initial opt-out screen of all post-assessments received credit for a daily assignment.

The procedure for conducting the assessments ensured that students received the information and had adequate time to complete them. Students were introduced to the assessments during the first class period by the class instructor. After class on the first day, all students received an e-mail invitation with links to the assessments and a brief explanation of the purpose and procedures of the study. Each assessment was run through Survey Monkey™ and remained open for one week. A reminder e-mail was sent one day before the assessments closed. A similar process occurred with the post-test for each instrument.

To ensure that all individuals responsible for or affected by this research were informed and protected, appropriate permissions and reviews were completed prior to data collection including permission from the mathematics department and institutional research board of the institution. Additional permission was granted to use CAOS and SATS© data for the control group from an ongoing National Science Foundation study from the principal investigator of the project. Students were assured of the confidentiality of their responses in the invitation. Informed consent was given through an initial opt-out screen for each assessment. This ensured students that they had the opportunity to not participate if they were uncomfortable with an assessment.

3.5 Data Analysis

Robust data analysis procedures were used throughout this research. Prior to any analysis, thorough data screening was employed to ensure that no outliers distorted the data. The threshold to determine and remove univariate outliers was observations beyond five standard deviations of the sample mean. Observations that violated three or more diagnostic measures were removed as bivariate outliers.

Appropriate statistical analyses were employed to address both research questions. An alpha level of .05 was used for all tests. A measure of effect size was calculated for all analyses as it provides an index of the magnitude of the differences between means which is independent of sample size (Warner, 2013). Using Cohen’s (1988) index guidelines, large effect sizes represented measures of .4 and greater, medium effects between .25 and .4 and small effect sizes between .1 and .25. The analysis for each research question follows. A post hoc power analysis indicated adequate power to detect large effects with ANCOVA for the treatment group (NMale = 32, NFemale = 32, d = .40, 1 − β = .88) and medium to large effects for the control group (d = .3, 1 − β = .88, NFemale = 58, NMale = 53); (Faul, Erdfelder, Buchner, & Lang, 2009).

What differences exist by gender in the change in students’ attitudes toward statistics for students who received training in an incremental mind-set and those who did not when controlling for initial attitudes?

The dependent variables for this research question were the post-test components of the SATS© score with covariates of the pre-test components of the SATS© score. The independent variable was the student’s gender: male or female. ANCOVA was used to assess differences in post-test attitude scores while controlling for pre-test SATS© score by gender.

What differences exist by gender in mastery of statistics for students who received training in an incremental mind-set and for those who did not when controlling for initial mastery?

The dependent variable for this research question was the post-test CAOS score with the covariate pre-test CAOS score. The independent variable was the student’s gender: male or female. An ANCOVA was used to assess differences in post-test mastery scores while controlling for pre-test mastery score by gender. The next section will share the results of this research.

4 Results

Section four examines the results of an intervention of incremental mind-set training in a college introductory statistics course. Areas examined included student attitudes toward statistics and student mastery of statistical content. The section opens with an examination of the response rate and sample demographics. The section then explores particular findings for each research question.

4.1 Response Rate and Demographics

The sample included all students who completed pre-test and post-test assessments in the introductory statistics classes between August 2013 and May 2015. The gender breakdown in the treatment group was evenly distributed with 32 females and 32 males. Adequate power was achieved to detect large effects (d = .4, 1 − β = .88, NFemale = 32, NMale = 32) (Faul et al., 2009). The control group consisted of students enrolled in the introductory statistics course prior to the treatment between August 2013 and May 2014. The gender breakdown in this group was evenly distributed with 58 females and 53 males. Adequate power was achieved to detect medium to large effects (d = .3, 1 − β = .88, NFemale = 58, NMale = 53) (Faul et al., 2009).

4.2 Attitude Toward Statistics

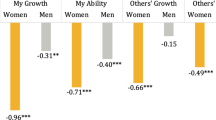
Research question one states: What differences exist by gender in the change in students’ attitudes toward statistics for students who received training in an incremental mind-set and those who did not when controlling for initial attitudes? Table 9.1 depicts the results for the treatment group on each component using a seven-point Likert scale with higher scores indicating more favourable attitudes. An encouraging finding for females demonstrated greater growth in comparison to males regarding their attitudes towards statistics. Statistically significant results were present for the effort and value components.

Table 9.1 Post-test SATS© scores by gender controlling for pre-test SATS© in treatment group
Full size table

Table 9.2 depicts the results for the control group on the change in attitudes for the students who did not receive growth mind-set treatments. No statistically significant differences between attitudes of males and females were present with the exception of the effort component.

Table 9.2 Post-test SATS© scores by gender controlling for pre-test SATS© in control group
Full size table

The effort component measured students’ perceptions regarding the amount of work they expend to learn statistics (Schau, 2003). While motivation is difficult to measure and can include unconscious aspects, effort is a description of behaviour which is “a dependable manifestation of motivation” (Hannula, 2006, p. 167). It is typical on the SATS© to observe a decrease in the effort component from the pre-test to post-test as students refer to intended effort on the pre-test prior to the semester and the post-test is a closer measure of their actual effort. The effort component decreased for both males and females during the treatment semesters, but males decreased at a statistically significantly greater rate than females (F(1, 63) = 4.41, MSE = 4.07, p = .040). Students in the control group that did not receive growth mind-set treatments showed similar, although weaker, findings by gender as females decreased in the effort component at a statistically significant lesser rate than males (F(1, 110) = 3.98, MSE = 2.64, p = .049).

Value increased for both genders in the treatment group with females gaining at a statistically greater rate than males (F(1, 63) = 9.40, MSE = 3.78, p = .003). The value component measured students’ views regarding the usefulness, relevance, and worth of statistics in their personal and professional life (Schau, 2003). Students in the control group did not demonstrate statistically significant differences by gender for the value component (F(1, 110) = 3.15, MSE = 1.40, p = .079). The next section will examine students’ mastery of statistics.

4.3 Mastery of Statistics

Research question two states: What differences exist by gender in mastery of statistics for students who received training in an incremental mind-set and for those who did not when controlling for initial mastery?

Table 9.3 depicts the results including an encouraging finding that females in the treatment group demonstrated statistically significant growth in their mastery of statistics compared to males. No significant difference by gender was present for mastery in the control group. This provides strong evidence of a difference by gender in response to incremental mind-set training.

Table 9.3 Post-test CAOS scores by gender controlling for pretest CAOS scores
Full size table

5 Summary, Conclusions, Discussions, and Recommendations

The final section of this paper will summarise, make conclusions, discuss findings, and provide recommendations for future practice and research.

5.1 Summary

This research examined the effects by gender of an intervention of incremental mind-set training on students’ attitudes toward statistics and mastery of statistical content in an introductory statistics course.

A quasi-experimental, pre-test/post-test design was used in this quantitative research and robust statistical analysis procedures were used throughout. The population was undergraduate students at a small, faith-based, liberal arts university in the Midwest. The students were predominantly Caucasian and of traditional college age. While the sample was not randomly selected, it was representative of students who typically enrol in this course.

The results of this study add to the research of implicit theories of knowledge in undergraduate statistics courses and support continuous improvement in undergraduate statistics pedagogy. A noteworthy contribution of this research is the positive results for females with mind-set training regarding attitudes toward statistics and mastery of statistics.

5.2 Conclusions

Based on this sample the following conclusions emerged regarding the benefit to females of incremental mind-set treatments in this introductory statistics course.

Females in the mind-set treatment condition increased their value of statistics at a significantly higher rate than males did on the SATS© component of value. This is a significant finding given the historical underrepresentation of women in mathematics and STEM in general (Dweck, 2008; Good et al., 2003). The increase in female’s value compared to males supports the notion that environments that communicate an incremental view of mathematics will improve the achievement of females in mathematics and science (Good et al., 2012).

Females in the mind-set treatment decreased in their effort towards statistics at a statistically significant lesser amount than males on the effort component of the SATS©. The effort component gives insight into motivation as it implies that an individual is “moved to do something” (Ryan & Deci, 2000, p. 54). This smaller decrease in effort for females is an indicator that females believed that they could “produce desired effects by their actions” allowing them to persevere when they faced challenges (Bandura, 1999, p. 28).

Females in the mind-set treatment demonstrated greater growth in their mastery of statistics compared to males as measured on the CAOS instrument. This concurs with Pinxten and colleagues’ (2014) findings regarding the strong correlation between maths achievement and maths competence beliefs as growth mind-set training, at its core, addressed students’ beliefs about their ability to learn mathematics.

5.3 Discussion

The purpose of the study was to determine the effects by gender of training of incremental mind-sets on students’ attitudes towards statistics and their mastery of statistics. The first section examines effort, followed by value and mastery.

5.3.1 Effort

Effort is an important behaviour to examine as time spent studying is the second-best predictor of college readiness, following only socioeconomic status (Strayhorn, 2014). The statistically significant lesser decrease in effort reported by females than males in the treatment group is an important finding as “academic effort expenditure has been frequently investigated in relation to students’ goal orientations and causal attributions of success and failure” because of its internal, controllable nature (Pinxten, Marsh, De Fraine, Van Den Noortgate, & Van Damme, 2013, p. 156). This provides evidence that training in a growth mind-set which includes goal setting and discussions of maladaptive attributions had a positive effect on females and the effort that they applied.

There is evidence that the valuation of effort and ability change with development as well. Harari and Covington (1981) found that early elementary students emphasised the role of effort in intelligence. This valuation gradually shifted throughout the educational experience to an emphasis on the role of ability in college students. As a result, many undergraduate students equate effort with lack of ability (Boekaerts, 1999). This is unfortunate since effort is required for students to work through struggle and is a normal part of learning mathematics (Su, 2016).

5.3.2 Value

Similar to effort, value of mathematics also declines as students enter middle school and high school (Turner & Meyer, 2009). This research notes an encouraging finding, demonstrating a statistically significant improvement for females in the treatment group compared to males on the SATS© value component. This is important to motivation in light of expectancy-value theory which states that motivation is a product of both the expectation that an action will produce an outcome and the value placed on that outcome (Bandura, 1999). Additionally, if incremental mind-set training helps females value mathematics, it may also improve their performance to help diminish a persistent stereotype in the mathematics community that males are more capable of mathematical thinking and quantitative reasoning than females (Dweck, 2008; Good et al., 2003, 2012).

5.3.3 Mastery

The statistically significant improvement in mastery of statistics, demonstrated by females in the treatment group when compared to males, is evidence of the importance of implicit theories of knowledge on student attitudes and behaviours. It provides evidence to support Urbina-Lilback’s (2016) assertion that students should adopt a growth mind-set to gain an appreciation of effort and productive struggle in learning. The following section provides recommendations for future practice and research based on these encouraging findings.

5.4 Recommendations

Recommendations for practice include creating classroom environments that communicate an incremental view of mathematics. This is an important step toward increasing the representation and achievement of females in mathematics and science (Good et al., 2012). An understanding of the malleable role of intelligence should permeate all aspects of the classroom including discourse, assessment, and pedagogy (Urbina-Lilback, 2016). Good et al. (2012) conjectured that the disengagement of females with mathematics may result not from a disinclination, but from a decreased sense of belonging. In a large study of undergraduate students in calculus, they found that the perception of an entity-oriented environment and stereotyping were significant predictors of a sense of belonging for females. Fortunately, an incremental mind-set can help stereotyped individuals counteract the effects of stereotyping (Good et al., 2003).

Recommendations for future research include replication, as it is necessary to learn more about the effects of growth mind-set training on achievement and attitudes for both males and females. Research should replicate the current quantitative study to increase the sample size, but also add an aspect of qualitative research to understand why males and females respond in different ways. Additionally, more research on the role of mind-sets and incremental mind-set training should be conducted in various mathematics settings including elementary, secondary, and undergraduate classrooms to improve the generalisability of results.