Keywords

1 Introduction

Over recent decades the importance of motivation, beliefs, and emotions in learning has been highlighted (DeBellis & Goldin, 2006; Middleton, 2013; Schunk & Mullen, 2012). Motivation, according to Kanfer (1994), is the force or impulse that drives individuals to perform an activity, regulating its direction and intensity.

When the reasons, or motivation, for an action are external to it, such as obtaining a reward or avoiding punishment, this type of behaviour ceases when the stimulus or the deterrent is removed. In contrast, if someone chooses to do an activity because they find it interesting, enjoyable and satisfying, their attention is focused on it and their motivation is permanent. In fact, this kind of motivation, intrinsic motivation, is the most intense and sustained action (Deci & Ryan, 1985).

2 Flow Theory

The term flow was introduced by Csikszentmihalyi (1975) after observing and interviewing a large number of individuals who dedicated a great deal of time and effort to activities which afforded them little money or recognition. He wanted to know how they felt when they were doing these activities and why they found them so rewarding.

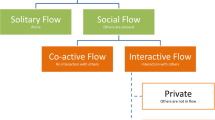
Surgeons, athletes, dancers, and chess players, among many others, described their experiences (flow) in a similar way. They faced challenging situations that required the total use of their skills, aimed at a well-defined goal, receiving frequent information about their progress towards achieving it. They were so focused on their activity that they isolated themselves from what was happening around them, forgetting everything about themselves and their problems, and sometimes losing track of time. They felt in control of their performance and of the activity, and experienced a feeling of effortlessness. All these factors resulted in an intrinsically rewarding experience that individuals would subsequently repeat in order to feel these same sensations over and over again (Csikszentmihalyi & Csikszentmihalyi, 1988). All of the flow dimensions are summarized in Fig. 13.1.

Fig. 13.1
figure 1

Flow dimensions

Full size image

Nakamura and Csikszentmihalyi (2002) argued that providing clear goals, immediate feedback, and a balance between personal skills and the challenges posed by the activity are necessary conditions for flow to occur, rather than the characteristics of the experience itself. Among these three aspects, the level of challenges and skills perceived by the subject has acquired special relevance. After exploring the quality of everyday life experiences, it became apparent that flow occurred when individuals perceived a high level of challenges and skills. Apathy and boredom were linked to the perception of low challenges, and anxiety occurred when individuals perceived that the challenge of the activity was above and beyond their abilities. Much research has been carried out using this model, the Quadrant Model of Flow, to measure flow experiences (Hektner & Csikszentmihalyi, 1996; Rathunde & Csikszentmihalyi, 1993).

The Quadrant Model of flow evolved from data gathered using the Experience Sample Method (ESM), which relies on a device which emits random signals and prompts participants to fill in a brief questionnaire. Using open-ended and scale-type questions (Hektner et al., 2007) information is gathered at the time of the prompt about the activity they were doing, and their cognitive, affective and motivational state. Quadrant Model of Flow evolved to another one with eight channels (Strati, Shernoff, & Dornbusch, 1996).

2.1 Flow Experiences in Education

Although the Flow theory was first tested in the art world in which artists spend many hours in deep concentration working on their paintings and sculptures, it has been applied to many other settings, including education (Shernoff, Abdi, Anderson, & Csikszentmihalyi, 2014).

Research work showed that when students experience flow in academic tasks they attain higher levels of achievement (Larson, 1998) and motivation in the subjects studied, choosing courses that include these activities in future stages of their education or in extracurricular activities (Whalen, 1998). This is one of the most important reasons for doing further research and applying the flow theory to education. In the words of Csikszentmihalyi:

The flow experience acts as a magnet for learning, that is, for developing new levels of challenges and skills. In an ideal situation, a person would be constantly growing while enjoying whatever he or she did. (Csikszentmihalyi, 1997, p. 33)

Using the Quadrant model of flow, Csikszentmihalyi, Rathunde, and Whalen (1993) found that the school environment and home study were surroundings in which gifted students most frequently experienced flow. On the other hand, the activities in which children aged from 9 to 15 most often undergo the flow experience were sports, play and study. Specifically, 20% of the students who took part in the survey claimed they experienced flow when studying (Mesurado, 2010).

2.2 Flow and Mathematics Education

Heine (1997) carried out a study with seven groups of students who attended a course focused on improving mathematical skills in gifted learners. He found that intrinsically motivated students achieved higher outcomes than those who were extrinsically motivated. Furthermore, he compared the flow levels of the seven groups and noticed a decrease in the initial level in five of the groups participating in the course. These groups spent more time listening to their teachers’ explanations and memorizing concepts, whereas the other two groups focused on their work, either individually or in groups, discussing or explaining their ideas. Moreover, they spent time working on problems that required the application of known concepts to new situations. Thus, applying algorithms or doing common or routine problems was considered boring and novel problems were perceived as too difficult.

Schweinle, Turner, and Meyer (2002) found that typical 5th and 6th grade students enrolling in compulsory mathematical courses had the best experiences when they perceived challenges slightly above those they usually encountered. However, their skills perception far outweighed the challenges of the tasks. As seen above, this situation lies outside the Flow Channel and so the Quadrant model of flow predicts boredom. In fact, they found that positive emotions only increase with challenges if the perception of mathematical skills is high. When ability is perceived as low, increasing the level of challenges produces a decrease in students’ perception of self-efficacy (Schweinle, Turner, & Meyer, 2008). In 2006 the same authors compared the learning strategies and environment created by four teachers whose classrooms were classified as provoking flow, apathy, anxiety, and boredom using the Quadrant model of flow. The main differences were the kind of feedback and evaluation provided, the importance given to the tasks, and the way in which they introduced challenges and supported autonomy, cooperation, and persistence (Schweinle, Turner, & Meyer, 2006).

Along the same lines, Liljedahl (2016) proposed the flow theory as a tool for analyzing teachers’ professional practices. Specifically, he compared the extent to which teachers clarify goals, give feedback, and establish challenges in their classrooms, and also the way in which they did it. Observing these practices, he was able to predict in which classroom flow is more likely to occur.

Sedig (2007) designed educational software to enable university students to experience flow while learning geometric plane figure translations, rotations and symmetry. To this end, mathematical tasks were perfectly integrated into a game (interest), SuperTangrams, which sets simple and well-defined rules (clear goals), gives players freedom to choose what they want to do, and allows learners to go through tasks at their own pace (autonomy and control). The game also has several levels of difficulty and a learning module of mathematical concepts that is fully integrated and aimed at the goal of the game. Likewise, it provokes epistemic conflicts and promotes reflection (challenges-skills balance). It also contains background music, special effects, and colourful graphics to engage full attention.

2.3 Flow in Pre-service Teachers and In-Service Teachers

Our first approach to flow theory in mathematics (Montoro, Gil, & Moreno, 2013) addressed two questions. As noted above, Schweinle et al. (2008) found that Quadrant Model of Flow did not fit well to data from primary school students in mathematical classes. This result, and the fact that the majority of flow theory research had been carried out with talented students (Nakamura, 1998) or using freely chosen activities, had raised questions about the necessity of having great mathematical skills to flow when doing mathematics.

Furthermore, after reviewing the methodology used to identify flow experiences, in addition to ESM and the Quadrant Model of Flow, many closed questionnaires were found. Most of them used the flow dimensions proposed by Csikszentmihalyi (1990) and summarized in Fig. 13.1 (González-Cutre, Sicilia, Moreno, & Fernández-Balboa, 2009; Heine, 1997; Jackson & Csikszentmihalyi, 1999). However, some authors eliminated some of these dimensions because they considered them to be prerequisites or consequences of the flow experience (Rodríguez-Sánchez et al., 2009; Whalen, 1998).

Moreover, Jackson and Csikszentmihalyi (1999) highlighted that not all dimensions are present in all activities. For example, a long-distance runner does not experience losing track of time because, by the nature of the activity, he or she must monitor time to regulate the speed required to reach the goal. Taking this into account, it was necessary to know which dimensions of flow are linked with mathematical flow situations.

In Montoro et al. (2013) an adaptation of an open questionnaire, used by Whalen (1998) to identify flow activities with talented student, was distributed to 35 mathematics students, 32 engineering students, and 54 pre-service primary school teachers. The questionnaire asks students to name mathematical activities and everyday activities that make them feel each of the flow dimensions, and also the activities where most of these dimensions are present. The data obtained supported Rodríguez-Sánchez, Cifre, Salanova, and Åborg (2008) and Ghani and Deshpande’s (1994) approach to identify flow through high levels of concentration and enjoyment. That is, an activity provokes flow in someone if they are deeply concentrated, lose all track of the time, isolated from what is happening around them, and enjoy doing it. Moreover, the percentage of pre-service teachers who claimed to flow with mathematical activities in some moment of their lives was more than 80% of the survey respondents. That suggests that it is not necessary to have great mathematical skills to flow when doing mathematics, specially, taking into account the gaps in the mathematical knowledge of pre-service teachers found in different research (MECD, 2013). Problem solving was the main flow activity.

Zhu (2001), Gray (2003) and Bakker (2005) pointed out that it is more likely for students to experience flow doing a task when their teachers are also in flow. We could assume, then, that teachers would need the skill to match the challenge of teaching their subjects. Mathematics is considered one of the most demanding and anxiety-provoking subjects (Shernoff, Knauth, & Makris, 2000). In fact, a high percentage of Spanish pre-service teachers claimed they felt anxious about mathematics, experienced low self-confidence and, therefore, had given up mathematics as soon as it was possible for them to do so (Pérez-Tyteca, 2012). Helping to instill flow in mathematics teachers’ training could have an indirect influence on their students’ flow experience in mathematics classes.

Although flow depends on individuals, tasks, and environments in which the tasks are performed, the research described in this chapter starts by analyzing the tasks as they represent the most controllable variable. Teachers are responsible for selecting, designing and implementing the tasks used in their classrooms.

Until now, most of the research into flow in education had assessed its frequency in courses using questionnaires completed at the end of the course. This methodology has a limitation: the problem of knowing which tasks made them experience this feeling. In fact, in our previous study (Montoro et al., 2013), this limitation was also present since the concept of problem can range from a routine exercise to an unknown situation without an immediately available answer.

3 The Present Study

The primary purpose of the present study is to explore the characteristics of mathematical tasks that enable the occurrence of flow in pre-service primary teachers. To achieve these goal, quantitative and qualitative data were combined to analyze flow as experienced by pre-service teachers facing mathematical tasks set in their training courses. In the first phase, a closed questionnaire was used to compare the percentage of pre-service teachers who experienced flow in different mathematical tasks. Likewise, we sought to obtain information about how interesting, useful, complex and demanding the task had proved to be, how clear the goal of the task had been and if feedback had been forthcoming. Using the data from this phase, one task was selected to be analyzed in depth. Specifically, the behaviour of a group of students solving a problem and their emotions were examined and video-taped. Problems referring to these tasks need to be explored further because an effective way of obtaining solutions is not yet known.

4 Phase 1

The main aims of this phase of the study were to find out which mathematical tasks provoked flow in a higher percentage of pre-service teachers and to analyze how these tasks were perceived by them.

4.1 Participants

For reasons of availability, it was decided to explore the flow experienced by 230 pre-service primary school teachers who attended the compulsory “Teaching and Learning Measurement in Primary Education” course at the University of Almeria. They were divided into four different groups of roughly 60 students who were taught by the two authors of this paper.

The sample was heterogeneous: 45% of the students had started the teacher training degree after completing the social sciences baccalaureate at secondary school, 20% from secondary school science baccalaureate, 20% from professional/vocational training courses, 8% from humanities baccalaureate at secondary school and 7% after passing the university entry exam for mature students (over 25 years of age). Thus, we found a wide range of mathematical training among our sample. In fact, most participants began the course without a good command of school mathematical contents such us operations with decimal numbers, area-perimeter relationship and solving elementary problems.

While we did not find a great difference in students’ percentage by gender (58% female and 42% male), there was a great variety of ages: 36% of students were 21 years old when they attended this course (so they had started this degree as soon as they finished high school), 53% were between 22 and 27, and 11% ranged from 28 to 51 years old.

4.2 Tasks

The course “Teaching and Learning Measurement in Primary Education” was structured in theoretical and practical sessions. In the theoretical sessions, comparison, measurement, and estimation situations were proposed by the teacher and discussed jointly with the group. Likewise, the main mistakes made and difficulties encountered by primary school pupils in similar tasks were explained by the teacher. In the practical sessions, students worked in groups of four or five to solve mathematical tasks. The tasks were designed bearing in mind that participants were expected to find them easy enough to do without becoming mentally blocked, but they were not trivial exercises. Thus, difficulties arose when they faced these tasks. However the pre-service teachers managed to overcome obstacles and re-direct their strategies working as a group. They also expanded their mental structures to include these new situations and saw examples of tasks easily adaptable to primary school ages. Table 13.1 contains a brief description of the tasks.

Table 13.1 Description of the five tasks
Full size table

These five tasks were chosen to be analyzed for several reasons. Firstly, several researchers found that in student-focused classrooms performing tasks individually or with peers can attain a higher level of flow (Heine, 1997; Shernoff, Knauth, & Makris, 2000). Choosing these activities gave us more opportunities to analyze flow experiences in our course. The second reason is methodological: it was easier to observe feelings in our students while working in groups since they had to talk to one another to find a solution.

The results obtained by Heine (1997) led us to expect that these tasks would provoke flow in a high percentage of students because, objectively, there were only two novel problems. One was the section of task 2 which consisted of measuring the capacity of the lungs and the other was task 4, which sought to discover formulas to calculate the area of plane figures using triangular (instead of a square) units.

4.3 The Flow Questionnaire

As our purpose was to measure the level of flow experienced by each student at the end of each of the five tasks described above, a brief questionnaire written in Spanish was required. Moreover, the tasks selected here promoted autonomous work, so the experience might vary greatly from one student to another and their perception of the tasks could be very different.

For this reason, the questionnaire had two parts. The first part was composed of those items used to identify flow experiences: two items about concentration and four about enjoyment. In the second part, there were items referring to aspects considered in previous research work as necessary conditions for flow to occur, namely: clear goals, feedback, complexity, interest, and relevance.

For each one of these variables, a positive and a negative item were developed. For example, for deep concentration, the following items were used: “My attention was completely focused on the activity” and “My concentration was easily interrupted by any distraction”. In their answers, participants indicated the extent to which they agreed with each sentence on a five-point scale ranging from 1 (strongly disagree) to 5 (strongly agree).

For each student’s response to the questionnaire, negative items were inverted and average scores on each scale were calculated. Considering that flow is characterized by a high level of both concentration and enjoyment as discussed above, in instances where students averaged 4 or above (equivalent to agree on all questions) in both concentration and enjoyment, they were considered to be in flow.

An exploratory factor analysis of the data collected in the two first tasks suggested using concentration and enjoyment to identify flow experiences. Interest and loss track of the time are used as enjoyment indicators with the activity (Montoro & Gil, 2011).

A Confirmatory Factor Analysis was carried out using the data from the five tasks described above, and the two-factor model including concentration and enjoyment showed a good fit. Specifically, as can be seen in Fig. 13.2, the model presented loadings above 0.6 which is established as appropriate (Ruiz, Pardo, & San Martín, 2010), and the indicators’ reliability exceed 0.5 which is considered appropriated (Andrade & Coba, 2006), excepting the case of the negative item of concentration (ConcentrN).

Fig. 13.2
figure 2

Two factor model of flow. Reliability indicators and loadings

Full size image

The goodness of fit of the model was evaluated using absolute and relative goodness of fit indices. Although the Chi-square test is the best known, it was not used here because it assumes multivariate normality and it is sensitive to sample size, rejecting models when large samples are used, and accepting models with very small samples (Byrne, 2010). Researchers have developed different goodness-of fit indices to address these limitations, and suggest to combine them rather than using only one of them. As can be seen in Table 13.2, the Goodness of Fit Index (GFI) and Comparative Fit Index (CFI) values were higher than 0.9, and Root Mean square Residual (RMR) value was less than 0.05, which indicated good fit. Moreover, the Root Mean Square Error of Approximation (RMSEA) values lower than 0.08 represent reasonable errors of approximation in the population. To know more about the items design, the validation process and the fit of other possible models, see Montoro and Gil (2013) and Montoro (2015).

Table 13.2 Relative goodness of fit indices
Full size table

4.4 Results

Differences in flow experienced in the various tasks are shown below. Table 13.3 shows the number of students who performed each task and how many of them claimed to have attained a high level of concentration and enjoyment doing the task. The percentage of students who experienced flow with each task is shown within a frame.

Table 13.3 Percentage of students who experienced concentration and enjoyment (flow)
Full size table

As expected, 67.2% of the responses corresponded to flow states. Although these tasks were associated with pleasant situations for most students (at least 50% experienced flow), there were differences among the percentages of students who experienced flow in all tasks (Table 13.3). For example, while tasks about using measurement instruments, comparing magnitudes, and measuring parts of the body provoked flow in more than 70% of students, the percentage of students in flow during task 4, which consisted of obtaining formulas to calculate areas, was roughly 50%. In this task, although the percentage of students concentrating on it was similar to that obtained in the other tasks, the percentage of students who enjoyed doing it was considerably lower.

Once differences on percentage of students in flow among tasks were found, mean and standard deviation of enjoyment and concentration in each task were calculated. As can be seen in Table 13.4, the lower the mean on each variable, the higher the standard deviation. Thus, there was greater agreement in concentration and enjoyment scores given by students when the task had a higher capacity to provoke high concentration and enjoyment. Furthermore, there was generally more agreement in the level of concentration achieved in the task than in the degree of enjoyment students felt in its execution.

Table 13.4 Descriptive statistics. Concentration and enjoyment of each task
Full size table

In order to find out if the differences on the mean among tasks were significant Bonferroni adjustment for repeated t tests were applied. We determined statistically significant differences when P-value was less than 0.01. Moreover, when statistical significance differences on mean were found, effect sizes were calculate with Cohen’s d formula (Table 13.5). We determined a “small” effect size when d was less than 0.25; a “medium” effect size if d was from 0.25 to 0.50, and a “large” effect size if d was greater than 0.5 (Morales, 2012).

Table 13.5 Statistical significance and effect size on concentration and enjoyment
Full size table

As can be seen, the only statistical significance difference on the mean on concentration was found between task 4 and task 1, with medium effect size. However, differences statistically significant were found between task 4 and the rest of the tasks, and between task 1 and 3. The differences between 3 and task 1 and 4 has a moderate effect, since the rest was large. In sum, the main differences were found in the level of enjoyment of task 4.

If task 4 is analysed objectively it could be said that it is more complex because it requires using high-order thinking skills (analysis, evaluation, and creation of new ideas). The other tasks required applying and adapting known concepts and procedures to new situations. Moreover, the task was designed to make students feel like a child learning formulas for calculating the area of plane shapes with a similar task. Although the task is easily adaptable to primary school levels, the task is not contextualised in real life and there are not surprising results.

But, how did the student evaluate the tasks? To make the results easier to understand and describe, similar tables to 13.4 and 13.5 with the rest of the variables from the questionnaire (complexity, clear goal, feedback, utility and interest) were combined. Table 13.6 shows descriptive statistics of each variable, ranked by mean, and d and p values, when differences were statistically significant and relevant. In this way, the effect size of the differences between the mean of two tasks is always equal or higher than the d-value shown in the sixth column of Table 13.6 and any row between them. For example, the d-value corresponding with the difference of means in complexity between task 5 and 2 is 0.316, between task 5 and task 2 is 0.801, and between task 5 and 4 is 1.677 (the highest d-value obtained in all the variables).

Table 13.6 Descriptive statistics, significance and size effect of facilitators in tasks (part 1)
Full size table

As can be seen in Table 13.6, statistically significant differences in the level of complexity were found between all the tasks, except between task 1 and 3. Task 4 was perceived as the most complex task, with a 3.6 average score on a 5-point scale. Compared with the other tasks the difference in average scores of complexity was statistically significant and the size effect was high.

Moreover, statistically significant differences and a medium size effect were found in average scores on clear goals between task 4 and tasks 3 and 5, and large size effect between task 4 and tasks 1 and 2. The goal of task 4 was less clear for students than the other.

Moreover, task 4 was considered the least interesting task. Similar to the clear goals, relevant and statistically significant differences was found between task 4 and the rest, with a large effect on differences between task 4 and task 1.

In the case of the usefulness of the tasks significant and relevant differences were only found between task 1 and tasks 4 and 3. These differences were also found on the feedback provided, and between task 4 and task 5. All of these differences have medium size effect. Furthermore, students may have considered these tasks useful for their training (Table 13.7).

Table 13.7 Descriptive statistics, significance and size effect of facilitators in tasks (part 2)
Full size table

5 Phase 2: Factors Influencing Flow

The results from the last phase led us to analyze task 4 in detail in order to identify aspects of it that hinder flow experiences, and thus, if possible, to modify them in order to raise the percentage of students in flow in future courses.

To this end, groups of students were asked to volunteer to be videotaped while solving each task. Finally, it was decided to analyze the responses to the questionnaire of one group in which the members had all concentrated hard on the tasks and found them all enjoyable, except that of obtaining formulas to calculate the area of plane shapes which was the only task that did not provoke flow in them.

The group was composed of the following members:

  • One student who passed but did not obtain a high mark. She is confident of her abilities and strategies when facing easy tasks. However, she has doubts when the task is complex or when she is with classmates who have a good command of mathematics and do not think in the same way as she does (P1).

  • Two students who passed the subject without a high mark, who like mathematics, have high self-confidence, and persevere to overcome obstacles and correct mistakes (P2 and P3).

  • One student who obtained a distinction in the course, loves mathematics, and has wanted to be a teacher since she was a child. She has high self-confidence and does not give up when faced with difficulties (P4).

  • Videos were analyzed using Atlas.ti 7 software, which allowed us to select extracts, codify them, and create comments that facilitated idea-links without losing the richness of the audiovisual data.

To codify the videos we used 16 categories. Some of these were codes to identify flow experiences: concentration/lack of concentration, enjoyment/lack of enjoyment, and positive emotions/negative emotions. Other categories represented the presence or absence of aspects linked to flow in previous research work that were included in the questionnaire described above: perceived complexity, clear goals, feedback, relevance, and interest. The third column in Tables 13.8, 13.9 and 13.10 shows examples of the coding system.

Subsequently, we focused our attention on changes that occurred in the reported level of concentration, enjoyment or emotions, in order to find the causes of these changes. We specifically looked for an increase in the complexity of the task, interaction between students, interaction with the teacher, and other possible aspects of the task and surroundings. In this case, it was essential to pay attention to what the students were doing at that moment in time, what they were saying, how they said it, their body language, their facial expressions, and their gestures.

Firstly, “key elements” were identified in the video. These were segments that were especially rich in positive or negative emotion or that depicted changes in students’ behaviour or emotion. For reasons of consistency, in addition to the authors, independent researchers familiar with flow theory watched the video and noted segments that were particularly emotionally charged. Subsequently, the key elements of the video were transcribed in two columns, one transcribing the student’s speech and another describing how it was delivered or expressed and what the student was doing at each moment (see examples in Tables 13.8, 13.9 and 13.10). It was necessary to watch the videos numerous times to ensure that no important fact or detail had been overlooked.

Other categories emerged from this analysis. In addition to lack of feedback, of clear goals, increased complexity of the task, and how interesting the task was, changes in students’ behaviour could be largely explained by their level of self-confidence and the interest shown by their colleagues in the group when expressing their ideas.

5.1 Results

The session began with the teacher’s description of the aim of the tasks: to acquire a significant teaching and learning method in order to obtain formulas to calculate the area of plane figures and to confront the difficulties of this learning process. The teacher then explained what the task consisted of: obtaining formulas to calculate the area of different plane figures, and taking as a unit an equilateral triangle with sides measuring one centimetre. To ensure that they understood the goal, it was necessary to solve the first example together. Even though the participants solved rapidly the first shape proposed (equilateral triangle), they found the task complex (Table 13.8).

Table 13.8 Perceived complexity of the task
Full size table

Finding the formula for equilateral triangles, regular hexagons, rhombi and rhomboids is a task of intermediate complexity. It can be solved using decomposition geometric or numeric (searching patterns) methods. Each member of the group discovered the formula for one of these plane figures (P1, P3, P4, and P2, respectively) and was able to understand and evaluate the ideas of their peers. Therefore, their colleagues, and the Geoboards, provided them with immediate feedback.

At the beginning of the task, P4 (nominated by the group) was responsible for completing the working document for this task. In some situations this activity deprived her of time to reflect on the pattern of the task, which was, in the students’ opinions, the most interesting aspect. Something similar happened to P1 who needed more time than P2 and P3 to discover formulas. They were sometimes so absorbed in their discussions or in the search for formulas that they did not listen to P1’s ideas or even try to involve her in the activity (Table 13.9).

Table 13.9 Working on hexagon formula
Full size table

In this situation P4 asked her partners for help to complete the document. P2 usually organised the ideas proposed using geometric terminology and saying what to put into the document, although in general everybody contributed. However, although in this situation P4 asked her partners for help to complete the document. P2 usually organized the ideas proposed using geometric terminology and saying what to write in the document, although in general everybody contributed. However, although P1 was still working and suggesting ideas, her interventions become fewer as the task advanced. She only tried to understand the ideas proposed by her peers and drew the plane figures on the Geoboard. She seemed unwilling to continue doing the task. In contrast, the rest of the group showed signs of enjoying it, especially P2 and P3.

The rest of the figures required composition and decomposition strategies and the creation of new ideas such as measuring height with 60° instead of 90°. However, to continue measuring the height in the usual way (90°), it would have been necessary to calculate the height of the equilateral triangle used as unit and to adjust the formulas.

This increased complexity was reflected in the mental block caused by the need to change strategy. The lack of suitable and useful alternatives among those proposed provoked mixed feelings in the group. Except P1, who seemed to have resigned herself to trying to understand the ideas of her peers, the other students seemed a little confused and cross (Table 13.10). Nevertheless, they persevered despite the difficulties and suggested new ideas. For example, P3 observed that they needed to know the height of the equilateral triangle in order to continue. They decided to assume it measured 1 cm. (the same as the side), and obtained the same formula as for the rhomboid figure (Fig. 13.3). Although P3 thought it was strange that the two shapes had the same formula, they were convinced that it was the correct answer because it worked for all the rectangles drawn on the Geoboard. In the right-angle triangle they considered that putting two right-angle triangles together they could get one rectangle with the same base and height. Thus, their formula also worked for all the right-angle triangles drawn on the Geoboard.

Table 13.10 Working on scalene triangle
Full size table
Fig. 13.3
figure 3

Resolution of rectangle

Full size image

However, the scalene triangle produced in them a mental block because they did not know how to count the triangles inside. It seemed that they wanted all the triangles inside the scalene triangle to fit completely or be divided exactly in half in order to keep using the same strategy.

As soon as the teacher arrived she suggested thinking about different strategies and asked them how they had solved the rectangle formula. At that moment she made them aware of the fact that they had made a mistake supposing that the height of the equilateral triangle was the same as its sides (Fig. 13.3). Their formulas would not work if they used a ruler to measure. The Geoboard had given them misleading feedback in this situation. P1 and P3 did not understand why it was not valid but they did not say anything until the end of the session. They might have failed to understand the problem or they might not have been aware of the need to use a common unit to measure the base and the height of the rectangle in order to find a useful formula for any shape drawn on white paper. This might have been caused by a conflict between the students’ goal, which could have been to discover a pattern or rule for calculating the area of plane figures using the Geoboard, and the teacher’s goal, which was to find a valid formula to do this calculation in general.

With the exception of P1, all students continued working on a solution to the problem. P3 and P4 showed flexible thinking. P3 found a decomposition of the scalene triangle in figures with formulas already known to them (Fig. 13.4). She felt proud of her achievement but realized that getting an algebraic formula was a really complex task. As soon as she tried, and encountered difficulties, she began to doubt the validity of her decomposition. Since the teacher had told them that the rectangle formula was incorrect, her self-confidence decreased. The group finally completed the problem with the teacher’s help.

Fig. 13.4
figure 4

Resolution of the scalene triangle

Full size image

Having succeeded with other figures, and solved this one, encouraged students to continue working. However their affective mood was different: none of them were enthusiastic. In short, P2 and P3 showed signs of enjoyment and of being focused on finding patterns. However, explaining their ideas and expressing them in algebraic language was perceived as tedious. Thus, it can be stated that they were in and out of flow states during the first part of the session. Nevertheless, the inconsistency that emerged between the feedback provided by the Geoboard and teacher’s feedback, the fast increase in complexity of the task, and a potential conflict between the teacher’s and the students’ goals that became apparent in the second part of the task, hindered the occurrence of flow experiences.

In the case of P1, it was observed that the speed with which her peers made further progress in the task stopped her from developing new skills to solve rhomboids and from being be able to solve the next shape, thus, she regarded her skills as unequal to the challenges of the task. Something similar happened with P4 who started to participate finding patterns after the second figure. However, she showed signs of willingness to do this task when she tried to get another colleague to complete the working document so that she could look for the rule.

6 Conclusion and Discussion

As stated in the introduction, our main goal, as a researcher and a teacher-trainer, is to create educational environments in which pre-service primary education teachers can have more opportunities to experience flow. Specifically, we decided to focus on analyzing the mathematical tasks that provoked flow in pre-service primary school teachers working in groups.

Data from 230 pre-service primary students show tasks which provoked flow for over 70% of the students when working in groups. These data suggest that under certain conditions almost every student can experience flow when learning mathematics. In our case, the tasks were considered useful for their training and future working life. The students found the tasks neither too easy nor too difficult but realized that their previous ideas were wrong and led them to make mistakes when tackling this activity. However, in group discussions they were able to adapt their procedures and overcome difficulties. Subsequently, they felt they had learned from their work and that their future students would also learn if they, as teachers, adapted the tasks to their pupils’ ages. Thus, they acquired useful learning as both mathematics students and future teachers.

Although the environment in which these five tasks were carried out was the same (teacher, classroom, members of each group, time to finish it, topic of study…), the percentage of students who experienced flow changed from one task to another. It was discovered that the easier the task was perceived to be, the higher percentage of students experienced flow. However, none of the tasks analyzed was considered either too easy or too difficult. Therefore, it is necessary to analyze what happened in this situation.

The highest percentage of students in flow was found in a task that consisted of using measurement instruments and reproducing what the teacher had done with another object. The next percentage of students in flow was found in magnitude comparison and body measurement tasks that required modification of a known procedure or concept to be applied to new situations, thus presenting a medium level of complexity (Anderson & Krathwohl, 2001). In contrast, the only task considered to be problem-solving showed the lowest percentage of students in flow. Conversely, in Montoro et al. (2013), university students named problem solving as the main flow activity in mathematics. This fact could be explained by the ambiguity of the term problem-solving. Text books usually use this term referring to contextualized exercises.

Students found Task 4 complex, their results were unsurprising, and the task was not contextualized in the real life.

After analyzing the development of problem-solving tasks with a group of students, clear goals and feedback were found to be crucial to flow experiences. We believe that when task complexity levels increase rapidly, using heterogeneous groups hinders the flow experience in students with lower mathematical skills, as they lack time to reflect on the tasks or to draw their own conclusions. This might also influence their self-confidence in a negative way. In these situations we suggest using homogeneous groups and/or collaborative work techniques to ensure that all members have the opportunity to think about task solutions.

In conclusion, to facilitate the emergence of flow when working in groups, in addition to the fact that the tasks must be interesting and useful for their real life or their training, our data suggest the necessity for all the three factors proposed in previous research to be present: pre-service primary school teachers must be clear about task requirements, receive immediate feedback on their performance, and feel able to face challenges and overcome difficulties. Moreover, they must notice that they significantly contribute to the group.

Further research currently being conducted indicates that the closed questionnaire, described in part four, is a useful tool for identifying flow in primary and secondary school students learning mathematics (Berenguel et al., 2016; Gil, Torres, & Montoro, 2017).

In Gil et al. (2017), the flow produced in students when listening to their teacher’s explanations and carrying out similar exercises to those the teacher had just done, was greater than that which occurred when performing open tasks, external to the textbook.

This suggests that some teachers are able to produce flow in students with their explanations. One reason for this result is that students with average skills find clear goals in repetition and know how to start working on a procedure. Furthermore, this helps them to avoid becoming mentally blocked and boosts their self-confidence.

It would be interesting to analyze the differences between average students attending compulsory mathematics classes and those studying mathematics as an extracurricular activity. Specifically, it would be enlightening to examine the influence on flow of problem solving exercises for which students learn metacognition techniques and heuristics, and then to analyze in depth the role of challenges and self-confidence in average students attending compulsory curricular mathematics classes.