Keywords

1 Introduction

Internet of Things (IoT) technology has been actively studied in academic and industry fields due to its useful applications, ranging from home automation, surveillance system, and health–care services. Unlike traditional service models, the IoT applications are able to provide highly customized services for each user by recognizing the customer’s needs or preferences through actively collected data from remotely deployed IoT devices. However, the low-end IoT sensors are usually placed in the public space (building, road, and street), which are easily accessible and manipulated by any legitimate or malicious users. If the adversaries illegally capture the installed IoT devices and perform the sophisticated reverse engineering or any effective hacking measures, the secret information can be easily leaked.

In order to prevent the potential threats, the information of the IoT devices should be securely encrypted through the cryptography algorithm, namely Public Key Cryptography (PKC). However, the PKC requires the complicated computations and the low-end IoT devices have very limited resources, in terms of storage, energy, and computation power. In order to meet the sufficient service availabilities, the careful optimization techniques of implementations should be considered. The PKC instantiations such Elliptic Curve Cryptography (ECC) in pre-quantum case or Supersingular Isogeny Diffie–Hellman key exchange (SIDH) in post-quantum case highly rely on the efficient implementation of modular multiplication, which is the most expensive operations in finite field arithmetic. For this reason, the execution timing of modular multiplication determines the service availability for the low-end microprocessors (e.g., 8-bit AVR and 16-bit MSP430X embedded processors).

In this paper, we present new optimal modular multiplication techniques based on interleaved Montgomery multiplication on 16-bit MSP430X microprocessors, which are effective for special modulus of NIST curves, SM2 curves, and SIDH. In the proposed interleaved Montgomery multiplication, the multiplication part is performed in a hardware multiplier, while the reduction part is performed in a basic Arithmetic Logic Unit (ALU) with optimal routine. Specially, we applied the proposed method to the NIST P–256 curve, of which the implementation improves the previous modular multiplication and squaring operations by 39% and 37.1% for 16-bit MSP430X microprocessors, respectively. Moreover, secure countermeasures against timing attack and simple power analysis are applied to the scalar multiplication on NIST P–256 curve, which achieves the 9,285,578 clock cycles and only requires 0.575 s (@16 MHz). Our implementations imply that the proposed Montgomery multiplication would have broad applications to more cryptographic schemes (e.g., SM2 and SIDH) and microprocessors (e.g., 8-bit AVR).

The rest of this paper is organized as follows. In Sect. 2, we explore the previous works of Montgomery multiplication and target MSP430X processor. In Sect. 3, we present implementations of Montgomery multiplication and NIST P-256 on the MSP430X processor. In Sect. 4, we evaluate the proposed implementations on the target embedded processors. Finally, we conclude the paper in Sect. 5.

2 Preliminaries and Related Works

2.1 Montgomery Multiplication

The modular reduction in School-book approach requires an expensive division operation, which is a high overheads on the low-end devices. Such expensive division operation can be transformed to the relatively cheap multiplication operation through Montgomery reduction, of which the detailed description is given in Algorithm 1.

figure a

The Montgomery reduction is proceeded as: given the intermediate result of multiplication \(T=A\cdot B\) or \(T=A\cdot A\) (where A and B are operands), T is multiplied by the inverse of modulus (\(M'\)) and then the results are reduced by R and stored into Q. Afterward, the equation (\((T+Q\times M)/R\)) is performed. Finally, the calculation of the Montgomery multiplication may require a final subtraction of the modulus (M) to get a reduced result in the range of [0, M). Recently, Gueron and Krasnov presented the implementation of Montgomery multiplication friendly modulus [6]. When the modulus has a special pattern (0xFFFFFFFF in hexadecimal), this can be performed in addition and subtraction operations rather than multiplication. The approach is widely used in recent ECC and SIDH implementations and shows the highest performance [2, 4, 8,9,10].

2.2 Target Processors

The MSP430 family of microcontrollers are widely used in IoT fields, such as small satellite applications [12]. The most popular IoT platform is TelosB and TmoteSky. The MSP430 microcontrollers have 16-bit instruction sets and 12 general-purpose registers. The specifications of clock frequency and ROM/RAM varies for each model. The MSP430 supports a number of instruction sets, including addition, subtraction, and basic operations. The detailed basic arithmetic is given in Table 1.

Table 1. Instruction set summary for MSP
Full size table

In particular, the integer multiplication is carried out with a memory–mapped hardware multiplier. The cost of multiplication is the cost of writing the operands and reading the result to/from a multiplier’s memory address in the MSP430 embedded processors. The operands can be accessed by four different addressing modes, including register direct, indexed, register indirect, and indirect with auto-increment.

Recently, advanced MSP430X microcontrollers have been introduced. The MSP430X supports 20-bit addressing pointers and a new 32-bit hardware multiplier. This sophisticated 32-bit hardware multiplier significantly improves the performance of traditional MSP430 implementation based on 16-bit hardware multiplier. The hardware multiplier supports both 32-bit multiplication and 32-bit Multiplication & ACcumulation (MAC) modes. In order to select the multiplication modes, the 32-bit operands should be written into specific memory addresses (multiplication: MPY32L, MPY32H, MAC: MAC32L, MAC32H) by two 16-bit. Particularly, the MAC mode efficiently accumulates the intermediate results into the result memory (RES0, RES1, RES2, RES3) and sets the carry bit into the carry memory (SUMEXT). The multiplier is triggered by writing the 32-bit operands into the operand memory (OP2L, OP2H). Afterward, the 65-bit results are accessible through result and carry memory addresses (RES0, RES1, RES2, RES3, SUMEXT).

Many previous works used the product-scanning multiplication over MSP430X hardware multiplier since the MAC mode efficiently accumulates the intermediate results in a column-wise fashion with small number of memory accesses [5, 14]. In this work, we also adopted the product-scanning method for multiplication, but we used a basic ALU for reduction over the MSP430X microprocessors for special modulus.

3 Proposed Montgomery Multiplication

In this section, we explore the efficient implementation of Montgomery multiplication for special modulus. The target modulus consists of special patterns (0x00000000, 0x00000001, and 0xFFFFFFFF in hexadecimal), which can be performed in simple addition and subtraction operations rather than complicated multiplication. Though we target the NIST P–256, the proposed method can be applied to the other cryptographic algorithms, such as SM2 and SIDH.

3.1 Constant Modular Addition/Subtraction for Special Modulus

Finite field addition (resp. subtraction) operation requires the final subtraction (resp. addition) with target modulus after addition (resp. subtraction) to fit the intermediate results in the range of target field. When the data format is unsigned, the reduced result should not generate the overflow bits. If we perform the conditional final subtraction or addition operation, the execution timing or power consumption becomes varied depending on the conditional statements. Since the program routines are highly correlated with secret values, the adversary may get the secret information from conditional execution of final subtraction for reduction [18].

In order to avoid the conditional statements, the constant-time reduction is introduced by Liu et al. in [11], which utilizes the conditional reduction (i.e. a multi-precision subtraction) of field arithmetic with the mask. After executing the first part of modular addition (i.e. \(A + B\)), it first generates the 2’s complement of carry, and it can be the value (mask). When the carry bit is set, the mask is always set to 0xFF. Otherwise, the value is set to zero (0x00). The masked modulo is then subtracted without the comparison. In [19], the optimized reduction technique for special modulus is introduced. For the NIST P-256 curve, the modulus \(p_{256}=2^{256}-2^{224}+2^{192}+2^{96}-1\) can be rewritten as 0xFFFFFFFF00000001000000000000000000000000FFFFFFFFFFFFFFFFFFFFFFFF

in hexadecimalFootnote 1, which consists of only three special patterns as 0xFFFF, 0x0000, and 0x0001, in 16-bit wise hexadecimal way. Among them two patterns (i.e. 0xFFFF and 0x0001) are only masked and utilized them for reduction since 0x0000 pattern does not require the masked reduction. These features are highly utilized in MSP430X microprocessors. The pattern (0x0001) is obtained from carry and the remaining pattern is obtained through one subtraction with ZERO register and CARRY register (i.e. 0x0000 - 0x0001 = 0xFFFF). The details are given in Algorithm 2.

figure b

As above demonstration, the MASK register is firstly set to zero, and then subtracted by CARRY register. When the CARRY register is set to 1, the MASK register is always set to 0xFFFF (in hexadecimal). Otherwise, both CARRY and MASK registers are set to 0. By using an efficient memory based operation of MSP430X processor, the masked values are directly subtracted from the intermediate results (i.e. RESULT). For the case of modular subtraction, the borrow bit is used for MASK register and the least significant bit of MASK register is extracted to CARRY register through AND instruction with value (0x0001).

3.2 Interleaved Montgomery Multiplication/Squaring for Special Modulus

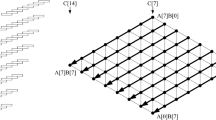
Generic n-word Montgomery multiplication requires (\(n^2+n\)) multiplication. The Montgomery multiplication consists of multiplication and reduction parts. Both parts can be implemented in interleaved or separated way. On one hand, the advantage of separated version combines any multiplication and reduction methods without difficulties. On the other hand, the interleaved version optimizes the number of memory access for intermediate results. In this paper, the interleaved version is adopted since the hardware multiplier of MSP430X is very efficient to handle the accumulation of intermediate results. In Fig. 1, the comparison of procedures for interleaved Montgomery multiplication in hardware utilization are described.

Fig. 1.
figure 1

Procedures for Montgomery multiplication in hardware utilization, MUL: multiplication, RED: reduction, RES: result

Full size image

Note that previous methods only utilized the hardware multiplier for both multiplication and reduction. This approach is efficient for original Montgomery multiplication. However, the proposed method performs the multiplication in the hardware multiplier and the reduction in the basic arithmetic logic unit. This approach shows better performance than previous work when it comes to special modulus.

Register and Memory Utilization. Since the performance is highly relied on the number of memory accesses, the optimized register utilization is very important for high-speed implementations. MSP430X microprocessor equips only 12 general purpose registers, among which five, two, one, and three registers are assigned for intermediate results, temporal storage, memory address of intermediate results in hardware multiplier, and memory address of operands as well as results, respectively. Every operand of multiplication is directly assigned to hardware multiplier and the 96-bit wise intermediate results are cached in the five 16-bit registers, which is used for efficient reduction based on the basic arithmetic. Montgomery multiplication needs to keep Q operands to perform the reduction, which are dynamically loaded/stored from/to the STACK.

Modular Reduction. Our modular multiplication combined both hardware-aided multiplication and basic Arithmetic Logic Unit (ALU) based modular reduction. At first we follow the product–scanning multiplication (i.e. column-wise multiplication) routines, which can be implemented with Multiplication–and–ACcumulation mode of hardware multiplier. Afterward the intermediate results are loaded to some 16-bit registers and then reduced. Different from previous Montgomery reduction which utilizes the product–scanning based multiplication, in our reduction we exploited the properties of special modulus and thus replaced the expensive multiplication into addition/subtraction operations.

figure c

For example, the modulus for NIST P-256 curve consists of three patterns in hexadecimal way, which includes 0x00000000, 0x00000001, and 0xFFFFFFFF. Since the 0x00000000 pattern does not require any computations, the routine is optimized away. The 0x00000001 pattern only requires five 16-bit wise addition, and the operands are directly loaded from memory and added to the memory. The 0xFFFFFFFF pattern requires three 16-bit wise addition and five 16-bit wise subtraction operations, where both operations requires identical 32-bit operands. We firstly load the 32-bit operands to two 16-bit registers (temporal storages) and used the operands twice for 32-bit addition and 32-bit subtraction, respectively. When the 0xFFFFFFFF pattern appears before operand generation, five 16-bit wise subtraction operations are optimized away because the least significant double-word is always set to zero.

The detailed descriptions of Montgomery multiplication in second column for NIST P-256 on MSP430X are given in Algorithm 3. It can be viewed that from Step 1 to 15, two partial products are obtained in the product-scanning way, while from Step 16 to 34, Montgomery reduction with 0xFFFFFFFFFFFFFFFF is performed in simple addition and subtraction.

Final Reduction. The last step of Montgomery multiplication may require the final subtraction to get reduced results. We adopted the masked subtraction described in Algorithm 2.

Modular Squaring. The squaring operation is also frequently called in the cryptographic implementations. For the straight-forward squaring implementation, we can directly use the multiplication for squaring by setting both operands to identical values. However, the multiplication routine does not ensure the highest performance for squaring operation since some memory accesses/partial products can be optimized by loading/performing once rather than twice. The detailed descriptions are given in Algorithm 4. Note that from Step 1 to 6, the partial product is obtained. When the part of operand for partial product is identical, we only need to assign it rather than full operands.

figure d

3.3 Implementation of NIST P–256 on MSP430X Microprocessors

The first implementation of ECC on MSP430X belongs to Gouvêa et al. [5], where they utilized the new 32-bit hardware multiplier instructions of MSP430X. Particularly, the new 32-bit hardware multiplier enhances the previous 16-bit hardware multiplier based prime field multiplication by about 45%. The combination of optimized algorithms and hardware shows that ECC at the security level of 128-bit is feasible for the MSP430X. Seo et al. intensively studied on multi-precision multiplication and squaring operations on MSP430 processors [15,16,17], where they optimized the register usages by caching the operands and memory access through incremental addressing mode.

In LatinCrypt’14, Hinterwälder et al. suggested Curve25519 for MSP430 microcontrollers [7], in which they avoided conditional jumps and loads to prevent timing attacks. Moreover, they provided a comprehensive evaluation of different implementations of the modular multiplication, based on which the Curve25519 implementations on MSP430X having 16-bit and 32-bit hardware multipliers achieved 9.1M and 6.5M cycles, respectively. Düll et al. in [3] optimized the X25519 key-exchange protocol for MSP430X 16-bit microcontrollers, and their implementations for MSP430X takes 5,301,792 cycles (32-bit multiplier) and 7,933,296 cycles (16-bit multiplier) for the computation of Diffie–Hellman key exchange. The computation is performed in less than a second if clocked at 16 MHz for a security level of 128 bits. Recently, Seo in [14] presented size optimized implementation of Curve25519, where he utilized hardware multiplier and accelerated the performance through the optimized multiplication routines in product-scanning way.

In this work, we targeted the special modulo of NIST P–256, and implemented desired cryptographic primitives. The NIST P–256 elliptic curve is given by

$$\begin{aligned} E/\mathbb {F}_{p_{256}}: y^2=x^3-3\cdot x+b,~p_{256}=2^{256}-2^{224}+2^{192}+2^{96}-1, \end{aligned}$$

and other details can be referred to the FIPS 186-2 standard [1]. For finite field arithmetic, we mainly follow the proposed techniques described in Sect. 3 to do the modular addition/subtraction and modular multiplication/squaring operations. Moreover, we adopted the constant-time finite field inversion of NIST P–256, which is performed by powering \(p_{256}-2\). Such inversion can be computed at a cost of 255S + 13M by following Algorithm 2 in [19]. For elliptic curve group arithmetic, we utilized the Montgomery ladder using co-Z Jacobian arithmetic with X and Y coordinates only, which ensures the fast and regular Montgomery ladder algorithm for scalar multiplication [13]. Since the regular Montgomery ladder algorithm does not require conditional statements, the implementation is always constant timing, and thus secure against the simple power analysis and timing attacks.

4 Evaluation

We implemented the NIST P–256 by using the proposed method on 16-bit MSP430X microprocessors (i.e. MSP430F5529) and evaluated the performance of implementations in execution time (clock cycles).

In Table 2, the detailed descriptions of performance evaluation for finite field operations are given. Note that addition and subtraction operations are much cheaper than multiplication and squaring operations (i.e., 8.x faster). It is also natural that the squaring operation is faster (by \(4.6\%\)) than multiplication through dedicated squaring routine in this paper. What’s more, the inversion is implemented based on Fermat’s little theorem, which is a regular fashion and ensures constant timing.

Table 2. Performance evaluation (execution timing in clock cycles) of finite field addition, subtraction, multiplication, squaring and inversion operations for NIST P–256 on 16-bit MSP430X microprocessors.
Full size table

We also give the comparison results of NIST P–256 with previous work as Table 3. For the most performance-critical operations, our proposed modular multiplication and squaring operations improve the performance of those in [5] by 39% and 37.1%, respectively. Such performance enhancements are achieved through optimized memory access, register utilization, and efficient modular reduction techniques. Moreover, this performance improvement directly influences the performance of scalar multiplication.

Table 3. Comparison of NIST P–256 implementations on 16-bit MSP430X microprocessors
Full size table

Though previous implementation of scalar multiplication requires 5,321,776 clock cycles [5], which is faster than ours. This is mainly because their implementation utilized the NAF method for scalar multiplication, which requires pre-computed Look-Up Table (LUT) to accelerate the performance. However, the frequent LUT access increases cache hit rates and may cause cache attack. It should be noted that in [5] the point addition and doubling chain is not a regular fashion, which would be vulnerable to timing attack and leak the secret information.

In order to avoid the potential side channel attacks, we also implemented the scalar multiplication on NIST P–256 in regular fashion as the Montgomery ladder algorithm. Thus constant timing finite field arithmetic and regular elliptic curve group arithmetic result in constant timing scalar multiplication implementation. Even though we sacrifice the performance, the implementation is much secure than previous works.

5 Conclusion

In this paper, we present new optimal modular multiplication techniques for special modulus based on interleaved Montgomery multiplication on 16-bit MSP430X microprocessors. The multiplication part of Montgomery multiplication is performed in the hardware multiplier, while the reduction operation is performed in the basic Arithmetic Logic Unit (ALU) with an optimal routine. Furthermore, the final subtraction is efficiently handled through masked subtraction for the target embedded processors.

The proposed implementation improves the previous modular multiplication and squaring operations for NIST P–256 curve by 39% and 37.1% for 16-bit MSP430X microprocessors, respectively. Based on the improved Montgomery multiplication, the scalar multiplication of NIST P–256 is efficiently constructed. The implementation utilized the Co-Z representation and security countermeasures against timing attack and simple power analysis. The proposed implementation of scalar multiplication achieves 9,122,988 clock cycles and requires only 0.575 s (@16 MHz).

We hope that such techniques for modular multiplication with special modulus on MSP430X microprocessor would improve the performance (as well as implementation security) of cryptographic primitives, which are thus applicable for more cryptographic schemes (such as SM2/NIST ECC and SIDH) and more platforms (such as 8-bit AVR).