Abstract
We analyze the effect of supply constraints on the dynamics of house prices in the Netherlands. In particular, we look at whether income shocks lead to stronger house price increases in regions characterized with higher supply constraints. We use a panel dataset that contains 316 municipalities over the years 1987–2016. Municipalities are divided in three equally sized groups according to the extent of supply constraints present in each municipality. Our results suggest that income shocks lead to significantly larger increases in house prices in municipalities that are relatively more supply constrained. This holds both in the short- and the long-term. The degree of mean reversion and persistence, however, do not seem to significantly differ between the three groups of municipalities.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
1 Introduction
After having sharply declined during the Great Financial Crisis (GFC), house prices in the Netherlands have been increasing strongly since 2014. There is substantial heterogeneity between regions, however. In 2018Q1, nominal house prices in Amsterdam stood 32% above their pre-crisis peak of 2008Q3, whereas in the more rural province of Friesland they were still 8% below their pre-crisis peak. Due to the relevance of house price swings for macroeconomic stability and the existence of spillover effects between regions (Teye and Ahelegbey 2017), it is of great importance for policymakers to gain a good understanding of the heterogeneity in house price developments across regions.
A typical feature of the Dutch housing market is that the price elasticity of housing supply is low, which is partly related to the relatively high population density (Caldera and Johansson 2013). Moreover, the supply elasticity is generally lower in the major cities compared to the rest of the country (Michielsen et al. 2017). If housing supply inadequately adjusts to changes in housing demand, this might lead to house prices deviating from their equilibrium values for an extended period of time (Capozza et al. 2002). In the literature, a low supply elasticity is often linked to physical supply constraints related to geography (Saiz 2010) or a rigid planning system (Hilber and Vermeulen 2016). For the Netherlands, both sources of supply restrictions are relevant. New construction is restricted by physical constraints, mostly in urban areas, because a considerable share of land is already developed. In addition, new housing supply is further hampered by a planning system that is fairly restrictive (Vermeulen and Rouwendal 2007).
It is often found that regions where housing supply is more restricted due to physical and/or regulatory constraints exhibit different house price dynamics. Glaeser et al. (2008) show that areas with stronger supply constraints in the United States experienced a larger housing boom in the 1982–2007 period. Extending on this research, Huang and Tang (2012) find that these areas also experienced larger housing busts during the GFC. In addition, Capozza et al. (2002), the closest work to ours, analyze house price dynamics in various US metropolitan areas and find that areas that face stronger supply constraints also experience stronger serial correlation (i.e. persistence in house price growth) and slower mean reversion of prices (i.e. the speed of adjustment to the long-run equilibrium house price). Similarly, Galati et al. (2011) find that the speed of mean reversion is the lowest in the most urbanized areas of the Netherlands. This finding seems to be in line with the findings of Capozza et al. (2002), assuming that more urbanized areas also face stronger supply constraints. However, in a somewhat more recent study, Galati and Teppa (2017) come to a different conclusion and find that mean reversion is lowest in both the least and most urbanized segments of the Dutch housing market.
The goal of this chapter is to study the interaction between supply constraints and house price dynamics in the Netherlands. Our hypothesis is that a shock in real household income will have a stronger effect on house prices in municipalities with stronger supply constraints. A well-known measure of supply constraints is developed by Saiz (2010), who measures physical supply constraints in the United States by making use of elevation in the landscape. This measure, however, is not suitable for our study as the variation in elevation levels is very low in the Netherlands. Instead, we use the measure developed by Hilber and Vermeulen (2016). Based on this methodology, we create an index for the extent of supply constraints in a given region (i.e. municipality) by relating the amount of already developed land to total available developable land. Note that physical and regulatory supply constraints are highly correlated in practice (Saiz 2010) and our observed supply constraints are driven by both physical and regulatory constraints. We divide the sample into three equally-sized groups: municipalities with weak, medium, and strong supply constraints, labeled as “least developed”, “medium developed” and “most developed”, respectively. We then study the relationship between house prices and income shocks, using an error correction model. Our results suggest that income shocks are associated with significantly larger increases in house prices in municipalities that face relatively strong supply constraints.
The contribution of our work to the literature is twofold. First, we employ a rich dataset that allows us to study the short- and long-run dynamics of house prices at a more granular (i.e. municipality) level than done by previous work on the Dutch housing market. Second, we add to the existing literature by studying the interaction between income shocks and housing supply constraints.
2 Data
For our dependent variable, i.e. house prices, we estimate a hedonic annual house price index at the municipality level using individual transaction data from the Dutch Association of Real Estate Brokers and Real Estate Experts (NVM), covering the period 1987 until 2016. In order to estimate the model for smaller municipalities with fewer transactions, we use the Hierarchical Trend Model of Francke and De Vos (2000) and Francke and Vos (2004). For a more detailed description of the house price index estimation method, see Öztürk et al. (2018).
We are somewhat limited in our selection of explanatory variables as these should ideally exhibit both time- and cross-sectional variation. In line with the literature, we include household income, the unemployment rate, population, construction costs, the mortgage interest rate, and the loan-to-value ratio of first-time buyers (LTV) in our analysis (Table 12.1). House prices, disposable household income, construction costs, and the mortgage rate are deflated by the Consumer Price Index (CPI). During our sample period several municipalities merged, which we account for by computing the weighted average for a merged municipality (weights based on population). For a more detailed description of this procedure see Burgers (2017). In total, we have complete data for 316 out of the 388 municipalities, determined by the availability of data on regional disposable household income.
Our main explanatory variable of interest is household income. We expect that an increase in income leads to an increase in house prices as this enables households to afford a more expensive house. The unemployment rate is expected to be negatively related to house prices since it reduces the number of people who can afford a house. Population should be positively related to house prices as the demand for housing will increase with the number of people living in a region. Construction costs should be positively related to house prices as this determines the structure value of the house, which is part of the total house price. The latter is usually defined as the sum of land and structure value (Francke and van de Minne 2017). The real mortgage interest rate is expected to have a negative relationship with house prices as debt financing becomes cheaper when interest rates fall, driving up house prices.Footnote 1 Finally, we include the LTV of first-time buyers as a proxy for credit conditions (we assume that a higher LTV reflects looser credit standards), and expect it to be positively related to house prices. This variable is usually seen as exogenous to house prices, since first-time buyers are assumed to be credit constrained (Francke et al. 2015). For a more detailed description of this variable see Verbruggen et al. (2015). We purposefully do not employ the housing stock as an explanatory variable as it is directly related to the degree of supply constraints, which we account for by the variable share developed land. Including the housing stock would possibly absorb the heterogeneous relationship between household income and house prices across regions, which is the centroid of our research.
The data used to construct the variable share developed land, which accounts for the extent of supply constraints in a given municipality, come from the Dutch land cover map (Het Landelijk Grondgebruiksbestand Nederland, LGN5) and are based on aerial photos taken in 2003 and 2004. We follow Hilber and Vermeulen (2016) as closely as possible and categorize land into developed land, developable land and non-developable land. The share of developed land (termed as “share developed” below) is the amount of developed land divided by the total amount of developable land (already developed and potentially developable). Note that we only have data for one moment in time. However, we expect that the level of the share developed remains fairly constant over time. We divide our sample into three equally-sized groups (in terms of the number of municipalities) according to the variable share developed land, i.e. municipalities that are the least (value lower than 0.14), medium (value between 0.14–0.25), and the most (value higher than 0.25) developed.
3 Methodology
We are interested in both the long- and short-run effects of income shocks on house prices. Therefore, our framework should model both the long-run underlying equilibrium relationship and the short-run deviations. In the literature, these are usually modelled in an error-correction (ECM) framework (Francke et al. 2009). Given the fact that we are especially interested in heterogeneous cross-sectional effects, we estimate the model with panel data. In an ECM, the long-run equation estimates the underlying equilibrium relationship in levels. In the short-run, deviations from this long-run equilibrium are modeled. Important components in the short-run equation are the speed of adjustment to the long-run equilibrium value (i.e. the error-correction term, ECT) and the degree of serial correlation.
As our goal is to explore the role of supply constraints on house price dynamics as mentioned above, we run our analysis for each of the three groups of municipalities (least-, medium-, and most developed) separately. In other words, we allow for the possibility that supply constraints impact house prices via their interaction with all explanatory variables. The main focus is, however, on the interaction of supply constraints with the income variable.
We employ a two-step Engle-Granger approach by first estimating the long-run equilibrium Eq. (12.1) and subsequently the short-run error-correction Eq. (12.2):
Here subscript i denotes the municipality for i ∈ {1, N}, t the year for t ∈ {1, T}, and j the group based on the share developed land for j ∈ {least, medium, most}. The dependent variable, h, is log house prices. Further, x is a 1xK row-vector of house price determinants that vary over time and municipality, \( {\beta}_j^0 \) and \( {\gamma}_j^0 \) are the Kx1 corresponding long- and short-run coefficient vectors, respectively. Additionally, z is a 1xL row-vector of house price determinants that vary over time only, \( {\beta}_j^1 \) and \( {\gamma}_j^1 \) are the Lx1 corresponding long- and short-run coefficient vectors, respectively.
Next, di is a municipal-specific intercept, αj is the coefficient on lagged house price changes that represents the degree of serial correlation, and δj measures the speed of adjustment. The barred variables include the cross-sectional averages of the variables that vary over the cross-section and time, and θ(0 … 3), j are their respective loadings.Footnote 2
We estimate the long-run Eq. (12.1) with Dynamic OLS (DOLS) and heteroscedasticity- and autocorrelation-consistent (HAC) standard errors clustered at the municipality level. The short-run Eq. (12.2) is estimated with OLS and HAC standard errors clustered at the municipality level. Because we correct for cross-sectional dependence in the short-run equation, we are not able to include the variables that only exhibit time-variation due to perfect multicollinearity (e.g. the mortgage rate and construction costs).
Admittedly, some of our variables might be endogenous to house prices. For our long-run equation this should not be a major issue, as this relationship is simply a long-run relationship between the variables and does not imply causality. Yet, we impose only one co-integrating relationship and do not allow for feedback effects through other variables. However, the literature on panel (V)ECMs is not very well developed in this respect, and there is no standard accepted method as how to approach this problem. The implication for our findings is that some effects are probably over- or underestimated. For example, in our regression equations we do not allow for the housing stock to change in response to a demand shock. This implies that the effect of a positive income shock on house prices might be overstated (i.e. if supply would be able to increase in response to a positive demand shock, the long-run effect on prices would be lower). We are, however, mainly interested in the differences in the effect of income shocks on house prices between regions with respect to the degree of supply restrictiveness. Assuming that supply is less (more) elastic in more (less) constrained regions, the negligence of these dynamics implies that our estimates of these differences are actually on the conservative side.
4 Results
Our empirical analysis consists of two stages. First, we estimate both the long- and short-run relationship for real house prices as given by Eqs. (12.1) and (12.2) for the whole sample, without taking into account the role of supply constraints. Second, we estimate these equations separately for each of the three subsamples of municipalities, allowing supply constraints to interact with all our explanatory variables in an unrestricted manner.Footnote 3
4.1 The Long-Run Relation Between Income and House Prices
We begin by estimating the long-run relationship in Eq. (12.1); the results are shown in Table 12.2. Note that all variables except for the mortgage rate, the unemployment rate, and the LTV are in logs, and can thus be interpreted as elasticities. As shown in Column 1 of Table 12.2, all variables have the expected sign. The results imply that a 1% increase in real income is associated with a 0.7% increase in real house prices in the long-run. The size of this coefficient is relatively small compared to the coefficient estimated by Kranendonk et al. (2005) (i.e. 1.4).
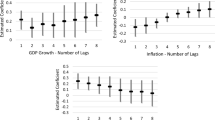
As a next step, we estimate the long-run price relationship for each of the three subsamples separately. The results indicate that in municipalities that are characterized by weak supply constraints (“least developed”), a 1% increase in real income leads to a 0.38% increase in house prices in the long-run (Table 12.2, Column 2.) In municipalities that are characterized by medium and strong supply constraints (“medium developed” and “most developed”), a 1% increase in real income increases house prices by around 0.75% and 0.92%, respectively (Table 12.2, Columns 3–4). Figure 12.1 shows the 95% confidence intervals of these coefficients. F-tests show that the coefficients of the medium- and most developed groups are statistically significantly higher than the coefficient of the least developed group. While the point estimate for the most developed group is larger than that of the medium developed group, this difference is not statistically significant. In line with our hypothesis, the income elasticity of house prices increases with the extent of supply constraints. Intuitively, this confirms that supply elasticities in supply-constrained areas are relatively low. As a result, a given increase in income leads to a strong response in equilibrium house price that is not offset by the relative muted supply response (as it would in less constrained areas).
4.2 The Short-Run (Dynamic) Relation Between Income and House Prices
We estimate the short-run relationship for real house prices according to Eq. (12.2).Footnote 4 As in the first stage, we first run the regression on the whole sample and then separately for each of the three subsamples. Table 12.3 summarizes the main findings. As given by Column 1, the coefficient on real household income is significant and positive (0.06).
Next, we estimate the short-run price relationship for each of the three subsamples separately. The results yield statistically significant coefficients for the real income variable only for the medium and most developed group. Although the coefficients are small, our hypothesis is confirmed since the effect of an income shock on house price growth is significantly larger in these groups compared to the least developed group. That the coefficient is small might be related to the fact that the purchase of a house—often the biggest purchase item in a consumer’s lifetime—requires some time for orientation, leading to a muted response of house prices in the short-run. For the other variables we do not find any heterogeneity in house price responses between municipalities with weak and strong supply constraints.
As mentioned earlier, the short-run relationship includes the first lag of the dependent variable to account for the degree of serial correlation (persistence). If house prices were to adjust to local economic shocks fully in the short run, the coefficient of this variable would be 0 (Capozza et al. 2002). Yet, the empirical literature has generally found a positive and large coefficient for this variable, hinting at backward-looking price setting behavior by sellers (Van Dijk and Francke 2018). As shown in Column 1 of Table 12.3, the coefficient of the first lag of the dependent variable is positive (0.38) and statistically significant, and in line with earlier findings for the United States. Capozza et al. (2002) find a serial correlation coefficient of 0.33 for the based on a panel data set of 62 US metro areas from 1979–1995. Similarly, Case and Shiller (1989) find that annual serial correlation ranges from 0.25 to 0.50 across the four cities that they study.Footnote 5 When the coefficients are estimated seperately by subsample, the coefficients of the serial correlation variable appear to be of similar size (see Columns 2–4). Thus, we do not find the degree of serial correlation to be heterogeneous across regions with different supply constraints.
Finally, we also look at the error-correction term to see how fast house prices converge to their long-run equilibrium, and whether this speed differs across regions with different supply constraints. For house prices to revert to their long-run equilibrium values, the coefficient of the lagged error-correction term should be negative. As shown by Column 1 of Table 12.3, the coefficient of the lagged error-correction term is indeed negative (−0.12) and statistically significant for the whole sample. This suggests that actual house prices adjust by 12% of the difference from their long-run values each year. The serial correlation coefficient (0.38) and the error-correction term together indicate how long it takes for house prices to adjust to a shock. As an example: a 10% income shock at t = 1 increases equilibrium house prices instantaneously by 7%, and first period prices by 0.6%. In the next periods, the error correction mechanism and the serial correlation coefficient will move house prices closer to their new equilibrium value until they eventually fully converge to their new equilibrium.
Figure 12.2 illustrates the effect of such a 10% shock and the adjustment process of house prices in the least, medium and most developed regions. A shock in income indeed has a larger effect on house prices in the medium and most developed regions than in the least developed regions, as expected. On the other hand, the time it takes for house prices to make up for half of the shock is more or less equal across the three groups: 4.5 years for the least, 3.5 years for the medium and the most developed regions.Footnote 6
5 Conclusion and Future Research
We have shown that house price dynamics in the Netherlands differ significantly between the least and most supply constrained municipalities. Our results suggest that positive income shocks are associated with significantly larger house price increases in municipalities that face strong supply constraints compared to municipalities with weaker supply constraints.Footnote 7 The response of house prices to an income shock is found to be generally muted in the short-run, but significantly stronger in municipalities with strong supply constraints. Contrary to findings for the United States by Capozza et al. (2002), we find no difference in the extent of persistence and mean reversion of house prices across municipalities with different supply constraints. We further find that after an income shock it takes between 3.5 and 4.5 years for house prices to make up for half of their initial deviation from the equilibrium price.
Future research in this area could explore ways to refine our measure of supply constraints for the Netherlands. As was previously discussed, the ratio of developed land to developable land is an imperfect measure of supply constraints. Not only does it imperfectly capture physical constraints to construction, it cannot distinguish physical constraints from regulatory constraints. Furthermore, in an ideal setting, such a measure should be exogenous to house prices and vary over time in order to find a causal effect of supply constraints on house prices.
Notes
- 1.
Between 1987 and 2002, the real mortgage interest rate is the average 5-year mortgage rate for new mortgages and between 2003 and 2016 the rate is calculated as the average of the 1 to 5-year rate and 5 to 10-year rate on new mortgages.
- 2.
It might be expected that there are spillovers between regions. Therefore, we correct for this possible cross-sectional dependence by including cross-sectional averages of all our explanatory variables (Pesaran 2006). We assume that this cross-sectional dependence is stationary and should therefore be accounted for in the short-run equation. Intuitively, this implies that these spillovers mainly affect the short-run dynamics of the housing market.
- 3.
In this chapter, we focus mainly on the effect of income on house prices. For a more detailed discussion of the other variables, please refer to Öztürk et al. (2018).
- 4.
In Öztürk et al., we show the results of various panel unit root- and cointegration tests which confirm that our level variables all contain a unit root (except unemployment) and that the residual (ECT) and the first differences are all stationary.
- 5.
Atlanta, Chicago, Dallas and San Francisco.
- 6.
These differences are insignificant since the differences between serial correlation coefficients and error-correction terms are insignificant.
- 7.
We performed various robustness checks and our main result always holds. These checks include regressions for different time periods, without unemployment (which is not I(1)), without population (since some of the long-run population coefficients were puzzling) and performed a weighted regression (with population weights).
References
Burgers, S. (2017). Determinants of regional house price dynamics: The role of supply constraints and sales activity. University of Amsterdam Thesis.
Caldera, A., & Johansson, Å. (2013). The price responsiveness of housing supply in OECD countries. Journal of Housing Economics, 22(3), 231–249.
Capozza, D. R., Hendershott, P. H., Mack, C., & Mayer, C. J. (2002). Determinants of real house price dynamics. NBER Working Paper, No w9262.
Case, K. E., & Shiller, R. J. (1989). The efficiency of the market for single-family homes. American Economic Review, 79(1), 125–137.
Francke, M., & De Vos, A. (2000). Efficient computation of hierarchical trends. Journal of Business & Economic Statistics, 18(1), 51–57.
Francke, M. K., & van de Minne, A. (2017). Land, structure and depreciation. Real Estate Economics, 45(2), 415–451.
Francke, M., & Vos, G. (2004). The hierarchical trend model for property valuation and local price indices. Journal of Real Estate Finance and Economics, 28(2), 179–208.
Francke, M., Vujic, S., & Vos, G. (2009). Evaluation of house price models using an ECM approach: The case of the Netherlands. Ortec Finance Working Paper Series, Methodological Paper No. 2009–05.
Francke, M., van de Minne, A., & Verbruggen, J. (2015). De sterke gevoeligheid van woningprijzen voor kredietvoorwaarden. Economisch-Statistische Berichten, 100(4713–4714), 426–429.
Galati, G., & Teppa, F. (2017). Heterogeneity in house price dynamics. DNB Working Paper No. 564.
Galati, G., Teppa, F., & Alessie, R. J. (2011). Macro and micro drivers of house price dynamics: An application to Dutch data. DNB Working Paper No. 288.
Glaeser, E. L., Gyourko, J., & Saiz, A. (2008). Housing supply and housing bubbles. Journal of Urban Economics, 64(2), 198–217.
Hilber, C. A., & Vermeulen, W. (2016). The impact of supply constraints on house prices in England. The Economic Journal, 126(591), 358–405.
Huang, H., & Tang, Y. (2012). Residential land use regulation and the US housing price cycle between 2000 and 2009. Journal of Urban Economics, 71(1), 93–99.
Kranendonk, H., van Leuvensteijn, M., Toet, M., & Verbruggen, J. (2005). Welke factoren bepalen de ontwikkeling van de huizenprijs in Nederland? CPB Document, 81.
Michielsen, T., Groot, S., & Maarseveen, R. (2017). Prijselasticiteit van het woningaanbod. CPB Notitie.
Öztürk, B., Van Dijk, D., Van Hoenselaar, F., & Burgers, S. (2018). The relationship between supply constraints and house price dynamics in the Netherlands. DNB Working Paper, 601.
Pesaran, M. H. (2006). Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica, 74(4), 967–1012.
Saiz, A. (2010). The geographic determinants of housing supply. Quarterly Journal of Economics, 125(3), 1253–1296.
Teye, A. L., & Ahelegbey, D. F. (2017). Detecting spatial and temporal house price diffusion in the Netherlands: A Bayesian network approach. Regional Science and Urban Economics, 65, 56–64.
Van Dijk, D., & Francke, M. (2018). Internet search behavior, liquidity and prices in the housing market. Real Estate Economics, 46(2), 368–403.
Verbruggen, J., Van der Molen, R., Jonk, S., Kakes, J., & Heeringa, W. (2015). Effects on further reductions in the LTV limit. DNB Occasional Study, 13(2).
Vermeulen, W., & Rouwendal, J. (2007). Housing supply and land use regulation in the Netherlands. CPB Discussion Paper No 87.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Öztürk, B., van Dijk, D., van Hoenselaar, F., Burgers, S. (2019). The Relationship Between Supply Constraints and House Price Dynamics in the Netherlands. In: Nijskens, R., Lohuis, M., Hilbers, P., Heeringa, W. (eds) Hot Property. Springer, Cham. https://doi.org/10.1007/978-3-030-11674-3_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-11674-3_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-11673-6
Online ISBN: 978-3-030-11674-3
eBook Packages: Economics and FinanceEconomics and Finance (R0)