Dynamic Hierarchies in Temporal Directed Networks

Abstract

The outcome of interactions in many real-world systems can be often explained by a hierarchy between the participants. Discovering hierarchy from a given directed network can be formulated as follows: partition vertices into levels such that, ideally, there are only forward edges, that is, edges from upper levels to lower levels. In practice, the ideal case is impossible, so instead we minimize some penalty function on the backward edges. One practical option for such a penalty is agony, where the penalty depends on the severity of the violation. In this paper we extend the definition of agony to temporal networks. In this setup we are given a directed network with time stamped edges, and we allow the rank assignment to vary over time. We propose 2 strategies for controlling the variation of individual ranks. In our first variant, we penalize the fluctuation of the rankings over time by adding a penalty directly to the optimization function. In our second variant we allow the rank change at most once. We show that the first variant can be solved exactly in polynomial time while the second variant is NP-hard, and in fact inapproximable. However, we develop an iterative method, where we first fix the change point and optimize the ranks, and then fix the ranks and optimize the change points, and reiterate until convergence. We show empirically that the algorithms are reasonably fast in practice, and that the obtained rankings are sensible. Code related to this paper is available at: https://bitbucket.org/orlyanalytics/temporalagony/.

1 Introduction

The outcome of interactions in many real-world systems can be often explained by a hierarchy between the participants. Such rankings occur in diverse domains, such as, hierarchies among athletes [3], animals [8, 14], social network behaviour [11], and browsing behaviour [10].

Discovering a hierarchy in a directed network can be defined as follows: given a directed graph $G = (V, E)$, find an integer r(v), representing a rank of v, for each vertex $v \in V$, such that ideally $r(u) < r(v)$ for each edge $(u, v) \in E$. This is possible only if G is a DAG, so in practice, we penalize each edge with a penalty q(r(u), r(v)), and minimize the total penalty. One practical choice for a penalty is agony [6, 15, 16], $q(r(u), r(v)) = \max (r(u) - r(v) + 1, 0)$. If $r(u) < r(v)$, an ideal case, then the agony is 0. On the other hand, if $r(u) = r(v)$, then we penalize the edge by 1, and the penalty increases as the edge becomes more ‘backward’. The major benefit of computing agony is that we can solve it in polynomial time [6, 15, 16].

In this paper we extend the definition of agony to temporal networks: we are given a directed network with time stamped edges¹ and the idea is to allow the rank assignment to vary over time; in such a case, the penalty of an edge with a time stamp t depends only on the ranks of the adjacent vertices at time t.

We need to penalize or constrain the variation of the ranks, as otherwise the optimization problem of discovering dynamic agony reduces to computing the ranks over individual snapshots. In order to do so, we consider 2 variants. In our first variant, we compute the fluctuation of the rankings over time, and this fluctuation is added directly to the optimization function, multiplied by a parameter $\lambda$. In our second variant we allow the rank to change at most once, essentially dividing the time line of a single vertex into 2 segments.

We show that the first variant can be solved exactly in $\mathcal {O} \mathopen {}\left( m^2\log m\right)$ time. On the other hand, we show that the second variant is NP-hard, and in fact inapproximable. However, we develop a simple iterative method, where we first fix the change points and optimize the ranks, and then fix the ranks and optimize the change points, and reiterate until convergence. We show that the resulting two subproblems can be solved exactly in $\mathcal {O} \mathopen {}\left( m^2\log m\right)$ time.

We show empirically that, despite the pessimistic theoretical running times, the algorithms are reasonably fast in practice: we are able to compute the rankings for a graph with over $350\,000$ edges in 5 min.

The remainder of the paper is organized as follows. We introduce the notation and formalize the problem in Sect. 2. In Sect. 3 we review the technique for solving static agony, and in Sect. 4 we will use this technique to solve the first two variants of the dynamic agony. In Sect. 5, we present the iterative solution for the last variant. Related work is given in Sect. 6. Section 7 is devoted to experimental evaluation, and we conclude the paper with remarks in Sect. 8. The proofs for non-trivial theorems are given in Appendix in supplementary material.

2 Preliminaries and Problem Definition

We begin with establishing preliminary notation, and then continue by defining the main problem.

The main input to our problem is a weighted temporal directed graph which we will denote by $G = (V, E)$, where V is the set of vertices and E is a set of tuples of form $e = (u, v, w, t)$, meaning an edge e from u to v at time t with a weight w. We allow multiple edges to have the same time stamp, and we also allow two vertices u and v to have multiple edges. If w is not provided we assume that an edge has a weight of 1. To simplify the notation we will often write w(e) to mean the weight of an edge e. Let T be the set of all time stamps.

A rank assignment ${r}:{V \times T} \rightarrow {\mathbb {N}}$ is a function mapping a vertex and a time stamp to an integer; the value r(u; t) represents the rank of a vertex u at a time point t.

Our next step is to penalize backward edges in a ranking r. In order to do so, consider an edge $e = (u, v, w, t)$. We define the penalty as

$$ p \mathopen {}\left( e; r\right) = w\times \max (0, r(u; t) - r(v; t) + 1). $$

This penalty is equal to 0 whenever $r(v; t) > r(u; t)$, if $r(v; t) = r(u; t)$, then the $p \mathopen {}\left( e; r\right) = w$, and the penalty increases as the difference $r(u; t) - r(v; t)$ increases.

We are now ready to define the cost of a ranking.

Definition 1

Assume an input graph $G = (V, E)$ and a rank assignment r. We define a score for r to be

$$ q \mathopen {}\left( r, G\right) = \sum _{e \in E} p \mathopen {}\left( e; r\right) . $$

Static Ranking: Before defining the main optimization problems, let us first consider the optimization problem where we do not allow the ranking to vary over time.

Problem 1

( agony). Given a graph $G = (V, E)$, an integer k, find a ranking r minimizing $q \mathopen {}\left( r, G\right)$, such that $0 \le r(v; t) \le k - 1$ and $r(v; t) = r(v; s)$, for every $v \in V$ and $t, s \in T$.

Note that agony does not use any temporal information, in fact, the exact optimization problem can be defined on a graph where we have stripped the edges of their time stamps. This problem can be solved exactly in polynomial time, as demonstrated by Tatti [16]. We should also point out that k is an optional parameter, and the optimization problem makes sense even if we set $k = \infty$.

Dynamic Ranking: We are now ready to define our main problems. The main idea here is to allow the rank assignment to vary over time. However, we should penalize or constrain the variation of a ranking. Here, we consider 2 variants for imposing such a penalty.

In order to define the first variant, we need a concept of fluctuation, which is the sum of differences between the consecutive ranks of a given vertex.

Definition 2

Let r be a rank assignment. Assume that T, the set of all time stamps, is ordered, $T = t_1, \ldots , t_\ell$. The fluctuation of a rank for a single vertex u is defined as

$$ fluc \mathopen {}\left( u; r\right) = \sum _{i = 1}^{\ell - 1} {\left| r(u, t_{i + 1}) - r(u, t_{i})\right| }. $$

Note that if r(u, t) is a constant for a fixed u, then $fluc \mathopen {}\left( u; r\right) = 0$. We can now define our first optimization problem.

Problem 2

( fluc-agony). Given a graph $G = (V, E)$, an integer k, and a penalty parameter $\lambda$, find a rank assignment r minimizing

$$ q \mathopen {}\left( r, G\right) + \lambda \sum _{v \in V} fluc \mathopen {}\left( v; r\right) , $$

such that $0 \le r(v; t) \le k - 1$ for every $v \in V$ and $t \in T$.

The parameter $\lambda$ controls how much emphasis we would like to put in constraining $fluc$: If we set $\lambda = 0$, then the $fluc$ term is completely ignored, and we allow the rank to vary freely as a function of time. In fact, solving fluc-agony reduces to taking snapshots of G at each time stamp in T, and applying agony to these snapshots individually. On the other hand, if we set $\lambda$ to be a very large number, then this forces $fluc \mathopen {}\left( v; r\right) = 0$, that is the ranking is constant over time. This reduces fluc-agony to the static ranking problem, agony.

In our second variant, we limit how many times we allow the rank to change. More specifically, we allow the rank to change only once.

Definition 3

We say that a rank assignment r is a rank segmentation if each u changes its rank r(u; t) at most once. That is, there are functions $r_1(u)$, $r_2(u)$ and $\tau (v)$ such that

$$ r(u; t) = {\left\{ \begin{array}{ll} r_1(u), &{} t < \tau (u), \\ r_2(u), &{} t \ge \tau (u). \end{array}\right. } $$

This leads to the following optimization problem.

Problem 3

( seg-agony). Given a graph $G = (V, E)$ and an integer k, find a rank segmentation r minimizing $q \mathopen {}\left( r; G\right)$ such that $0 \le r(v; t) \le k - 1$ for every $v \in V$ and $t \in T$.

Note that the obvious extension of this problem is to allow rank to change $\ell$ times, where $\ell > 1$. However, in this paper we focus specifically on the $\ell = 1$ case as this problem yields an intriguing algorithmic approach, given in Sect. 5.

3 Generalized Static Agony

In order to solve the dynamic ranking problems, we need to consider a minor extension of the static ranking problem.

To that end, we define a static graph $H=(W, A)$ to be the graph, where W is a set of vertices and A is a collection of directed edges (u, v, c, b), where $u, v \in V$, c is a positive—possibly infinite—weight, and b is an integer, negative or positive.

Problem 4

( gen-agony). Given a static graph $H = (W, A)$ find a function ${r}:{W} \rightarrow {\mathbb {Z}}$ minimizing

$$ \sum _{(u, v, c, b) \in A} \max (c \times (r(u) - r(v) + b), 0). $$

Note that c in (u, v, c, b) may be infinite. This implies that if the solution has a finite score, then $r(u) + b \le r(v)$.²

We can formulate the static ranking problem, agony, as an instance of gen-agony: Assume a graph $G = (V, E)$, and a(n optional) cardinality constraint k. Define a graph $H = (W, A)$ as follows. The vertex set W consists of the vertices V and two additional vertices $\alpha$ and $\omega$. For each edge $(u, v, w, t) \in E$, add an edge $(u, v, c = w, b = 1)$ to A. If there are multiple edges from u to v, then we can group them and combine the weights. This guarantees that the sum in gen-agony corresponds exactly to the cost function in agony. If k is given, then add edges $(\alpha , u, c = \infty , b = 0)$ and $(u, \omega , c = \infty , b = 0)$ for each $u \in V$. Finally, add $(\omega , \alpha , c = \infty , b = 1 - k)$. This guarantees that the for the optimal solution we must have $r(\alpha ) \le r(u) \le r(\omega ) \le r(\alpha ) + k - 1$, so now the ranking defined $r(u; t) = r(u) - r(\alpha )$ satisfies the constraints by agony.

Example 1

Consider a temporal network given in Fig. 1a. The corresponding graph H is given in Fig. 1b.

Fig. 1.

Graph G, and the corresponding graphs H used in agony and fluc-agony. In (b), the edges with omitted parameters have $c = \infty$ and $b = 0$. In (c), vertices $\alpha$ and $\omega$, and the adjacent edges, are omitted.

As argued by Tatti [16], gen-agony is a dual problem of capacitated circulation, a classic variant of a max-flow optimization problem. This problem can be solved using an algorithm by Orlin [13] in $\mathcal {O} \mathopen {}\left( {\left| A\right| }^2\log {\left| W\right| }\right)$ time. In practice, the running time is faster.

4 Solving fluc-agony

In this section we provide a polynomial solution for fluc-agony by mapping the problem to an instance of gen-agony.

Assume that we are given a temporal graph $G = (V, E)$, a parameter $\lambda$ and a(n optional) constraint on the number of levels, k.

We will create a static graph $H = (W, A)$ for which solving gen-agony is equivalent of solving fluc-agony for G. First we define W: for each vertex $v \in V$ and a time stamp $t \in T$ such that there is an edge adjacent to v at time t, add a vertex $v_t$ to W. Add also two vertices $\alpha$ and $\omega$. The edges A consists of three groups $A_1$, $A_2$ and $A_3$:

• (i) For each edge $e = (u, v, w, t) \in E$, add an edge $(u_t, v_t, c = w, b = 1)$.

• (ii) Let $v_t, v_s \in W$ such that $s > t$ and there is no $v_o \in W$ with $t< o < s$, that is $v_t$ and $v_s$ are ‘consecutive’ vertices corresponding to v. Add an edge $(v_t, v_s, c = \lambda , b = 0)$, also add an edge $(v_s, v_t, c = \lambda , b = 0)$.

• (iii) Assume that k is given. Connect each vertex $u_t$ to $\omega$ with $b = 0$ and weight $c = \infty$. Connect $\alpha$ to each vertex $u_t$ with $b = 0$ and weight $c = \infty$. Connect $\omega$ to $\alpha$ with $b = 1 - k$ and $c = \infty$. This essentially forces $r(\alpha ) \le r(u_t) \le r(\omega ) \le r(\alpha ) + k - 1$.

Example 2

Consider a temporal graph in Fig. 1a. The corresponding graph, without $\alpha$ and $\omega$, is given in Fig. 1c.

Let r be the rank assignment for H with a finite cost, and define a rank assignment for G, $r'(v; t) = r(v_t)$. The penalty of edges in $A_1$ is equal to $q \mathopen {}\left( r', G\right)$ while the penalty of edges in $A_2$ is equal to $\lambda \sum _{v \in V} fluc \mathopen {}\left( v, r'\right)$. The edges in $A_3$ force $r'$ to honor the constraint k, otherwise $q \mathopen {}\left( r, H\right) = \infty$. This leads to the following proposition.

Proposition 1

Let r be the solution of gen-agony for H. Then $r'(v; t) = r(v_t) - r(\alpha )$ solves fluc-agony for G.

We conclude with the running time analysis. Assume G with n vertices and m edges. A vertex $v_t \in W$ implies that there is an edge $(u, v, w, t) \in E$. Thus, ${\left| W\right| } \in \mathcal {O} \mathopen {}\left( m\right)$. Similarly, ${\left| A_1\right| } + {\left| A_2\right| } + {\left| A_3\right| } \in \mathcal {O} \mathopen {}\left( m\right)$. Thus, solving gen-agony for H can be done in $\mathcal {O} \mathopen {}\left( m^2 \log m\right)$ time.

5 Computing seg-agony

In this section we focus on seg-agony. Unlike the previous problem, seg-agony is very hard to solve (see Appendix for the proof).

Proposition 2

Discovering whether there is a rank segmentation with a 0 score is an NP-complete problem.

This result not only states that the problem is hard to solve exactly but it is also very hard to approximate: there is no polynomial-time algorithm with a multiplicative approximation guarantee, unless $\mathbf NP =\mathbf P$.

5.1 Iterative Approach

Since we cannot solve the problem exactly, we have to consider a heuristic approach. Note that the rank assignment of a single vertex is characterized by 3 values: a change point, the rank before the change point, and the rank after the change point. This leads to the following iterative algorithm: (i) fix a change point for each vertex, and find the optimal ranks before and after the change point, (ii) fix the ranks for each vertex, and find the optimal change point. Repeat until convergence.

More formally, we need to solve the following two sub-problems iteratively.

Problem 5

( change2ranks). Given a graph $G = (V, E)$ and a function $\tau$ mapping a vertex to a time stamp, find ${r_1}:{V} \rightarrow {N}$ and ${r_2}:{V} \rightarrow {N}$ mapping a vertex to an integer, such that the rank assignment r defined as

$$ r(v; t) = {\left\{ \begin{array}{ll} r_1(v), &{} t < \tau (v), \\ r_2(v), &{} t \ge \tau (v) \end{array}\right. } $$

minimizes $q \mathopen {}\left( r; G\right)$.

Problem 6

( ranks2change). Given a graph $G = (V, E)$ and two functions ${r_1}:{V} \rightarrow {N}$ and ${r_2}:{V} \rightarrow {N}$ mapping a vertex to an integer, find a rank segmentation r minimizing $q \mathopen {}\left( r; G\right)$ such that there is a function $\tau$ such that

$$ r(v; t) = {\left\{ \begin{array}{ll} r_1(v), &{} t < \tau (v), \\ r_2(v), &{} t \ge \tau (v). \end{array}\right. } $$

Surprisingly, we can solve both sub-problems exactly as we see in the next two subsections. This implies that during the iteration the score will always decrease. We still need a starting point for our iteration. Here, we initialize the change point of a vertex v as the median time stamp of v.

5.2 Solving change2ranks

We begin by solving the easier of the two sub-problems.

Assume that we are given a temporal network $G = (V, E)$ and a function ${\tau }:{V} \rightarrow {T}$. We will map change2ranks to gen-agony. In order to do so, we define a graph $H = (W, A)$. The vertex set W consists of two copies of V; for each vertex $v \in V$, we create two vertices $v^1$ and $v^2$, we also add vertices $\alpha$ and $\omega$ to enforce the constraint k. For each edge $e = (u, v, w, t) \in E$, we introduce an edge $(u^i, v^j, c = w, b = 1)$ to A, where

$$ i = {\left\{ \begin{array}{ll} 1 &{} \text { if } t< \tau (u), \\ 2 &{} \text { if } t \ge \tau (u), \\ \end{array}\right. } \quad \text {and}\quad j = {\left\{ \begin{array}{ll} 1 &{} \text { if } t < \tau (v), \\ 2 &{} \text { if } t \ge \tau (v). \end{array}\right. } $$

Finally, like before, we add $(\alpha , v, c = \infty , b = 0)$, $(v, \omega , c = \infty , b = 0)$ and $(\omega , \alpha , c = \infty , b = 1 - k)$ to enforce the constraint k.

We will denote this graph by $G(\tau )$.

Example 3

Consider the toy graph given in Fig. 1a. Assume $\tau (u) = 1$ and $\tau (v) = 2$. The resulting graph $G(\tau )$ is given in Fig. 2a.

The following proposition shows that optimizing agony for H is equivalent of solving change2ranks. We omit the proof as it is trivial.

Proposition 3

Let r be a ranking for H. Define $r'$ as

$$ r'(v; t) = {\left\{ \begin{array}{ll} r(v^1) - r(\alpha ), &{} t < \tau (v), \\ r(v^2) - r(\alpha ), &{} t \ge \tau (v). \end{array}\right. } $$

Then $q \mathopen {}\left( r', G\right) = q \mathopen {}\left( r, H\right)$. Reversely, given a ranking $r'$ satisfying conditions of change2ranks, define a ranking r for G by setting $r(v^i) = r_i(v)$. Then $q \mathopen {}\left( r', G\right) = q \mathopen {}\left( r, H\right)$.

We conclude with the running time analysis. Assume G with n vertices and m edges. We have at most $2n + 2$ vertices in W and ${\left| A\right| } \in \mathcal {O} \mathopen {}\left( m\right)$. Thus, solving change2ranks for H can be done in $\mathcal {O} \mathopen {}\left( m^2 \log n\right)$ time.

5.3 Solving ranks2change

Our next step is to solve the opposite problem, where we are given the two alternative ranks for each vertex, and we need to find the change points. Luckily, we can solve this problem in polynomial time. To solve the problem we map it to gen-agony, however unlike in previous problems, the construction will be quite different.

Assume that we are given a graph $G = (V, E)$, and the two functions $r_1$ and $r_2$. To simplify the following definitions, let us first define

$$ r_{ min } \mathopen {}\left( v\right) = \min (r_1(v), r_2(v)) \quad \text {and}\quad r_{ max } \mathopen {}\left( v\right) = \max (r_1(v), r_2(v)). $$

Assume an edge $e = (u, v, w, t) \in E$. A solution to ranks2change must use ranks given by $r_1$ and $r_2$, that is the rank of u is either $r_{ min } \mathopen {}\left( u\right)$ or $r_{ max } \mathopen {}\left( u\right)$, and the rank of v is either $r_{ min } \mathopen {}\left( v\right)$ or $r_{ max } \mathopen {}\left( v\right)$, depending where we mark the change point for u and v. This means that there are only 4 possible values for the penalty of e. They are

$$ \begin{aligned} p_{00}(e)&= w\times \max (0, r_{ min } \mathopen {}\left( u\right) - r_{ min } \mathopen {}\left( v\right) + 1), \\ p_{10}(e)&= w\times \max (0, r_{ max } \mathopen {}\left( u\right) - r_{ min } \mathopen {}\left( v\right) + 1), \\ p_{01}(e)&= w\times \max (0, r_{ min } \mathopen {}\left( u\right) - r_{ max } \mathopen {}\left( v\right) + 1), \\ p_{11}(e)&= w\times \max (0, r_{ max } \mathopen {}\left( u\right) - r_{ max } \mathopen {}\left( v\right) + 1). \end{aligned} $$

Among these penalties, $p_{01}(e)$ is the smallest, and ideally we would pay only $p_{01}(e)$ for each edge. This is rarely possible, so we need to design a method that takes other penalties into account.

Next we define a static graph $H = (W, A)$ that will eventually solve ranks2change. For each vertex $v \in V$ and a time stamp $t \in T$ such that there is an edge adjacent to v at time t, add a vertex $v_t$ to W. Add also two additional vertices $\alpha$ and $\omega$. We will define the edges A in groups. The first two sets of edges in A essentially force $r(u_t) = 0, 1$, and that the ranking is monotonic as a function of t. Consequently, there will be at most only one time stamp for each vertex u, where the ranking changes. This will be the eventual change point for u. The edges are:

• (i) Connect each vertex $u_t$ to $\omega$ with $b = 0$ and weight $c = \infty$. Connect $\alpha$ to each vertex $u_t$ with $b = 0$ and weight $c = \infty$. Connect $\omega$ to $\alpha$ with $b = -1$ and $c = \infty$. Connect $\alpha$ to $\omega$ with $b = 1$ and $c = \infty$. This forces $r(\alpha ) \le r(u_t) \le r(\omega ) = r(\alpha ) + 1$.

• (ii) Let $v_t, v_s \in W$ such that $s > t$ and there is no $v_o \in W$ with $t< o < s$. If $r_2(v) \ge r_1(v)$, then connect $v_t$ to $v_s$ with $b = 0$ and $c = \infty$. This forces $r(v_s) \ge r(v_t)$. If $r_2(v) < r_1(v)$, then connect $v_s$ to $v_t$ with $b = 0$ and $c = \infty$. This forces $r(v_s) \le r(v_t)$.

For notational simplicity, let us assume that $r(\alpha ) = 0$. The idea is then that once we have obtained the ranking for H, we can define the ranking for G as

$$ r'(v; t) = r_{ min } \mathopen {}\left( v\right) + ( r_{ max } \mathopen {}\left( v\right) - r_{ min } \mathopen {}\left( v\right) )r(v_t). $$

Our next step is to define the edges that correspond to the penalties in the original graph. We will show later in Appendix that the agony of $r'$ is equal to $P_1 + P_2 + P_3 + const$, where

$$ \begin{aligned} P_1&= \sum _{v_t \mid r(v_t) = 0} \sum _{e = (u, v, w, t) \in E} p_{00}(e) - p_{01}(e), \\ P_2&= \sum _{u_t \mid r(u_t) = 1} \sum _{e = (u, v, w, t) \in E} p_{11}(e) - p_{01}(e), \\ P_3&= \sum _{e = (u, v, w, t) \in E \atop r(v_t) = 0, r(u_t) = 1} p_{10}(e) - p_{00}(e) - p_{11}(e) + p_{01}(e). \end{aligned} $$

Let us first define the edges that lead to these penalties.

• (i) Connect $\omega$ to each vertex $v_t$ with $b = 0$ and weight

  $$ c = \sum _{e = (u, v, w, t) \in E} p_{00}(e) - p_{01}(e). $$

  In the sum v and t are fixed, and correspond to $v_t$. This edge penalizes vertices with $r(v_t) = 0$ with a weight of c. Summing these penalties yields $P_1$.

• (ii) Connect each vertex $u_t$ to $\alpha$ with $b = 0$ and weight

  $$ c = \sum _{e = (u, v, w, t) \in E} p_{11}(e) - p_{01}(e). $$

  In the sum u and t are fixed, and correspond to $u_t$. This edge penalizes vertices with $r(u_t) = 1$ with a weight of c. Summing these penalties yields $P_2$.

• (iii) For each edge $e = (u, v, w, t) \in E$, connect $u_t$ and $v_t$ with $b = 0$ and

  $$ c = p_{10}(e) - p_{00}(e) - p_{11}(e) + p_{01}(e). $$

  This edge penalizes cases when $r(u_t) = 1$ and $r(v_t) = 0$, and constitute $P_3$.

We will denote the resulting H by $G(r_1, r_2)$.

Example 4

Consider the toy graph given in Fig. 1a. Assume that the rank assignments are $r_1(u) = 0$, $r_1(v) = 1$, $r_2(u) = 2$, $r_2(v) = 3$. The resulting graph $G(r_1, r_2)$ is given in Fig. 2b. The optimal ranking for $G(r_1, r_2)$ assigns 0 to $\alpha$, $u_0$, $v_0$, and $v_1$; the rank for the remaining vertices is 1.

Fig. 2.

Graphs used for solving seg-agony. In both figures, the edges with omitted parameters have $c = \infty$ and $b = 0$. For clarity, we omit edges between $\alpha$ and $\omega$ in both figures, in addition, in (b) we omit parameters for the edges $(x, \alpha )$ and $(\omega , x)$ with $c = 0$.

Before we show the connection between the ranks in G and $H = G(r_1, r_2)$, we first need to show that the edge weights are non-negative. This is needed to guarantee that we can find the optimal ranking of H using gen-agony.

Proposition 4

The weights of edges in H are non-negative.

The proof is given in Appendix.

We will state our main result: we can obtain the solution for ranks2change using the optimal ranking for H; see Appendix for the proof.

Proposition 5

Let r be the optimal ranking for H. Then

$$ r'(v; t) = r_{ min } \mathopen {}\left( v\right) + ( r_{ max } \mathopen {}\left( v\right) - r_{ min } \mathopen {}\left( v\right) ) (r(v_t) - r(\alpha )) $$

solves ranks2change.

We conclude this section with the running time analysis. Assume G with n vertices and m edges. A vertex $v_t \in W$ implies that there is an edge $(u, v, w, t) \in E$. Thus, ${\left| W\right| } \in \mathcal {O} \mathopen {}\left( m\right)$. Similarly, ${\left| A\right| } \in \mathcal {O} \mathopen {}\left( m\right)$. Thus, solving ranks2change for H can be done in $\mathcal {O} \mathopen {}\left( m^2 \log m\right)$ time.

6 Related Work

Perhaps the most classic way of ranking objects based on pair-wise interactions is Elo rating proposed by Elo [3], used to rank chess players. A similar approach was proposed by Jameson et al. [8] to model animal dominance.

Maiya and Berger-Wolf [11] proposed discovering directed trees from weighted graphs such that parent vertices tend to dominate the children. A hierarchy is evaluated by a statistical model where the probability of an edge is high between a parent and a child. A good hierarchy is then found by a greedy heuristic.

Penalizing edges using agony was first considered by Gupte et al. [6], and a faster algorithm was proposed by Tatti [15]. The setup was further extended to handle the weighted edges, which was not possible with the existing methods, by Tatti [16], as well to be able to limit the number of distinct ranks (parameter k in the problem definitions).

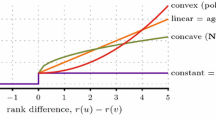
An alternative to agony is a penalty that penalizes an edge (u, v) with $r(u) \ge r(v)$ with a constant penalty. In such a case, optimizing the cost is equal to feedback arc set (FAS), an APX-hard problem with a coefficient of $c = 1.3606$ [2]. Moreover, there is no known constant-ratio approximation algorithm for FAS, and the best known approximation algorithm has ratio $O(\log n \log \log n)$ [4]. In addition, Tatti [16] demonstrated that minimizing agony is NP-hard for any concave penalties while remains polynomial for any convex penalty function.

An interesting direction for future work is to study whether the rank obtained from minimizing agony can be applied as a feature in role mining tasks, where the goal is to cluster vertices based on similar features [7, 12].

seg-agony essentially tries to detect a change point for each vertex. Change point detection in general is a classic problem and has been studied extensively, see excellent survey by Gama et al. [5]. However, these techniques cannot be applied directly for solving seg-agony since we would need to have the ranks for individual time points.

The difficulty of solving seg-agony stems from the fact that we allow vertices to have different change points. If we require that the change point must be the equal for all vertices, then the problem is polynomial. Moreover, we can easily extend such a setup for having $\ell$ segments. Discovering change points then becomes an instance of a classic segmentation problem which can be optimized by a dynamic program [1].

7 Experiments

In this section we present our experimental evaluation.

Datasets and Setup: We considered 5 datasets. The first 3 datasets, Mention, Retweet, and Reply, obtained from SNAP repository [9], are the twitter interaction networks related to Higgs boson discovery. The 4th dataset, Enron consists of the email interactions between the core members of Enron. In addition, for illustrative purposes, we used a small dataset: NHL, consisting of National Hockey League teams during the 2015–2016 regular season. We created an edge (x, y) if team x has scored more goals against team y in a single game during the 2014 regular season. We assign the weight to be the difference between the points and the time stamp to be the date the game was played. We used hours as time stamps for Higgs datasets, days for Enron. The sizes of the graphs are given in Table 1.

Table 1. Basic characteristics of the datasets and the experiments. The third data column, ${\left| T\right| }$, represents the number of unique time stamps, while the last column is the number of unique (v, t) pairs such that the vertex v is adjacent to an edge at time t, $\big | \bigcup _{(u, v, w, t) \in E} \left\{ (v, t), (u, t)\right\} \big |$.

Table 2. Agony, running time, and number of unique ranks in the ranking.

For each dataset we applied fluc-agony, seg-agony, and the static variant, agony. For fluc-agony we set $\lambda = 1$ for the Higgs datasets, $\lambda = 2$ for NHL and Enron.

We implemented the algorithms in C++, and performed experiments using a Linux-desktop equipped with a Opteron 2220 SE processor.³

Computational Complexity: First, we consider the running times, reported in Table 2. We see that even though the theoretical running time is $\mathcal {O} \mathopen {}\left( m^2 \log n\right)$ for fluc-agony and for a single iteration of seg-agony, the algorithms perform well in practice. We are able to process graphs with 300 000 edges in 5 min. Naturally, seg-agony is the slowest as it requires multiple iterations—in our experiments 3–5 rounds—to converge.

Table 3. Statistics measuring fluctuation of the resulting rankings: $fluc$ is equal to the fluctuation $fluc \mathopen {}\left( u; r\right)$ averaged over u, $maxdiff$ is the maximum difference between the ranks of a single vertex u, averaged over u, $change$ is the number of times rank is changed for a single vertex u, averaged over u. Note that $fluc = maxdiff$ for seg-agony as the assignment is allowed to change only once.

Statistics of Obtained Rankings: Next, we look at the statistics of the obtained rankings, given in Table 2. We first observe that the agony of the dynamic variants is always lower than the static agony, as expected.

Let us compare the constraint statistics, given in Table 3. First, we see that fluc-agony yields the smallest $fluc$ in Higgs databases. seg-agony produces smaller $fluc$ in the other two datasets but it also produces a higher agony.

Interestingly enough, fluc-agony yields a surprisingly low average number of change points for Higgs datasets. The low average is mainly due to most resulting ranks being constant, and only a minority of vertices changing ranks over time. However, this minority changes its rank more often than just once.

Agony vs Fluctuation: The parameter $\lambda$ of fluc-agony provides a flexible way of controlling the fluctuation: smaller values of $\lambda$ leads to smaller agony but larger fluctuation while larger values of $\lambda$ leads to larger agony but smaller fluctuation. This can be seen in Table 2, where relatively large $\lambda$ forces small fluctuation for the Higgs datasets, while relatively small $\lambda$ allows variation and a low agony for Enron dataset. This flexibility comes at a cost: we need to have a sensible way of selecting $\lambda$. One approach to select this value is to study the joint behavior of the agony and the fluctuation as we vary $\lambda$. This is demonstrated in Fig. 3 for Enron data, where we scatter plot the agony versus the average fluctuation, and vary $\lambda$. We see that agony decreases steeply as we allow some fluctuation over time but the obtained benefits decrease as we allow more variation.

Use Case: Finally, let us look on the rankings by seg-agony of NHL given in Fig. 4. We limit the number of possible rank levels to $k = 3$.

The results are sensible: the top teams are playoff teams while the bottom teams have a significant losing record. Let us highlight some change points that reflect significant changes in teams: for example, the collapse of Montreal Canadiens (MTL) from the top rank to the bottom rank coincides with the injury of their star goaltender. Similarly, the rise of the Pittsburgh Penguins (PIT) from the middle rank to the top rank reflects firing of the head coach as well as retooling their strategy, Penguins eventually won the Stanley Cup.

Fig. 3.

Agony plotted against $fluc$ of the optimal ranking for fluc-agony by varying the parameter $\lambda$ (Enron).

Fig. 4.

Rank segmentations for NHL with $k = 3$. The bottom figure shows only the teams whose rank changed. The y-axis is used only to reduce the clutter.

8 Concluding Remarks

In this paper we propose a problem of discovering a dynamic hierarchy in a directed temporal network. To that end, we propose two different optimization problems: fluc-agony and seg-agony. These problems vary in the way we control the variation of the rank of single vertices. We show that fluc-agony can be solved in polynomial time while seg-agony is NP-hard. We also developed an iterative heuristic for seg-agony. Our experimental validation showed that the algorithms are practical, and the obtained rankings are sensible.

fluc-agony is the more flexible of the two methods as the parameter $\lambda$ allows user to smoothly control how much rank is allowed to vary. This comes at a price as the user is required to select an appropriate $\lambda$. One way to select $\lambda$ is to vary the parameter and monitor the trade-off between the agony and the fluctuation. An interesting variant of fluc-agony—and potential future line of work—is to minimize agony while requiring that the fluctuation should not increase over some given threshold.

The relation between seg-agony and the sub-problems ranks2change and change2ranks is intriguing: while the joint problem seg-agony is NP-hard not only the sub-problems are solvable in polynomial time, they are solved with the same mechanism.

A straightforward extension for seg-agony is to allow more than just one change point, that is, in such a case we are asked to partition the time line of each vertex into $\ell$ segments. However, we can no longer apply the same iterative algorithm. More specifically, the solver for ranks2change relies on the fact that we need to make only one change. Developing a solver that can handle the more general case is an interesting direction for future work.