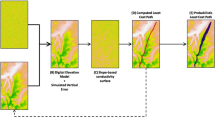
Abstract
GIS-based digital modelling tools, such as the well-known least cost paths (LCP), have been widely used in archaeology in recent years as ways of approaching forms of mobility in the past. Roman roads are among the best-known examples of ancient networks of paths and have been widely studied using such approaches. In this paper, we shall make a general reflection on the applicability of those tools for the modelling and analysis of ancient routes, with a special focus on Roman roads. Drawing from a case study in the NW Iberian Peninsula, we shall discuss certain aspects related to the potential and limits of Cumulative Costs, LCP and other related tools for the modelling and analysis of ancient roads. We will illustrate how the use of tools which explore potential mobility in less restricted ways can help to overcome some of the limitations of LCP.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction: Tradition and Innovation in the Analysis of Roman Roads
The Roman road system is one of the largest and most widely studied (in archaeological terms) networks of ancient roads in the world. They were an essential tool for the expansion of the Empire and the administration and control of its territory. It has been argued that the network of roads reached a remarkable extension of 120,000 km at its height (Fasolo 2014, 3875), consisting of a vast range of different pathways, from long-distance roads to short-range, local paths. As is to be expected, knowledge of these routes is rather uneven, with most archaeological research focusing on the main, long-distance routes, for which abundant epigraphic and textual documentation exists. A brief account of the case of the NW Iberian Peninsula may be representative of research trends elsewhere.
The study of Roman roads in Iberia has, for a long time, attracted the attention of a heterogeneous group of scholars. Unlike other specialized topics, archaeologists have traditionally occupied a secondary position in this debate. While historians have mainly focused on the analysis of epigraphic (e.g. milestones) and ancient literary sources (itinera) (Roldán Hervás 1975; Rabanal Alonso 2006; Fernández Ochoa et al. 2012; Roldán Hervás and Caballero Casado 2014), engineers and other professionals have paid more attention to historical cartography, to the technical problems relating to the construction of the roads and to other elements linked to the latter, such as bridges (Moreno Gallo 2006, 2011a; Vicente González 2013; Alonso Trigueros 2014).
The landscape of the north-western area of the Iberian Peninsula is characterized by its heterogeneity. This aspect has naturally had a strong impact on the degree of preservation of ancient roads and, therefore, on the information we currently have about them. In densely populated areas or in regions where smallholdings are predominant, the conservation of archaeological remains tends to be worse. For instance, the lack of reliable archaeological data and certain scholarly traditions have shaped an intense historiographical debate about the original route of Roman roads in some areas (Estefanía Álvarez 1960; Sáez Taboada 1999; Franco Maside 2000, 2001; Rodríguez Colmenero et al. 2004; Gómez Vila 2005). On the contrary, the local topography in mountainous areas led to the recurrent use of certain natural passages from prehistoric times to our days, thus making the general outline of these routes more easily detectable or, it could be said, less debatable (González Álvarez 2011).
To a great extent, ancient infrastructures are still recognizable on the open fields of the northern Spanish plateau. Where they are no longer in use as modern roads, they may still be detectable as abandoned hollow tracks or via place names. This situation has also made them prone to detection via the use of more comprehensive approaches, such as aerial surveying (Del Olmo Martín 2006). This is the reason why the reconstruction of old itineraries has become more consistent over time, albeit, in general, with small changes when compared to the work of the pioneers on the subject (Loewinsohn 1965; Moreno Gallo 2011b).
In fact, when we are deprived of the (occasionally biased) contribution of ancient written sources, the differences between most ancient routes, either Roman or later, are very small in terms of materiality. The dating and characterization of these paths as Roman roads is, therefore, a significant issue. Moreno Gallo (2006) has argued that “archaeology does not have enough resources to deal with this problem” (p. 186) and that the stratigraphic methodology traditionally used for their study has actually been “par excellence destructive” (p. 223). Far from being an incendiary statement, what this author stresses is the lack of multidisciplinary, holistic approaches for the study of these structures and the general lack of awareness of archaeologists regarding certain basic notions of Roman engineering. Being an engineer himself, his criticism is quite understandable and it is, actually, extremely similar to what an archaeologist might say about those scholars who overuse ancient sources. Regardless of its certitude, the assertion is not entirely original, since the problem had already been pointed out by certain archaeologists (Abásolo Álvarez 1990).
In recent times, the extensive use of new resources and techniques, such as geophysical surveying or airborne LiDAR technology, is slowly transforming the study of Roman roads through the development of more systematic multi-disciplinary surveys (Gethin and Toller 2014; Small 2016). Among these new approaches, digital modelling has contributed to a renewed analysis of Roman roads in different ways, in Spain as well as elsewhere in Europe. The digital modelling of human movement with GIS, based on the use of tools and concepts such as friction, cumulative cost or least cost paths (LCPs onwards), has been one of the most significant contributions. In the following paragraphs, we shall briefly outline some of these recent approaches.
2 GIS-Based Modelling of Roman Roads
GIS-based digital modelling tools, such as the well-known LCPs, among others, have been widely used in archaeology in recent years as ways of understanding forms of mobility in the past. A growing body of literature exists presenting both theoretical and methodological proposals, as well as multiple examples of application in different geographical and archaeological contexts (e.g. White and Surface-Evans 2012; Herzog 2013, 2014; Polla and Verhagen 2014; Howey and Brouwer Burg 2017; Supernant 2017, among many others). The analysis of Roman roads is just one of the fields to which those approaches have contributed significantly.
To put it quite simplistically, most of these contributions can be classified either as predictive or “postdictive” approaches. In other words, the former are aimed at reconstructing the layout of ancient networks of paths, while the latter focus on understanding the logic behind the layout of an existing road network. Obviously, there is no sharp division between them, but rather a different emphasis. A review of some examples can help in understanding this difference.
Most GIS-based models of ancient mobility apply slope-dependent cost functions, whereby costs for movement are basically, or exclusively, computed according to the influence of variations in terrain gradient on human mobility. A number of functions exist to compute costs (measured either in energy, changes in speed or any other currency) from slope changes (usually represented in a GIS environment as a slope map). However, other cost factors have also been considered in some cases. The work of Verhagen and Jeneson (2012) is a good example of an explicitly predictive approach whereby other cost factors beyond terrain slope are considered. Their work is based on the explicitly predictive objective of finding plausible hypotheses for the original route of a given Roman road, on a detailed geographical scale:
Given the uncertainties regarding the way in which Roman engineers chose routes through difficult terrain, it seems logical to apply least cost path (LCP) models to try to find the most plausible ones. (Verhagen and Jeneson 2012, 125)
Taking as a starting point a series of locations where the existence of the road is known, LCP is the mechanism used to predict the most probable routes to link them and, consequently, to “join the dots” and predict the probable route of the road in its entirety. In contrast with other approaches, Verhagen and Jeneson consider other factors besides movement costs. In particular, they include visual control over the surrounding landscape as a possible additional factor influencing the layout of the road, considering that this Via Belgica was originally a military route. The different combinations of these factors (anisotropic costs and visual control measured in different ways) produce a range of LCPs, which aid in the validation of the different existing proposals regarding the actual route of the road and provide some plausible hypotheses for ground-truthing in the field.
In a series of recent papers, Van Lanen et al. have developed a detailed predictive model for the identification of Roman and Medieval routes in the Netherlands (Van Lanen et al. 2015a, b, 2016). Within a mostly flat geographical region, with little topographical variation, their proposal stands out for not relying on the use of cost surfaces but on what they call “network friction”:
Traditional GIS modelling of past routes has largely focussed on correctly defining cost-surface modules [...]. In low-lying regions such as the Netherlands these approaches are less useful when modelling route networks. In these regions, other landscape factors greatly will have determined route networks and local translocation conditions (e.g. the presence of mires, peat bogs, rivers). Network friction calculates regional accessibility conditions based on environmental data and locates transport obstacles and corridors, and therefore can be used to model historical route networks. (Van Lanen et al. 2015b, 145)
It could be argued that these factors can also be quantified in terms of costs and that they are, actually, producing and using cost surfaces (albeit based not on topographical costs and using relative measurements of friction). Nevertheless, their proposal is a detailed approach to detect the most probable routes (rather than specific roads) connecting a known distribution of Roman and Medieval settlements (High Density Settlement Clusters), considering the likely influence of secondary settlements (Isolated Settlements) in the layout of those routes. Theoretical routes are calculated with two different friction surfaces (terrestrial and maritime) but using direct connections between pairs of points as LCPs do; that is, given certain friction values, the single best connection between points is calculated. The results are tested with archaeological data related to the location of “infrastructural” and “isolated finds” from the Roman period which are used as the ground evidence to measure (with good results) the likelihood of the routes obtained through the modelling analysis.
Equally predictive is the recent proposal by Verbrugghe et al. (2017) in Flanders:
Despite this long research tradition the routes of Roman roads in the Civitas Menapiorum (the Roman region covering what are now the Belgian provinces of West and East Flanders, the French Departement du Nord and the Dutch province of Zealand) are still uncertain. (Verbrugghe et al. 2017, 76)
Again, they do not rely on the common use of slope-based cost surfaces but on a combination of morphometric and land cover analysis to build their cost surfaces, something that is, once more, justified by the specific conditions of the regional landscape:
Since the study area is characterised by a large number of dry ridges and wet depressions, two cost surfaces were created based on an ASCII version of the DTM (cell size five metres) for Flanders (2001 and 2004) and a shapefile version of the Belgian soil map of 2001 (cell size five metres). […] The cost ascribed to the DTM was based on the method used by Wiedemann, Antrop and Vermeulen. They used the raster calculator in ArcGIS to give depressions (negative height values) and higher areas (positive height values) a respective high and low cost, since hilltops and ridges were favoured for routes. […] Subsequently, a cost surface based on the Belgian soil map was created. […] The cost ascribed to the resulting map was based on a division into four soil types. Dry sand, dry soils, moist soils and wet soils were ascribed respectively costs of one, two, three and ten. […] Since no objective data on cost preferences in Roman decision making are available, no weights were ascribed to the calculated cost surfaces when combining them. After multiplying the cost surfaces, the resulting cost surface was calibrated in the same way, on a scale of zero to ten. (Verbrugghe et al. 2017, 79)
Using that friction surface, they calculate the LCP which would probably have joined the “accepted junctions of supralocal Roman roads in Flanders” (ibid, 79). The use of LCPs leads again to obtaining a network composed of the single best route connecting the points in question. To validate their results, they compare those routes with the known location of Roman settlements, with possible ancient paths identified via aerial prospection and with modern-day road segments with names allegedly referring to a Roman origin. In contrast with the preceding papers, in this case, their results are only partially positive, for which the authors themselves give a plausible reason:
The choice of costs is one of the explanations why only little similarity could be observed by comparing the buffers for the calculated least cost paths, the known archaeological sites from the CAI and the crop and soil marks on oblique and vertical photographs. (Verbrugghe et al. 2017, 84)
This is a good case to illustrate why a predictive approach must always rely on an explicit hypothesis where the measurement of movement costs is based on reliable evidence. As in predictive modelling in general, there are two main ways to build these hypotheses: either inductively or deductively (Verhagen and Whitley 2012). In the case of ancient roads in general, and Roman roads in particular, we have seen how most authors agree that one of the main things which remain to be explored is precisely what criteria guided cost preferences in Roman decision making. This has encouraged some authors to take an inductive approach and model Roman roads from a ‘postdictive’ point of view: taking some cases in which a substantial amount of evidence remains about the actual route of roads in the past. These approaches aim not to reconstruct the routes, but to understand the pieces of evidence which inform us about them. In other words, their objective is:
to understand the rationale behind the layout of a Roman road […] to understand, via the use of a modelling process, the criteria and factors which were taken into account when choosing a particular route for this road. (Fonte et al. 2017, 164)
A good example of this is the recent contribution by Herzog (2017). Although she is not dealing with Roman roads, she provides an interesting example of a combination of predictive and “postdictive” modelling. She starts with a collection of maps representing ancient roads, which are carefully transferred into their actual geographical position. In parallel, she uses LCPs to calculate the most likely routes to join the places depicted in the historical maps. A comparison between them allows her to further refine the cost factors considered in order to achieve the theoretical LCP which best match the known historical roads (what we would call a “postdictive” approach). This implies unveiling the factors considered in the development of those roads, which in this case were avoiding wet soils and terrains with a critical slope of 12% and giving preference to certain fords which were historically documented. Having refined the model of cost, she was able to obtain a map of the route of those ancient roads on a very detailed scale (a predictive approach), which can be used to guide a prospection based on the identification of hollow tracks in high-resolution airborne LiDAR data.
In summary, these (and other) recent contributions have proved the potential of GIS-based modelling to improve our understanding of Roman roads. Firstly, they illustrate how a reliable prediction must always be based on a previous understanding of the factors which might have influenced their layout and on accurate modelling of them in a digital environment. Secondly, when compared to each other, they show that the relative importance of the factors influencing the layout of Roman roads seems to have been different depending both on the regional geography and on the historical context of their development. Although slope-dependent cost functions have proved to be useful in many cases (e.g. Herzog 2017), their relevance should not be universally taken for granted (a recent good example is Supernant 2017). Again, a deep understanding of the cost factors involved in each specific context is needed. Thirdly, these papers are also informative of both the potential and limits of the widely used LCPs: despite being extremely useful tools, they provide a somehow restricted illustration of mobility, limited to the single best possible connection between points.
In the following sections, we shall attempt to explore some of these issues in more detail, elaborating on our previous work on the analysis of Roman roads in the north-western Iberian Peninsula (Güimil-Fariña and Parcero-Oubiña 2015; Fonte et al. 2017).
3 The Case Study: Approaches to Roman Roads in the NW Iberian Peninsula
Our recent approaches to the digital modelling of Roman roads in the north-western Iberian Peninsula have been based on an explicitly “postdictive” perspective aimed at exploring which cost factors best explain the route of some of the main roads which are known in sufficient detail. As the north-west of the Iberian Peninsula is a region with a rugged topography, we relied on the calculation of LCP based on slope-dependent cost functions to approach the rationale behind the layout of the best-known sections of the Roman roads in the region.
An initial paper (Güimil-Fariña and Parcero-Oubiña 2015) enabled us to understand some of the basic factors behind the road network on a general scale and from a pedestrian perspective. We found that, in most cases, the distribution of material indicators related with the Roman roads (essentially milestones, which are reasonably abundant in this region) was highly coincident with the route of the LCPs calculated for pedestrian movement, in which changes in slope were the only influence. Besides slope-dependent friction, we only added an extra cost to river courses, which in this region have gentler slopes than most of the surrounding terrain, to prevent the software from considering them as theoretically good areas for movement and producing LCPs running through rivers. Although good results were obtained for some of the roads, others proved to be dependent on different factors which we were not able to identify at that point.
A second paper (Fonte et al. 2017) focused on a more detailed analysis of a specific road: the so-called Via XVII from the Antonine Itinerary¸ connecting Bracara Augusta (Braga, Portugal) and Asturica Augusta (Astorga, Spain). This analysis provided further arguments to understand the influence of some other physical factors in the layout of the roads. In particular, we focused on the modelling of the movement of animal-drawn wheeled vehicles, finding that the known layout of the road analysed showed a very good coincidence with the theoretical LCP which, besides considering the effect of the slope on pedestrian movement, avoids higher altitudes and prioritizes terrain below a given critical slope. In our case, dealing with a succession of regions of sharp topographical contrast, between hilly terrain and open flat land, the threshold for the critical slope was found to occur between 8 and 16%, depending on the sector. Table 14.1 summarizes the model of friction which we found useful in understanding the layout of the Via XVII road.
This approach allowed us to acquire a good understanding of the rationale behind the Via XVII and, to our view, provided a perspective which was complementary to the more traditional approaches aimed at the reconstruction of the route of the road based on what we call a “joining the dots” approach (for this particular road, Lemos 2000; Rodríguez Colmenero et al. 2004; Maciel and Maciel 2004; Moreno Gallo 2011a; Fontes and Andrade 2012). In a way, drawing from the proposals of Limp and Opitz regarding the impact of digital measurement tools in archaeology (Opitz and Limp 2015; Limp 2016), our results could be seen as an “independent measure”, against which the likelihood of the existing archaeological interpretations can be tested.
However, these results opened up a number of new questions and/or avenues for further research. One obvious possibility would be to use the more refined results of this second analysis to fuel a predictive approach in order to find the most plausible routes of the roads, or sections of roads, for which a greater degree of uncertainty exists. Although we have already begun exploring this approach, it extends beyond the limits available for this publication. In this case, we shall focus on certain parts of the Via XVII in an attempt to explore the utility of certain tools which allow movement to be modelled less restrictively than is the case with LCPs.
4 Beyond Least Cost Paths: Finding Multiple Optimal Routes Between Points
4.1 Combining Optimal Routes for Different Friction Models
One of the main limitations of LCP-based approaches is that, given a specific model of friction, it is possible to find only the first optimal connection between points. One simple way to overcome this limitation is to use multiple models of friction, as some authors have done to obtain and compare, for instance, optimal terrestrial and maritime routes (Howey 2007; Van Lanen et al. 2015b) or to calculate various potential optimal paths based on different factors (Verhagen and Jeneson 2012; Surface-Evans 2012; De Gruchy 2016). However, even in those cases, for each single friction model, the results are always limited to the first single optimal connection between points. Therefore, the outcome is a collection of multiple single optimal connections, based on different criteria.
Although this is not necessarily a problem in many cases, in others it might be relevant to explore the possibility of multiple potential pathways to connect a network of points (Howey 2011). This can also occur in the case of highly formalized road networks such as the main Roman roads where different branches are sometimes supposed to have connected two points. A section of the Via XVII around Aquae Flauiae (Chaves, Portugal) which we previously analysed in Fonte et al. (2017) provides a good case in point (Fig. 14.1).
As was observed in our previous paper, it seems that Aquae Flauiae acted as a primary node in the layout of this road, something which is in accordance with its importance as a central place of secondary level in Roman times. The topography around Aquae Flauiae is especially rugged, which must have implied some limitations to mobility in the past: less than 50% of the area represented in Fig. 14.1 has a slope below 16%, and only 22.5% below 8%, referring to the range of slopes which is usually assumed to limit the movement of wheeled vehicles.
The most recent proposals (Rodríguez Colmenero et al. 2004; Fontes and Andrade 2012) agree in suggesting the existence of two branches to the west of Aquae Flauiae, both of which are indicated by the presence of milestones and/or bridges. These branches cross the Terva valley (Boticas, Portugal), where an important Roman mining area is located (Fontes et al. 2011) (Fig. 14.1). Less consensus exists towards the east of Aquae Flauiae. Although some authors propose the existence of just one single branch through the Rabaçal valley (Valpaços, Portugal) (Rodríguez Colmenero et al. 2004), others have argued for the existence of a second branch northwards, through the Tuela valley (Vinhais, Portugal), to which direct evidence such as milestones and possible Roman bridges could be associated (Lemos 1993, 2000; Maciel and Maciel 2004) (Fig. 14.1, top). A third proposal has been put forward by P. Soutinho, who agrees on the existence of that route to the north but interprets it not as a branch of the main Via XVII but as part of a secondary road coming from the south (Fig. 14.1, bottom).Footnote 1 In any case, both branches, or both roads, would have come together around Castro de Avelãs (Bragança, Portugal).
The context is open to different interpretations. There are some locations where direct material evidence points to the passing of a Roman pathway (milestones and bridges), although some of the connections between them are largely uncertain. The proposals summarized in Fig. 14.1 rely on different, indirect, evidence, but it is hard to definitively affirm which one is more accurate or reliable. As mentioned above, this is a section of the larger road (Via XVII) which was analysed in Fonte et al. (2017). In that case, we arrived at the friction model summarized in Table 14.1. The LCP it produced showed a good match with the distribution of most of the known milestones along the whole road and is also largely coincident with (1) the northern branch of the road to the west of Aquae Flauiae and (2) the southern and most agreed-on branch to the east. But what could be the logic of the other two branches? Do they privilege other types of movement, such as pedestrian routes? Do they lead to secondary places of interest which deviate from the optimal route? Are they earlier or later routes, suitable for different criteria and cost factors? Are they seasonal branches?
If we limit our analysis to the use of LCP, we can only test those hypotheses by designing alternative friction models and checking their coincidence with the available evidence. For other sections of this same road, the possible existence of changes in time has been already suggested (Fernández Ochoa et al. 2012): a road initially developed in a context of military conquest was later turned into an administrative and commercial route, which would have implied some redesign. This is an idea worth exploring, with a possible hypothesis being that any of the branches could correspond to optimal pedestrian paths which were later replaced, or complemented, by more adequate routes for wheeled vehicles (Fig. 14.2).
To test this possibility, we returned to the area around Aquae Flauiae in order to carry out further analyses. In this case, we used a higher definition DEM, with a spatial resolution of 10 m, built using the elevation data (contours and height points) of the Portuguese Army Geographical Institute (IGeoE) 1:25,000 cartography.
Our first step was to calculate the LCP for pedestrian movement between three nodes which are assumed to have been located along the road in this sector: Aquae Flauiae (without a doubt a central node of the road), Castro de Avelãs (whose Roman name is uncertain but its relationship to the road seems clear) and the supposed location of the mansio Caladunum (the site is unknown, but there is general agreement that the road ran through the place we have chosen and direct evidence for this theory). We also re-calculated the LCP for wheeled vehicles, using the same parameters as in our previous work, but with the more detailed DEM now available.
None of the results were satisfactory. On the one hand, on this more detailed scale, the LCP designed for wheeled vehicles provides only a partial coincidence with the assumed main route of the road, especially to the east of Aquae Flauiae. This deviation, which was not noticeable in our previous analysis on a more general scale, might suggest that the selection of a specific point to cross the River Rabaçal must have also had a local influence on the route of the road (as seems to occur, on a more general scale, with other bridges (Güimil-Fariña and Parcero-Oubiña 2015). For this reason, we have included the Ponte do Arquinho bridge as a fourth node in our calculation of the wheeled LCP. In this case, the match is very good, and the LCP aligns well with the milestones and bridges located there. Although this looks like a good solution, we shall return to this issue later on to see whether there might be a subtler explanation for this particular question.
On the other hand, the pedestrian LCP shows only a partial coincidence with the known evidence about the branches. Towards the west of Aquae Flauiae, the pedestrian LCP follows practically the same corridor as the LCP for vehicles. To the east, the pedestrian LCP takes a rather straighter route towards Castro de Avelãs, a route which aligns with a couple of milestones and a bridge before crossing the Rabaçal river, but which runs far from the two milestones to the northwest of Castro de Avelãs. This might make it possible to argue that part of the northern branch of the road to the east of Aquae Flauiae could correspond to optimal routes for other criteria. Unfortunately, we have had no chance to test if they could also have corresponded to the second or third best routes for wheeled vehicles which may have been in use for whatever reason. Besides this, and even if we consider that pedestrian movement can help to understand part of the northern branch to the east of Aquae Flauiae, it is of little help in clarifying the southern branch to the west.
4.2 Overcoming the Limitations of the Single Least-Cost Path Model
This is where the use of LCPs can take us. If we wish to explore further the possible logic of these branches, we need to resort to other methodological tools which reach beyond the restrictions of LCPs. These restrictions have recently been discussed, and some alternate methods have been proposed, such as “circuit theory” (Howey and Brouwer Burg 2017) or the exploration of potential movement in terms of “flows” or as “topographies of movement” (Fábrega-Álvarez 2006; Frachetti 2006; Llobera et al. 2011; Mlekuž 2014; Frachetti et al. 2017). We decided to use Focal Mobility Networks, or MADO in its Spanish acronym (Llobera et al. 2011), for two main reasons. Firstly, because we are more familiar with its operation, as one of us (C.P-O) was one of the authors who developed it, and we have previous experience in applying it. Secondly, because MADOs can be calculated using any desktop GIS software, thus simplifying our analysis, since we could limit ourselves to using one single piece of software (ArcGIS in our case).
MADO has been defined as “the network of most likely paths towards a given destination”. It is based on the application of hydrological tools (flow direction and accumulation) to cumulative cost surfaces. The final result, a raster image of “cumulative probability of movement”, can be reclassified into a network of potential paths towards the destination of choice (Llobera et al. 2011; an example of a similar approach in Fábrega-Álvarez et al. 2011).
Applying this approach to our case study, we calculated the MADO towards the three nodes on which the Roman roads in our area are based (Aquae Flauiae, Castro de Avelãs and Caladunum) and obtained a map of the potential natural corridors heading towards any of the three destinations (Fig. 14.3).Footnote 2 Even though, according to the LCP analysis, Ponte do Arquinho also seemed to be a primary node in the area, we intentionally decided to leave it out in this case so as to double check the preliminary idea.
This led to an initial interpretation of the most probable corridors of mobility towards the four destinations we have chosen. A measure of the reliability of these corridors with respect to mobility in Roman times can be obtained by quantifying their proximity to the material elements related with Roman roads (milestones and bridges). In the area of interest for our analysis, six bridges with a Roman origin have been documented and a total of 73 milestones are known (Rodríguez Colmenero et al. 2004). Since some of them are clustered in one single location, the actual number of milestone locations is 53. While bridges are obviously in situ elements, most of the milestones known in the area are found today in secondary locations. The exact place of origin is known only for a few of them (12) and, although most of the remaining ones are thought to be placed near their original location, we have considered them separately for our purpose here.
Table 14.2 summarizes the results of this measurement, showing a relatively high proximity between all the in situ elements and the closest MADO route: only one in situ milestone location is more than 500 m far from any MADO route. A complementary quantification, taking into account the density of MADO routes in the area, is shown in Table 14.3. Almost all the in situ elements are located within a buffer distance of 500 m of the MADO lines depicted in Fig. 14.3, which represents around 23% of the total area under analysis.
4.3 From MADO Meshes to Multiple Discrete Optimal Connections
All the above seems to indicate that the potential routes modelled with our MADO analysis show a high degree of coincidence with the actual routes used by Roman mobility in the area. In turn, this reinforces the conclusions of Fonte et al. (2017) in relation to the suitability of the friction model developed for modelling Roman mobility in this region. However, if we want this MADO analysis to be more useful in understanding the logic behind the different branches of the Via XVII which seem to have existed here, we still need to simplify the extremely dense network of potential routes shown in Fig. 14.3. In fact, MADO analysis does not by definition provide connections between points, but rather potential paths with no specific origin. This is clearly obvious in some routes in Fig. 14.3 which “lead to nowhere”, while some others are prolonged across the whole area and do indeed connect the destination points of choice. This happens when MADO lines leading to one location (for instance, Aquae Flauiae) overlap at some point with MADO lines leading to any other of the two given positions (Castro de Avelãs or Caladunum). Thus, there is an intrinsic network of multiple LCPs hidden behind the larger complete mesh of MADO lines.
In order to extract the network of multiple LCP, we followed the proposal of Lynch and Parcero-Oubiña (2017): simply selecting the overlapping segments of the lines obtained from all sites independently and merging them into one single path connecting the three nodes. Prior to this, we calculated a line density map in order to see which corridors had a higher concentration of potential mobility. This, together with the elimination of the lines with a centrifugal direction, ended up in the multiple LCP shown in Fig. 14.4.
The most probable routes between the different nodes considered, compared in relative terms of length and cost. Top: line thickness is proportional to length (longest routes correspond to thicker lines); labels indicate how much longer each route is with respect to the shortest one. Bottom: line thickness is proportional to accumulated friction crossed (higher frictions correspond to thicker lines); labels indicate, in relative terms, how much more accumulated friction each route implies with respect to the least cost one. An independent relative scale is used, respectively, for the routes to the east and west of Aquae Flauiae
This network of multiple optimal connections can also be organized in a hierarchy using different criteria, which might help us to further understand why some of them seem to correspond better than others with the distribution of material indicators of the Roman roads. Cost distance measurements are a combination of linear distance and terrain friction, two factors which can be explored separately in order to obtain two complementary path hierarchies. Firstly, we can look at the length of each path. Figure 14.4, top, shows that line width is proportional to the length of each path with the labels quantifying the relative length of each one, with 1 being the shortest in each direction (to the west and east of Aquae Flauiae, respectively). To the west, the shortest path is also the LCP in terms of cost (see Fig. 14.2). However, the most remarkable result is the extremely good coincidence of the second shortest path with the distribution of milestones marking the supposed route of the southern branch (compare with Fig. 14.1). The third potential path takes a substantial detour and is almost 40% longer than the shortest one.
Between Aquae Flauiae and Castro de Avelãs, the network of potential paths is denser. In this case, the LCP obtained in Fig. 14.2 is not the shortest one, but only the fourth in length: three shorter routes exist northwards, which converge in crossing the Rabaçal river around Ponte de Picões and, when combined, are not too different from some of the reconstructions proposed for the northern branch of the Via XVII in this area. One of them is also rather similar to the pedestrian LCP, as shown in Fig. 14.2. Among the options to the south, and with respect to the LCP represented in Fig. 14.2, this analysis shows how the connection via the bridge of Ponte do Arquinho is, actually, one of the optimal choices to travel between Aquae Flauiae and Castro de Avelãs, even if the path is not obliged to go over that bridge. Finally, there is one more optimal path with a significantly longer route which implies an extra 12–16 km.
A complementary, and perhaps more illuminating, hierarchy emerges if we quantify the total friction of the terrain crossed by each path. This quantification is made by adding the friction values of all the cells that each path goes across. To ease comparison, we have also represented these values in relative magnitudes, with 1 being the sum of frictions of the less costly path in each direction independently (to the west and east of Aquae Flauiae, respectively).
To the west of Aquae Flauiae, this friction-based hierarchy, once more, defines the first LCP as the optimal one (as should be expected). The second shortest path is also in second place in terms of friction travelled. The longer detour to the north also implies a higher cost and, although the differences are not very high, when combined with length, it is clear that this is the least optimal of the three most probable routes. Again, it must be highlighted that the two first optimal paths are those which coincide well with the distribution of milestones in this sector.
To the east of Aquae Flauiae, the situation is somewhat more complicated and interesting. Quite surprisingly, the LCP though Ponte do Arquinho is now the best option (i.e. the pathway which implies crossing a terrain with a lower degree of overall friction), and it is only due to the fact that it is slightly longer (2 more km) that it does not come out as the optimal connection between Aquae Flauiae and Castro de Avelãs when a LCP approach is used. This is an interesting result which also helps to qualify the true influence of Ponte do Arquinho as a node in this section: rather than it being a direct conditioning factor for the layout of the road, it could be interpreted as the crossing point coinciding with one of the best “natural corridors” across the area.Footnote 3 The extra distance implied by this route with respect to the first optimal choice (ca. 2 km), as calculated by the LCP analysis, seems to have been less relevant in Roman times than the lower overall friction that it offered.
As far as the northern routes, which were shorter in length, are concerned, they now imply a more substantial extra friction of 30–67% when compared to the two southern routes. In this case, the existence of a possible branch of the road in this area would not be fully explained merely in terms of an alternative optimal route for wheeled vehicles. It seems clear that certain other factors must have come into play.
5 Final Comments
The results of our analysis seem to imply that a balance between terrain friction and distance lay behind the apparent selection of the routes that were followed at some point to travel across this region in Roman times. Between Aquae Flauiae and Caladunum, the shortest and least costly path was complemented by the second-best choice in terms of both cost and length, facilitating the access to a southern area of the Terva valley which, at some point in time, became important for the mines located nearby. What our analysis shows is that the route across this part of the valley was chosen following the same criteria which lay behind the selection of the first route northwards: the preference for terrain suitable for wheeled vehicles, according to the friction model summarized in Table 14.1.
Between Aquae Flauiae and Castro de Avelãs, the situation is a little more complex, since the hierarchy of best routes changes depending on how it is measured: in terms of length or travelled friction. The analysis based on the use of MADO for the calculation of multiple LCP shows that a single LCP analysis may imply an over-simplification of a subtler case. Although the path that best matches the distribution of known milestones and bridges is not the first LCP between Aquae Flauiae and Castro de Avelãs, it is, however, among the optimal choices available. Indeed, it is the path which implies travelling over terrain with a lower degree of friction, despite being slightly longer. The MADO-based calculation of multiple LCP has allowed us to better understand that the rationale behind this section of the road is no different from what was proposed for the road as a whole. The apparent influence of Ponte do Arquinho as a primary node is also lessened by this analysis.
The location of the elements signalling the supposed northern branch of the road in this sector shows, in general, a rather good coincidence with other potentially optimal routes, which would have implied higher costs to traverse, despite being shorter. It should be noted that a large section of these routes is coincident with the pedestrian LCP calculated for this area, and the combination of these two factors may provide an argument to help understand the logic of this branch: a shorter connection for pedestrian travel, allowing access to a different portion of the territory which, although it is only a secondary option for wheeled movement, is also among the “natural corridors” to cross the area in those circumstances.
The analysis we have summarized here offers just a brief example of the potential of using tools other than LCP to digitally explore and predict the possible routes of ancient roads. Undoubtedly, a more refined approach is needed than that shown here, but hopefully this example will illustrate the benefits of using tools, such as MADO, to explore potential mobility in less restrictive ways.
Notes
- 1.
This proposal is developed on the website http://ww.viasromanas.pt, which includes a detailed mapping of the proposed routes and the location of a large number of material remains related to Roman roads in Portugal.
- 2.
- 3.
Rather than being the only, or best, possible way to cross the Rabaçal river, as seems to have been the case with other bridges in the region, such as Ponte Bibei on a nearby road (Güimil-Fariña and Parcero-Oubiña 2015).
References
Abásolo Álvarez JA (1990) El conocimiento de las vías romanas. Un problema arqueológico. In: Simposio sobre la red viaria en la Hispania romana. Institución Fernando el Católico, Zaragoza, pp 7–20
Alonso Trigueros JM (2014) Modelo gráfico para la datación de las vías romanas empedradas a partir del estudio de sus estados de frecuentación y del análisis superficial de roderas. Universidad Politécnica de Madrid, Madrid. Available at http://oa.upm.es/32697/. Accessed on 12 May 2018
De Gruchy MW (2016) Beyond replication: the quantification of route models in the North Jazira, Iraq. J Archaeol Method Theory 23(2):427–447. https://doi.org/10.1007/s10816-015-9247-x
Del Olmo Martín J (2006) Arqueología Aérea de las Ciudades Romanas en la Meseta Norte. Algunos ejemplos de urbanismo de la primera Edad del Hierro, segunda Edad del Hierro y Romanización. In: Moreno Gallo I (ed) Nuevos Elementos de Ingeniería Romana, III Congreso de las Obras Públicas Romanas. Junta de Castilla y León / Colegio de Ingenieros Técnicos de Obras Públicas, Astorga, pp 313–340, Available at http://www.traianvs.net/pdfs/2006_12olmo.pdf. Accessed on 12 May 2018
Estefanía Álvarez D (1960) Vías romanas de Galicia. Zephyrus 11:5–104
Fábrega-Álvarez P (2006) Moving without destination. A theoretical GIS–based determination of movement from a given origin. Archaeol Comput Newsl 64:7–11. Available from http://digital.csic.es/handle/10261/15993. Accessed on 12 May 2018.
Fábrega-Álvarez P, Fonte J, González García FJ (2011) Las sendas de la memoria. Sentido, espacio y reutilización de las estatuas-menhir en el noroeste de la Península Ibérica. Trab Prehist 68(2):313–330. https://doi.org/10.3989/tp.2011.11072
Fasolo M (2014) Infrastructure in the Roman world: roads and aqueducts. In: Smith C (ed) Encyclopedia of global archaeology. Springer, New York, pp 3873–3882. https://doi.org/10.1007/978-1-4419-0465-2_1458
Fernández Ochoa C, Morillo Cerdán Á, Gil Sendino F (2012) El «Itinerario de Barro». Cuestiones de autenticidad y lectura. Zephyrus 70:151–179
Fonte J, Parcero-Oubiña C, Costa-García JM (2017) A GIS-based analysis of the rationale behind Roman roads. The case of the so-called via XVII (NW Iberian Peninsula). Mediterr Archaeol Archaeometry 17(3):163–189. https://doi.org/10.5281/zenodo.1005562
Fontes L, Alves M, Martins CMB, Delfim B, Loureiro E (2011) Paisagem, povoamento e mineração antigas no vale alto do rio Terva, Boticas. In: CMB M, AMS B, Martins JIFP, Carvalho J (eds) Povoamento e Exploração dos Recursos Mineiros na Europa Atlântica Ocidental. CITCEM/APEQ, Braga, pp 203–219
Fontes, LFO, Andrade F (2012) O traçado da via romana Bracara-Asturica, por Aguae Flaviae, no concelho de Boticas. Unidade de Arquelogia, Universidade do Minho, Braga. Available at http://repositorium.sdum.uminho.pt/handle/1822/16561. Accessed on 12 May 2018
Frachetti MD (2006) Digital archaeology and the scalar structure of pastoral landscapes. In: Evans TL, Daly P (eds) Digital archaeology: bridging method and theory. Routledge, London, pp 128–147
Frachetti MD, Smith CE, Traub CM, Williams T (2017) Nomadic ecology shaped the highland geography of Asia’s Silk Roads. Nature 543(7644):193–198. https://doi.org/10.1038/nature21696
Franco Maside RM (2000) Rutas naturais e vías romanas na provincia de A Coruña. Gallaecia 19:162–166. Available at https://dialnet.unirioja.es/servlet/articulo?codigo=83901. Accessed on 12 May 2018
Franco Maside RM (2001) La vía per loca maritima: un estudio sobre vías romanas en la mitad Norocidental de Galicia. Gallaecia 20:224–229. Available at https://dialnet.unirioja.es/servlet/articulo?codigo=83925. Accessed on 12 May 2018
Gethin B, Toller H (2014) The Roman marching camp and road at Loups Fell, Tebay. Britannia 45:1–10. https://doi.org/10.1017/S0068113X13000548
Gómez Vila J (2005) Vías romanas de la actual provincia de Lugo. University of Santiago de Compostela, Santiago de Compostela. Available at https://minerva.usc.es/xmlui/handle/10347/9615. Accessed on 12 May 2018
González Álvarez D (2011) Vías romanas de montaña entre Asturias y León: La integración de la «Asturia transmontana» en la red viaria de Hispania. Zephyrus 67:171–192
Güimil-Fariña A, Parcero-Oubiña C (2015) “Dotting the joins”: a non-reconstructive use of Least Cost Paths to approach ancient roads. The case of the Roman roads in the NW Iberian Peninsula. J Archaeol Sci 54:31–44. https://doi.org/10.1016/j.jas.2014.11.030
Herzog I (2013) The potential and limits of optimal path analysis. In: Bevan A, Lake M (eds) Computational approaches to archaeological spaces. Left Coast Press, Walnut Creek (CA), pp 179–211
Herzog I (2014) A review of case studies in archaeological least cost analysis. Archeologia e Calcolatori 25:223–239. Available at http://www.archcalc.cnr.it/indice/PDF25/12_Herzog.pdf. Accessed on 12 May 2018
Herzog I (2017) Reconstructing pre-industrial long distance roads in a hilly region in Germany, based on historical and archaeological data. Stud Digit Herit 1(2):642–660. https://doi.org/10.14434/sdh.v1i2.23283
Howey MCL (2007) Using multi-criteria cost surface analysis to explore past regional landscapes: a case study of ritual activity and social interaction in Michigan, AD 1200–1600. J Archaeol Sci 34(11):1830–1846. https://doi.org/10.1016/j.jas.2007.01.002
Howey MCL (2011) Multiple pathways across past landscapes: circuit theory as a complementary geospatial method to least cost path for modeling past movement. J Archaeol Sci 38(10):2523–2535. https://doi.org/10.1016/j.jas.2011.03.024
Howey MCL, Brouwer Burg M (2017) Assessing the state of archaeological GIS research: unbinding analyses of past landscapes. J Archaeol Sci 84:1–9. https://doi.org/10.1016/j.jas.2017.05.002
Lemos FS (1993) Povoamento romano de Trás-os-Montes Oriental. Universidade do Minho, Braga
Lemos FS (2000) A Via Romana entre Bracara Augusta e Asturica Augusta, por Aquae Flaviae. Revista de Guimarães 110:15–51
Limp WF (2016) Measuring the face of the past and facing the measurement. In: Forte M, Campana S (eds) Digital methods and remote sensing in archaeology. Springer, Cham, pp 349–369. https://doi.org/10.1007/978-3-319-40658-9_16
Llobera M, Fábrega-Álvarez P, Parcero-Oubina C (2011) Order in movement: a GIS approach to accessibility. J Archaeol Sci 38(4):843–851. https://doi.org/10.1016/j.jas.2010.11.006
Llobera M, Sluckin TJ (2007) Zigzagging: theoretical insights on climbing strategies. J Theor Biol 249:206–217. https://doi.org/10.1016/j.jtbi.2007.07.020
Loewinsohn E (1965) Una calzada y dos campamentos romanos del conuentus asturum. Arch Esp Arqueol 38:26–43
Lynch J, Parcero-Oubiña C (2017) Under the eye of the Apu. Paths and mountains in the Inka settlement of the Hualfín and Quimivil valleys, NW Argentina. J Archaeol Sci Rep 16:44–56. https://doi.org/10.1016/j.jasrep.2017.09.019
Maciel T, Maciel MJ (2004) Estradas romanas no território de Vinhais: a antiga rede viária e as suas pontes. Câmara Municipal de Vinhais, Vinhais
Mlekuž D (2014) Exploring the topography of movement. In: Polla S, Verhagen P (eds) Computational approaches to movement in archaeology. Theory, practice and interpretation of factors and effects of long term landscape formation and transformation. De Gruyter, Berlin, pp 5–22. https://doi.org/10.1515/9783110288384.5
Moreno Gallo I (2006) Vías romanas. Ingeniería y técnica constructiva. CEHOPU/Ministerio de Fomento, Madrid
Moreno Gallo I (2011a) Identificación y descripción de la vía de Astorga a Braga por Chaves. De Asturica a Veniata. In: Vías romanas en Castilla y León. Junta de Castilla y León, Valladolid, pp 2–38. Available at http://www.viasromanas.net/pdf/00_Vias_romanas_en_Castilla_y_Leon.pdf. Accessed on 12 May 2018
Moreno Gallo I (2011b) Vías romanas en Castilla y León. Available at http://www.viasromanas.net/. Accessed on 12 May 2018
Opitz R, Limp F (2015) Recent developments in high-density survey and measurement (HDSM) for archaeology: implications for practice and theory. Annu Rev Anthropol 44(1):347–364. https://doi.org/10.1146/annurev-anthro-102214-013845
Polla S, Verhagen P (eds) (2014) Computational approaches to the study of movement in archaeology, theory, practice and interpretation of factors and effects of long term landscape formation and transformation. De Gruyter, Berlin. https://doi.org/10.1515/9783110288384
Rabanal Alonso MA (2006) Las vías romanas en las provincias de Zamora y León. Instituto de Estudios Zamoranos “Florian de Ocampo”/Diputación de Zamora/UNED, Zamora
Rodríguez Colmenero A, Ferrer Sierra S, Álvarez Asorey R (2004) Miliarios e outras inscricións viarias romanas no Noroeste Hispánico (conventus Bracarense, Lucense y Asturicense). Consello da Cultura Galega, Santiago de Compostela. Available at http://consellodacultura.gal/mediateca/extras/CCG_2004_Miliarios-e-outras-inscricions-viarias-romanas-do-noroeste-hispanico-conventos-bracarense-lucense-e-asturicense.pdf. Accessed on 12 May 2018
Roldán Hervás JM (1975) Itineraria Hispana. Fuentes antiguas para el estudio de las vías romanas en la península ibérica. Universidad de Valladolid, Valladolid
Roldán Hervás JM, Caballero Casado C (2014) Itineraria Hispana. Estudio de las vías romanas en Hispania a partir del Itinerario de Antonino, el Anónimo de Rávena y los Vasos de Vicarello. El Nuevo Miliario 17:1–255
Sáez Taboada B (1999) Vías 19 y 20: Trazado y función. University of Sevilla, Sevilla
Small F (2016) The lost Roman road from Chichester to Arundel. Hist Engl Res 4:3–8. Available at https://historicengland.org.uk/images-books/publications/historic-england-research-4. Accessed on 12 May 2018
Supernant K (2017) Modeling Métis mobility? Evaluating least cost paths and indigenous landscapes in the Canadian west. J Archaeol Sci 84:63–73. https://doi.org/10.1016/j.jas.2017.05.006
Surface-Evans S (2012) Cost catchments: a least cost application for modeling hunter-gatherer land use. In: White DA, Surface-Evans SL (eds) Least cost analysis of social landscapes: Archaeological case studies. University of Utah Press, Salt Lake City, pp 128–151
Van Lanen RJ, Jansma E, Van Doesburg J, Groenewoudt BJ (2016) Roman and early-medieval long-distance transport routes in north-western Europe: modelling frequent-travel zones using a dendroarchaeological approach. J Archaeol Sci 73:120–137. https://doi.org/10.1016/j.jas.2016.07.010
Van Lanen RJ, Kosian MC, Groenewoudt BJ, Jansma E (2015a) Finding a way: modeling landscape prerequisites for Roman and early-medieval routes in the Netherlands. Geoarchaeology 30(3):200–222. https://doi.org/10.1002/gea.21510
Van Lanen RJ, Kosian MC, Groenewoudt BJ, Spek T, Jansma E (2015b) Best travel options: modelling Roman and early-medieval routes in the Netherlands using a multi-proxy approach. J Archaeol Sci Rep 3:144–159. https://doi.org/10.1016/j.jasrep.2015.05.024
Verbrugghe G, De Clercq W, Van Eetvelde V (2017) Routes across the Civitas Menapiorum: using least cost paths and GIS to locate the Roman roads of Sandy Flanders. J Hist Geogr 57:76–88. https://doi.org/10.1016/j.jhg.2017.06.006
Verhagen P, Jeneson K (2012) A Roman puzzle. Trying to find the via Belgica with GIS. In: Chrysanthi A, Murrieta Flores P, Papadopoulos C (eds) Thinking beyond the tool. Archaeological computing and the interpretive process. Archaeopress, Oxford, pp 123–130
Verhagen P, Whitley T (2012) Integrating archaeological theory and predictive modeling: a live report from the scene. J Archaeol Method Theory 19:1–52. https://doi.org/10.1007/s10816-011-9102-7
Vicente González JL (2013) Vías romanas del Noroeste Hispano: génesis, trazado y una nueva metodología para su estudio. Revista Mapping 22(160):48–67. Available at http://www.jlvg.es/Publicaciones/2013_05_06_VIAS_ROMANAS_NW_HISPANO_JLVG.pdf. Accessed on 12 May 2018
White DA, Surface-Evans SL (eds) (2012) Least cost analysis of social landscapes. Archaeological case studies. University of Utah Press, Salt Lake City
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Parcero-Oubiña, C., Güimil-Fariña, A., Fonte, J., Costa-García, J.M. (2019). Footprints and Cartwheels on a Pixel Road: On the Applicability of GIS for the Modelling of Ancient (Roman) Routes. In: Verhagen, P., Joyce, J., Groenhuijzen, M.R. (eds) Finding the Limits of the Limes. Computational Social Sciences(). Springer, Cham. https://doi.org/10.1007/978-3-030-04576-0_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-04576-0_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-04575-3
Online ISBN: 978-3-030-04576-0
eBook Packages: Social SciencesSocial Sciences (R0)