Abstract
The notion of non-interactive secure computation (NISC) first introduced in the work of Ishai et al. [EUROCRYPT 2011] studies the following problem: Suppose a receiver R wishes to publish an encryption of her secret input y so that any sender S with input x can then send a message m that reveals f(x, y) to R (for some function f). Here, m can be viewed as an encryption of f(x, y) that can be decrypted by R. NISC requires security against both malicious senders and receivers, and also requires the receiver’s message to be reusable across multiple computations (w.r.t. a fixed input of the receiver).
All previous solutions to this problem necessarily rely upon OT (or specific number-theoretic assumptions) even in the common reference string model or the random oracle model or to achieve weaker notions of security such as super-polynomial-time simulation.
In this work, we construct a NISC protocol based on the minimal assumption of one way functions, in the stateless hardware token model. Our construction achieves UC security and requires a single token sent by the receiver to the sender.
A. Jain—This research was supported in part by a DARPA/ARL Safeware Grant W911NF-15-C-0213.
R. Ostrovsky—Research supported in part by NSF grant 1619348, DARPA SafeWare subcontract to Galois Inc., DARPA SPAWAR contract N66001-15-1C-4065, US-Israel BSF grant 2012366, OKAWA Foundation Research Award, IBM Faculty Research Award, Xerox Faculty Research Award, B. John Garrick Foundation Award, Teradata Research Award, and Lockheed-Martin Corporation Research Award. The views expressed are those of the authors and do not reflect position of the Department of Defense or the U.S. Government.
I. Visconti—Research supported in part by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 780477 (project PRIViLEDGE) and in part by University of Salerno through a FARB grant.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
A motivating scenario [1]. Suppose there is a public algorithm D that takes as input the DNA data of two individuals and determines whether or not they are related. Alice would like to use this algorithm to find family relatives, but does not want to publish her DNA data in the clear. Instead, she would like to publish an “encryption” of her DNA data b so that anyone else with DNA data a can send back a single message to Alice that reveals D(a, b), i.e., whether or not Alice is related to that person. This process must be such that it prevents either party from influencing the output (beyond the choice of their respective inputs), while also ensuring the privacy of their DNA data.
Non-interactive Secure Computation. The notion of non-interactive secure computation (NISC), introduced by Ishai et al. [25], provides a solution to the above problem. In its general form, NISC allows a receiver party R to publish an encryption of her input y such that any sender party S with input x can then send a message m that reveals f(x, y) to R (for some function f), where m can be viewed as an encryption of f(x, y) that can be decrypted by R. NISC achieves security against malicious senders and receivers, and also allows the receiver’s message to be reusable across multiple computations (w.r.t. a fixed input of the receiver).
Note that if malicious security was not required, then one could readily obtain a solution via Yao’s secure computation protocol [33]. However, NISC guarantees malicious security, and is therefore impossible in the plain model w.r.t. polynomial-time simulation [20].
The work of Ishai et al. [25] gave the first solution for NISC in a hybrid model where the parties have access to the oblivious transfer (OT) functionality. Subsequently, efficient solutions for NISC based on cut-and-choose techniques were investigated in the common reference string (CRS) model [1, 29], the global random oracle model [9], as well as the plain model with super-polynomial-time simulation [2].
Our Goal. All of these works, however, necessarily rely upon OT [2, 25] (or specific number-theoretic assumptions, as in [1, 9, 29]). In this work, we ask whether it is possible to construct NISC protocols based on the minimal assumption of one-way functions?
Since OT is necessary for secure computation (even in CRS and random oracle model), we investigate the above question in the tamper-proof hardware token model, namely, where parties can send hardware tokens to each other.
Starting from the work of Katz [26], there is a large body of research work on constructing secure computation protocols in the hardware token model (see Sect. 3 for a detailed discussion). However, all known solutions require two or more rounds of interaction between the parties (after an initial token transfer phase) regardless of the assumptions and the number of tokens used in the protocol. Thus, so far, the problem of NISC in the hardware token model has remained open.
Our Result. In this work, we construct a UC-secure NISC protocol based on one-way functions that uses a single, stateless hardware token. Note that this is optimal both in terms of complexity assumption as well as the number of tokens.
Concretely, our solution uses the following template: first, a receiver R sends out a hardware token that has its input y hardwired. Upon communicating with the token, a sender S sends out a single message to R, who can then evaluate the output. Note that by using the transformation of [27] which involves adding a single message from R to S, we can also support the case where we want both parties to learn the output.
We remark that prior work on cryptography using hardware tokens has studied the use of both stateful and stateless hardware tokens. The latter is considered to be a more desirable model since it is more realistic, and places weaker requirements on the token manufacturer. Our protocol, therefore, only relies on a stateless hardware token. Moreover, following prior work, we do not make any assumptions on the token if R is malicious; in particular, in this case, the adversarial token may well be stateful.
2 Technical Overview
We now describe the techniques used in our non-interactive secure computation (NISC) protocol using one stateless token and assuming one way functions.
Token Direction. Recall that in a NISC protocol, the receiver R first sends her input y in some encrypted manner such that any sender S with input x computes on this encrypted input and sends back a message m that the receiver can then decrypt to recover the output f(x, y). For different choices of the function f and input x, the sender can generate a fresh message m using the same encrypted input of the receiver. Therefore, to follow this paradigm, in the setting of stateless hardware tokens, we require that the receiver first sends a stateless token T (containing her input) which can be followed by a communication message from the sender. Another approach is to perhaps have the receiver first send a communication message followed by a token sent by the sender. However, such an approach has the drawback that to reuse the receiver’s first message, each time, the sender has to generate and send a fresh token. Hence, we stick to the setting of the receiver first sending a token.
A natural first approach then is to start with the large body of secure computation protocols based on stateless tokens [11, 18, 23, 24] and try to squish one of them into a protocol that comprises of just one token from the receiver and one communication message from the sender. However, in all these works, it is the sender who first sends a token to the receiver (as opposed to our setting where the direction of token transfer is reversed) and this is followed by at least two rounds of interaction between the two parties. As such, it is completely unclear how this could be done even if we were to rely on assumptions stronger than one-way functions.
Therefore, we significantly depart from the template followed in all prior works, and start from scratch for constructing NISC in the stateless hardware token model.
Input authentication. In the stateless hardware token model, an important desideratum is to prevent an adversary from gaining undue advantage by resetting the stateless token that it receives from the honest party. In all prior works, to prevent the adversary from resetting the token and changing its input in each interaction with the token and observing the output (which may potentially allow it learn more information), the token recipient’s input encoding is first authenticated by the token creator before interaction with the token. However, such an approach necessarily requires at least two rounds of communication between S and R after the exchange of tokens which is not feasible in our setting. To overcome this issue, we in fact do allow S to potentially reset the token and interact with the token using different inputs! While this might seem strange at first, the key observation is that S performs only “encrypted” computation in its interaction with the token. Therefore, even if S resets and interacts with the token using different inputs, he learns no information whatsoever about R’s input from his interaction with the token. Thus, resetting attacks are nullified even without authentication. We now describe how to perform such “encrypted” computation.
Protocol structure. At a very high level, our construction follows the garbled circuit based approach to secure computation [33]. That is, the sender S with input x sends a garbled version of a circuit \(C_x\) that computes f(x, z) for any input z. Since we are in the setting of malicious adversaries, an immediate question is how does S prove correctness of the garbled circuit? Clearly, a proof of correctness to the receiver will require more than one message of interaction. Instead, we make S prove to the token T that the garbled circuit \(\mathsf {GC}\) was correctly generated. At the end of the proof, T outputs a signature on \(\mathsf {GC}\) which is sent by the sender S to the receiver R (along with \(\mathsf {GC}\)) as authentication that this garbled circuit was indeed correctly generated.
To make this approach work, one question that naturally arises is how does R receive the labels corresponding to her input in order to evaluate the garbled circuit? Recall that we wish to rely on only one way functions and hence can’t assume stronger primitives like oblivious transfer (OT). Also, previous stateless token based OT protocols rely on multiple rounds of interaction and in some cases, multiple tokens and stronger assumptions. We instead do the following: S sends the garbled circuit \(\mathsf {GC}\) to T and additionally discloses the randomness \(\mathsf {rand}\) used to generate the garbled circuit. The token can use this randomness to compute on its own the labels corresponding to R’s input y. It then responds with a ciphertext \(\mathsf {CT}\) of these labels, and further proves that this ciphertext was indeed correctly generated using the receiver’s input y and the randomness \(\mathsf {rand}\). Then, if the proof verifies, S sends \(\mathsf {CT}\) along with the garbled circuit \(\mathsf {GC}\) and its signature to R. The receiver R decrypts the ciphertext \(\mathsf {CT}\) to recover the labels and then evaluates the garbled circuit. To prevent S from tampering with the ciphertext in its message to R, we will additionally require that the token T signs the ciphertext as well. In fact, we require that the signature queries on \(\mathsf {GC}\) and \(\mathsf {CT}\) are performed jointly as a single query to prevent an adversarial sender from resetting the token and getting signatures from the token on a garbled circuit \(\mathsf {GC}\) computed using randomness \(\mathsf {rand}\), and an encryption \(\mathsf {CT}\) of the wire labels corresponding to R’s input computed using different randomness \(\mathsf {rand}'\ne \mathsf {rand}\). Indeed, such an attack may allow the sender to force an incorrect output on R.
Selective Abort. One issue with the above protocol is that if R is malicious, the token could launch an aborting attack as follows: on being queried with the garbled circuit \(\mathsf {GC}\) and randomness \(\mathsf {rand}\) used for garbling, reconstruct the circuit \(C_x\), thereby learning the sender’s input x and output \(\bot \) if x begins with 0 (for example). Now, if R received a valid message from S, she knows that S’s input begins with 1. The observation is that it is crucial for the token T to not learn both the garbled circuit \(\mathsf {GC}\) and the randomness \(\mathsf {rand}\) used for garbling. Since it is necessary for T to know \(\mathsf {rand}\) to generate the encrypted labels, we tweak the protocol to have S query the token only with a commitment to the garbled circuit (along with the randomness used for garbling) and prove that this commitment is correctly computed. T then produces a signature on this commitment. In his message to R, S now sends the commitment, the signature on it and the decommitment to help R recover the garbled circuit.
Subliminal Channel. Another attack that a malicious receiver could launch is by embedding information about the randomness \(\mathsf {rand}\) in the ciphertext and signatures it generates. Note that even though the token proves that the signature and the ciphertext were correctly generated, a malicious token could still choose the randomness for generating the ciphertext/signature as a function of \(\mathsf {rand}\). Now, even though the proof verifies successfully, the receiver, using the knowledge of the encryption key/signing key, might be able to recover the randomness used for encrypting/signing and learn information about \(\mathsf {rand}\) thus breaking the security of the garbled circuit \(\mathsf {GC}\) (which, in turn, can reveal S’s input). To prevent such an attack, it is necessary to enforce that the randomness used by the token to generate the ciphertext and signature is independent of \(\mathsf {rand}\), but unknown to the sender. We do this by making the token fix this randomness ahead of time (using a commitment) and proving that the randomness used to encrypt and sign was the one committed to before knowing \(\mathsf {rand}\). Additionally, we ensure (using pseudorandom functions) that a malicious sender, via resetting attacks, can not learn this randomness used for encrypting and signing.
Finally, note that to deal with resetting attacks in the proofs, we use a resettably sound zero-knowledge argument for the proof given by the sender to the token and a resettable zero-knowledge argument of knowledge for the proof from the token to the sender. Both these arguments are known assuming just one way functions [12,13,14,15]. Here, we need the argument of knowledge property in order to extract the receiver’s input in the security proof. To extract the sender’s input in the ideal world, the simulator uses knowledge of the garbled circuit (sent to the receiver) and the randomness for garbling (sent to the simulated token). We refer the reader to the main body for more details about our construction and other issues that we tackle.
3 Related Work
We briefly review prior work on cryptography using hardware tokens. The seminal work of Katz [26] initiated the study of secure computation protocols using tamper-proof hardware tokens and established the first feasibility results using stateful hardware tokens. Subsequently, this stateful token model has been extensively explored in several directions with the purpose of improving upon the complexity assumptions, round-complexity of protocols and the number of required tokens [16, 17, 21, 28, 30].
The study of secure computation protocols in the stateless hardware token model was initiated by Chandran et al. [10]. They constructed a polynomial round two-party computation protocol for general functions where each party exchanges one token with the other party, based on enhanced trapdoor permutations. Subsequent to their work, Goyal et al. [23] constructed constant-round protocols assuming collision-resistant hash functions (CRHFs). However, these improvements were achieved at the cost of requiring a polynomial number of tokens. Choi et al. [11] subsequently improved upon their result by decreasing the number of required tokens to only one, while still using only constant rounds and CRHFs. Recently, two independent works [18, 24] obtained the first protocols for secure two party computation based on the minimal assumption of one-way functions. Specifically, Döttling et al. [18] construct a secure constant round protocol using only one token. Hazay et al. [24] construct two-round two-party computation in this model using a polynomial number of tokens.
All the above works, including ours, focus on achieving Universally Composable (UC) [6] securityFootnote 1.
4 Preliminaries
UC-Secure Two Party Computation. We follow the standard real-ideal paradigm for defining secure two party computation. We include the formal definitions in Appendix A.
Non-interactive Secure Computation (NISC). A secure two party computation protocol in the stateless hardware token model between a sender S and a receiver R where only R learns the output is called a NISC protocol if it has the following structure: first, R sends a token to S and then the sender S sends a single message to R. We require security against both a malicious sender and a malicious receiver (who can create the token to be stateful). Further, note that we work in the stand-alone security model and don’t consider composability.
Token functionality. We model a tamper-proof hardware token as an ideal functionality \(\mathcal {F}_{\mathsf {WRAP}} \), following Katz [26]. A formal definition of this functionality can be found in Appendix A. Note that our ideal functionality models stateful tokens. Although all our protocols use stateless tokens, an adversarially generated token may be stateful (Fig. 3).
Cryptographic primitives. In our constructions, we use the following cryptographic primitives all of which can be constructed from one way functions: pseudorandom functions, digital signatures, commitments, garbled circuits, private key encryption [19, 31,32,33].
Additionally, we also use the following advanced primitives that were recently constructed based on one way functions: resettable zero knowledge argument of knowledge and resettably sound zero knowledge arguments. [3,4,5, 8, 12,13,14,15].
Interactive proofs for a “stateless” player. We consider the notion of an interactive proof system for a “stateless” prover/verifier. By “stateless”, we mean that the verifier has no extra memory that can be used to remember the transcript of the proof so far. Consider a stateless verifier. To get around the issue of not knowing the transcript, the verifier signs the transcript at each step and sends it back to the prover. In the next round, the prover is required to send this signed transcript back to the verifier and the verifier first checks the signature and then uses the transcript to continue with the protocol execution. Without loss of generality, we can also include the statement to be proved as part of the transcript. It is easy to see that such a scenario arises in our setting if the stateless token acts as the verifier in an interactive proof with another party.
5 Construction
In this section, we construct a non-interactive secure computation (NISC) protocol based on one-way functions using only one stateless hardware token. Formally, we prove the following theorem:
Theorem 1
Assuming one-way functions exist, there exists a non-interactive secure computation (NISC) protocol that is UC-secure in the stateless hardware token model using just one token.
Notation. We first list some notation and the primitives used.
-
Let \(\lambda \) denote the security parameter.
-
Let’s say the sender \({\mathcal S} \) has private input \(\mathsf {x}\in \{0,1\}^{\lambda }\) and receiver \({\mathcal R} \) has private input \(\mathsf {y}\in \{0,1\}^\lambda \) and they wish to evaluate a function f on their joint inputs.
-
Let \(\mathsf {PRF}: \{0,1\}^\lambda \times \{0,1\}^{\lambda ^2} \rightarrow \{0,1\}^\lambda \) be a pseudorandom function.
-
Let \(\mathsf {Commit}\) be a non-interactiveFootnote 2 computationally hiding and statistically binding commitment scheme that uses n bits of randomness to commit to one bit.
-
Let\((\mathsf {Gen},\mathsf {Sign},\mathsf {Verify})\) be a signature scheme.
-
Let \((\mathsf {ske.setup}, \mathsf {ske.enc}, \mathsf {ske.dec})\) be a private key encryption scheme.
-
Let \(\mathsf {RSZK}= (\mathsf {RSZK.Prove},\mathsf {RSZK.Verify})\) be a resettably-sound zero-knowledge argument system for a “stateless verifier” and \(\mathsf {RZKAOK}= (\mathsf {RZKAOK.Prove},\mathsf {RZKAOK.Verify})\) be a resettable zero knowledge argument of knowledge system for a “stateless prover” as defined in Sect. 4.
-
Let \((\mathsf {Garble}, \mathsf {Garble.KeyGen}, \mathsf {Eval})\) be a garbling scheme for poly sized circuits.
Note that all the primitives can be constructed assuming the existence of one-way functions.
NP languages. We will use the following NP languages in our protocol.
-
1.
NP language \(L^{T}\) characterized by the following relation \(R^{T}\). Statement : \(\mathsf {st}= (\mathsf {c}_{\mathcal {GC}}, \mathsf {ct}, \sigma , \mathsf {c}_\mathsf {y}, \mathsf {c}_\mathsf {ek}, \mathsf {c}_\mathsf {sk}, \mathsf {c}_\mathsf {k}, \mathsf {toss}, \mathsf {vk}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})})\) Witness : \(\mathsf {w}=(\mathsf {y}, \mathsf {r}_\mathsf {y}, \mathsf {ek}, \mathsf {r}_\mathsf {ek}, \mathsf {sk}, \mathsf {r}_\mathsf {sk}, \mathsf {k}, \mathsf {r}_\mathsf {k}, \ell _\mathsf {y}, \mathsf {r}_\mathsf {Sign})\) \(R^{T}_2(\mathsf {st},\mathsf {w})=1\) if and only if :
-
\(\mathsf {c}_\mathsf {y}= \mathsf {Commit}(\mathsf {y};\mathsf {r}_\mathsf {y})\) (AND)
-
\(\mathsf {c}_\mathsf {ek}= \mathsf {Commit}(\mathsf {ek};\mathsf {r}_\mathsf {ek})\) (AND)
-
\(\mathsf {c}_\mathsf {sk}= \mathsf {Commit}(\mathsf {sk};\mathsf {r}_\mathsf {sk})\) (AND)
-
\(\mathsf {c}_\mathsf {k}= \mathsf {Commit}(\mathsf {k};\mathsf {r}_\mathsf {k})\) (AND)
-
\(\ell _\mathsf {y}= \mathsf {Garble.KeyGen}(\mathsf {y}; \mathsf {toss}) \) (AND)
-
\(\mathsf {ct}= \mathsf {ske.enc}(\mathsf {ek}, \ell _\mathsf {y}; \mathsf {PRF}(\mathsf {k}, \mathsf {r}_\mathsf {ske.enc}))\) (AND)
-
\((\mathsf {vk}, \mathsf {sk}) = \mathsf {Gen}(\mathsf {r}_\mathsf {Sign})\) (AND)
-
\(\sigma = \mathsf {Sign}(\mathsf {sk}, (\mathsf {c}_{\mathcal {GC}},\mathsf {ct}); \mathsf {PRF}(\mathsf {k}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}))\).
-
-
2.
NP language L characterized by the following relation R. Statement : \(\mathsf {st}= (\mathsf {toss}, \mathsf {c}_{\mathcal {GC}}, f)\) Witness : \(\mathsf {w}=(\mathsf {x}, \mathcal {GC}, \mathsf {r}_{\mathcal {GC}})\) \(R(\mathsf {st},\mathsf {w})=1\) if and only if :
-
\(\mathcal {GC}= \mathsf {Garble}({\mathcal C}; \mathsf {toss})\) (AND)
-
\({\mathcal C} (\cdot ) = f(\mathsf {x}, \cdot )\) (AND)
-
\(\mathsf {c}_{\mathcal {GC}} = \mathsf {Commit}(\mathcal {GC};\mathsf {r}_{\mathcal {GC}})\)
-
5.1 Protocol
The NISC protocol \(\pi \) is described below:
Token Transfer:
\({\mathcal R} \) does the following:
-
1.
Pick a random key
 for the function \(\mathsf {PRF}\).
for the function \(\mathsf {PRF}\). -
2.
Pick random strings \(\mathsf {r}_\mathsf {y}, \mathsf {r}_\mathsf {ek}, \mathsf {r}_\mathsf {sk}, \mathsf {r}_\mathsf {k}, \mathsf {r}_\mathsf {Sign}\).
-
3.
Compute \((\mathsf {sk},\mathsf {vk}) \leftarrow \mathsf {Gen}(\lambda ; \mathsf {r}_\mathsf {Sign})\) and \(\mathsf {ek}\leftarrow \mathsf {ske.setup}(\lambda )\).
-
4.
Create a token \({\mathbf T} \) containing the code in Fig. 1.
-
5.
Send token \({\mathbf T} \) to \({\mathcal S} \).
Communication Message:
The sender \({\mathcal S} \) does the following:
-
1.
Query the token with input “\(\mathsf {Start}\)” to receive \((\mathsf {c}_\mathsf {y}, \mathsf {c}_\mathsf {ek}, \mathsf {c}_\mathsf {sk}, \mathsf {c}_\mathsf {k}, \mathsf {vk})\).
-
2.
Pick random strings \((\mathsf {toss}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})})\). Compute \(\mathcal {GC}= \mathsf {Garble}({\mathcal C} _\mathsf {x};\mathsf {toss})\) where \(\mathsf {toss}\) is the randomness for garbling and \({\mathcal C} _\mathsf {x}\) is a circuit that on input a string \(\mathsf {y}\), outputs \(f(\mathsf {x},\mathsf {y})\). Then, compute \(\mathsf {c}_{\mathcal {GC}} = \mathsf {Commit}(\mathcal {GC};\mathsf {r}_{\mathcal {GC}})\).
-
3.
Using the prover algorithm \((\mathsf {RSZK.Prove})\), engage in an execution of an RSZK argument with \({\mathbf T} \) (who acts as the verifier) for the statement \(\mathsf {st}= (\mathsf {toss}, \mathsf {c}_{\mathcal {GC}}, f) \in L\) using witness \(\mathsf {w}=(\mathsf {x}, \mathcal {GC}, \mathsf {r}_{\mathcal {GC}})\). That is, as part of the RSZK, if the next message of the prover is \(\mathsf {msg}\), query \({\mathbf T} \) with input (“\(\mathsf {RSZK}\)”, \(\mathsf {toss}, \mathsf {c}_{\mathcal {GC}}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}, \mathsf {msg})\).Footnote 3
-
4.
At the end of the above argument, receive \((\mathsf {ct}, \sigma _{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})})\) from \({\mathbf T} \).
-
5.
Then, using the verifier algorithm \((\mathsf {RZKAOK.Verify})\), engage in an execution of a RZKAOK with \({\mathbf T} \) (who acts as the prover) for the statement \(\mathsf {st}^{\mathbf T} = (\mathsf {c}_{\mathcal {GC}},\mathsf {ct}, \sigma _{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}, \mathsf {c}_\mathsf {y}, \mathsf {c}_\mathsf {ek}, \mathsf {c}_\mathsf {sk}, \mathsf {c}_\mathsf {k}, \mathsf {toss}, \mathsf {vk}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}) \in L^{{\mathbf T}}\). That is, as part of the RZKAOK, if the next message of the verifier is \(\mathsf {msg}\), query \({\mathbf T} \) with input (“\(\mathsf {RZKAOK}\)”, \(\mathsf {toss}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}, \mathsf {msg})\). Output \(\bot \) if the argument does not verify successfully.
-
6.
Send \((\mathsf {c}_{\mathcal {GC}}, \mathcal {GC}, \mathsf {r}_{\mathcal {GC}}, \mathsf {ct}, \sigma _{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})})\) to the receiver \({\mathcal R} \).
Output Computation Phase:
\({\mathcal R} \) does the following to compute the output:
-
1.
Abort if \(\mathsf {Verify}_{\mathsf {vk}}((\mathsf {c}_{\mathcal {GC}},\mathsf {ct}),\sigma _{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}) =0\).
-
2.
Abort if \(\mathsf {c}_{\mathcal {GC}} \ne \mathsf {Commit}(\mathcal {GC};\mathsf {r}_{\mathcal {GC}})\).
-
3.
Compute \(\ell = \mathsf {ske.dec}(\mathsf {ek}, \mathsf {ct})\).
-
4.
Evaluate the garbled circuit \(\mathcal {GC}\) using the labels \(\ell \) to compute the output. That is, \(\mathsf {out}= \mathsf {Eval}(\mathcal {GC}, \ell )\).
Remark: In the above description, we were assuming non-interactive commitments (which require injective one way functions) to ease the exposition. In order to rely on just one way functions, we switch our commitment scheme to a two message protocol where the receiver of the commitment sends the first message. Now, we tweak our protocol as follows: after receiving the token, \(\mathsf {P}_1\) sends the first message of the commitment which is then used by the token \({\mathbf T} \) to compute \(\mathsf {c}_\mathsf {y}\). Similarly, \(\mathsf {P}_1\) computes \(\mathsf {c}_1\) after receiving a first message receiver’s commitment message from \({\mathbf T} \). Note that this doesn’t affect the round complexity of the NISC protocol.
5.2 Correctness
The correctness of the protocol follows from the correctness of all the underlying primitives.
6 Security Proof: Malicious Receiver
Let’s first consider the case where the receiver \({\mathcal R} ^*\) is malicious. Let the environment be denoted by \({\mathcal Z} \). Initially, the environment chooses an input \(\{\mathsf {x}\} \in \{0,1\}^{\lambda }\) and sends it to the honest sender \({\mathcal S} \) as his input.
6.1 Simulator Description
The strategy for the simulator \(\mathsf {Sim}\) against a malicious receiver \({\mathcal R} ^*\) is described below:
Token Exchange Phase:
Receive token \({\mathbf T} \) from \({\mathcal R} ^*\).
Token Interaction:
-
1.
Query the token with input “\(\mathsf {Start}\)” to receive \((\mathsf {c}_\mathsf {y}, \mathsf {c}_\mathsf {ek}, \mathsf {c}_\mathsf {sk}, \mathsf {c}_\mathsf {k}, \mathsf {vk})\).
-
2.
Pick random strings \((\mathsf {toss}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})})\). Compute \(\mathsf {c}_{\mathcal {GC}} = \mathsf {Commit}(0^\lambda ;\mathsf {r}_{\mathcal {GC}})\).
-
3.
Using the simulator \(\mathsf {Sim}_\mathsf {RSZK}\), engage in an execution of an RSZK argument with \({\mathbf T} \) (who acts as the verifier) for the statement \(\mathsf {st}= (\mathsf {toss}, \mathsf {c}_{\mathcal {GC}},f) \in L\). That is, as part of the RSZK, if the next message of \(\mathsf {Sim}_\mathsf {RSZK}\) is \(\mathsf {msg}\), query \({\mathbf T} \) with input (“\(\mathsf {RSZK}\)”, \(\mathsf {toss}, \mathsf {c}_{\mathcal {GC}}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})},\) \(\mathsf {msg})\). Note that \(\mathsf {Sim}\) forwards the code \({\mathsf M} \) of the token \({\mathbf T} \) that it received from \(\mathcal {F}_{\mathsf {WRAP}} \) to \(\mathsf {Sim}_{\mathsf {RSZK}}\).
-
4.
At the end of the above argument, receive \((\mathsf {ct}, \sigma _{(\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}},\mathsf {ct})})\) from \({\mathbf T} \).
-
5.
Then, using the verifier algorithm \((\mathsf {RZKAOK.Verify})\), engage in an execution of a RZKAOK with \({\mathbf T} \) (who acts as the prover) for the statement \(\mathsf {st}^{\mathbf T} = (\mathsf {c}_{\mathcal {GC}},\mathsf {ct}, \sigma _{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}, \mathsf {c}_\mathsf {y}, \mathsf {c}_\mathsf {ek}, \mathsf {c}_\mathsf {sk}, \mathsf {c}_\mathsf {k}, \mathsf {toss}, \mathsf {vk}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}) \in L^{{\mathbf T}}\). That is, as part of the RZKAOK, if the next message of the verifier is \(\mathsf {msg}\), query \({\mathbf T} \) with input (“\(\mathsf {RZKAOK}\)”, \(\mathsf {toss}, \mathsf {r}_\mathsf {ske.enc}, \mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}, \mathsf {msg})\). Output \(\bot \) if the argument does not verify successfully.
Query to Ideal Functionality:
-
1.
Run \(\mathsf {Ext}_{\mathsf {RZKAOK}}\) on the transcript of the above argument to extract a witness \((\mathsf {y}, \mathsf {r}_\mathsf {y}, \mathsf {ek},\mathsf {r}_\mathsf {ek}, \mathsf {sk}, \mathsf {r}_\mathsf {sk}, \mathsf {k}, \mathsf {r}_\mathsf {k}, \ell _\mathsf {y},\mathsf {r}_\mathsf {Sign})\). Note that \(\mathsf {Sim}\) forwards the code \({\mathsf M} \) of the token \({\mathbf T} \) that it received from \(\mathcal {F}_{\mathsf {WRAP}} \) to \(\mathsf {Ext}_{\mathsf {RZKAOK}}\).
-
2.
Query the ideal functionality with input \(\mathsf {y}\) to receive as output \(\mathsf {out}\). The honest sender does not receive any output from the ideal functionality.
Communication Message:
-
1.
Using the output \(\mathsf {out}\), generate a simulated garbled circuit and simulated labels. That is, compute \((\mathsf {Sim}.\mathcal {GC},\mathsf {Sim}.\ell _{\mathsf {y}}) \leftarrow \mathsf {Sim.GC}(\mathsf {out})\).
-
2.
Compute a commitment to the garbled circuit. That is, compute \(\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}} = \mathsf {Commit}(\mathsf {Sim}.\mathcal {GC};\mathsf {r}_{\mathsf {Sim}.\mathcal {GC}})\).
-
3.
Recompute the ciphertext and the signature using the same keys and randomness as done by the token. That is, compute \(\mathsf {ct}= \mathsf {ske.enc}(\mathsf {ek},\) \(\mathsf {Sim}.\ell _{\mathsf {y}};\mathsf {PRF}\) \((\mathsf {k},\mathsf {r}_\mathsf {ske.enc}))\), \(\sigma _{(\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}},\mathsf {ct})} = \mathsf {Sign}(\mathsf {sk}, (\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}},\mathsf {ct}); \mathsf {PRF}\) \((\mathsf {k},\mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}))\).
-
4.
Send \((\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}}, \mathsf {Sim}.\mathcal {GC}, \mathsf {r}_{\mathsf {Sim}.\mathcal {GC}}, \mathsf {ct}, \sigma _{(\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}},\mathsf {ct})})\) to the receiver \({\mathcal R} ^*\).
6.2 Hybrids
We now show that the real and ideal worlds are computationally indistinguishable via a sequence of hybrid experiments where \(\mathsf {Hyb}_0\) corresponds to the real world and \(\mathsf {Hyb}_{4}\) corresponds to the ideal world.
-
\(\mathsf {Hyb}_0\) - Real World: Consider a simulator \(\mathsf {Sim}_{\mathsf {Hyb}}\) that performs exactly as done by the honest sender \({\mathcal S} \) in the real world.
-
\(\mathsf {Hyb}_1\) - Extraction: In this hybrid, \(\mathsf {Sim}_{\mathsf {Hyb}}\) runs the “Query to Ideal Functionality” phase as in the ideal world. That is, run the algorithm \(\mathsf {Ext}_\mathsf {RZKAOK}\) to extract \((\mathsf {y}, \mathsf {r}_\mathsf {y}, \mathsf {ek},\mathsf {r}_\mathsf {ek}, \mathsf {sk}, \mathsf {r}_\mathsf {sk}, \mathsf {k}, \mathsf {r}_\mathsf {k}, \ell _\mathsf {y},\mathsf {r}_\mathsf {Sign})\), then query the ideal functionality with the value \(\mathsf {y}\) to receive output \(\mathsf {out}\). Note that \(\mathsf {Sim}_{\mathsf {Hyb}}\) continues to use the honest circuit \(\mathcal {GC}\) and its commitment \(\mathsf {c}_{\mathcal {GC}}\) in its interaction with \({\mathbf T} \) and the receiver.
-
\(\mathsf {Hyb}_2\) - Simulate RSZK: In this hybrid, in its interaction with the token \({\mathbf T} \), \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes the RSZK argument by running the simulator \(\mathsf {Sim}_\mathsf {RSZK}\) instead of running the honest prover algorithm \(\mathsf {RSZK.Prove}\). Note that \(\mathsf {Sim}_{\mathsf {Hyb}}\) forwards the code \({\mathsf M} \) of the token \({\mathbf T} \) that it received from \(\mathcal {F}_{\mathsf {WRAP}} \) to \(\mathsf {Sim}_{\mathsf {RSZK}}\).
-
\(\mathsf {Hyb}_3\) - Simulate Garbled Circuit: In this hybrid, \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes the message sent to the receiver as in the ideal world. That is, after interacting with the token, \(\mathsf {Sim}_{\mathsf {Hyb}}\) does the following:
-
Using the output \(\mathsf {out}\), generate a simulated garbled circuit and simulated labels. That is, compute \((\mathsf {Sim}.\mathcal {GC},\mathsf {Sim}.\ell _{\mathsf {y}}) \leftarrow \mathsf {Sim.GC}(\mathsf {out})\).
-
Compute a commitment to the garbled circuit. That is, compute \(\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}} = \mathsf {Commit}(\mathsf {Sim}.\mathcal {GC};\mathsf {r}_{\mathsf {Sim}.\mathcal {GC}})\).
-
Recompute the ciphertext and the signature using the same keys and randomness as done by the token. That is, compute \(\mathsf {ct}= \mathsf {ske.enc}(\mathsf {ek},\) \(\mathsf {Sim}.\ell _{\mathsf {y}};\mathsf {PRF}(\mathsf {k},\mathsf {r}_\mathsf {ske.enc}))\), \(\sigma _{(\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}},\mathsf {ct})} = \mathsf {Sign}(\mathsf {sk}, (\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}},\) \(\mathsf {ct}); \mathsf {PRF}(\mathsf {k},\mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}))\).
-
Send \((\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}}, \mathsf {Sim}.\mathcal {GC}, \mathsf {r}_{\mathsf {Sim}.\mathcal {GC}}, \mathsf {ct}, \sigma _{(\mathsf {c}_{\mathsf {Sim}.\mathcal {GC}},\mathsf {ct})})\) to the receiver \({\mathcal R} ^*\).
-
-
\(\mathsf {Hyb}_4\) - Switch Commitment: In this hybrid, \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes \(\mathsf {c}_{\mathcal {GC}} = \mathsf {Commit}(0^\lambda ;\mathsf {r}_{\mathcal {GC}})\) and uses this in its interaction with the token. This hybrid corresponds to the ideal world.
We now prove that every pair of consecutive hybrids is computationally indistinguishable and this completes the proof.
Claim
Assuming the argument of knowledge property of the \(\mathsf {RZKAOK}\) system, \(\mathsf {Hyb}_0\) is computationally indistinguishable from \(\mathsf {Hyb}_1\).
Proof
The only difference between the two hybrids is that in \(\mathsf {Hyb}_1\), \(\mathsf {Sim}_{\mathsf {Hyb}}\) also runs the extractor \(\mathsf {Ext}_\mathsf {RZKAOK}\) to extract the adversary’s input \(\mathsf {y}\). Therefore, by the argument of knowledge property of the \(\mathsf {RZKAOK}\) system, we know that the extractor \(\mathsf {Ext}_\mathsf {RZKAOK}\) is successful except with negligible probability given the transcript of the argument and the code of the prover (that is, the token’s code \({\mathsf M} \)). Hence, the two hybrids are computationally indistinguishable.
Here, note that \(\mathsf {Sim}_{\mathsf {Hyb}}\) forwards the code \({\mathsf M} \) of the token \({\mathbf T} \) that it received from \(\mathcal {F}_{\mathsf {WRAP}} \) to the algorithm \(\mathsf {Ext}_{\mathsf {RZKAOK}}\).
Claim
Assuming the zero knowledge property of the \(\mathsf {RSZK}\) system, \(\mathsf {Hyb}_1\) is computationally indistinguishable from \(\mathsf {Hyb}_2\).
Proof
The only difference between the two hybrids is the way in which the \(\mathsf {RSZK}\) argument is computed. In \(\mathsf {Hyb}_1\), \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes the \(\mathsf {RSZK}\) by running the honest prover algorithm \(\mathsf {RSZK.Prove}\), while in \(\mathsf {Hyb}_2\), \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes the \(\mathsf {RSZK}\) by running the simulator \(\mathsf {Sim}_\mathsf {RSZK}\). Thus, it is easy to see that if there exists an adversary that can distinguish between these two hybrids with non-negligible probability, \(\mathsf {Sim}\) can use that adversary to break the zero knowledge property of the \(\mathsf {RSZK}\) argument system with non-negligible probability which is a contradiction.
Here, note that \(\mathsf {Sim}_{\mathsf {Hyb}}\) forwards the code \({\mathsf M} \) of the token \({\mathbf T} \) that it received from \(\mathcal {F}_{\mathsf {WRAP}} \) to the external challenger which it uses to run the algorithm \(\mathsf {Sim}_{\mathsf {RSZK}}\).
Claim
Assuming the security of the garbling scheme \((\mathsf {Garble},\mathsf {Eval})\) and the argument of knowledge property of the RZKAOK system, \(\mathsf {Hyb}_2\) is computationally indistinguishable from \(\mathsf {Hyb}_3\).
Proof
The only difference between the two hybrids is the way in which the garbled circuit and the labels that are sent to the receiver are computed. We show that if there exists an adversary \({\mathcal A} \) that can distinguish between the two hybrids, then there exists an adversary \({\mathcal A} _\mathsf {GC}\) that can break the security of the garbling scheme. The reduction is described below.
\({\mathcal A} _\mathsf {GC}\) interacts with the adversary \({\mathcal A} \) as done by \(\mathsf {Sim}_{\mathsf {Hyb}}\) in \(\mathsf {Hyb}_2\) except for the changes below. \({\mathcal A} _\mathsf {GC}\) first runs the token interaction phase and the query to ideal functionality phase as done by \(\mathsf {Sim}_{\mathsf {Hyb}}\) in \(\mathsf {Hyb}_2\). In particular, it picks a random string \(\mathsf {toss}\), computes \(\mathsf {c}_{\mathcal {GC}}\) as a commitment to an honest garbled circuit, generates a simulated RSZK argument, extracts the adversary’s input \(\mathsf {y}\) and learns the output \(\mathsf {out}\).
Then, \({\mathcal A} _\mathsf {GC}\) interacts with the challenger \(\mathsf {Chall}_\mathsf {GC}\) of the garbling scheme and sends the tuple \(({\mathcal C} _\mathsf {x},\mathsf {y}, \mathsf {out})\). Here, \({\mathcal C} _\mathsf {x}\) is a circuit that on input any string z outputs f(x, z). \(\mathsf {Chall}_\mathsf {GC}\) sends back a tuple \(({\mathcal C} ^*, \ell ^*_\mathsf {y})\) which is a tuple of garbled circuit and labels that are either honestly generated or simulated. Then, \({\mathcal A} _\mathsf {GC}\) computes \(\mathsf {c}^* = \mathsf {Commit}({\mathcal C} ^*;\mathsf {r}^*)\), \(\mathsf {ct}^* = \mathsf {ske.enc}(\mathsf {ek},\ell ^*_\mathsf {y};\mathsf {PRF}(\mathsf {k},\mathsf {r}_\mathsf {ske.enc}))\), \(\sigma _{(\mathsf {c}^*,\mathsf {ct}^*)} = \mathsf {Sign}(\mathsf {sk}, (\mathsf {c}^*,\mathsf {ct}^*); \mathsf {PRF}(\mathsf {k},\mathsf {r}_{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct}^*)}))\). Finally, \({\mathcal A} _\mathsf {GC}\) sends \((\mathsf {c}^*, {\mathcal C} ^*, \mathsf {r}^*,\) \(\mathsf {ct}^*, \sigma _{(\mathsf {c}^*,\mathsf {ct}^*)})\) to the adversary \({\mathcal A} \) as the message from the sender.
Observe that when \(\mathsf {Chall}_\mathsf {GC}\) computes the garbled circuit and keys honestly, the interaction between \({\mathcal A} _\mathsf {GC}\) and \({\mathcal A} \) corresponds exactly to \(\mathsf {Hyb}_2\). This is true because even though in \(\mathsf {Hyb}_2\), its the token that generates the ciphertext \(\mathsf {ct}\) and the signature \(\sigma _{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}\), from the argument of knowledge property of the scheme \(\mathsf {RZKAOK}\), we know that except with negligible probability, they were generated using the message and randomness exactly as computed by \({\mathcal A} _\mathsf {GC}\). Then, when \(\mathsf {Chall}_\mathsf {GC}\) simulates the garbled circuit and keys, the interaction between \({\mathcal A} _\mathsf {GC}\) and \({\mathcal A} \) corresponds exactly to \(\mathsf {Hyb}_3\). Now, note that the adversary \({\mathcal A} \) does not get access to the randomness \(\mathsf {toss}\) or the commitment \(\mathsf {c}_{\mathcal {GC}}\) sent to the token \({\mathbf T} ^*\) by the reduction \({\mathcal A} _\mathsf {GC}\). Also, crucially, the randomness used in either the ciphertext generation or the signature generation is completely independent of the message being encrypted or signed and hence they don’t leak any subliminal information from the token \({\mathbf T} ^*\) to the adversary \({\mathcal A} \). Finally, \({\mathcal A} _\mathsf {GC}\) does not require any of the randomness used by \(\mathsf {Chall}_\mathsf {GC}\) to generate the garbled circuit and labels since \({\mathcal A} _\mathsf {GC}\) simulates the RSZK argument in its interaction with \({\mathbf T} ^*\). Thus, if the adversary \({\mathcal A} \) can distinguish between these two hybrids with non-negligible probability, \({\mathcal A} _\mathsf {GC}\) can use the same guess to break the security of the garbling scheme with non-negligible probability which is a contradiction.
Claim
Assuming the hiding property of the commitment scheme \(\mathsf {Commit}\), \(\mathsf {Hyb}_3\) is computationally indistinguishable from \(\mathsf {Hyb}_4\).
Proof
The only difference between the two hybrids is the way in which the value \(\mathsf {c}_{\mathcal {GC}}\) is computed. In \(\mathsf {Hyb}_3\), it is computed as a commitment to the garbled circuit \(\mathcal {GC}\) while in \(\mathsf {Hyb}_4\), it is computed as a commitment to \(0^\lambda \). Note that the value committed to or the randomness for commitment is not used anywhere else since the \(\mathsf {RSZK}\) argument is now simulated. Thus, it is easy to see that if there exists an adversary that can distinguish between these two hybrids with non-negligible probability, \(\mathsf {Sim}\) can use that adversary to break the hiding property of the commitment scheme \(\mathsf {Commit}\) with non-negligible probability, which is a contradiction.
7 Security Proof: Malicious Sender
Consider a malicious sender \({\mathcal S} ^*\). Let the environment be denoted by \(\mathcal {Z}\). Initially, the environment chooses an input \(\{\mathsf {y}\} \in \{0,1\}^{\lambda }\) and sends it to the honest receiver \({\mathcal R} \) as his input.
7.1 Simulator Description
The strategy for the simulator \(\mathsf {Sim}\) against a malicious sender \({\mathcal S} ^*\) is described below:
Token Exchange Phase:
\(\mathsf {Sim}\) does the following:
-
1.
Pick a random key
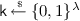 for the function \(\mathsf {PRF}\).
for the function \(\mathsf {PRF}\). -
2.
Pick random strings \(\mathsf {r}_\mathsf {y}, \mathsf {r}_\mathsf {ek}, \mathsf {r}_\mathsf {sk}, \mathsf {r}_\mathsf {k}, \mathsf {r}_\mathsf {Sign}\).
-
3.
Compute \((\mathsf {sk},\mathsf {vk}) \leftarrow \mathsf {Gen}(\lambda ; \mathsf {r}_\mathsf {Sign})\) and \(\mathsf {ek}\leftarrow \mathsf {ske.setup}(\lambda )\).
-
4.
Create a token \({\mathbf T} _\mathsf {Sim}\) almost exactly as in the honest protocol execution with the only difference that instead of the honest receiver’s input \(\mathsf {y}\), the token uses a random string \(\mathsf {y}^*\) as input. For completeness, we describe the functionality of the simulated token’s code in Fig. 2.
-
5.
Send token \({\mathbf T} _\mathsf {Sim}\) to \({\mathcal S} ^*\).
Communication Message:
Receive \((\mathsf {c}_{\mathcal {GC}}, \mathcal {GC}, \mathsf {r}_{\mathcal {GC}}, \mathsf {ct}, \sigma _{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})})\) from the sender \({\mathcal S} ^*\).
Query to Ideal Functionality:
-
1.
Abort if \(\mathsf {Verify}_{\mathsf {vk}}((\mathsf {c}_{\mathcal {GC}},\mathsf {ct}),\sigma _{(\mathsf {c}_{\mathcal {GC}},\mathsf {ct})}) =0\).
-
2.
Abort if \(\mathsf {c}_{\mathcal {GC}} \ne \mathsf {Commit}(\mathcal {GC};\mathsf {r}_{\mathcal {GC}})\).
-
3.
Amongst the queries made to the token \({\mathbf T} _\mathsf {Sim}\), pick one containing the tuple \((\mathsf {c}_\mathcal {GC},\mathsf {toss})\) for which the RSZK argument verified. Note that the queries to the token are known to \(\mathsf {Sim}\) by the observability property of the token.
-
4.
Using this randomness \(\mathsf {toss}\) from the above query and the garbled circuit \(\mathcal {GC}\) sent by \({\mathcal S} ^*\), recover \({\mathcal S} ^*\)’s input \(\mathsf {x}\). Recall that \(\mathcal {GC}= \mathsf {Garble}({\mathcal C} _\mathsf {x};\mathsf {toss})\) where \({\mathcal C} _\mathsf {x}(\cdot ) = f(\mathsf {x},\cdot )\).
-
5.
Send \(\mathsf {x}\) to the ideal functionality and instruct it to deliver output to the honest receiver.
7.2 Hybrids
We now show that the real and ideal worlds are computationally indistinguishable via a sequence of hybrid experiments where \(\mathsf {Hyb}_0\) corresponds to the real world and \(\mathsf {Hyb}_{5}\) corresponds to the ideal world.
-
\(\mathsf {Hyb}_0\) - Real World: Consider a simulator \(\mathsf {Sim}_{\mathsf {Hyb}}\) that performs exactly as done by the honest receiver \({\mathcal R} \) in the real world.
-
\(\mathsf {Hyb}_1\) - Extraction: In this hybrid, \(\mathsf {Sim}_{\mathsf {Hyb}}\) also runs the “Query to Ideal Functionality” phase as in the ideal world. That is, \(\mathsf {Sim}_{\mathsf {Hyb}}\) extracts the malicious sender’s input, sends it to the ideal functionality and instructs it to deliver output to the honest party.
-
\(\mathsf {Hyb}_2\) - Simulate RZKAOK: In this hybrid, in case 3 of the token’s description, \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes the RZKAOK argument by using the simulator \(\mathsf {Sim}_\mathsf {RZKAOK}\) instead of running the honest prover algorithm. Note that this happens only internally in the proof and not in the final simulator’s description. Hence, the final simulator will not require the code of the environment or need to rewind it.
-
\(\mathsf {Hyb}_3\) - Switch Commitment: In this hybrid, in case 1 of the token’s description, \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes \(\mathsf {c}_\mathsf {y}= \mathsf {Commit}(\mathsf {y}^*;\mathsf {r}_\mathsf {y})\).
-
\(\mathsf {Hyb}_4\) - Switch Ciphertext: In this hybrid, in case 2 of the token’s description, \(\mathsf {Sim}_{\mathsf {Hyb}}\) sets \(\ell _\mathsf {y}= \mathsf {Garble.KeyGen}(\mathsf {y}^*;\mathsf {toss})\) and computes \(\mathsf {ct}= \mathsf {ske.enc}(\mathsf {ek}, \ell _\mathsf {y}\) \(;\mathsf {r}_\mathsf {ske.enc})\) as in the ideal world.
-
\(\mathsf {Hyb}_5\) - Honest RZKAOK: In this hybrid, in case 3 of the token’s description, \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes the RZKAOK argument by running the honest prover algorithm as in the ideal world. This hybrid corresponds to the ideal world.
We now prove that every pair of consecutive hybrids is computationally indistinguishable and this completes the proof.
Claim
Assuming the unforgeability property of the signature scheme \((\mathsf {Gen},\mathsf {Sign},\)
\(\mathsf {Verify})\), the binding property of the commitment scheme \(\mathsf {Commit}\), the soundness of the \(\mathsf {RSZK}\) argument system, \(\mathsf {Hyb}_0\) is computationally indistinguishable from \(\mathsf {Hyb}_1\).
Proof
The only difference between the two hybrids is that in \(\mathsf {Hyb}_1\), \(\mathsf {Sim}_{\mathsf {Hyb}}\) extracts the adversary’s input \(\mathsf {x}\) as in the ideal world. We now argue that this extraction is successful except with negligible probability and this completes the proof that the two hybrids are computationally indistinguishable.
First, from the soundness of the argument system \(\mathsf {RSZK}\), we know that except with negligible probability, in one of the arguments given by the malicious sender to the token containing the tuple \((\mathsf {c}_{\mathcal {GC}},\mathsf {toss})\), there exists \((\mathsf {x}, \mathcal {GC}, \mathsf {r}_{\mathcal {GC}})\) such that \({\mathcal C} (\cdot ) = f(\mathsf {x}, \cdot )\), \(\mathcal {GC}= \mathsf {Garble}({\mathcal C}; \mathsf {toss})\) and \(\mathsf {c}_{\mathcal {GC}} = \mathsf {Commit}(\mathcal {GC};\mathsf {r}_{\mathcal {GC}})\). Then, from the unforegability of the signature scheme, we know that except with negligible probability, the commitment \(\mathsf {c}_{\mathcal {GC}}\) sent by \({\mathcal S} ^*\) in the first message is indeed the same as the one used in the above \(\mathsf {RSZK}\) argument. Similarly, from the binding property of the commitment scheme, we know that except with negligible probability, the commitment \(\mathsf {c}_{\mathcal {GC}}\) sent by \({\mathcal S} ^*\) in the first message is indeed a commitment to the same value \(\mathcal {GC}\) that was used as witness in the above \(\mathsf {RSZK}\) argument. Hence, the value \(\mathsf {x}\) extracted by \(\mathsf {Sim}_{\mathsf {Hyb}}\) is the adversary’s input except with negligible probability. There is no difference in the adversary’s view between the two hybrids. Thus the joint distribution of the adversary’s view and honest party’s input is indistinguishable between both the hybrids.
Claim
Assuming the resettable zero knowledge property of the \(\mathsf {RZKAOK}\) system, \(\mathsf {Hyb}_1\) is computationally indistinguishable from \(\mathsf {Hyb}_2\).
Proof
The only difference between the two hybrids is the way in which the \(\mathsf {RZKAOK}\) argument is computed. In \(\mathsf {Hyb}_1\), \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes the \(\mathsf {RZKAOK}\) by running the honest prover algorithm \(\mathsf {RZKAOK.Prove}\), while in \(\mathsf {Hyb}_2\), \(\mathsf {Sim}_{\mathsf {Hyb}}\) computes the \(\mathsf {RZKAOK}\) by running the simulator \(\mathsf {Sim}_\mathsf {RZKAOK}\). Thus, it is easy to see that if there exists an adversary that can distinguish between the joint distribution of the malicious sender’s view and the honest party’s output in these two hybrids with non-negligible probability, \(\mathsf {Sim}\) can use that adversary to break the resettable zero knowledge property of the \(\mathsf {RZKAOK}\) system with non-negligible probability, which is a contradiction.
Note: This is a non-black box reduction - that is, in this reduction, \(\mathsf {Sim}_{\mathsf {Hyb}}\) needs the adversary’s code. However, this is only within this specific reduction. In particular, we stress again that the final simulator will not require the code of the environment or need to rewind it and hence the protocol achieves UC security.
Claim
Assuming the hiding property of the commitment scheme \(\mathsf {Commit}\), \(\mathsf {Hyb}_2\) is computationally indistinguishable from \(\mathsf {Hyb}_3\).
Proof
The only difference between the two hybrids is the way in which the value \(\mathsf {c}_\mathsf {y}\) is computed. In \(\mathsf {Hyb}_2\), it is computed as a commitment to the string \(\mathsf {y}\) while in \(\mathsf {Hyb}_3\), it is computed as a commitment to \(0^\lambda \). Note that the value committed to or the randomness for commitment is not used as a witness in the \(\mathsf {RZKAOK}\) since the argument is now simulated. We only need the value \(\mathsf {y}\) to generate the ciphertext which is not a problem. Thus, it is easy to see that if there exists an adversary that can distinguish between the joint distribution of the malicious sender’s view and the honest party’s output in these two hybrids with non-negligible probability, \(\mathsf {Sim}\) can use that adversary to break the hiding property of the commitment scheme \(\mathsf {Commit}\) with non-negligible probability, which is a contradiction.
Claim
Assuming the semantic security of the encryption scheme \((\mathsf {ske.setup},\) \(\mathsf {ske.enc}, \mathsf {ske.dec})\), \(\mathsf {Hyb}_3\) is computationally indistinguishable from \(\mathsf {Hyb}_4\).
Proof
The only difference between the two hybrids is the way in which the ciphertext \(\mathsf {ct}\) is computed. In \(\mathsf {Hyb}_3\), it is computed as an encryption of the string \(\ell _\mathsf {y}= \mathsf {Garble.KeyGen}(\mathsf {y};\mathsf {toss})\) while in \(\mathsf {Hyb}_4\), it is computed as an encryption of \(\ell _\mathsf {y}= \mathsf {Garble.KeyGen}(\mathsf {y}^*;\mathsf {toss})\). Note that the message encrypted, the randomness for encryption or the secret key of the encryption scheme are not used as a witness in the RZKAOK since the argument is now simulated. We only need the value \(\mathsf {y}^*\) to generate the ciphertext which is not a problem. Thus, it is easy to see that if there exists an adversary that can distinguish between the joint distribution of the malicious sender’s view and the honest party’s output in these two hybrids with non-negligible probability, \(\mathsf {Sim}\) can use that adversary to break the semantic security of the encryption scheme with non-negligible probability which is a contradiction.
Claim
Assuming the resettable zero knowledge property of the \(\mathsf {RZKAOK}\) system, \(\mathsf {Hyb}_4\) is computationally indistinguishable from \(\mathsf {Hyb}_5\).
Proof
This is identical to the proof of Subsect. 7.2.
8 Extension
Output for Both parties:
By using the transformation of [27] which involves the receiver’s output also containing a signed copy of the sender’s output that is then sent to the sender using an extra message from the receiver, we can get a two message protocol where both parties receive output. Formally:
Corollary 2
Assuming one-way functions exist, there exists a two message UC-secure two party computation protocol in the stateless hardware token model using just one token, where both parties receive output.
Notes
- 1.
- 2.
To ease the exposition, we use non-interactive commitments that are based on injective one-way functions. We describe later how the protocol can be modified to use a two-message commitment scheme that relies only on one-way functions without increasing the message complexity of the protocol.
- 3.
Looking ahead, note that a malicious sender can’t change the value of \(\mathsf {toss}\) across different rounds of the RSZK argument because the token checks the signed copy of the transcript at each step.
References
Afshar, A., Mohassel, P., Pinkas, B., Riva, B.: Non-interactive secure computation based on cut-and-choose. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 387–404. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_22
Badrinarayanan, S., Garg, S., Ishai, Y., Sahai, A., Wadia, A.: Two-message witness indistinguishability and secure computation in the plain model from new assumptions. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 275–303. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_10
Barak, B., Goldreich, O., Goldwasser, S., Lindell, Y.: Resettably-sound zero-knowledge and its applications. In: FOCS (2001)
Bitansky, N., Paneth, O.: On the impossibility of approximate obfuscation and applications to resettable cryptography. In: STOC (2013)
Bitansky, N., Paneth, O.: On non-black-box simulation and the impossibility of approximate obfuscation. SIAM J. Comput. 1383, 44–1325 (2015)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: FOCS (2001)
Canetti, R., Dodis, Y., Pass, R., Walfish, S.: Universally composable security with global setup. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 61–85. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_4
Canetti, R., Goldreich, O., Goldwasser, S., Micali, S.: Resettable zero-knowledge (extended abstract). In: STOC (2000)
Canetti, R., Jain, A., Scafuro, A.: Practical UC security with a global random oracle. In: Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014, pp. 597–608 (2014)
Chandran, N., Goyal, V., Sahai, A.: New constructions for UC secure computation using tamper-proof hardware. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 545–562. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_31
Choi, S.G., Katz, J., Schröder, D., Yerukhimovich, A., Zhou, H.-S.: (Efficient) universally composable oblivious transfer using a minimal number of stateless tokens. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 638–662. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_27
Chung, K.-M., Ostrovsky, R., Pass, R., Venkitasubramaniam, M., Visconti, I.: 4-round resettably-sound zero knowledge. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 192–216. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_9
Chung, K., Ostrovsky, R., Pass, R., Visconti, I.: Simultaneous resettability from one-way functions. In: FOCS (2013)
Chung, K., Pass, R., Seth, K.: Non-black-box simulation from one-way functions and applications to resettable security. In: STOC (2013)
Chung, K., Pass, R., Seth, K.: Non-black-box simulation from one-way functions and applications to resettable security. SIAM J. Comput. 45, 415–458 (2016)
Döttling, N., Kraschewski, D., Müller-Quade, J.: Unconditional and composable security using a single stateful tamper-proof hardware token. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 164–181. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_11
Döttling, N., Kraschewski, D., Müller-Quade, J.: Statistically Secure linear-rate dimension extension for oblivious affine function evaluation. In: Smith, A. (ed.) ICITS 2012. LNCS, vol. 7412, pp. 111–128. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32284-6_7
Döttling, N., Kraschewski, D., Müller-Quade, J., Nilges, T.: From stateful hardware to resettable hardware using symmetric assumptions. In: Au, M.-H., Miyaji, A. (eds.) ProvSec 2015. LNCS, vol. 9451, pp. 23–42. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-26059-4_2
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM (1986)
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994)
Goldwasser, S., Kalai, Y.T., Rothblum, G.N.: One-time programs. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 39–56. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_3
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18, 186–208 (1989)
Goyal, V., Ishai, Y., Sahai, A., Venkatesan, R., Wadia, A.: Founding cryptography on tamper-proof hardware tokens. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 308–326. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_19
Hazay, C., Polychroniadou, A., Venkitasubramaniam, M.: Composable security in the tamper-proof hardware model under minimal complexity. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 367–399. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_15
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Prabhakaran, M., Sahai, A.: Efficient non-interactive secure computation. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 406–425. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_23
Katz, J.: Universally composable multi-party computation using tamper-proof hardware. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 115–128. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_7
Katz, J., Ostrovsky, R.: Round-optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_21
Kolesnikov, V.: Truly efficient string oblivious transfer using resettable tamper-proof tokens. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 327–342. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_20
Mohassel, P., Rosulek, M.: Non-interactive secure 2PC in the Offline/online and batch settings. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 425–455. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_15
Moran, T., Segev, G.: David and goliath commitments: UC Computation for asymmetric parties using tamper-proof hardware. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 527–544. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_30
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4, 151–158 (1991)
Rompel, J.: One-way functions are necessary and sufficient for secure signatures. In: Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing, pp. 387–394. ACM (1990)
Yao, A.C.: How to generate and exchange secrets (extended abstract). In: FOCS (1986)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A UC Framework and Ideal Functionalities
A UC Framework and Ideal Functionalities
For simplicity, we define the two-party protocol syntax, and then informally review the two-party UC-framework, which can be extended to the multi-party case. For more details, see [6].
Protocol syntax. Following [22], a protocol is represented as a system of probabilistic interactive Turing machines (ITMs), where each ITM represents the program to be run within a different party. Specifically, the input and output tapes model inputs and outputs that are received from and given to other programs running on the same machine, and the communication tapes model messages sent to and received from the network. Adversarial entities are also modeled as ITMs.
The construction of a protocol in the UC-framework proceeds as follows: first, an ideal functionality is defined, which is a “trusted party” that is guaranteed to accurately capture the desired functionality. Then, the process of executing a protocol in the presence of an adversary and in a given computational environment is formalized. This is called the real-life model. Finally, an ideal process is considered, where the parties only interact with the ideal functionality, and not amongst themselves. Informally, a protocol realizes an ideal functionality if running of the protocol amounts to “emulating” the ideal process for that functionality.
Let \(\varPi =(P_{1},P_2)\) be a protocol, and \(\mathcal {F}\) be the ideal-functionality. We describe the ideal and real world executions.
The real-life process. The real-life process consists of the two parties \(P_{1}\) and \(P_2\), the environment \(\mathcal {Z}\), and the adversary \({\mathcal A} \). Adversary \({\mathcal A} \) can communicate with environment \(\mathcal {Z}\) and can corrupt any party. When \({\mathcal A} \) corrupts party \(P_i\), it learns \(P_i\)’s entire internal state, and takes complete control of \(P_i\)’s input/output behavior. The environment \(\mathcal {Z}\) sets the parties’ initial inputs. Let \(\mathsf {REAL}^{}_{\varPi , {\mathcal A}, \mathcal {Z}}\) be the distribution ensemble that describes the environment’s output when protocol \(\varPi \) is run with adversary \({\mathcal A} \).
We also consider a \(\mathcal {G}\)-hybrid model, where the real-world parties are additionally given access to an ideal functionality \(\mathcal {G}\). During the execution of the protocol, the parties can send inputs to, and receive outputs from, the functionality \(\mathcal {G}\). We will use \(\mathsf {REAL}^{\mathcal {G}}_{\varPi , {\mathcal A}, \mathcal {Z}}\) to denote the distribution of the environment’s output in this hybrid execution.
The ideal process. The ideal process consists of two “dummy parties” \(\hat{P}_1\) and \(\hat{P}_2\), the ideal functionality \(\mathcal {F}\), the environment \(\mathcal {Z}\), and the ideal world adversary \(\mathsf {Sim} \), called the simulator. In the ideal world, the uncorrupted dummy parties obtain their inputs from environment \(\mathcal {Z}\) and simply hand them over to \(\mathcal {F}\). As in the real world, adversary \(\mathsf {Sim} \) can corrupt any party. Once it corrupts party \(\hat{P}_i\), it learns \(\hat{P}_i\)’s input, and takes complete control of its input/output behavior. Let \(\mathsf {IDEAL}^{\mathcal {F}}_{\mathsf {Sim} , \mathcal {Z}}\) be the distribution ensemble that describes the environment’s output in the ideal process.
Definition 1
(UC-Realizing an Ideal Functionality). Let \(\mathcal {F}\) be an ideal functionality, and \(\varPi \) be a protocol. We say that \(\varPi \) UC-realizes \(\mathcal {F}\) in the \(\mathcal {G}\)-hybrid model if for any hybrid-model PPT adversary \({\mathcal A} \), there exists an ideal process expected PPT adversary \(\mathsf {Sim} \) such that for every PPT environment \(\mathcal {Z}\):
Note that the above equation, says that in the ideal world, the simulator \(\mathsf {Sim} \) has no access to the ideal functionality \(\mathcal {G}\). However, when \(\mathcal {G}\) is a set-up assumption, this is not necessarily true and the simulator may have access to \(\mathcal {G}\) even in the ideal world. Indeed, there exist different formulations of the UC framework, capturing different requirements on the set-assumptions (e.g., [7]). In [7] for example, the set-up assumption is global, which means that the environment has direct access to the set-up functionality \(\mathcal {G}\). Hence, the simulator \(\mathsf {Sim} \) needs to have oracle access to \(\mathcal {G}\) as well.
The Ideal Token Functionality. We now describe the ideal token functionality. Note that our ideal functionality models stateful tokens. Although all our protocols use stateless tokens, an adversarially generated token may be stateful.
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Badrinarayanan, S., Jain, A., Ostrovsky, R., Visconti, I. (2018). Non-interactive Secure Computation from One-Way Functions. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11274. Springer, Cham. https://doi.org/10.1007/978-3-030-03332-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-03332-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03331-6
Online ISBN: 978-3-030-03332-3
eBook Packages: Computer ScienceComputer Science (R0)


 for the function
for the function 
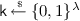 for the function
for the function 

