Abstract
Lattice signature schemes generally require particular care when it comes to preventing secret information from leaking through signature transcript. For example, the Goldreich-Goldwasser-Halevi (GGH) signature scheme and the NTRUSign scheme were completely broken by the parallelepiped-learning attack of Nguyen and Regev (Eurocrypt 2006). Several heuristic countermeasures were also shown vulnerable to similar statistical attacks.
At PKC 2008, Plantard, Susilo and Win proposed a new variant of GGH, informally arguing resistance to such attacks. Based on this variant, Plantard, Sipasseuth, Dumondelle and Susilo proposed a concrete signature scheme, called DRS, that has been accepted in the round 1 of the NIST post-quantum cryptography project.
In this work, we propose yet another statistical attack and demonstrate a weakness of the DRS scheme: one can recover some partial information of the secret key from sufficiently many signatures. One difficulty is that, due to the DRS reduction algorithm, the relation between the statistical leak and the secret seems more intricate. We work around this difficulty by training a statistical model, using a few features that we designed according to a simple heuristic analysis.
While we only recover partial information on the secret key, this information is easily exploited by lattice attacks, significantly decreasing their complexity. Concretely, we claim that, provided that \(100\,000\) signatures are available, the secret key may be recovered using BKZ-138 for the first set of DRS parameters submitted to the NIST. This puts the security level of this parameter set below 80-bits (maybe even 70-bits), to be compared to an original claim of 128-bits.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
At Crypto’97, Goldreich, Goldwasser and Halevi proposed the encryption and signature schemes [16] whose security relies on the hardness of lattice problems. Concurrently, a practical scheme, NTRUEncrypt was proposed, and adapted for signatures a few years later (NTRUSign [18]). In 2006, Nguyen and Regev presented a celebrated statistical attack [23] and completely broke GGH and NTRUSign in practice. The starting point of NR attack is a basic observation that any difference between signature and message always lies in the parallelepiped spanned by secret key. Thus each signature leaks partial information about the secret key, which allows to fully recover the secret key from sufficiently many signatures. In 2012, Ducas and Nguyen revisited NR attack [13] and showed that it could be generalized to defeat several heuristic countermeasures [18, 19].
Designing secure and efficient lattice based signatures remains a challenging problem. To get rid of information leaks, the now standard method is to use a delicate sampling algorithm for trapdoor inversion [15, 25].Footnote 1 Following such setting, it can be proved that signatures are independent of the secret key. Yet this provable guarantee doesn’t come cheap in terms of efficiency and simplicity: it remains very tempting to make more aggressive design choices.
Such a design was proposed by Plantard, Susilo and Win [27]. It is very close to the original GGH scheme, with a modified reduction algorithm that produces signatures falling in a known hypercube, independent of the secret key. According to the authors, such property should prevent the NR attack. The main idea of [27] is to reduce vectors under \(\ell _\infty \)-norm instead of Euclidean norm. Recently, Plantard, Sipasseuth, Dumondelle and Susilo updated this scheme, and submitted it to the NIST post-quantum cryptography project, under the name of DRS [26], standing for Diagonal-dominant Reduction Signature. Currently DRS is in the list of round 1 submissions to the NIST post-quantum cryptography project.
Our results. In this work, we present a statistical attack against the DRS scheme [26, 27]. We first notice that while the support of the transcript distribution is indeed fixed and known, the distribution itself is not, and is related to the secret key. More concretely, in the DRS signature, the reduction algorithm will introduce some correlations among coordinates \(w_i\)’s of the signature, and these correlations are strongly related to certain coefficients of the secret key \(\mathbf {S}\).
In more details, we assume that the coefficient \(\mathbf {S}_{i,j}\) can be well approximated by some function of the distribution of \((w_i,w_j)\) and proceed to profile such a function according to known instances (the training phase). Once we have the function, we can measure over sufficient signatures and obtain the guess for an unknown secret \(\mathbf {S}\).
With a few extra amplification tricks, we show this attack to be rather effective: for the first set of parameters, \(100\,000\) signatures suffice to locate all the large coefficients of the secret matrix \(\mathbf {S}\) and to determine most of their signs as well. Finally, we can feed this leaked information back into lattice attacks (BDD-uSVP attack), significantly decreasing their cost. Concretely, we claim that the first set of parameters offers at most 80-bits of security, significantly less than the original claim of 128-bits.
As a by-product, we formalize how to accelerate BDD attack when given some known coefficients of the solution. More specifically, we are able to construct a lattice of the same volume but smaller dimension for this kind of BDD instances.
Our scripts are open source for checking, reproduction or extension purposes, available at https://github.com/yuyang-Tsinghua/DRS_Cryptanalysis.
Related work. Very recently, Li, Liu, Nitaj and Pan proposed a chosen message attack [17] against the randomized version of Plantard-Susilo-Win GGH signature variant [27]. Their starting observation is that the difference between two signatures of a same message is a relatively short lattice vector in the randomized Plantard-Susilo-Win scheme, then from enough such short lattice vectors one may recover some short vectors of the secret matrix by lattice reduction. The randomized modification is a crucial weakness of Plantard-Susilo-Win scheme exploited by the attack in [17]. To fix such weakness, the authors mentioned two strategies: storing previous messages and padding a random nonce in the hash function. In comparison, our targeted scheme and technical idea are different from those in [17]. More importantly, the weakness of the DRS scheme that we demonstrate does not seem to be easily fixed.
Roadmap. In Sect. 2, we introduce notations and background on lattices. In Sect. 3, we provide a brief description of DRS signature scheme. Then we explain how to learn large coefficients of the secret matrix in Sect. 4, and how to combine partial information and lattice techniques to recover the full key in Sect. 5. Finally, we conclude and discuss potential countermeasure in Sect. 6.
2 Preliminaries
We use bold lowercase letters for vectors and denote by \(v_i\) the i-th entry of the vector \(\mathbf {v}\). We denote by \(\Vert \mathbf {v}\Vert \) (resp. \(\Vert \mathbf {v}\Vert _\infty \)) the Euclidean norm (resp. \(\ell _\infty \)-norm) of \(\mathbf {v}\). For simplicity and matching programming, we assume the script of each entry of \(\mathbf {v}\in \mathbb {R}^n\) is an element of \(\mathbb {Z}_n = \{0,\cdots , n-1\}\).
Let \(\mathbf {rot}_i(\mathbf {v}) = (v_{-i},\cdots ,v_{-i+n-1})\) be a rotation of \(\mathbf {v}\in \mathbb {R}^n\). We denote by \(\mathbf {srot}_i(\mathbf {v})\) the vector generated by \(\mathbf {rot}_i(\mathbf {v})\) with each entry changing the sign independently with probability 1 / 2. We define the set
We use bold capital letters for matrices and denote by \(\mathbf {v}_i\) the i-th row of the matrix \(\mathbf {V}\), i.e. \(\mathbf {V}= (\mathbf {v}_0,\cdots , \mathbf {v}_{n-1})\). We use \(\mathbf {V}_{i,j}\) to represent the entry in the i-th row and j-th column of \(\mathbf {V}\). Let \(\mathbf {I}_n\) be the n-dimensional identity matrix. We denote by \(\mathbf {ROT}(\mathbf {v})\) (resp. \(\mathbf {SROT}(\mathbf {v})\)) the matrix  (resp.
(resp.  ). Note that all \(\mathbf {srot}_i(\mathbf {v})\)’s in \(\mathbf {SROT}(\mathbf {v})\) are generated independently. A matrix \(\mathbf {V}\) is diagonal dominant if \(\mathbf {V}_{i,i} > \sum _{j\ne i} |\mathbf {V}_{i,j}|\) for all i.
). Note that all \(\mathbf {srot}_i(\mathbf {v})\)’s in \(\mathbf {SROT}(\mathbf {v})\) are generated independently. A matrix \(\mathbf {V}\) is diagonal dominant if \(\mathbf {V}_{i,i} > \sum _{j\ne i} |\mathbf {V}_{i,j}|\) for all i.
For a distribution D, we write \(X\leftarrow D\) when the random variable X is sampled from D. Given a finite set S, let U(S) be the uniform distribution over S. We denote by \(\mathbb {E}(X)\) the expectation of random variable X.
A (full-rank) n-dimensional lattice \(\mathcal {L}\) is the set of all integer combinations of linearly independent vectors  , i.e.
, i.e.  . We call
. We call  a basis of
a basis of  and write
and write  . For a unimodular matrix \(\mathbf {U}\in \mathbb {Z}^{n\times n}\), we have \(\mathbf {U}\mathbf {B}\) is also a basis of \(\mathcal {L}(\mathbf {B})\), i.e. \(\mathcal {L}(\mathbf {B}) = \mathcal {L}(\mathbf {U}\mathbf {B})\). Let \((\mathbf {b}_0^*,\cdots ,\mathbf {b}_{n-1}^*)\) be the Gram-Schmidt vectors of \(\mathbf {B}\). The volume of the lattice \(\mathcal {L}(\mathbf {B})\) is \(\text {vol}(\mathcal {L}(\mathbf {B})) = \prod _i \Vert \mathbf {b}_i^*\Vert \) that is an invariant of the lattice. Given \(\mathcal {L}\subseteq \mathbb {R}^n\) and \(\mathbf {t}\in \mathbb {R}^n\), the distance between \(\mathbf {t}\) and \(\mathcal {L}\) is \(\text {dist}(\mathbf {t}, \mathcal {L}) = \min _{\mathbf {v}\in \mathcal {L}} \Vert \mathbf {t}-\mathbf {v}\Vert \).
. For a unimodular matrix \(\mathbf {U}\in \mathbb {Z}^{n\times n}\), we have \(\mathbf {U}\mathbf {B}\) is also a basis of \(\mathcal {L}(\mathbf {B})\), i.e. \(\mathcal {L}(\mathbf {B}) = \mathcal {L}(\mathbf {U}\mathbf {B})\). Let \((\mathbf {b}_0^*,\cdots ,\mathbf {b}_{n-1}^*)\) be the Gram-Schmidt vectors of \(\mathbf {B}\). The volume of the lattice \(\mathcal {L}(\mathbf {B})\) is \(\text {vol}(\mathcal {L}(\mathbf {B})) = \prod _i \Vert \mathbf {b}_i^*\Vert \) that is an invariant of the lattice. Given \(\mathcal {L}\subseteq \mathbb {R}^n\) and \(\mathbf {t}\in \mathbb {R}^n\), the distance between \(\mathbf {t}\) and \(\mathcal {L}\) is \(\text {dist}(\mathbf {t}, \mathcal {L}) = \min _{\mathbf {v}\in \mathcal {L}} \Vert \mathbf {t}-\mathbf {v}\Vert \).
Lattice reduction is an important tool for solving lattice problems and estimating the security of lattice-based cryptosystems. The goal of lattice reduction is to find a basis of high quality. The quality of a basis \(\mathbf {B}\) is related to its root Hermite factor \({{\mathrm{\mathbf {rhf}}}}(\mathbf {B})=\left( \frac{\Vert \mathbf {b}_0\Vert }{\text {vol}(\mathcal {L}(\mathbf {B}))^{1/n}}\right) ^{1/n}.\) Currently, the most practical lattice reduction algorithms are BKZ [28] and BKZ 2.0 [10]. We denote by BKZ-\(\beta \) the BKZ/BKZ 2.0 with blocksize \(\beta \). In general, we assume the root Hermite factor of a BKZ-\(\beta \) basis is bounded by
when \(n\gg \beta >50\).
3 The DRS Signature Scheme
In this section, we are to make a brief description of the DRS scheme. We may omit some details that are unnecessary for understanding our attack. For more details on the algorithms and implementations we refer to [26].
To start with, we introduce several public parameters of DRS:
-
n : the dimension
-
D : the diagonal coefficient of the secret key
-
b : the magnitude of the large coefficients (i.e.
 ) in the secret key
) in the secret key -
\(N_b\) : the number of large coefficients per vector in the secret key
-
\(N_1\) : the number of small coefficients (i.e.
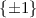 ) per vector in the secret key
) per vector in the secret key
Following the setting provided in [26], the parameter D is chosen to be n and satisfies that \(D > b\cdot N_b + N_1\).
The secret key of DRS is a matrix
where \(\mathbf {M}= \mathbf {SROT}(\mathbf {v})\) with \(\mathbf {v}\leftarrow U\left( \mathcal {T}(n, b, N_b, N_1) \bigcap \{\mathbf {v}\in \mathbb {Z}^n \mid v_0=0\}\right) \) is the noise matrix. It is easily verified that \(\mathbf {S}\) is diagonal dominant. The public key is a matrix \(\mathbf {P}\) such that \(\mathcal {L}(\mathbf {P}) = \mathcal {L}(\mathbf {S})\) and the vectors in \(\mathbf {P}\) are much longer than those in \(\mathbf {S}\).
Hash space. The specification submitted to the NIST [26] is rather unclear about the message space. Namely, only a bound of \(2^{28}\) is mentioned, which suggests a hash space \(\mathcal {M}={(-2^{28},2^{28})}^n\), following the original scheme [27]. Yet, we noted that the implementation seems to instead use the message space \(\mathcal {M}={(0,2^{28})}^n\): the sign randomization is present, but commented out. Discussion with the designersFootnote 2 led us to consider this as an implementation bug, and we therefore focus on the analysis with \(\mathcal {M}={(-2^{28},2^{28})}^n\), following both the original scheme [27] and the intention of [26].
We strongly suspect that taking \(\mathcal {M}={(0,2^{28})}^n\) would not be an effective countermeasure against the kind attack analyzed in this paper. Preliminaries experiments on this variant suggested that leak was stronger, but its relation to the secret key seemed more intricate.
For our experiments, we generated directly uniform points in that space rather than hashing messages to this space; according to the Random Oracle Model, this should make no difference.
Signature. The signature algorithm of DRS follows the one in [27] and its main component is a message reduction procedure in \(\ell _\infty \)-norm. It is summarized below as Algorithm 1.

In brief, the message reduction is reducing successively each large coefficient \(m_i\) of the message \(\mathbf {m}\) by qD such that \(|m_i - qD| < D\) but adding \(\pm q, \pm qb\) to \(m_j\) with \(j\ne i\) according to the entries of \(\mathbf {M}\), until all coefficients of the reduced message are within \((-D, D)\). Since \(\mathbf {S}\) is diagonal dominant, the message can be reduced within bounded steps as proved in [26, 27].
Besides the reduced message \(\mathbf {w}\), an auxiliary vector \(\mathbf {k}\) is also included in the signature and used to accelerate the verification. To verify the signature, one would first check whether \(\Vert \mathbf {w}\Vert _\infty < D\) and then check whether \(\mathbf {m}-\mathbf {w}=\mathbf {k}\mathbf {P}\). In later discussions, we shall ignore the auxiliary vector, because it can be calculated in polynomial time from \(\mathbf {w},\mathbf {m}\) and the public key \(\mathbf {P}\).
4 Learning Coefficients of the Secret Matrix
All DRS signatures \(\mathbf {w}\) lie in and fill the region \((-D, D)^n\). Unlike the GGH scheme, the signature region is a known hypercube and independent of the secret matrix, thus the DRS scheme was deemed to resist statistical attacks. However, the distribution of random signature in \((-D, D)^n\) may be still related to the secret key, which would leak some key information.
In later discussion, we aim at a concrete parameter set
that is submitted to the NIST and claimed to provide at least 128-bits of security in [26].
4.1 Intuition on a Potential Leak
Our approach is to try to recover \(\mathbf {S}_{i, j}\) by studying the distribution \(W_{i,j}\) of \((w_i, w_j)\). Indeed, when a reduction happens at index i: \(\mathbf {w}\leftarrow \mathbf {w}- q \mathbf {s}_i\), and when \(\mathbf {S}_{i,j} \ne 0\) some correlation is introduced between \(w_i\) and \(w_j\). Symmetrically, correlation is also introduced when \(\mathbf {S}_{j,i} \ne 0\). Another source of correlations is created by other reductions at index \(k \not \in \{i,j\}\) when both \(\mathbf {S}_{k,i}\) and \(\mathbf {S}_{k,j}\) are non-zero; these events create much less correlations since the diagonal coefficients are much larger, but those correlations accumulate over many k’s. One is tempted to model the accumulated correlations as those of some bi-variate Gaussians with a certain covariance.
Of course, there are complicated “cascading” phenomena: by modifying a coefficient, a reduction may trigger another reduction at an other index. But let us ignore such phenomena, and just assume that several reductions at indices \(k \ne i,j\) occur, followed by one reduction at index i with \(q=\pm 1\), before the algorithm terminates. We depict our intuition as Fig. 1.
In this simple model, we note that there are 4 degrees of liberty, 3 for the shape of the ellipsoid, and 1 for \(\mathbf {S}_{i,j}= -b, 0, b\).Footnote 3 Therefore, one may expect to be able to recover all the parameters using 4 statistical measures. One natural choice is the following. First, measure the covariance matrix of the whole distribution, which gives 3 parameters. Assuming the clipped caps have small weights, this would roughly give the shape of the ellipsoid. For the last measure, one would select only sample for which \(|w_i|\) is small, so as to focus on the superimposed displaced caps. With a bit of effort one would find an appropriate measurement.
Unfortunately, it seems rather hard to determine mathematically what will precisely happen in the full reduction algorithm, and to construct by hand a measurement on the distribution of \((w_i, w_j)\) directly giving \(\mathbf {S}_{i,j}\), i.e. a function f such that \(f(W_{i,j}) = \mathbf {S}_{i,j}\).
4.2 Training
While constructing such a function f by a mathematical analysis may be hard, our hope is that such function may be easy to learn using standard techniques, ranging from least-square method to convolutional neural networks. Indeed, going back to Fig. 1, recovering \(\mathbf {S}_{i,j}\) from \(W_{i,j}\) can essentially be viewed as a grey-scale image classification problem (the lightness of the pixel (x, y) corresponding to the density of \(W_{i,j}\) at (x, y)).
Features. We therefore proceed to design a few features, according to the intuition built above. The average of each \(w_i\) is supposed to be 0, thus we do not treat it as a feature. Certainly, the covariance information is helpful, but we also introduce extra similar statistics to allow the learning algorithm to handle extra perturbations not captured by our simple intuition. We restrict our features to being symmetric: a sample (x, y) should have the same impact as \((-x, -y)\). Indeed, while quite involved, the whole reduction process preserves this symmetry.
More specifically, by scaling a factor of D, consider the distribution W to have support \((-1, 1)^2\). For a function f over \((-1,1)^2\), we write \(f(W) = \mathbb {E}_{(x,y) \leftarrow W}(f(x))\). The features mentioned before are listed belowFootnote 4:
-
\(f_1(W) = D\cdot \mathbb {E}_{(x,y) \leftarrow W}(x \cdot y)\);
-
\(f_2(W) = D\cdot \mathbb {E}_{(x,y) \leftarrow W}(x \cdot |x|^{1/2}\cdot y)\);
-
\(f_3(W) = D\cdot \mathbb {E}_{(x,y) \leftarrow W}(x \cdot |x|\cdot y)\);
We could go on with higher degrees, but this would cause some trouble. First, higher degree moments converge much slower. Secondly, taking too many features would lead to over-fitting.
Then, following our intuition, we want to also consider features that focus on the central region. Still, we do not want to give too much weight to samples with x very close to 0. Indeed, there will be some extra perturbation after the reduction at index i, which could flip the sign of x. A natural function to take this into account is the following.
-
\(f_4(W) = D\cdot \mathbb {E}_{(x,y) \leftarrow W}(x(x-1)(x+1)\cdot y)\).Footnote 5
The most contributing sample will be the one for which \(x = \pm 1/\sqrt{3}\), and it is not clear that this is the optimal range to select. We therefore offer to the learning algorithm a few variants of the above that select samples with smaller values of x, hoping that it can find a good selection by combining all of them:
-
\(f_5(W) = D\cdot \mathbb {E}_{(x,y) \leftarrow W}(2x(2x-1)(2x+1)\cdot y \mid |2x| \le 1)\);
-
\(f_6(W) = D\cdot \mathbb {E}_{(x,y) \leftarrow W}(4x(4x-1)(4x+1)\cdot y \mid |4x| \le 1)\);
-
\(f_7(W) = D\cdot \mathbb {E}_{(x,y) \leftarrow W}(8x(8x-1)(8x+1)\cdot y \mid |8x| \le 1)\);
For any function f over \(\mathbb {R}^2\), we call  the transpose of f. So far, we have introduced 13 different features, i.e.
the transpose of f. So far, we have introduced 13 different features, i.e.  and their transposes
and their transposes  .Footnote 6 We plot these functions in Fig. 2.
.Footnote 6 We plot these functions in Fig. 2.
Generating data. Then, we proceed to measure each \(W_{i,j}\) for known values of \(\mathbf {S}_{i,j}\), say, using \(400\,000\) samples for each key \(\mathbf {S}\), and using 30 different keys \(\mathbf {S}\). This is implemented by our script gen_training.py. This took about 38 core-hours.
Training. We naturally considered using advanced machine learning techniques (support vector regression [7], random forest regression [20] and artificial neural networks) to construct a model, with the precious support of Han Zhao. Despite some effort, he was unable to find a method that outperforms what we achieved with a linear model \(f = \sum _{\ell =1}^{13} x_\ell f_\ell \) trained using the least-square fit method. Yet his exploration was certainly far from exhaustive, and we do not conclude that least-square fit is the best method.
Evaluating and refining our model. After preliminary experiments, we noted that, depending on their position \(i-j\), some coefficients \(\mathbf {S}_{i,j}\) seem easier to learn than others. In this light, it is not clear that one should use the same function f for all indices i, j. Instead, we constructed two functions \(f^+ = \sum x^+_\ell f_\ell \), \(f^{-} = \sum x^-_\ell f_\ell \) respectively for indices such that \(i-j \bmod n \ge n/2\) and \(i-j \bmod n < n/2\). The model obtained by the least-square fit method is provided in Table 1 and plotted in Fig. 3. Moreover, the distributions of \(f^{+}(W_{i,j})\), \(f^{-}(W_{i,j})\) for \(\mathbf {S}_{i,j}=\pm b, \pm 1, 0\) are illustrated in Figs. 4 and 5.
Remark 1
For other set of parameters, or even to refine our attack and recover more secret information, it is of course possible to cut our modeling in more than 2 pieces, but this requires more training data, and therefore more computational resources.
The impact from sample sizes on the measured distributions of \(f^{-}(W_{i,j})\), \(f^{+}(W_{i,j})\). The left graphs correspond to \(f^-\) and the right graphs correspond to \(f^+\). The upper graphs measure over 20 instances and \(400\,000\) samples per instance, and the lower graphs measure over 20 instances and \(50\,000\) samples per instance.
Remark 2
As shown in Figs. 4 and 5, predicted values \(f(W_{i,j})\) for large coefficients are usually of larger size than those for \(-1,0,1\). Compared with large coefficients far from the main diagonal, those near the main diagonal tend to be predicted as a number of larger size. Furthermore, the variances of \(f(W_{i,j})\) decrease with sample size growing, which provides a sanity check for our models.
4.3 Learning
Following the previous method, we obtain a matrix \(\mathbf {S}'\) consisting of all guesses of \(\mathbf {S}_{i,j}\)’s.Footnote 7 While clear correlations between the guess \(\mathbf {S}'\) and \(\mathbf {S}\) were observed, the guess was not good enough by itself for the limited number of samples that we used. In the following, we exploit the “absolute-circulant” structure of the secret key to improve our guess. The experimental results described below are based on our script attack.py.
Determining the locations. Notice that all \(\mathbf {S}_{i,j}\)’s in a same diagonal are of the same absolute value, hence we used a simple trick to enhance the contrast between large and small coefficients. It consists in calculating
as the weight of the k-th diagonal. Since we used two different features for coefficients near/far from the main diagonal, for better comparison, the first \(n/2-1\) weights were scaled by their maximum and so were the last n / 2 weights. We denote by \(\mathcal {W}^-_k\) the first \(n/2-1\) scaled weights and by \(\mathcal {W}^+_k\) the last n / 2 ones.
As illustrated in Fig. 6, the scaled weights of those diagonals consisting of large coefficients are significantly larger than others. A straightforward method to locate large coefficients is to pick the \(N_b\) largest scaled weights.
Verified by experimental results, we were able to perfectly locate all large coefficients, provided we collected sufficient signatures. For different sample size, i.e. the number of signatures, we respectively tested 20 instances and checked the accuracy of locations for large coefficients. All experimental data is illustrated in Table 2.
Determining the signs. We straightforward assumed the sign of measured feature \(f(W_{i,j})\) is the same as that of \(\mathbf {S}_{i,j}\), when \(\mathbf {S}_{i,j}=\pm b\). Unlike guessing locations, we could not recover all signs of large coefficients exactly, but as the sample size grows, we were still able to get a high accuracy, denoted by p. Then, we may expect to recover all signs of large coefficients in each row exactly with a probability \(p_{row}=p^{N_b}\) (in our case \(N_b=16\)).
Moreover, we noticed that the accuracy of guessing signs for large coefficients in the lower triangle, i.e. \(\mathbf {S}_{i,j}\) with \(i > j\), is higher than that for large coefficients in the upper triangle, thus we denote by \(p_l\) and \(p_u\) the accuracy corresponding to the lower and upper triangle. That may suggest us to guess the signs of large coefficients from the last row to the first row. Table 3 exhibits the experimental data for \(p_l, p_u, p\) and \(p_{row}\).
Comparing guessing locations, guessing signs is much more sensitive to the number of signatures. That is because the sign information of \(\mathbf {S}_{i,j}\) only comes from \(f(W_{i,j})\) rather than all features in the same diagonal so that it requires a more precise measurement. Furthermore, we tried a modified model for guessing signs: in training phase, we mapped \(\mathbf {S}_{i,j}\) to \(\lfloor \mathbf {S}_{i,j}/b\rceil \) and then find \(x_\ell \)’s determining the global feature. Intuitively, the modified model further emphasizes large coefficients, but it performed almost the same as the current model in practice.
5 Exploiting Partial Secret Key Knowledge in Lattice Attacks
Using the technique described in last section, we are able to recover exactly all off-diagonal large coefficients in a row, with high probability (in addition to the diagonal coefficient D). First, we show how to adapt the BDD-uSVP attack, by exploiting the known coefficients of a row \(\mathbf {s}_k\) to decrease the distance of the BDD target to the lattice, making the problem easier. Then, we show a more involved version, where we also decrease the dimension of the lattice while maintaining its volume. While not much is gained to recover a first secret row \(\mathbf {s}_k\), this technique makes guessing the rest of the key much faster.
In later discussion, assume that we have already successfully determined all \(-b,b\) and D coefficients in \(\mathbf {s}_k\). Let \(M=\{m_0,\cdots ,m_{N_b}\}\) be the set of all m’s such that \(\mathbf {S}_{k,m} \in \{-b,b,D\}\) where \(m_0< \cdots < m_{N_b}\). We still focus on the concrete parameter set \((n, D, b, N_b, N_1)=(912,912,28,16,432)\).
5.1 Direct BDD-uSVP Attack
Let \(\mathbf {t}\in \mathbb {Z}^n\) such that, if \(|\mathbf {S}_{k,i}|>1\), \(t_i = \mathbf {S}_{k,i}\), otherwise \(t_i = 0\), then \(\text {dist}(\mathbf {t}, \mathcal {L})=\sqrt{N_1}\). We construct a new lattice \(\mathcal {L}'\) with a basis
we have \(\text {vol}(\mathcal {L}') = \text {vol}(\mathcal {L}) \approx D^n\) and \(\mathcal {L}'\) contains a vector of Euclidean norm \(\sqrt{N_1 + 1}\ll D\). Thus, to recover \(\mathbf {s}_k\), it suffices to solve uSVP on \(\mathcal {L}'\).
New estimations of the blocksize required by BKZ to solve uSVP were given in [4] and have been confirmed by theoretical analysis and experiments in [2]. Following these results, we claim that \(\mathbf {s}_k\) could be recovered by BKZ-\(\beta \) when \(\beta \) satisfies:
We conclude that running BKZ-\(\beta \) with \(\beta = 146\) should be sufficient to break the scheme. Typically [1, 8], it is estimated that BKZ-\(\beta \) converges after about 16 tours, therefore making \(16(n+1)\) calls to \(\text {SVP-}\beta \):
Though the factor 16 may shrink by increasing the blocksize \(\beta '\) progressively from 2 to \(\beta \). Estimation of the cost of \(C_{\text {SVP-}\beta }\) varies a bit in the literature, also depending on the algorithm used. The standard reference for estimating the cost enumeration is [10], which gives a cost of \(2^{0.270\beta \ln \beta -1.019\beta +16.10}\) [3, 9] clock-cycles. Alternatively, the Gauss-Sieve algorithm [22] with dimension for free and other tricks showed a running time of \(2^{0.396\beta + 8.4}\) clock cycles [11].
Those two methods lead respectively to estimates of \(2^{78}\) and \(2^{80}\) clock-cycles to recover one secret row. One could of course repeat the attack over each row, but below, we present a strategy that slightly reduces the cost of guessing a first row, and greatly reduces the cost of guessing all the other rows.
Remark 3
These numbers are likely to be over-estimates. Indeed, while cost predictions have not been provided, the enumeration algorithms have been sped up in practice recently with the discrete-pruning technique [5, 14, 29]. Unfortunately, the record timing on SVP challenges up to SVP-150 are difficult to use, as they only solve SVP up to an approximation factor of 1.05, which is significantly easier than the exact SVP typically used in BKZ. Similarly, avenues for improvements are discussed in [11], such as using a faster sieve, or amortizing certain costs inside the BKZ loop. Moreover, a long-standing question remains open: could it be more efficient to use an approx-SVP oracle with a larger blocksize in BKZ to achieve similar reduction faster.
5.2 BDD-uSVP Attack with Dimension Reduction
Next we detail how to also reduce the dimension of \(\mathcal {L}'\) but maintain its volume, when exploiting known coefficients of a BDD solution.
Let \(\mathbf {H}= (h_{i,j})_{i,j}\) be the HNF (Hermite Normal Form) of \(\mathbf {P}\) satisfying:
-
\(h_{i,i} > 0\);
-
\(h_{j,i} \in \mathbb {Z}_{h_{i,i}}\) for any \(j > i\).
-
\(h_{j,i} = 0\) for any \(j < i\).
Let \(I = \{i\mid h_{i,i} > 1\}\). In general, |I| is very small (say \(\le 5\)), for example \(|I| = 1\) if \(\det (\mathbf {H})\) is square-free. Thus we have, with a high probability, that \(I \cap M = \emptyset \), i.e. \(h_{m,m}=1\) for any \(m\in M\). If not so, we choose another row \(\mathbf {s}_{k'}\) of \(\mathbf {S}\). Let \(\{l_0,\cdots , l_{n-2-N_b}\} = \mathbb {Z}_n \setminus M\) where \(l_0< \cdots < l_{n-2-N_b}\).
Let \(\mathbf {H}'=(h'_{i,j})_{i,j}\) be a matrix of size \((n-N_b-1)\times (n-N_b-1)\), in which \(h'_{i,j} = h_{l_i,l_j}\). Let \(\mathbf {a}=(a_0,\cdots ,a_{n-N_b-2})\) where \(a_i=\sum _{m\in M}\mathbf {S}_{k,m}h_{m,l_i}\). Let \(\mathcal {L}'\) be the lattice generated by
We first have that
Secondly, we can prove that \(\mathcal {L}'\) has an unusually short vector corresponding to all small coefficients of \(\mathbf {s}_k\). Indeed, let \(\mathbf {c}\in \mathbb {Z}^n\) such that \(\mathbf {c}\mathbf {H}=\mathbf {s}_k\), then \(c_m = \mathbf {S}_{k,m}\) for any \(m\in M\) thanks to \(h_{m,m}=1\). Let \(\mathbf {c}'=(c_{l_0},\cdots ,c_{l_{n-2-N_b}})\), then
Notice that \(\Vert \mathbf {v}'\Vert = \sqrt{N_1+1} \ll \text {vol}(\mathcal {L}')^{\frac{1}{n-N_b}}\approx D^{\frac{n}{n-N_b}}\), we may use uSVP oracle to find \(\mathbf {v}'\).
Using the same argument as in the previous subsection, we could recover \(\mathbf {v}'\), namely \(\mathbf {s}_k\), by BKZ-\(\beta \) when \(\beta \) satisfies:
This condition is satisfied for \(\beta = 138\). Based respectively on [10] and [11], this gives attack in \(2^{73}\) and \(2^{77}\) clock-cycles. Again, these numbers should be taken with a grain of salt (see Remark 3).
5.3 Cheaply Recovering All the Other Rows
Once a vector \(\mathbf {s}_k\) has been fully recovered, we have much more information on all the other secret rows. In particular, we know all the positions of the 0, and this allows to decrease the dimension from n to \(N_b + N_1 + 1\).
As in previous section we are able to construct a \((N_b + N_1 + 1)\)-dimensional lattice \(\mathcal {L}'\) of the same volume as \(\mathcal {L}\) and containing a vector of length \(\sqrt{N_b\cdot b^2 + N_1 + 1}\). Then, using BKZ-50 is enoughFootnote 8 to recover the target vector and the cost is negligible compared to the cost of the first step.
6 Conclusion
We have shown that the DRS scheme is in principle susceptible to a statistical attack: signatures do leak information about the secret key. More concretely, for the first set of parameters submitted to the NIST [26], we have shown its security should be considered below 80-bits after \(100\, 000 \approx 2^{17}\) signatures have been released, contradicting the original claim of 128-bits of security. While such a large number of signatures may not be released in many applications, it remains much lower than the bound of \(2^{64}\) signatures given by the NIST call for proposal [24, Sect. 4.A.4].
We also warn the reader that for demonstrating the principle of our attack, we have only focused on the easiest secret coefficients. But from Fig. 4, it seems also possible to deduce more information on the key. We strongly suspect that, focusing on the very near-diagonal coefficients, it could be possible to get the locations of a few 0’s and \(\pm 1\)’s as well, using more signatures, a more focused statistical model, and the diagonal amplification trick. This may lead to a full break in practice of this parameter set. Moreover, our estimates do not take account of the recent discrete pruning technique for enumeration [5, 14, 29], that has unfortunately not yet been the object of easily usable predictions.
While we view it likely that the attack can be pushed further, it is not clear how much effort this question deserves. In our view, our current attack suffices to demonstrate the need to fix the leak of the DRS scheme [26], and maybe to re-parametrize it.
In addition, we would like to clarify our views on lattice-based crypto security estimates. While we did stick to the best known attack methodology in this paper so as to not overclaim our cryptanalytic result, we do not recommend this approach for design and security claims, considering that the state of the art in lattice reduction is still making significant progress [5, 11, 14, 29].
6.1 Viability of the DRS Design, and Potential Countermeasure
We note nevertheless that this statistical attack seems much less powerful than the statistical attacks presented in [13, 23] against the original schemes GGH [16] and NTRUSign [18]. Indeed, our attack requires much more signatures, and still only recovers partial secret key information. In this light, we do not conclude that the approach of [26] is to be discarded at once, at least if it shows competitive performances. We therefore suggest several directions to improve the security of the scheme.
Disclaimer. These suggestions should however not be understood as a pledge for the DRS scheme [26]. We believe a much more thorough analysis of the statistical properties of the scheme should be provided to sustain its security. We think that a statistical argument would be much more reassuring than the experimental failure of the type of attack described in this paper.
Randomization. In [26, 27], it is suggested that the orders of the indices j for the reductions \(\mathbf {w}\leftarrow \mathbf {w}- q\mathbf {s}_j\) could be randomized. As claimed in [17], this modification should not be applied directly. For our attack, such randomization does not affect the intuition developed in Sect. 4.1. We suspect it might make the attack somewhat simpler. Indeed, in the current deterministic version, the coefficients far from the diagonal seemed harder to learn, forcing us to use two different models \(f^-\) and \(f^+\). We believe that this complication could be removed against the randomized variant.
Set of secret coefficients. Rather than a sparse yet wide set \(\{0,\pm 1, \pm b\}\) for the coefficients of \(\mathbf {S}\), we recommend an interval of integers \(\{-u, \dots , u\}\), where u is chosen such that the Euclidean length of the rows is maintained (say, on average). As we saw (Fig. 4), larger coefficients are easier to detect, and the gap between 1 and b allows one to make a guess with much more confidence. Note that this could only mitigate the attack, but would not fully seal the leak.
Structure of the secret matrix. Secondly, the “absolute-circulant” structure could be removed without affecting the size of the secret key; indeed, the whole matrix, could be streamed by a PRG, only keeping the seed as the new secret key.Footnote 9 Again, this may only mitigate the attack, but would not fully seal the leak.
Perturbation/drowning. Depending on the situation, adding well-designed perturbation may [25] or may not [13, 18] be an effective countermeasure against statistical attacks. Given the track record of heuristic countermeasures, we find the formal approach preferable. Drowning is a similar idea in spirit, but the added noise has a fixed distribution, typically much larger than what is to be hidden.
We note that the problem of directly trying to forge a signature seems harder than recovering the secret key with the current parameters of DRS [26]. This means that allowing larger vectors for signatures (up to a certain cross-over point) should not affect security. This gives a lot of room for perturbation or drowning, for which ad-hoc concrete statistical statements could plausibly be made, maybe exploiting Rényi divergence as in [4, 6].
Notes
- 1.
- 2.
- 3.
In fact, two of those degrees are fixed by the shape of the secret matrix: each rows of \(\mathbf {S}\) has fixed Euclidean length, fixing the variance of \(w_i\) and \(w_j\).
- 4.
We introduced a re-normalization factor D in our experiments. We keep it in this paper for consistency.
- 5.
As we are only going to consider linear models in our features, we could equivalently replace this feature by \(\mathbb {E}_{(x,y) \leftarrow W}(x^3 \cdot y)\) because of the presence of \(f_1\).
- 6.
Since \(f_1\) is a symmetric function of \((w_i,w_j)\), we did not count its transpose.
- 7.
We ignore diagonal elements because they are public.
- 8.
- 9.
Variants can be designed so that each row can be generated on demand.
References
Albrecht, M.R.: On dual lattice attacks against small-secret LWE and parameter choices in HElib and SEAL. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 103–129. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_4
Albrecht, M.R., Göpfert, F., Virdia, F., Wunderer, T.: Revisiting the expected cost of solving uSVP and applications to LWE. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 297–322. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_11
Albrecht, M.R., Player, R., Scott, S.: On the concrete hardness of learning with errors. J. Math. Cryptol. 9(3), 169–203 (2015)
Alkim, E., Ducas, L., Pöppelmann, T., Schwabe, P.: Post-quantum key exchange—a new hope. In: USENIX Security 2016, pp. 327–343 (2016)
Aono, Y., Nguyen, P.Q.: Random sampling revisited: lattice enumeration with discrete pruning. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 65–102. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_3
Bai, S., Langlois, A., Lepoint, T., Stehlé, D., Steinfeld, R.: Improved security proofs in lattice-based cryptography: Using the rényi divergence rather than the statistical distance. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 3–24. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_1
Basak, D., Pal, S., Patranabis, D.C.: Support vector regression. Neural Inf. Process. Lett. Rev. 11(10), 203–224 (2007)
Chen, Y.: Réduction de réseau et sécurité concrète du chiffrement complètement homomorphe. PhD thesis (2013)
Chen, Y., Nguyen, P.Q.: BKZ 2.0: Better lattice security estimates (full version). http://www.di.ens.fr/~ychen/research/Full_BKZ.pdf
Chen, Y., Nguyen, P.Q.: BKZ 2.0: better lattice security estimates. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 1–20. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_1
Ducas, L.: Shortest vector from lattice sieving: a few dimensions for free. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 125–145. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_5
Ducas, L., Durmus, A., Lepoint, T., Lyubashevsky, V.: Lattice signatures and bimodal Gaussians. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 40–56. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_3
Ducas, L., Nguyen, P.Q.: Learning a zonotope and more: cryptanalysis of NTRUSign countermeasures. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 433–450. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_27
Fukase, M., Kashiwabara, K.: An accelerated algorithm for solving SVP based on statistical analysis. J. Inf. Process. 23(1), 67–80 (2015)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC 2008, pp. 197–206 (2008)
Goldreich, O., Goldwasser, S., Halevi, S.: Public-key cryptosystems from lattice reduction problems. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 112–131. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052231
Li, H., Liu, R., Nitaj, A., Pan, Y.: Cryptanalysis of the randomized version of a lattice-based signature scheme from PKC’08. In: Susilo, W., Yang, G. (eds.) ACISP 2018. LNCS, vol. 10946, pp. 455–466. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93638-3_26
Hoffstein, J., Howgrave-Graham, N., Pipher, J., Silverman, J.H., Whyte, W.: NTRUSign: digital signatures using the NTRU lattice. In: Joye, M. (ed.) CT-RSA 2003. LNCS, vol. 2612, pp. 122–140. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36563-X_9
Hu, Y., Wang, B., He, W.: NTRUSign with a new perturbation. IEEE Trans. Inf. Theor. 54(7), 3216–3221 (2008)
Liaw, A., Wiener, M., et al.: Classification and regression by randomforest. R News 2(3), 18–22 (2002)
Lyubashevsky, V.: Fiat-Shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_35
Micciancio, D., Voulgaris, P.: Faster exponential time algorithms for the shortest vector problem. In: SODA 2010, pp. 1468–1480 (2010)
Nguyen, P.Q., Regev, O.: Learning a parallelepiped: cryptanalysis of GGH and NTRU signatures. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 271–288. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_17
NIST: Submission requirements and evaluation criteria for the post-quantum cryptography standardization process, December 2016. https://csrc.nist.gov/CSRC/media/Projects/Post-Quantum-Cryptography/documents/call-for-proposals-final-dec-2016.pdf
Peikert, C.: An efficient and parallel gaussian sampler for lattices. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 80–97. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_5
Plantard, T., Sipasseuth, A., Dumondelle, C., Susilo, W.: DRS : diagonal dominant reduction for lattice-based signature. Submitted to the NIST Post-Quantum Cryptography Project. https://csrc.nist.gov/projects/post-quantum-cryptography/round-1-submissions
Plantard, T., Susilo, W., Win, K.T.: A digital signature scheme based on CVP\(_\infty \). In: Cramer, R. (ed.) PKC 2008. LNCS, vol. 4939, pp. 288–307. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78440-1_17
Schnorr, C.P., Euchner, M.: Lattice basis reduction: improved practical algorithms and solving subset sum problems. Math. Program. 66(1–3), 181–199 (1994)
Teruya, T., Kashiwabara, K., Hanaoka, G.: Fast lattice basis reduction suitable for massive parallelization and its application to the shortest vector problem. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 437–460. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_15
Yu, Y., Ducas, L.: Second order statistical behavior of LLL and BKZ. In: Adams, C., Camenisch, J. (eds.) SAC 2017. LNCS, vol. 10719, pp. 3–22. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-72565-9_1
Acknowledgements
We thank Thomas Plantard, Arnaud Sipasseuth, and Han Zhao for helpful discussions and comments. We are also grateful to Yanbin Pan for sharing their work. Yang Yu is supported by the National Key Research and Development Program of China (No. 2017YFA0303903) and Zhejiang Province Key R & D Project (No. 2017C01062). Léo Ducas is supported by a Veni Innovational Research Grant from NWO under project number 639.021.645.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Yu, Y., Ducas, L. (2018). Learning Strikes Again: The Case of the DRS Signature Scheme. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11273. Springer, Cham. https://doi.org/10.1007/978-3-030-03329-3_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-03329-3_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03328-6
Online ISBN: 978-3-030-03329-3
eBook Packages: Computer ScienceComputer Science (R0)





 ) in the secret key
) in the secret key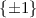 ) per vector in the secret key
) per vector in the secret key





