Abstract
A mixed variational formulation of some problems in L 2-based Sobolev spaces is used to define the Newtonian and layer potentials for the Stokes system with L ∞ coefficients on Lipschitz domains in \({\mathbb R}^3\). Then the solution of the exterior Dirichlet problem for the Stokes system with L ∞ coefficients is presented in terms of these potentials and the inverse of the corresponding single layer operator.
Dedicated to Professor H. Begehr on the occasion of his 80th birthday
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The trace operators defined on Sobolev spaces of vector fields on Ω± or \({\mathbb R}^3\) are also denoted by γ ± and γ, respectively.
References
M.S. Agranovich, Sobolev Spaces, Their Generalizations, and Elliptic Problems in Smooth and Lipschitz Domains (Springer, Heidelberg, 2015)
F. Alliot, C. Amrouche, The Stokes problem in \({\mathbb R}^n\): an approach in weighted Sobolev spaces. Math. Models Methods Appl. Sci. 9, 723–754 (1999)
F. Alliot, C. Amrouche, Weak solutions for the exterior Stokes problem in weighted Sobolev spaces. Math. Methods Appl. Sci. 23, 575–600 (2000)
C. Amrouche, M. Meslameni, Stokes problem with several types of boundary conditions in an exterior domain. Electron. J. Diff. Equ. 2013(196), 1–28 (2013)
C. Amrouche, H.H. Nguyen, L p-weighted theory for Navier-Stokes equations in exterior domains. Commun. Math. Anal. 8, 41–69 (2010)
I. Babus̆ka, The finite element method with Lagrangian multipliers. Numer. Math. 20, 179–192 (1973)
C. Băcuţă, M.E. Hassell, G.C. Hsiao, F-J. Sayas, Boundary integral solvers for an evolutionary exterior Stokes problem. SIAM J. Numer. Anal. 53, 1370–1392 (2015)
A. Barton, Layer potentials for general linear elliptic systems. Electron. J. Diff. Equ. 2017(309), 1–23 (2017)
K. Brewster, D. Mitrea, I. Mitrea, M. Mitrea, Extending Sobolev functions with partially vanishing traces from locally (𝜖, δ)-domains and applications to mixed boundary problems. J. Funct. Anal. 266, 4314–4421 (2014)
F. Brezzi, On the existence, uniqueness and approximation of saddle points problems arising from Lagrange multipliers. R.A.I.R.O. Anal. Numer. R2, 129–151 (1974)
F. Brezzi, M. Fortin, Mixed and Hybrid Finite Element Methods. Springer Series in Computational Mathematics, vol. 15 (Springer, New York, 1991)
O. Chkadua, S.E. Mikhailov, D. Natroshvili, Analysis of direct boundary-domain integral equations for a mixed BVP with variable coefficient, I: Equivalence and invertibility. J. Integr. Equ. Appl. 21, 499–543 (2009)
O. Chkadua, S.E. Mikhailov, D. Natroshvili, Localized boundary-domain singular integral equations based on harmonic parametrix for divergence-form elliptic PDEs with variable matrix coefficients. Integr. Equ. Oper. Theory. 76, 509–547 (2013)
O. Chkadua, S.E. Mikhailov, D. Natroshvili, Analysis of direct segregated boundary-domain integral equations for variable-coefficient mixed BVPs in exterior domains. Anal. Appl. 11(4), 1350006 (2013)
J. Choi, K-A. Lee, The Green function for the Stokes system with measurable coefficients. Commun. Pure Appl. Anal. 16, 1989–2022 (2017)
J. Choi, M. Yang, Fundamental solutions for stationary Stokes systems with measurable coefficients. J. Diff. Equ. 263, 3854–3893 (2017)
M. Costabel, Boundary integral operators on Lipschitz domains: elementary results. SIAM J. Math. Anal. 19, 613–626 (1988)
R. Dautray, J. Lions, Mathematical Analysis and Numerical Methods for Science and Technology. Integral Equations and Numerical Methods, vol. 4 (Springer, Berlin, 1990)
M. Dindos̆, M. Mitrea, The stationary Navier-Stokes system in nonsmooth manifolds: the Poisson problem in Lipschitz and C 1 domains. Arch. Ration. Mech. Anal. 174, 1–47 (2004)
A. Ern, J.L. Guermond, Theory and Practice of Finite Elements (Springer, New York, 2004)
E. Fabes, C. Kenig, G. Verchota, The Dirichlet problem for the Stokes system on Lipschitz domains. Duke Math. J. 57, 769–793 (1988)
E. Fabes, O. Mendez, M. Mitrea, Boundary layers on Sobolev-Besov spaces and Poisson’s equation for the Laplacian in Lipschitz domains. J. Funct. Anal. 159, 323–368 (1998)
G.P. Galdi, An Introduction to the Mathematical Theory of the Navier–Stokes Equations. Steady-State Problems, 2nd edn. (Springer, New York, 2011)
G.N. Gatica, W.L. Wendland, Coupling of mixed finite elements and boundary elements for linear and nonlinear elliptic problems. Appl. Anal. 63, 39–75 (1996)
V. Girault, P.A. Raviart, Finite Element Methods for Navier-Stokes Equations, Theory and Algorithms. Springer Series in Comp. Math., vol. 5 (Springer, Berlin, 1986)
V. Girault, A. Sequeira, A well-posed problem for the exterior Stokes equations in two and three dimensions. Arch. Ration. Mech. Anal. 114, 313–333 (1991)
J. Giroire, Étude de quelques problèmes aux limites extérieurs et résolution par équations intégrales. Thése de Doctorat d’État, Université Pierre-et-Marie-Curie (Paris-VI), 1987
B. Hanouzet, Espaces de Sobolev avec poids – application au probl\(\grave {e}\)me de Dirichlet dans un demi-espace. Rend. Sere. Mat. Univ. Padova. 46, 227–272 (1971)
S. Hofmann, M. Mitrea, A.J. Morris, The method of layer potentials in L p and endpoint spaces for elliptic operators with L ∞ coefficients. Proc. Lond. Math. Soc. 111, 681–716 (2015)
G.C. Hsiao, W.L. Wendland, Boundary Integral Equations (Springer, Heidelberg, 2008)
D.S. Jerison, C. Kenig, The inhomogeneous Dirichlet problem in Lipschitz domains. J. Funct. Anal. 130, 161–219 (1995)
M. Kohr, I. Pop, Viscous Incompressible Flow for Low Reynolds Numbers (WIT Press, Southampton, 2004)
M. Kohr, M. Lanza de Cristoforis, W.L. Wendland, Nonlinear Neumann-transmission problems for Stokes and Brinkman equations on Euclidean Lipschitz domains. Potential Anal. 38, 1123–1171 (2013)
M. Kohr, M. Lanza de Cristoforis, S.E. Mikhailov, W.L. Wendland, Integral potential method for transmission problem with Lipschitz interface in \({\mathbb R}^3\) for the Stokes and Darcy-Forchheimer-Brinkman PDE systems. Z. Angew. Math. Phys. 67(5), 1–30, 116 (2016)
M. Kohr, M. Lanza de Cristoforis, W.L. Wendland, On the Robin-transmission boundary value problems for the nonlinear Darcy-Forchheimer-Brinkman and Navier-Stokes systems. J. Math. Fluid Mech. 18, 293–329 (2016)
M. Kohr, S.E. Mikhailov, W.L. Wendland, Transmission problems for the Navier-Stokes and Darcy-Forchheimer-Brinkman systems in Lipschitz domains on compact Riemannian manifolds. J. Math. Fluid Mech. 19, 203–238 (2017)
J. Lang, O. Méndez, Potential techniques and regularity of boundary value problems in exterior non-smooth domains: regularity in exterior domains. Potential Anal. 24, 385–406 (2006)
W. McLean, Strongly Elliptic Systems and Boundary Integral Equations (Cambridge University Press, Cambridge, 2000)
D. Medková, Transmission problem for the Brinkman system. Complex Var. Elliptic Equ. 59, 1664–1678 (2014)
S.E. Mikhailov, Traces, extensions and co-normal derivatives for elliptic systems on Lipschitz domains. J. Math. Anal. Appl. 378, 324–342 (2011)
S.E. Mikhailov, Solution regularity and co-normal derivatives for elliptic systems with non-smooth coefficients on Lipschitz domains. J. Math. Anal. Appl. 400, 48–67 (2013)
M. Mitrea, M. Wright, Boundary value problems for the Stokes system in arbitrary Lipschitz domains. Astérisque. 344, viii+241 pp. (2012)
M. Mitrea, S. Monniaux, M. Wright, The Stokes operator with Neumann boundary conditions in Lipschitz domains. J. Math. Sci. (New York). 176(3), 409–457 (2011)
J.-C. Nédélec, Approximation des Équations Intégrales en Mécanique et en Physique. Cours de DEA, 1977
D.A. Nield, A. Bejan, Convection in Porous Media, 3rd edn. (Springer, New York, 2013)
F-J. Sayas, V. Selgas, Variational views of Stokeslets and stresslets. SEMA J 63, 65–90 (2014)
H. Triebel, Interpolation Theory, Function Spaces, Differential Operators (North-Holland, Amsterdam, 1978)
W. Varnhorn, The Stokes Equations (Akademie Verlag, Berlin, 1994)
Acknowledgements
The research has been supported by the grant EP/M013545/1: “Mathematical Analysis of Boundary-Domain Integral Equations for Nonlinear PDEs” from the EPSRC, UK. Part of this work was done in April/May 2018, when M. Kohr visited the Department of Mathematics of the University of Toronto. She is grateful to the members of this department for their hospitality.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Mixed Variational Formulations and Their Well-Posedness Property
Appendix: Mixed Variational Formulations and Their Well-Posedness Property
Here we make a brief review of well-posedness results due to Babus̆ka [6] and Brezzi [10] for mixed variational formulations related to bounded bilinear forms in reflexive Banach spaces. We follow [20, Section 2.4], [11], and [25, §4].
Let X and \({\mathcal M}\) be reflexive Banach spaces, and let X
∗ and \({\mathcal M}^*\) be their dual spaces. Let  ,
,  be bounded bilinear forms. Then we consider the following abstract mixed variational formulation.
be bounded bilinear forms. Then we consider the following abstract mixed variational formulation.
For f ∈ X ∗ , \(g\in {\mathcal M}^{*}\) given, find a pair \((u,p)\in X\times {\mathcal M}\) such that
Let A : X → X ∗ be the bounded linear operator defined by
where  is the duality pairing of the dual spaces X
∗ and X. We also use the notation 〈⋅, ⋅〉 for the duality pairing \(_{{\mathcal M}^{*}}\langle \cdot ,\cdot \rangle _{\mathcal M}\). Let \(B:X\to {\mathcal M}^{*}\) and \(B^{*}:{\mathcal M}\to X^{*}\) be the bounded linear and transpose operators given by
is the duality pairing of the dual spaces X
∗ and X. We also use the notation 〈⋅, ⋅〉 for the duality pairing \(_{{\mathcal M}^{*}}\langle \cdot ,\cdot \rangle _{\mathcal M}\). Let \(B:X\to {\mathcal M}^{*}\) and \(B^{*}:{\mathcal M}\to X^{*}\) be the bounded linear and transpose operators given by
In addition, we consider the spaces
Then the following well-posedness result holds (cf., e.g., [20, Theorem 2.34]).
Theorem 1
Let X and \({\mathcal M}\) be reflexive Banach spaces, f ∈ X ∗ and \(g\in {\mathcal M}^{*}\) , and \(a(\cdot ,\cdot ):X\times X\to {\mathbb R}\) and \(b(\cdot ,\cdot ):X\times {\mathcal M}\to {\mathbb R}\) be bounded bilinear forms. Let V be the subspace of X defined by (4). Then the variational problem (1) is well-posed if and only if a(⋅, ⋅) satisfies the conditions
and b(⋅, ⋅) satisfies the inf-sup (Ladyzhenskaya-Babus̆ka-Brezzi) condition,
Moreover, there exists a constant C depending on β, λ and the norm of a(⋅, ⋅), such that the unique solution \((u,p)\in {X}\times {\mathcal M}\) of (1) satisfies the inequality
In addition, we have (see [20, Theorem A.56, Remark 2.7], [4, Theorem 2.7]).
Lemma 2
Let \(X,{\mathcal M}\) be reflexive Banach spaces. Let \(b(\cdot ,\cdot ):X\times {\mathcal M}\to {\mathbb R}\) be a bounded bilinear form. Let  and
and  be the operators defined by (3), and let
be the operators defined by (3), and let  . Then the following results are equivalent:
. Then the following results are equivalent:
-
(i)
There exists a constant β > 0 such that b(⋅, ⋅) satisfies condition (7).
-
(ii)
\(B:{X/V}\to {\mathcal M}^{*}\) is an isomorphism and
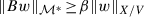 for any
for any
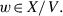
-
(iii)
 is an isomorphism and
is an isomorphism and
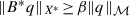 for any
\(q\in {\mathcal M}.\)
for any
\(q\in {\mathcal M}.\)
Remark 3
Let X be a reflexive Banach space and V be a closed subspace of X. If a bounded bilinear form \(a(\cdot ,\cdot ):V\times V\to {\mathbb R}\) is coercive on V , i.e., there exists a constant c a > 0 such that
then the conditions (6) are satisfied as well (see, e.g., [20, Lemma 2.8]).
The next result known as the Babus̆ka-Brezzi theorem is the version of Theorem 1 for Hilbert spaces (see [6], [10, Theorems 0.1, 1.1, Corollary 1.2]).
Theorem 4
Let X and \({\mathcal M}\) be two real Hilbert spaces. Let \(a(\cdot ,\cdot ):X\times X\to {\mathbb R}\) and \(b(\cdot ,\cdot ):X\times {\mathcal M}\to {\mathbb R}\) be bounded bilinear forms. Let f ∈ X ∗ and \(g\in {\mathcal M}^{*}\) . Let V be the subspace of X defined by (4). Assume that \(a(\cdot ,\cdot ):V\times V\to {\mathbb R}\) is coercive and that \(b(\cdot ,\cdot ):X\times {\mathcal M}\to {\mathbb R}\) satisfies the inf-sup condition (7). Then the variational problem (1) is well-posed.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Kohr, M., Mikhailov, S.E., Wendland, W.L. (2019). Newtonian and Single Layer Potentials for the Stokes System with L∞ Coefficients and the Exterior Dirichlet Problem. In: Rogosin, S., Çelebi, A. (eds) Analysis as a Life. Trends in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-02650-9_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-02650-9_12
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-02649-3
Online ISBN: 978-3-030-02650-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


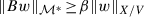 for any
for any
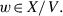
 is an isomorphism and
is an isomorphism and
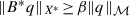 for any
for any