A-Contrario Horizon-First Vanishing Point Detection Using Second-Order Grouping Laws

Abstract

We show that, in images of man-made environments, the horizon line can usually be hypothesized based on a-contrario detections of second-order grouping events. This allows constraining the extraction of the horizontal vanishing points on that line, thus reducing false detections. Experiments made on three datasets show that our method, not only achieves state-of-the-art performance w.r.t. horizon line detection on two datasets, but also yields much less spurious vanishing points than the previous top-ranked methods.

1 Introduction

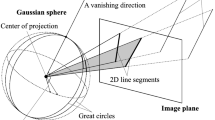
Accurate detection of vanishing points (VPs) is a prerequisite for many computer vision problems such as camera self-calibration [16], single view structure recovery [7], video compass [6], robot navigation [10] and augmented reality [4], among many others. Under the pinhole camera model, a VP is an abstract point on the image plane where 2-D projections of a set of parallel line segments in 3-D space appear to converge. In the Gestalt theory of perception [3], such a spatial arrangement of perceived objects is called a grouping law, or a gestalt. More specifically, as a 2-D line segment (LS) is in itself a gestalt (grouping of aligned points), a VP is qualified as a second-order gestalt [3].

In this paper, we are interested in VP detection from uncalibrated monocular images. As any two parallel lines intersect in a VP, LSs grouping is a difficult problem that often yields a large number of spurious VPs. However, many tasks in computer vision, including the examples mentioned above, only require that the vertical (so-called zenith) VP and two or more horizontal VPs (hVPs) are detected. In that case, a lot of spurious VPs may be avoided by first detecting the zenith and the horizon line (HL), and then constraining the hVPs on the HL. The zenith is generally easy to detect, as many lines converge towards that point in man-made environments. However, until recently, the HL was detected as an alignment of VPs, in other words, a third-order gestalt. This led to a “chicken-and-egg” situation, that motivated e.g. the authors of [14], to minimize an overall energy across the VPs and the HL, at the expense of a high computational cost.

Following [12], we show that, as soon as the HL is inside the image boundaries, this line can usually be detected as an alignment of oriented LSs, that is, a second-order gestalt (at the same perceptive level as the VPs). This comes from a simple observation, that any horizontal LS at the height of the camera’s optical center projects to the HL regardless of its 3-D direction (red LSs in Fig. 1). In practice, doors, windows, floor separation lines but also man-made objects such as cars, road signs, street furniture, and so on, are often placed at eye level, so that alignments of oriented LSs around the HLs are indeed observed in most images from urban and indoor scenes. Going one step further than [12], we effectively put the HL detection into an a-contrario framework. This transposal along with other improvements allows us to obtain top-ranked results in terms of both rapidity of computation and accuracy of the HL, along with more relevant VPs than with the previous top-ranked methods.

Fig. 1.

The horizon line can be detected as a meaningful alignment of image line segments orthogonal to the zenith line. (Color figure online)

2 Related Work and Contributions

There is a vast body of literature on the problem of VP detection in uncalibrated images. [6] use an Expectation-Maximization (EM) algorithm, which iteratively estimates the coordinates of VPs as well as the probabilities of individual LSs belonging to a particular vanishing direction. Although EM is often sensitive to initialization, a very rough procedure is used for this step. Several attempts have been made to obtain a more accurate initialization. [13] estimate VP hypotheses in the image plane using pairs of edges and compute consensus sets using the J-linkage algorithm. The same framework is used in [17], though a probabilistic consistency measure is proposed, which shows better performance. [16] present a RANSAC-based approach using a solution for estimating three orthogonal VPs and focal length from a set of four lines, aligned with either two or three orthogonal directions.

All these methods have been compared on the same datasets (DSs), York Urban (YU) [2] and Eurasian Cities (EC) [14] (see Sect. 5) and with the same protocol of [14]. It is difficult to establish a ground truth (GT) for the VPs, as selecting relevant VPs among hundreds e.g. in an urban scene is a subjective task. For that reason, the evaluation in [14] is focused on the accuracy of the HL. It is easy to show that the HL is orthogonal to the zenith line (ZL), which is the line connecting the principal point (PP) and the zenith (Fig. 1). The HL can then be found by performing a 1-D search along the ZL, and a weighted least squares fit, where the weight of each detected VP equals the number of corresponding lines. The horizon error is then defined as the maximum Euclidean distance between the estimated HL and the GT HL within the image boundaries, divided by the image height. To represent this error over a DS, a cumulative histogram of it is plotted. The plots are reported in Fig. 5. [15] also proposed to report a numerical value as the percentage of area under the curve (AUC) in the subset $[0,0.25]\times [0,1]$. These values are also reported in Fig. 5. It can be seen that each new method improves the accuracy, from $74.34\%$ AUC for YU and $68.62\%$ for EC with the earliest method of [6] to $93.45\%$ for YU and $89.15\%$ for EC with the state of the art method in 2013 [17].

A-Contrario Methods. Some authors proposed to detect meaningful VPs in the sense of the Gestalt Theory. This theory was translated by Desolneux et al. into a mathematics and computer vision program [3]. According to the Helmholtz principle, which states that “we immediately perceive whatever could not happen by chance”, a universal variable adaptable to many detection problems, the Number of False Alarms (NFA) was defined. The NFA of an event is the expectation of the number of occurrences of this event under a white noise assumption. From this variable, a meaningful event in the phenomenological sense can be detected as a so-called $\epsilon$-meaningful event, namely an event whose NFA is less than $\epsilon$. Most problems of computer vision have been solved efficiently by simply setting $\epsilon$ to 1. When $\epsilon \le 1$, the event is said meaningful. The Helmholtz principle has been applied to the VP detection problem in [1] and [8]. In [1], a practical application of the Santaló’s theory [11] is used to partition the infinite image plane into a finite family of so-called vanishing regions. Meaningful VPs are then detected from large votes of lines meeting in a vanishing region, thus producing low NFA. Although this method was only qualitatively assessed, it presents interesting matter for the building of our own method, and especially the use of the Santaló’s theory. In [8], a point alignment detector based on the Helmholtz principle [9] is used twice: in the image domain, to group LSs into more precise lines, and in dual domains where converging lines become aligned points. This method achieved state-of-the-art accuracy in 2014 ($94.51\%$ for YU, $89.20\%$ for EC).

Horizon-First VP Detection. Horizon-first VP detection was simultaneously introduced in two recent works [12, 18], both based on the same principle: propose candidate HLs, score them, and keep the best. In [18], a deep convolutional neural network (CNN) is used to extract global image context and guide the generation of a set of candidate HLs. For each candidate, they identify VPs by solving a combinatorial optimization process (see Sect. 5.3) followed by a constrained nonlinear optimization. The final score for each candidate HL is based on the consistency of the lines in the image w.r.t. the selected VPs. This method achieved state-of-the-art accuracy in 2016: $94.78\%$ for YU, $90.80\%$ for EC. In Sect. 5, we closely compare their results with ours and discuss the strengths and weaknesses of each approach. In [12] (our previous work) the ZL is first obtained using a brute force algorithm. Centroids of the LSs orthogonal to the ZL are then projected to the ZL and candidate HLs are taken at the peaks of a histogram of the obtained coordinates. A decreasing density sampling is then performed along each candidate HL. Each sample point is scored by the number of LSs consistent with that point, based on an angular consistency measure, and the VPs are found as peaks in the score curve. The final score for each candidate HL is finally the sum of the best two scores at the peaks (or the best score in case there is only one peak). This method is fast in execution and easy to implement, but middle rank in terms of accuracy ($90.40\%$ for YU, $85.64\%$ for EC).

Contributions. In this paper, we build on the advances of several of these works, and especially [1, 12, 18], to obtain a novel and more accurate HL and VP detection algorithm. In particular: (i) as in [1, 8] we put the method into a mathematically, well founded a-contrario framework. However, by fractioning the 2-D search of meaningful VPs into three 1-D searches of meaningful events (ZL, HL and VPs), we avoid computationally expensive processes encountered using the previous a-contrario approaches; (ii) the ZL itself is obtained based on the Helmholtz principle. One benefit of doing so is to allow considering several orientations for the candidate HLs, therefore succeeding where other methods fail in cases where the vertical of the scene is masked by another near-vertical direction; (iii) As in [18], a set of candidate HLs is sampled around the meaningful HLs. We use a Gaussian mixture model (GMM) for that step, whose modes are the offsets of the meaningful HLs. This step significantly improves the accuracy w.r.t. [12], where no other candidates than the peaks of the histogram are considered; (iv) as in [12] and [18], VPs are hypothesized along the candidate HLs. However, thanks to the Helmholtz principle, we get more meaningful VPs. Moreover, our procedure does not require using any consistency measure, which have proven to be biased [17] and/or expensive to compute. Thanks to these improvements, our approach is top-ranked in terms of accuracy on the usual DSs ($95.35\%$ on YU, $91.10\%$ on EC), without compromising neither the easiness of implementation, nor the efficiency of computation. Our method is actually even faster than [12]. It is also much faster than [8] and slightly faster than [18], the two previous state-of-the-art methods. In the next section, we describe how ZLs and HLs are hypothesized based on the Helmholtz principle. VP detection along the candidate HLs and candidate scoring are presented in Sect. 4. Experimental results are finally provided and discussed in Sect. 5.

3 Candidate Horizon Lines

3.1 A-Contrario Zenith Line Detection

As mentioned in introduction, the ZL $\mathcal{L}_z$ is the line connecting the PP and the zenith VP. An initial guess of this line is obtained based on the fact that the vertical LSs in the scene are aligned with $\mathcal{L}_z$ when passing through the PP, and near-parallel to $\mathcal{L}_z$ in a narrow strip around the PP (Fig. 1). This yields a second-order parallelism gestalt, which can be detected by finding the maximal meaningful modes (MMMs) [3] of an orientation histogram. More specifically, our procedure for detecting hypothesized ZLs consists of the following steps (Fig. 2): (i) a set of M LSs with orientations $\theta _i\in [0,\pi [$ are detected using the LSD algorithm [5], (ii) LSs far from the PP ($|\mathbf{l}_i^T\mathbf{c}|>d_{PP}$, with $\mathbf{l}_i$ the homogeneous coordinates of the LSs normalized so that $\sqrt{{l_i}_1^2+{l_i}_2^2}=1$ and $\mathbf{c}$ the homogeneous coordinates of the PP) or far from being vertical in the image ($|\theta _i-~\pi /2|<\theta _v$) are discarded (Fig. 2-A1 shows the LSs remaining at the end of this step), (iii) a $L_z$-bin orientation histogram of the remaining LSs is built (Fig. 2-A2) and the MMMs of this histogram are computed (blue bins in Fig. 2-A3); the middle orientations of the highest bins of the MMMs are chosen as rough estimates of the hypothesized ZLs (colored circles in Fig. 2-A3), (iv) for each estimate, a set of candidate vertical LSs is selected by thresholding the angles between all image LSs and the estimate ($|\theta _i-\theta _{\mathcal{L}_z}|<\theta _z$, with $\theta _{\mathcal{L}_z}\in [0,\pi [$ the orientation of $\mathcal{L}_z$ (Fig. 2-B1, the LSs are drawn using the same color as the corresponding circles in Fig. 2-A3); the intersection point of these LSs (in direction of the colored dashed lines in Fig. 2-B2) and a set of inlier LSs are obtained using a RANSAC algorithm; finally, the intersection point (the hypothesized zenith VP) is refined from the set of inliers, based on SVD.

Step (iv) is the same as in [18]. MMMs are computed using the large deviation estimate of the NFA¹, with

$$\begin{aligned} p(a, b) = (b-a+1)/L \end{aligned}$$

(1)

($L=L_z$) the prior probability for a LS to have its orientation in a bin between [a, b] (a uniform distribution is used as null hypothesis). In most cases, only one MMM is detected. However, it can happen, as in Fig. 2, that several modes are obtained (a mean of 1.71 MMMs is obtained in our experiments on YU, 1.66 on EC) while the mode with highest NFA does not correspond to the expected direction. A benefit of using an a-contrario approach here, is that all hypotheses can be used to generate candidate HLs, so that the correct solution can still be found in such difficult cases (Fig. 2-B2, the GT HL is drawn in dashed yellow, the estimated HL in cyan). This is a key improvement in comparison with [12] and [18], where only one candidate is obtained at that stage, leading to incorrect results in such cases (e.g. with [18] in Fig. 2-B3). Rarely, a histogram has no MMM. In that case, the vertical direction of the image is taken as an initial guess for the ZL, and refined according to step (iv).

Fig. 2.

A-contrario detection of the zenith line (see the text). (Color figure online)

3.2 A-Contrario Horizon Line Detection

The detection of the HL is based on following geometric properties (Fig. 1): (i) the HL is perpendicular to the ZL, (ii) any horizontal LS at the height of the camera’s optical center projects to the HL regardless of its 3-D direction. From these properties we get that all horizontal LSs at height of the optical center in the scene accumulate on a line in the image plane, perpendicular to the ZL. This yields a second-order alignment gestalt, which is detected by finding the MMMs of an offset histogram. More specifically, our method for detecting the HL is as follows (Fig. 1): (i) LSs far from being perpendicular to the ZL ($||\theta _i-\theta _{\mathcal{L}_z}|-\pi /2|<\theta _{h}$) are discarded, (ii) the centroids of the remaining LSs are orthogonally projected on the ZL and their offsets are computed relative to the projection of the PP, (iii) a $L_h$-bin offset histogram is generated and the MMMs of this histogram are computed (red bins in Fig. 1). Again, though more rarely than for the ZL, this procedure can yield several MMMs (a mean of 1.03 MMMs is obtained on YU, 1.06 on EC). The centers of the highest peaks of the $N_{init}$ MMMs are all considered as candidate HLs (blue dashed line in Fig. 1).

3.3 Line Sampling

This estimate of the HL can be inaccurate in some cases, due to the histogram binning and, sometimes, to some offsets between the position of the accumulated LSs and the HL. Following the approach used in [18], we tackle this issue by sampling additional candidate HLs perpendicularly to the ZL, around the initial candidates. In [18], the offset probability density function (PDF) used for this sampling is a Gaussian model, fit from the CNN categorical probability distribution outputs. As we can have several initial candidates, we use a Gaussian mixture model (GMM) where the modes are the offsets of the initial candidates and the standard deviations are identically equal to $\sigma H$, with H the image height and $\sigma$ provided in Table 1. We draw $S-N_{init}$ additional candidates, equally divided between the $N_{init}$ initial candidates. In the case where no MMM is found, we have no a priori knowledge on the position of the HL along the ZL. The offsets of the S candidate HLs are then sampled linearly between $[-2H,2H]$.

4 Candidate Vanishing Points

All S candidate HLs are assessed against the success of detecting VPs along the line. Let us assume a line candidate $\mathcal{L}$ with polar coordinates $(\theta , \rho )$ is indeed the HL. Then, intersecting all image LSs (extended indefinitely beyond their endpoints) with $\mathcal{L}$ should lead to an accumulation of intersection points around the VPs (Fig. 3-A, B). In the same spirit as previously, these accumulations can be detected by finding the MMMs of a coordinate histogram of the intersection points. However, the prior probability for the coordinates along the HL is not uniform, leading to incorrect or inaccurate MMMs if p(a, b) is taken as in Eq. (1) (e.g. Fig. 3-B, the MMM, shown in red, is very large and its highest bin does not correspond to a VP). In this section, we provide the prior (null hypothesis) suited to this problem and describe how the VPs and the HL are finally obtained.

Fig. 3.

Left: each line segment gives rise to an intersection point with the horizon line (A). The modes of a coordinate histogram of these intersections (in red and yellow) should appear at the positions of the vanishing points. Different results are shown (B, C, D) depending on the choice of the null hypothesis and the way the histogram is built. Right: computation of p depending on whether the line meets the circle or not. (Color figure online)

4.1 Null-Hypothesis

For simplicity, we shall consider the image domain as a circle $\mathcal{C}$ of center O and radius 1 (Fig. 3-A). The polar coordinates of the detected LSs are assumed uniformly distributed over this domain. The prior probability p(a, b) can then be derived from a result obtained by Luis A. Santaló in the late 1970s [11]:

If $K_1,K_2$ are two bounded convex sets in the plane (which may or may not overlap) and $L_1,L_2$ the lengths of the boundaries $\partial K_1,\partial K_2$, the probability that a random chord of $K_1$ intersects $K_2$ is $p=\frac{L_i-L_e}{L_1},$ where $L_e$ is the length of the external cover $C_e$ of $K_1$ and $K_2$, and $L_i$ is the length of the internal cover $C_i$ of $K_1$ and $K_2$ if $K_1\cap K_2=\emptyset$, or $L_i=L_1+L_2$ if $K_1$ and $K_2$ overlap².

This result is applied to our problem as follows. Let $O'$ be the orthogonal projection of O onto the candidate HL $\mathcal{L}$ and let X be a point on $\mathcal{L}$ at a signed distance x from $O'$ (Fig. 3, right). We use $K_1=\mathcal{C}$ ($L_1=2\pi$) and $K_2=[O'X]$ ($L_2=2|x|$). The probability of a LS meeting $\mathcal{L}$ between $O'$ and X depends on whether or not $\mathcal{L}$ meets $\mathcal{C}$.

Case 1: $\mathcal{C}\cap \mathcal{L}=\emptyset$ (Fig. 3, top-right). Let A, B (resp. C, D) be the points of contact of the tangents to the circle $\mathcal{C}$ from point $O'$ (resp. X). We have:

$$\begin{aligned} L_e= & {} O'X+XD+\widehat{DA}+AO' = O'X+XC+\widehat{DA}+BO',\\ L_i= & {} XO'+O'B+\widehat{BD}+\widehat{DA}+\widehat{AC}+CX,\\ p= & {} \frac{L_i-L_e}{L_1} = \frac{\widehat{BD}+\widehat{AC}}{2\pi } = \frac{\widehat{EF}}{\pi }, \end{aligned}$$

where $\widehat{}$ denotes a counterclockwise arc of $\mathcal{C}$, and E, F are the intersection points of the circle $\mathcal C$ with lines $(OO')$ and (resp.) (OX)³. Finally:

$$\begin{aligned} p(x) = \frac{1}{\pi }{\tan ^{-1}\frac{x}{\rho }}. \end{aligned}$$

(2)

It may be noticed that this expression is similar to the inverse of the sampling function $s(k) = L \tan (k\varDelta \theta )$ used in [12], though the term $\rho$ is also involved here.

Case 2: $\mathcal{C}\cap \mathcal{L}\ne \emptyset$. In that case, we have $p=(L_1+L_2-L_e)/L_1$ with $L_e$ depending on whether X is inside or outside the circle $\mathcal C$. In the sub-case where X is inside the circle, $L_e=L_1$ and

$$\begin{aligned} p(x)=\frac{x}{\pi }, \end{aligned}$$

(3)

which is independent from $\rho$. In the sub-case where X is outside the circle (Fig. 3, bottom-right), $L_e=L1-\widehat{AB}+AX+BX$ and $p=(2|x|+2\tan ^{-1}(AX)-2AX)/2\pi$, where A, B denote the points of contact of the tangents to the circle $\mathcal{C}$ from point X. This yields to:

$$\begin{aligned} p(x) = \frac{1}{\pi }\left( x+\tan ^{-1}\left( x\sqrt{1+\frac{\rho ^2-1}{x^2}}\right) -x\sqrt{1+\frac{\rho ^2-1}{x^2}}\right) . \end{aligned}$$

(4)

Finally, given a coordinate histogram of the intersection points and given a bin range [a, b], the prior probability p(a, b) is given by:

$$\begin{aligned} p(a,b) = p(r(b))-p(l(a)), \end{aligned}$$

(5)

where l(a), r(a) denote the min and (resp.) max values of the histogram bin a.

4.2 A-Contrario VP Detection and Line Scoring

Figure 3-C shows an example of the PDF $r(x)=\frac{\partial p}{\partial x}(x)$, obtained for a line $\mathcal L$ in case 2 (purple curve). In this figure, the red and yellow MMMs are obtained using p(a, b) provided by Eq. (5): both VPs are correctly detected. However, the coordinates of the intersection points can be large, depending on the orientations of the detected LSs w.r.t. the HL. For a given bin width, this results in an arbitrary and potentially very large number of bins, yielding poor time performance for the MMM detection. For that reason, we rather use the following approach: (i) the coordinates of the intersection points are transformed using the function p(x), yielding new coordinates, theoretically uniformly distributed (except at the VPs) between $-1/2$ and 1/2, (ii) a histogram with a fixed number $L_{vp}$ of bins is computed from the new coordinates and the MMMs of this histogram are detected using the prior probability p(a, b) provided by Eq. (1), with $L=L_{vp}$. The histogram and MMMs obtained by following this procedure are shown in Fig. 3-D. Both VPs are still detected, while the histogram is much more compact (46 bins against 3630) for the same accuracy (30 bins) inside the image domain. The accuracy may be worse outside the image domain but, as a counterpart, the propagated error e.g. on the inferred 3-D vanishing directions, decreases as the distance between the PP and the VP increases⁴. Finally, an initial set of candidate VPs are extracted at the centers of the highest bins of the MMMs. These candidate VPs are refined using an EM-like algorithm similar to the one used in [18]. This algorithm relies on the consistency measure $f_c(\mathbf{v}_i,\mathbf{l}_j)=\max (\theta _{con}-|\cos ^{-1}(\mathbf{v}_i^\top \mathbf{l}_j)|,0)$, where $\mathbf{l}_j$ is a LS whose consistency with a VP $\mathbf{v}_i$ is measured. At the end of this procedure, we select the two highest weighted VPs $\left\{ \mathbf{v}_i\right\} _{best}$ (or one if there is only one candidate) and compute the score of the candidate HL as $\sum _{\left\{ \mathbf{v}_i\right\} _{best}}\sum _{\left\{ \mathbf{l}_j\right\} }f_c(\mathbf{v}_i,\mathbf{l}_j)$.

Fig. 4.

Horizon lines obtained at the 1st, 25th, 50th, 75th and 100th percentiles of the horizon error (Col. 1–5, resp.) for YU (Row A), EC (Row B) and HLW (Row C). The GT HL is shown in yellow dashed line, the MMMs in blue dashed lines and the estimated HL in cyan solid line. The horizon error is displayed on the top-left corner of each image result. LSs participating to a VP are shown using one color per VP. (Color figure online)

It is important to notice that the consistency measure is used to refine the VPs, but not to detect them. This is a great difference in comparison with [18], where the consistency measure is used both to detect and refine the VPs, yielding more spurious VPs (see Sect. 5). Moreover, our 1-D search of the VPs has several advantages over the previous a-contrario approaches [1, 8] that operated in 2-D space. With regard to [1], we avoid computationally expensive local maximization of meaningfulness as well as filtering of spurious vanishing regions, due to artificial mixtures of different segment orientations. With regard to [8], we avoid highly combinatorial point alignment detection in the dual space, along with tricky parameters tuning (sizes of rectangles, local windows, boxes – see [9] for details).

5 Experimental Results

5.1 Implementation

The source code of our method is available at https://members.loria.fr/GSimon/v/. Algorithm parameters are provided in Table 1. Those were tuned manually using a few images from the DSs. We used the same number of line samples, $S=300$, as in [18]. The PP is assumed at image center. In order quantify the parameters’ sensitivity, we did the following experiment. For each parameter p, we run our method 9 times, multiplying p by $\frac{1}{2},\frac{5}{8},\frac{6}{8},\frac{7}{8},1,\frac{5}{4},\frac{6}{4},\frac{7}{4},2$, respectively, and leaving the other parameters unchanged (the first 20 images of YU and EC were used). For each parameter, we report the relative decrease from the maximum to the minimum AUC obtained over the 9 runs (last row). The consistency thresholds $\theta _z,\theta _h$, and particularly $\theta _{con}$ (also used in [17]) are the most sensitive parameters. The number of bins in the histograms ($L_z,L_h,L_{vp}$) are not very sensitive, though $L_h$ is more sensitive than the other two. $d_{pp},\theta _v$ and $\sigma$ are not sensitive. The number of samples S is not as sensitive as one might expect (from $S=150$ to $S=600$, the AUC increases from $93.7\%$ to $94.3\%$).

Table 1. Algorithm parameters. First row: parameters’ values (W is the image width). Second row: parameters’ sensitivity.

5.2 Accuracy of the Horizon Line

Computation of the HL was first evaluated on the two usual DSs: (i) York Urban (YU) [2], consisting of 102 images of resolution $640 \times 480$, taken indoor and outdoor and mostly following the Manhattan world assumption, and (ii) Eurasian City (EC) [14], consisting of 114 images of resolution $1920 \times 1080$, including scenes from different parts of the world, more varied viewpoints, and poorer fit to the Manhattan assumption. Example results are provided in Fig. 4, first and second rows (resp. YU and EC). We show the images where the horizon error is the lowest (column 1), the highest (column 5), and at the 25th, 50th and 75th percentiles (columns 2, 3, 4, resp.). The table in Fig. 5 shows the performance of our method, based on the cumulative histogram of the horizon error and the AUC (Sect. 2). We achieve state-of-the-art performance on both DSs. On YU, we improve upon the previous best of Zhai et al. [18] by a relative improvement $\varDelta AUC=(AUC_{new}-AUC_{old})/(1-AUC_{old})=10.9\%$. This is a significant improvement, especially considering their improvement relative to the previous state of the art [8] was $5\%$. On EC, the relative improvement upon the previous best is $3.3\%$. To further investigate our results, we replaced our PDF-based sampling method by a linear sampling between $[-2H, 2H]$. The new AUC are shown in the table of Fig. 5 (“Linear samp”). The accuracy is similar to that with our sampling PDF and higher to that with the PDF of [18]. This signifies that YU is a easy DS (two large sets of parallel lines are detected in most images), that does not require fine sampling as long as it covers the range $[-2H, 2H]$ with sufficient density. This tends to attribute the improvement of accuracy w.r.t. to [18] to our scoring procedure. It indeed appears that the method of [18] gets much more spurious VPs than ours on both YU and EC (see Sect. 5.3 below). By contrast, the best result obtained by our method on EC may be interpreted slightly differently, as here both our sampling PDF and the one of [18] improve the accuracy compared to that with a linear sampling, so that both sampling and scoring of the candidate HLs contribute to our performance.

Fig. 5.

Performance results w.r.t. HL detection.

Our method was then evaluated on Horizon Lines in the Wild (HLW), a DS introduced recently by Zhai et al. [18], and consisting of 2018 images of various resolutions. This DS is not only larger but also much more challenging than the previous ones. Most of the photos look like holiday photos, showing man-made environments, but also groups of people, statues occupying a large part of the image, and so on. Furthermore, the roll and tilt angles of the camera have very large range of values, often leading to HLs far from the image boundaries, and ZL angles out of the assumed range (e.g. Fig. 4-C5). Example results and AUCs obtained with our method are shown in Fig. 4-Row C, and (resp.) in the third column of the table in Fig. 5. The approach of Zhai et al. outperforms our method on that DS and we get a relative decrease of $9.1\%$ w.r.t. them. The AUC with a linear sampling is much lower than with our PDF (a relative decrease of $19.4\%$), which indicates that sampling plays a crucial role on this DS. To closely compare our PDF with the one of [18] and establish which parameters of the PDFs, among the modes and the spreads, are the most critical, we tested both methods using only one sample ($S=1$), namely the mode of the GMM with highest NFA with our method, and the center of the PDF with the method of Zhai et al. The results are shown in the last two rows of the table in Fig. 5. The AUC with our method is now quite the same as with [18]. This indicates that, in HLW, the spread of the sampling is the key element of the difference in performance between [18] and our method. In [18], $\sigma$ is re-estimated each frame from the CNN output, while we take a constant, empirical value in our method. A way to improve our results may be to consider the NFAs of the candidate HLs as uncertainty measures, that may be used to generate more relevant values of $\sigma$.

The predictive power of the CNN is interesting in bad images where analytical vision fails, assuming a large DS of similar examples is provided, along with a GT, to the learning process. By contrast, our method may provide accurate results in some images where the CNN fails due to insufficient representation in the learning DS. For instance, Fig. 6-A1 shows an example of an image acquired in an industrial environment. Our method succeeds in predicting the HL, refining it and getting meaningful VPs (Fig. 6-A1), while the method of Zhai et al. poorly estimates the sampling PDF and finally the HL (Fig. 6-A2).

5.3 Relevance of the Vanishing Points

Figure 6-B1, B3, C1, C3 show some example VPs (represented by the LSs consistent with them) obtained by using our method. Performance w.r.t. the previous two best of [8, 18] was measured by counting the number of good and spurious VPs obtained on the YU and EC DSs. We chose to use these two DSs, as those are representative of different resolutions (low and high) and get higher accuracy regarding HL detection. In our experiment, a “good VP” is a VP that indeed corresponds to a set of parallel, horizontal lines, while a spurious VP can be of two kinds: “spurious VPs” that correspond to fortuitous convergences of non parallel lines, and “split VPs”, issued from undesirable splittings of parallel, horizontal lines normally corresponding to the same VP. In the latter case, one “good VP” plus one “split VP” per added VP are counted. Figure 7-Left shows the total number of good VPs, spurious VPs and split VPs obtained on the two DSs for each method. Our method is the most relevant regarding the three criteria. We obtain the highest number of good VPs, very few spurious VPs and no split VP at all, whatever the DS is.

Fig. 6.

Qualitative comparisons between our method (Col. 1) and the method of Zhai et al. [18] (Col. 2) on the one hand, and between our method (Col. 3) and the method of Lezama et al. [8] (Col. 4) on the other hand. Plotting conventions are as in Fig. 4. (Color figure online)

The method in [18] detects slightly less good VPs than ours (a mean of 2.11 per image–p.i. on the two DSs, against 2.14 with our method) but much more spurious VPs, about one for 2 good VPs, against one for 23 with our method. It also obtains a non-negligible number of split VPs (one for 29 good, against 0 with our method). These relatively poor results are mainly due to the approach used by [18] to initialize VPs along the candidate HLs. This approach consists in randomly selecting a subset of LSs $\left\{ \mathbf{l}_j\right\}$ and computing their intersection with the HL. An optimal subset of VPs $\mathbf{v}_i$ is extracted from the intersections, so that the sum of weights $\sum _{\mathbf{v}_i}\sum _{\mathbf{l}_j}f_c(\mathbf{v}_i,\mathbf{l}_j)$ is maximal, while ensuring no VPs in the final set are too close. A distance threshold between two VPs has therefore to be fixed, which can lead to split LSs into several groups while they correspond to the same VP (e.g. the blue and yellow LSs on the building’s facade in Fig. 6-B2). Moreover, random selection of LSs can prevent detecting a VP represented by few LSs (e.g. the VP consistent with the yellow LSs in Fig. 6-C1, not found in Fig. 6-C2). Finally, as another threshold has to be fixed for the consistency measure, any set of LSs that meet accidentally “near” the same point on the HL can generate a spurious VP (e.g. the yellow LSs in Fig. 6-C2). All these threshold problems are inherently handled when using our a-contrario framework.

While also relying on an a-contrario framework, the method in [8] gets poor results regarding the detected VPs: the lowest number of found VPs (1.80 p.i.), the second highest number of spurious VPs (one for 3 good) and the highest number of split VPs (one for 4 good). The low number of good VPs (see e.g. the VPs consistent with the orange LSs in Fig. 6-B3 and C3, not found in Fig. 6-B4 and C4, resp.) may be explained by the fact that a VP can appear as meaningful along the HL, but not in the whole image dual domain. The high number of spurious VPs (e.g. the VPs consistent with the cyan, green, red and yellow LSs Fig. 6-C4) is mainly due to accidental intersections of LSs, that appear more frequently in the whole image dual domain than on the HL. Finally, the high number of split VPs is mainly due to the fact that aligned points in the dual domain (meeting LSs in the primal domain) can be scattered in the direction orthogonal to the alignment, producing several meaningful alignments with slightly different orientations (Fig. 6-A4 and B4). Using our method, LSs corresponding to the same VP can meet the HL at coordinates scattered along the HL, but generally in contiguous bins of the coordinate histogram, so that those are fused in a single MMM (Fig. 6-A3 and B3).

Fig. 7.

Left: performance results w.r.t. VP detection. Right: computation times in sec.

5.4 Computation Times

The method was implemented in Matlab and run on a HP EliteBook 8570p laptop with I7-3520M CPU. Computation times are given in Fig. 7-Right. Our method is faster than the previous methods whose code is available. Moreover, contrary to e.g. [8], it is only slightly affected by increases in the image size, which generally yield larger numbers of LSs. Indeed, our method is in $O(L_z^2+L_h^2+S(L_{vp}^2+M))$, therefore only linearly affected by the number of LSs.

6 Conclusion

As soon as one wishes to detect Manhattan directions, hVPs and/or the HL in an image, which are common tasks in computer vision, our experimental results show that horizon-first strategies are definitely faster and more accurate than all previous methods. In particular, our method achieves state-of-the-art performance w.r.t. HL detection on two over three DSs. Moreover, it provides more relevant VPs than the previous two state-of-the-art approaches, which can be of great interest for any practical use of the VPs (e.g. finding the Manhattan directions). Finally, it performs well in any kind of environment, as soon as man-made objects are visible at eye level. The method of Zhai et al. [18] stays, however, an alternate method that may be more suited to specific environments, learned from large GT DSs, especially when the later condition is not met.