Intact Connectional Morphometricity Learning Using Multi-view Morphological Brain Networks with Application to Autism Spectrum Disorder

Abstract

The morphology of anatomical brain regions can be affected by neurological disorders, including dementia and schizophrenia, to various degrees. Hence, identifying the morphological signature of a specific brain disorder can improve diagnosis and better explain how neuroanatomical changes associate with function and cognition. To capture this signature, a landmark study introduced, brain morphometricity, a global metric defined as the proportion of phenotypic variation that can be explained by brain morphology derived from structural brain MRI scans. However, this metric is limited to investigating morphological changes using low-order measurements (e.g., regional volumes) and overlooks how these changes can be related to each other (i.e., how morphological changes in region A are influenced by changes in region B). Furthermore, it is derived from a pre-defined anatomical similarity matrix using a Gaussian function, which might not be robust to outliers and constrains the locality of data to a fixed bandwidth. To address these limitations, we propose the intact connectional brain morphometricity (ICBM), a metric that captures the variation of connectional changes in brain morphology. In particular, we use multi-view morphological brain networks estimated from multiple cortical attributes (e.g., cortical thickness) to learn an intact space that first integrates the morphological network views into a unified space. Next, we learn a multi-view morphological similarity matrix in the intact space by adaptively assigning neighbors for each data sample based on local connectivity. The learned similarity capturing the shared traits across morphological brain network views is then used to derive our ICBM via a linear mixed effect model. Our framework shows the potential of the proposed ICBM in capturing the connectional neuroanatomical signature of brain disorders such as Autism Spectrum Disorder.

1 Introduction

Brain disorders affect the brain construct on multiple levels including neural activity quantified using functional magnetic resonance imaging (MRI) and brain tissue morphology measured using structural T1-weighted MRI. While several studies focused on identifying the functional signature (or fingerprint) of brain disorders [1,2,3], a few works investigated the morphological fingerprint of a specific brain disorder (Alzheimer’s disease, Autism Spectrum Disorder, Parkinson’s disease). To fill this gap, [4] proposed a statistical metric called brain ‘morphometricity’ (BM) that describes the associations between brain morphology and multiple risk factors such as age and gender. Using structural MRI, volumetric measurements of noncortical structures and thickness measurements of cortical regions were generated. To capture the similarity between brain morphologies of brains drawn from distinct groups (e.g., normal controls and ASD patients), they computed a similarity matrix for each of these measurements separately, and then averaged them to produce the global anatomical similarity matrix. Ultimately, a Linear Mixed Effect model (LME) was applied to estimate the variance captured by the similarity matrix to unravel the morphological signature of a specific phenotypic trait (e.g., clinical diagnosis).

However, the proposed morphometricity metric is limited to investigating morphological changes using low-order measurements (e.g., regional volumes) and overlooks how these changes can be related to each other (i.e., how morphological changes in region A are influenced by changes in region B). In other words, it does not look at morphological connectivity of anatomical regions of interest (ROIs), where a morphological connection quantifies the (dis)similarity in shape between two brain ROIs –i.e., how their morphologies are related. This can be modeled using multi-view morphological brain networks (MBN) as proposed in [5,6,7,8]. These showed great potential for brain disorder diagnosis [5,6,7] and morphological connectional biomarker identification [8] using supervised [5, 6] or unsupervised learning [7] techniques trained on structural T1-weighted MRI data. More importantly, each view-specific MBN models the relationship in morphology between brain regions using a specific measurement (e.g., curvature).

To fill this gap, we unprecedentedly propose to use multi-view MBNs for ‘connectional brain morphometricity’ (CBM) estimation. We note that in the landmark work [4] of BM, the similarity matrix is computed using a pre-defined similarity function such as Gaussian metric, which (i) may not be robust to outliers, (ii) may not handle well multi-view data drawn from multiple sources, and (iii) may fail to capture data sample distributions with varying bandwidths. To address these limitations, we propose to learn the data similarity matrix by levering the intact-awareness similarity learning model developed in [9]. More precisely, the proposed approach aims to recover an intact space [10] that captures the complementarity between multiple data views. A practical example of this is the medical diagnosis of neurological diseases, such as dementia. Each morphological feature (e.g., cortical thickness) alone captures insufficient information and thus cannot comprehensively describe the brain atrophy, which can only be fully recovered by integrating all the features. To leverage the complementary of multi-view MBNs, we propose a novel intact connectional brain morphometricity (ICBM) learning framework to identify the connectional morphology-driven fingerprint of specific traits. Specifically, we use the intactness-aware similarity learning method [9] to estimate the similarity that has the maximum dependence with its intact space, where shared traits across views are well captured. First, we learn the complementarity between different MBNs by constructing an intact connectomic space. Within a joint framework, we simultaneously learn a multi-view morphological similarity matrix in the intact space by adaptively assigning neighbors for each data sample based on local connectivity. The learned similarity capturing the shared traits across morphological brain network views is then used to derive our ICBM via a linear mixed effect model. The main contributions of our work can be summarized as follows:

• We propose to learn a morphological intact space that models the complementarity between different morphological brain networks by integrating them in one space, thereby catching partial information from each individual view.

• We learn the multi-view morphological similarity matrix that is in harmony with the morphological intact space of multi-view MBNs.

• We introduce the intact connectional brain morphometricity, a metric that could reveal novel insights into morphological connectivity fingerprinting brain disorders.

Fig. 1.

Proposed framework for intact connectional brain morphometricity (ICBM) learning. (A) Feature extraction from different multi-view morphological brain networks, each driven from a specific morphological brain measurement (e.g., curvature). Multi-view feature vectors are concatenated to create a multi-view training matrix including all subjects. (B) Intact similarity matrix construction. We learn an intact connectomic space, which captures the complementarity between all views $\{ \mathbf {F}^k \}$, and where the intact similarity matrix $\mathbf {S}$ is jointly learned. (C) ICBM estimation. Given the learned similarity matrix along with the phenotype vector (e.g., subject label as normal control or autistic) and the population covariance matrix, we compute ICBM using linear mixed effect (LME) model.

Table 1. Major mathematical notations used in this paper

2 Intact Connectional Brain Morphometricity Learning

In the following, we present the main steps of our intact connectional brain morphometricity (ICBM) learning framework. To clarify the reading, we summarized the major mathematical notation in Table 1. Figure 1 illustrates the proposed pipeline for estimating the intact connectional morphometricity in three major steps: (1) construction of multi-view morphological networks, (2) learning of the intact multi-view similarity matrix, and (3) estimation of the ICBM using LME model.

Multi-view Morphological Network. Inspired by the foundational works of [7, 8], we define a morphological brain network $\mathbf {V}$ as a graph comprising a set of nodes, each node representing a brain ROI. The connection between two nodes quantifies the dissimilarity in shape between two ROIs i and j by computing the absolute difference between ROI-based average morphological measurements (e.g., mean curvature). By diversifying the morphological measurements, we generate a set of MBNs $\mathbf {\mathcal {M}_v}=\{V^1,V^2,\dots ,V^k\}$, each capturing a specific view of the morphological brain construct. Since each MBN can be defined as a symmetric matrix, we only vectorize the off-diagonal upper triangular part to generate a feature vector $\mathbf {F}^{k}_{s}$ for each subject s and each view k (Fig. 1-A).

Intact Morphological Similarity Learning. This step is the core of our framework as it describes the connectional similarity between the morphological views. Basically, we first propose to learn an intact space that represents the complementary information of multiple views. As reported in [10], an individual view is insufficient for learning, thus integrating multiple views is necessary to learn a comprehensive representation of the data. Given specific views $\mathbf {V^i}$ and $\mathbf {V^j}$ generated from the intact space $\mathbf {X}$, the view insufficiency can be expressed by $\mathbf {I}(\mathbf {X};\mathbf {V}^j | \mathbf {V}^i)$ that measures how much information is shared between the intact space $\mathbf {X}$ and the newly generated view $\mathbf {V^j}$ given the known view $\mathbf {V^i}$. Given, multiple views $\mathbf {\mathcal {M}_v}$ generated from the complete intact space $\mathbf {X}$, the information obtained to learn $\mathbf {X}$ is measured by:

$$\begin{aligned} \mathbf {I}(\mathbf {X}; {\mathbf {V}^1,\mathbf {V}^2,\dots ,\mathbf {V}^k}) = \sum _{i=1}^{k} \mathbf {I}(\mathbf {X};\mathbf {V}^{i-1},\mathbf {V}^{i-2},\dots ,\mathbf {V}^{1}) \end{aligned}$$

(1)

Thus, learning $\mathbf {X}$ can be formulated as a minimization problem based on Eq. 1 so that $\mathbf {X} = \min _{\mathbf {X}} L(X ; {V^1, V^k})$ where L(.) is the loss function l(.) over the samples on different views. Considering $\mathbf {W}^{k}$ a mapping function of a specific feature view $\mathbf {F}^k$ representing all subjects in the intact space $\mathbf {X}$, the intact space $\mathbf {X}$ learning is formulated as follows:

$$\begin{aligned} \min _{\mathbf {X},\mathbf {W}^{k}} \frac{1}{\mathbf {K}} \sum _{k=1}^{K} \parallel ^{2}_{F} + \lambda _{1}\parallel ^{2}_{F} \end{aligned}$$

(2)

where $\lambda _{1}\parallel ^{2}_{F}$ is a regularization term used to penalize the intact space $\mathbf {X}$ and $\lambda _{1}$ is a non-negative parameter.

Following the learning of the intact space $\mathbf {X}$, one can learn an intact similarity matrix $\mathbf {S}^{c}$ between subjects across views by maximizing its dependence with the intact space $\mathbf {X}$. This results in connecting the data points based on their locality –i.e., only the nearest neighbors observations of a specific point can be connected to this point rather than all other observations. Hence, the multi-view morphological similarity learning can be formulated as follow:

$$\begin{aligned} \min _{\mathbf {S}^{c}} \lambda _{2}\sum _{i=1}^{n}\sum _{j=1}^{n} \parallel _{1}\mathbf {S}_{ij}^{c} + \gamma \parallel ^{2}_F \end{aligned}$$

(3)

where $\gamma \parallel ^{2}_{F}$ is used to prevent $\mathbf {S}^{c}$ from converging to identity matrix. $\lambda _{2}$ and $\gamma$ are non-negative parameters. Additionally, in order to handle noisy samples, we adopted the $l_1$ distance instead of $l_2$.

Since the connectional similarity matrix $\mathbf {S}^{c}$ is derived from the intact connectomic space $\mathbf {X}$, we combine both models of Eqs. 2 and 3 into a joint alternating optimization framework where the learning of the intact space is influenced by the learning of the similarity matrix and vice versa:

$$\begin{aligned} \min _{\mathbf {X},\mathbf {W}^{k},\mathbf {S}^{c}} \frac{1}{K} \sum _{k=1}^{K} \parallel ^{2}_{F}+\lambda _{2} \sum _{i=1}^{n}\sum _{j=1}^{n} ||\mathbf {X}_{i} - \mathbf {X}_{j}||_1 \mathbf {S}_{ij}^{c} + \gamma \parallel ^{2}_{F} \end{aligned}$$

(4)

Intact Connectional Brain Morphometricity Estimation. Next, we propose to use the learned intact morphological similarity matrix $\mathbf {S}^{c}$ to estimate the intact connectional morphometricity. Specifically, we are using the Restricted Maximum Likelihood (ReML) [11] to fit the Linear Mixed Effect (LME) model described as follows:

$$\begin{aligned} \mathbf {y} = \mathbf {\Sigma } * \mathbf {f}_{e} + \mathbf {r}_{e} + \mathbf {\epsilon }, \end{aligned}$$

(5)

where $\mathbf {y}$ denotes the phenotype vector that describes the clinical state of samples (e.g., healthy or disordered subject), $\mathbf {\Sigma }$ is the covariance matrix that contains data of covariate variables such as age and gender, $\mathbf {f}_e$ is the fixed effect vector, $\mathbf {r}_e\sim N(0,v_{a} \mathbf {S}^c)$ is a random effect vector resulted from a zero-mean multivariate Gaussian distribution with a covariance matrix $\mathbf {S}^{c}$, and $\mathbf {\epsilon }$ denotes the noise vector with variance $v_{e}$. We then define the intact connectional brain morphometricity $m_{c}$ as:

$$\begin{aligned} m_{c} = \frac{v_a}{v_a+v_e} = \frac{v_a}{v_c} \end{aligned}$$

(6)

where $v_a$ is the variance captured by $\mathbf {S}^{c}$ and $v_c$ is the phenotypic variance. The proposed ICBM can thus described as the proportion of phenotypic variation that can be explained by morphological brain connectivity.

Fig. 2.

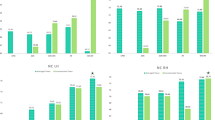
Intact connectional brain morphometricity (ICBM) estimates using three different combinations of brain four views: mean maximum principal curvature, mean cortical thickness, mean sulcal depth, mean of average curvature. (A) ICBM estimated while fixing the model parameters using the left hemisphere (LH). (B) ICBM estimated while fixing the model parameters using the right hemisphere (RH). Blue bars display ICBM for the LH and orange bars display ICBM for the RH.

3 Results and Discussion

Data Parameters. We evaluate the proposed framework on 341 subjects (155 ASD and 186 NC) from Autism Brain Imaging Data Exchange (ABIDE)¹, each represented using four morphological brain networks constructed using the following cortical measurements in the right and left hemispheres: mean maximum principal curvature, mean cortical thickness, mean sulcal depth, mean of average curvature. For more details about MBN construction strategy, we kindly refer the reader to [6, 8]. Three parameters were tuned using grid search: the dimension of the intact space, $\lambda _{2}$ is a non-negative trade-off parameter and $n_k$ is the number of nearest neighbor of a specific sample in ${\mathbf {X}}$. Specifically, using a grid search strategy we tuned one parameter by fixing the others using 5-fold cross-validation for the left and the right hemispheres, independently.

Estimating ICBM Using Different Combinations of Brain Network Views. Given our 4 brain network views, we first constructed all possible combinations using 2, 3, and 4 views, respectively. This allows to investigate the ICBM using different combinations of views as mapped onto the intact space. For instance, using two views, we generate $C_4^2$ ICBMs, each for a specific pair of views. Next, we report in Fig. 2 the average ICBM across all pairings along with the standard deviation. For comparing the estimated intact connectional brain morphometricity across hemispheres, we report in Fig. 2-A ICBM estimates when tuning the parameters for the left hemisphere (LH) and then fixing them for the right hemisphere (RH), whereas in Fig. 2-B, the ICBM parameters are tuned using the RH.

Figure 2 shows the association between multi-view morphological networks and ASD, assessed using the ICBM. Specifically, our preliminary analyses indicate that this particular clinical condition is not significantly morphometric since all intact connectional brain morphometricity estimates were smaller than 0.8 as explained in [4]. Figure 2 also shows that the right hemisphere (orange bars) is more morphometric than the left hemisphere on a ‘connectional’ level. This is in line with the findings of [7], where MBNs derived from the right hemisphere produced the best classification accuracy in distinguishing between ASD and NC subjects, which might indicate that right hemispheric connectional features have more discriminative power than the left hemisphere when leveraging high-order morphological information such as correlation between cortical measurements. We also note that both Fig. 2-A and B exhibit similar trends where the estimated of ICBM for RH is higher than LH for three- and four-view based combinations. As for two-view based combination, we note that ICBN is somewhat invariant across cortical hemispheres.

4 Conclusion

In this work, we introduced the intact connectional brain morphometricity, a metric that is learned using multi-view morphological brain network data for identified the connectional morphometric fingerprint of a specific trait (e.g., autism spectrum disorder). Our preliminary results revealed that autism is not significantly morphometric on a connectional level. However, we found that the right hemisphere is more morphometric than the left one. In our future work, we will evaluate the proposed ICBM learning framework on other disordered datasets (e.g., dementia). It would be also interesting to compare conventional brain morphometricity [4] to the connectional one.