Skip to main content
SpringerLink
Log in

Internet Bubble Examination with Mean-Variance Ratio

  • Reference work entry
  • First Online:
Handbook of Financial Econometrics and Statistics

Abstract

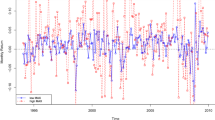
To evaluate the performance of the prospects X and Y, financial professionals are interested in testing the equality of their Sharpe ratios (SRs), the ratios of the excess expected returns to their standard deviations. Bai et al. (Statistics and Probability Letters 81, 1078–1085, 2011d) have developed the mean-variance-ratio (MVR) statistic to test the equality of their MVRs, the ratios of the excess expected returns to its variances. They have also provided theoretical reasoning to use MVR and proved that their proposed statistic is uniformly most powerful unbiased. Rejecting the null hypothesis infers that X will have either smaller variance or larger excess mean return or both leading to the conclusion that X is the better investment. In this paper, we illustrate the superiority of the MVR test over the traditional SR test by applying both tests to analyze the performance of the S&P 500 index and the NASDAQ 100 index after the bursting of the Internet bubble in the 2000s. Our findings show that while the traditional SR test concludes the two indices being analyzed to be indistinguishable in their performance, the MVR test statistic shows that the NASDAQ 100 index underperformed the S&P 500 index, which is the real situation after the bursting of the Internet bubble in the 2000s. This shows the superiority of the MVR test statistic in revealing short-term performance and, in turn, enables investors to make better decisions in their investments.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 849.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Hardcover Book
USD 549.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    We note that Bai et al. (2009a, b, 2011c) have also used the same framework as in 53.5.

  2. 2.

    The results of the one-sided test which draw a similar conclusion are available on request.

References

  • Agarwal, V., & Naik, N. Y. (2004). Risk and portfolios decisions involving hedge funds. Review of Financial Studies, 17, 63–98.

    Article  Google Scholar 

  • Bai, Z. D., Liu, H. X., & Wong, W. K. (2009a). Enhancement of the applicability of Markowitz’s portfolio optimization by utilizing random matrix theory. Mathematical Finance, 19, 639–667.

    Article  Google Scholar 

  • Bai, Z. D., Liu, H. X., & Wong, W. K. (2009b). On the markowitz mean-variance analysis of self-financing portfolios. Risk and Decision Analysis, 1, 35–42.

    Google Scholar 

  • Bai, Z. D., Wong, W. K., & Zhang, B. Z. (2010). Multivariate linear and non-linear causality tests. Mathematics and Computers in Simulation, 81, 5–17.

    Article  Google Scholar 

  • Bai, Z. D., Li, H., Liu, H. X., & Wong, W. K. (2011a). Test statistics for prospect and markowitz stochastic dominances with applications. Econometrics Journal, 14, 278–303.

    Article  Google Scholar 

  • Bai, Z. D., Li, H., Wong, W. K., & Zhang, B. Z. (2011b). Multivariate causality tests with simulation and application. Statistics and Probability Letters, 81, 1063–1071.

    Article  Google Scholar 

  • Bai, Z. D., Liu, H. X., & Wong, W. K. (2011c). Asymptotic properties of eigenmatrices of a large sample covariance matrix. Annals of Applied Probability, 21, 1994–2015.

    Article  Google Scholar 

  • Bai, Z. D., Wang, K. Y., & Wong, W. K. (2011d). Mean-variance ratio test, a complement to coefficient of variation test and Sharpe ratio test. Statistics and Probability Letters, 81, 1078–1085.

    Article  Google Scholar 

  • Bai, Z. D., Hui, Y. C., Wong, W. K., & Zitikis, R. (2012). Evaluating prospect performance: Making a case for a non-asymptotic UMPU test. Journal of Financial Econometrics, 10(4), 703–732.

    Google Scholar 

  • Baker, M., & Stein, J. C. (2004). Market liquidity as a sentiment indicator. Journal of Financial Markets, 7, 271–300.

    Article  Google Scholar 

  • Broll, U., Wahl, J. E., & Wong, W. K. (2006). Elasticity of risk aversion and international trade. Economics Letters, 91, 126–130.

    Article  Google Scholar 

  • Broll, U., Egozcue, M., Wong, W. K., & Zitikis, R. (2010). Prospect theory, indifference curves, and hedging risks. Applied Mathematics Research Express, 2010, 142–153.

    Google Scholar 

  • Cadsby, C. B. (1986). Performance hypothesis testing with the Sharpe and Treynor measures: A comment. Journal of Finance, 41, 1175–1176.

    Article  Google Scholar 

  • Chan, C. Y., de Peretti, C., Qiao, Z., & Wong, W. K. (2012). Empirical test of the efficiency of UK covered warrants market: Stochastic dominance and likelihood ratio test approach. Journal of Empirical Finance, 19, 162–174.

    Article  Google Scholar 

  • Chen, S. X. (2008). Nonparametric estimation of expected shortfall. Journal of Financial Econometrics, 6, 87–107.

    Article  Google Scholar 

  • Egozcue, M., & Wong, W. K. (2010). Gains from diversification on convex combinations: A majorization and stochastic dominance approach. European Journal of Operational Research, 200, 893–900.

    Article  Google Scholar 

  • Egozcue, M., Fuentes García, L., Wong, W. K., & Zitikis, R. (2011). Do investors like to diversify? A study of Markowitz preferences. European Journal of Operational Research, 215, 188–193.

    Article  Google Scholar 

  • Eling, M., & Schuhmacher, F. (2007). Does the choice of performance measure influence the evaluation of hedge funds? Journal of Banking and Finance, 31, 2632–2647.

    Article  Google Scholar 

  • Fong, W. M., Wong, W. K., & Lean, H. H. (2005). International momentum strategies: A stochastic dominance approach. Journal of Financial Markets, 8, 89–109.

    Article  Google Scholar 

  • Fong, W. M., Lean, H. H., & Wong, W. K. (2008). Stochastic dominance and behavior towards risk: The market for internet stocks. Journal of Economic Behavior and Organization, 68, 194–208.

    Article  Google Scholar 

  • Gasbarro, D., Wong, W. K., & Zumwalt, J. K. (2007). Stochastic dominance analysis of iShares. European Journal of Finance, 13, 89–101.

    Article  Google Scholar 

  • Gregoriou, G. N., & Gueyie, J. P. (2003). Risk-adjusted performance of funds of hedge funds using a modified Sharpe ratio. Journal of Wealth Management, 6, 77–83.

    Article  Google Scholar 

  • Hanoch, G., & Levy, H. (1969). The efficiency analysis of choices involving risk. Review of Economic Studies, 36, 335–346.

    Article  Google Scholar 

  • Jobson, J. D., & Korkie, B. (1981). Performance hypothesis testing with the Sharpe and Treynor measures. Journal of Finance, 36, 889–908.

    Article  Google Scholar 

  • Lam, K., Liu, T., & Wong, W. K. (2010). A pseudo-Bayesian model in financial decision making with implications to market volatility, under- and overreaction. European Journal of Operational Research, 203, 166–175.

    Article  Google Scholar 

  • Lam, K., Liu, T., & Wong, W. K. (2012). A new pseudo Bayesian model with implications to financial anomalies and investors’ behaviors. Journal of Behavioral Finance, 13(2), 93–107.

    Article  Google Scholar 

  • Lean, H. H., Phoon, K. F., & Wong, W. K. (2012). Stochastic dominance analysis of CTA funds. Review of Quantitative Finance and Accounting, doi:10.1007/s11156-012-0284-1.

    Google Scholar 

  • Leung, P. L., & Wong, W. K. (2008). On testing the equality of the multiple Sharpe ratios, with application on the evaluation of iShares. Journal of Risk, 10, 1–16.

    Google Scholar 

  • Li, C. K., & Wong, W. K. (1999). Extension of stochastic dominance theory to random variables. RAIRO Recherche Opérationnelle, 33, 509–524.

    Google Scholar 

  • Lintner, J. (1965). The valuation of risky assets and the selection of risky investment in stock portfolios and capital budgets. Review of Economics and Statistics, 47, 13–37.

    Article  Google Scholar 

  • Lo, A. (2002). The statistics of Sharpe ratios. Financial Analysis Journal, 58, 36–52.

    Article  Google Scholar 

  • Ma, C., & Wong, W. K. (2010). Stochastic dominance and risk measure: A decision-theoretic foundation for VaR and C-VaR. European Journal of Operational Research, 207, 927–935.

    Article  Google Scholar 

  • Markowitz, H. M. (1952). Portfolio selection. Journal of Finance, 7, 77–91.

    Google Scholar 

  • Matsumura, E. M., Tsui, K. W., & Wong, W. K. (1990). An extended multinomial-Dirichlet model for error bounds for dollar-unit sampling. Contemporary Accounting Research, 6, 485–500.

    Article  Google Scholar 

  • Memmel, C. (2003). Performance hypothesis testing with the Sharpe ratio. Finance Letters, 1, 21–23.

    Google Scholar 

  • Ofek, E., & Richardson, M. (2003). A survey of market efficiency in the internet sector. Journal of Finance, 58, 1113–1138.

    Article  Google Scholar 

  • Perkins, A. B., & Perkins, M. C. (1999). The internet bubble: Inside the overvalued world of high-tech stocks. New York: Harper Business.

    Google Scholar 

  • Schultz, P., & Zaman, M. (2001). Do the individuals closest to internet firms believe they are overvalued? Journal of Financial Economics, 59, 347–381.

    Article  Google Scholar 

  • Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance, 19, 425–442.

    Google Scholar 

  • Sharpe, W. F. (1966). Mutual funds performance. Journal of Business, 39, 119–138.

    Article  Google Scholar 

  • Sortino, F. A., & van der Meer, R. (1991). Downside risk. Journal of Portfolio Management, 17, 27–31.

    Article  Google Scholar 

  • Sriboonchitta, S., Wong, W. K., Dhompongsa, D., & Nguyen, H. T. (2009). Stochastic dominance and applications to finance, risk and economics. Boca Raton: Chapman and Hall/CRC.

    Google Scholar 

  • Statman, M. (2002). Lottery players/stock traders. Journal of Financial Planning, 14–21.

    Google Scholar 

  • Tobin, J. (1958). Liquidity preference as behavior towards risk. Review of Economic Studies, 25, 65–86.

    Article  Google Scholar 

  • Wong, W. K. (2006). Stochastic dominance theory for location-scale family. Journal of Applied Mathematics and Decision Sciences, 2006, 1–10.

    Article  Google Scholar 

  • Wong, W. K. (2007). Stochastic dominance and mean-variance measures of profit and loss for business planning and investment. European Journal of Operational Research, 182, 829–843.

    Article  Google Scholar 

  • Wong, W. K., & Bian, G. (2000). Robust Bayesian inference in asset pricing estimation. Journal of Applied Mathematics & Decision Sciences, 4, 65–82.

    Article  Google Scholar 

  • Wong, W. K., & Chan, R. (2004). The estimation of the cost of capital and its reliability. Quantitative Finance, 4, 365–372.

    Article  Google Scholar 

  • Wong, W. K., & Chan, R. (2008). Markowitz and prospect stochastic dominances. Annals of Finance, 4, 105–129.

    Article  Google Scholar 

  • Wong, W. K., & Li, C. K. (1999). A note on convex stochastic dominance theory. Economics Letters, 62, 293–300.

    Article  Google Scholar 

  • Wong, W. K., & Ma, C. (2008). Preferences over location-scale family. Economic Theory, 37, 119–146.

    Article  Google Scholar 

  • Wong, W. K., & Miller, R. B. (1990). Analysis of ARIMA-noise models with repeated time series. Journal of Business and Economic Statistics, 8, 243–250.

    Google Scholar 

  • Wong, W. K., Chew, B. K., & Sikorski, D. (2001). Can P/E ratio and bond yield be used to beat stock markets? Multinational Finance Journal, 5, 59–86.

    Google Scholar 

  • Wong, W. K., Manzur, M., & Chew, B. K. (2003). How rewarding is technical analysis? Evidence from Singapore stock market. Applied Financial Economics, 13, 543–551.

    Article  Google Scholar 

  • Wong, W. K., Thompson, H. E., Wei, S., & Chow, Y. F. (2006). Do winners perform better than losers? A stochastic dominance approach. Advances in Quantitative Analysis of Finance and Accounting, 4, 219–254.

    Article  Google Scholar 

  • Wong, W. K., Phoon, K. F., & Lean, H. H. (2008). Stochastic dominance analysis of Asian hedge funds. Pacific-Basin Finance Journal, 16, 204–223.

    Article  Google Scholar 

  • Wong, W. K., Wright, J. A., Yam, S. C. P., & Yung, S. P. (2012). A mixed Sharpe ratio. Risk and Decision Analysis, 3(1–2), 37–65.

    Google Scholar 

Download references

Acknowledgment

We would like to thank the editor C.-F. Lee for his substantive comments that have significantly improved this manuscript. The third author would also like to thank Professors Robert B. Miller and Howard E. Thompson for their continuous guidance and encouragement. The research is partially supported by grants from North East Normal University, National University of Singapore, Hong Kong Baptist University and the Research Grants Council of Hong Kong. The first author thanks the financial support from NSF China grant 11171057, Program for Changjiang Scholars and Innovative Research Team in University, and the Fundamental Research Funds for the Central Universities and NUS grant R-155-000-141-112.

Author information

Authors and Affiliations

  1. KLAS MOE & School of Mathematics and Statistics, Northeast Normal University, Changchun, China

    Zhidong D. Bai

  2. Department of Statistics and Applied Probability, National University of Singapore, Singapore, Singapore

    Zhidong D. Bai

  3. Department of Economics, Hong Kong Baptist University, Kowloon, Hong Kong

    Wing-Keung Wong

  4. School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, China

    Yongchang C. Hui

Authors
  1. Zhidong D. Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yongchang C. Hui
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wing-Keung Wong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhidong D. Bai .

Editor information

Editors and Affiliations

  1. Department of Finance and Economics, Rutgers Business School, Rutgers, The State University of New Jersey, Piscataway, New Jersey, USA

    Cheng-Few Lee

  2. Center for PBBEF Research, North Brunswick, New Jersey, USA

    John C. Lee

Rights and permissions

Reprints and permissions

Copyright information

© 2015 Springer Science+Business Media New York

About this entry

Cite this entry

Bai, Z.D., Hui, Y.C., Wong, WK. (2015). Internet Bubble Examination with Mean-Variance Ratio. In: Lee, CF., Lee, J. (eds) Handbook of Financial Econometrics and Statistics. Springer, New York, NY. https://doi.org/10.1007/978-1-4614-7750-1_53

Download citation

  • DOI: https://doi.org/10.1007/978-1-4614-7750-1_53

  • Published:

  • Publisher Name: Springer, New York, NY

  • Print ISBN: 978-1-4614-7749-5

  • Online ISBN: 978-1-4614-7750-1

  • eBook Packages: Business and Economics

Publish with us

Policies and ethics

Search

Navigation