Abstract
In this study, we address issues arising in system identification-based plant modeling for the purpose of tuning PID controllers. We discuss some of the more celebrated tuning methods and make an attempt to anticipate future directions of identification procedures in the effort to provide reliable answers to more involved problems. The algorithmic progression of the different methods starts with easy-to-estimate, minimal information about the plant, in the form of a single frequency point in the Nyquist plot or a couple of parameters of the step response, aiming to produce the tuning parameters with back-of-the-envelope calculations. High order general models from either first-principles modeling or system identification were then used in a variety of off-line or on-line optimization problems to produce optimal PID tunings, and were often converted to the always elusive set of quick calculations that could tune a PID controller in the field. Highest in complexity, are the most recent methods which involve maximal information about the plant, in the form of one or more nominal models and a description of uncertainty, and aim for a tuning that combines high performance, adequate robustness, and high reliability. The latter appears to be the key qualitative difference between early and late identification and controller tuning procedures, that is, the ability to provide a reliable tuning with minimal trial-and-error. An alternative implementation of the same concepts can be performed as a direct optimization of the PID parameters, that can be readily converted to an attractive on-line tuning application. Finally, employing more complex, min–max identification methods can safeguard against performance deterioration problems due to disturbances or poorly designed excitation, albeit with a significant increase in computational load and identification time.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
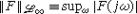 . If F is stable,
. If F is stable, 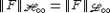 .
. - 2.
The Sensitivity crossover is related to the closed-loop crossover (Complementary Sensitivity) but it is better behaved in cases of right half-plane zeros near the desired bandwidth.
References
Astrom, K.J., Hagglund, T.: PID Controllers: Theory, Design, and Tuning, 2nd edn. ISA (1995)
Voda, A.A., Landau, I.D.: A method for the auto-calibration of PID controllers. Automatica 31(1), 41–53 (1995)
Harris, S., Mellichamp, D.: Controller tuning using optimization to meet multiple closed-loop criteria. AIChE J. 31(3), 484–487 (1985)
Schei, T.S.: Automatic tuning of PID controllers based on transfer function estimation. Automatica 30(12), 1983–1989 (1994)
Nishikawa, Y., Sannomiya, N., Ohta, T., Tanaka, H.: A method for auto-tuning of PID control parameters. Automatica 20(3), 321–332 (1984)
Tan, W., Liu, J., Chen, T., Marquez, H.: Comparison of some well-known PID tuning formulas. Comput. Chem. Eng. 30, 1416–1423 (2006)
Kristansson, B., Lennartson, B.: Evaluation and simple tuning of PID controllers with high-frequency robustness. J. Process Control 16, 91–102 (2006)
de Callafon, R.A., Van den Hof, P.M.J.: Control relevant identification for H ∞-norm based performance specifications. In: Proc. 34th CDC, pp. 3498–3503 (1995)
Gevers, M., Anderson, B.D.O., Codrons, B.: Issues in modeling for control. In: Proc. 1998 ACC, pp. 1615–1619 (1998)
Reinelt, W., Garulli, A., Ljung, L.: Comparing different approaches to model error modeling in robust identification. Automatica 38, 787–803 (2002)
Bombois, X., Gevers, M., Scorletti, G., Anderson, B.: Robustness analysis tools for an uncertainty set obtained by prediction error identification. Automatica 37(10), 1629–1636 (2001)
Gevers, M., Bombois, X., Codrons, B., Scorletti, G., Anderson, B.: Model validation for control and controller validation in a prediction error identification framework. Automatica 39(3), 403–427 (2003)
Rivera, D.E., Gaikwad, S.V.: Digital PID controller tuning using prefiltered ARX estimation. In: Proc. 31st CDC, pp. 68–69 (1992)
Grassi, E., Tsakalis, K.S.: PID controller tuning by frequency loop shaping. In: Proc. 35th CDC (1996)
Adusumilli, S., Rivera, D.E., Dash, S., Tsakalis, K.: Integrated MIMO identification and robust PID controller design through loop shaping. In: Proc. 1998 ACC, pp. 1230–1234 (1998)
Grimble, M.J.:
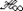 controllers with a PID structure. J. Dyn. Syst. Meas. Control 112, 325–336 (1990)
controllers with a PID structure. J. Dyn. Syst. Meas. Control 112, 325–336 (1990)
Panagopoulos, H., Astrom, K.J., Hagglund, T.: Design of PID controllers based on constrained optimization. IEE Proc., Control Theory Appl. 149(1), 32–40 (2002)
Astrom, K.J., Panagopoulos, H., Hagglund, T.: Design of PI controllers based on nonconvex optimization. Automatica 34(5), 585–601 (1998)
Ender, D.: Process control performance: Not as good as you think. In: Control Engineering, pp. 180–190 (1993)
Gaikwad, S.V., Dash, S.K., Tsakalis, K.S., Stein, G.: Auto-tuning controller using loop-shaping. U.S. Patent No. 7,024,253, 4 April 2006
Grassi, E., Tsakalis, K., Dash, S., Gaikwad, S.V., MacArthur, W., Stein, G.: Integrated identification and PID controller tuning by frequency loop-shaping. IEEE Trans. Control Syst. Technol. 9(2), 285–294 (2001)
Gevers, M.: Identification for control: from early achievements to the revival of experiment design. Eur. J. Control 11, 1–18 (2005)
Hjalmarsson, H.: From experiment to closed-loop control. Automatica 41, 393–438 (2005)
Lee, W.S., Anderson, B.D.O., Kosut, R.L., Mareels, I.M.Y.: A new approach to adaptive robust control. Int. J. Adapt. Control Signal Process. 7(3), 183–211 (1993)
Lee, W.S., Anderson, B.D.O., Mareels, I.M.Y., Kosut, R.L.: On some key issues in the windsurfer approach to adaptive robust control. Automatica 31(11), 1619–1636 (1995)
Ziegler, J.G., Nichols, N.B.: Optimum settings for automatic controllers. Trans. Am. Soc. Mech. Eng. 64(11), 759–768 (1942)
Astrom, K.J., Hagglund, T.: A frequency domain method for automatic tuning of simple feedback loops. In: Proc. 23rd IEEE Conf. Dec. Contr., Las Vegas, NV, December 1984, pp. 299–304 (1984)
Gaikwad, S., Dash, S., Stein, G.: Auto-tuning PID using loop-shaping ideas. In: Proc. 1999 IEEE Intl. Conf. on Control Applications, Hawaii, August 1999, pp. 589–593 (1999)
Grassi, E., Tsakalis, K.S., Dash, S., Gaikwad, S.V., Stein, G.: Adaptive/self-tuning PID control by frequency loop-shaping. In: Proc. 39th IEEE Conf. on Decision and Control, Sydney, December 2000, pp. 1099–1101 (2000)
Jun, M., Safonov, M.G.: Automatic PID tuning: An application of unfalsified control. In: Proc. IEEE CCA/CACSD, Kohala Coast Island of Hawaii, 22–27 August 1999, pp. 328–333 (1999)
Morse, A.S., Mayne, D.Q., Goodwin, G.C.: Application of hysteresis switching in parameter adaptive control. IEEE Trans. Autom. Control 37(9), 1343–1354 (1992)
Safonov, M.G., Tsao, T.: The unfalsified control concept and learning. IEEE Trans. Autom. Control 42(6), 843–847 (1997)
Hespanha, J.P., Liberzon, D., Morse, A.S.: Hysteresis-based switching algorithms for supervisory control of uncertain systems. Automatica 39(2), 263–272 (2003)
Dehghani, A., Anderson, B.D.O., Lanzon, A.: Unfalsified adaptive control: a new controller implementation and some remarks. In: Proc. of the European Control Conference 2007, Kos, Greece, 2–5 July 2007, pp. 709–716 (2007)
Stefanovic, M., Safonov, M.G.: Safe adaptive switching control: Stability and convergence. IEEE Trans. Autom. Control 53(9), 2012–2021 (2008)
Khalil, H.: Nonlinear Systems, 3rd edn. Prentice Hall, Upper Saddle River (2002)
Francis, B.: A Course in H ∞ Control Theory. Springer, Berlin (1987)
Barnes, T.J.D., Wang, L., Cluett, W.R.: A frequency domain design method for PID controllers. In: Proc. Amer. Contr. Conf., San Francisco, pp. 890–894 (1993)
Wang, L., Barnes, T.J.D., Cluett, W.R.: A new frequency domain design method for PID controllers. IEE Proc., Control Theory Appl. 142(4), 265–271 (1995)
Rivera, D.E., Morari, M., Skogestad, S.: Internal model control 4. PID controller design. Ind. Eng. Chem. Process Des. Dev. 25, 252–265 (1986)
Grassi, E., Tsakalis, K.: PID controller tuning by frequency loop-shaping: Application to diffusion furnace temperature control. IEEE Trans. Control Syst. Technol. 8(5), 842–847 (2000)
Ljung, L.: System Identification. Prentice Hall, New York (1987)
Vidyasagar, M.: Nonlinear Systems Analysis, 2nd edn. Prentice Hall, New York (1987)
Safonov, M.G.: Stability margins of diagonally perturbed multivariable feedback systems. Proc. IEEE 129(6), 251–256 (1982)
Adusumilli, S., Rivera, D.E., Dash, S., Tsakalis, K.: Integrated identification and robust PID controller design through loop shaping for multi-input multi-output processes. In: Proc. ACC, June 1998, pp. 1230–1234 (1998)
McFarlane, D.C., Glover, K.: A loop shaping design procedure using H ∞ synthesis. IEEE Trans. Autom. Control 37(6), 759–769 (1992)
Alexander, C., Tsakalis, K.S.: Control of an inverted pendulum: A classical experiment revisited. In: Proc. of 1995 Soc. for Comp. Sim. Western Multi-Conference, Las Vegas, NV, January 1995
Papadopoulos, A., Tsakalis, K.: Adaptive control of an inverted pendulum. In: Proc. 23rd IASTED int’l conf. on modeling, identification and control, Grindelwald, Switzerland, February 2004, vol. 412-051, pp. 461–466 (2004)
Limanond, S., Si, J., Tsakalis, K.S.: Monitoring and control of semiconductor manufacturing processes. IEEE Control Syst. 18(6), 46–58 (1998)
Tsakalis, K.S., Stoddard, K.D.: Integrated identification and control for diffusion/CVD furnaces. In: Proc. 6th IEEE Int. Conference on Emerging Technologies and Factory Automation, Los Angeles, September 1997, pp. 514–519 (1997)
Tsakalis, K., Flores-Godoy, J.-J., Stoddard, K.: Temperature control of diffusion/CVD furnaces using robust multivariable loop-shaping techniques. In: Proc. 38th Conf. Decision and Contr., Phoenix, AZ, December 1999, vol. 4, pp. 4192–4197 (1999)
McCormack, A.S., Godfrey, K.R.: Rule-Based autotuning based on frequency domain identification. IEEE Trans. Control Syst. Technol. 6(1), 43–61 (1998)
Fox, P.D., Godfrey, K.R.: Multiharmonic perturbations for nonparametric autotuning. IEE Proc., Control Theory Appl. 146, 1–8 (1999)
Zhu, Y.-C.: Identification and control of MIMO industrial processes: An integration approach. Ph.D. dissertation. Eindhoven Univ. of Technology, Dept. of Electr. Engr., The Netherlands (1990)
Ioannou, P.A., Sun, J.: Robust Adaptive Control. Prentice Hall, New York (1996)
Grassi, E., Tsakalis, K., Dash, S., Gaikwad, S., Stein, G.: Adaptive/self-tuning PID control by frequency loop-shaping. In: Proc. IEEE 39th Conf. Decision and Control, Sydney, 12–15 December 2000, vol. 2, pp. 1099–1101 (2000)
Krause, J.M., Khargonekar, P.P.: Robust parameter adjustment. In: Proc. 1988 ACC, Atlanta, GA, pp. 331–336 (1988)
Tsakalis, K., Dash, S.: Adaptive PID control using Filter-Banks and frequency loop shaping. In: European Control Conference 2007, Kos, Greece, 2–5 July 2007, pp. 1340–1347 (2007)
Astrom, K.J., Rundkwist, L.: Integrator wind up and how to avoid it. In: Proc. 1989 ACC, pp. 1693–1698 (1989)
Teel, A.R., Kapoor, N.: The L-2 anti-windup problem: its definition and solution. In: Proc. of Europ. Contr. Conf. (1997)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag London Limited
About this chapter
Cite this chapter
Tsakalis, K.S., Dash, S. (2012). Identification for PID Control. In: Vilanova, R., Visioli, A. (eds) PID Control in the Third Millennium. Advances in Industrial Control. Springer, London. https://doi.org/10.1007/978-1-4471-2425-2_10
Download citation
DOI: https://doi.org/10.1007/978-1-4471-2425-2_10
Publisher Name: Springer, London
Print ISBN: 978-1-4471-2424-5
Online ISBN: 978-1-4471-2425-2
eBook Packages: EngineeringEngineering (R0)


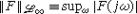 . If F is stable,
. If F is stable, 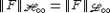 .
.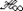 controllers with a PID structure. J. Dyn. Syst. Meas. Control 112, 325–336 (1990)
controllers with a PID structure. J. Dyn. Syst. Meas. Control 112, 325–336 (1990)