Abstract
With the aid of Volterra multiplier, we study ecological equations for both tree system and cycle system. We obtain a set of sufficient conditions for the ultimate boundedness to nonautonomous n-dimensional Lotka–Volterra tree systems with continuous time delay. The criteria are applicable to cooperative model, competition model, and predator–prey model. As to cycle system, we consider a three-dimensional predator–prey Lotka–Volterra system. In order to get a condition under which the system is globally asymptotic stable, we obtain a Volterra multiplier, so that in a parameter region the system is with the Volterra multiplier it is globally stable. We have also proved that in regions in which the condition is not satisfied, the system is unstable or at least it is not globally stable. Therefore, we say that the three-dimensional cycle system is with global bifurcation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
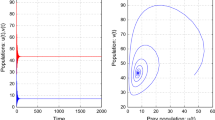
Similar content being viewed by others
References
K. Gopalsamy, Exchange of equilibria in two species Lotka–Volterra competition models, Journal of Australian Mathematical Society Series B, 24, 160–170, (1982)
Xinhua Ji, The existence of globally stable equilibria of n-dimensional Lotka–Volterra systems, Applicable Analysis, 62(1), 11–28, (1996)
Xue-Zhi Li, G. Gupur and Xin-Hua Ji, The criteria of ultimate boundedness for nonautonomous Lotka–Volterra tree systems, Applied Mathematics Letters, 14(4), 469–476, (2001)
Xue-Zhi Li, Chun-Lei Tang and Xin-Hua Ji, Global asymptotic stability for Lotka–Volterra tree systems, Differential Equations and Dynamical Systems, 8.2, 141–149, (2000)
Fen-guo Peng and Zhi-ming Zhou, Global stability for 3-dimensional prey–predator Volterra systems with loop, Journal of Biomathematics, 3(2), 159–170, (1988)
F. Solimano and E.Beretta, Existence of a globally asymptotical stable equilibrium in Volterra models with continuous time delay, Journal of Mathematical Biology, 18, 93–102, (1983)
Y. Takeuchi, Global dynamical properties of Lotka–Volterra system, World Scientific, Singapore (1996)
A. Wörz-Busekros, Global stability in ecological systems with continuous time delay, SIAM Journal of Applied Mathematics, 35, 123–134, (1978)
Acknowledgements
This research was supported by the Deutsche Forschungsgemeinschaft.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer Science+Business Media, LLC
About this chapter
Cite this chapter
Gürlebeck, K., Ji, X. (2011). Lotka–Volterra System with Volterra Multiplier. In: Arabnia, H., Tran, QN. (eds) Software Tools and Algorithms for Biological Systems. Advances in Experimental Medicine and Biology, vol 696. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-7046-6_66
Download citation
DOI: https://doi.org/10.1007/978-1-4419-7046-6_66
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4419-7045-9
Online ISBN: 978-1-4419-7046-6
eBook Packages: Biomedical and Life SciencesBiomedical and Life Sciences (R0)