Abstract
Computational models based on the structural and functional properties of the human brain have seen impressive gains since the mid-1980s, owing to significant discoveries in neuroscience and advancements in computing technology. Among these models, cortical algorithms (CAs) have emerged as a biologically inspired approach, modeled after the human visual cortex, which stores sequences of patterns in an invariant form and which recalls those patterns autoassociatively. This chapter details the structure and mathematical formulation of CA. We then present a case study of CA generalization accuracy in identifying isolated Arabic speech using an entropy-based weight update.
If you just have a single problem to solve, then fine, go ahead and use a neural network. But if you want to do science and understand how to choose architectures, or how to go to a new problem, you have to understand what different architectures can and cannot do.
You have full access to this open access chapter, Download chapter PDF
Keywords
- Mean Square Error
- Speech Recognition
- Speech Recognition System
- Machine Learn Repository
- Handwritten Digit
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
—Marvin MinskyFootnote 1
Computational models inspired by the structural and functional properties of the human brain have seen impressive gains since the mid-1980s, owing to significant discoveries in neuroscience and advancements in computing technology. Among these models, cortical algorithms (CAs) have emerged as a biologically inspired approach, modeled after the human visual cortex, which stores sequences of patterns in an invariant form and recalls those patterns autoassociatively. This chapter details the structure and mathematical formulation of CA then presents a case study of CA generalization accuracy in identifying isolated Arabic speech using an entropy-based weight update.
Cortical Algorithm Primer
Initially developed by Edelman and Mountcastle (1978), and inspired by the visual human cortex, CAs are positioned to be superior to the early generations of artificial neural networks (ANNs), which do not use temporal and spatial relationships in data for building machine learning models.
The CA model consists of a multilayered network, with the cortical column as the basic structure. The network is trained in a two-stage manner: the first learning stage is unsupervised and trains the columns to identify independent features from the patterns occurring; the second stage relies on supervised feedback learning to create invariant representations.
Cortical Algorithm Structure
The human brain is a six-layered structure consisting of a very large number of neurons strongly connected via feedforward and feedback connections. An important property of the neocortex is its structural and functional uniformity: all units in the network seem similar, and they perform the same basic operation. Like this brain architecture, CA architecture has minicolumns of varying thickness (Edelman and Mountcastle 1978). A minicolumn is a group of neurons that share the same receptive field: neurons belonging to a minicolumn are associated with the same sensory input region. The minicolumn is the basic structure in a cortical network, in contrast to neurons in a classical ANN. An association of minicolumns is called a hypercolumn or layer (in what follows, the terms column and minicolumn are used interchangeably). Connections in a CA network occur in two directions: horizontally, between columns in the same layer, and vertically, between columns of consecutive layers. Although connections between nonconsecutive layers are present in the human cortex, these connections are omitted in CA, for the sake of simplicity.
Figure 8-1 displays a representation of a cortical network. The lateral inhibiting connections are not shown explicitly in the figure because their functionality is not physical; that is, these connections do not represent data propagated between neurons, but serve as a means of communication between the columns.
The notation adopted hereafter is given in Figure 8-2, where  represents the weight of the connection between the jth neuron of the ith column of layer r and the kth column of the previous layer (r-1) during the training epoch t. Bold variables stand for vector entities, underlined variables represent matrices, and italic variables represent scalar entities.
represents the weight of the connection between the jth neuron of the ith column of layer r and the kth column of the previous layer (r-1) during the training epoch t. Bold variables stand for vector entities, underlined variables represent matrices, and italic variables represent scalar entities.
During the learning process a connection is disabled by assigning to it a zero weight. If the network is fully connected, each neuron j in the column is connected to all the columns in the previous layer. All connections are elastic; that is, if a connection is disabled during the feedforward process, it can be restored during the feedback learning, and vice versa.
The weight matrix representing the state of a column composed of M nodes during the training epoch t is defined by

The weight vector
 of the connections entering neuron j of column i in layer r, composed of L
r columns, is given by
of the connections entering neuron j of column i in layer r, composed of L
r columns, is given by

where  is the number of columns in the layer (r-1), L
r represents the number of columns in the layer r, and the superscript ' stands for the transpose operator.
is the number of columns in the layer (r-1), L
r represents the number of columns in the layer r, and the superscript ' stands for the transpose operator.
Expanding  yields
yields

The output vector Z r,t of layer r for epoch t is given by

where  is the output of column i in the layer for the same training epoch.
is the output of column i in the layer for the same training epoch.
Considering the output of a neuron to be the result of the nonlinear activation function f(.), in response to the weighted sum of the connections entering the neuron, the output of the column is defined as the sum of the outputs of the neurons constituting the column.
 is the output of the jth neuron of the ith column in the rth layer at the training epoch t, given by
is the output of the jth neuron of the ith column in the rth layer at the training epoch t, given by

 is the output of the jth neuron constituting the ith column of the rth layer, and
is the output of the jth neuron constituting the ith column of the rth layer, and  is defined by
is defined by

where T is a tolerance parameter empirically selected and constant for all epochs and columns. It is assumed that all weights are normalized and bounded between –1 and 1.
The nonlinear activation function is analogous to the propagation of the action potential through an axon in the neural system.
Training of Cortical Algorithms
Connectivity within the columns is modeled through the value of the synaptic weights. Initially, there is no specific connectivity between cortical columns. It is assumed that the network is fully connected before training. Also, all synaptic weights are initialized to random values that are very close to 0 to avoid preference to any particular pattern.
The training process, as introduced by Edelman and Mountcastle (1978) and developed further by Hashmi (2010), is described in the following sections, according to its main phases: unsupervised feedforward, supervised feedback, and weight update.
Unsupervised Feedforward
Feedforward learning trains columns to identify features via random firing and repeated exposure. When a pattern is presented, the input is propagated through the network. Each column has a small probability of firing, which means that most of the columns in a particular layer stay inactive. When the random firing of a particular column coincides with a particular input pattern, this activation is enforced. In other words, when activation is enforced, the column firing strengthens its weights, according to the strengthening weight update rule. At the same time, the column firing inhibits neighboring columns in the same layer from firing by weakening the weights, as presented in the inhibiting update rule.
The weight update rules are as follows:
-
Inhibiting:

-
Strengthening:

where Ω( ) is given by
) is given by

and where ρ is a tuning parameter, and ε is the firing threshold chosen empirically to be constant for all epochs and columns.
With repeated exposure the network learns to extract certain features of the input data, and the columns learn to fire for specific patterns. Layers in the network extract aspects of the input in increasing complexity. Thus, lower layers detect simple features, whereas higher stages learn concepts and more complex abstractions of the data.
Supervised Feedback
Feedforward learning trains columns to identify features of the data, such that the hierarchical network starts to recognize patterns. When the network is exposed to a variation of a pattern that is quite different from the previous one, the top layer of columns that are supposed to fire for that pattern do not, and only some of the columns in the hierarchy may fire, which leads to a misclassification. Through the CA feedback mechanism, the error occurring at the top layer generates a feedback signal that forces the column firing for the original pattern to fire, while inhibiting the column that is firing for the variation. Over multiple exposures the top layer should reach the desired firing scheme (also called stable activation). More specifically, designated columns in the top layer learn to fire for a particular pattern. Once the columns start to give a stable activation for pattern variations, the feedback signal is propagated back to the previous layers. Each layer is then trained until a convergence criterion, expressed as an error term in function of the actual output, and a desired output (firing scheme) are reached. The feedback signal is sent to the preceding layers only once the error in the layer concerned converges to a value below a certain, predefined tolerance threshold. The excitatory and inhibiting signals follow the same update rules as for the feedforward learning.
When used for the feedback learning of the network, CA can be summarized by the following steps:
-
1.
Following the feedforward unsupervised batch learning (i.e., after the training data are entirely propagated through the network), a desired output scheme per layer is formed by averaging the column outputs. If
 is the output of the ith column in the rth layer of the network for a certain training instance denoted by k and given N instances in total; the desired output for this particular column
is the output of the ith column in the rth layer of the network for a certain training instance denoted by k and given N instances in total; the desired output for this particular column  is given by:
is given by:

-
2.
Starting with the last layer, compare the measured output of each column as a response to each instance k,
 with the desired value of
with the desired value of  . If the desired output of a column is a firing state, whereas the actual is different, the column is strengthened (see Equation 8-8; the column is inhibited (see Equation 8-7) if the opposite occurs (i.e., if the actual output is firing, whereas a nonfiring state is desired).
. If the desired output of a column is a firing state, whereas the actual is different, the column is strengthened (see Equation 8-8; the column is inhibited (see Equation 8-7) if the opposite occurs (i.e., if the actual output is firing, whereas a nonfiring state is desired). -
3.
Repeat step 2 until the error threshold is met.
-
4.
Follow the same procedure for the previous layers, one layer at a time.
Weight Update
In CA, good accuracy is taxed with computationally expensive and lengthy training. This cost is mainly due to the computation of the exponential function invoked during the weight update process for each neuron while the weights of the network are learned.
For a particular node  , Equation 8-8 may be written as:
, Equation 8-8 may be written as:

Here, α, β, and δ are variables that depend on the training epoch as well as the column considered; therefore, a suitable nomenclature would be in the form  . For the sake of simplicity, one can omit the subscripts and superscripts for these variables, referring to Ω(
. For the sake of simplicity, one can omit the subscripts and superscripts for these variables, referring to Ω( ) as Ω.
) as Ω.
As demonstrated in Equation 8-11, the parameters of the exponential weight update rule—α, β, δ, Ω, and T—depend on the state of the column considered. Therefore, it can be inferred that the strengthening rule is a family of exponential functions with varying parameters for each column. The update of a column requires the computation of the exponential function for each of the nodes—hence, the lengthy training.
Figure 8-3 shows a plot of θ, with respect to the value of the neuron weight for a random node.
The computational cost involved in the strengthening rule also comes from the calculation of the exponential function. For example, MATLAB software uses the binomial theorem (see Equation 8-12) to compute the approximate value of an exponential, and this approximation is computed up to orders ranging from 5 to 10 (Mohler 2011):

The number of operations required to compute the exponential function is summarized in Table 8-1.
The workflow for CA training is displayed in Figure 8-4.
Experimental Results
Experimental results for various pattern recognition databases obtained from the University of California, Irvine, Machine Learning Repository (Bache and Lichman 2013) show CA superior performance, as detailed for the following datasets:
-
Letter Recognition dataset: This dataset consists of a collection of 20,000 black-and-white images to be classified as one of the 26 capital letters of the English alphabet (Slate 1991). Each instance is represented by a set of 16 features of integer type, normalized into a range of 0-15 representing aspects of the image, such as horizontal and vertical position, and width and length. The best accuracy reported for this dataset is 97.58 percent (Bagirov and Ugon 2011).
-
Image Segmentation dataset: This dataset is collection of images sized 3 × 3 each, represented by 19 attributes describing features of the image, such as average intensity, saturation, and hue (Vision Group 1990). The dataset is divided into a training set consisting of 210 instances and a testing set of 2,100 instances; each image belongs to one of 7 classes. Dash et al. (2003) achieved an accuracy of 98.6 percent.
-
ISOLET (Isolated Letter Speech Recognition) dataset: The task in this experiment is to classify a collection of isolated spoken English letters as one of 26 classes (A-Z). The dataset is composed of 2,800 instances uttered by 150 speakers, each instance represented by a set of 617 features, including spectral coefficients, contour features, sonorant features, presonorant features, and postsonorant features (Cole and Fanty 1994). The reported accuracy of this database is 96.73 percent (Dietterich 1994).
-
PENDIGITS (Pen-Based Recognition of Handwritten Digits) dataset: This experiment consists of pen-based recognition of handwritten digits. The database collects 10,992 samples from 44 writers, each sample being a sequence of (x, y) coordinates representing the trajectory of the pen during the writing process. The sequences have been resampled to obtain a fixed-length attribute vector equal to 16 (eight pairs of (x, y) coordinates) and normalized to eliminate the effect of artifacts resulting from different handwritings. The 10,992 samples are divided into a training set of 7,494 instances and 3,498 instances for testing. The accuracy of this dataset reached 98.6 percent (Alpaydin and Alimoglu 1998).
-
Multiple Features dataset: This dataset consists of 649 features, for a total of 2,000 patterns of handwritten numerals (`0'--`9') extracted from a collection of Dutch utility maps (Duin 2013). These digits are represented in terms of six feature sets: 76 Fourier coefficients of the character shapes; 216 profile correlations; 64 Karhunen-Loève coefficients; 240 pixel averages, in 2 × 3 windows; 47 Zernike moments; and six morphological features. The best accuracy achieved is 98 percent (Perkins and Theiler 2003).
-
Abalone dataset: The task for this dataset is to classify the age of a collection of 4,177 abalones from a total of eight physical measurements, such as height, weight, diameter, and length. This dataset is characterized by a highly unbalanced class distribution and has achieved an accuracy of 79.0 percent (Tan and Dowe 2003).
Table 8-2 compiles the recognition rate, training time, and total number of required iterations for convergence, based on a fourfold cross-validation, using the mean squared error (MSE) and the well-formed cross-entropy (CE) cost functions at the output layer.
Two experiments were performed:
-
Experiment 1: CA with the exponential weight update rule and MSE as a cost function
-
Experiment 2: CA with the exponential weight rule and CE as a cost function
On average the CE cost function results in better classification accuracy. However, this is achieved at the expense of an increase in computational complexity and training time.
Note
Despite their superior hypothetical performance, CAs remain less widely used than ANNs, owing to their longer and more expensive training and computational requirements. These make them unattractive for online learning, energy-aware computing nodes, and large datasets with stringent restrictions on the training duration.
Modified Cortical Algorithms Applied to Arabic Spoken Digits: Case Study
Because CAs have not been extensively implemented for automatic speech recognition (in particular for the Arabic language), the following sections show how CA strengthening and inhibiting rules originally employed during feedback were modified with weighted entropy concepts that were added to the CA cost function and the weight update rule.
Entropy-Based Weight Update Rule
During the feedback learning stage of a CA, the output of each layer is compared with a desired state of firing, and the weights are updated until an error term is reduced to a minimum threshold value. Using the least squares criterion, large error values influence the learning process much more than smaller ones. For a class of problems, the gradient descent algorithm, with the MSE as a criterion for weight updates, can be trapped in a local minimum and so it will fail to find the optimal solution. In contrast, the well-formed CE criterion, employing a gradient descent algorithm, guarantees convergence to the optimal solution during learning (Wittner and Denker 1988).
The three properties of a well-formed error function of the form  are as follows:
are as follows:
-
For all
 the derivative of
the derivative of  , defined as
, defined as  , must be negative.
, must be negative. -
There must exist an ϵ
 , such that
, such that 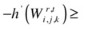 for all
for all  .
. -
The function h must be differentiable and bounded.
CE as a cost function criterion can be written as

where  is the desired output of the ith column of layer r at epoch t.
is the desired output of the ith column of layer r at epoch t.
If you adopt the same procedure for the feedback learning, and assume that training convergence of each layer happens when the entropy measure falls below a predetermined threshold value, the weight update rule becomes:
-
Inhibiting:

-
Strengthening:

One advantage of using the proposed gradient descent weighted rules is that the CE cost function diverges if one of the outputs converges to the wrong extreme; hence, the gradient descent reacts quickly. In contrast, the MSE cost function approaches a constant, and the gradient descent on the least square will wander on a plateau, even though the error may not be small.
Experimental Validation
Using a CA of six hidden layers, starting with 2,000 columns of 20 nodes for the first hidden layer and decreasing the number of columns by half between consecutive layers, four experiments, employing the weighted entropy weight update rule, were performed based on a fivefold cross-validation:
-
Experiment 1: CA trained using the MSE cost function and the original weight update rule
-
Experiment 2: CA trained using the MSE cost function and the proposed weight update rule
-
Experiment 3: CA trained using the CE cost function and the original weight update rule
-
Experiment 4: CA trained using the CE function and the proposed weight update rule
Simulations were executed, using MATLAB R2011a software on an Intel i7 at 2GHz and 6GB RAM on a Windows 7 Home Premium operating system, using a modified central nervous system (CNS) library. Developed at the Massachusetts Institute of Technology, by Mutch, Knoblich, and Poggio (2010), the CNS library is a framework for simulating cortically organized networks.
The database was obtained from the UCI Machine Learning Repository and consists of a collection of 13 Mel frequency cepstral coefficient (MFCC) frames representing 8,800 spoken Arabic digits—one of ten classes (0-9), uttered by 88 different speakers, obtained after filtering the spoken digits, using a moving Hamming window. Several techniques were validated on this database; the best achieved result shows a 97.03 percent recognition rate, based on a threefold cross-validation, using a multiclass SVM classifier (Ji and Sun 2011).
Tree Representation for Arabic Phonemes
As the first language in 22 countries, Arabic ranks fifth among the most spoken languages in the world (Mosa and Ali 2009). Although applications treating speech recognition have increased significantly (e.g., iPhone 4S Siri interface), implementation for the Arabic language is limited, mainly because of its morphological complexity. For Arabic automatic speech recognition, the recognition of phonemes constitutes an important step in continuous speech analysis. Most research proceeds by extracting isolated phonemes or small phonetic segments (El-Obaid, Al-Nassiri, and Maaly 2006; Awais 2003; Gevaert, Tsenov, and Mladenov 2010; Al-Manie, Alkanhal, and Al-Ghamdi 2009) for analysis of longer speech signals (Abushariah et al. 2010) and broadcast news (Al-Manie, Alkanhal, and Al-Ghamdi 2009), using several techniques, such as ANN (Essa, Tolba, and Elmougy 2008), fuzzy HMM (Shenouda, Zaki, and Goneid 2006), fuzzy logic, concurrent self-organizing maps (Sehgal, Gondal, and Dooley 2004), and HMM (Satori, Harti, and Chenfour 2007; Bourouba et al. 2010; Biadsy, Moreno, and Jansche 2012).
Spoken in the Middle East and North Africa, Arabic has different dialects. However, Literary Arabic (also called Modern Standard Arabic) is the official form used in documents and for formal speaking in all Arabic-speaking countries. One of the differences between spoken and written Arabic is the presence in the latter of diacritics (marks used to indicate how a letter should be pronounced). The complexity of Arabic is the result of its unusual morphology: words are formed using a root-and-pattern scheme, in which the root is composed of 3 consonants, leading to several possibilities from one root. Phonetically, Arabic has 28 consonant segments and 6 vowels (Newman 1984). Phonemes can be grouped according to the articulation of the lips and tongue during speech, as shown in the classification of Arabic phonemes.

Note
MFCCs can model the acoustic content of speech independently of the source (speaker). MFCCs are calculated by mapping the logarithm of the spectrum into the Mel scale and converting the obtained signal back to the time domain, using discrete cosine transform (Klatau 2005).
For consistency, the first experiment with the data used the 13 MFCCs provided and then added the first and second derivatives of the MFCCs, that is, coefficients with a feature vector of size 39. Tables 8-3 and 8-4 show a comparison of the results obtained for all experiments with the average recognition rate obtained, training time, and number of epochs required for convergence.
Tables 8-3 and 8-4 demonstrate that training of the cortical network, using the entropy cost function and the proposed weight update rule, performed better than the original training parameters. This improvement is achieved at the expense of a small worsening of the required training time. Despite the lengthy training time, however, the proposed weight update rule requires fewer training epochs to converge, compared with the original weight update rule. This is because the amount of strengthening added using the proposed rule is proportional to the gradient of the cost function, meaning that fewer training epochs are necessary to reach convergence. The proposed weight update rule involves computing the entropy gradient, which is computationally more expensive, compared with the original weight update rule.
The confusion matrices in Figure 8-5, obtained for the image segmentation dataset using both cost functions, demonstrate that although a significant trend is observed in the confusion between classes 1, 7, and 8 with the classical distance measure, the proposed entropy-based update rule was able to correct this trend partially.
Figure 8-6 compares the CE cost function with the training epochs obtained while training the cortical network using the entropy cost function for the proposed and the regular weight update rules. Note that the proposed weight update converges to a smaller MSE value, compared with the regular update, which is consistent with the recognition rates obtained earlier.
References
Abushariah, Mohammad A. M., Raja N. Ainon, Roziati Zainuddin, Moustafa Elshafei, and Othman O. Khalifa. “Natural Speaker-Independent Arabic Speech Recognition System Based on Hidden Markov Models Using Sphinx Tools.” In Proceedings of the 2010 International Conference on Computer and Communication Engineering, Kuala Lumpur, Malaysia, May 11–12, 2010, 1–6. Piscataway, NJ: Institute of Electrical and Electronic Engineers, 2010.
Awais, M. M. “Recognition of Arabic Phonemes Using Fuzzy Rule Base System.” In Proceedings of the 7th International Multitopic Conference, Islamabad, Pakistan, December 8–9, 2003, 367–370. Piscataway, NJ: Institute of Electrical and Electronic Engineers, 2003.
Bache, K., and M. Lichman. “University of California, Irvine, Machine Learning Repository.” Irvine: University of California, 2013. http://archive.ics.uci.edu/ml/index.html.
Bagirov, A. M., J. Ugon, and D. Webb. “An Efficient Algorithm for the Incremental Construction of a Piecewise Linear Classifier.” Journal of Information Systems 36, no. 4 (2011): 782–790.
Biadsy, Fadi, Pedro J. Moreno, and Martin Jansche. “Google's Cross-Dialect Arabic Voice Search.” In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech, and Signal Processing, Kyoto, Japan, March 25–30, 2012, 4441–4444. Piscataway, NJ: Institute of Electrical and Electronic Engineering, 2012.
Bourouba, H., R. Djemili, M. Bedda, and C. Snani. “New Hybrid System (Supervised Classifier/HMM) for Isolated Arabic Speech Recognition.” In Proceedings of the 2nd Conference on Information and Communication Technologies, Damascus, Syria, April 24–28, 2006, 1264–1269. Piscataway, NJ: Institute of Electrical and Electronic Engineering, 2006.
Cole, Ron, and Mark Fanty. “ISOLET Data Set.” University of California, Irvine, Machine Learning Repository. Irvine: University of California, 1994. https://archive.ics.uci.edu/ml/datasets/ISOLET.
Dash, Manoranjan, Huan Liu, Peter Scheuermann, and Kian Lee Tan. “Fast Hierarchical Clustering and Its Validation.” Data and Knowledge Engineering 44, no. 1 (2003): 109–138.
Dietterich, Thomas G., and Ghulum Bakiri. “Solving Multiclass Learning Problems via Error-Correcting Output Codes.” Journal of Artificial Intelligence Research 2, no. 1 (1995): 263–286.
Duin, Robert P. W. “Multiple Features Data Set.” University of California, Irvine, Machine Learning Repository. Irvine: University of California, 2013. http://archive.ics.uci.edu/ml/datasets/Multiple+Features.
Edelman, Gerald M., and Vernon B. Mountcastle. The Mindful Brain: Cortical Organization and the Group-Selective Theory of Higher Brain Function. Cambridge, MA: Massachusetts Institute of Technology Press, 1978.
Essa, E. M., A. S. Tolba, and S. Elmougy. “A Comparison of Combined Classifier Architectures for Arabic Speech Recognition.” In Proceedings of the 2008 International Conference on Computer Engineering and Systems, Cairo, Egypt, November 25–27, 2008, 149–153. Piscataway, NJ: Institute of Electrical and Electronic Engineering, 2008.
Gevaert, Wouter, Georgi Tsenov, and Valeri Mladenov. “Neural Networks Used for Speech Recognition.” Journal of Automatic Control 20, no. 1 (2010): 1–7.
Ji, You, and Shiliang Sun. “Multitask Multiclass Support Vector Machines.” In Proceedings of the 11th International Conference on Data Mining Workshops), Vancouver, BC, December 11, 2011, 512–518. Piscataway, NJ: Institute of Electrical and Electronic Engineering, 2011.
Klautau, Aldebaro. “The MFCC,” 2012. www.cic.unb.br/∼lamar/te073/Aulas/mfcc.pdf.
Hashmi, Artif G., and Mikko. H. Lipasti. “Discovering Cortical Algorithms”. In Proceedings of the International Conference on Fuzzy Computation and International Conference on Neural Computation, Valencia, Spain, October 24–26, 2010, 196–204.
Manie, Mohammed A. Al-, Mohammed I. Alkanhal, and Mansour M. Al-Ghamdi. “Automatic Speech Segmentation Using the Arabic Phonetic Database.” In Proceedings of the 10th WSEAS International Conference on Automation and Information, Prague, Czech Republic, March 23–25, 76–79. Stevens Point, Wisconsin: World Scientific and Engineering Academy and Society, 2009.
Mohler, Cleve. “Exponential Function.” Chap. 8 in Experiments with MATLAB. MathWorks, 2011. www.mathworks.com/moler/exm/chapters/exponential.pdf.
Mosa, Ghassaq S., and Abduladhem Abdulkareem Ali. “Arabic Phoneme Recognition Using Hierarchical Neural Fuzzy Petri Net and LPC Feature Extraction.” Signal Processing: An International Journal 3, no. 5 (2009): 161–171.
Mutch, Jim, Ulf Knoblich, and Tomaso Poggio. “CNS: A GPU-Based Framework for Simulating Cortically-Organized Networks.” Technical Report, Massachusetts Institute of Technology, 2010.
Newman, Daniel. “The Phonetics of Arabic.” Journal of the American Oriental Society 46 (1984): 1–6.
Obaid, Manal El-, Amer Al-Nassiri, and Iman Abuel Maaly. “Arabic Phoneme Recognition Using Neural Networks.” In Proceedings of the 5th WSEAS International Conference on Signal Processing, Istanbul, Turkey, May 27–29, 2006, 99–104. Stevens Point, Wisconsin: World Scientific and Engineering Academy and Society, 2006.
Perkins, Simon, and James Theiler. “Online Feature Selection Using Grafting.” In Proceedings of the Twentieth International Conference on Machine Learning, Washington, DC, August 21–24, 2003, 592–599. Menlo Park, CA: Association for the Advancement of Artificial Intelligence, 2003.
Satori, Hassan, Mostafa Harti, and Nouredine Chenfour. “Introduction to Arabic Speech Recognition Using CMU Sphinx System.” In Proceedings of the Information and Communication Technologies International Symposium, Fez, Morocco, April 3–5, 2007, edited by Mohammad Essaaidi, Mohammed El Mohajir, Badreddine El Mohajir, and Paolo Rosso, 139–142. Piscataway, NJ: Institute of Electrical and Electronic Engineers, 2007.
Sehgal, M. S. B., Iqbal Gondal, and Laurence Dooley. “A Hybrid Neural Network Based Speech Recognition System for Pervasive Environments.” In Proceedings of the 8th International Multitopic Conference, Lahore, Pakistan, December 24–26, 2004, 309–314. Piscataway, NJ: Institute of Electrical and Electronic Engineers, 2004.
Shenouda, Sinout D., Fayez W. Zaki, and A. M. R. Goneid. “Hybrid Fuzzy HMM System for Arabic Connectionist Speech Recognition.” In Proceedings of the Twenty-Third National Radio Science Conference, Monufia, Egypt, March 14–16, 1–8. Piscataway, NJ: Institute of Electrical and Electronic Engineers, 2006.
Slate, David J. “Letter Recognition Data Set.” University of California, Irvine, Machine Learning Repository. Irvine: University of California, 1991. http://archive.ics.uci.edu/ml/datasets/Letter+Recognition.
Tan, Peter J., and David L. Dowe. “MML Inference of Decision Graphs with Multi-Way Joins and Dynamic Attributes.” In AI 2003: Advances in Artificial Intelligence; Proceedings of the 16th Australian Conference on AI, Perth, Australia, December 3–5, 2003, edited by Tamás Domonkos Gedeon and Lance Chun Che Fung, 269–281. Berlin: Springer, 2003.
Alpaydin, E., and Fevzi Alimoglu. ”Pen-Based Recognition of Handwritten Digits Data Set.” University of California, Irvine, Machine Learning Repository. Irvine: University of California, 1998. https://archive.ics.uci.edu/ml/datasets/Pen-Based+Recognition+of+Handwritten+Digits.
Vision Group. “Image Segmentation Data Set.” University of California, Irvine, Machine Learning Repository. Irvine: University of California, 1990. https://archive.ics.uci.edu/ml/datasets/Image+Segmentation.
Wittner, Ben S., and John S. Denker. “Strategies for Teaching Layered Networks Classification Tasks.” In Neural Information Processing Systems: Denver, CO, 1987, edited by Dana Z. Anderson, 850–859. Berlin: Springer, 1988.
Notes
- 1.
Marvin Minsky, “Scientist on the Set: An Interview with Marvin Minsky,” in HAL’s Legacy: 2001’s Computer as Dream and Reality, by David G. Stork (Massachusetts Institute of Technology Press, 1998), p. 18.
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits any noncommercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this chapter or parts of it.
The images or other third party material in this chapter are included in the chapter’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2015 Apress Media, LLC
About this chapter
Cite this chapter
Awad, M., Khanna, R. (2015). Cortical Algorithms. In: Efficient Learning Machines. Apress, Berkeley, CA. https://doi.org/10.1007/978-1-4302-5990-9_8
Download citation
DOI: https://doi.org/10.1007/978-1-4302-5990-9_8
Published:
Publisher Name: Apress, Berkeley, CA
Print ISBN: 978-1-4302-5989-3
Online ISBN: 978-1-4302-5990-9
eBook Packages: Professional and Applied ComputingProfessional and Applied Computing (R0)Apress Access Books





 is the output of the ith column in the rth layer of the network for a certain training instance denoted by k and given N instances in total; the desired output for this particular column
is the output of the ith column in the rth layer of the network for a certain training instance denoted by k and given N instances in total; the desired output for this particular column  is given by:
is given by: with the desired value of
with the desired value of  . If the desired output of a column is a firing state, whereas the actual is different, the column is strengthened (see Equation 8-8; the column is inhibited (see Equation 8-7) if the opposite occurs (i.e., if the actual output is firing, whereas a nonfiring state is desired).
. If the desired output of a column is a firing state, whereas the actual is different, the column is strengthened (see Equation 8-8; the column is inhibited (see Equation 8-7) if the opposite occurs (i.e., if the actual output is firing, whereas a nonfiring state is desired).
 versus
versus 

 the derivative of
the derivative of  , defined as
, defined as  , must be negative.
, must be negative. , such that
, such that 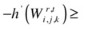 for all
for all  .
.
