Abstract
Multiobjective optimization caters to achieving multiple goals, subject to a set of constraints, with a likelihood that the objectives will conflict with each other. Multiobjective optimization can also be explained as a multicriteria decision-making process, in which multiple objective functions have to be optimized simultaneously. In many cases, optimal decisions may require tradeoffs between conflicting objectives. Traditional optimization schemes use a weight vector to specify the relative importance of each objective and then combine the objectives into a scalar cost function. This strategy reduces the complexity of solving a multiobjective problem by converting it into a single-objective problem. Solution techniques for multiobjective optimization involve a tradeoff between model complexity and accuracy. Examples of multiobjective optimization can be found in economics (setting monetary policy), finance (risk–return analysis), engineering (process control, design tradeoff analysis), and many other applications in which conflicting objectives must be obtained.
All men seek one goal: success or happiness. The only way to achieve true success is to express yourself completely in service to society. First, have a definite, clear, practical ideal—a goal, an objective. Second, have the necessary means to achieve your ends: wisdom, money, materials, and methods. Third, adjust all your means to that end.
—Aristotle
You have full access to this open access chapter, Download chapter PDF
Multiobjective optimization caters to achieving multiple goals, subject to a set of constraints, with a likelihood that the objectives will conflict with each other. Multiobjective optimization can also be explained as a multicriteria decision-making process, in which multiple objective functions have to be optimized simultaneously. In many cases, optimal decisions may require tradeoffs between conflicting objectives. Traditional optimization schemes use a weight vector to specify the relative importance of each objective and then combine the objectives into a scalar cost function. This strategy reduces the complexity of solving a multiobjective problem by converting it into a single-objective problem. Solution techniques for multiobjective optimization involve a tradeoff between model complexity and accuracy. Examples of multiobjective optimization can be found in economics (setting monetary policy), finance (risk–return analysis), engineering (process control, design tradeoff analysis), and many other applications in which conflicting objectives must be obtained.
One of the prerequisites of multiobjective optimization is to determine whether one solution is better than another. However, no simple method exists for reaching such a conclusion. Instead, multiobjective optimization methods commonly adopt a set of Pareto optimal solutions (also called nondominated solutions), which are alternatives with different tradeoffs between the various objectives. In the solution defined by a Pareto optimal set, one objective cannot be improved without degrading at least one other objective in the set. It is up to the decision maker to select the Pareto optimal solution that best fits preferred policy or guidelines. Pareto graphs illustrate the attributes of the tradeoff between distinct objectives. The solution can be represented in the shape of a curve, or a three-dimensional surface that trades off different zones in the multiobjective space.
This chapter discusses machine learning methodologies for solving Pareto-based multiobjective optimization problems, using an evolutionary approach. The goal is to find a set of nondominated solutions with the minimum distance to the Pareto front in each generation. Successive solutions are built as part of the evolutionary process, in which one set of selected individual solutions gives rise to another set for the next generation. Solutions with higher fitness measures are more likely to be selected to the mating pool, on the assumption that they will produce a fitter solution in the next generation (next run), whereas solutions with weaker fitness measures are more likely to be discarded. Such solutions possess several attributes that make them suitable for problems involving (1) a large and complex search space and (2) mutually conflicting objectives.
Formal Definition
A multiobjective optimization problem deals with a finite number of objective functions. In an optimization problem with n objectives of equal importance, all need to be minimized (or maximized) to serve a performance criterion. Mathematically, the problem can be expressed as a vector of objectives f
i(x) that must be traded off in some manner,

where X (see Equation 10-2) is a set of n decision vectors (a decision space) that represents parameters for the values selected to satisfy constraints and optimize a vector function,

The relative significance of these objectives cannot be determined until the tradeoffs between them are distinctly understood. Because F(x) is a vector, competing objective functions will prevent it from achieving a unique solution. You can associate each solution x in a decision space X with a point in objective space Y, such that

In multiobjective optimization the sets X and Y are known as decision variable space and objective function space, respectively. Figure 10-1 illustrates the mapping of the search space to the objective space. Every iteration of search space leads to a set of objective vectors that defines the objective space, in which several optimal objective vectors may represent different tradeoffs between the objectives.
Pareto Optimality
Pareto optimality is a concept built on multiobjective optimization that facilitates optimization of a vector of multiple goals through tradeoffs between combinations of multiple objectives. Tradeoffs are formulated to improve the performance of one objective at the cost of one or more other objectives. As displayed in Figure 10-1, each point in the objective space represents a unique set of model variables, such that Pareto optimality categorizes multiple Pareto optimal solutions. The term honors Vilfredo Pareto (1848–1923), an Italian economist who demonstrated that income follows a power law probability distribution.
For an ideal case the optimal solution of a multiobjective problem is generally denoted as a Pareto set
 . The corresponding outcome, or objective vector, is represented by a Pareto front
. The corresponding outcome, or objective vector, is represented by a Pareto front
 . In practice an ideal solution is nonexistent, and solving multiobjective optimization does not typically produce an optimally unique solution. Instead, we use Pareto optimal solutions, in which one objective cannot be improved without degrading at least one of the other objectives. Therefore, when using evolutionary techniques, knowledge of the optimal Pareto set (X*, Y*) assists in finding a best-compromise solution.
. In practice an ideal solution is nonexistent, and solving multiobjective optimization does not typically produce an optimally unique solution. Instead, we use Pareto optimal solutions, in which one objective cannot be improved without degrading at least one of the other objectives. Therefore, when using evolutionary techniques, knowledge of the optimal Pareto set (X*, Y*) assists in finding a best-compromise solution.
Dominance Relationship
A solution x
1 dominates another solution  if the following conditions are met:
if the following conditions are met:
-
1.
For all objectives, solution x 1 is better than or equal to x 2, such that
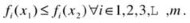
-
2.
For at least one objective, solution x 1 is strictly better than x 2, such that
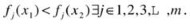
If either of these conditions is violated, then x
1 does not (Pareto) dominate the solution x
2. The dominance relationship is nonsymmetrical. For example, if the solution x
1 does not dominate the solution  that does not imply that x
2 dominates
that does not imply that x
2 dominates  therefore, both solutions can be nondominated. However, the dominance relationship is also transitive. For instance, if
therefore, both solutions can be nondominated. However, the dominance relationship is also transitive. For instance, if  and
and  then
then  This property allows us to identify which solutions are not dominated
This property allows us to identify which solutions are not dominated  (Xˆ) by any member of the solution set X. These nondominated sets
(Xˆ) by any member of the solution set X. These nondominated sets  (Xˆ) of the entire feasible search space are called globally Pareto-optimal sets.
(Xˆ) of the entire feasible search space are called globally Pareto-optimal sets.
Generating a Pareto set can be computationally expensive. Therefore, you need to select a computationally efficient method for determining the Pareto-optimal set of a multiobjective optimization algorithm. Although you may employ many different approaches to solve a multiobjective optimization problem, much work has been done in the area of evolutionary multiobjective optimization on the approximation of the Pareto set.
Performance Measure
To evaluate the performance of a solution, it is essential to develop a measurement scheme that quantifies the quality of the nondominant Pareto front. The general performance criteria for multiobjective optimization algorithms can be summarized as follows:
-
1.
Convergence (γ): Estimates the proximity of the candidate nondominated (Pareto) solutions to the best-known prediction or known set of Pareto optimal solutions. For each solution obtained using an algorithm, you can use the minimum Euclidian distance (Deb, Pratap, and Agarwal 2002) to the Pareto optimal front. The average distance can be used as the convergence measure. A smaller γ value indicates a better convergence.
-
2.
Diversity (Δ): Provides a decision maker with efficient choices. Because you are interested in the solution that covers the entire Pareto-optimal region, you need to evaluate the degree of spread between the solutions obtained.
-
3.
Displacement (D): In the case of algorithmic approximations or the presence of a discontinuous Pareto-optimal front, only a portion of true optimal front may be reflected. Displacement is used to overcome this limitation. Displacement measures the relative proximity of the candidate solution set to a known set of Pareto-optimal solutions. Mathematically, displacement can be expressed as

where,
P* = Uniformly spaced solutions from the true Pareto-optimized front
Q = Final solution
d(I, j) = Euclidean distance between the ith solution of P* and jth solution of Q
A lower displacement value represents better convergence and coverage.
Each algorithm may select one or more performance criteria to test the quality of a solution. In many cases, the performance criteria may depend on the availability (or nonavailability) of a known collection of Pareto-optimal sets. The rest of this chapter looks at various multiobjective optimization solutions based on evolutionary learning methodologies.
Machine Learning: Evolutionary Algorithms
Generating the Pareto set can be computationally expensive, because multiobjective optimization problems no longer have a single optimal solution, but a whole set of potential solutions. Classical optimizers (Marler and Arora 2004) include weighted-sum approaches, perturbation methods, Tchybeshev methods, goal programming, and min–max methods. Although these methods can be used for multicriteria optimization, you can only obtain a single solution for each simulation run; simulation needs to execute multiple times, with an expectation that one of the solutions may lead to the Pareto-optimal solution. Evolutionary algorithms (EAs) are well suited to solving multiobjective optimization problems, because they mimic natural processes that are inherently multiobjective; a number of Pareto-optimal solutions can be captured in a single simulation run. Additionally, EAs are less sensitive to the shape or continuity of the Pareto front. These algorithms have been successfully applied to a wide range of combination problems, in which information from multiple sources is brought together to achieve an optimal solution. Such algorithms are particularly useful in applications involving design and optimization, in which there are a large number of variables and in which procedural algorithms are either nonexistent or extremely complicated. Generally, evolutionary methods are population-based, metaheuristic optimization algorithms that mimic the principles of natural evolution. These methods use the initial population of a solution and update in each generation to converge to a single optimal solution. Although EAs do not guarantee a true optimal solution, they attempt to find a good approximation, representing a near-Pareto-optimal solution.
EAs are typically classified into four major categories: (1) genetic algorithms (GAs), (2) genetic programming (GP), (3) evolutionary programming (EP), and (4) evolution strategy (ES). Although these algorithms employ different approaches, they all derive inspiration from the principle of natural selection. Fundamental processes involved in EAs are selection, mutation, and crossover. The first stage of an EA entails applying a fitness factor to evaluate the population in the objective space (which represents the quality of the solution). Next, a mating pool is created by selecting the population from previous step, using a random selection or likelihood-based selection criterion. Once the mating pool is organized, it is subjected to recombination and mutation, which produce a new population set. The recombination process performs an n-point crossover, with a configurable probability that allows fragments of one parent to combine with fragments of another parent to create an entirely new child population. Mating selection is a critical step in the EA process, inasmuch as it attempts to select promising solutions, on the assumption that future mating pools derived as a consequence of a high-quality selection tend to be superior. A mutation operator modifies individuals by making small changes to the associated vectors, according to a given mutation rate. Given the probabilistic nature of the mating and mutation processes, certain populations may not undergo any variation and simply replicate to the next generation.
Analogous to natural evolution, individuals represent possible solutions, and a set of individuals (or possible solutions) is called a population. Each individual is encoded, using a problem-specific encoding scheme that can be decoded and evaluated by a fitness function. The mating process iterates through the process of modifying an existing population via recombination and mutation to evolve a new population. Each loop iteration is called a generation, which represents a timeline in the evolutionary process.
Early work in the area of multiobjective EAs is credited to David Schaffer, who implemented the vector-evaluated GA (VEGA) (Schaffer 1985). Goldberg(1989) proposed calculating individual fitness according to Pareto dominance. Many variants of multiobjective EAs have since been suggested (of which this chapter considers some of the more popular).
Genetic Algorithm
GAs follow the principle of natural selection (see Figure 10-2), in which each solution is represented as a binary (or real) coded string (chromosomes) and an associated fitness measure. Successive solutions are built as part of the evolutionary process, in which one set of selected individual solutions gives rise to another set for the next generation. Individuals with a high fitness measure are more likely to be selected to the mating pool, on the assumption that they will produce a fitter solution in the next generation. Solutions with the weaker fitness measures are naturally discarded. Typically, you can use roulette-wheel selection to simulate natural selection, in which elimination of solutions with a higher functional fitness is, although possible, less likely. In this method each possible selection is assigned a portion of the wheel that is proportional to its fitness value, followed by a random selection, analogous to spinning a roulette wheel. A small likelihood also exists that some weaker solutions will survive the selection process, because they may include components (genes) that prove useful after the crossover process. Mathematically, the likelihood of selecting a potential solution is given by

where P i represents the likelihood of ith solution’s being selected for the mating pool, F i stands for the operating fitness of ith individual solution, and N is the total number of solution elements in a population. GAs have proven useful in solving complex problems with large search spaces that are less understood by reason of little domain knowledge. The chromosomes of a GA represent the building blocks (alleles) of a solution to the problem that is suitable for the genetic operators and the fitness function. Candidate solutions undergo modification, using crossover and mutation functions, and result in new candidate solutions that undergo evaluation for candidacy in new mating pools.
Genetic Programming
GP is an evolutionary technique that expands the genetic learning paradigm into an autonomous synthesis of computer programs that, when executed, lead to candidate solutions. Unlike GAs, in which populations are fixed-length encoded character strings representing candidate solutions, in GP, populations are programs represented by syntax trees (also called parse trees). GP iteratively evolves the populations of programs, transforming one set of programs into another set by exercising the genetic operations crossover and mutation. Crossover function is implemented by exchanging subtrees at a random crossover point of two parent individuals (selected according to fitness criteria) in the population. Crossover creates an offspring by replacing the subtree at the crossover point of the first parent with the subtree of the second parent. In subtree mutation (the most commonly used form of mutation) the subtree of a randomly selected mutation point is replaced by the subtree of a randomly generated tree.
Figure 10-3 demonstrates the general flow and crossover operation of a GP methodology using two variables x and y and prefix notation to express mathematical operators. Parent 1 [+(*(x, y),2)] crosses over with parent 2 [*(+(x,1),/(y,2))] and produces an offspring represented by [+(/(y,2)),2)]. It is customary to use such prefix notation to represent expressions in GP.
Multiobjective Optimization: An Evolutionary Approach
In single-objective optimization, to evaluate the quality of the solution, you simply measure the value of the objective function. In the case of multiobjective optimization, it may not be possible to evaluate the quality of the solution relative to optimal Pareto approximations, because you may not possess the relevant information, with respect to objective space or coverage, and thus may not be able to define the quality of solution, in terms of closeness to the optimal Pareto set and diversity of coverage. Even if one solution dominates the other solution, you may still not be able to quantify the relative improvement, because relative distance and diversity alone are not sufficient to quantify the Pareto set approximation. This brings us to the fundamental requirements for defining the strategy for implementing multiobjective EAs. These requirements can be summarized as follows:
-
Fitness: Guiding the solution closer to the Pareto set. This requires constructing a scalar fitness function that fulfills multiple optimization criteria.
-
Diversity improvement: Improving coverage by selecting a diverse set of nondominated solutions. This avoids a situation in which identical solutions exist, relative to objective space and decision space.
-
Elitism: Preventing nondominated solutions from being eliminated.
Most EAs differ in the manner in which they handle fitness, diversity, and elitism. Listed here are some of the most popular multiobjective EA (MOEA) approaches:
-
Weighted-Sum approach
-
Vector-Evaluated GA (VEGA) (Schaffer 1985)
-
Multiobjective GA (MOGA) (Fonseca and Fleming 1993)
-
Niched Pareto GA (NPGA) (Horn, Nafpliotis, and Goldberg 1994)
-
Nondominated sorting GA (NSGA) (Nidamarthi and Deb 1994)
-
Strength Pareto EA (SPEA) (Zitzler and Thiele 1999)
-
Strength Pareto EA II (SPEA-II) (Zitzler, Laumanns, and Thiele 2001)
-
Pareto archived evolutionary strategy (PAES) (Knowles and Corne 1999)
-
Pareto envelope-based selection algorithm (PESA) (Corne, Knowles, and Oates 2000)
-
Pareto envelope-based selection algorithm II (PESA-II) (Corne et al. 2001)
-
Elitist nondominated sorting GA (NSGA-II) (Deb, Pratap, and Agarwal 2002)
These approaches are presented in turn in the following sections.
Weighted-Sum Approach
The weighted-sum method for multiobjective optimization delivers multiple solution points by varying the weights consistently. Different objectives are merged into a single objective, and the composite function is minimized, using configurable weights. Mathematically, the weighted-sum approach can be represented as

For positive weights, minimizing F can result in a Pareto optimal solution. Although this method is computationally efficient, the major drawback is that it cannot determine the weights that can optimally scale the objective functions for a problem with little or no information.
Vector-Evaluated Genetic Algorithm
VEGA is a population-based algorithm that extends the selection operator of a simple GA (SGA), such that each generation produces a number of disjoint subpopulations, as a result of a proportional selection scheme, and is governed by different objectives. For a problem with m objectives and a total population of size N, m subpopulations of size N / m are generated by their respective fitness functions. As depicted in Figure 10-4, these subpopulations are shuffled together to generate a new population of size N. The scheme is efficient and easy to implement, because only the selection method of SGA is modified.
Because of proportional selection, the shuffling and merging operations of all the subpopulations in VEGA result in an aggregating approach. The drawback of this scheme is its inability to find a large number of points on the Pareto optimal front because each solution executes its own objective function. VEGA is prone to finding extreme solutions, owing to the parallel search directions of the axes in the objective space or simultaneous execution of multiple-objective functions.
Multiobjective Genetic Algorithm
MOGA is another variant of SGA, differing in the way fitness is assigned to a solution. In this scheme, rank R is assigned to each solution, using the expression

where n
i is the number of solutions that dominate the ith solution x
i in generation t. Once the ranking process is completed, the fitness of individuals is assigned by interpolating between the best rank (1) and the worst rank  via a user-defined function. The fitness of individuals of the same rank is averaged, allowing sampling at the similar rate, while maintaining selection pressures. The fitness of certain individuals may degrade more than others, depending on the size of the ranked population. Ranking guides the search to converge only on global optima. Solutions exhibiting good performance in many objective dimensions are more likely to participate in the mating process.
via a user-defined function. The fitness of individuals of the same rank is averaged, allowing sampling at the similar rate, while maintaining selection pressures. The fitness of certain individuals may degrade more than others, depending on the size of the ranked population. Ranking guides the search to converge only on global optima. Solutions exhibiting good performance in many objective dimensions are more likely to participate in the mating process.
Although the ranking process assigns the nondominated solutions the correct fitness, it does not always guarantee sampling uniformity in the Pareto set. When dealing with multiple objectives, genetic drift triggers a suboptimal behavior, in which a large number of solutions tend to converge on a lesser number of objectives, owing to an imperfect selection process. To prevent premature convergence and to diversify the population, a niche-formation method is adopted to distribute the population over the Pareto region, in the objective space. If the fitness of two individuals is closer than a certain niching distance, they are considered part of same niche (i.e., sharing the same fitness). Niche formation discourages convergence to a single region of the fitness function by introducing competitive pressures among niches that reduce the fitness of such locally optimal solutions. Niche formation leads to discovery of diverse regions of the fitness landscape. In nature a niche is regarded as an organism’s task in the environment, and a species is the collection of organisms with the same features. Niching segments the GA population into disjoint sets in such a manner that at least one member in each region of fitness function covers more than one local optimal. In one such method, you define a parameter niche radius (σ radius). Any two individuals closer than this distance are considered part of the same niche, sharing the same fitness value. Niching lets the GA operate on the new shared fitness instead of on the original fitness of an individual. Niching reduces interspecies competition and helps synthesize a stable subpopulation around different niches. In multiobjective optimization problems, a niche is ordinarily represented by the locale of each optimum in the search space, with fitness as the resource of that niche.
Niched Pareto Genetic Algorithm
NPGA is a tournament selection scheme based on Pareto dominance, in which a comparison set of randomly selected individuals participates to determine the winner between two candidate solutions. Each of the candidates is tested to determine dominance. The candidate that is nondominated by the comparison set is selected for the mating pool. If both candidates are either dominated or nondominated by the comparison set, then they are likely to belong to the same equivalence class. As shown in Figure 10-5, for a given niche radius (σ share) the selection for the mating pool is determined by the niche class count. Candidates with the least number of individuals in the equivalence class (least niche count) have the best fitness. In this example, because both candidates are nondominated, Candidate 1 is selected to the mating pool, on the basis of lower niche class count.
MOGA and NPGA suffer from similar drawbacks; both methods are highly sensitive to selection of niche radius (σ share).
Nondominated Sorting Genetic Algorithm
NSGA is another Pareto-based nonelitist approach that differs from SGA in the manner in which the selection operator is used. All the nondominant solutions are selected first and classified as the first nondominant front in the population. To determine the members of the second nondominant front, members of the first nondominant front are eliminated from the evaluation process, and the search for nondominance continues with the remaining population. This process of level elimination and nondominance search within a shrinking population continues until all the individuals of the population have been categorized to a level of nondominance. Levels of nondominance range from 1 to p. Fitness is assigned to each category of the subpopulation proportionally to the population size. Solutions belonging to the lower levels of nondominance have higher fitness than those belonging to higher levels. This mechanism maintains the selection pressure to select individuals to the mating pool with higher fitness (members of lower levels of nondominance), in a direction toward the Pareto-optimal front.
In the first step the initial dummy fitness, equal to the population size, is assigned to individuals in the first level of the nondominance front. Based on the number of neighboring solutions (niche class count for a given niche radius σ
share) sharing the same front and the same level, the fitness value of an individual is reduced by a factor of the niche count, and a new shared fitness value is recomputed for each individual in this level. For the individuals in the second nondominance level, a dummy fitness smaller than the lowest shared fitness of the first nondominance level is assigned. Similarly, individuals that are members of the third and all subsequent levels are assigned fitnesses in decreasing order, relative to the lowest fitness of the lower levels. This guarantees that the fitness of individuals belonging to higher levels of nondominance is always lower than that of individuals in the lower levels. This process continues until all individuals in the entire population have been assigned their shared fitness. Once all the fitness values have been assigned, traditional GA processes related to selection, crossover, and mutation apply. Mathematically, this process can be explained as follows: for k individuals with a dummy fitness of f
p and niche count of  , as part of p nondominance level, the shared fitness of each individual i can be calculated as
, as part of p nondominance level, the shared fitness of each individual i can be calculated as

dummy fitness for individuals in the subsequent nondominance level is given as

where ε is a small positive number.
NSGA shares the same drawback as other algorithms in this category: high sensitivity to the niche radius σ share.
Strength Pareto Evolutionary Algorithm
SPEA implements elitism and nondominance by merging several features of previous implementations of multiobjective EAs. Elitist selection prevents the quality of good solutions from degrading, from one generation to the next. In one of its variants, the best individuals from the current generation are carried to the next, without alteration.
Zitzler et al. (2001) defined the characteristics of SPEA by referencing the following attributes:
-
1.
Creates an external and continuously updating nondominated population set by archiving previously found nondominated solutions. At each generation the nondominated solutions are copied to the external nondominated set. Unlike other EAs, in SPEA the relative dominance of one solution by other solutions within the population is irrelevant.
-
2.
Applies external nondominated solutions from step 1 to the selection process by evaluating an individual’s fitness, based on the strength of its solutions that dominate the candidate solution.
-
3.
Preserves population diversity, using the Pareto dominance relationship. This EA does not require a distance parameter (such as niche radius).
-
4.
Incorporates a clustering procedure to prune the nondominated external set without destroying its characteristics.
As stated, this algorithm implements elitism explicitly by maintaining an external nondominant population set  . The algorithm flow consists of the following steps:
. The algorithm flow consists of the following steps:
-
1.
Initialize the population P of size n.
-
2.
Initialize an empty population
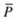 representing an external nondominant solution set archive.
representing an external nondominant solution set archive. -
3.
Copy the nondominated solutions of P to
 .
. -
4.
Remove solutions contained in
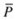 that are covered by other members of
that are covered by other members of  (or dominated solutions).
(or dominated solutions). -
5.
If the number of solutions in
 exceeds a given threshold, prune
exceeds a given threshold, prune 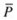 , using clustering.
, using clustering. -
6.
Compute the fitness of each member of P and the strength of each member of
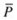 .
. -
7.
Perform binary tournament selection (with replacement) to select individuals for the mating pool from the multiset union of P and
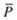 (
(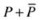 ). Tournament selection creates selection pressure by holding a “tournament” among randomly selected individuals from the current population (
). Tournament selection creates selection pressure by holding a “tournament” among randomly selected individuals from the current population ( ). The winner of each tournament (the individual with the best fitness) is inducted into the mating pool. The mating pool has higher average fitness, compared with the average population fitness, and helps build selection pressure, which improves the average fitness of successive generations.
). The winner of each tournament (the individual with the best fitness) is inducted into the mating pool. The mating pool has higher average fitness, compared with the average population fitness, and helps build selection pressure, which improves the average fitness of successive generations. -
8.
Apply problem-specific mutation and crossover operators, as usual.
-
9.
Go to step 3, and repeat (unless termination criteria are reached).
Strength of 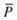 Solutions
Solutions
Each solution is assigned a strength  S
i is proportional to the number of individuals
S
i is proportional to the number of individuals  such that i dominates j. The fitness of the solution in an external nondominated set
such that i dominates j. The fitness of the solution in an external nondominated set  is given by
is given by

where n is the number of individuals in P dominated by i, and N is the total population of P.
Fitness of PSolutions
The fitness of solution  is calculated by summing the strength of all external nondominated solutions
is calculated by summing the strength of all external nondominated solutions  that cover (or dominate) j. The fitness of a solution in set P is given by
that cover (or dominate) j. The fitness of a solution in set P is given by

with 1 added to the fitness to maintain better fitness of the external nondominant solution. Because the fitness is minimized, lower fitness results in a higher likelihood of being selected to the mating pool.
Clustering
In SPEA the size of the external nondominated solution set  is key to the success of the algorithm. Because of its participation in the selection process, an extremely large nondominated solution set may reduce selection pressure and slow down the search. Yet, unbalanced distribution in the population may bias the solutions toward certain regions of the search space. Therefore, a pruning process is needed to eliminate individuals in the external nondominated population set, while maintaining its diversity. Zitzler, Laumanns, and Thiele (2001) used the average linkage method (Morse 1980) to prune the external nondominated solution set. The clustering steps are as follows:
is key to the success of the algorithm. Because of its participation in the selection process, an extremely large nondominated solution set may reduce selection pressure and slow down the search. Yet, unbalanced distribution in the population may bias the solutions toward certain regions of the search space. Therefore, a pruning process is needed to eliminate individuals in the external nondominated population set, while maintaining its diversity. Zitzler, Laumanns, and Thiele (2001) used the average linkage method (Morse 1980) to prune the external nondominated solution set. The clustering steps are as follows:
-
1.
Initialize a cluster C, such that each individual
 in the external nondominated solution set is a member of a distinct cluster.
in the external nondominated solution set is a member of a distinct cluster. -
2.
Calculate the distance between all possible pairs of clusters. Let d m,n be the distance between two clusters c m and
 then,
then,
where
 is the Euclidian distance between the objective space of two individuals, and
is the Euclidian distance between the objective space of two individuals, and  is the population of cluster c
k.
is the population of cluster c
k. -
3.
Merge two clusters with minimum distance d m,n into the larger cluster.
-
4.
Identify the individual in each cluster set with the minimum average distance to all other individuals in the cluster.
-
5.
Cycle steps 2–4 until reaching a threshold of maximum number of allowed clusters
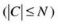
.
SPEA introduces elitism into evolutionary multiobjective optimization. One advantage that stands out is that this algorithm is not dependent on niche distance (σ radius), as are MOGA or NSGA. The success of SPEA largely depends on the fitness assignment methodology, based on the strength of the archive members. In the worst-case scenario, if the archive contains a single member, then every member of P will have the same rank. The clustering process also remains the critical consideration for the success of the algorithm. Although essential for maintaining diversity, this technique may not be able to preserve boundary solutions, which can lead to nonuniform spread of nondominated solutions.
Strength Pareto Evolutionary Algorithm II
SPEA-II is an enhanced version of SPEA. In SPEA-II each individual in both the main population and the elitist archive is assigned a strength value (S i) representing the number of solutions it dominates,

On the basis of the strength value S i, the raw fitness value R i is calculated by summing the strengths of the individuals that dominate the existing one i,

where 
Unlike SPEA, in which fitness is determined only by the cumulative strength of the dominating archive members, in SPEA-II, fitness is determined by the cumulative strength of the dominating members in both the archive and the population. Because the fitness is minimized, a higher fitness value signifies that the candidate individual is dominated by a large number of individuals.
To distinguish individuals with identical raw fitness scores, SPEA uses the k–nearest neighbors (k-NN) method (Silverman 1986) for estimating additional density information for each individual. Here, kis calculated as the square root of the combined sample size of P and  . Each individual i measures, stores, and sorts its distance in objective space, relative to all other individuals j in the archive and the population. The kth element (distance) of the sorted list, in increasing order, is represented by
. Each individual i measures, stores, and sorts its distance in objective space, relative to all other individuals j in the archive and the population. The kth element (distance) of the sorted list, in increasing order, is represented by  . Density D
i is given by
. Density D
i is given by

where 
Finally, adding R i (raw fitness) and D i yields the fitness of individual i, represented by

Unlike SPEA, SPEA-II maintains a constant number of individuals in the archive. After the fitness evaluation is completed, the next step is to copy all nondominated individuals from archive  and population (P
t) to the archive of the next generation
and population (P
t) to the archive of the next generation 

If the number of nondominated solutions is less than the threshold N, then the  best-dominated solutions
best-dominated solutions  from the sorted list of the previous archive
from the sorted list of the previous archive  and population (P
t) are moved to the new archive
and population (P
t) are moved to the new archive  . If, however, the number of nondominated solutions exceeds the threshold N, then the truncation process takes place by removing
. If, however, the number of nondominated solutions exceeds the threshold N, then the truncation process takes place by removing  individuals with minimum distance, relative to each other. In the case of a tie, the second-smallest distances are considered, and so on.
individuals with minimum distance, relative to each other. In the case of a tie, the second-smallest distances are considered, and so on.
Also unlike SPEA, in which binary tournament selection (with replacement) selects individuals for the mating pool from the multiset population of P
t and  SPEA-II selects individuals from the archive population
SPEA-II selects individuals from the archive population  only.
only.
Pareto Archived Evolutionary Strategy
PAES is a simple multiobjective EA capable of generating diverse Pareto-optimal solutions. It is a single-parent, single-child EA that resembles (1+1)-Evolutionary Strategy. PAES uses binary representation and bitwise mutation operators to fulfill local search and create offspring. A bitwise mutation operator flips the bits (genes) of the binary coded solution (chromosomes) with a fixed probability, thereby creating a new solution. A reference archive stores and updates the best nondominated solutions found in previous generations. The best solution is the one that either dominates or remains nondominated in a less crowded region in the parameter space. This archive is used for ranking the dominance of all the resulting solutions.
First, a child is created, and its objective functions are computed. Next, the child is compared with the parent. If the child dominates the parent, the child is accepted as a parent for the next generation, and its copy is added to the archive. If the parent dominates the child, the child is discarded, and a new mutated solution is generated from the parent.
In the event that the parent and the child are nondominating, with respect to each other, then both are compared with the archive of best solutions to make an appropriate selection. If any member of the archive dominates the child, the child is discarded, and a new mutated solution is generated from the parent. If the child dominates any member of the archive, the child is accepted as a parent for the next generation, and all dominated solutions in the archive are eliminated. If the child does not dominate any solution in the reference archive, then the child is checked for its proximity to the solutions in the archive. The child is accepted as a parent in the next generation if it resides in a less crowded region in the parameter space. A copy of the child is also added to the archive.
The PAES algorithm consists of the following steps:
-
1.
Initialize a parent, evaluate its objective function, and add it to the archive.
-
2.
Mutate the parent, generate a child, and evaluate its objective function.
-
3.
Compare the parent and child.
-
a.
If the parent dominates the child, discard the child, and go to step 2.
-
b.
If the child dominates the parent, accept the child as a parent for the next generation, and add it to the archive.
-
4.
Compare the child with members in the archive.
-
a.
If any member of the archive dominates the child, discard the child, and go to step 2.
-
b.
If the child dominates any member of the archive, accept the child as a parent for the next generation, add it to the archive, and remove all dominated solutions in the archive.
-
5.
If the child does not dominate any solution in the reference archive, then check the child for proximity to the solutions in the archive; accept the child as a parent in next generation if it resides in a less crowded region in the parameter space. Copy the child to the archive.
-
6.
Go to step 2, and repeat until a predefined number of generations is reached.
Pareto Envelope-Based Selection Algorithm
PESA is a multiobjective EA that uses features from both SPEA and PAES. The difference is attributed to the part of the algorithm in which PESA integrates selection and diversity, using a hypergrid-based crowding scheme. Like SPEA, PESA employs a smaller internal population and larger external population. Whereas the external population archives the existing Pareto front approximation, the internal population comprises new candidates competing for inclusion in the external archive. Similar to PAES, to maintain diversity, PESA uses the hypergrid division of objective space to measure the scale of crowding in distinct regions of the external archive. Like PAES and SPEA, PESA’s solution replacement scheme (archiving the best nondominated solutions) for the external archive is based on the crowding measure; however, unlike PAES (which uses parent mutation) and SPEA (which uses the fitness measure, based on the strength of the dominating solutions), the selection scheme in PESA is also based on the crowding measure.
The PESA algorithm uses two population sets: P I representing the internal population and P E representing the external population (also called archive population). The steps of PESA are as follows:
-
1.
Initialize the external population (P E) to an empty set.
-
2.
Initialize the internal population
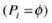 .
. -
3.
Evaluate each individual in the internal population.
-
4.
Update the external population archive P E.
-
a.
Copy the nondominated solution (in P I and any member of P E) of P I into P E.
-
b.
Remove the solution of P E that is dominated by the newly added nondominated solution of P I.
-
c.
If the solution of P I neither dominates nor is dominated by P E, then add the solution to P E.
-
d.
If |P E| exceeds a threshold, randomly choose a solution from the most crowded hypergrids to be removed.
-
5.
Check the termination criteria.
-
a.
IF a termination criterion has been reached, STOP; return P E.
-
b.
OTHERWISE,
-
1.
Delete the internal population
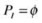 .
. -
2.
Repeat (until a new P I is generated).
-
a.
Select two parents from P E, from the less crowded hypergrid (based on the density information).
-
b.
Create new offspring, based on crossover and mutation.
-
6.
Go to to step 3, and repeat.
The crowding methodology in PESA forms a hypergrid that divides objective space into hyperboxes. Each individual in the external archive is associated with a particular hyperbox in objective space. An attribute defined as the squeeze factor represents the total number of other individuals that reside in the same hyperbox. The squeeze factor narrows down the choice of solutions from among randomly selected solutions (from the external archive) by picking the ones with lower squeeze factors. The squeeze factor drives the search toward an emerging Pareto front by selecting members of the under represented population.
The squeeze factor is also used to regulate the population of the external archive. When the archive population |P E| exceeds a certain threshold, a random individual from the region with a maximum squeeze factor is chosen to be removed.
Pareto Envelope-Based Selection Algorithm II
PESA-II is an extension of PESA that exercises a region-based selection approach, in which the selection criteria are satisfied using a hyperbox instead of random individuals in the hyperbox. A sparsely populated hyperbox has a higher likelihood of being selected than a crowded one. Once the cell is selected, individuals with the cell are randomly selected to participate in the mating and mutation processes. Although this algorithm is computationally efficient, it requires prior information about the objective space to tune the grid size.
Elitist Nondominated Sorting Genetic Algorithm
NSGA-II improves the nonelitist nature of NSGA with a crowded tournament selection scheme that uses crowding distance to facilitate selection. In NSGA-II, once the population is initialized, individuals in the population undergo nondominated sorting and ranking, as in NSGA. To find the first nondominated front, each individual in the population is compared with every other individual in the population to find if that individual is dominated. The nondominated individuals in the first front are removed from the population and placed in temporary (level 1) storage. To find the next front, the procedure is repeated with the remainder of the population. The process continues until all the members of the population are assigned a front. In the worst-case scenario, each front contains only one solution. Each individual in each front is given a fitness value (or rank), based on the front it belongs to; for instance, an individual in the nth front is given a fitness of n. Additionally, crowding distance is measured for each individual. Crowding distance represents the measure of an individual’s proximity to its neighbors, which drives the population toward better diversity. Parents are admitted into the mating pool, using binary tournament selection, based on rank and crowding distance. On completion of the nondominated sort, a crowding distance value is assigned to each individual.
If two solutions are compared during tournament selection, the winning solution is selected, based on the following criteria:
-
If the solutions belong to two different ranks, the solution with the better rank wins the selection.
-
If the solutions belong to the same rank, the solution with the higher crowding distance (or lesser crowding region) wins.
Once the mating pool is populated, crossover and mutation operators are applied to generate the offspring population. To implement elitism, the parent and child populations are combined, and the nondominated individuals from the combined population are propagated to the next generation. The NSGA-II algorithm is summarized as follows:
Initialization
-
1.
Initialize a random population P 0 of size N.
-
2.
Sort and rank the population by creating nondomination fronts.
-
3.
Assign fitness, according to the ranks of the population.
-
4.
Create offspring Q 0 of size N, using crossover and mutation operators.
Selection
-
5.
The start of each generation has a combined population
 of size 2N .
of size 2N .
-
6.
Sort and rank the population by creating nondomination fronts (F 1 (t), F 2 (t), F 3 (t),…,F n (t)).
-
7.
Select fronts F 1 (t) to F n (t) until the sum of the combined population of selected fronts exceeds N.
-
8.
Copy the entire populations of selected fronts F 1 (t) to F n-1 (t) to the mating pool of the next generation.
-
9.
Sort the population of the last selected front F n (t) in decreasing order, by crowding distance.
-
10.
Select the best individuals from the last front F n (t) needed to fill the mating pool slot of N.
-
11.
The mating pool now comprises the entire population of fronts F 1 to F n-1 and the partial population (sorted by crowding distance) of front Fn to create a parent population (mating pool) of population N.
-
12.
Use crossover and mutation operators to create N offspring.
-
13.
Go to step 5, and repeat.
The crowding distance guides the selection process toward a uniformly spread-out Pareto optimal front. The crowding distance of the ith solution D[i] is calculated as the sum of individual distance values corresponding to each objective m. Each objective function is normalized before calculating the crowding distance. The following steps summarize the crowding distance computation of all solutions in a nondominated set I:
-
1.
 Number of solutions
Number of solutions
-
2.
I = {0}Initialize all solutions to 0 ---------[For all objectives k = 1 to k = m]----------
-
3.
I = Sort (I,k ) Sort by the kth objective
-
4.
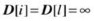 --------[For i = 2 to i £ (l −1) ]-----------------------
--------[For i = 2 to i £ (l −1) ]-----------------------
-
5.

Step 5 is a recursive operation, in which each successive iteration evaluates the crowding distance of the sorted solutions, based on the objective fitness. Step 5 is invoked for each objective fitness. Here, I[i].k represents the kth objective function value of the ith individual in the set I. The crowding distance is the Euclidian distance between each individual in the m–dimensional hyperspace. The individuals in the boundary are always selected, because they have infinite distance assignment. To ensure elitism, the offspring and parent populations of the current generation are combined to select the mating pool of the next generation. The population is subsequently sorted by nondomination. As illustrated in Figure 10-6, the new population for the mating pool is generated by filling the populations of each front F j (low to high) until the population size exceeds a threshold size of the parent population. If by including individuals in the front F j the total population exceeds N, then individuals in the front F j are selected in descending order of crowding distance until the population of size N is reached. This concludes the creation of the mating pool for the next generation. In the figure the nondominated fronts F 1(t), F 2(t), and F 3(t) are included fully, and the crowding distance–sorted front F 4(t) is included partially, in the mating pool P(t + 1).
Example: Multiobjective Optimization
Cloud computing allows us to host workloads with variable resource requirements and service-level objectives or performance guarantees. Furthermore, the cloud enables us to share resources efficiently, thereby reducing operational costs. These shared resources primarily relate to compute, memory, input/output (I/O), and storage. Variability of resources creates thermal imbalances, over- or underprovisioning, performance loss, and reliability issues. If these problems remain unchecked, their cumulative effect can increase the cost of running a datacenter as well as degrade workload performance, owing to unplanned provisioning and unanticipated demands. The solution for efficient datacenter management rests in satisfying multidimensional constraints that may be dynamic in nature and mutually conflicting. Environmental stresses vary from time to time and create resource pressures, which may be either global or regional, creating dynamic constraints that result in revised goals that need to be achieved.
As illustrated in Figure 10-7, the operational constraints in this example can be classified as four objective functions:
-
1.
Reducing thermal stresses (F T ): Thermal stresses occur when one or more devices approach their throttling limit or generate hot or cold spots, relative to other devices (or clusters of systems). Thermal stresses can be relieved by regulating fan speed, input airflow, or resource utilization.
-
2.
Meeting power targets (F P ): Power targets are set by an external management agent, according to fair usage and availability of maximum power. System power targets can be regulated by resource utilization; fan speed; or hosting workloads that do not exceed power demands and that are nonnoisy, relative to other workloads already running on different cores.
-
3.
Meeting performance guarantees (F S ): Performance guarantees are the fitness matrices defined by applications to measure service-level objectives (SLOs). For example, query response time is a measure that can quantify the quality of service when hosted on a system or cluster of systems. Performance guarantees are delivered via regulated resource utilization or by hosting workloads that are nonnoisy, relative to other workloads running on different cores.
-
4.
Meeting resource utilization targets (F U ): Resource utilization targets are enforced to maximize the server usage in a unit volume of rack space, leading to a reduction in idle periods. In some cases, resource utilization is regulated to deliver service assurance or reduce thermal hot spots. Resource utilization enforcement is generally realized by using an appropriate distribution of workloads in different cores in a manner that ultimately leads to the most efficient resource utilization with the least amount of mutual noise (cache, prefetching) or contention.
The multiobjective optimization problem can be represented as a function of these four objectives,

where x represents the parameters for the values selected to satisfy thermal, power, utilization, and performance constraints. These parameters can be summarized as follows:
-
Fan speed (x 1)
-
Central processing unit (CPU) power limit (x 2)
-
Memory power limit (x 3)
-
Input airflow (x 4)
-
Workload type ID (x 5)
-
Number of CPU cores (x 6)
These parameters x = (x 1 , x 2, x 3, x 4, x 5, x 6) regulate the operating states of the resources, which result in environmental as well as system-specific perturbations that may need to be corrected as part of exploring a true Pareto-optimal front or stable system.
Objective Functions
Individual objective functions measure the quality of solutions. Multiobjective optimization methods trade off the performance between various objectives. Here, a suitable tradeoff between power, thermal, performance, and utilization objectives is sought, using the EAs. Equations 10-21–10-24 represent the objective functions for these objectives. Each of the objectives is contingent on the values of parameters (decision vectors) that define the search space to satisfy the vectors of multiple goals through tradeoffs between combinations of multiple objectives,

where T
d and U
d are temperature and utilization of device d, respectively;  and
and  are the respective temperature and utilization thresholds; P is the current power consumption of the complete system; and Q is the service-level agreement (SLA), or performance score, of the workload running on the system. The solution x impacts the process output, represented by the corresponding functions
are the respective temperature and utilization thresholds; P is the current power consumption of the complete system; and Q is the service-level agreement (SLA), or performance score, of the workload running on the system. The solution x impacts the process output, represented by the corresponding functions  which influence the output of the objective functions. (Note that power and performance are system specific and not device specific in this context.)
which influence the output of the objective functions. (Note that power and performance are system specific and not device specific in this context.)
The solution x evolves by maneuvering multiple dimensions of the decision space and anticipating an optimal tradeoff between all four objectives. Forinstance, setting a higher fan speed (x 1) will improve cooling (F T) but increase power consumption, thereby degrading F P . Similarly, the CPU power limit (x 1) may regulate power consumption but degrade performance (F S). Therefore, the goal of the EAs is to synthesize a near-optimal solution that attempts to fulfill the inherent and often conflicting constraints of all the objectives. Solutions should reflect optimal decisions in the presence of tradeoffs between the four objectives. These decision vectors match certain workloads on specific systems, such that there is the least amount of conflict between objectives. Additional controls regulate the fan speed, CPU and memory power limits, input airflow, and allocation (or deallocation) of additional CPU cores.
Figure 10-8 displays the process of selecting the best compute node (from among a large number of nodes) for workload hosting.
Whenever a new workload is staged for hosting on one of the compute nodes, it undergoes fingerprinting. This process involves matching the distinctive attributes of multidimensional features to a preexisting database. Fingerprints correlate resource utilization patterns and estimate resource requirements. Swarm intelligence acts as a mechanism whereby a few candidate host nodes are selected from hundreds of possible host nodes for further evaluation. Some nodes are eliminated because of the low likelihood of their ability to deliver enough contention-free resources. Once shortlisted, the candidate nodes represent compute resources that can host incoming workloads, although with varying degrees of resource handling. All the shortlisted nodes are evaluated for quality of hosting the new workload by running MOEA in parallel, in an effort to generate multiple Pareto-optimal fronts, one for each node. The node corresponding to the best solution is selected for hosting the workload. The MOEA evaluates the solutions (see Equation 10-20) by measuring the collective efficiency of power, performance, utilization, and temperature and iterates toward finding the tradeoff representing the best solution. The process repeats each time a new workload appears in the staging queue to be serviced by one of the compute nodes.
References
Corne, David W., Nick R. Jerram, Joshua D. Knowles, and Martin J. Oates. “PESA-II: Region-Based Selection in Evolutionary Multiobjective Optimization.” In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2001). San Francisco: Morgan Kaufmann, 2001.
Corne, David W., Joshua D. Knowles, and Martin J. Oates. “The Pareto Envelope-Based Selection Algorithm for Multiobjective Optimization.” Parallel Problem Solving from Nature—PPSN VI: Proceedings of the 6th International Conference, edited by Marc Schoenauer, Kalyanmoy Deb, Günter Rudolph, Xin Yao, Evelyne Lutton, Juan Julian Merelo, and Hans-Paul Schwefel, 839–848. Berlin: Springer, 2000.
Deb, Kalyanmoy, Amrit Pratap, Sameer Agarwal, and T. Meyarivan. “A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II.” IEEE Transactions on Evolutionary Computation 6, no. 2 (2002): 182–197.
Fonseca, Carlos M., and Peter J. Fleming. “Genetic Algorithms for Multiobjective Optimization: Formulation Discussion and Generalization.” In Proceedings of the 5th International Conference on Genetic Algorithms, edited by Stephanie Forrest, pp. 416–423. San Francisco: Morgan Kaufmann, 1993.
Goldberg, David E. Genetic Algorithms in Search, Optimization, and Machine Learning. Reading, MA: Addison-Wesley, 1989.
Horn, J., N. Nafpliotis, and D. E. Goldberg. “A Niched Pareto Genetic Algorithm for Multiobjective Optimization.” In Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, 82–87. Piscataway, NJ: Institute of Electrical and Electronic Engineers, 1994.
Knowles, J. D., and D. W. Corne. “The Pareto Archived Evolution Strategy: A New Baseline Algorithm for Pareto Multiobjective Optimisation.” In Proceedings of the 1999 Congress on Evolutionary Computation, 98–105. Piscataway, NJ: Institute of Electrical and Electronic Engineers, 1999.
Marler, R. Timothy, and Jasbir S. Arora. “Survey of Multi-Objective Optimization Methods for Engineering.” Structural and Multidisciplinary Optimization 26, no. 6 (2004): 369–395.
Morse, J. N. “Reducing the Size of the Nondominated Set: Pruning by Clustering.” Computers and Operations Research 7, nos. 1–2 (1980): 55–66.
Nidamarthi, Srinivas, and Kalyanmoy Deb. “Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms.” Evolutionary Computation 2, no. 3 (1994): 221–248.
Schaffer, J. David. 1985. “Multiple Objective Optimization with Vector Evaluated Genetic Algorithms.” In Proceedings of the 1st International Conference on Genetic Algorithms, edited by John J. Grefenstette, 93–100. Hillsdale, NJ: L. Erlbaum, 1985.
Silverman, B. W. Density Estimation for Statistics and Data Analysis. London: Chapman and Hall, 1986.
Zitzler, E., M. Laumanns, and L. Thiele. “SPEA2: Improving the Strength Pareto Evolutionary Algorithm.” Technical report, Swiss Federal Institute of Technology, 2001.
Zitzler, E., and L. Thiele. “Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach” IEEE Transactions on Evolutionary Computation 3, no. 4 (1999): 257–271.
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits any noncommercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this chapter or parts of it.
The images or other third party material in this chapter are included in the chapter’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2015 Apress Media, LLC
About this chapter
Cite this chapter
Awad, M., Khanna, R. (2015). Multiobjective Optimization. In: Efficient Learning Machines. Apress, Berkeley, CA. https://doi.org/10.1007/978-1-4302-5990-9_10
Download citation
DOI: https://doi.org/10.1007/978-1-4302-5990-9_10
Published:
Publisher Name: Apress, Berkeley, CA
Print ISBN: 978-1-4302-5989-3
Online ISBN: 978-1-4302-5990-9
eBook Packages: Professional and Applied ComputingProfessional and Applied Computing (R0)Apress Access Books








 representing an external nondominant solution set archive.
representing an external nondominant solution set archive. .
.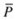 that are covered by other members of
that are covered by other members of  (or dominated solutions).
(or dominated solutions). exceeds a given threshold, prune
exceeds a given threshold, prune 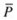 , using clustering.
, using clustering.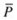 .
.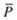 (
(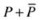 ). Tournament selection creates selection pressure by holding a “tournament” among randomly selected individuals from the current population (
). Tournament selection creates selection pressure by holding a “tournament” among randomly selected individuals from the current population ( ). The winner of each tournament (the individual with the best fitness) is inducted into the mating pool. The mating pool has higher average fitness, compared with the average population fitness, and helps build selection pressure, which improves the average fitness of successive generations.
). The winner of each tournament (the individual with the best fitness) is inducted into the mating pool. The mating pool has higher average fitness, compared with the average population fitness, and helps build selection pressure, which improves the average fitness of successive generations.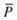 Solutions
Solutions in the external nondominated solution set is a member of a distinct cluster.
in the external nondominated solution set is a member of a distinct cluster. then,
then,
 is the Euclidian distance between the objective space of two individuals, and
is the Euclidian distance between the objective space of two individuals, and  is the population of cluster c
k.
is the population of cluster c
k.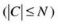
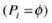 .
.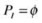 .
. of size 2N .
of size 2N .
 Number of solutions
Number of solutions
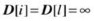 --------[For i = 2 to i £ (l −1) ]-----------------------
--------[For i = 2 to i £ (l −1) ]-----------------------



