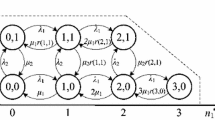
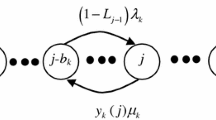
Abstract
We describe a diffusion approximation model for an ATM statistical multiplexer using the instantaneous return model approach (Gelenbe, 1975). Two Cell Loss Estimates are proposed for multiclass traffic. Our aim is to provide a novel conservative, accurate and computationally efficient method for predicting cell loss probabilities which we call the Finite Buffer Diffusion Cell Loss Estimate (FBDCLE) and Infinite Buffer Diffusion Cell Loss Estimate (IBDCLE). We evaluate their accuracy by comparing them with simulation results using a wide variety of input traffic characteristics. In particular we test the model with traffic which is a mixture of different “On-Off” sources with varying loads. Both homogeneous and heterogeneous aggregated arrival processes have been taken into account. These comparisons, which include evaluations of the statistical confidence of the simulation runs, show that our model predictions are very close to the simulation results. In particular, FBDCLE is a conservative upper bound to cell loss ratio, while the other (IBDCLE) provides an accurate predictor which may slightly under-estimate or over-estimate cell loss.
Chapter PDF
Similar content being viewed by others
Keywords
References
D. R. Cox and P. A. W. Lewis (1966). The Statistical Analysis of Series of Events. Methuen, London.
A. Duda (1986). Diffusion approximations for time-dependent queueing systems. IEEE J. SAC, SAC–4(6), 905–18.
E. Gelenbe (1975). On approximate computer system models. J. ACM, 22, 261–3.
R. Guerin and L. Gun (1992). A unified approach to bandwidth allocation and access control in fast packet-switched networks. Proc. INFOCOM’92, 1–12.
E. Gelenbe and G. Pujolle (1976) An approximation to the behaviour of a single queue in a network. Acta Informatica, 7, 123–36.
H. Akimaru, T. Okuda and K. Nagai (1994) A Simplified Performance Evaluation for Bursty Multiclass Traffic in ATM Systems. IEEE Transactions on Communications, COM–42(5), 2078–83.
H. Heffes and D. M. Lucantoni (1986) A markov modulated characterization of packetized voice and data traffic and related statistical multiplexer performance. IEEE J. SAC, SAC–4(6), 856–67.
H. Kobayashi (1974) Application of the diffusion approximation to queueing networks: Parts I and II. J. ACM, 21, 316–28.
H. Kobayashi and Q. Ren (1993) A diffusion approximation analysis of an ATM statistical multiplexer with multiple state solutions: Part I: Equilibrium state solutions. Proc. ICC’93, 1047–53.
J. Medhi (1991) Stochastic Models in Queueing Theory. Academic Press, New York.
K. Sriram and W. Whitt (1986) Characterizing superposition arrival processes in packet multiplexers for voice and data. IEEE J. SAC, SAC–4 (6), 833–46.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1996 IFIP International Federation for Information Processing
About this chapter
Cite this chapter
Gelenbe, E., Mang, X., Feng, Y. (1996). A Diffusion Cell Loss Estimate for ATM with Multiclass Bursty Traffic. In: Kouvatsos, D.D. (eds) ATM Networks. ATM 1995. IFIP Advances in Information and Communication Technology. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-35068-4_13
Download citation
DOI: https://doi.org/10.1007/978-0-387-35068-4_13
Publisher Name: Springer, Boston, MA
Print ISBN: 978-1-5041-2902-2
Online ISBN: 978-0-387-35068-4
eBook Packages: Springer Book Archive