Abstract
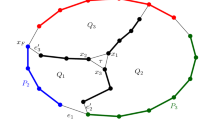
Given a graph G=(V, E), four distinct vertices u 1,u2,u3,u4 ∈ V and four natural numbers n 1, n2, n3, n4 such that \(\sum\nolimits_{i = 1}^4 {n_i = |V|}\), we wish to find a partition V 1, V2, V3, V4 of the vertex set V such that u i ∈ Vi, ¦Vi¦=ni and V i induces a connected subgraph of G for each i, 1 ≤ i ≤ 4. In this paper we give a simple linear-time algorithm to find such a partition if G is a 4-connected planar graph and u 1, u2, u3, u4 are located on the same face of a plane embedding of G. Our algorithm is based on a “4-canonical decomposition” of G, which is a generalization of an st-numbering and a “canonical 4-ordering” known in the area of graph drawings.
Chapter PDF
Similar content being viewed by others
References
M.E. Dyer and A.M. Frieze, On the complexity of partitioning graphs into connected subgraphs, Discrete Applied Mathematics, 10 (1985) 139–153.
S. Even, Graph Algorithms, Computer Science Press, Potomac (1979).
E. Györi, On division of connected subgraphs, Proc. 5th Hungarian Combinational Coll., (1978) 485–494.
E. Györi, Private communication, March 21, 1996.
L. Jou, H. Suzuki and T. Nishizeki, A linear algorithm for finding a nonseparating ear decomposition of triconnected planar graphs, Tech. Rep. of Information Processing Society of Japan, AL40-3 (1994).
G. Kant, A more compact visibility representation, Proc. of the 19th International Workshop on Graph Theoretic Concepts in Computer Science (WG'93), LNCS 790 (1994) 411–424.
G. Kant and X. He, Two algorithms for finding rectangular duals of planar graphs, Proc. of the 19th International Workshop on Graph Theoretic Concepts in Computer Science (WG'93), LNCS 790 (1994) 396–410.
L. Lovász, A homology theory for spanning trees of a graph, Acta Math. Acad. Sci. Hunger, 30 (1977) 241–251.
J. Ma and S. H. Ma, An O(k 2n2) algorithm to find a k-partition in a k-connected graph, J. of Computer Sci. & Technol., 9, 1 (1994) 86–91.
H. Suzuki, N. Takahashi and T. Nishizeki, A linear algorithm for bipartition of biconnected graphs, Information Processing Letters 33, 5 (1990) 227–232.
H. Suzuki, N. Takahashi, T. Nishizeki, H. Miyano and S. Ueno, An algorithm for tripartitioning 3-connected graphs, Journal of Information Processing Society of Japan 31, 5 (1990) 584–592.
K. Wada and K. Kawaguchi, Efficient algorithms for triconnected graphs and 3-edge-connected graphs, Proc. of the 19th International Workshop on Graph Theoretic Concepts in Computer Science (WG'93), LNCS 790 (1994) 132–143.
K. Wada, A. Takaki and K. Kawaguchi, Efficient algorithms for a mixed k-partition problem of graphs without specifying bases, Proc. of the 20th International Workshop on Graph Theoretic Concepts in Computer Science (WG'94), LNCS 903 (1995) 319–330.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1997 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Nakano, Si., Rahman, M.S., Nishizeki, T. (1997). A linear-time algorithm for four-partitioning four-connected planar graphs. In: North, S. (eds) Graph Drawing. GD 1996. Lecture Notes in Computer Science, vol 1190. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-62495-3_58
Download citation
DOI: https://doi.org/10.1007/3-540-62495-3_58
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-62495-0
Online ISBN: 978-3-540-68048-2
eBook Packages: Springer Book Archive