Keywords

1 Introduction

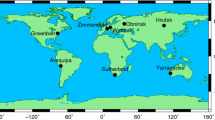
The combination of the space geodetic techniques constituting the ITRF is performed using the local ties at fundamental sites (Ray and Altamimi 2005). However, multiple sites show discrepancies beyond the requirements of the Global Geodetic Observing System (GGOS): positions ≤1 mm and velocities ≤0.1 mm/yr (Rothacher et al. 2009). For instance, based on the tie discrepancies of the ITRF2014, Fig. 1 shows that the differences in east, north and up components for a GNSS-to-GNSS baseline surpasses largely the 1 mm requirement at several sites (Altamimi et al. 2016). The same can be observed for baselines with GNSS to SLR, and GNSS to VLBI, with discrepancies in the cm-level. Some sites, such as the Geodetic Observatory Wettzell in Germany (Fig. 2), are equipped with more than one instrument of the same technique. Thus, very short baselines of the same technique can be formed. These short baselines provide the perfect opportunity to study technique-specific systematic and time-dependent biases, as the baselines are known precisely from terrestrial measurements (local ties), the relative atmospheric delays can be modelled and a common clock can be used. In particular for Wettzell, a VLBI short baseline, a SLR short baseline, and multiple GNSS short baselines are available. Within the scope of this project, several experiments with short baselines have been performed to continuously monitor the local ties, and detect technique-specific systematic and time-dependent biases which are affecting the performance of the different geodetic techniques. The study of intra-technique experiments is expected to lead to a better understanding of system-specific error sources, biases and delays and constitutes an essential step for the realisation of a highly precise terrestrial reference frame that fulfils the demanding requirements of today and the future.

Fig. 1
figure 1

ITRF2014 tie discrepancies [mm] at selected co-location sites according to Altamimi et al. (2016)

Full size image
Fig. 2
figure 2

Co-located instruments at the Geodetic Observatory Wettzell. Credits: IAPG TU-München

Full size image

2 Multi-Year Analysis of GNSS Short Baselines at Co-location Sites

The first of these intra-technique co-location experiments deals with GNSS short baselines. For the network of GNSS stations in Wettzell, 15 years of GNSS data were reprocessed, using a tailored parameterisation, based on double differences with ambiguity fixing, with six different solutions: Single frequency L1 and L2, ionosphere-free linear combination (L3), with (TR) and without (NT) the estimation of relative tropospheric delays. The assumption is that for such a small distance and small height difference, tropospheric delays can be modelled (Beutler et al. 1987; Dilßner et al. 2008; Saastamoinen 1972), or cancelled out. This reprocessing yielded highly consistent time series, with repeatabilities for the east and north component below 1 mm, and 2 mm for the up component. Figure 3 shows the repeatability for the up component of the station WTZZ with respect to WTZR, for each investigated solution, where seasonal outliers associated with snow on the antennas, noise variations due receiver changes and, in general, site-specific events can be observed. This analysis shows that single-frequency solutions without estimation of the relative troposphere have better performance in terms of repeatabilities, than the linear combinations or the solutions with the estimation of relative troposphere. In particular, the solution L3-TR shows an amplified noise and considerably larger outliers. It is worth mentioning that this solution is equivalent to that used for global solutions, hence the relevance of its characterisation.

Fig. 3
figure 3

Repeatabilities for the up component of station WTZZ (with respect to WTZR)

Full size image

In addition, we compare the GNSS-based solutions with the local tie at the epoch of the local tie. According to the log files of the stations, the Wettzell site has reported local ties with a precision better than 2 mm (IGS 2017). Figure 4 shows the differences for all the baselines at Wettzell, where the worst performance for the baseline WTZZ-WTZR is given by the L3 solution with troposphere estimates. The general performance at the site includes discrepancies up to 9 mm for the height component, when the estimation of the relative troposphere is involved. A detailed analysis for this and several other co-location sites part of the ITRF2014 solution is shown in Herrera Pinzón and Rothacher (2018).

Fig. 4
figure 4

Differences between GNSS-based baselines and local ties [mm] in Wettzell, at the epoch of the local tie

Full size image

3 Assessment of the VLBI Short Baseline at Wettzell

The second type of intra-technique co-location experiment performed uses the short VLBI baseline at Wettzell, realised by the 20 m RTW telescope and the 13m TWIN1 telescope. We used 57 VLBI sessions of the IVS campaign, which contain the baseline RTW–TWIN1, between July 2015 and June 2016 (Behrend 2013). The local Wettzell baseline is not present after January 26th, 2016. Similarly to GNSS, four different approaches have been studied, where the modelling of the dry atmosphere, the solid Earth tides and ocean loading were common for all these solutions. The first approach (GLO) is a global solution, where all VLBI observations are used. Zenith wet delays are estimated as a piece-wise linear function with 2 h intervals using the wet VMF model for mapping. Receiver clock offsets are parametrised as a linear polynomial during the session, for each station except for RTW. The second processing approach (BAS) is a short baseline solution, where only the RTW-TWIN1 baseline observations are used. Receiver clock offsets are calculated each 24 h for TWIN1, for each session. The main feature of this approach is that the troposphere delays between the two stations are not estimated, based on the assumption that for such a small distance and small height difference, differences in tropospheric delays can be modelled, e.g. with the dry part of the Saastamoinen (1972) model. Similarly, the third approach (BA2) is also a baseline solution. However, in this solution zenith wet tropospheric delays are estimated piece-wise linearly with a time resolution of 2 h and mapped with the wet VMF model for RTW. Finally, for the outage of data in 2016, the (BA3) solution uses the station NYALES20, in Ny-Alesund (Svalbard, Norway) to connect the two Wettzell telescopes. Receiver clock offsets are defined as in the BA2 solution and zenith wet tropospheric delays are set up as for the GLO solution. Figure 5 shows the standard deviation of the residuals of the estimation process, where the local solutions have evidently lower level of noise. A deeper explanation of the modelling and parameterisation used to obtain these results can be found in Herrera Pinzón et al. (2018). Based on these solutions, we performed the comparison of the VLBI-based solution and the local ties, regarding the baseline length (123.3070 m ± 0.7 mm) (Kodet et al. 2018). The differences obtained for these solutions have an overall satisfactory mean behaviour, with a mean over the time series below 1 mm, even for the global solution. However, the largest difference is the scatter of these time series: The global solutions have standard deviations of about 5 mm, while the local solutions display a standard deviation of around 1 mm.

Fig. 5
figure 5

Time series of the standard deviation of the residuals of the VLBI processing for each investigated solution

Full size image

Similarly to the processing of GNSS short baselines, the BAS solution (without estimation of relative troposphere) shows the best time series of results (Fig. 6). The mean of the differences over time for each solution are at the sub-mm level, namely GLO: − 0.8 ± 4.9, BA3: − 0.2 ± 4.6, BAS: − 0.3 ± 0.8, BA2: − 0.1 ± 1.3. A more comprehensive discussion of these results can be found in Herrera Pinzón et al. (2018).

Fig. 6
figure 6

Comparison of the VLBI-based baseline and the baseline derive from the local ties between the telescopes at Wettzell

Full size image

4 Differencing Approaches for SLR Short Baselines

Forming differences is a standard approach in GNSS processing. But simultaneous SLR observations from one telescope to two satellites are impossible. However, Pavlis (1985) and Svehla et al. (2013) introduced the concept of quasi-simultaneity to build differences. Two observations are considered quasi-simultaneous if they lie within a specified time window. Figure 7 shows the concept of quasi-simultaneity for an SLR baseline, where time windows for the observation from telescope 2 with respect to telescope 1 are t1 and t2 for satellite 1 and 2, respectively. With this idea, the goal is to test the potential of the differencing approaches, namely single- and double-differences, for the estimation of geodetic parameters. It is expected that single-difference observations from two stations to one satellite will remove biases related to the satellite orbit and the retro-reflectors. Similarly, quasi-simultaneous single-differences to two satellites can remove station-dependent range errors. These differences, together with the original ranges (zero-differences), are used to get estimates of both satellite- and station-specific error sources, so that systematic effects common to both stations can be identified at mm-level. Moreover, this approach can be potentially used to improve the processing of classical SLR observations of GNSS and LEO satellites, and to estimate accurate local ties. Initially, the residuals of the zero-difference processing are used to build the single- and double-differences. These observables are then used in a so-called zero test, where no geodetic parameters are estimated. Instead, coordinates of the stations are fixed to the local tie values and the atmospheric parameters are calculated with the standard model of Marini and Murray (1973). The zero-difference residuals for the short SLR baseline at Wettzell, realised by the telescopes WLRS and SOS-W, for July 3rd, 2018, are displayed in Fig. 8. Only GLONASS and Galileo satellites were used for this initial assessment.

Fig. 7
figure 7

Concept of quasi-simultaneity for the differencing SLR observations, together with the error sources targeted with these approaches

Full size image
Fig. 8
figure 8

Skyplot of the residuals of the zero-test, as seen at each SLR station, using the original observations (zero-differences)

Full size image

4.1 Single-Difference Residuals [2 Telescopes to 1 Satellite]

Figure 9 shows the single-difference residuals grouped by constellation, allowing for mis-synchronisation of 3 h (quasi-simultaneity). This analysis reveals that the residuals are evidently biased, with a mean value of −26.3 mm, a value related to the range biases of WLRS and SOS-W. An extensive analysis of these biases is discussed in details in Riepl et al. (2019). Not only range biases can be observed within these differences, but, after removing the mean bias, errors associated to the orbits are also noticeable (Fig. 10), especially for Galileo satellites. The identification of orbital errors is therefore an advantage of this approach.

Fig. 9
figure 9

Single-differences from 2 telescopes to 1 satellite. Left: Galileo satellites. Right: GLONASS satellites

Full size image
Fig. 10
figure 10

Single-differences from 2 telescopes to 1 satellite, after removing the mean bias. Left: Galileo satellites. Right: GLONASS satellites

Full size image

4.2 Single-Difference Residuals [1 Telescope to 2 Satellites]

Single-differences of residuals from the same telescope to two satellites can also be built. Allowing a quasi-simultaneity of 24 h, the time series of differenced residuals per station is depicted in Fig. 11. The blue coloured residuals indicate two Galileo satellites, the red coloured two GLONASS satellites, and the green colour is used when the difference is built using one satellite from each system. One feature stands out in the time series: the poor performance of some Galileo satellites, due to their orbit errors, produces the largest residuals throughout the time series. In particular Galileo satellites E01 and E05 show the largest residuals. This is observed for both telescopes. This identification, and also the removal of orbital issues is a great advantage of the differencing approaches.

Fig. 11
figure 11

Time series of single-differences from 1 telescope to 2 satellites. Top: Telescope SOS-W. Bottom: WLRS. The x-axis indicates the time difference between the two observations used to build the differences, namely the quasi-simultaneity

Full size image

4.3 Double-Difference Residuals

Finally, in the same fashion, the double-difference residuals are built. Figure 12 shows all the possible differences that can be built when allowing a quasi-simultaneity of 24 h. Based on the single differences from one telescope to two satellites, for SOS-W in the x-axis and WLRS in the y-axis, 63,452 differences were available. These residuals range from −10 to 10 cm, with a mean value of 1.2 mm and a scatter of 24 mm. This behaviour is heavily influenced by the bad performances of the aforementioned Galileo satellites. Considering only those double differences of GLONASS satellites during the first 30 min of the simultaneity (t1 < 30 &t2 < 30), the differenced residuals improve considerably in terms of scatter, with an standard deviation of 5.3 mm, with a mean value of −0.7 mm, for 150 differences. These results indicate that quasi-simultaneous SLR differences are feasible, and that it is possible to obtain double-difference residuals close to the sub-mm level. In turn, the use of SLR differenced observations constitutes a valuable observable for the estimation of geodetic parameters through SLR.

Fig. 12
figure 12

Double-differences of SLR residuals. The x-axis indicates the time difference allowed to build the single differences from the SOS-W telescope to two satellites. Similarly, the y-axis shows the time difference allowed to build the single-differences from the WLRS telescope to two satellites. Finally, the colour bar indicates the value of the residual

Full size image

5 Conclusions and Outlook

The overarching goal of this work lies in determining the potential of intra-technique studies on short baselines for the understanding of technique-specific biases and errors and the monitoring of local ties. Experiments on GNSS to GNSS, SLR to SLR and VLBI to VLBI short baselines are assessed, where multiple local and environmental effects are investigated. In particular, the analysis of GNSS short baselines showed cm-level discrepancies with respect to local ties, for a processing strategy which is equivalent to that used in global solutions. On the other hand, the study of a short VLBI baseline showed mm to sub-mm agreement of the estimated baseline with the local tie. The benefits from the accurate and common timing estimation, for the determination of height and troposphere, were investigated. Finally, a concept for the differencing of SLR observables was studied, where mm-level double-difference residuals were found. Besides allowing the identification of station- and orbital biases, and based on the size of these residuals, this method is expected to be suitable for the estimation of geodetic parameters. These findings are expected to be extended in future experiments. Replacing the estimation of clock corrections, by a Two Way Optical Time and Frequency System is expected to make the estimation of VLBI clock corrections unnecessary. The SLR differencing approaches are expected to be useful for the estimation of coordinates and the assessment of local ties. Finally inter-technique experiments on very short baselines, including GNSS and VLBI observations are foreseen, where the challenge will be the assessment of biases among the space geodetic techniques and the study of the benefits from a rigorous GNSS-VLBI combination of all common parameter types.