Abstract
This paper describes a practical implementation of the International Height Reference System (IHRS) in Argentina. The contribution deals with the determination of potential values W(P) at five Argentinean stations proposed to be included in the reference network of the International Height Reference Frame (IHRF). All sites are materialized with GNSS stations of the Argentine continuous satellite monitoring network and most of them are included in the SIRGAS Continuously Operating Network. Not all the stations are connected to the National Vertical Reference System 2016 and most of them are near to an absolute gravity station measured with an A10 gravimeter.
This paper also discusses the approach for the computation of W(P) at the IHRF stations using the Argentinean geoid model GEOIDE-Ar 16 developed by the Instituto Geográfico Nacional, Argentina together with the Royal Melbourne Institute of Technology (RMIT) University, Australia using the remove-compute-restore technique and the GOCO05s satellite-only Global Gravity Model. Then, geoid undulations (N) were transformed to height anomalies (ζ) in order to infer W(P) at the stations located on the Earth’s surface. The transformation from N to ζ must be consistent with the hypothesis used for the geoid determination. Special emphasis is made on the standards, conventions and constants applied.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Argentinean stations to the IHRF reference network
- GEOIDE-Ar 16
- International Height Reference System and Frame
1 Introduction
During the 26th General Assembly of the International Union of Geodesy and Geophysics (IUGG) held from June 22 to July 2, 2015 in Prague, Czech Republic, the International Association of Geodesy (IAG) released the Resolution No. 1 that outlines five conventions for the definition and realization of an International Height Reference System (IHRS; Drewes et al. 2016). The definition is given, cf. Ihde et al. (2017, Section 5) and cf. Sánchez and Sideris (2017, Section 1), by:
-
1.
The vertical coordinate is given in terms of geopotential quantities: potential values W(P) or geopotential numbers C(P) referred to an equipotential surface of the Earth’s gravity field realized by the conventional value W0 = 62636853.40 m2 s−2 (Sánchez et al. 2016):
$$\displaystyle \begin{aligned} C(P)=W_0 - W(P)=-\varDelta W(P). {} \end{aligned} $$(1) -
2.
The spatial reference of the position P for the gravity potential W(P) = W(X) is given by the coordinate vector X of the International Terrestrial Reference Frame (ITRF; Altamimi et al. 2016).
-
3.
The estimation of X(P), W(P) or C(P) includes their variation with time; i.e., \(\dot {X}(P)\), \(\dot {W}(P)\) or \(\dot {C}(P)\).
-
4.
This resolution also states that parameters, observations and data shall be related to the mean tidal system/mean crust.
-
5.
The unit of length is the meter and the unit of time is the second (SI).
The realization of the IHRS is called International Height Reference Frame (IHRF) and it corresponds to a set of physical points (continuously operated stations) with precise potential values W(P), or geopotential numbers C(P) and geometrical coordinates X(P), see Ihde et al. (2017).
Five sites have been selected along Argentina to be included in the IHRF, from north to south: Salta (UNSA), San Juan (OAFA), La Plata (AGGO), Rio Gallegos (UNPA) and Rio Grande (RIO2). Figure 1 illustrates the location of each station and the space geodetic and gravimetric techniques that are operated in each station. Figure 1 also shows the topography.
The Argentinean-German Geodetic Observatory (AGGO) is a fundamental geodetic observatory located in the east-central part of Argentina, close to the city of La Plata. The observatory was moved in 2015 from Concepcion, Chile, to La Plata and is currently operated jointly by the German Federal Agency for Cartography and Geodesy (BKG) and the National Scientific and Technical Research Council of Argentina (CONICET). Very Long Baseline Interferometry (VLBI) and Satellite Laser Ranging (SLR) techniques are co-located with Global Navigation Satellite System (GNSS). A gravity laboratory is established at AGGO where the superconducting gravimeter (SG) SG038 has been continuously recording gravity changes since December 16th, 2015 (Antokoletz et al. 2017). Moreover, on January 2018, an absolute gravimeter FG5 was installed to set an absolute gravity reference for the station. AGGO is a reference station of the new International Gravity Reference Frame (IGRF). As precise time keeping is essential, different atomic clocks are also installed at AGGO.
All GNSS stations with the exception of OAFA contribute to the continuously operating reference network of the Geocentric Reference System for the Americas (SIRGAS-CON; Sánchez and Brunini 2009) but all the stations are included in the Argentine Continuous Satellite Monitoring Network (RAMSAC; Piñón et al. 2018). UNSA, AGGO and RIO2 belong to the global network of the International GNSS Service (IGS; Johnston et al. 2017).
The current terrestrial reference frame of Argentina is Posiciones Geodesicas Argentina 2007 (POSGAR07), based on ITRF2005 with epoch 2006.632 (Cimbaro et al. 2009).
At present, only AGGO is connected to the National Vertical Reference System 2016 (SRVN16) (Piñón et al. 2016) for vertical datum unification.
2 Computation of Potential Values W(P)
This contribution presents the calculation of potential values recovered from the existing Argentinean geoid model GEOIDE-Ar 16 (Piñón 2016), described in the next section and also shows the computation of potential values based on Global Gravity Models (GGMs) of high-degree.
2.1 Potential Values W(P) Recovered from an Existing Geoid Model
The potential value W(P) can be understood as the sum of the disturbing potential T(P) determined as a solution of a geodetic boundary value problem (GBVP) at the known position P(X) on the Earth’s surface plus the normal gravity potential U(P) at the same point using the formula (2-224) from Hofmann-Wellenhof and Moritz (2005):
with:
where U0 is the normal potential at the reference ellipsoid, hP is the ellipsoidal height and the gradient of the normal potential \(\frac {\partial U_0}{\partial h}\) is the normal gravity value (γP) at P.
Equation (2) can be written as:
In Argentina, the disturbing potential and geoid were solved applying the classical Stokes approach (Piñón 2016). The disturbing potential was determined at a point P0 on the geoid. Spherical harmonics of degrees zero and one were not considered in the geoid heights derived from the GBVP solution (NGBVP). The zero-degree term (Eq. (5)) was added to NGBVP. Then, geoid heights (N = NGBVP + N0) were converted to height anomalies (ζ). The zero-degree term takes into account the difference between the Earth’s and reference ellipsoid’s geocentric gravitational constant (GM) and also the difference between the reference potential W0 value adopted by the IHRS and the normal potential U0 on the reference ellipsoid.
The zero-degree term can be derived with:
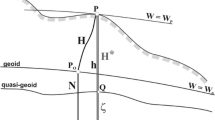
where the GMGGM is the geocentric gravitational constant of the GGM, GMGRS80 is the geocentric gravitational constant of the Geodetic Reference System 1980 (GRS80; Moritz 2000), \(\gamma _{Q_0}\) is the normal gravity on the reference ellipsoid and \(r_{P_0}\) is the geocentric radial distance of the point P0. See Fig. 2 for the position of P0, Q0, P and Q.
Heights and reference surfaces (modified from Sánchez et al. 2018)
The basic relation for the geoid–quasigeoid separation is obtained using the formula (8-113) of Hofmann-Wellenhof and Moritz (2005):
where \(\overline {\gamma }\) is the mean normal gravity between a point Q0 on the ellipsoid and the corresponding point Q on the telluroid; \(\overline {g}\) is the mean gravity along the real plumbline between P0 on the geoid and P on the Earth’s surface, H the orthometric height and ΔgB is the Bouguer gravity anomaly.
The transformation from N to ζ must be consistent with the hypothesis of masses applied for the geoid computation (Sánchez et al. 2018), that in the case of Argentina, it was the Helmert’s second method of condensation: the topographic masses are shifted and condensed to a surface layer on the geoid (Hofmann-Wellenhof and Moritz 2005).
Once the geoid is transformed to quasigeoid, the potential values W(P) can be inferred using Eq. (4) as:
Since the IAG resolution No. 1 has also stated that parameters, observations, and data should be related to the mean tidal system/mean crust, the ITRF ellipsoidal heights were transformed from tide-free system (TF) to mean-tide system (MT) following Petit and Luzum (2010) and Sánchez and Sideris (2017):
where φ is the ellipsoidal latitude.
Regarding geoid undulations, they were transformed from the tide-free system to the mean-tide system following (Ekman 1989):
where k = 0.30190, being consistent with the Love numbers proposed in Petit and Luzum (2010).
2.2 Estimation of Potential Values W(P) with Global Gravity Models
Potential values W(P) can be estimated by the combination of ITRF positions with global gravity models in terms of Stokes spherical harmonics coefficients (Cnm, Snm) of high degree, where n is the degree, nmax the maximum degree and m the order (Eq. (10); Hofmann-Wellenhof and Moritz 2005):
where \(P_{nm}(\sin \phi )\) represents the first class Legendre associated functions evaluated in \(\sin \phi \), a is the semi-major axis of the Earth and Φ is the centrifugal potential at point P. (r, λ, ϕ) are the spherical geocentric coordinates of the computation point (P) transformed from ellipsoidal coordinates (h, λ, φ) using the transformation formulas found in Hofmann-Wellenhof and Moritz (2005).
3 Data Used
3.1 Geoid Model GEOIDE-Ar 16
GEOIDE-Ar 16 is the current official geoid model for Argentina (Piñón 2016). It is the result of a gravimetric geoid model with a spatial resolution of 1′× 1′, fitted to the Argentinean vertical datum though the determination of a corrective trend surface, which was computed using the co-located GPS/Levelling benchmarks. GEOIDE-Ar 16 was developed by the Instituto Geográfico Nacional (IGN), Argentina together with the Royal Melbourne Institute of Technology (RMIT) University, Australia using the remove-compute-restore technique (Schwarz et al. 1990) and the GOCO05s GGM (Mayer-Gürr et al. 2015) up to degree 280, together with 671,547 gravity measurements referred to the International Gravity Standardization Net 1971 (IGSN71; Morelli et al. 1972), on the Argentine continental territory, its neighboring countries, Islas Malvinas and the coastal (marine) areas. For the regions with lack of gravity observations, the DTU13 world gravity model (Andersen et al. 2013) was applied to fill in the gravity voids.
For the determination of the potential values in this contribution, the “pure gravimetric geoid” before fitting it to the Argentinean vertical datum is used. The zero-degree term previously computed with Eq. (5) has been added to the “pure gravimetric geoid” since it was not taken into account for the geoid computation (Piñón 2016).
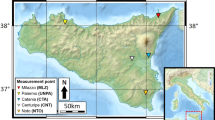
3.2 Gravity Data Around the Proposed IHRF Stations
The distribution of relative terrestrial and shipborne gravity data used for the determination of the gravimetric geoid around each IHRF station can be seen in Fig. 3 (blue points). Figure 3 also shows the nearest absolute gravity stations that belong to the Red Argentina de Gravedad Absoluta (RAGA, Lauría et al. 2017), which were measured with a Micro-g LaCoste A10 (red points). The absolute gravity measurement made at AGGO with a Micro-g LaCoste FG5 is also included (yellow point).
Different buffer radius of 10, 50, 110 and 200 km are depicted in Fig. 3. Following Sánchez et al. (2017), the minimum amount of gravity points required is 5 inside the radius of 10 km, 15 inside the 50 km, 30 inside the 110 km and 45 inside the 210 km. Each circle is divided into 1, 4, 7 and 11 compartments, respectively. From Fig. 3, we can observe that the gravity data do not fulfill the requirements of density and distribution around each IHRF station. Approximately, one hundred stations homogeneously distributed around the IHRF stations up to a distance of 200 km are required (Sánchez et al. 2017). Since UNSA and OAFA are located in a rough area in the Andes, more stations homogeneously distributed are needed.
3.3 Standards
Some standards used for the computation of the “pure gravimetric geoid” were examined, following some agreements for the computation of the station potential values as IHRF coordinates, geoid undulations and height anomalies within the Colorado 1 cm geoid experiment (Sánchez et al. 2018). The numerical values for the constant of gravitation (G), the geocentric gravitational constant (GM), the mean angular velocity of the Earth (ω), the average density of the topographic masses (ρ) used to apply gravity reductions for geoid computation were the same as those proposed in Sánchez et al. (2018).
The GRS80 that provides the numerical value for the parameters of the geodetic Earth model was used. GOCO05s was the GGM taken into account for the remove-compute-restore technique in the geoid computation of Argentina. First-degree Stokes coefficients were assumed to be zero (Earth’s center of masses aligned with the ITRF coordinates).
In Sect. 2.1, the parameters involved in the equations are listed below:
-
W0 = 62636853.40 m2 s−2, is the reference potential value adopted by the IHRS.
-
U0 = 62636860.85 m2 s−2, is the normal potential on the GRS80 reference ellipsoid.
-
GMGGM = 3.986004415 × 1014 m3 s−2.
-
GMGRS80 = 3.986005 × 1014 m3 s−2.
Atmospheric correction was applied to the terrestrial gravity data (Piñón 2016).
4 Results and Discussion
To determine the potential values W(P), the “pure gravimetric” geoid (see Sect. 3.1) was used and the zero-degree term of the geoid (Eq. (5)) was added. The resulted geoid was then transformed from tide-free system to mean-tide system using Eq. (9).
Geoid undulations were converted into height anomalies taking into account the N-ζ transformation according to Eq. (6), using the refined Bouguer gravity anomalies computed with SRTMv4.1 and SRTM30_plus_v10 (Jarvis et al. 2008; Becker et al. 2009).
Table 1 shows N and ζ for each IHRF station in Argentina and the potential value W(P) computed applying Eq. (7). It can be seen that for those stations located near the coast, N and ζ are practically identical while for those stations located near the Andes the differences reach 10 cm for OAFA and 20 cm for UNSA.
For AGGO, IGN has provided a geopotential number C(P) = 230.284 m2 s−2 from gravity and levelling survey (Piñón et al. 2016). Then, the potential value can be estimated with W(P) = W0 − C(P) = 62636623.12 m2 s−2. The difference of 0.67 m2 s−2 (∼6 cm) with the potential value estimated in this contribution can be attributed to the fact that C(P) was obtained from levelling survey referred to a local vertical datum (long-term mean sea level measured at a selected tide-gauge).
Potential values from several high-degree (up to nmax = 2190) GGMs were obtained in order to compare them with those computed in this contribution. EGM2008 model (Pavlis et al. 2012), EIGEN-6C4 model (Förste et al. 2014) and the experimental gravity field model XGM2019e_2159 (Zingerle et al. 2019), were evaluated. The computations were done using the International Centre for Global Earth Models computation service (ICGEM; http://icgem.gfz-potsdam.de/; Ince et al. 2019). The tidal system and reference ellipsoid were selected being consistent with what is previously discussed. Table 2 and Fig. 4 shows the differences between the obtained potential values and those derived from the GGMs. Differences are consistent between models: those stations located near the coast (AGGO, UNPA and RIO2) present differences between 1 to 2 m2 s−2, while for stations located near the Andes (UNSA and OAFA), differences are larger. These results become more clear analyzing the differences between potential values computed from the selected GGMs (see also Table 2). Regarding the expected accuracy of the potential values derived from GGMs, Rummel et al. (2014) and Sánchez and Sideris (2017) proposed that the mean accuracy applying one GGM is ± 0.4 to ± 0.6 m2 s−2 in well-surveyed areas, and about ± 2 to ± 4 m2 s−2 with extreme cases of ± 10 m2 s−2 in sparsely surveyed regions. In this sense, the results shown in Table 2 allow to conclude that: more terrestrial gravity data should be included to improve the accuracy of the potential values, especially in regions with rough heights; and, at present, GGMs of high-degree are not accurate enough to derive potential values of the IHRF stations in Argentina.
Finally, the certainty of the potential values presented in this paper is mainly limited by three aspects:
-
1.
The accuracy of the geoid model taken into account. In order to improve it, more terrestrial gravity data should be included in the geoid computation, especially in the vicinity of the selected IHRF stations;
-
2.
the approximation used in Eq. (6) to transform from N to ζ, which could cause errors of several cm in mountain areas (Flury and Rummel 2009). An extensive approach (e.g. Flury and Rummel 2009; Sjöberg 2010) for the transformation should be evaluated in the future; and,
-
3.
the transformation from N to ζ itself. More reliable W(P) could be obtain by computing a local quasigeoid model for each station.
5 Conclusions and Future Work
This contribution presents the five Argentinean stations that were selected to belong to the global reference network of the IHRF. These stations are named UNSA, OAFA, AGGO, UNPA and RIO2.
All these stations are continuously monitored to detect deformations of the reference frame and they are referred to the ITRS/ITRF to know with high-precision the geometric coordinates. It is desirable that OAFA would be included in the SIRGAS-CON network (Sánchez and Brunini 2009). Currently, UNSA, UNPA, OAFA and RIO2 are not connected to the local vertical datum (SRVN16; Piñón et al. 2016). The connection will be done in the future.
AGGO is a fundamental geodetic observatory where several geodetic techniques are co-located with absolute and superconducting gravity meters, enabling the connection between X, W and gravity.
Preliminary potential values were obtained for the stations selected. They were recovered from the existing geoid model for Argentina GEOIDE-Ar 16 without fitting it to GPS/Levelling benchmarks. Potential values were also derived from high-degree GGMs. Differences between models show that present GGMs are not accurate enough for the estimation of potential values of the selected stations in Argentina to integrate the IHRF.
For a precise transformation from geoid values to height anomalies, orthometric heights and gravity observations should be available for all stations. Moreover, two aspects should be evaluated in the future: (a) the transformation applied from geoid undulations to height anomalies, which could be not accurate enough; and (b) the gravity data around the stations. In this sense, homogeneously gravity data should be distributed around the IHRF reference stations up to 210 km (∼2∘) with a minimum accuracy of the gravity values of ±20 μGal, especially for those stations located in the Andes region (OAFA and UNSA).
As a consistent comparison of the obtained potential values, geopotential numbers should also be available from gravity and levelling surveys connected to the national vertical reference system (SRVN16).
References
Altamimi Z, Rebischung P, Métivier L, Collilieux X (2016) ITRF2014: a new release of the international terrestrial reference frame modeling nonlinear station motions. J Geophys Res Solid Earth 121:6109–6131. https://doi.org/10.1002/2016JB013098
Andersen OB, Knudsen P, Kenyon SC, Factor JK, Holmes S (2013) The DTU13 global marine gravity field. Ocean Surface Topography Science Team meeting 2013. Boulder, USA
Antokoletz ED, Wziontek H, Tocho C (2017) First six months of superconducting gravimetry in Argentina. In: Vergos G, Pail R, Barzaghi R (eds) International symposium on gravity, geoid and height systems 2016. International association of geodesy symposia, vol 148. Springer, Cham. https://doi.org/10.1007/1345_2017_13
Becker JJ, Sandwell DT, Smith WHF, Braud J, Binder B, Depner J, Fabre D, Factor J, Ingalls S, Kim S-H, Ladner R, Marks K, Nelson S, Pharaoh A, Trimmer R, Von Rosenberg J, Wallace G, Weatherall P (2009) Global bathymetry and elevation data at 30 arc seconds resolution: SRTM30_PLUS. Mar Geod 32(4):355–371. https://doi.org/10.1080/01490410903297766
Cimbaro SR, Lauría EA, Piñón DA (2009) Adopción del Nuevo Marco de Referencia Geodésico Nacional. Paper presented to Instituto Geográfico Militar, Buenos Aires, Argentina
Drewes H, Kuglitsch F, Adám J, Rózsa S (2016) The geodesist’s handbook 2016. J Geod 90:907. https://doi.org/10.1007/s00190-016-0948-z
Ekman M (1989) Impacts of geodynamic phenomena on systems for height and gravity. Bull Géod 63(3):281–296. https://doi.org/10.1007/BF02520477
Flury J, Rummel R (2009) On the geoid–quasigeoid separation in mountain areas. J Geod 83(9):829–847. https://doi.org/10.1007/s00190-009-0302-9
Förste C, Bruinsma SL, Abrikosov O, Lemoine J-M, Marty JC, Flechtner F, Balmino G, Barthelmes F, Biancale R (2014) EIGEN-6C4 the latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Services. http://doi.org/10.5880/icgem.2015.1
Hofmann-Wellenhof B, Moritz H (2005) Physical geodesy. Springer, New York
Ihde J, Sánchez L, Barzaghi R, Drewes H, Foerste C, Gruber T, Liebsch G, Marti U, Pail R, Sideris MG (2017) Definition and proposed realization of the International Height Reference System (IHRS). Surv Geophys 38(3):549–570. https://doi.org/10.1007/s10712-017-9409-3
Ince ES, Barthelmes F, Reißland S, Elger K, Förste C, Flechtner F, Schuh H (2019) ICGEM – 15 years of successful collection and distribution of global gravitational models, associated services and future plans. Earth Syst Sci. Data 11:647–674. http://doi.org/10.5194/essd-11-647-2019
Jarvis A, Reuter HI, Nelson A, Guevara E (2008) Hole-filled SRTM for the globe Version 4. http://www.cgiar-csi.org/data/srtm-90m-digital-elevation-database-v4-1
Johnston G, Riddell A, Hausler G (2017) The international GNSS service. In: Teunissen PJG, Montenbruck O (eds) Springer handbook of global navigation satellite systems, 1st edn. Springer, Cham, pp 967–982. https://doi.org/10.1007/978-3-319-42928-1
Lauría E, Pacino MC, Blitzkow D, Cimbaro S, Piñón DA, Miranda S, Bonvalot S, Gabalda G, Tocho CN (2017) Red Argentina de Gravedad Absoluta (RAGA). In I Simposio Internacional de Geomática Aplicada y Soluciones Geoespaciales (GEODATA 2017). Rosario, 3 al 7 de abril de 2017. http://sedici.unlp.edu.ar/handle/10915/75806
Mayer-Gürr T, Pail R, Gruber T, Fecher T, Rexer M, Schuh W-D, Kusche J, Brockmann J-M, Rieser D, Zehentner N, Kvas A, Klinger B, Baur O, Höck E, Krauss S, Jäggi A (2015) The combined satellite gravity field model GOCO05s. Presentation at EGU 2015, Vienna, April 2015
Morelli C, Gantar C, McConnell RK, Szabo B, Uotila U (1972) The international gravity standardization net 1971 (IGSN 71). Osservatorio Geofisico sperimentale Trieste (Italy). Available at https://apps.dtic.mil/dtic/tr/fulltext/u2/a006203.pdf. Accessed 20 Dec 2019
Moritz H (2000) Geodetic reference system 1980. J Geod 74(1):128–133. https://doi.org/10.1007/s001900050278
Pavlis NK, Holmes SA, Kenyon SC, Factor JK (2012) The development of the Earth gravitational model 2008 (EGM2008). J Geophys Res 117:B04406. https://doi.org/10.1029/2011JB008916
Petit G, Luzum B (eds) (2010) IERS conventions 2010. IERS Technical Note 36. Verlag des Bundesamtes für Kartographie und Geodäsie, Frankfurt a.M.
Piñón D (2016) Development of a precise gravimetric geoid model for Argentina. Masters by Research, Mathematical and Geospatial Sciences, RMIT University. http://researchbank.rmit.edu.au/view/rmit:161742
Piñón DA, Guagni H, Cimbaro SR (2016) Nuevo Sistema Vertical de la República Argentina. Simposio SIRGAS 2016. https://www.ign.gob.ar/descargas/geodesia/2016_Nuevo_Sistema_Vertical_de_Referencia.pdf
Piñón DA, Gómez DD, Smalley JrR, Cimbaro SR, Lauría EA, Bevis MG (2018) The history, state, and future of the Argentine continuous satellite monitoring network and its contributions to geodesy in Latin America. Seismol Res Lett 89(2A):475–482. https://doi.org/10.1785/0220170162
Rummel R, Gruber TH, Ihde J, Liebsch G, Rülke A, Schäfer U, Sideris M, Rangelova E, Woodworth PH, Hughes CH (2014) STSE-GOCE+ , height system unification with GOCE, Doc. No. GOHSU-PL-002, issue 1, 24-02-2014
Sánchez L, Brunini C (2009) Achievements and challenges of SIRGAS. In: Drewes H (ed) Geodetic reference frames. International association of geodesy symposia, vol 134. Springer, Berlin/Heidelberg. https://doi.org/10.1007/978-3-642-00860-3_25
Sánchez L, Sideris MG (2017) Vertical datum unification for the International Height Reference System (IHRS). Geophys J Int 209(2):570–586. https://doi.org/10.1093/gji/ggx025
Sánchez L, Cunderlík R, Dayoub N, Mikula K, Minarechová Z, Sima Z, Vatrt V, Vojtíšková M (2016) A conventional value for the geoid reference potential W0. J Geod 90(9):815–835. https://doi.org/10.1007/s00190-016-0913-x
Sánchez L, Ihde J, Pail R, Gruber T, Barzaghi R, Marti U, Ågren J, Sideris M, Novák P (2017) Towards a first realization of the International Height Reference System (IHRS). Geophysical Research Abstracts, vol 19, EGU2017-17104. European Geosciences Union General Assembly 2017. Available at https://ihrs.dgfi.tum.de/fileadmin/JWG_2015/Sanchez_et_al_Towards_a_IHRS_Realization_EGU2017.pdf. Accessed 19 Dec 2019
Sánchez L, Ågren J, Huang J, Wang YM, Forsberg R (2018) Basic agreements for the computation of station potential values as IHRS coordinates, geoid undulations and height anomalies within the Colorado 1 cm geoid experiment. Work document. Version 0.5, October 30, 2018. Available at https://ihrs.dgfi.tum.de/fileadmin/JWG_2015/Colorado_Experiment_Basic_req_V0.5_Oct30_2018.pdf. Accessed 20 Dec 2019
Schwarz KP, Sideris MG, Forsberg R (1990) The use of FFT techniques in physical geodesy. Geophys J Int 100(3):485–514. https://doi.org/10.1111/j.1365-246X.1990.tb00701.x
Sjöberg LE (2010) A strict formula for geoid-to-quasigeoid separation. J Geod 84(11):699–702. https://doi.org/10.1007/s00190-010-0407-1
Zingerle P, Pail R, Gruber T, Oikonomidou X (2019) The experimental gravity field model XGM2019e. GFZ Data Services. http://doi.org/10.5880/ICGEM.2019.007
Acknowledgements
The authors would like to thank the anonymous reviewers for their careful reading of our manuscript and their many useful and constructive comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this paper
Cite this paper
Tocho, C.N., Antokoletz, E.D., Piñón, D.A. (2020). Towards the Realization of the International Height Reference Frame (IHRF) in Argentina. In: Freymueller, J.T., Sánchez, L. (eds) Beyond 100: The Next Century in Geodesy. International Association of Geodesy Symposia, vol 152. Springer, Cham. https://doi.org/10.1007/1345_2020_93
Download citation
DOI: https://doi.org/10.1007/1345_2020_93
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-09856-7
Online ISBN: 978-3-031-09857-4
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)