Keywords

1 Introduction

In this paper we report on the status of the determination of monthly Earth gravity field models from orbit positions and K-band satellite-to-satellite tracking measurements of the GRACE and GRACE Follow-On (GRACE-FO) low Earth orbiters at Leibniz Universität’s Institut für Erdmessung. We give an overview on the processing approach of the LUH-GRACE2018 time series of monthly solutions from GRACE data. We briefly report on the first monthly solutions from GRACE-FO data that will be described in detail in an upcoming article.

The first batch of the LUH-GRACE2018 time series, covering 7 years (2003–2009), was presented and published in 2018 (Naeimi et al. 2018). In September 2019, a second batch containing monthly solutions from the years 2010 to 2016 was published. The processing approach for the solutions is the method of dynamic orbit and gravity field determination based on the equations of motion, also often referred to as the variational equations approach, e.g. Montenbruck and Gill (2005), Vallado (2013). We implemented it in a compact all-MATLAB program named GRACE-Satellite orbit Integration and Gravity field analysis in MAtlab (GRACE-SIGMA). The code uses strongly vectorized modules for numerical integration of reference orbits and the contributions to the design matrix (state transition matrix, sensitivity matrix). To allow for the vectorization, a modified Gauss-Jackson numerical integrator was developed. The least-squares parameter estimation is done in a two-step procedure: in the first step, a suitable reference orbit and accelerometer calibration parameters are estimated as a fit to reduced-dynamic orbit positions. In the second step, K-Band Range Rate (KBRR) observations are added to estimate updates to spherical harmonic gravity field coefficients. In order not to constrain the solutions towards the background force models of the pre-adjusted orbits, arc-specific parameters from step 1 are estimated together with the coefficients of the Earth’s time-variable potential (Meyer et al. 2015). To allow for an efficient data handling and processing, observations, parameters and force model data are stored and updated in arc-wise data capsules.

The implementation of the force effects was validated in comparison with computation results from other GRACE ACs within the new COmbination Service for Time-variable Gravity solutions (COST-G) (Meyer et al. 2018). It must be noted that we used RL05 Atmosphere and Ocean De-aliasing (AOD) models to correct for rapid mass variations, as our processing started before the more recent and more accurate RL06 AOD models were available. Also, we used RL02 Level-1B data products as the reprocessed RL03 Level-1B data were not yet available for the first batch of our processing. For the GRACE-FO gravity field solutions RL06 AOD models and RL04 data products were used. For a future time series of monthly GRACE solutions, we plan to use updated data and models.

The LUH-GRACE2018 monthly solutions were in principle estimated up to spherical harmonic degree and order 80. The monthly parameter estimation was done by stacking normal equations from orbital arcs of 3 h each; initial satellite state corrections, 3-axes accelerometer instrument biases and empirical range-rate corrections were estimated arc-wise. Our current stochastic model uses uniform weights for the reduced-dynamic orbit position pseudo-observations on the one hand and the K-band range-rate observations on the other.

Obtained results are compared to the solutions of other ACs in terms of error degree standard deviations that show the level of time-variable signal, modeling errors and random measurement errors with respect to a long-term reference model. In addition, obtained results are compared to those of other ACs in terms of mass variation time series for selected geophysical processes. This evaluation shows that for most months the quality of our results is similar to results from other ACs. For some months with poorer and more heterogeneous data quality, we have obtained a similar quality level by estimating spherical harmonic parameters up to degree 60 only. For other months with an even more difficult data situation, the results are not yet satisfactory and therefore not yet published.

One of the future goals of our group is to test how inhomogeneous data quality as seen, e.g., in post-fit range-rate residuals, propagates in the gravity recovery processing. We expect that changes in the parametrization or modifications of the input sensor data can help to identify and disentangle some of the involved effects.

2 Overview of the Gravity Field Recovery Method

Here, we mention the main elements of dynamic orbit and gravity field determination from GRACE and GRACE-FO sensor data. A paper with more details on our implementation is in preparation. We refer to Fig. 1 for a generalized overview. As the problem is highly nonlinear, a reference orbit that closely matches the true orbit (represented by the GRACE Level-1B data products) is determined using dynamic orbit integration from a priori force models. Then reduced observations are computed. After the linearization, the reduced observations are used to estimate parameter updates.

Fig. 1
figure 1

Simplified procedure of gravity field recovery from satellite-to-satellite tracking data with the variational equations approach. STM: state transition matrix, SM: sensitivity matrix, non-grav. acc: non-gravitational acceleration

Full size image

Orbit integration is based on the equations of motion

$$\displaystyle \begin{aligned} \mathbf{\ddot{r}} = -\dfrac{GM_{\oplus}}{r^3} \mathbf{r} + \mathbf{\ddot{r}}_{\mbox{p}}\end{aligned} $$
(1)

with the central (Keplerian) term and a sum of accelerations due to perturbing forces \(\mathbf {\ddot {r}}_{\mbox{p}} \). The perturbing forces include the higher harmonics of the time-variable gravity field, direct and indirect tidal forces, forces from non-tidal mass re-distribution, and non-gravitational forces acting on the satellites.

The reference orbit is obtained by numerically integrating the first order ordinary differential equations

$$\displaystyle \begin{aligned} \left.\begin{array}{rl} \mathbf{\dot{r}} &= \mathbf{v}\\ \mathbf{\dot{v}} &= -\dfrac{GM_{\oplus}}{r^3} \mathbf{r} + \mathbf{\ddot{r}}_{\mbox{p}} \quad \end{array}\right\}{}{} . \end{aligned} $$
(2)

For the non-gravitational forces, the accelerometer observations of each satellite are used, considering bias and scale calibration parameters. For the perturbing forces, frame transformations between geocentric and inertial frames or between satellite body frames and inertial frame need to be applied; for the latter, star camera based attitude data are used.

In the first estimation step, the orbit is iteratively fitted to orbit positions from a reduced-dynamic orbit as pseudo-observations, in order to ensure a sufficiently good linearization for the second estimation step. The partial derivatives in the design matrix of the estimation require the integration of the state transition and sensitivity matrices along with the orbit integration. In the second step, K-band range-rate observations are added, and updates to spherical harmonic coefficients are introduced as main unknown parameters.

3 Data

For the GRACE processing, we used the Level-1B data products of the release 2 (RL02) (Case et al. 2010). These data products include K-band range-rate observations (KBR1B), reduced-dynamic positions and velocities (GNV1B), accelerometer measurements representing the non-gravitational accelerations (ACC1B) and satellite attitude (SCA1B). All quantities of the Level-1B data products were used with 5s sampling during numerical integration. For K-band range-rates, light-time and antenna offset corrections from the KBR1B data products were included. In the processing the standard GNV1B reduced-dynamic orbit positions were used as pseudo-observations. We assume that they allow for a sufficiently good linearization in the first estimation step. Nevertheless, the influence of the orbit type and their characteristics, e.g. dynamic information in reduced-dynamic orbits or high frequency noise in kinematic orbits, on the recovered gravity field solutions may deserve further systematic investigations in the future.

4 Force Modeling

Force models needed for the numerical integration of the satellite trajectory and the state transition and sensitivity matrices are summarized in Table 1. The force models consider gravitational effects of tidal and non-tidal nature as well as non-gravitational effects. The non-gravitational effects are measured by the onboard accelerometers and have to be corrected for scale factors and biases during processing. Except for the acceleration due to the Earth’s gravity potential and the non-gravitational acceleration, all effects were pre-computed using the GNV1B reduced-dynamic orbits and were not altered during numerical orbit integration. We assume that future releases of the LUH-GRACE monthly gravity field solutions will benefit from updated ocean tide models such as FES2014 (Carrere et al. 2015) and from the AOD1B RL06 de-aliasing products (Dobslaw et al. 2017).

Table 1 Force models applied for the LUH-GRACE2018 time series of monthly gravity field solutions. d/o: indicates the utilized maximum degree/order of the spherical harmonic coefficients
Full size table

5 Numerical Integration

An accurate numerical integration of the satellite orbits and the state transition and sensitivity matrices can be regarded as the most time-consuming processing part of gravity field recovery. In order to save computational time while ensuring an integration accuracy suitable for gravity field recovery, we developed a modified version of the widely used predictor-corrector Gauss-Jackson integrator, e.g. Berry and Healy (2004), Montenbruck and Gill (2005), Vallado (2013). The impact of the corrector step on a GRACE-like orbit (near circular with an eccentricity of 0.001 and an altitude of about 500 km) was validated for different integration orders and step sizes. For the typical GRACE integration step size of 5 s and the integration order of 8, the impact of the corrector step is in the order of 10−13 m for the position and 10−13 m/s for the velocity and thus can be neglected (Naeimi 2018). However, the corrector formulas can be used to simplify the formulation of the predictor step considerably, allowing a straightforward, vectorized and thus efficient implementation. While more details of this integration technique will be covered in an upcoming publication, the modified Gauss-Jackson equations and ancillary sets of coefficients needed for an implementation can be found below. The modified Gauss-Jackson equations for state prediction have the following form:

$$\displaystyle \begin{aligned} \left.\begin{array}{rl} {\mathbf{r}}_{i+1} &= {\mathbf{r}}_i + h\mathbf{\dot{r}}_i + h^2 \mathbf{p}\mathbf{B}\mathbf{A} \quad \\ \mathbf{\dot{r}}_{i+1} &=\mathbf{\dot{r}}_i + h \mathbf{q}\mathbf{B}\mathbf{A}\\ \end{array}\right\} \end{aligned} $$
(3)

where ri+1, \(\mathbf {\dot {r}}_{i+1}\) (row vectors) are the predicted position and velocity vectors; ri and \(\mathbf {\dot {r}}_i\) (row vectors) are the position and velocity vectors at a current time and h is the integration step size. pBA and qBA represent the summation parts of the integrator, where the specific integration order is considered. For the computation of the results presented in this study an integration order of 12 was used. In the modified version of the Gauss-Jackson integrator this integration order corresponds to a summation over indices j = [1, m] where m is the integration order decreased by one. The row vectors p and q contain the coefficients pj and qj that are defined in Table 2. Matrix A contains row-wise the acceleration vector at the current time stamp i as well as the accelerations of m − 1 back points. The result of multiplying matrix B with matrix A are the acceleration backward differences up to order m − 1. The entries of matrix B are summarized in Table 3. For initialization a Runge-Kutta integrator of order 4 is used.

Table 2 Parameters \(p_j=\delta _{j+1}-\gamma _j^*-\delta _{j+1}^*\) and \(q_j=\gamma _j-\gamma _j^*\) for the numerical integration with the modified Gauss-Jackson integrator
Full size table
Table 3 Entries of the matrix B for the vectorized computation of backward differences
Full size table

6 Parametrization

The parametrization chosen for the two-step approach is summarized in Table 4. The main idea behind the two-step approach is to reduce the number of iterations during gravity field recovery and therefore to save computational time. This is achieved by estimating appropriate a priori values for the initial satellite states as well as accelerometer calibration parameters using only reduced-dynamic orbit positions as observations in the orbit pre-adjustment (Wang et al. 2015). For this release of monthly gravity field solutions the accelerometer biases are estimated arc-wise while the scale factors are held fixed to a priori values reported in Bettadpur (2009). The satellite orbits are parametrized by an arc length of 3 h. The aim of this arc length is to allow a more precise orbit fit to observations, as inaccuracies, e.g. in force modeling, can be balanced by the very frequent estimation of local arc parameters. Compared to the usual arc length of one day, no constrained dynamic empirical parameters, such as cycle per revolution accelerations or more frequent stochastic parameters, have to be co-estimated in order to achieve a good orbit fit. In the second step the K-band range-rates are used as main observations, along with reduced-dynamic positions. As additional unknowns, kinematic empirical KBRR parameters are introduced. In total 8 empirical parameters consisting of bias and bias-rates as well as periodic bias and bias-rates are estimated per arc (Kim 2000). We solve for the bias and bias-rates every 90 min and for periodic bias and bias-rates every 180 min. Range-rates and reduced-dynamic orbit positions are combined on normal equation level using a technique-specific weighting. The spherical harmonic coefficients of the Earth’s gravity potential are obtained together with the arc-specific parameters without any constraints, regularizations or stochastic accelerations. The number of parameters to be estimated in the second step of the procedure equals 6557 global parameters representing the normalized spherical harmonic coefficients of the Earth’s potential (for maximum degree 80) as well as 6448 arc-specific parameters if 31 days of observations are considered.

Table 4 Specifics of the two-step approach applied for the LUH-GRACE2018 time series of monthly gravity field solutions
Full size table

7 GRACE-FO Solutions

In Sect. 8 we will jointly evaluate the LUH-GRACE2018 gravity field solutions (2003–2016) as well as first GRACE-FO results (June 2018–August 2019). For the GRACE-FO results a slightly modified processing strategy was applied. The most recent de-aliasing product AOD1B RL06 (Dobslaw et al. 2017) up to degree and order 180 was used. In addition, atmospheric tides were considered according to Biancale and Bode (2006). Accelerometer scale factors were estimated arc-wise along with the biases. The Earth’s gravity potential was estimated up to degree and order 96.

8 Results and Evaluation

The convergence of exemplary gravity field solutions in terms of the error degree standard deviation for March 2006 (good ground track coverage) and September 2004 (sparse ground track coverage) are shown in Fig. 2. Arcs with a length of 3 h are stacked successively, overall leading to a decrease of the error degree standard deviations of the corresponding solutions. Figure 2a, b shows the convergence from the beginning, highlighting the rapid convergence during the first seven days. For the remainder of a month, the convergence rate is much slower as can be seen in Fig. 2c, d. The results demonstrate that satisfactory sub-monthly gravity field solutions of the time-variable Earth’s gravity potential can often be obtained without any constraints, regularizations or a priori information such as solutions from previous months or weeks. Note that the convergence rate can vary significantly depending on sensor data quality and distribution of ground tracks.

Fig. 2
figure 2

Exemplary successive stacking of 3 hourly orbital arcs and the error degree standard deviations of the corresponding gravity field solution for March 2006 (good ground track coverage) and September 2004 (sparse ground track coverage) with respect to the gravity field model GIF48. The error degree standard deviations for 1 day, 2 days, 7 days, 2 weeks and 3 weeks of observation data are highlighted. (a) March 2006. (b) September 2004. (c) March 2006 zoom. (d) September 2004 zoom

Full size image

The computed monthly gravity field solutions are compared to the solutions of the three official ACs: CSR (Center for Space Research, The University of Texas at Austin), GFZ (German Research Centre for Geosciences) and JPL (Jet Propulsion Laboratory, California Institute of Technology). Since we used AOD1B RL05 products for the correction of rapid mass variations, our solutions are compared to the RL05 previous generation solutions, in order to allow for a fair comparison. The reference solutions CSR RL05 (Bettadpur 2012), GFZ RL05a (Dahle et al. 2012) and JPL RL05 (Watkins and Yuan 2014) are obtained from the International Centre for Global Earth Models (ICGEM) (Ince et al. 2019).

Error degree standard deviations of the monthly solutions are illustrated in Fig. 4. The mean error degree standard deviations are computed for the two periods 2003–2009 and 2010–2016 separately. As a reference field the recent static gravity field model GOCO06s (Kvas et al. 2019) was subtracted from the solutions of all 4 ACs. It can be seen that in general the noise characteristics of the solutions are similar, not considering degree 2. In general the amplitudes of the LUH error degree standard deviations are slightly larger when compared to the other ACs. Degree 4 for both periods as well as degree 3 for the second period show larger error degree standard deviations indicating a larger noise for these degrees. A comparison on the coefficients level showed that the degree 4 deviation is caused by the \(\overline {C}_{44}\) and \(\overline {S}_{44}\) coefficients. We presume that this deviation is caused by the applied parametrization, since the mean error degree standard deviations of about one year of GRACE-FO processing with a slightly changed parametrization does not show any significant deviations in the low degrees. Nevertheless, further investigations are needed. Error degree standard deviations show effects of orbital resonances (Cheng and Ries 2017) near degrees 31 and 46. The orbital resonance near degree 62 is missing in the second period leading to a smaller noise for the higher degrees 62–80 compared to period 1.

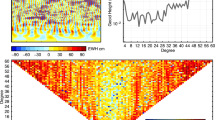
A comparison of exemplary global maps of mass variations in terms of Equivalent Water Height (EWH) can be seen in Fig. 3. Global maps based on CSR RL05 and the LUH-GRACE2018 solutions for every second month of the year 2008 are shown with respect to the static model GOCO06s. The \(\overline {C}_{20}\) coefficients of all solutions were replaced by values obtained from Satellite Laser Ranging (SLR) (Cheng and Ries 2017). In order to mitigate the meridional North-South stripes, the spherical harmonic coefficients differences were smoothed using the Gaussian filter (Wahr et al. 1998) with a half width of 400 km before computing the EWH. It can be seen that larger mass variations such as in the Amazon region, central Africa, India, Southeast Asia, Greenland and Northeast Canada can be localized equally well in both CSR and LUH solutions. The meridional stripes in the LUH maps are slightly stronger, which is consistent with the slightly higher error degree standard deviations in Fig. 4, and their characteristics suggest differences in the analysis noise that should be further studied.

Fig. 3
figure 3

Global Equivalent Water Height (EWH) for every second month of the year 2008. Left side: CSR RL05 solutions; right side: LUH solutions. The \(\overline {C}_{20}\) coefficients were replaced by SLR values in all solutions. As a reference model the static gravity field model GOCO06s (reference epoch: 2010-01-01) was subtracted. The spherical harmonic coefficients differences were smoothed using the Gaussian filter with a half width of 400 km

Full size image
Fig. 4
figure 4

Mean of error degree standard deviations of the four analysis centers for degrees 2–80 with respect to the static model GOCO06s. The solutions were divided into two periods: 2003–2009 (a) and 2010–2016 (b). The \(\overline {C}_{20}\) coefficients were not replaced. All solutions are zero-tide. A specific month is considered when a solution from all 4 centers is available. We define a monthly solution as a solution that is based on satellite data from one calendar month, i.e. solutions combining sensor data of neighboring months are not considered. Periods when regualrizations were applied are excluded

Full size image

Exemplary Equivalent Water Height time series for Greenland and the Amazon and Ganges basins based on the same processing as applied for the global EWH maps are shown in Fig. 5. The time series cover the GRACE period and additionally include the first available GRACE-FO solutions. The EWH signals of all four ACs covering a time span of more than 16 years show a high degree of consistency for all three regions. This indicates that the signal content of the four ACs’ solutions does not exhibit large differences. The degradation of the GRACE sensor data manifests as gaps in the second half of the time series.

Fig. 5
figure 5

Equivalent Water Heights (EWH) in three regions: (a) Greenland, (b) Amazon basin, (c) Ganges basin. EWH values are region mean values. The \(\overline {C}_{20}\) coefficients in all solutions were replaced by SLR values. As a reference model the static gravity field model GOCO06s (reference epoch: 2010-01-01) was subtracted. The spherical harmonic coefficients differences were smoothed using the Gaussian filter with a half width of 400 km

Full size image