A Wavelet-Based Outlier Detection and Noise Component Analysis for GNSS Position Time Series

Abstract

Various signals of crustal deformation and mass loading deformation are contained in a GNSS position time series. However, a GNSS position time series is also polluted by outliers and various colored noise, which must be reasonably modelled before estimating deformation signals. Since temporal signals of the GNSS position time series are non-linear and complicated, we propose a wavelet-based approach for outlier detection, which first retrieves the temporal signals from the GNSS position time series by using wavelet analysis, and then detect outliers in the residual position time series by using the interquartile range. After the detected outliers are eliminated from the residual time series, the noise components, including white noise and flicker noise, are estimated by using MINQUE approach. Our proposed approach is used to process the real GNSS position time series of the Crustal Movement Observation Network of China (CMONOC) over the period spanning 1999–2018. The results demonstrate that our approach can detect the outliers more efficiently than the traditional approach, which retrieves the temporal signals by using a functional model with trend and periodic variations. As a result, the noise components estimated with our proposed approach are smaller than those with the traditional approach for the GNSS position time series of all CMONOC stations.

1 Introduction

The position time series of various GNSS station networks are widely used to study the geophysical phenomena such as plate tectonics (Tobita 2016), post-glacial rebound (Peltier et al. 2015) and sea level change (Wöppelmann et al. 2007). Due to multipath effects, station-related error (such as electromagnetic interference), orbital anomaly and other unknown reasons, outliers inevitably exist in the GNSS position time series, which will lead to bias estimates in both functional and stochastic models (Koch 1999; Khodabandeh et al. 2012). There are several approaches for detecting outliers in the GNSS position time series, such as three sigma method (3σ) (Mao et al. 1999), Bayesian method (Zhang and Gui 2013), as well as Detection Identification Adaptation (DIA) procedure (Amiri-Simkooei et al. 2015). Besides these methods, the window-opening test algorithm based on the Interquartile Range (IQR) statistic is another commonly used approach for outlier detection in the GNSS position time series (Nikolaidis 2002; Li and Shen 2018). This algorithm is fast and robust since the median and IQR values of a time series are less affected by outliers. Due to its superior performance, the outlier detection approach based on IQR criterion has been widely applied in the open source software or packages for GNSS position time series analysis, such as iGPS (Tian 2011), Hector (Bos et al. 2013) and TSAnalyzer (Wu et al. 2017).

Apart from outliers, the GNSS position time series are also polluted by temporally correlated noise, which is a combination of white noise plus flicker noise (Mao et al. 1999). The maximum likelihood estimation (MLE) is widely used for estimating the noise components of a GNSS time series. Besides, the existing methods of Variance Component Estimation (VCE), such as Helmert (1907), Minimum Norm Quadratic Unbiased Estimation (MINQUE) (Rao 1971), Best Invariant Quadratic Unbiased Estimation (BIQUE) (Koch 1999), as well as LS_VCE (Teunissen and Amiri-Simkooei 2008), are identical under the normal distribution (Teunissen and Amiri-Simkooei 2008). Therefore we use MINQUE method to estimate noise components in this paper.

The traditional least squares (LS) outlier detection based on IQR criterion (LS_IQR) and noise component estimation based on MINQUE method (LS_MINQUE) are all based on the harmonic functional model (Nikolaidis 2002) in which a position time series is described as a combination of linear trend, quasi-annual and semi-annual signals with constant amplitude and phase. However, the amplitudes and phases of seasonal variation signals in GNSS position time series also vary slightly over time due to the variation of surface-mass loading (Blewitt and Lavallée 2002), atmospheric and hydrological loadings (Bogusz and Figurski 2014). Consequently, a harmonic model isn’t sufficient to reflect the nonlinear variation signals of GNSS position time series, especially the time-varying seasonal variation due to the irrationality of the model itself. Therefore, when a harmonic functional model is used to describe the GNSS position time series, the LS residuals still contains partial signal, which will affect the performance of outlier detection and lead to imprecise estimation of noise components. For this reason, we propose a wavelet-based algorithm for outlier detection and noise component analysis, which extracts the time variable signals by wavelet analysis and thereby named as WA_IQR and WA_MINQUE for the correspondent outlier detection and noise component algorithm. The remainder of the paper is organized as follows. Section 2 presents the main methodology, including dyadic wavelet analysis, outlier detection based on IQR criterion and noise component estimation using MINQUE method. Section 3 presents the results of real data analysis of CMONOC over the period from 1999 to 2018, and conclusions are summarized in Sect.4.

2 Methodology

2.1 Dyadic Wavelet Analysis

When φ(t) is denoted as a basic wavelet function, a set of wavelet functions can be derived by means of dilation a and translation b of φ(t) as (Daubechies 1992)

$$ {\varphi}_{a,b}(t)=\frac{1}{\sqrt{a}}\varphi \left(\frac{t-b}{a}\right) $$

(1)

Taking a = 2^j, b = 2^jk, where j, k are integers, we can obtain the dyadic wavelet functions as

$$ {\varphi}_{j,k}(t)={2}^{-j/2}\varphi \left({2}^{-j}t-k\right) $$

(2)

For a discrete time series x = [x₀ x₁ ⋯ x_N − 1]^T, its j-th dyadic wavelet transform is defined as (Walnut 2013)

$$ w\left(j,k\right)=\sum \limits_{i=0}^{N-1}{x}_i{\int}_{S_i}{\varphi}_{j,k}(t) dt $$

(3)

where w(j, k) is the k-th value of j-th wavelet coefficient and S_i is the i-th sampling interval. Rewriting Eq. (3) with vector and matrix form as

$$\vspace*{3pt} {\mathbf{w}}_j={\mathbf{W}}_j\mathbf{x}\vspace*{3pt} $$

(4)

where w_j is a vector of j-th wavelet coefficient with the size of n_j = N/2^j + 1 and $\vspace*{3pt}{\mathbf{W}}_j={\left[\begin{array}{cccc}{\mathbf{W}}_{j,0}^T& {\mathbf{W}}_{j,1}^T& \cdots & {\mathbf{W}}_{j,{n}_{j-1}}^T\end{array}\right]}^T\vspace*{3pt}$ is j-th wavelet transform matrix with the size of n_j × N, where,${\mathbf{W}}_{j,k}=\big[\begin{array}{cccc}{\int}_{S_0}{\varphi}_{j,k}(t) dt& {\int}_{S_1}{\varphi}_{j,k}(t) dt& \cdots & {\int}_{S_{N-1}}{\varphi}_{j,k}(t) dt\end{array}\big]$.

Stacking the wavelet coefficients from small to large scale and subjoining the scale coefficient v_J − 1, where J denotes the number of layers to be decomposed. For the GNSS position time series, the reconstructed seventh and eighth components of basic wavelet function represent time-varying signals with periods of about 182 and 365 days, which denote the semi-annual and annual signals (Klos et al. 2018), respectively. For this reason, we take J as 8. Then we obtain the wavelet transform of x in matrix form as

$$ \mathbf{w}=\mathbf{Wx} $$

(5)

where $\mathbf{w}{=}{\big[\begin{array}{cccc}{\mathbf{w}}_0^T {\cdots} {\mathbf{w}}_{J{-}1}^T {\mathbf{v}}_{J{-}1}^T\end{array}\big]}^T,\mathbf{W}{=}{\big[\begin{array}{cccc}{\mathbf{W}}_0^T \!\!{\cdots} {\mathbf{W}}_{J-1}^T {\mathbf{V}}_{J-1}^T\end{array}\big]}^T$. V_J − 1 is the scale transform matrix, which is orthogonal to W_j and the wavelet transform matrix W is a standard orthogonal matrix. The original time series x can be reconstructed by the wavelet coefficients and transform matrix as follows:

$$ \mathbf{x}={\mathbf{W}}^T\mathbf{w}=\sum \limits_{j=0}^{J-1}{\mathbf{d}}_j+{\mathbf{a}}_{J-1} $$

(6)

where ${\mathbf{d}}_j={\mathbf{W}}_j^T{\mathbf{w}}_j$ represents the j-th detail component and ${\mathbf{a}}_{J-1}={\mathbf{V}}_{J-1}^T{\mathbf{v}}_{J-1}$ represents the appropriate component of the time series.

2.2 Outlier Detection in Residual with IQR

The original time series x can be decomposed into components of different frequencies which represent either signal or noise after multi-resolution analysis (Mallat 1988). The signal and noise can be separated by the correlation coefficient method (Zhang et al. 2018), which calculates the correlation coefficient between the original time series and the reconstructed component of each layer, and the layer where the correlation coefficient firstly appears local minimum is considered to be the boundary layer. The correlation coefficient between x and i-th reconstructed component d_i can be calculated as

$$\vspace*{-3pt} R\left(x,{d}_i\right)=\frac{\sum \limits_{t=1}^N\left({x}_t-\overline{x}\right)\left({d}_{t,i}-{\overline{d}}_i\right)}{\sqrt{\sum \limits_{t=1}^N{\left({x}_t-\overline{x}\right)}^2}\sqrt{\sum \limits_{t=1}^N{\left({d}_{t,i}-{\overline{d}}_i\right)}^2}} \vspace*{-3pt}$$

(7)

where x_t and d_{t, i} represent t-th element of x and d_i, $\overline{x}$ and ${\overline{d}}_i$ represent the average value of x and d_i, respectively.

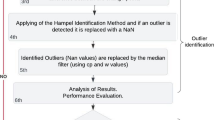
After the multi-resolution analysis of the original time series, we obtain the residual vector v, in which outliers are mostly reflected. Sorting residual in ascending order, and then dividing it into several equal parts with the window length L, which was commonly taken as 182 (Nikolaidis 2002; Wu et al. 2017). Performing a window check on each part of the data set using the Z-ratio statistic (Nikolaidis 2002).

$$\vspace*{-3pt} Z=\frac{v_i- med\left({v}_{i-L/2},{v}_{i+L/2}\right)}{IQR\left({v}_{i-L/2},{v}_{i+L/2}\right)} \vspace*{-3pt}$$

(8)

where v_i represents the i-th residual, med(∗) and IQR(∗) denote the operators for computing the median and interquartile range of a series, respectively. According to IQR criterion (Nikolaidis 2002; Bos et al. 2013), when Z > 3, the i-th value of the original time series is detected as an outlier.

2.3 Noise Component Estimation Using MINQUE Approach

After the outliers are detected and then eliminated, the noise amplitudes of residual time series, including white noise and flicker noise are estimated by MINQUE method. The fundamental equation of variance component estimation (VCE) is (Li et al. 2010)

$$\vspace*{-3pt} {\mathbf{R}\boldsymbol{\Sigma}}_{\mathbf{y}}{\mathbf{R}}^T={\mathbf{vv}}^T\vspace*{-3pt} $$

(9)

where $\mathbf{v}=\mathbf{Ry},\mathbf{R}=\mathbf{I}-\mathbf{A}{\big({\mathbf{A}}^T{\boldsymbol{\Sigma}}_y^{-1}\mathbf{A}\big)}^{-1}{\mathbf{A}}^T{\boldsymbol{\Sigma}}_y^{-1}$, A is the coefficient matrix of the observational equation. The covariance matrix Σ_y is a combination of two cofactor matrices for white noise and flicker noise as

$$\vspace*{-3pt} {\boldsymbol{\Sigma}}_{\mathbf{y}}={\sigma}_w^2\mathbf{I}+{\sigma}_f^2{\mathbf{Q}}_f \vspace*{-3pt}$$

(10)

where ${\sigma}_w^2,{\sigma}_f^2$ are the white and flicker noise components to be estimated, Q_f is the cofactor matrix of flicker noise. For the calculation of Q_f, one can refer to Mao et al. (1999).

According to the MINQUE estimation by Rao (1971), the equation to compute the white and flicker noise components is given as follows

$$\vspace*{-3pt} \mathbf{N}\boldsymbol{\uptheta } =\mathbf{q}\vspace*{-3pt} $$

(11)

where, $\boldsymbol{\uptheta} ={\left({\sigma}_w^2,{\sigma}_f^2\right)}^T$. N is a 2 × 2 matrix and q is a 2 vector, the elements are given by

$$ {\displaystyle \begin{array}{l}{n}_{11}= tr\left(\mathbf{WW}\right),\kern0.5em {n}_{12}={n}_{21}= tr\left({\mathbf{WWQ}}_f\right),\\ {}{n}_{22}= tr\left({\mathbf{WQ}}_f{\mathbf{WQ}}_f\right),\kern0.75em {q}_1={\mathbf{v}}^T\mathbf{WWv},\\ {}{q}_2={\mathbf{v}}^T{\mathbf{WQ}}_f\mathbf{Wv}\end{array}} $$

(12)

where $\mathbf{W}={\boldsymbol{\Sigma}}_{\mathbf{y}}^{-1}\mathbf{R}$, tr(∗) is the operator for computing the trace of a matrix. Since R contains unknown noise components, Eq. (11) needs to be iteratively solved with given initial value of noise components.

Fig. 1

Geographic locations of 27 stations in CMONOC (Shen et al. 2014)

Fig. 2

Position time series of BJFS station. (a): Original one; (b): After missing values complemented and discontinuities corrected

Fig. 3

Reconstructed 9 layer’s components of BJFS station using wavelet analysis

3 Real GNSS Position Time Series Analysis

The real position time series of 27 permanent GNSS stations of CMONOC are processed with our proposed approach and their locations are shown in Fig. 1. All the GNSS position time series are processed by a homogeneous state-of-the-art method using the processing package GAMIT/GLOBK (Ver.10.4) in the frame of ITRF 2000 (see processing details in ftp://ftp.cgps.ac.cn/doc/processing_manual.pdf and download data in http://www.cgps.ac.cn/).

Figure 2a presents position time series of Up, North, and East coordinates for BJFS station and it shows that position time series of three coordinates contain some outliers. Wavelet analysis requires that involved time series should be stable and equally spaced (Walnut 2013), however missing data inevitably occur in the position time series (Shen et al. 2014). We adopt the iterative interpolation scheme to handle data missing problem. Besides, some abrupt changes called discontinuities or offsets occur in the GNSS position time series due to various reasons such as brakes in station operation and change of antennas. Vitti (2012) provided a tool (sigseg) for the detection of position discontinuities in geodetic time series based on Blake-Zisserman variational model. This tool is used to detect and repair the discontinuities in position time series. The new position time series after complementing the missing values and correcting the discontinuities are presented in Fig. 2b.

Fig. 4

Signals of BJFS station extracted by WA and LS method

3.1 Signal and Noise Separation

The detrend BJFS time series in Fig. 2b is then decomposed with coif-5 wavelet, and the reconstructed components of each layer are presented in Fig. 3 and correlation coefficients between the original time series and the reconstructed component of each layer are presented in Table 1. Signals extracted by WA and LS estimation are presented in Fig. 4. Obviously, WA can well capture the nonlinear variation of position time series, while LS estimation based on harmonic model characterizes the nonlinear variation as a periodic signal with constant amplitude, which is clearly inconsistent with the actual change.

Table 1 Correlation coefficient between the original time series and reconstructed component of each wavelet layer

3.2 Outlier Detection

The IQR criterion is used to detect outliers in the residuals of three coordinates by WA and LS estimation, and results are presented in Fig. 5. Obviously, WA_IQR can detect much more outliers than LS_IQR. In Fig. 5, LS_IQR fails to detect a lot of outliers, especially in the epochs of the non-stationary part, which are caused by the poor fitting to the harmonic model. Figure 5 also presents the detected outliers by the 3σ method, it seems that the 3σ method can only detect a few outliers. The new time series after eliminating outliers from the original position time series are presented in Fig. 6, from which we can see that more outliers remain in the LS_IQR and the 3σ detected time series (i.e. between 1999 and 2003) than WA_IQR detected time series. However, none of them can recognize some outliers, of which the magnitude is quite small (i.e. outliers near epoch of 2015).

Fig. 5

Residuals derived by WA (Up) and LS (middle) for North, East and Up coordinates of BJFS station, and outliers detected by IQR and 3σ are marked with red dot

Fig. 6

The new time series of BJFS station after outliers removed based on WA_IQR(left), LS_IQR(middle) and 3σ (right)

Figure 7 presents the proportion of detected outliers in position time series of 27 stations for three coordinates. For the BJFS station, the proportion of detected outliers for the whole data for three coordinates are 0.77%, 0.19% and 0.84% by 3σ, 1.78%, 1.47% and 2.11% by LS_IQR, and 4.50%, 5.55% and 3.65% by WA_IQR, respectively. From the remaining stations in Fig. 7, we can clearly see that WA_IQR can detect more outliers than LS_IQR and 3σ for all stations, the mean detected proportion of 27 stations are 0.16%, 0.50% and 0.39% by 3σ, 1.62%, 1.92% and 1.62% by LS_IQR, and 4.61%, 4.65% and 2.59% by WA_IQR, respectively.

Fig. 7

Proportions of detected outliers in 27 stations using WA_IQR, LS_IQR and 3σ

3.3 Noise Components Estimation

After detected outliers are eliminated, WA_MINQUE and LS_MINQUE are employed to estimate noise components for the 27 stations, the results are presented in Figs. 8 and 9. The noise amplitude estimates of σ_w and σ_f in Figs. 8 and 9 clearly show that the noise component of Up coordinate is much larger than those of horizontal coordinates, and the flicker noise is larger than white noise. Therefore, as confirmed by Amiri-Simkooei et al. (2007), flicker noise is dominant in the GNSS position time series. Also, both the white and flicker noise derived by WA_MINQUE are all smaller than those by LS_MINQUE.

Fig. 8

Estimates of σ_w for 27 stations by two algorithms

Fig. 9

Estimates of σ_f for 27 stations by two algorithms

4 Conclusions and Remarks

The traditional LS_IQR for outlier detection and LS_MINQUE for noise component estimation are all based on the harmonic functional model, which cannot well describe the time-variable seasonal signals of GNSS position time series. Consequently, the residuals derived by traditional LS estimation still contain partial signal, which will definitely affect the performance of outlier detection and lead to an imprecise estimate of the noise component. This paper develops a wavelet-based algorithm of outlier detection and noise component estimation, namely WA_IQR and WA_MINQUE. The basic idea of our new algorithm is to separate the signal and noise of the GNSS position time series by wavelet analysis firstly, then detect outliers in residual time series using IQR statistic and then estimate noise components of the residual time series after outliers eliminated. The new algorithm is verified by the real data of CMONOC and the results show that WA_IQR is more effective than LS_IQR to detect outliers and WA_MINQUE can obtain the more reasonable noise component estimates than LS_MINQUE. The noise components estimated by WA_MINQUE approach are all smaller than those by the traditional LS_MINQUE approach for all 27 CMONOC stations.