Abstract
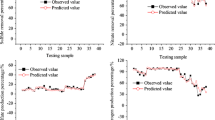
Mathematical models are normally used to calculate the component concentrations in biological wastewater treatment. However, this work deals with the wastewater from a coke plant and it implies inhibition effects between components which do not permit the use of said mathematical models. Due to this, feed-forward neural networks were used to estimate the ammonium concentration in the effluent stream of the biological plant. The architecture of the neural network is based on previous works in this topic. The methodology consists in performing a group of different sizes of the hidden layer and different subsets of input variables.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Hornik, K., Stinchcombe, M., White, H.: Multilayer feedforward networks are universal approximators. Neural Networks 2, 359–366 (1989)
Funahashi, K.: On the approximate realization of continuous mappings by neural networks. Neural Networks 2, 192–193 (1989)
Cybenko, G.: Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals, and Systems 2, 303–314 (1989)
Hartman, E., Keeler, J., Kowalski, J.: Layered neural networks with gaussian hidden units as universal approximations. Neural Computation 2, 210–215 (1990)
Levenberg, K.: A method for the solution of certain problems in least squares. Quart. Appl. Math., 164–168 (1944)
Marquardt, D.: An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 11, 431–441 (1963)
Moré, J.: The levenberg-marquardt algorithm: Implementation and theory. Numerical Analysis 630, 105–116 (1977)
LeCun, Y., Denker, J., Solla, S.: Optimal brain damage. Advances in Neural Information Processing Systems 2, 598–605 (1990)
López, H., González, R., Machón, I., Ojea, G., Peregrina, S., González, J., de Abajo, N.: Identification of melting and brightening section of a tinplate facility by means of neural networks. In: Proc. European Control Conference, Porto (2001)
Norgaard, M., Ravn, O., Poulsen, N., Hansen, L.: Neural Networks for Modelling and Control of Dynamic Systems. Springer, London (2000)
Norgaard, M., Ravn, O., Poulsen, N.: Nnsysid-toolbox for system identification with neural networks. Mathematical and Computer Modelling of Dynamical Systems 8, 1–20 (2002)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
García, H.L., González, I.M. (2006). Ammonium Estimation in a Biological Wastewater Plant Using Feedforward Neural Networks. In: Schwenker, F., Marinai, S. (eds) Artificial Neural Networks in Pattern Recognition. ANNPR 2006. Lecture Notes in Computer Science(), vol 4087. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11829898_12
Download citation
DOI: https://doi.org/10.1007/11829898_12
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-37951-5
Online ISBN: 978-3-540-37952-2
eBook Packages: Computer ScienceComputer Science (R0)