Abstract
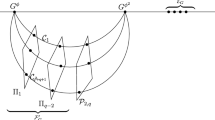
In this paper, we use the undetermined coefficient method to find a desirable pair of cubic Bezier spirals and a desirable pair of quintic PH spirals to generate planar G2 transition curve between two separated circles. The G2 transition curve can be gotten by the rooting formula, which simplifies the computation, and the ratio of two radii has no restriction, which extends the application area.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Guggenheimer, H.W.: Differential geometry. McGraw-Hill, New York (1963)
Baass, K.G.: The use of clothoid templates in highway design. Transportation Forum 1, 47–52 (1984)
Meek, D.S., Walton, D.J.: The use of Cornu spirals in drawing planar curves of controlled curvature. Journal of Computational and Applied Mathematics 25, 69–78 (1989)
Walton, D.J., Meek, D.S.: A planar cubic Bezier spiral. Journal of Computational and Applied Mathematics 72, 85–100 (1996)
Walton, D.J., Meek, D.S.: A Pythagorean hodograph quintic spiral. Computer Aided Design 28, 943–950 (1996)
Walton, D.J., Meek, D.S.: Planar G2 transition curves composed of cubic Bezier spiral segments. Journal of Computational and Applied Mathematics 157, 453–476 (2003)
Walton, D.J., Meek, D.S.: Planar G2 transition with a fair Pythagorean hodograph quintic curve. Journal of Computational and Applied Mathematics 138, 109–126 (2002)
Walton, D.J., Meek, D.S.: G2 curve composed of cubic and Pythagorean hodograph quintic spirals. Computer Aided Geometry Design 15, 547–566 (1998)
Li, Z., Meek, D.S.: Smoothing an arc spline. Computers & Graphics 29, 576–587 (2005)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Li, Z., Ma, L., Zhao, M., Mao, Z. (2006). Improvement Construction for Planar G2 Transition Curve Between Two Separated Circles. In: Alexandrov, V.N., van Albada, G.D., Sloot, P.M.A., Dongarra, J. (eds) Computational Science – ICCS 2006. ICCS 2006. Lecture Notes in Computer Science, vol 3992. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11758525_47
Download citation
DOI: https://doi.org/10.1007/11758525_47
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-34381-3
Online ISBN: 978-3-540-34382-0
eBook Packages: Computer ScienceComputer Science (R0)