Abstract
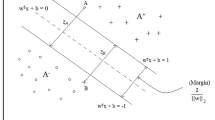
In this paper, we propose a fuzzy extension to proximal support vector classification via generalized eigenvalues. Here, a fuzzy membership value is assigned to each pattern, and points are classified by assigning them to the nearest of two non parallel planes that are close to their respective classes. The algorithm is simple as the solution requires solving a generalized eigenvalue problem as compared to SVMs, where the classifier is obtained by solving a quadratic programming problem. The approach can be used to obtain an improved classification when one has an estimate of the fuzziness of samples in either class.
Chapter PDF
Similar content being viewed by others
Keywords
References
Mangasarian, O.L., Wild, E.W.: Multisurface Proximal Support Vector Classification via Generalized Eigenvalues. Data Mining Institute Technical Report. 04-03 June (2004)
Fung, G., Mangasarian, O.L.: Proximal Support Vector Machines. In: Proc. KDD-2001, San Francisco, August 26-29, pp. 77–86 (2001)
Burges, C.: A Tutorial on Support Vector Machines for Pattern Recognition. Data Mining and Knowledge Discovery 2 (1998)
Tikhonov, A.N., Arsenin, V.Y.: Solution of Ill Posed Problems. John Wiley and Sons, New York (1977)
Parlett, B.N.: The symmetric Eigen value Problem. SIAM, Philadelphia (1998)
Blake, C.L., Merz, C.J.: UCI Repository for Machine Learning database. Department of Information and Computer Sciences. University of California, Irvine, On-line at, http://www.ics.uci.edu/~mlearn/MLRepository.html
Jayadeva, Khemchandani, R., Chandra, S.: Fast and Robust Learning Through Fuzzy Linear Proximal Support Vector Machines. Journal of Neurocomputing 61, 401–411 (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Jayadeva, Khemchandani, R., Chandra, S. (2005). Fuzzy Proximal Support Vector Classification Via Generalized Eigenvalues. In: Pal, S.K., Bandyopadhyay, S., Biswas, S. (eds) Pattern Recognition and Machine Intelligence. PReMI 2005. Lecture Notes in Computer Science, vol 3776. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11590316_54
Download citation
DOI: https://doi.org/10.1007/11590316_54
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-30506-4
Online ISBN: 978-3-540-32420-1
eBook Packages: Computer ScienceComputer Science (R0)