Abstract
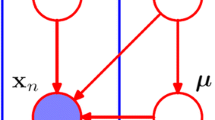
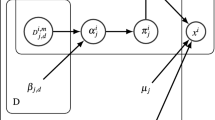
The problem of image segmentation can be formulated in the framework of Bayesian statistics. We use a Markov random field as the prior model of the spacial relationship between image pixels, and approximate an observed image by a Gaussian mixture model. In this paper, we introduce into the statistical model a hierarchical prior structure from which model parameters are regarded as drawn. This would give an efficient Gibbs sampler for exploring the joint posterior distribution of all parameters given an observed image and could make the estimation more robust.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Barker, S.A.: Image Segmentation using Markov Random Field Models, PhD thesis, University of Cambridge (1998)
Besag, J.E.: Spatial Interaction and The Statistical Analysis of Lattice Systems. Journal of the Royal Statistical Society B 36, 192–236 (1974)
Besag, J.E.: On The Statistical Analysis of Dirty Pictures. Journal of the Royal Statistical Society B 48, 259–302 (1986)
Cowles, M.K., Carlin, B.P.: Markov Chain Monte Carlo Convergence Diagnostics: A Comparative Review. Journal of the American Statistical Association 91, 883–904 (1996)
Geman, S., Geman, D.: Stochastic Relaxation, Gibbs Distribution, and the Bayesian Restoration of Images. IEEE Transactions on Pattern Analysis and Machine Intelligence 6(6), 721–741 (1984)
Kato, Z.: Bayesian Color Image Segmentation Using Reversible Jump Markov Chain Monte Carlo, Research Report PNA-R9902, CWI (1999)
Richardson, S., Green, P.J.: On Bayesian Analysis of Mixtures with An Unknown Number of Components. Journal of the the Royal Statistical Society B 59, 731–792 (1997)
Stephens, M.: Bayesian Methods for Mixture of Normal Distributions, PhD thesis, University of Oxford (1997)
Tu, Z., Zho, S.-C.: Image Segmentation By Data-Driven Markov Chain Monte Carlo. IEEE Transactions on Pattern Analysis and Machine Intelligence 24(5), 657–673 (2002)
Zhang, J.: The Mean Field Theory in EM Procedures for Markov Random Fields. IEEE Transactions on Signal Processing 40(10), 2570–2583 (1992)
Zhang, Y., Brady, M., Smith, S.: Segmentation of Brain MR Images Through a Hidden Markov Random Field Model and the Expectation-Maximization Algorithm. IEEE Transactions on Medical Imaging 20(1), 45–57 (2001)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2005 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Aoki, K., Nagahashi, H. (2005). Bayesian Image Segmentation Using MRF’s Combined with Hierarchical Prior Models. In: Kalviainen, H., Parkkinen, J., Kaarna, A. (eds) Image Analysis. SCIA 2005. Lecture Notes in Computer Science, vol 3540. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11499145_8
Download citation
DOI: https://doi.org/10.1007/11499145_8
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-26320-3
Online ISBN: 978-3-540-31566-7
eBook Packages: Computer ScienceComputer Science (R0)