Abstract
In game semantics, a computation is represented by a play, which is traditionally a sequence of messages exchanged by a program and an environment. Because of the sequentiality of plays, most game models for concurrent programs are a kind of interleaving semantics. Several frameworks for truly concurrent game models have been proposed, but no model has yet been applied to give a semantics of a complex concurrent calculus such as the \(\pi \)-calculus (with replication).
This paper proposes a truly concurrent version of the HO/N game model in which a play is not a sequence but a directed acyclic graph (DAG) with two kinds edges, justification pointers and causal edges. By using this model, we give the first truly concurrent game semantics for the asynchronous \(\pi \)-calculus. In order to illustrate a possible application, we propose an intersection type system for the asynchronous \(\pi \)-calculus by means of our game model, and discuss when a process can be completely characterised by the intersection type system.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Game semantics succeeded to give semantics for variety of programming languages such as PCF [1, 21] and Idealized Algol [2].
The idea of game semantics has been applied to give models for concurrent calculi such as CSP [23], Idealized Parallel Algol [18] and the asynchronous \(\pi \)-calculus [24]. However, the sequential nature of plays forces these models to be a kind of interleaving semantics; the causalities between events are obfuscated.
Hence it is natural to investigate a concurrent extension of the traditional game models. Several frameworks for concurrent game models have been proposed by several researchers [3, 27, 29, 34], but no model has yet been applied to give a semantics of a complex concurrent calculus such as the \(\pi \)-calculus (with replication), as pointed out in [10]. The goal of this paper is to develop a truly concurrent game model by which the asynchronous \(\pi \)-calculus can be interpreted.
The starting point of our development is an observation by Melliès [27]: in the HO/N innocent game model [21, 32], only a part of the sequential information is really relevant. For example, the order of consecutive occurrences of O- and P-moves are indispensable, whereas that of consecutive occurrences of P- and O-moves can be safely forgotten (unless the O-move is justified by the P-move).
Now it is natural to think of a play in which the relevant order information is made explicit. Consider a traditional sequential play on the left side in Fig. 1, where \(\bullet \) (resp. \(\circ \)) represents an O-move (resp. a P-move) and a pointer is a justification pointer. By making the relevant sequential information explicit, we obtain a representation in the middle in Fig. 1. Then because all the relevant sequential information has been explicitly indicated by edges, we can simply forget the sequential information, resulting in the right representation in Fig. 1. This is our representation of a play that we call a DAG-based play.
A DAG-based play generated by this way from a sequential play satisfies a certain property, which reflects the sequential nature of the target language of the innocent game model [21]. In order to model a concurrent calculus, the condition required for DAG-based plays should be weakened. This is the idea that leads us to the definition of plays in this paper.
Following this idea, we develop a DAG-based game model for the asynchronous \(\pi \)-calculus, guided by the sequential game model of Laird [24]. Our model is truly concurrent in the sense that it distinguishes between \(a.\bar{b} \,|\, c.\bar{d}\) and \(a.(\bar{b} \,|\, c.\bar{d}) + c.(a.\bar{b} \,|\, \bar{d})\). Laird’s model can be reconstructed by lining up the nodes of DAG-based plays of our model. We prove the soundness of our model by reducing it to that of Laird’s model, using this relationship.
As a possible application of our model, we give an intersection type system based on the relationship between intersection types and game semantics which has been studied in the case of \(\lambda \)-calculus [7, 14, 37]. Based on a game-semantic consideration, we characterise a class of processes that are completely described by the intersection type system.
Organisation of the paper. Section 2 defines our target language, a variant of the asynchronous \(\pi \)-calculus. In Sect. 3, we define our truly concurrent game model and relate it with sequential game models. A semantics of the \(\pi \)-calculus is given in Sect. 4. Section 5 illustrates a possible application of our game model, giving an intersection type system for a fragment of the \(\pi \)-calculus. Section 6 discusses related work and Sect. 7 concludes the paper.
2 Simply-Typed Asynchronous \(\pi \)-Calculus
We define the target language of the paper: the simply-typed asynchronous polyadic \(\pi \)-calculus with distinction between input and output channels. This is the calculus studied in the previous work of Laird [24], in which he gave an interleaving (or sequential) game model.
We assume countably infinite sets of input names and of output names. Unlike the standard \(\pi \)-calculus in which an input name a is a priori connected to the output name \(\bar{a} \), we do not assume any relationship between input and output names but a connection is established by \(\nu \) constructor. This design choice significantly simplifies the denotational semantics.
The processes are defined by the following grammar:  Here x (resp. \(\bar{x} \)) ranges over input (resp. output) names and \(\varvec{x}\) (resp. \(\bar{\varvec{x}}\)) represents a (possibly empty) sequence of input (resp. output) names. Name creation \(\nu \) creates a pair of input and output names. We abbreviate \(\nu (\bar{x}_1, y_1). \dots . \nu (\bar{x}_n, y_n). P \) as \(\nu (\bar{x}_1 \dots \bar{x}_n, y_1 \dots y_n).P \).
Here x (resp. \(\bar{x} \)) ranges over input (resp. output) names and \(\varvec{x}\) (resp. \(\bar{\varvec{x}}\)) represents a (possibly empty) sequence of input (resp. output) names. Name creation \(\nu \) creates a pair of input and output names. We abbreviate \(\nu (\bar{x}_1, y_1). \dots . \nu (\bar{x}_n, y_n). P \) as \(\nu (\bar{x}_1 \dots \bar{x}_n, y_1 \dots y_n).P \).
The structural congruence \(\equiv \) is defined as usual. The one-step reduction relation \(\longrightarrow \) on processes is defined by the following rule:
It is worth emphasising here that the communication only occurs over names that are bound by \(\nu \). The reduction relation \(\longrightarrow ^* \) is the reflexive transitive closure of \(({\longrightarrow } \cup {\equiv }) \). We write \(P{\Downarrow }_{\bar{x}} \) if \(P \longrightarrow ^* \nu (\bar{\varvec{y}}, \varvec{z}).(\bar{x}\langle \bar{\varvec{y}}', \varvec{z}' \rangle \mid Q)\) for some Q, where \(\bar{x}\) is free. Note that we can observe only an output action.
We require that processes are well-typed. The syntax of types is given by  . We write \(x : \mathbf {ch}[S_1 \ldots S_m, T_1 \ldots T_n] \) to mean that x is an input name by which one receives m output names and n input names at once. Similarly for \(\bar{y} : \mathbf {ch}[S_1 \ldots S_m, T_1 \ldots T_n] \). A sequence \(S_1 \ldots S_m \) of types is often written as \(\varvec{S} \) and the empty sequence is written as \(\_ \). The type \(\mathbf {ch}[\_, \_] \) is abbreviated as \(\mathbf {ch}[] \). An input type environment is a finite sequence of type bindings of the form x : T and an output type environment is that of the form \(\bar{y} : S \). A type judgement is of the form \(\varGamma \vdash P; \varSigma \), where \(\varGamma \) and \(\varSigma \) are input and output type environments, respectively. Typing rules are listed in Fig. 2.
. We write \(x : \mathbf {ch}[S_1 \ldots S_m, T_1 \ldots T_n] \) to mean that x is an input name by which one receives m output names and n input names at once. Similarly for \(\bar{y} : \mathbf {ch}[S_1 \ldots S_m, T_1 \ldots T_n] \). A sequence \(S_1 \ldots S_m \) of types is often written as \(\varvec{S} \) and the empty sequence is written as \(\_ \). The type \(\mathbf {ch}[\_, \_] \) is abbreviated as \(\mathbf {ch}[] \). An input type environment is a finite sequence of type bindings of the form x : T and an output type environment is that of the form \(\bar{y} : S \). A type judgement is of the form \(\varGamma \vdash P; \varSigma \), where \(\varGamma \) and \(\varSigma \) are input and output type environments, respectively. Typing rules are listed in Fig. 2.
Remark 1
(1) A calculus with a priori connection between an input name x and an output name \(\bar{x} \) can be simulated by passing/receiving a pair \((x, \bar{x}) \) of input and output names. Via this translation our game semantics is applicable to a calculus with a priori connection because the translation reflects may-testing equivalence. (2) The standard parallel composition, which invokes communications of the two processes, can be expressed as \(\nu (\bar{\varvec{a}}\bar{\varvec{b}}, \varvec{a}\varvec{b}). (P|Q| (\varvec{a}' \!\rightarrow \! \bar{\varvec{a}}) | (\varvec{b} \!\rightarrow \! \bar{\varvec{b}}'))\) where \(\varvec{a} \) and \(\bar{\varvec{b}} \) are free names in P and Q, and \(\varvec{a}' \rightarrow \bar{\varvec{a}} \) is a “forwarder”, a process forwarding names received from \(a_i' \) to \(\bar{a}_i \).
3 Concurrent HO/N Game Model
This section introduces a truly concurrent game model in which a play is not a sequence but a directed acyclic graph (DAG). A node of a play is labelled by a move representing an event; an edge represents either a justification pointer or causality. The key is the notion of plays (Sect. 3.2) and of interactions (Sect. 3.3). The other parts are relatively straightforward adaptation of the techniques in the standard HO/N game model (e.g. [21]) or Laird’s model [24].
3.1 Arenas
The definition of arenas is (essentially) the same as the definition of arenas in the case of the sequential game model of \(\pi \)-calculus [24]. The differences from the standard definition (e.g. [21]) are (1) all moves are questions, and (2) the owner of moves does not have to alternate.
Definition 1
(Arena). An arena is a triple \(A = (\mathcal {M}_{A}, \lambda _{A}, \vdash _{A})\), where \(\mathcal {M}_{A}\) is a set of moves, \(\lambda _A :\mathcal {M}_{A} \rightarrow \{P, O\}\) is an ownership function and \({\vdash _{A}} \subseteq (\{\star \} + \mathcal {M}_{A}) \times \mathcal {M}_{A}\) is an enabling relation that satisfies: for every \(m \in \mathcal {M}_{A}\), there uniquely exists \(x \in \{\star \} + \mathcal {M}_{A}\) such that \(x \vdash _{A} m\).
We say that m is a P-move if \(\lambda _{A}(m) = P\); it is an O-move if \(\lambda _A(m) = O \). Every move represents an output action: a P-move is an output action of the process and an O-move is that of the environment (see a discussion after Definition 4). Let \(\lambda _{A}^{\bot }\) denote the negation of \(\lambda _{A}\) i.e. \(\lambda _{A}^{\bot }(m) = O\) (resp. \(\lambda _{A}^{\bot }(m) = P\)) if \(\lambda _{A}(m) = P\) (resp. \(\lambda _{A}(m) = O\)). A move m is initial if \(\star \vdash _A m\). An arena is negative (resp. positive) if all initial moves are O-moves (resp. P-moves). In what follows, we shall consider only negative arenas (hence we often use arenas to mean negative arenas). The empty arena is defined by \(I := (\emptyset , \emptyset , \emptyset )\).
Negative and positive arenas correspond to input and output type environments, respectively. Hence a judgement, which consists of a pair of input and output type environments, should be expressed as a pair of arenas.
Definition 2
(Arena pair). An arena pair is a pair (A, B) of (negative) arenas. We write \(\mathcal {M}_{A, B} \) for \(\mathcal {M}_{A} + \mathcal {M}_{B}\). The ownership function is defined by \(\lambda _{A, B} = [\lambda _{A}^{\bot }, \lambda _{B}]\). The enabling relation \(\vdash _{A, B}\) is given by: \(m \vdash _{A, B} m' \) if and only if \(m \vdash _{A} m'\) or \(m \vdash _{B} m'\). (In particular, \(\star \vdash _{A, B} m\) iff \(\star \vdash _{A} m\) or \(\star \vdash _{B} m'\).)
Note that an arena pair is not a negative arena since it has an initial P-move.
Example 1
Three (negative) arenas A, B and C are illustrated in Fig. 3, as well as the arena pair (A, B). Those arenas are used in examples in this paper. Nodes are labelled by moves and edges represent the enabling relation. If a name is overlined, the move is a P-move; otherwise it is an O-move. The arena pair (A, B) corresponds to the pair of the output type environment \( \varGamma = \bar{a}_1 : \mathbf {ch}[\_,\mathbf {ch}[]],\, \bar{a}_2 :\mathbf {ch}[] \) and the input type environment \( \varSigma = b_1:\mathbf {ch}[\mathbf {ch}[], \mathbf {ch}[\mathbf {ch}[],\_]]\). (Channel names do not have to coincide with move names.)
3.2 DAG-based Plays
In the standard HO/N game model [21], a play is a sequence of moves equipped with pointers, called justification pointers. The justification pointers express the binder-bindee relation and the sequential structure expresses the temporal relation between the events in the sequence (e.g. in the sequence \(s_1\,a\,s_2\,b\,s_3 \), the event b occurs after a). The causal relation is left implicit (cf. Sect. 3.5).
In the proposed game model, we explicitly describe the causal relation as well as the justification pointers.
Definition 3
(Justified graph). A justified graph over an arena pair (A, B) is a tuple  where:
where:
-
\(V_s\) is a finite set called the vertex set
-
\(l_s\) is the vertex labelling, that is \(l_s :V_s \rightarrow \mathcal {M}_{A, B}\)
-
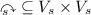 is the justification relation
is the justification relation
-
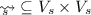 is the causality relation
is the causality relation
such that
-
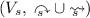 is a DAG i.e. there is no cycle
is a DAG i.e. there is no cycle 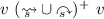 .
. -
If \(l_s(v)\) is initial, then there is no node \( v'\) such that
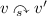 .
. -
If \(l_s(v)\) is not initial, then there exists a unique node \( v'\) such that
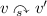 . Furthermore this \( v'\) satisfies \(l_s(v') \vdash _{A, B} l_s(v)\).
. Furthermore this \( v'\) satisfies \(l_s(v') \vdash _{A, B} l_s(v)\).
Note that  and
and  do not have to be disjoint. We define
do not have to be disjoint. We define  . The set of justified graphs over an arena pair (A, B) is denoted by \(J_{A, B}\).
. The set of justified graphs over an arena pair (A, B) is denoted by \(J_{A, B}\).
In what follows, we shall identify isomorphic justified graphs.
Given a justified graph s over (A, B), a P-node (resp. an O-node) is a node \(v \in V_s \) whose label is a P-move (resp. an O-move). We write \(V_s^P \) for the set of P-nodes and \(V_s^O \) for the set of O-nodes (e.g. \(V_s^P := \{ v \in V_s \mid \lambda _{A, B}(l_s(v)) = P \} \)).
Definition 4
(Play). Let  be a justified graph over (A, B). It is a play if it satisfies the following conditions:
be a justified graph over (A, B). It is a play if it satisfies the following conditions:
-
(P1) for every \(v, v' \in V_s \),
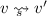 implies \(v \in V_s^P \) and \(v' \in V_s^O \),
implies \(v \in V_s^P \) and \(v' \in V_s^O \), -
(P2) for every \(v_p \in V_s^P\) and \(v_o \in V_s^O\), if
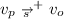 , then
, then 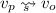 , and
, and -
(P3) for every \(v_o \in V^o_s \), there exists \(v_p \in V_s^P \) such that
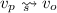 .
.
We write \(P_{A, B}\) for the set of plays over (A, B).
Condition (P1) reflects the asynchronous nature of the target language. Recall that a P-move corresponds to an output action of a process and an O-move to an output action of the environment. No P-node should be causally related to P-nodes since an output action of the process cannot cause any other output of the process. Similarly no O-node should be causally related to O-nodes since an output action of the environment cannot cause any other output of the environment (provided that the environment is also described by the asynchronous \(\pi \)-calculus). An output action of a process may cause an output action of the environment; however it is a matter of the environment and a play describes the behaviour of a process, not the environment. Hence  .
.
Condition (P2) comes from a purely technical requirement. (We need this condition to establish Lemma 2, as well as a proposition stating the copycat strategy is the identity.)
Condition (P3) is the counterpart of the even-length condition. Here we regard the even-length condition for sequential plays as the requirement that every O-move in the sequence should be responded by a P-move.
Example 2
Figure 4 shows three different plays over the arena pair (A, B) in Fig. 3. The solid arrows represent justification pointers, and squiggly arrows represent causalities. Nodes are labelled by moves and different nodes may be labelled by a same move. Note that plays may have a join point, i.e. a node that is linked to two “incomparable” nodes, like the node labelled by \(\bar{a}_{11}\) in \(s_2\).
Examples of plays over the arena pair (A, B) in Fig. 3.
Remark 2
A play can be seen as a process, e.g. the play \(s_2\) in Fig. 4 corresponds to the process \(\nu (\bar{a}_{11}, a_{11}).(b_1(\_, b_{12}). b_{12}(\bar{b}_{121},\_).(\bar{a}_{11} \,|\, \bar{b}_{121}) \,|\, \bar{a}_1\langle \_,a_{11}\rangle )\) (whose type differs from that described by the arena pair). The formal description of the connection to the linear internal \(\pi \)-calculus is left for the future work.
3.3 Strategies and Composition
Strategy. In most variants of sequential game models, a strategy \(\sigma \) is a collection of plays that is (even-length) prefix closed: if \(s m_O m_P \in \sigma \), then \(s \in \sigma \). The set of strategies in our game model is defined by the same way, though the notion of prefix should be adapted to our setting.
Definition 5
(Prefix). Let  be a play. Let \( U \subseteq V_s \) be a subset that satisfies (1) \(v \in U \) and
be a play. Let \( U \subseteq V_s \) be a subset that satisfies (1) \(v \in U \) and  implies \(v' \in U \) and (2) for all \(v_o \in U^{O}\) there exists \(v_p \in U^{P}\) such that
implies \(v' \in U \) and (2) for all \(v_o \in U^{O}\) there exists \(v_p \in U^{P}\) such that  . The prefix \(s[U] := (U, l, \curvearrowright , \rightsquigarrow ) \) of s induced by U is the restriction of s to U, i.e.,
. The prefix \(s[U] := (U, l, \curvearrowright , \rightsquigarrow ) \) of s induced by U is the restriction of s to U, i.e.,

We write \(s' \sqsubseteq s \) if \(s' \) is a prefix of s. A prefix of a play is a play.
Example 3
In Fig. 4, the play \(s_3\) is a prefix of \(s_2\) induced by the set of nodes labelled by \(m \in \{\bar{a}_1, \bar{a}_{11}, b_1, b_{12}\}\).
Definition 6
(Strategy). Let (A, B) be an arena pair. A set \(\sigma \subseteq P_{A,B} \) of plays over (A, B) is a strategy of (A, B), written as \(\sigma :A \rightarrow B \), if it satisfies prefix-closedness (S1):
-
(S1) If \(s \in \sigma \) and \(s' \sqsubseteq s \), then \(s' \in \sigma \).
Composition. The composition of strategies is defined by using the notion of interactions. Since plays are not sequences but graphs, an interaction should also be represented by a graph that we call an interaction graph.
Definition 7
Let (A, B, C) be a triple of arenas. The set \(\mathcal {M}_{A, B, C} \) of moves of (A, B, C) is the disjoint union \(\mathcal {M}_A + \mathcal {M}_B + \mathcal {M}_C \). The enabling relation \(\vdash _{A,B,C}\) is defined by: \(x \vdash _{A,B,C} m\) if \(x \vdash _{X} m\) for some \(X \in \{A, B, C\}\). The ownership function is defined by: \(\lambda _{A, B, C} := [\lambda _A, \lambda _B, \lambda _C]\). The set \(J_{A, B, C}\) of justified graphs of (A, B, C) is defined by the same way as in Definition 3.
For \(X \in \{ A, B, C, (A, B), (B, C), (A, C) \} \), we write \(V_X\) for the set of nodes restricted to the component X and \(V_X^P \) and \(V_X^O \) for the sets of nodes labelled by P-moves and by O-moves in the component X. For example, \(v \in V_{A,B}^P \) means either (1) \(l_{u}(v) \in \mathcal {M}_{B} \) and \(\lambda _B(l_{u}(v)) = P \), or (2) \(l_{u}(v) \in \mathcal {M}_A \) and \(\lambda _A(l_{u}(v)) = O \).
Definition 8
(Restriction). Let \(u = (V, l, {\curvearrowright }, {\rightsquigarrow })\) be a justified graph over (A, B, C) and \(X \in \{(A, B), (B, C), (A, C)\}\). The restriction  of u to X is defined by
of u to X is defined by  , where
, where

The definition of  needs some care. If
needs some care. If  , then
, then  is just the restriction of the original causal relation, i.e.
is just the restriction of the original causal relation, i.e.  (cf. Condition (P1)). If \(X = (A, C)\), then
(cf. Condition (P1)). If \(X = (A, C)\), then  relates moves linked through the intermediate component B, i.e.
relates moves linked through the intermediate component B, i.e.  .
.
Example 4
Figure 5 shows a justified graph u over the triple (A, B, C) (in Fig. 3) and its restrictions to components (A, B), (B, C) and (A, C).
Note that although  , we have
, we have  because
because  .
.
Definition 9
(Interaction graph). Let \(u \in J_{A, B, C} \) be a justified graph over (A, B, C) and V be the set of nodes of u. We say that u is an interaction graph if it satisfies the following conditions.
-
(I1) If
 , then \((v, v') \in V_X^P \times V_X^O \) for some \(X \in \{ (A, B), (B, C) \} \).
, then \((v, v') \in V_X^P \times V_X^O \) for some \(X \in \{ (A, B), (B, C) \} \). -
(I2) Both
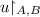 and
and 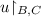 are plays.
are plays.
Condition (I1) is a variant of the switching condition. The set of interaction graphs over (A, B, C) is denoted as \(\mathrm {Int}(A, B, C)\).
In fact u in Example 4 is an interaction graph.
Definition 10
(Composition). Let \(\sigma :A \rightarrow B\) and \(\tau :B \rightarrow C\) be strategies. The composition of \(\sigma \) and \(\tau \) is defined by

Note that the definition of composition is applicable to sets of plays that are not necessarily strategies. By abuse of notation, we shall write \(\tau \circ \sigma \) even if \(\sigma \) and \(\tau \) are not strategies but just sets of plays.
Theorem 1
The composite of strategies is a strategy. The composition is associative.
Category. We define the category \(\mathcal {P}\) of negative arenas and strategies: an object of \(\mathcal {P}\) is a (negative) arena and a morphism from A to B is a strategy \(\sigma :A \rightarrow B \). The composite of \(\sigma :A \rightarrow B \) and \(\tau :B \rightarrow C \) is given by the composition \(\tau \circ \sigma \) of strategies defined above. Given an arena A, the identity morphism \(\mathrm {id}_A :A \rightarrow A \) is the “copycat strategy”: when the environment makes a move m in one component, then it responds by making a copy of m in the other component. It is the set of copycat plays, whose construction is illustrated in Fig. 6: (a) take a “justified graph without causality” of the arena (in this example, the arena is B in Fig. 3); (b) make positive and negative copies and connect the corresponding nodes by a causal edge \(\rightsquigarrow \) in the appropriate direction; and (c) add causal edges so as to satisfy Condition (P2), resulting in a play over (B, B).
3.4 Distributive-Closed Freyd Category
In this section, we define the categorical structures of \(\mathcal {P}\), which is used in Sect. 4 to give an interpretation of the \(\pi \)-calculus. A category with the structures below is called a distributive-closed Freyd category [24]. The definitions in this section are adapted from the interleaving game model for the \(\pi \)-calculus [24].
Monoidal product. Let \(A = (\mathcal {M}_A, \lambda _{A}, \vdash _{A})\) and \(B = (\mathcal {M}_{B}, \lambda _{B}, \vdash _{B})\) be arenas. The arena \(A \odot B\) is defined as \((\mathcal {M}_{A} + \mathcal {M}_{B}, [\lambda _{A}, \lambda _{B}], \vdash _{A, B})\), where \(\vdash _{A, B}\) is the enabling relation defined in Definition 2. Given strategies \(\sigma :A \rightarrow B \) and \(\tau :C \rightarrow D \), the strategy \(\sigma \odot \tau :A \odot C \rightarrow B \odot D \) is defined by the juxtaposition of plays in \(\sigma \) and \(\tau \), namely \(\sigma \odot \tau := \{s \uplus t \mid s \in \sigma , t \in \tau \}\) where \(s \uplus t \) is the juxtaposition of plays. Then the triple \((\mathcal {P}, \odot , I)\) is a symmetrical monoidal category.
Closed Freyd structure. An input prefixing \(a(\bar{\varvec{x}}, \varvec{y}).P \) should be interpreted by using a kind of closed structure (intuitively because the input prefix bounds variables in P like \(\lambda \)-abstraction). Laird [24] used closed Freyd categories [33].
A Freyd category consists of a symmetric (pre)monoidal category \(\mathcal {P}\), a cartesian category \(\mathcal {A}\) and an identity-on-object strict (pre)monoidal functor  . Intuitively \(\mathcal {P}\) is that of types and “terms” whereas \(\mathcal {A}\) is the category of types and “values”; the functor ! gives us a way to regard a “value” as a “term”. In our context, “terms” are processes and “values” are processes of the form \(\sum _i a_i(\bar{\varvec{x}_i}, \varvec{y}_i).P_i \), where \(P_i \) has no free input channel except for those in \(\varvec{y}_i \).
. Intuitively \(\mathcal {P}\) is that of types and “terms” whereas \(\mathcal {A}\) is the category of types and “values”; the functor ! gives us a way to regard a “value” as a “term”. In our context, “terms” are processes and “values” are processes of the form \(\sum _i a_i(\bar{\varvec{x}_i}, \varvec{y}_i).P_i \), where \(P_i \) has no free input channel except for those in \(\varvec{y}_i \).
We define the game-semantic counterpart of the processes of the this form.
Definition 11
(Well-opened play, strategy). A play s is well-opened if it contains precisely one initial O-node \(v_0 \) to which all other nodes are connected (i.e.  for every \(v \in V_s\)). We write \(W_{A, B}\) for the set of well-opened plays over (A, B). A well-opened strategy from arena A to arena B, written as \(\sigma :A \mathop {\rightarrow }\limits ^{\bullet } B \), is a set \(\sigma \) of well-opened plays that is prefix-closed (S1).
for every \(v \in V_s\)). We write \(W_{A, B}\) for the set of well-opened plays over (A, B). A well-opened strategy from arena A to arena B, written as \(\sigma :A \mathop {\rightarrow }\limits ^{\bullet } B \), is a set \(\sigma \) of well-opened plays that is prefix-closed (S1).
Then we define an operator !, a mapping from well-opened strategies to strategies and the composition of well-opened strategies by using !.
Definition 12
Let \(\sigma :A \mathop {\rightarrow }\limits ^{\bullet } B\) be a well-opened strategy. The strategy \(!\sigma :A \rightarrow B\) is defined by \(!\sigma := \{s_1 \uplus \cdots \uplus s_n \mid n \ge 0,\ \forall i \le n.\, s_i \in \sigma \}\) where \(s_1 \uplus \dots \uplus s_n \) is the juxtaposition of plays \(s_1, \dots , s_n \).
Definition 13
(Composition of well-opened strategies). Let \(\sigma :A \mathop {\rightarrow }\limits ^{\bullet } B \) and \(\tau :B \mathop {\rightarrow }\limits ^{\bullet } C \) be well-opened strategies. We define \(\tau \circ _{\mathcal {A}} \sigma := \tau \circ {{!}\sigma } \).
Lemma 1
The composite of well-opened strategies with respect to \(\circ _{\mathcal {A}} \) is a well-opened strategy. The composition \(\circ _{\mathcal {A}} \) of well-opened strategies is associative.
The category \(\mathcal {A}\) of negative arenas and well-opened strategies is defined by the following data: an object is a negative arena, a morphism from A to B is a well-opened strategy \(\sigma :A \mathop {\rightarrow }\limits ^{\bullet } B \), the composition is given by \(\circ _{\mathcal {A}} \). The identity morphism is \(\mathrm {id}_A \cap W_{A, A} \), where \(\mathrm {id}_A \) is the copycat strategy. The category \(\mathcal {A}\) is cartesian: the cartesian product of A and B is \(A \odot B \).
By defining \({!}A := A \) for objects, the operation ! becomes a functor  . This is identity on objects and strict symmetric monoidal functor and thus \((\mathcal {A}, \mathcal {P}, !) \) is a Freyd category.
. This is identity on objects and strict symmetric monoidal functor and thus \((\mathcal {A}, \mathcal {P}, !) \) is a Freyd category.
Lemma 2
The Freyd category \((\mathcal {A}, \mathcal {P}, {!}) \) is closed, i.e. for every arena A, the functor \({!}({-}) \odot A :\mathcal {A}\rightarrow \mathcal {P}\) has the right-adjoint \(A \rightharpoonup ({-}) :\mathcal {P}\rightarrow \mathcal {A}\).
The action of \(A \rightharpoonup ({-}) \) on objects and on morphisms is illustrated in Fig. 7. We write \(\varLambda \) for the bijective map \(\mathcal {P}({!}A \odot B, C) \rightarrow \mathcal {A}(A, B \rightharpoonup C) \) and \(\mathbf {app}_{A,B} :{!}(A \rightharpoonup B) \odot A \rightarrow B \) for the counit. The bijection \(\mathcal {P}({!}A \odot B, C) \cong \mathcal {A}(A, B \rightharpoonup C) \) induced by the adjunction intuitively corresponds to the following bijection of the \(\pi \)-calculus processes: \( \bar{\varvec{x}} : \varvec{S}, \bar{\varvec{y}} : \varvec{T} \vdash P ; \varvec{z} : \varvec{U} \;\;\longleftrightarrow \;\; \bar{\varvec{x}} : \varvec{S} \vdash a(\bar{\varvec{y}}, \varvec{z}). P ; a : \mathbf {ch}[\varvec{T}, \varvec{U}]. \)
Distributive law. The process obtained by (the \(\pi \)-term representation of) the above adjunction has the input prefix \(a(\bar{\varvec{y}}, \varvec{z}) \) as expected but it has only one free input channel. We use the distributive law of the distributive-closed Freyd category to model a process with multiple free input channel. By using the syntax of the \(\pi \)-calculus, the distribution law can be seen as the following map:
Definition 14
(Distributive-closed Freyd category [24]). A closed Freyd category  is distributive-closed if there is a family of morphisms \(\varrho _{A}:{!}(A \rightharpoonup (B \odot C)) \;\longrightarrow \; B \odot {!}(A \rightharpoonup C)\) in \(\mathcal {P}\), natural in B and C which makes certain diagrams commute.
is distributive-closed if there is a family of morphisms \(\varrho _{A}:{!}(A \rightharpoonup (B \odot C)) \;\longrightarrow \; B \odot {!}(A \rightharpoonup C)\) in \(\mathcal {P}\), natural in B and C which makes certain diagrams commute.
Theorem 2
The game model \({!} :\mathcal {A}\rightarrow \mathcal {P}\) is distributive-closed.
Trace. The operator \(\nu (\bar{x}, y). P \) is interpreted as a trace operator. We define \(Tr_{A, C}^{B}(f) := \mathbf {app}_{B, C} \circ \mathbf {symm}_{B, B\rightharpoonup C} \circ \varrho _{B, B, C} \circ {!\varLambda (\mathbf {symm}_{B,C} \circ f)}\), given a morphism \(f:A \odot B \rightarrow C \odot B\) in \(\mathcal {P}\). Then Tr is the trace operator for the symmetrical monoidal category \(\mathcal {P}\) [24].
Additional structures. Some additional structures are required to interpret the \(\pi \)-calculus: the minimum strategy \(\bot _{A, B}\) (with respect to the set-inclusion), the diagonal \(\varDelta _A :A \mathop {\rightarrow }\limits ^{\bullet } A \odot A \), the codiagonal \(\nabla _A :A \odot A \mathop {\rightarrow }\limits ^{\bullet } A \) (defined by \(\nabla _A := \pi _1 \cup \pi _2 \) where \(\pi _i :A \odot A \mathop {\rightarrow }\limits ^{\bullet } A \) is the projection), and the dereliction \( der _A :A \rightarrow A \) (defined as \(\mathrm {id}_A \cap W_{A, A} \)).
3.5 Relation to Sequential Game Models
Laird’s interleaving game model. Our model can be seen as a truly concurrent version of the interleaving game model \(\mathcal {P}_{\mathrm {L}}\) of Laird [24]. The idea is to relate a (concurrent) play  to an interleaving play by lining up the nodes in \(V_{s} \) in such a way that if
to an interleaving play by lining up the nodes in \(V_{s} \) in such a way that if  , then \(v_2 \) appears before \(v_1 \). We write |s| for the set of sequential plays obtained by this way.
, then \(v_2 \) appears before \(v_1 \). We write |s| for the set of sequential plays obtained by this way.
Example 5
Let \(s_2\) be the play in Fig. 4. Then \(|s_2|\) is given as:

Theorem 3
\(|{-}| \) induces an identity-on-object functor from \(\mathcal {P}\) to \(\mathcal {P}_{\mathrm {L}}\), which preserves the structure of distributed-closed Freyd categories (and the additional structures). Furthermore \(|\sigma | \) is the minimum strategy if and only if so is \(\sigma \).
Sequential HO/N game model. The standard sequential HO/N game model [21] is a subcategory of our concurrent model. Since our game model only have question moves, we compare our model with the HO/N game model without answer (and thus without well-bracketing).
An arena A is alternating if \(m \vdash _A m' \) implies \(\lambda _A(m) = \lambda ^{\bot }_A(m') \). Let \(\mathcal {G} \) be the category of negative alternating arenas and innocent strategies (we omit the definition, which is standard). We write \(\ulcorner {\hat{s}}\urcorner \) for the P-view [21] of the sequential play \(\hat{s} \). Given a sequential play \(\hat{s} = m_1 \dots m_n \), a DAG-based play is given by
where \(V_{\hat{s}} := \{ 1, \dots , n \} \), \(l_{\hat{s}}(i) := m_i \) and \(\rho _{\hat{s}} \) is the partial function describing the justification pointer. Note that the occurrence \(m_i \) of a P-move is causally related to an occurrence \(m_j \) of an O-move if and only if \(m_j \) appears in the P-view of \(m_i \). This map is naturally extended to strategies, namely \(\Vert \hat{\sigma } \Vert := \{ \Vert \hat{s} \Vert \mid \hat{s} \in \hat{\sigma } \} \).
Theorem 4
\(\Vert {-}\Vert \) induces a faithful functor from \(\mathcal {G} \) to \(\mathcal {P}\).
Remark 3
It is natural to ask if one can give a similar map from Laird’s interleaving model. The answer seems negative: all maps that we have checked are not functorial. See [8] for a related result.
4 Game Semantics of the \(\pi \)-calculus
We give an interpretation of the \(\pi \)-calculus, following the result of Laird [24] applicable to every distributive-closed Freyd category with additional structures.
A type and a type environment are interpreted as objects of \(\mathcal {P}\). The interpretation of a type \(\mathbf {ch}[\varvec{S}, \varvec{T}] \) and a sequence \(\varvec{S} \) of types are defined by:

The interpretation of an input type environment is given by the tensor product of elements, e.g. \(\llbracket x_1 : S_1, \dots , x_n : S_n \rrbracket := \llbracket S_1 \rrbracket \odot \dots \odot \llbracket S_n \rrbracket \).
A process \(\varGamma \vdash P ; \varSigma \) is interpreted as a morphism  in \(\mathcal {P}\). The interpretation is defined by induction on the type derivations. The rules are listed in Fig. 8.
in \(\mathcal {P}\). The interpretation is defined by induction on the type derivations. The rules are listed in Fig. 8.
The distributive-closed Freyd structure together with additional structures (of \(\varDelta \), \(\nabla \), \(\bot \), der) gives a (weak) soundness result with respect to the reduction.
Theorem 5
Let \(\varGamma \vdash P; \varSigma \) and \(\varGamma \vdash Q; \varSigma \) be processes of the same type.
-
1.
If \(P \equiv Q\), then \(\llbracket \varGamma \vdash P; \varSigma \rrbracket = \llbracket \varGamma \vdash Q; \varSigma \rrbracket .\)
-
2.
If \(P \longrightarrow Q\), then \(\llbracket \varGamma \vdash P; \varSigma \rrbracket \supseteq \llbracket \varGamma \vdash Q; \varSigma \rrbracket .\)
The relationship to Laird’s model (Theorem 3) gives a finer result, which does not follow from the general theory of the distributive-closed Freyd categories.
Lemma 3
(Adequacy). \(P\Downarrow _{\bar{x}}\) iff \(\llbracket P \rrbracket \ne \bot \) for every process \(\bar{x}:\mathbf {ch}[] \vdash P;\_\).
Proof
Because of Theorem 3, we have  , where \(\llbracket P \rrbracket _L \) is the interpretation of the process in Laird’s game model [24]. Laird [24] shows that \(P \Downarrow _{\bar{x}} \) if and only if \(\llbracket P \rrbracket _L \ne \bot \). Since \(|{-}| \) preserves \(\bot \), we obtain the claim. \(\square \)
, where \(\llbracket P \rrbracket _L \) is the interpretation of the process in Laird’s game model [24]. Laird [24] shows that \(P \Downarrow _{\bar{x}} \) if and only if \(\llbracket P \rrbracket _L \ne \bot \). Since \(|{-}| \) preserves \(\bot \), we obtain the claim. \(\square \)
Lemma 3 and monotonicity of the interpretation lead to the next theorem.
Theorem 6
Let \(\bar{x}\) be a testing name that does not occur in \(\varGamma \). If \(\llbracket \varGamma \vdash P; \varSigma \rrbracket \subseteq \llbracket \varGamma \vdash Q; \varSigma \rrbracket \), then \(C[P] \Downarrow _{\bar{x}}\) implies \(C[Q] \Downarrow _{\bar{x}}\) for all context \(C[\,]\).
Unlike Laird’s model [24], our model is not complete since our model is truly concurrent. For example, \(\llbracket a().\bar{b}\langle \rangle \mid c().\bar{d}\langle \rangle \rrbracket \ne \llbracket \nu (\bar{x}, x).( \bar{x}\langle \rangle \mid x().a().(\bar{b}\langle \rangle \mid c().\bar{d}\langle \rangle ) \mid x().c().(a().\bar{b}\langle \rangle \mid \bar{d}\langle \rangle )) \rrbracket \) in our model, whereas they are testing equivalent.
5 Discussion: Relationally-Describable Process
Using our game model, we study the relational interpretations of process in the form of intersection type system that describes the behaviour of processes. The intersection type system is a fully abstract model for a class of process which we characterise with the help of “interaction graph”.
The syntax of types and intersections are defined by the following grammar:
where \(\langle \cdots \rangle \) is a finite multiset defined by an enumeration of the elements. A type environment is a sequence of type bindings of the form \(x{:}\xi \) (or \(\bar{y}{:}\zeta \)). Given intersections \(\xi = \langle \varphi _1, \dots , \varphi _n \rangle \) and \(\zeta = \langle \psi _1, \dots , \psi _k \rangle \), we write \(\xi \wedge \zeta \) for \(\langle \varphi _1, \dots , \varphi _n, \psi _1, \dots , \psi _k \rangle \). This operation is extended to type environments by pointwise application. The typing rules are listed below (some rules are omitted):

This type system is inspired by the correspondence between intersection type systems and the operation called time forgetting map [4], which is an operation that forgets the temporal structure of plays, in sequential game models (see, e.g., [37]). Time forgetting map is the operation that forgets the causal relation in the case of our concurrent game model.
Completeness of the type system holds for every process, but soundness does not; the reason is explained by a game-semantic consideration. We would thus like to find a class for which the relational interpretation is sound.
Let \(s \in P_{A, B} \) and \(t \in P_{B, C} \) be plays. We say that s and t are composable if  coincides with
coincides with  except for the causal relations. Then it would be natural to think of an “interaction graph” by composing them (see Fig. 9). Unfortunately the resulting “interaction graph” may not be acyclic and hence not be an interaction graph; in this case we say that the pair (s, t) contains a cycle.
except for the causal relations. Then it would be natural to think of an “interaction graph” by composing them (see Fig. 9). Unfortunately the resulting “interaction graph” may not be acyclic and hence not be an interaction graph; in this case we say that the pair (s, t) contains a cycle.
This notion of cycle can be extended to strategies and processes. The composition of strategies \(\tau \circ \sigma \) is cycle-free if every pair of composable plays \(s \in \sigma \) and \(t \in \tau \) is cycle-free. A process P is relationally-describable if every composition in the definition of \(\llbracket P \rrbracket \) is cycle-free.
Theorem 7
Let \(\varGamma \vdash P ;~ \varSigma \) be a relationally-describable process and let \(\bar{x} \in \mathrm {dom}(\varGamma ) \). Then \(P \Downarrow _{\bar{x}} \) if and only if \(\bar{x} : \mathbf {ch}[\varvec{\xi }, \varvec{\zeta }] \vdash P ;~ \emptyset \) for some \(\varvec{\xi } \) and \(\varvec{\zeta } \).
This is because the operation of forgetting the causal relation commutes with cycle-free composition. Note that the notion of cycle is stronger than deadlock: \(\nu (\bar{a}\bar{b}, ab). (a_1.\bar{b}_2 | b_3.\bar{a}_4 | \bar{a}_5) \) (subscripts are used to distinguish occurrences) is not relationally-describable because connecting \(a_1 \) to \(\bar{a}_4 \) and \(b_3 \) to \(\bar{b}_2 \) creates a cycle.
Restricting the form of processes by focusing on cycles is a reminiscent of the correctness criterion for MLL proof nets. The formal relationship between our notion of cycle in an interaction graph and the correctness criterion, and the connection between cycle (in our sense) and the type system, which gives a typed \(\pi \)-calculus corresponding to polarised proof-nets satisfying the correctness criterion, proposed by Honda and Laurent [19] are worth investigating.
6 Related Work
Melliès [27] studied HO/N innocent strategies from a truly concurrent point of view. Among others, he introduced the notions of alternating homotopy and diagrammatic innocence, which influence to this work. These ideas were subsequently developed by Melliès and Mimram [29, 30], who introduced asynchronous games. They focused on the fact that some moves of a play in an innocent strategy can be exchanged, and studied games whose rules explicitly describe which moves should be commutable. Our game model is also inspired by [27] (and [28]) but we focused on a different aspect of the alternating homotopy, that is, the fact that the connection between a successive pair of O- and P-moves (in HO/N innocent strategies) are quite tight (see also [25, 36]); in our game model, a strategy explicitly describes indispensable connections \(\rightsquigarrow \) between events. Because of these differences, their game model differs from ours; indeed our strategy is not necessarily positional. Nevertheless those models seems closely related; for example, it seems worth investigating the connection between scheduled strategies [30] and cycle-free composition.
A related approach using a map of event structures has been proposed by Rideau and Winskel [34] and extensively studied recently [9, 10]. In this game model, a strategy is a map from an event structure describing the internal causal relation to another event structure expressing the observable events. We think that their model should be closely related to the (pre)sheaf version [36] of our game model, although we have not established any formal relationship yet.
From a technical point of view, an important difference between above models and our model is the way to deal with duplication of moves. Our model uses HO/N-style justification pointers, whereas the above models use the idea of thread indexing [10, 26] in the style of AJM game model [1]. Both approaches have advantages and disadvantages (for example, an advantage of the HO/N-style is that a morphism is a strategy, not an equivalence class of strategies modulo reindexing). Hence we think that it is good to have a truly concurrent model using justification pointers.
Laird [24] briefly discussed an idea of a truly concurrent version of his interleaving game model, introducing the notion of justified pomset. His idea is very closed to ours; indeed a play s in our game model can be seen as a pomset  ordered by (reflexive transitive closure of) the adjacent relation
ordered by (reflexive transitive closure of) the adjacent relation  .
.
A DAG-based reformulation of the HO/N game model is a reminiscent of L -nets [13, 17]. The conditions required for L-nets are essentially the same as those we require for plays, though L-nets corresponds to strategies, not to plays. An interpretation of the \(\pi \)-calculus using differential nets [15] seems to be relevant to our development.
The game-semantics study of this paper has many parallels to the syntactic study of the \(\pi \)-calculus. The relationship between the HO/N game model for PCF [21] and the \(\pi \)-calculus has originally been studied by Hyland and Ong themselves [20], who gave a translation from PCF terms to processes of the \(\pi \)-calculus based on the idea of their game model. The \(\pi \)-terms representing sequential functional computation can be characterised by a simple type system proposed by Berger, Honda and Yoshida [5], which lead to the type system of [19]. We conjecture that processes typed by the simple type system of [5, 19] is related to relationally-describable processes. Boreale [6] gave an encoding from the asynchronous \(\pi \)-calculus to the internal \(\pi \) -calculus [35]. Our game model can be seen as a variant of the encoding by regarding the plays as the processes of the linear internal \(\pi \)-calculus, in which each name must be used exactly once.
There are some pieces of work based on the techniques other than games but related to this work, such as event structure semantics of several variants of the \(\pi \)-calculus by Crafa, Varacca and Yoshida [11, 12] and Varacca and Yoshida [38], and a data-flow semantics by Jagadeesan and Jagadeesan [22].
7 Conclusion and Future Work
We have developed a truly concurrent version of the HO/N game model [21, 32], in which a computation is represented by a DAG of messages instead of a sequence. The resulting game model has the categorical structure needed to interpret the asynchronous \(\pi \)-calculus proposed by Laird [24]. By using the connection between our model and Laird’s model [24], we have proved soundness of the interpretation of the processes in our concurrent game model. This is the first truly concurrent game semantics for the \(\pi \)-calculus.
We have several topics left for future work:
-
Formal description of the connection between plays and processes mentioned in Remark 2. By this connection, our game semantics can be seen as an approximation of the processes of the \(\pi \)-calculus by a linear \(\pi \)-calculus, which is a reminiscent of the Taylor expansion of the \(\lambda \)-calculus [16] (see also [37]).
-
Development of the (pre)sheaf version of the game model [36], which would be related to the game model based on [34].
-
Development of a model of the synchronous \(\pi \)-calculus. This requires us to deal with causal edges from O-moves and/or to P-moves. To simply relax the requirements for \(\rightsquigarrow \) does not seem to work: for example, the copycat strategy of this paper is no longer the identity in the relaxed version.
-
Development of a model of the \(\pi \)-calculus with the matching primitive. We expect that a nominal game model [31] would be useful for this purpose.
References
Abramsky, S., Jagadeesan, R., Malacaria, P.: Full abstraction for PCF. Inf. Comput. 163(2), 409–470 (2000)
Abramsky, S., McCusker, G.: Linearity, sharing and state: a fully abstract game semantics for idealized algol with active expressions. Electr. Notes Theor. Comput. Sci. 3, 2–14 (1996)
Abramsky, S., Melliès, P.-A.: Concurrent games and full completeness. In: 14th Annual IEEE Symposium on Logic in Computer Science, pp. 431–442 (1999)
Baillot, P., Danos, V., Ehrhard, T., Regnier, L.: Timeless games. In: 11th International Workshop on Computer Science Logic, pp. 56–77 (1997)
Berger, M., Honda, K., Yoshida, N.: Sequentiality and the pi-calculus. In: TLCA, pp. 29–45 (2001)
Boreale, M.: On the expressiveness of internal mobility in name-passing calculi. Theor. Comput. Sci. 195(2), 205–226 (1998)
Boudes, P.: Thick subtrees, games and experiments. In: Curien, P.-L. (ed.) TLCA 2009. LNCS, vol. 5608, pp. 65–79. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02273-9_7
Castellan, S., Clairambault, P.: Causality vs. interleavings in concurrent game semantics. In: 27th International Conference on Concurrency Theory, CONCUR 2016, pp. 32:1–32:14 (2016)
Castellan, S., Clairambault, P., Winskel, G.: Symmetry in concurrent games. In: Joint Meeting of the Twenty-Third EACSL Annual Conference on Computer Science Logic (CSL) and the Twenty-Ninth Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), CSL-LICS 2014, pp. 28:1–28:10 (2014)
Castellan, S., Clairambault, P., Winskel, G.: The parallel intensionally fully abstract games model of PCF. In: 30th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2015, pp. 232–243 (2015)
Crafa, S., Varacca, D., Yoshida, N.: Compositional event structure semantics for the internal \(pi\)-calculus. In: CONCUR 2007 - Concurrency Theory, 18th International Conference, CONCUR 2007, pp. 317–332 (2007)
Crafa, S., Varacca, D., Yoshida, N.: Event structure semantics of parallel extrusion in the pi-calculus. In: Foundations of Software Science and Computational Structures - 15th International Conference, FOSSACS 2012, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2012, pp. 225–239 (2012)
Curien, P.-L., Faggian, C.: An approach to innocent strategies as graphs. Inf. Comput. 214, 119–155 (2012)
Di Gianantonio, P., Lenisa, M.: Innocent game semantics via intersection type assignment systems. In: Computer Science Logic 2013, CSL 2013, pp. 231–247 (2013)
Ehrhard, T., Laurent, O.: Interpreting a finitary pi-calculus in differential interaction nets. Inf. Comput. 208(6), 606–633 (2010)
Ehrhard, T., Regnier, L.: Uniformity and the taylor expansion of ordinary lambda-terms. Theor. Comput. Sci. 403(2–3), 347–372 (2008)
Faggian, C., Maurel, F.: Ludics nets, a game model of concurrent interaction. In: 20th IEEE Symposium on Logic in Computer Science (LICS 2005), pp. 376–385 (2005)
Ghica, D.R., Murawski, A.S.: Angelic semantics of fine-grained concurrency. Ann. Pure Appl. Logic 151(2–3), 89–114 (2008)
Honda, K., Laurent, O.: An exact correspondence between a typed pi-calculus and polarised proof-nets. Theor. Comput. Sci. 411(22–24), 2223–2238 (2010)
Hyland, J.M.E., Ong, C.-H.L.: Pi-calculus, dialogue games and PCF. In: Proceedings of the Seventh International Conference on Functional Programming Languages and Computer Architecture, FPCA 1995, pp. 96–107 (1995)
Hyland, J.M.E., Ong, C.-H.L.: On full abstraction for PCF: I, II, and III. Inf. Comput. 163(2), 285–408 (2000)
Jategaonkar Jagadeesan, L., Jagadeesan, R.: Causality and true concurrency: a data-flow analysis of the pi-calculus. In: Alagar, V.S., Nivat, M. (eds.) AMAST 1995. LNCS, vol. 936, pp. 277–291. Springer, Heidelberg (1995). doi:10.1007/3-540-60043-4_59
Laird, J.: A game semantics of idealized CSP. Electr. Notes Theor. Comput. Sci. 45, 232–257 (2001)
Laird, J.: A game semantics of the asynchronous \(\pi \)-calculus. In: 16th International Conference on CONCUR 2005 - Concurrency Theory, pp. 51–65 (2005)
Levy, P.B.: Morphisms between plays. In: Lecture Slides, GaLoP (2013)
Melliès, P.-A.: Asynchronous games 1: a group-theoretic formulation of uniformity (2003). (Unpublished manuscript)
Melliès, P.-A.: Asynchronous games 2: the true concurrency of innocence. Theor. Comput. Sci. 358(2–3), 200–228 (2006)
Melliès, P.-A.: Game semantics in string diagrams. In: Proceedings of the 27th Annual IEEE Symposium on Logic in Computer Science, LICS 2012, pp. 481–490 (2012)
Melliès, P.-A., Mimram, S.: Asynchronous games: innocence without alternation. In: Caires, L., Vasconcelos, V.T. (eds.) CONCUR 2007. LNCS, vol. 4703, pp. 395–411. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74407-8_27
Melliès, P.-A., Mimram, S.: From asynchronous games to concurrent games (2008). (Unpublished manuscript)
Murawski, A.S., Tzevelekos, N.: Nominal game semantics. Found. Trends Program. Lang. 2(4), 191–269 (2016)
Nickau, H.: Hereditarily sequential functionals. In: Nerode, A., Matiyasevich, Y.V. (eds.) LFCS 1994. LNCS, vol. 813, pp. 253–264. Springer, Heidelberg (1994). doi:10.1007/3-540-58140-5_25
Power, J., Thielecke, H.: Closed Freyd-and kappa-categories. In: Automata, Languages and Programming. In: 26th International Colloquium, ICALP 1999, pp. 625–634 (1999)
Rideau, S., Winskel, G.: Concurrent strategies. In: Proceedings of the 26th Annual IEEE Symposium on Logic in Computer Science, LICS 2011, pp. 409–418 (2011)
Sangiorgi, D.: pi-calculus, internal mobility, and agent-passing calculi. Theor. Comput. Sci. 167(1&2), 235–274 (1996)
Tsukada, T., Ong, C.-H.L.: Nondeterminism in game semantics via sheaves. In: 30th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2015, pp. 220–231 (2015)
Tsukada, T., Ong, C.-H.L.: Plays as resource terms via non-idempotent intersection types. In: Grohe, M., Koskinen, E., Shankar, N. (eds.) Proceedings of the 31st Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2016, New York, USA, July 5–8, 2016, pp. 237–246. ACM (2016)
Varacca, D., Yoshida, N.: Typed event structures and the linear pi-calculus. Theor. Comput. Sci. 411(19), 1949–1973 (2010)
Acknowledgements
We would like to thank Naoki Kobayashi and anonymous referees for useful comments. This work is partially supported by JSPS Kakenhi Grant Number 15H05706 and JSPS Kakenhi Grant Number 16K16004.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Sakayori, K., Tsukada, T. (2017). A Truly Concurrent Game Model of the Asynchronous \(\pi \)-Calculus. In: Esparza, J., Murawski, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2017. Lecture Notes in Computer Science(), vol 10203. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54458-7_23
Download citation
DOI: https://doi.org/10.1007/978-3-662-54458-7_23
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54457-0
Online ISBN: 978-3-662-54458-7
eBook Packages: Computer ScienceComputer Science (R0)








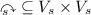 is the justification relation
is the justification relation
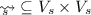 is the causality relation
is the causality relation
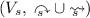 is a DAG i.e. there is no cycle
is a DAG i.e. there is no cycle 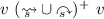 .
.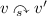 .
.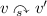 . Furthermore this
. Furthermore this 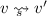 implies
implies 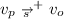 , then
, then 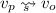 , and
, and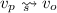 .
.


 , then
, then 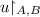 and
and 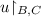 are plays.
are plays.


