Abstract
Symbolic models for security protocol verification, following the seminal ideas of Dolev and Yao, come in many flavors, even though they share the same ideas. A common assumption is that the attacker has complete control over the network: he can therefore intercept any message. Depending on the precise model this may be reflected either by the fact that any protocol output is directly routed to the adversary, or communications may be among any two participants, including the attacker — the scheduling between which exact parties the communication happens is left to the attacker. These two models may seem equivalent at first glance and, depending on the verification tools, either one or the other semantics is implemented. We show that, unsurprisingly, they indeed coincide for reachability properties. However, when we consider indistinguishability properties, we prove that these two semantics are incomparable. We also introduce a new semantics, where internal communications are allowed but messages are always eavesdropped by the attacker. We show that this new semantics yields strictly stronger equivalence relations. We also identify two subclasses of protocols for which the three semantics coincide. Finally, we implemented verification of trace equivalence for each of these semantics in the APTE tool and compare their performances on several classical examples.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Automated, symbolic analysis of security protocols, based on the seminal ideas of Dolev and Yao, comes is many variants. All of these models however share a few fundamental ideas:
-
messages are represented as abstract terms,
-
adversaries are computationally unbounded, but may manipulate messages only according to pre-defined rules (this is sometimes referred to as the perfect cryptography assumption), and
-
the adversary completely controls the network.
In this paper we will revisit this last assumption. Looking more precisely at different models we observe that this assumption may actually slightly differ among the models. The fact that the adversary controls the network is supposed to represent a worst case assumption.
In some models this assumption translates to the fact that every protocol output is sent to the adversary, and every protocol input is provided by the adversary. This is the case in the original Dolev Yao model and also in the models underlying several tools, such as AVISPA [6], Scyther [13], Tamarin [20], Millen and Shmatikov’s constraint solver [17], and the model used in Paulson’s inductive approach [18].
Some other models, such as those based on process algebras, e.g. work based on CSP [19], the Spi [3] and applied pi calculus [1], but also the strand space model [21], consider a slightly different communication model: any two agents may communicate. Scheduling whether communication happens among two honest participants, or a honest participant and the attacker is under the attacker’s control.
When considering reachability properties, these two communication models indeed coincide: intuitively, any internal communication could go through the adversary who acts as a relay and increases his knowledge by the transmitted message. However, when considering indistinguishability properties, typically modelled as process equivalences, these communication models diverge. Interestingly, when forbidding internal communication, i.e., forcing all communication to be relayed by the attacker, we may weaken the attacker’s distinguishing power.
In many recent work privacy properties have been modelled using process equivalences, see for instance [5, 14, 15]. The number of tools able to verify such properties is also increasing [9,10,11, 22]. We have noted that for instance the AKISS tool [10] does not allow any direct communication on public channels, while the APTE tool [11] allows the user to choose among the two semantics. One motivation for disallowing direct communication is that it allows for more efficient verification (as less actions need to be considered and the number of interleavings to be considered is smaller).
Our contributions. We have formalised three semantics in the applied pi calculus which differ by the way communication is handled:
-
the classical semantics (as in the original applied pi calculus) allows both internal communication among honest participants and communication with the adversary;
-
a private semantics allows internal communication only on private channels while all communication on public channels is routed through the adversary;
-
an eavesdropping semantics which allows internal communication, but as a side-effect adds the transmitted message to the adversary’s knowledge.
For each of the new semantics we define may-testing and observational equivalences. We also define corresponding labelled semantics and trace equivalence and bisimulation relations (which may serve as proof techniques).
We show that, as expected, the three semantics coincide for reachability properties. For equivalence properties we show that the classical and private semantics yield incomparable equivalences, while the eavesdropping semantics yields strictly stronger equivalence relations than both other semantics. The results are summarized in Fig. 7.
An interesting question is whether these semantics coincide for specific subclasses of processes. We first note that the processes that witness the differences in the semantics do not use replication, private channels, nor terms other than names, and no equational theory. Moreover, all except one of these examples only use trivial else branches (of the form \(\mathsf {else}\ 0\)); the use of a non-trivial else branch can however be avoided by allowing a single free symbol.
However conditions on the channel names may yield such a subclass. We first observe that the class of simple processes [12], for which already observational, testing, trace equivalence and labelled bisimulation coincide, do have this property. Simple processes may however be too restrictive for modelling some protocols that should guarantee anonymity (as no parallel processes may share channel names). We therefore identify a syntactic class of processes, that we call I/O-unambiguous. For this class we forbid communication on private channels, communication of channel names and an output may not be sequentially followed by an input on the same channel directly, or with only conditionals in between. Note that I/O-unambiguous processes do however allow outputs and inputs on the same channel in parallel. We show that for this class the eavesdropping semantics (which is the most strict relation) coincides with the private one (which is the most efficient for verification).
Finally, we extended the APTE tool to support verification of trace equivalence for the three semantics. Verifying existing protocols in the APTE example repository we verified that the results, fortunately, coincided for each of the semantics. We also made slight changes to the encodings, renaming some channels, to make them I/O-unambiguous. Interestingly, using different channels, significantly increased the performance of the tool. Finally, we also observed that, as expected, the private semantics yields more efficient verification. The results of our experiments are summarized in the table on page 21.
Outline. In Sect. 2 we define the three semantics we consider. In Sect. 3 we present our main results on comparing these semantics. We present subclasses for which (some) semantics coincide in Sect. 4 and compare the performances when verifying protocols for different semantics using APTE in Sect. 5, before concluding in Sect. 6.
Because of lack of space we did not include all proofs. Missing proofs are available in an extended [7].
2 Model
The applied pi calculus [1] is a variant of the pi calculus that is specialised for modelling cryptographic protocols. Participants in a protocol are modelled as processes and the communication between them is modelled by message passing on channels. In this section, we describe the syntax and semantics of the applied pi calculus as well as the two new variants that we study in this paper.
2.1 Syntax
We consider an infinite set \({\mathcal {N}}\) of names of base type and an infinite set \({\mathcal {C}}h\) of names of channel type. We also consider an infinite set of variables \({\mathcal {X}}\) of base type and channel type and a signature \({\mathcal {F}}\) consisting of a finite set of function symbols. We rely on a sort system for terms. In particular, the sort base type differs from the sort channel type. Moreover, any function symbol can only be applied and returns base type terms. We define terms as names, variables and function symbols applied to other terms. Given \(N \subseteq {\mathcal {N}}\), \(X \subseteq {\mathcal {X}}\) and \(F \subseteq {\mathcal {F}}\), we denote by \({\mathcal {T}}(F,X,N)\) the sets of terms built from X and N by applying function symbols from F. We denote \(fv(t)\) the sets of variables occurring in t. We say that t is ground if \(fv(t) = \emptyset \). We describe the behaviour of cryptographic primitives by the means of an equational theory \({\mathsf {E}}\) that is a relation on terms closed under substitutions of terms for variables and closed under one-to-one renaming. Given two terms u and v, we write \(u =_{\mathsf {E}}v\) when u and v are equal modulo the equational theory.
In the original syntax of the applied pi calculus, there is no distinction between an output (resp. input) from a protocol participant and from the environment, also called the attacker. In this paper however, we will make this distinction in order to concisely present our new variants of the semantics. Therefore, we consider two process tags \({{\mathsf {h}}}{{\mathsf {o}}}\) and \({{\mathsf {a}}}{{\mathsf {t}}}\) that respectively represent honest and attacker actions. The syntax of plain processes and extended processes is given in Fig. 1.
The process \({\mathsf {out}}^{\theta }(c,u)\) represents the output by \(\theta \) of the message u on the channel c. The process \({{\mathsf {i}}}{{\mathsf {n}}}^{\theta }(c,x)\) represents an input by \(\theta \) on the channel c. The input message will instantiate the variable x. The process \({\mathsf {eav}}(c,x)\) models the capability of the attacker to eavesdrop a communication on channel c. The process !P represents the replication of the process P, i.e. unbounded number of copies of P. The process \(P \mid Q\) represents the parallel composition of P and Q. The process \(\nu n. P\) (resp. \(\nu x. A\)) is the restriction of the name n in P (resp. variable x in A). The process \({{\mathsf {i}}}{{\mathsf {f}}}\ u = v \ {\mathsf {then}}\ P \ {\mathsf {else}}\ Q\) is the conditional branching under the equality test \(u = v\). The process \(\omega c\) records that a private channel c has been opened, i.e., it has been sent on a public or previously opened channel. Finally, the substitution \(\{ ^u/_x\}\) is an active substitution that replaces the variable x with the term u of base type.
We say that a process P (resp. extended process A) is an honest process (resp. honest extended process) when all inputs and outputs in P (resp. A) are tagged with \({{\mathsf {h}}}{{\mathsf {o}}}\) and when P (resp. A) does not contain eavesdropping processes and \(\omega c\). We say that a process P (resp. extended process A) is an attacker process (resp. attacker extended process) when all inputs and outputs in P (resp. A) are tagged with \({{\mathsf {a}}}{{\mathsf {t}}}\).
As usual, names and variables have scopes which are delimited by restrictions, inputs and eavesdrops. We denote \(fv(A), bv(A), fn(A), bn(A)\) the sets of free variables, bound variables, free names and bound names respectively in A. Moreover, we denote by \(oc(A)\) the sets of terms c of channel type opened in A, i.e. that occurs in a process \(\omega c\). We say that an extended process A is closed when all variables in A are either bound or defined by an active substitution in A. We define an evaluation context \(C[\_]\) as an extended process with a hole instead of an extended process. As for processes, we define an attacker evaluation context as an evaluation context where all outputs and inputs in the context are tagged with \({{\mathsf {a}}}{{\mathsf {t}}}\).
Note that our syntax without the eavesdropping process, opened channels and tags correspond exactly to the syntax of the original applied pi calculus.
Lastly, we consider the notion of frame that are extended processes built from 0, parallel composition, name and variable restrictions and active substitution. Given a frame \(\varphi \), we consider the domain of \(\varphi \), denoted \(dom(\varphi )\), as the set of free variables in \(\varphi \) that are defined by an active substitution in \(\varphi \). Given an extended process A, we define the frame of A, denoted \(\phi (A)\), as the process A where we replace all plain processes by 0. Finally, we write \(dom(A)\) as syntactic sugar for \(dom(\phi (A))\).
2.2 Operational Semantics
In this section, we define the three semantics that we study in this paper, namely:
-
the classical semantics from the applied pi calculus, where internal communication can occur on both public and private channels;
-
the private semantics where internal communication can only occur on private channels; and
-
the eavesdropping semantics where the attacker is able to eavesdrop on a public channel.
We first define the structural equivalence between extended processes, denoted \(\equiv \), as the smallest equivalence relation on extended processes that is closed under renaming of names and variables, closed by application of evaluation contexts, that is associative and commutative w.r.t. \(\mid \), and such that:

The three operational semantics of extended processes are defined by the structural equivalence and by three respective internal reductions, denoted \(\rightarrow _{\mathsf {c}}\), \(\rightarrow _{\mathsf {p}}\) and \(\rightarrow _{\mathsf {e}}\). These three reductions are the smallest relations on extended processes that are closed under application of evaluation context, structural equivalence and such that:


We emphasise that the application of the rule is closed under application of arbitrary evaluation contexts. In particular the context may restrict channels, e.g. the rule C-Open may be used under the context \(\nu c.\_\) resulting in a private channel c, but with the attacker input/output being in the scope of this restriction. It follows from the definition of evaluation contexts that the resulting processes are always well defined. We denote by \(\Rightarrow _s\) the reflexive, transitive closure of  for \(s \in \{ {\mathsf {c}},{\mathsf {p}},{\mathsf {e}}\}\). We note that the classical semantics
for \(s \in \{ {\mathsf {c}},{\mathsf {p}},{\mathsf {e}}\}\). We note that the classical semantics  is independent of the tags \(\theta , \theta '\), the eavesdrop actions and the \(\omega c\) processes.
is independent of the tags \(\theta , \theta '\), the eavesdrop actions and the \(\omega c\) processes.
Example 1
Consider the process
where d is a channel name and t a term of base type. Suppose \(\theta = \theta ' ={{\mathsf {h}}}{{\mathsf {o}}}\) then we have that communication is only possible in the classical semantics (using twice the Comm rule):

while no transitions are available in the two other semantics. To enable communication in the eavesdropping semantics we need to explicitly add eavesdrop actions. Applying the rules C-OEav and C-Eav we have that

We note that the first transition adds the information \(\omega d\) to indicate that d is now available to the environment.
Finally, if we consider that \({{\mathsf {a}}}{{\mathsf {t}}}\in \theta ,\theta '\) then internal communication on a public channel is possible and, using rules C-Open and C-Env we obtain for \(s\in \{ {\mathsf {p}}, {\mathsf {e}}\}\) that

2.3 Reachability and Behavioural Equivalences
We are going to compare the relation between the three semantics for the two general kind of security properties, namely reachability properties encoding security properties such as secrecy, authentication, and equivalence properties encoding anonymity, unlinkability, strong secrecy, receipt freeness, .... Intuitively, reachability properties encode that a process cannot reach some bad state. Equivalences define the fact that no attacker can distinguish two processes. This was originally defined by the (may)-testing equivalence [3] in the spi-calculus. An alternate equivalence, which was considered in the applied pi calculus [1], is observational equivalence.
Reachability properties can simply be encoded by verifying the capability of a process to perform an output on a given cannel. We define \(A \Downarrow ^{s,\theta }_c\) to hold when \(A \Rightarrow {\ }_s C[{\mathsf {out}}^{\theta }(c,t).P]\) for some evaluation context C that does not bind c, some term t and some plain process P, and \(A \Downarrow ^s_c\) to hold when \(A \Downarrow ^{s,\theta }_c\) for some \(\theta \in \{ {{\mathsf {a}}}{{\mathsf {t}}},{{\mathsf {h}}}{{\mathsf {o}}}\}\). For example the secrecy of s in the process \(\nu s. A\) can be encoded by checking whether for all attacker plain process I, we have that
where \(\mathsf {bad} \not \in fn(A)\).
Authentication properties are generally expressed as correspondence properties between events annotating processes, see e.g. [8]. A correspondence property between two events \(\mathsf {begin}\) and \(\mathsf {end}\), denoted \(\mathsf {begin} \Leftarrow \mathsf {end}\), requires that the event \(\mathsf {end}\) is preceded by the event \(\mathsf {begin}\) on every trace. A possible encoding of this correspondence property consists in first replacing all instances of the events in A by outputs \({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(ev,\mathsf {begin})\) and \({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(ev,\mathsf {end})\) where \(ev \not \in fn(A) \cup bn(A)\). This new process \(A'\) can then be put in parallel with a cell Cell that reads on the channel ev and stores any new value unless the value is \(\mathsf {end}\) and the current stored value in the cell is not \(\mathsf {begin}\). In such a case, the cell will output on the channel \(\mathsf {bad}\). The correspondence property can therefore be encoded by checking whether for all attacker plain process I, we have that \(I \mid \nu ev. (A' \mid Cell) \not \Downarrow _{\mathsf {bad}}^{s,{{\mathsf {h}}}{{\mathsf {o}}}}\).
We say that an attacker evaluation context \(C[\_]\) is \({\mathsf {c}}\)-closing for an extended process A if \(fv(C[A]) = \emptyset \). For \(s \in \{{\mathsf {p}},{\mathsf {e}}\}\), we say that \(C[\_]\) is s-closing for A if it is \({\mathsf {c}}\)-closing for A, variables and names are bound only once in \(C[\_]\) and for all channels \(c \in bn(C[\_]) \cap fn(A)\), if the scope of c includes \(\_\) then the scope of c also includes \(\omega c\).
We next introduce the two main notions of behavioural equivalences: may testing and observational equivalence.
Definition 1
((May-)Testing equivalences \(\approx _{m}^{{\mathsf {c}}}\) , \(\approx _{m}^{{\mathsf {p}}}\) , \(\approx _{m}^{{\mathsf {e}}}\) ). Let \(s \in \{ {\mathsf {c}}, {\mathsf {p}}, {\mathsf {e}}\}\). Let A and B two closed honest extended processes such that \(dom(A) = dom(B)\). We say that \(A \approx _{m}^{s} B\) if for all attacker evaluation contexts \(C[\_]\) s-closing for A and B, for all channels c, we have that \(C[A] \Downarrow ^s_c\) if and only if \(C[B] \Downarrow ^s_c\).
Definition 2
(Observational equivalences \(\approx _o^{{\mathsf {c}}}\) , \(\approx _o^{{\mathsf {p}}}\) , \(\approx _o^{{\mathsf {e}}}\) ). Let \(s \in \{ {\mathsf {c}}, {\mathsf {p}}, {\mathsf {e}}\}\). Let A and B two closed extended processes such that \(dom(A) = dom(B)\). We say that \(A \approx _{m}^{s} B\) if \(\approx _{m}^{s}\) is the largest equivalence relation such that:
-
\(A \Downarrow ^s_c\) implies \(B \Downarrow ^s_c\);
-
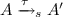 implies \(B \Rightarrow {\epsilon }_s B'\) and \(A' \approx _{m}^{s} B'\) for some \(B'\);
implies \(B \Rightarrow {\epsilon }_s B'\) and \(A' \approx _{m}^{s} B'\) for some \(B'\); -
\(C[A] \approx _{m}^{s} C[B]\) for all attacker evaluation contexts \(C[\_]\) s-closing for A and B.
For each of the semantics we have the usual relation between these two notions: observational equivalence implies testing equivalence.
Proposition 1
\({\approx _o^{s}} \subsetneq {\approx _{m}^{s}}\) for \(s \in \{ {\mathsf {c}}, {\mathsf {e}}, {\mathsf {p}}\}\).
Example 2
Consider processes A and B of Fig. 2. Process A computes a value \(h^n(a)\) to be output on channel c, where \(h^n(a)\) denotes n applications of h and \(h^0(a) = a\). The value is initially a and A may choose to either output the current value, or update the current value by applying the free symbol h. B may choose non-deterministically to either behave as A or output the fresh name s. (The non-deterministic choice is encoded by a communication on the private channel e which may be received by either the process behaving as A or the process outputting s.)
We have that \(A \not \approx _o^{s} B\). The two processes can indeed be distinguished by the context

Intuitively, when B outputs s the attacker context \(C[\_]\) can iterate the application of h the same number of times as would have done process A. Comparing the value computed by the adversary (\(h^n(a)\)) and the honestly computed value (either \(h^n(a)\) or s) the adversary distinguishes the two processes by outputting on the test channel \(c_t\).
However, we have that \(A \approx _{m}^{s} B\). Indeed, for any s-closing context \(D[\_]\) and all public channel ch we have that \(D[A] \Downarrow ^s_{ch}\) if and only if \(D[B] \Downarrow ^s_{ch}\). In particular for context \(C[\_]\) defined above we have that both \(C[A] \Downarrow ^s_{ch}\) and \(C[B] \Downarrow ^s_{ch}\) for \(ch \in \{ c_a, c_t, c \}\). Unlike observational equivalence, may testing does not require to “mimick” the other process stepwise and we cannot force a process into a particular branch.
2.4 Labelled Semantics
The internal reduction semantics introduced in the previous section requires to reason about arbitrary contexts. Similar to the original applied pi calculus, we extend the three operational semantics by a labeled operational semantics which allows processes to directly interact with the (adversarial) environment: we define the relation  ,
,  and
and  where \(\ell \) is part of the alphabet \({\mathcal {A}}= \{ \tau , out(c,d), eav(c,d), in(c,w),\nu k. out(c,k), \nu k. eav(c,k) \mid c,d \in {\mathcal {C}}h, k \in {\mathcal {X}}\cup {\mathcal {C}}h\text { and } w \text { is a term of any sort}\}\). The labeled rules are given in Fig. 3.
where \(\ell \) is part of the alphabet \({\mathcal {A}}= \{ \tau , out(c,d), eav(c,d), in(c,w),\nu k. out(c,k), \nu k. eav(c,k) \mid c,d \in {\mathcal {C}}h, k \in {\mathcal {X}}\cup {\mathcal {C}}h\text { and } w \text { is a term of any sort}\}\). The labeled rules are given in Fig. 3.
Consider our alphabet of actions \({\mathcal {A}}\) defined above. Given \(w \in {\mathcal {A}}^*\), \(s \in \{{\mathsf {c}}, {\mathsf {p}}, {\mathsf {e}}\}\) and an extended process A, we say that  when
when  for some extended processes \(A_1,\ldots , A_n\) and \(w = \ell _1 \cdot \ldots \cdot \ell _n\). By convention, we say that
for some extended processes \(A_1,\ldots , A_n\) and \(w = \ell _1 \cdot \ldots \cdot \ell _n\). By convention, we say that  where \(\epsilon \) is the empty word. Given \({{\mathsf {t}}}{{\mathsf {r}}}\in ({\mathcal {A}}\setminus \{\tau \})^*\), we say that
where \(\epsilon \) is the empty word. Given \({{\mathsf {t}}}{{\mathsf {r}}}\in ({\mathcal {A}}\setminus \{\tau \})^*\), we say that  when there exists \(w \in {\mathcal {A}}^*\) such that \({{\mathsf {t}}}{{\mathsf {r}}}\) is the word w where we remove all \(\tau \) actions and
when there exists \(w \in {\mathcal {A}}^*\) such that \({{\mathsf {t}}}{{\mathsf {r}}}\) is the word w where we remove all \(\tau \) actions and  .
.
Example 3
Coming back to Example 1, we saw that  and no \(\tau \)-actions in the other two semantics were available. Instead of explicitly adding eavesdrop actions, we can apply the rules Eav-OCh and Eav-T and obtain that
and no \(\tau \)-actions in the other two semantics were available. Instead of explicitly adding eavesdrop actions, we can apply the rules Eav-OCh and Eav-T and obtain that

We can now define both reachability and different equivalence properties in terms of these labelled semantics and relate them to the internal reduction. To define reachability properties in the labelled semantics, we define \(A \downdownarrows ^s_c\) to hold when  , \({{\mathsf {t}}}{{\mathsf {r}}}= {{\mathsf {t}}}{{\mathsf {r}}}_1 out(c,t) {{\mathsf {t}}}{{\mathsf {r}}}_2\) and \({{\mathsf {t}}}{{\mathsf {r}}}_1\) does not bind c for some \({{\mathsf {t}}}{{\mathsf {r}}},{{\mathsf {t}}}{{\mathsf {r}}}_1,{{\mathsf {t}}}{{\mathsf {r}}}_2 \in ({\mathcal {A}}\setminus \{\tau \})^*\), term t and extended process \(A'\).
, \({{\mathsf {t}}}{{\mathsf {r}}}= {{\mathsf {t}}}{{\mathsf {r}}}_1 out(c,t) {{\mathsf {t}}}{{\mathsf {r}}}_2\) and \({{\mathsf {t}}}{{\mathsf {r}}}_1\) does not bind c for some \({{\mathsf {t}}}{{\mathsf {r}}},{{\mathsf {t}}}{{\mathsf {r}}}_1,{{\mathsf {t}}}{{\mathsf {r}}}_2 \in ({\mathcal {A}}\setminus \{\tau \})^*\), term t and extended process \(A'\).
The following proposition states that any reachability property modelled in terms of \(A \Downarrow ^{s,\theta }_c\) and universal quantification over processes, can also be expressed using \(A \downdownarrows ^s_c\) without the need to quantify over processes.
Proposition 2
For all closed honest plain processes A, for all \(s \in \{ {\mathsf {c}}, {\mathsf {e}}, {\mathsf {p}}\}\), \(A \downdownarrows ^s_c\) iff there exists an attacker plain process \(I^s\) such that \(I^s \mid A \Downarrow ^{s,{{\mathsf {h}}}{{\mathsf {o}}}}_c\).
Next, we define equivalence relations using our labelled semantics that may serve as proof techniques for the may testing relation. First we need to define an indistinguishability relation on frames, called static equivalence.
Definition 3
(Static equivalence \(\sim \) ). Two terms u and v are equal in the frame \(\phi \), written \((u =_{\mathsf {E}}v)\phi \), if there exists \({\tilde{n}}\) and a substitution \(\sigma \) such that \({\phi \equiv \nu {\tilde{n}}.\sigma }\), \({\tilde{n}} \cap (fn(u) \cup fn(v)) = \emptyset \), and \(u\sigma =_{\mathsf {E}}v\sigma \).
Two closed frames \(\phi _1\) and \(\phi _2\) are statically equivalent, written \(\phi _1 \sim \phi _2\), when:
-
\(dom(\phi _1) = dom(\phi _2)\), and
-
for all terms u, v we have that: \((u =_{\mathsf {E}}v)\phi _1\) if and only if \((u =_{\mathsf {E}}v)\phi _2\).
Example 4
Consider the equational theory generated by the equation \({\mathsf{dec}}({\mathsf{enc}}(x,y) ,y) = x\). Then we have that
Intutively, the first equivalence confirms that encryption hides the plaintext when the decryption key is unknown. The second equivalence does not hold as the test \(({\mathsf{dec}}(x_1,x_2) =_{\mathsf {E}}a)\) holds on the left hand side, but not on the right hand side. Finally, the third equivalence again holds as two restricted names are indistinguishable.
Now we are ready to define two classical equivalences on processes, based on the labelled semantics: trace equivalence and labelled bisimulation.
Definition 4
(Trace equivalences \(\approx _t^{{\mathsf {c}}}\) , \(\approx _t^{{\mathsf {p}}}\) , \(\approx _t^{{\mathsf {e}}}\) ). Let \(s \in \{ {\mathsf {c}},{\mathsf {p}},{\mathsf {e}}\}\). Let A and B be two closed honest extended processes. We say that \(A \sqsubseteq _t^{s} B\) if for all \(A {\mathop \Rightarrow \limits ^{{{\mathsf {t}}}{{\mathsf {r}}}}}_s A'\) such that \(bn({{\mathsf {t}}}{{\mathsf {r}}}) \cap fn(B) = \emptyset \), there exists \(B'\) such that \(B {\mathop \Rightarrow \limits ^{{{\mathsf {t}}}{{\mathsf {r}}}}}_s B'\) and \(\phi (A') \sim \phi (B')\). We say that \(A \approx _t^{s} B\) when \(A \sqsubseteq _t^{s} B\) and \(B \sqsubseteq _t^{s} A\).
Definition 5
(Labeled bisimulations \(\approx _\ell ^{{\mathsf {c}}}\) , \(\approx _\ell ^{{\mathsf {p}}}\) , \(\approx _\ell ^{{\mathsf {e}}}\) ). Let \(s \in \{ {\mathsf {c}}, {\mathsf {p}}, {\mathsf {e}}\}\). Let A and B two closed honest extended processes such that \(dom(A) = dom(B)\). We say that \(A \approx _\ell ^{s} B\) if \(\approx _\ell ^{s}\) is the largest equivalence relation such that:
-
\(\phi (A) \sim \phi (B)\)
-
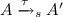 implies \(B {\mathop \Rightarrow \limits ^{\epsilon }}_s B'\) and \(A' \approx _\ell ^{s} B'\) for some \(B'\),
implies \(B {\mathop \Rightarrow \limits ^{\epsilon }}_s B'\) and \(A' \approx _\ell ^{s} B'\) for some \(B'\), -
 and \(bn(\ell ) \cap fn(B) = \emptyset \) implies \(B {\mathop \Rightarrow \limits ^{l}}_{s} B'\) and \(A' \approx _\ell ^{s} B'\) for some \(B'\).
and \(bn(\ell ) \cap fn(B) = \emptyset \) implies \(B {\mathop \Rightarrow \limits ^{l}}_{s} B'\) and \(A' \approx _\ell ^{s} B'\) for some \(B'\).
We again have, as usual that labelled bisimulation implies trace equivalence.
Proposition 3
\({\approx _\ell ^{s}} \subsetneq {\approx _t^{s}}\) for \(s \in \{ {\mathsf {c}}, {\mathsf {e}}, {\mathsf {p}}\}\).
In [1] it is shown that \({\approx _o^{{\mathsf {c}}}} = {\approx _\ell ^{{\mathsf {c}}}}\). We conjecture that for the new semantics \({\mathsf {p}}\) and \({\mathsf {e}}\) this same equivalence holds as well. Re-showing these results is beyond the scope of this paper, and we will mainly focus on testing/trace equivalence. As shown in [12], for the classical semantics trace equivalence implies may testing, while the converse does not hold in general. The two relations do however coincide on image-finite processes.
Definition 6
Let A be a closed extended process. A is image-finite for the semantics \(s\in \{ {\mathsf {c}}, {\mathsf {e}}, {\mathsf {p}}\}\) if for each trace \({{\mathsf {t}}}{{\mathsf {r}}}\) the set of equivalence classes  is finite.
is finite.
Note that any replication-free process is necessarily image-finite as there are only a finite number of possible traces for any given sequence of labels \({{\mathsf {t}}}{{\mathsf {r}}}\). The same relations among trace equivalence and may testing shown for the classical semantics hold also for the other semantics.
Theorem 1
\({\approx _t^{s}} \subsetneq {\approx _{m}^{s}}\) and \({\approx _t^{s}} = {\approx _{m}^{s}}\) on image-finite processes for \(s \in \{ {\mathsf {c}}, {\mathsf {e}}, {\mathsf {p}}\}\).
The proof of this result (for the classical semantics) is given in [12] and is easily adapted to the other semantics. To see that the implication is strict, we continue Example 2 on processes A and B defined in Fig. 2. We already noted that \(A \approx _{m}^{s} B\), but will now show that \(A \not \approx _t^{s} B\) (for \(s \in \{ {\mathsf {c}}, {\mathsf {e}}, {\mathsf {p}}\}\)). All possible traces of A are of the form  where \(\phi (A') = \{ ^{h^n(a)}/ x \}\) for \(n\in {\mathbb {N}}\). We easily see that \({A} {\not \approx _t^{s}} {B}\) as for any n we have that \(\{ ^{h^n(a)}/ _x \} \not \sim \{ ^s/ _x \}\), by testing \(x ={h^n(a)}\). On the other hand, given an image-finite process, we can only have a finite number of different frames for a given trace, and therefore we can bound the context size that is necessary for distinguishing the processes.
where \(\phi (A') = \{ ^{h^n(a)}/ x \}\) for \(n\in {\mathbb {N}}\). We easily see that \({A} {\not \approx _t^{s}} {B}\) as for any n we have that \(\{ ^{h^n(a)}/ _x \} \not \sim \{ ^s/ _x \}\), by testing \(x ={h^n(a)}\). On the other hand, given an image-finite process, we can only have a finite number of different frames for a given trace, and therefore we can bound the context size that is necessary for distinguishing the processes.
3 Comparing the Different Semantics
In this section we state our results on comparing these semantics. We first show that, as expected, all the semantics coincide for reachability properties.
Theorem 2
For all ground, closed honest extended processes A, for all channels d, we have that \(A \downdownarrows ^{\mathsf {p}}_d\) iff \(A \downdownarrows ^{\mathsf {c}}_d\) iff \(A \downdownarrows ^{\mathsf {e}}_d\).
The next result is, in our opinion, more surprising. As the private semantics force the adversary to observe all information, one might expect that his distinguishing power increases over the classical one. This intuition is however wrong: the classical and private trace equivalences, testing equivalence and labelled bisimulations appear to be incomparable.
Theorem 3
\( {{\approx _{r}^{{\mathsf {p}}}}} \not \subseteq {{\approx _{r}^{{\mathsf {c}}}}}\) and \({{\approx _{r}^{{\mathsf {c}}}}} \not \subseteq {{\approx _{r}^{{\mathsf {p}}}}}\) for \(r \in \{ \ell , t, m\}\).
Proof
We first show that there exist A and B such that \(A \approx _\ell ^{{\mathsf {p}}} B\), but \(A \not \approx _{m}^{{\mathsf {c}}} B\). Note that, as \({\approx _\ell ^{s}} \subset {\approx _t^{s}} \subseteq {\approx _{m}^{s}} \) for \(s \in \{{\mathsf {c}}, {\mathsf {p}}\}\) these processes demonstrate both that \({\approx _\ell ^{{\mathsf {p}}}} \not \subseteq {\approx _\ell ^{{\mathsf {c}}}}\), \({\approx _t^{{\mathsf {p}}}} \not \subseteq {\approx _t^{{\mathsf {c}}}}\) and \({\approx _{m}^{{\mathsf {p}}}} \not \subseteq {\approx _{m}^{{\mathsf {c}}}}\).
Consider processes A and B defined in Fig. 4. In short, the result follows from the fact that if A performs an internal communication on channel c followed by an output on d (from \(P_1\)), B has no choice other then performing the output on d in \(P_2\). In the private semantics, however, the internal communication will be split in an output followed by an input: after the output on c, the input \({{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,x).P_2(x)\) following the output becomes available. More precisely, to see that \(A \approx _\ell ^{{\mathsf {p}}} B\) we first observe that if  then \(B \xrightarrow {\nu z.out(c,z)}_{\mathsf {p}}B'\) and \(A' \equiv B'\), and vice-versa. If
then \(B \xrightarrow {\nu z.out(c,z)}_{\mathsf {p}}B'\) and \(A' \equiv B'\), and vice-versa. If  then \(B \xrightarrow {in(c,t)}_{\mathsf {p}}B'\). As \(t \not \in \{s_1, s_2 \}\) we have that \(P_1 (t) \approx _\ell ^{{\mathsf {p}}} 0 \approx _\ell ^{{\mathsf {p}}} P_2(t)\). Finally, if \(t \ne s_2\) we also have that \(P_1 (t) \approx _\ell ^{{\mathsf {p}}} P_2(t)\) as in particular \(P_1(s_1)\approx _\ell ^{{\mathsf {p}}} P_2(s_1)\). Therefore,
then \(B \xrightarrow {in(c,t)}_{\mathsf {p}}B'\). As \(t \not \in \{s_1, s_2 \}\) we have that \(P_1 (t) \approx _\ell ^{{\mathsf {p}}} 0 \approx _\ell ^{{\mathsf {p}}} P_2(t)\). Finally, if \(t \ne s_2\) we also have that \(P_1 (t) \approx _\ell ^{{\mathsf {p}}} P_2(t)\) as in particular \(P_1(s_1)\approx _\ell ^{{\mathsf {p}}} P_2(s_1)\). Therefore,
which allows us to conclude.
As A and B are image-finite, we have that \(A \approx _{m}^{{\mathsf {c}}} B\) if and only if \(A \approx _t^{{\mathsf {c}}} B\). To see that \(A \not \approx _t^{{\mathsf {c}}} B\) we observe that A may perform the following transition sequence, starting with an internal communication on a public channel:

In order to mimic the behaviour of A, B must perform the same sequence of observable transitions:

We conclude as  , but
, but  . This trace inequivalence has also been shown using APTE.
. This trace inequivalence has also been shown using APTE.
To show that \({{\approx _{r}^{{\mathsf {c}}}}} \not \subseteq {{\approx _{r}^{{\mathsf {p}}}}}\) for \(r \in \{ \ell , t, m\}\) we show that there exist processes A and B such that \(A \approx _\ell ^{{\mathsf {c}}} B\) and \(A \not \approx _{m}^{{\mathsf {p}}} B\). As in the first part of the proof, note that, as \({\approx _\ell ^{s}} \subset {\approx _t^{s}} \subseteq {\approx _{m}^{s}}\) for \(s \in \{{\mathsf {c}}, {\mathsf {p}}\}\) these processes demonstrate that \({\approx _\ell ^{{\mathsf {c}}}} \not \subseteq {\approx _\ell ^{{\mathsf {p}}}}\), \({\approx _t^{{\mathsf {c}}}} \not \subseteq {\approx _t^{{\mathsf {p}}}}\) and \({\approx _{m}^{{\mathsf {c}}}} \not \subseteq {\approx _{m}^{{\mathsf {p}}}}\).
Consider the processes A and B defined in Fig. 5. The proof crucially relies on the fact that B may perform an internal communication in the classical semantics to mimic A, which becomes visible in the attacker in the private semantics. To see that \(A \approx _\ell ^{{\mathsf {c}}} B\) we first observe that the only first possible action from A or B is an input. In particular, given a term t, there is a unique \(B'\) such that  where \(B' = \nu s. ({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,s). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a) \mid {{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,y). P(y))\). However, if
where \(B' = \nu s. ({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,s). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a) \mid {{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,y). P(y))\). However, if  then either \(A' = B'\) or \(A' = A''\) with \(A''\ \hat{=} \ \nu s. ({{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,x). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,s). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a) \mid P(t))\). Therefore, to complete the proof, we only need to find \(B''\) such that
then either \(A' = B'\) or \(A' = A''\) with \(A''\ \hat{=} \ \nu s. ({{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,x). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,s). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a) \mid P(t))\). Therefore, to complete the proof, we only need to find \(B''\) such that  and \(A'' \approx _\ell ^{{\mathsf {c}}} B''\). Such process can be obtain by applying an internal communication on \(B'\), i.e.
and \(A'' \approx _\ell ^{{\mathsf {c}}} B''\). Such process can be obtain by applying an internal communication on \(B'\), i.e.  . Note that \(t \ne s\) since s is bound, meaning that \(P(t) \approx _\ell ^{{\mathsf {c}}} {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a)\). Moreover, \(P(s) \approx _\ell ^{{\mathsf {c}}} {{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,x). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,s). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a)\). This allows us to conlude that \(\nu s. ({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a) \mid P(s)) \approx _\ell ^{{\mathsf {c}}} A''\).
. Note that \(t \ne s\) since s is bound, meaning that \(P(t) \approx _\ell ^{{\mathsf {c}}} {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a)\). Moreover, \(P(s) \approx _\ell ^{{\mathsf {c}}} {{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,x). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,s). {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a)\). This allows us to conlude that \(\nu s. ({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a) \mid P(s)) \approx _\ell ^{{\mathsf {c}}} A''\).
Again, as A and B are image-finite may and trace equivalence coincide. To see that \(A \not \approx _t^{{\mathsf {p}}} B\) we first observe that A may perform the following transition sequence:

We conclude as  but
but  . This trace disequivalence has also been shown using APTE. \(\square \)
. This trace disequivalence has also been shown using APTE. \(\square \)
One may also note that the counter-example witnessing that equivalences in the private semantics do not imply equivalences in the classical semantics is minimal: it does not use function symbols, equational reasoning, private channels, replication nor else branches. The second part of the proof relies on the use of else branches. We can however refine this result in the case of labeled bisimulation to processes without else branches, the counter-example being the same processes A and B described in the proof but where we replace each \({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,a)\) by 0. In the case of trace equivalence, we can also produce a counter-example without else branches witnessing that trace equivalences in the classical semantics do no imply trace equivalences in the private semantics but provided that we rely on a function symbol h. In the appendix of the technical report [7], we describe in more details these processes and give the proofs of them being counter-examples.
Next, we show that the eavesdropping semantics yields strictly stronger bisimulations and trace equivalences: the eavesdropping semantics is actually strictly included in the intersection of the classic and private semantics.
Theorem 4
\({\approx _\ell ^{{\mathsf {e}}}} \subsetneq {\approx _\ell ^{{\mathsf {p}}}} \cap {\approx _\ell ^{{\mathsf {c}}}}\).
Proof
(Sketch)
-
1.
We first show that \({\approx _\ell ^{{\mathsf {e}}}} \subseteq {\approx _\ell ^{{\mathsf {p}}}}\). Suppose \({A} {\approx _\ell ^{{\mathsf {e}}}} {B}\) and let \({{\mathcal {R}}}\) be the relation witnessing this equivalence. We will show that \({{\mathcal {R}}}\) is also a labelled bisimulation in the private semantics. Suppose \(A {{{\mathcal {R}}}} B\).
-
as \(A {\approx _\ell ^{{\mathsf {e}}}} B\), we have that \(\phi (A) \sim \phi (B)\).
-
if
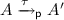 then, as
then, as  ,
,  . As \(A {\approx _\ell ^{{\mathsf {e}}}} B\) there exists \(B'\) such that
. As \(A {\approx _\ell ^{{\mathsf {e}}}} B\) there exists \(B'\) such that  and \(A' {{{\mathcal {R}}}} B'\). As B is a honest process no \(\textsc {Comm-Eav}\) transition is possible, and hence
and \(A' {{{\mathcal {R}}}} B'\). As B is a honest process no \(\textsc {Comm-Eav}\) transition is possible, and hence  .
. -
if
 and \(bn(\ell ) \cap fn(B) = \emptyset \) then we also have that
and \(bn(\ell ) \cap fn(B) = \emptyset \) then we also have that  (as
(as  and there exists \(B'\) such that
and there exists \(B'\) such that  and \(A' {{{\mathcal {R}}}} B'\). As no \(\textsc {Comm-Eav}\) are possible and \(\ell \) is not of the form eav(c, d) nor \(\nu y.eav(c,y)\) we have that
and \(A' {{{\mathcal {R}}}} B'\). As no \(\textsc {Comm-Eav}\) are possible and \(\ell \) is not of the form eav(c, d) nor \(\nu y.eav(c,y)\) we have that 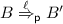 .
.
-
-
2.
We next show that \(A \approx _\ell ^{{\mathsf {e}}} B\) implies \(A \approx _\ell ^{{\mathsf {c}}} B\) for any A, B. We will show that \( \approx _\ell ^{{\mathsf {e}}}\) is also a labelled bisimulation in the classical semantics. The proof relies on similar arguments as in Item 2 of the proof of Theorem 5 and the facts that
-
\(\nu {\tilde{n}}. (A' \mid \{ ^{t}/_{x} \}) \approx _\ell ^{{\mathsf {e}}} \nu {\tilde{n}}. (B' \mid \{ ^{u}/_{x} \})\) implies \(\nu {\tilde{n}}. A' \approx _\ell ^{{\mathsf {e}}} \nu {\tilde{n}}. B'\),
-
\(A' \approx _\ell ^{{\mathsf {e}}} B'\) implies \(\nu c. A' \approx _\ell ^{{\mathsf {e}}} \nu c. B'\)
The first property is needed when an internal communication of a term or public channel is replaced by an eavesdrop action and an input. The second property handles the case when we replace the internal communication of a private channel by an application of the Eav-OCh rule and an input.
-
-
3.
We now show that the implication \({\approx _\ell ^{{\mathsf {e}}}} \subsetneq {\approx _\ell ^{{\mathsf {c}}}} \cap {\approx _t^{{\mathsf {c}}}} \) is strict, i.e., there exist A and B such that \(A \approx _\ell ^{{\mathsf {c}}} B\), \(A \approx _\ell ^{{\mathsf {p}}} B\) but \(A \not \approx _t^{{\mathsf {e}}} B\) (which implies \(A \not \approx _\ell ^{{\mathsf {e}}} B\)).
Consider the processes A and B defined in Fig. 6. This example is a variant of the one given in Fig. 4. The difference is the addition of “\( {{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,z). {{\mathsf {i}}}{{\mathsf {f}}}\ z = s_1 \ {\mathsf {then}}\ \)” in processes \(P_1(x)\) and \(P_2(x)\): this additional check is used to verify whether the adversary learned \(s_1\) or not. The proofs that \(A \approx _\ell ^{{\mathsf {c}}} B\) and \(A \approx _\ell ^{{\mathsf {p}}} B\) follow the same lines as in Theorem 3. We just additionally observe that \(\nu s_1. ({{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,z). {{\mathsf {i}}}{{\mathsf {f}}}\ z = s_1 \ {\mathsf {then}}\ {\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,s_2) ) \approx _\ell ^{s} \nu s_1.\ ({{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(d,z). 0)\) for \(s \in \{ {\mathsf {c}}, {\mathsf {p}}\}\).
The trace witnessing that \(A \not \approx _t^{{\mathsf {e}}} B\) (which implies \(A \not \approx _\ell ^{{\mathsf {e}}} B\)) is again similar to the one in Theorem 3, but starting with an eavesdrop transition which allows the attacker to learn \(s_1\), which in turn allows him to learn \(s_2\) and distinguish \(P_1(s_2)\) from \(P_2(s_2)\). We have verified \(A \not \approx _t^{{\mathsf {e}}} B\) using APTE which implies \(A \not \approx _\ell ^{{\mathsf {e}}} B\). \(\square \)
Again we note that the implications are strict, even for processes containing only public channels.
Theorem 5
\({\approx _t^{{\mathsf {e}}}} \subsetneq {\approx _t^{{\mathsf {p}}}} \cap {\approx _t^{{\mathsf {c}}}}\).
Proof
(Sketch)
-
1.
We first prove that \({\approx _t^{{\mathsf {e}}}} \subseteq {\approx _t^{{\mathsf {p}}}}\). Suppose that \(A \approx _t^{{\mathsf {e}}} B\). We need to show that for any \(A'\) such that
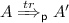 there exists \(B'\) such that
there exists \(B'\) such that  . It follows from the definition of the semantics that whenever
. It follows from the definition of the semantics that whenever  then we also have
then we also have  as
as 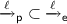 . As \(A \approx _t^{{\mathsf {e}}} B\), we have that there exists \(B'\), such that
. As \(A \approx _t^{{\mathsf {e}}} B\), we have that there exists \(B'\), such that  and \(\phi (A') \sim \phi (B')\). As \({{\mathsf {t}}}{{\mathsf {r}}}\) does not contain labels of the form eav(c, d) nor \(\nu y.eav(c,y)\) and as no \(\textsc {Comm-Eav}\) are possible (A and B are honest processes) we also have that
and \(\phi (A') \sim \phi (B')\). As \({{\mathsf {t}}}{{\mathsf {r}}}\) does not contain labels of the form eav(c, d) nor \(\nu y.eav(c,y)\) and as no \(\textsc {Comm-Eav}\) are possible (A and B are honest processes) we also have that 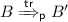 . Hence \(A\approx _t^{{\mathsf {p}}} B\).
. Hence \(A\approx _t^{{\mathsf {p}}} B\). -
2.
We next prove that \({\approx _t^{{\mathsf {e}}}} \subseteq {\approx _t^{{\mathsf {c}}}}\). Similar to Item 1 we suppose that \(A \approx _t^{{\mathsf {e}}} B\) and
 . From the semantics, we obtain that
. From the semantics, we obtain that  , where
, where-
\(\phi (A'_{\mathsf {c}}) \subseteq \phi (A'_{\mathsf {e}})\), i.e., \(dom(\phi (A'_{\mathsf {c}})) \subseteq dom(\phi (A'_{\mathsf {e}}))\) and the frames coincide on the common domain.
-
\(tr_{\mathsf {e}}\) is constructed from tr by replacing any \(\tau \) action resulting from the \(\textsc {Comm}\) rule by an application of an eavesdrop rule (\(\textsc {Eav-T}\), \(\textsc {Eav-Ch}\), or \(\textsc {Eav-OCh}\)).
The proof is done by induction on the length of tr and the proof tree of each transition. As \(A \approx _t^{{\mathsf {e}}} B\) we also have that
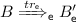 and \(A'_{\mathsf {e}}\sim B'_{\mathsf {e}}\). We show by the definition of the semantics that
and \(A'_{\mathsf {e}}\sim B'_{\mathsf {e}}\). We show by the definition of the semantics that  and \(\phi (B'_{\mathsf {c}}) \subseteq \phi (B'_{\mathsf {e}})\) (replacing each eavesdrop action by an internal communication). Due to the inclusions of the frames and \(A'_{\mathsf {e}}\sim B'_{\mathsf {e}}\) we also have that \(A'_{\mathsf {c}}\sim B'_{\mathsf {c}}\).
and \(\phi (B'_{\mathsf {c}}) \subseteq \phi (B'_{\mathsf {e}})\) (replacing each eavesdrop action by an internal communication). Due to the inclusions of the frames and \(A'_{\mathsf {e}}\sim B'_{\mathsf {e}}\) we also have that \(A'_{\mathsf {c}}\sim B'_{\mathsf {c}}\). -
-
3.
To show that the implication \({\approx _t^{{\mathsf {e}}}} \subsetneq {\approx _t^{{\mathsf {p}}}} \cap {\approx _t^{{\mathsf {c}}}}\) is strict, i.e., there exist processes A and B such that \(A \approx _t^{{\mathsf {c}}} B\), \(A \approx _t^{{\mathsf {p}}} B\) but \(A \not \approx _t^{{\mathsf {e}}} B\). The processes defined in Fig. 6 witness this fact (cf the discussion of these processes in the proof of Theorem 4). These trace (in)equivalences have also been verified using APTE.
We note from the processes defined in Fig. 6 that the implications are strict even for processes that do not communicate on private channels, do not use replication, nor else branches and terms are simply names (no function symbols nor equational theories).
Theorem 6
\({\approx _{m}^{{\mathsf {e}}}} \subsetneq {\approx _{m}^{{\mathsf {p}}}} \cap {\approx _{m}^{{\mathsf {c}}}}\).
Proof
(Sketch)
-
1.
We first prove that \({\approx _{m}^{{\mathsf {e}}}} \subseteq {\approx _{m}^{{\mathsf {p}}}}\). Suppose that \(A \approx _{m}^{{\mathsf {e}}} B\). Suppose that \(A \approx _{m}^{{\mathsf {e}}} B\). We need to show that for all channel c, for all \(C[\_]\) attacker evaluation contexts \({\mathsf {p}}\)-closing for A and B, \(C[A]\Downarrow ^{\mathsf {p}}_c\) is equivalent to \(C[B]\Downarrow ^{\mathsf {p}}_c\). It follows from the definition of the private semantics that any process \({\mathsf {eav}}(c,x).P\) in \(C[\_]\) has the same behaviour as the process 0. Hence, we generate a context \(C^1[\_]\) by replacing in \(C[\_]\) any instance of \({\mathsf {eav}}(c,x).P\) by 0, and thus obtaining \({C[A]\Downarrow ^{\mathsf {p}}_c} \Leftrightarrow {C'[A]\Downarrow ^{\mathsf {p}}_c}\) and \({C[B]\Downarrow ^{\mathsf {p}}_c} \Leftrightarrow {C'[B]\Downarrow ^{\mathsf {p}}_c}\). Notice that the definition of semantics gives us \({\rightarrow _{\mathsf {p}}} \subseteq {\rightarrow _{\mathsf {e}}}\). Hence, \(C'[A] \Downarrow ^{\mathsf {p}}_c\) implies \(C'[A] \Downarrow ^{\mathsf {e}}_c\) and \(C'[B] \Downarrow ^{\mathsf {p}}_c\) implies \(C'[B] \Downarrow ^{\mathsf {e}}_c\). Furthermore, since we built \(C'[\_]\) to not contain any process of the form \({\mathsf {eav}}(c,x).P\), we deduce that rules C-Eav and C-OEav can never be applied in a derivation of \(C'[A]\) or \(C'[B]\). It implies that \(C'[A] \Downarrow ^{\mathsf {p}}_c \Leftrightarrow C'[A] \Downarrow ^{\mathsf {e}}_c\) and \(C'[B] \Downarrow ^{\mathsf {p}}_c \Leftrightarrow C'[B] \Downarrow ^{\mathsf {e}}_c\). Thanks to \(A \approx _{m}^{{\mathsf {e}}} B\), we know that \({C'[A] \Downarrow ^{\mathsf {e}}_c} \Leftrightarrow {C'[B] \Downarrow ^{\mathsf {e}}_c}\) and so we conclude that \({C[A] \Downarrow ^{\mathsf {p}}_c} \Leftrightarrow {C[B] \Downarrow ^{\mathsf {p}}_c}\).
-
2.
We next prove that \({\approx _{m}^{{\mathsf {e}}}} \subseteq {\approx _{m}^{{\mathsf {c}}}}\). Similarly to Item 1, we consider a channel c and an attacker evaluation context \(C[\_]\) that is \({\mathsf {c}}\)-closing for A and B. The main difficulty of this proof is to match the application of the rule Comm in the classical semantics with the rules C-Eav and C-OEac. However, \(C[\_]\) does not necessarily contain eavesdrop process \({\mathsf {eav}}(d,x) \mid \omega c\). Moreover, as mentioned in Item 1, a process \({\mathsf {eav}}(d,x).P\) has the same behavior as 0 in the classical semantics but can have a completely different behaviour in the eavesdropping semantics if P is not 0. Thus, we remove from \(C[\_]\) the eavesdrop processes, obtaining \(C'[\_]\). Then, we define a new context \(C''[\_]\) based on \(C'[\_]\) where will add harmless eavesdrop process \({\mathsf {eav}}(d,y).0\). We first add in parallel the processes \(! {\mathsf {eav}}(a,y) \mid \omega a\) for all free channels a in \(C'[\_], A\) and B. Moreover, since private channels can be opened, we also replace any process \(\nu d. P\), \({{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {a}}}{{\mathsf {t}}}}(c,x).P\) where d, x are of channel type with \(\nu d. (P \mid ! {\mathsf {eav}}(d,y))\) and \({{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {a}}}{{\mathsf {t}}}}(c,x). (P \mid ! {\mathsf {eav}}(x,y))\). By induction of the derivations, we can show that \({C[A]\Downarrow ^{\mathsf {c}}_c} \Leftrightarrow {C''[A] \Downarrow ^{\mathsf {e}}_c}\) and \({C[B]\Downarrow ^{\mathsf {c}}_c} \Leftrightarrow {C''[B] \Downarrow ^{\mathsf {e}}_c}\). Since \(A \approx _{m}^{{\mathsf {e}}} B\), we deduce that \({C''[A] \Downarrow ^{\mathsf {e}}_c} \Leftrightarrow {C''[B]\Downarrow ^{\mathsf {e}}_c}\) and so \({C[A]\Downarrow ^{\mathsf {c}}_c} \Leftrightarrow {C[B]\Downarrow ^{\mathsf {c}}_c}\).
-
3.
To show that the implication \({\approx _{m}^{{\mathsf {e}}}} \subsetneq {\approx _{m}^{{\mathsf {p}}}} \cap {\approx _{m}^{{\mathsf {c}}}}\) is strict, i.e., there exist processes A and B such that \(A \approx _{m}^{{\mathsf {c}}} B\), \(A \approx _{m}^{{\mathsf {p}}} B\) but \(A \not \approx _{m}^{{\mathsf {e}}} B\). The processes defined in Fig. 6 witness this fact. They already were witness of the strict inclusion \({\approx _t^{{\mathsf {e}}}} \subsetneq {\approx _t^{{\mathsf {p}}}} \cap {\approx _t^{{\mathsf {c}}}}\) (see proof of Theorem 5) and since A and B are image finite, we know from Theorem 1 that may and trace equivalences between A and B coincide. \(\square \)
4 Subclasses of Processes for Which the Semantics Coincide
4.1 Simple Processes
The class of simple processes was defined in [12]. It was shown that for these processes observational and may testing equivalences coincide. Intuitively, these processes are composed of parallel basic processes. Each basic process is a sequence of input, test on the input and output actions. Moreover, importantly, each basic process has a distinct channel for communication.
Definition 7
(basic process). The set \({\mathcal {B}}(c,{\mathcal {V}})\) of basic processes built on \({c \in {\mathcal {C}}h}\) and \({\mathcal {V}} \subseteq {\mathcal {X}}\) (variables of base type) is the least set of processes that contains 0 and such that
-
if \(B_1,B_2\in {\mathcal {B}}(c,{\mathcal {V}})\), \(M,N\in {\mathcal {T}}({\mathcal {F}},{\mathcal {N}},{\mathcal {V}})\), then \({{\mathsf {i}}}{{\mathsf {f}}}\ M = N \ {\mathsf {then}}\ B_1 \ {\mathsf {else}}\ B_2 \;\in \; {\mathcal {B}}(c, {\mathcal {V}})\).
-
if \(B \in {\mathcal {B}}(c,{\mathcal {V}})\), \(u\in {\mathcal {T}}({\mathcal {F}},{\mathcal {N}},{\mathcal {V}})\), then \({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,u). B \;\in \; {\mathcal {B}}(c, {\mathcal {V}})\).
-
if \(B \in {\mathcal {B}}(c,{\mathcal {V}} \uplus \{x\})\), x of base type (\(x \notin {\mathcal {V}}\)), then \({{\mathsf {i}}}{{\mathsf {n}}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,x). B \,\in \, {\mathcal {B}}(c,{\mathcal {V}})\).
Definition 8
(simple process). A simple process is obtained by composing and replicating basic processes and frames, hiding some names:
where \(B_{j}\in {\mathcal {B}}(c_j,\emptyset )\), \(B_{j}'\in {\mathcal {B}}(c_j',\emptyset )\) and \(c_j\) are channel names that are pairwise distinct. The names \(p_1, \ldots , p_n\) are distinct channel names that do not appear elsewhere and \(\sigma _1, \ldots , \sigma _k\) are frames without restricted names (i.e. substitutions).
We have that for simple processes, all equivalences and semantics coincide.
Theorem 7
When restricted to simple processes, we have that \({\approx _{r_1}^{s_1}} = {\approx _{r_2}^{s_2}}\) for \(r_1,r_2 \in \{ \ell , o, m, t\}\) and \(s_1,s_2 \in \{ {\mathsf {c}}, {\mathsf {p}}, {\mathsf {e}}\}\).
Proof
The result when \(s_1 = s_2 = {\mathsf {c}}\) was shown in [12]. As for simple processes, all parallel processes have distinct channels, the internal communication rule may never be triggered, and therefore it is easy to show that the three semantics coincide.
4.2 I/O-Unambiguous Processes
Restricting processes to simple processes is often too restrictive. For instance, when verifying unlinkability and anonymity properties, two outputs by different parties should not be distinguishable due to the channel name. We therefore introduce another class of processes, that we call io-unambiguous for which we also show that the different semantics (although not the different equivalences) do coincide.
Intuitively, an io-unambiguous process forbids an output and input on the same public channel to follow each other directly (or possibly with only conditionals in between). For instance, we forbid processes of the form \({\mathsf {out}}^{\theta }(c,t). {{\mathsf {i}}}{{\mathsf {n}}}^{\theta }(c,x). P\), \({\mathsf {out}}^{\theta }(c,t).({{\mathsf {i}}}{{\mathsf {n}}}^{\theta }(c,x). P \mid Q)\) as well as \({\mathsf {out}}^{\theta }(c,t). {{\mathsf {i}}}{{\mathsf {f}}}\ \ t_1 = t_2\ \ {\mathsf {then}}\ P \ {\mathsf {else}}\ {{\mathsf {i}}}{{\mathsf {n}}}^{\theta }(c,x). Q\). We however allow inputs and outputs on the same channel in parallel.
Definition 9
We define an honest extended process A to be I/O-unambiguous when \({\mathsf{ioua}}(A, \_) = \top \) where

Note that an I/O-unambiguous process does not contain private channels and always input/output base-type terms. We also note that a simple way to enforce that processes are I/O-unambiguous is to use disjoint channel names for inputs and outputs (at least in the same parallel thread).
Theorem 8
When restricted to I/O-unambiguous processes, we have that \({\approx _{r}^{{\mathsf {p}}}} = {\approx _{r}^{{\mathsf {e}}}}\) but \({\approx _{r}^{{\mathsf {e}}}} \subsetneq {\approx _{r}^{{\mathsf {c}}}}\) for \(r \in \{ \ell , t\}\).
Proof
From Theorems 4 and 5, we already know that \({\approx _{r}^{{\mathsf {e}}}} \subseteq {\approx _{r}^{{\mathsf {p}}}}\) and \({\approx _{r}^{{\mathsf {e}}}} \subseteq {\approx _{r}^{{\mathsf {c}}}}\). Hence, we only need to show that \({\approx _{r}^{{\mathsf {p}}}} \subseteq {\approx _{r}^{{\mathsf {e}}}}\) and \({\approx _{r}^{{\mathsf {p}}}} \subsetneq {\approx _{r}^{{\mathsf {c}}}}\). The latter is easily shown by noticing that the processes A and B in Fig. 5 are I/O-unambiguous. Thus, we focus on \({\approx _{r}^{{\mathsf {p}}}} \subseteq {\approx _{r}^{{\mathsf {e}}}}\).
We start by proving that for all I/O-unambiguous processes A, for all  , we have that \(A'\) is I/O-unambiguous. Note that structural equivalence preserves I/O-unambiguity, i.e. for all extended processes A, B, for all channel name c, \(A \equiv B\) implies \({\mathsf{ioua}}(A,c) = {\mathsf{ioua}}(B,c)\). Hence, we assume w.l.o.g. that a name is bound at most once and the set of bound and free names are disjoint.
, we have that \(A'\) is I/O-unambiguous. Note that structural equivalence preserves I/O-unambiguity, i.e. for all extended processes A, B, for all channel name c, \(A \equiv B\) implies \({\mathsf{ioua}}(A,c) = {\mathsf{ioua}}(B,c)\). Hence, we assume w.l.o.g. that a name is bound at most once and the set of bound and free names are disjoint.
Second, we show that for all I/O-unambiguous processes A, for all  , we have that
, we have that  . To prove this property, denoted \({\mathcal {P}}\), let us assume w.l.o.g. that
. To prove this property, denoted \({\mathcal {P}}\), let us assume w.l.o.g. that  . The transition
. The transition  indicates that \(A \equiv \nu {\tilde{n}}. ({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,u).P \mid Q)\) and \(A_1 \equiv {\tilde{n}}. (P \mid Q \mid \{^u/_z\})\) for some \(P,Q,{\tilde{n}},c,u\). Note that A is I/O-unambiguous, and hence \({\mathsf{ioua}}(P, c) = \top \).
indicates that \(A \equiv \nu {\tilde{n}}. ({\mathsf {out}}^{{{\mathsf {h}}}{{\mathsf {o}}}}(c,u).P \mid Q)\) and \(A_1 \equiv {\tilde{n}}. (P \mid Q \mid \{^u/_z\})\) for some \(P,Q,{\tilde{n}},c,u\). Note that A is I/O-unambiguous, and hence \({\mathsf{ioua}}(P, c) = \top \).
As A is I/O-unambiguous implies that A does not contain private channels, we have that the rule applied in \(A_1 \rightarrow ^*_{\mathsf {p}}A_2\) is either the rule Then or Else. Therefore, there exists \(P'\) and \(Q'\) such that \(P \rightarrow ^*_{\mathsf {p}}P'\), \(Q \rightarrow ^*_{\mathsf {p}}Q'\), \(A_n \equiv \nu {\tilde{n}}. (P' \mid Q' \mid \{^u/_x\})\) and \({\mathsf{ioua}}(P', c) = \top \). Hence, we deduce that there exists \(Q_1, Q_2\) such that \(Q' \equiv \nu {\tilde{m}}.({{\mathsf {i}}}{{\mathsf {n}}}^{.}(c,x) Q_1 \mid Q_2)\) and \(A' \equiv \nu {\tilde{n}}.\nu {\tilde{m}}. (P' \mid Q_1\{^u/_x\} \mid Q_2)\). We conclude the proof of this property by noticing that we can first apply on A the reduction rules of \(Q \rightarrow ^*_{\mathsf {p}}Q'\), then apply the rule C-Eav and finally apply the rules of \(P \rightarrow ^*_{\mathsf {p}}P'\).
-
1.
To prove \({\approx _{t}^{{\mathsf {p}}}} \subseteq {\approx _{t}^{{\mathsf {e}}}}\), we assume that A,B are two closed honest extended processes such that \(A \approx _t^{{\mathsf {p}}} B\). For all
 , it follows from the semantics that
, it follows from the semantics that  where \({{\mathsf {t}}}{{\mathsf {r}}}_p\) is obtained by replacing in \({{\mathsf {t}}}{{\mathsf {r}}}\) each \(\nu z. eav(c,z)\) by \(\nu z. out(c,z). in(c,z)\). Since \(A \approx _t^{{\mathsf {p}}} B\), there exists \(B'\) such that
where \({{\mathsf {t}}}{{\mathsf {r}}}_p\) is obtained by replacing in \({{\mathsf {t}}}{{\mathsf {r}}}\) each \(\nu z. eav(c,z)\) by \(\nu z. out(c,z). in(c,z)\). Since \(A \approx _t^{{\mathsf {p}}} B\), there exists \(B'\) such that 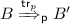 and \(\phi (A') \sim \phi (B')\). Thanks to the property \({\mathcal {P}}\), we conclude that
and \(\phi (A') \sim \phi (B')\). Thanks to the property \({\mathcal {P}}\), we conclude that 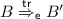 .
. -
2.
To prove \({\approx _{\ell }^{{\mathsf {p}}}} \subseteq {\approx _{\ell }^{{\mathsf {e}}}}\), we assume that A,B are two closed honest extended processes such that \(A \approx _\ell ^{{\mathsf {p}}} B\) and let \({\mathcal {R}}\) be the relation witnessing this equivalence. We will show that \({\mathcal {R}}\) is also a labelled bisimulation in the eavesdropping semantics. Suppose \(A {{{\mathcal {R}}}} B\).
-
as \(A \approx _\ell ^{{\mathsf {p}}} B\), we have that \(\phi (A) \sim \phi (B)\).
-
if
 then, as A is honest,
then, as A is honest,  . As \(A \approx _\ell ^{{\mathsf {p}}} B\) there exists \(B'\) such that
. As \(A \approx _\ell ^{{\mathsf {p}}} B\) there exists \(B'\) such that 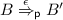 and \(A' {{{\mathcal {R}}}} B'\). As
and \(A' {{{\mathcal {R}}}} B'\). As  ,
, 
-
if
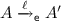 then, as A is I/O-unambiguous,
then, as A is I/O-unambiguous,  where \({{\mathsf {t}}}{{\mathsf {r}}}= \nu z.out(c,z).in(c,z)\) when \(\ell = \nu z. eav(c,z)\) else \({{\mathsf {t}}}{{\mathsf {r}}}= \ell \). As \(A \approx _\ell ^{{\mathsf {p}}} B\), there exists \(B'\) such that
where \({{\mathsf {t}}}{{\mathsf {r}}}= \nu z.out(c,z).in(c,z)\) when \(\ell = \nu z. eav(c,z)\) else \({{\mathsf {t}}}{{\mathsf {r}}}= \ell \). As \(A \approx _\ell ^{{\mathsf {p}}} B\), there exists \(B'\) such that  and \(A' {{{\mathcal {R}}}} B'\). When \({{\mathsf {t}}}{{\mathsf {r}}}= \ell \), the definition of the semantics directly gives us
and \(A' {{{\mathcal {R}}}} B'\). When \({{\mathsf {t}}}{{\mathsf {r}}}= \ell \), the definition of the semantics directly gives us  . When \({{\mathsf {t}}}{{\mathsf {r}}}= \nu z.out(c,z).in(c,z)\), the property \({\mathcal {P}}\) gives us
. When \({{\mathsf {t}}}{{\mathsf {r}}}= \nu z.out(c,z).in(c,z)\), the property \({\mathcal {P}}\) gives us  . \(\square \)
. \(\square \)
-
5 Different Semantics in Practice
As we have seen, in general, the three proposed semantics may yield different results. A conservative approach would consist in verifying always the eavesdropping semantics which is stronger than the two other ones, as shown before. However, this semantics seems also to be the least efficient one to verify.
We have implemented the three different semantics in the APTE tool, for processes with static channels, i.e. inputs and outputs may only have names in the channel position and not variables. This allowed us to investigate the difference in results and performance between the semantics.
In our experiments we considered several examples from APTE’s repository:
-
the Private Authentication protocol proposed by Abadi and Fournet [2];
-
the passive authentication protocol implemented in the European Passport protocol [4, 16];
-
the French and UK versions of the Basic Access Protocol (BAC) implemented in the European passport [5, 16].
For all these examples we found that the results, i.e., whether trace equivalence holds or not, was unchanged, independent of the semantics. However, as expected, performance of the private semantics was generally better. The existing protocol encodings generally used a single public channel. To enforce I/O-unambiguity, we introduced different channels and, surprisingly, noted that distinct channels significantly enhance the tool’s performance. (The model using different channels in the case of RFID protocols such as the electronic passport is certainly questionable.)
The results are summarised in the following table. For each protocol we considered the original encoding, and a slightly changed one which enforces I/O-unambiguity. In the results column we mark an attack by a cross (\(\times \)) and a successful verification with a check mark (\(\checkmark \)). In case of an attack we generally considered the minimal number of sessions needed to find the attack. In case of a successful verification we consider more sessions, which is the reason for the much higher verification times.
Protocol | # Sessions | Property | Time | Result | ||
|---|---|---|---|---|---|---|
\(\approx _t^{{\mathsf {e}}}\) | \(\approx _t^{{\mathsf {c}}}\) | \(\approx _t^{{\mathsf {p}}}\) | ||||
Private Authentication | 1 | Anonymity | 1 s | 1 s | 1 s | \(\checkmark \) |
2 | 53h 53 m 20 s | 47 h 46 m 40 s | 46 h 56 m 40 s | |||
I/O unambiguous | 1 | 1s | 1s | 1s | ||
2 | 31 m 39 s | 21 m 2 s | 19 m 39 s | |||
Passive Authentication | 2 | Anonymity | 4 s | 3 s | 3 s | \(\checkmark \) |
I/O unambiguous | 2 | 4 s | 4 s | 3 s | ||
3 | 6 h 38 m 34 s | 6 h 29 m 24 s | 6 h 36 m 40 s | |||
Passive Authentication | 2 | Unlinkability | 4 s | 4 s | 3 s | \(\checkmark \) |
I/O unambiguous | 2 | 3 s | 3 s | 3 s | ||
3 | 7 h 43 m 2 s | 6 h 39 m 14 s | 4 h 27 m 47 s | |||
FR BAC protocol | 2 | Unlinkability | 1 s | 1 m 29 s | 1 s | \(\times \) |
I/O unambiguous | 2 | 1 s | 1 s | 1 s | ||
UK BAC protocol | 2 | Unlinkability | 1 h 2 m 35 s | ? | 6 h 39 m 14 s | \(\times \) |
I/O unambiguous | 2 | 4s | 53s | 2s | ||
6 Conclusion
In this paper we investigated two families of Dolev-Yao models, depending on how the hypothesis that the attacker controls the network is reflected. While the two semantics coincide for reachability properties, they yield incomparable notions of behavioral equivalences, which have recently been extensively used to model privacy properties. The fact that forcing all communication to be routed through the attacker may diminish his distinguishing power may at first seem counter-intuitive. We also propose a third semantics, where internal communication among honest participants is permitted but leaks the message to the attacker. This new communication semantics entails strictly stronger equivalences than the two classical ones. We also identify two subclasses of protocols for which (some) semantics coincide. Finally, we implemented the three semantics in the APTE tool. Our experiments showed that the three semantics provide the same result on the case studies in the APTE example repository. However, the private semantics is slightly more efficient, as less interleavings have to be considered. Our results illustrate that behavioral equivalences are much more subtle than reachability properties and the need to carefully choose the precise attacker model.
References
Abadi, M., Fournet, C.: Mobile values, new names, and secure communication. In: Nielson, H.R.: 28th Symposium on Principles of Programming Languages (POPL 2001), pp. 104–115. ACM, London, January 2001
Abadi, M., Fournet, C.: Private authentication. Theor. Comput. Sci. 322(3), 427–476 (2004)
Abadi, M., Gordon, A.D.: A calculus for cryptographic protocols: the spi calculus. Inf. Comput. 148(1), 1–70 (1999)
Arapinis, M., Cheval, V., Delaune, S.: Verifying privacy-type properties in a modular way. In: Cortier, V., Zdancewic, S. (eds.) Proceedings of the 25th IEEE Computer Security Foundations Symposium (CSF 2012), pp. 95–109. IEEE Computer Society Press, Cambridge, June 2012
Arapinis, M., Chothia, T., Ritter, E., Ryan, M.: Analysing unlinkability and anonymity using the applied pi calculus. In: Proceedings of 23rd Computer Security Foundations Symposium (CSF 2010), pp. 107–121. IEEE Computer Society Press (2010)
Armando, A., et al.: The AVISPA tool for the automated validation of internet security protocols and applications. In: Etessami, K., Rajamani, S.K. (eds.) CAV 2005. LNCS, vol. 3576, pp. 281–285. Springer, Heidelberg (2005). doi:10.1007/11513988_27
Babel, K., Cheval, V., Kremer, S.: On communication models when verifying equivalence properties. Technical report, HAL (2017)
Blanchet, B.: Automatic verification of correspondences for security protocols. J. Comput. Secur. 17(4), 363–434 (2009)
Blanchet, B., Abadi, M., Fournet, C.: Automated verification of selected equivalences for security protocols. J. Logic Algebraic Program. 75(1), 3–51 (2008)
Chadha, R., Cheval, V., Ciobâcă, Ş., Kremer, S.: Automated verification of equivalence properties of cryptographic protocol. ACM Trans. Comput. Logic 17, 23 (2016)
Cheval, V., Comon-Lundh, H., Delaune, S.: Trace equivalence decision: negative tests and non-determinism. In: Proceedings of 18th ACM Conference on Computer and Communications Security (CCS 2011), ACM, October 2011
Cheval, V., Cortier, V., Delaune, S.: Deciding equivalence-based properties using constraint solving. Theor. Comput. Sci. 492, 1–39 (2013)
Cremers, C.J.F.: The scyther tool: verification, falsification, and analysis of security protocols. In: Gupta, A., Malik, S. (eds.) CAV 2008. LNCS, vol. 5123, pp. 414–418. Springer, Heidelberg (2008). doi:10.1007/978-3-540-70545-1_38
Delaune, S., Kremer, S., Ryan, M.D.: Verifying privacy-type properties of electronic voting protocols. J. Comput. Secur. 17(4), 435–487 (2009)
Dong, N., Jonker, H., Pang, J.: Analysis of a receipt-free auction protocol in the applied pi calculus. In: Degano, P., Etalle, S., Guttman, J. (eds.) FAST 2010. LNCS, vol. 6561, pp. 223–238. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19751-2_15
Force, P.T.: PKI for machine readable travel documents offering ICC read-only access. Technical report, International Civil Aviation Organization (2004)
Millen, J.K., Shmatikov, V.: Constraint solving for bounded-process cryptographic protocol analysis. In: Proceedings of 8th Conference on Computer and Communications Security, pp. 166–175. ACM Press (2001)
Paulson, L.C.: The inductive approach to verifying cryptographic protocols. J. Comput. Secur. 6(1/2), 85–128 (1998)
Ryan, P., Schneider, S., Goldsmith, M., Lowe, G., Roscoe, A.: Modelling and Analysis of Security Protocols. Addison Wesley, Boston (2000)
Meier, S., Schmidt, B., Cremers, C., Basin, D.: The TAMARIN prover for the symbolic analysis of security protocols. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 696–701. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39799-8_48
Fabrega, T.H., Javier, F., Herzog, J.C., Guttman, J.D.: Strand spaces: proving security protocols correct. J. Comput. Secur. 7(2/3), 191–230 (1999)
Tiu, A., Dawson, J.E.: Automating open bisimulation checking for the spi calculus. In: Proceedings of 23rd Computer Security Foundations Symposium (CSF 2010), pp. 307–321. IEEE Computer Society (2010)
Acknowledgments
We would like to thank Catherine Meadows and Stéphanie Delaune for interesting discussions, as well as the anonymous reviewers for their comments. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 645865-SPOOC) and the ANR project SEQUOIA ANR-14-CE28-0030-01.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Babel, K., Cheval, V., Kremer, S. (2017). On Communication Models When Verifying Equivalence Properties. In: Maffei, M., Ryan, M. (eds) Principles of Security and Trust. POST 2017. Lecture Notes in Computer Science(), vol 10204. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54455-6_7
Download citation
DOI: https://doi.org/10.1007/978-3-662-54455-6_7
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54454-9
Online ISBN: 978-3-662-54455-6
eBook Packages: Computer ScienceComputer Science (R0)






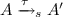 implies
implies 

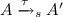 implies
implies  and
and 

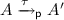 then, as
then, as  ,
,  . As
. As  and
and  .
. and
and  (as
(as  and there exists
and there exists  and
and 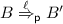 .
.
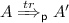 there exists
there exists  . It follows from the definition of the semantics that whenever
. It follows from the definition of the semantics that whenever  then we also have
then we also have  as
as 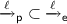 . As
. As  and
and 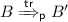 . Hence
. Hence  . From the semantics, we obtain that
. From the semantics, we obtain that  , where
, where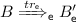 and
and  and
and 
 , it follows from the semantics that
, it follows from the semantics that  where
where 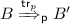 and
and 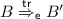 .
. then, as A is honest,
then, as A is honest,  . As
. As 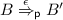 and
and  ,
, 
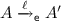 then, as A is I/O-unambiguous,
then, as A is I/O-unambiguous,  where
where  and
and  . When
. When  .
. 