Abstract
We introduce an efficient complementation technique for semi-deterministic Büchi automata, which are Büchi automata that are deterministic in the limit: from every accepting state onward, their behaviour is deterministic. It is interesting to study semi-deterministic automata, because they play a role in practical applications of automata theory, such as the analysis of Markov decision processes. Our motivation to study their complementation comes from the termination analysis implemented in Ultimate Büchi Automizer, where these automata represent checked runs and have to be complemented to identify runs to be checked. We show that semi-determinism leads to a simpler complementation procedure: an extended breakpoint construction that allows for symbolic implementation. It also leads to significantly improved bounds as the complement of a semi-deterministic automaton with n states has less than \(4^n\) states. Moreover, the resulting automaton is unambiguous, which again offers new applications, like the analysis of Markov chains. We have evaluated our construction against the semi-deterministic automata produced by the Ultimate Büchi Automizer. The evaluation confirms that our algorithm outperforms the known complementation techniques for general nondeterministic Büchi automata.
The research was supported through The Czech Science Foundation, grant P202/12/G061, by the German Research Council (DFG) as part of the Transregional Collaborative Research Center “Automatic Verification and Analysis of Complex Systems” (SFB/TR14 AVACS) and EPSRC grant EP/M027287/1.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The complementation of Büchi automata [6] is a classic problem that has been extensively studied [6, 11–13, 17, 19, 20, 22, 23, 25–27, 31–33, 37] for more than half a century; see [35] for a survey. The traditional line of research has started with a proof on the existence of complementation algorithms [19, 22] and continued to home in on the complexity of Büchi complementation, finally leading to matching upper [27] and lower [37] bounds for complementing Büchi automata. This line of research has been extended to more general classes of automata, notably parity [30] and generalised Büchi [29] automata.
The complementation of Büchi automata is a valuable tool in formal verification (cf. [18]), in particular when a property that all runs of a model shall have is provided as a Büchi automaton,Footnote 1 and when studying language inclusion problems of \(\omega \)-regular languages. With the growing understanding of the worst case complexity, the practical cost of complementing Büchi automata has become a second line of research. In particular the GOAL tool suite [33] provides a platform for comparing the behaviour of different complementation techniques on various benchmarks [32].
While these benchmarks use general Büchi automata, practical applications can produce or require subclasses of Büchi automata in specific forms. Our research is motivated by the observation that the program termination analysis in Ultimate Büchi Automizer [15] and the LTL software model checker Ultimate LTL Automizer [9] produce semi-deterministic Büchi automata (SDBA) [34, 36] during their run. Semi-deterministic Büchi automata are a special class of Büchi automata that behave deterministically after traversing the first accepting state. For this reason, they are sometimes referred to as limit deterministic or deterministic-in-the-limit Büchi automata.
Program termination analysis is a model checking problem, where the aim is to prove that a given program terminates on all inputs. In other words, it tries to establish (or disprove) that all infinite execution paths in the program flowgraph are infeasible. The Ultimate Büchi Automizer uses an SDBA to represent infinite paths that are already known to be infeasible. It needs to complement the SDBA and make the product with the program flowgraph to identify the set of infinite execution paths whose infeasibility still needs to be proven. One can use off-the-shelf complementation algorithms like rank based [12, 13, 17, 27] or determinisation based [24, 25, 28, 29] ones, but they make no use of the special structure of SDBAs.
We show that exploiting this structure helps: while the complementation of Büchi automata with n states leads to a \((cn)^n\) blow-up for a constant \(c \approx 0.76\) (cf. [27] for the upper and [37] for the lower bound), an SDBA with n states can be complemented to an automaton with less than \(4^n\) states. More precisely, if the deterministic part (the states reachable from the accepting states) contains d states, including a accepting states, the complement automaton has at most \(2^{n-d}3^a4^{d-a}\) states. The \(2^{\varTheta (n)}\) blow-up is tight as an \(\varOmega (2^n)\) lower bound is inherited from the complementation of nondeterministic finite automata. Another advantage of our construction is that it is suitable for the simplest class of Büchi automata: deterministic Büchi automata with a accepting and n non-accepting states are translated to \(2n-a\) states, which meets Kurshan’s construction for the complementation of deterministic Büchi automata [18].
Moreover, the resulting automata have further useful properties. For example, their structure is very simple: they are merely an extended breakpoint construction [21]. Like ordinary breakpoint constructions, this provides a structure that is well suited for symbolic implementation. This is quite different from techniques based on Safra style determinisation [24, 25, 28, 29]. In addition to this, they are unambiguous, i.e. there is exactly one accepting run for each word accepted by such an automaton. This is notable, because disambiguation is another automata transformation that seems to be more involved than complementation, but simpler than determinisation [16], and it has proven to be useful for the quantitative analysis of Markov chains [3, 7]. For our motivating application, this is particular good news, as the connection to Markov chains implies direct applicability to model checking stochastic models as well as nondeterministic ones. The connection to stochastic models closes a cycle of applications, as they form a second source for applying semi-deterministic automata: they appear in the classic algorithm for the qualitative analysis of Markov decision processes [8] and in current model checking tools for their quantitative analysis [14] alike.
With all of these favourable properties in mind, it would be easy to think that the complementation mechanism we develop forms a class of its own. But this is not the case: when comparing it with classic rank based complementation [17] and its improvements [12, 13, 27], semi-deterministic automata prove to be automata, where all states in all runs can be assigned just three ranks, ranks 1 through 3 in the terminology of [17]. Consequently, there are only states with a single even rank, and a rank based algorithm that has to guess the rank correctly for states that are reachable from an accepting state has very similar properties. From this perspective, one could say that complementation and disambiguation are easy to obtain, as very little needs to be guessed (only the point where the rank of a state goes down to 1) and very little has to be checked.
We also motivate and present an on-the-fly modification of our complementation, which does not need to know the whole automaton before the complementation starts. The price for the on-the-fly approach is a slightly worse upper bound on the size of the produced automaton for the complement: it has less than \(5^n\) states.
We have implemented our construction in the GOAL tool and the Ultimate Automata Library and evaluated it on semi-deterministic Büchi automata that were produced by Ultimate Büchi Automizer applied to programs of the Termination category of the software verification competition SV-COMP 2015 [4]. The evaluation confirms that the specific complementation algorithm realises its theoretical advantage and outperforms the traditional algorithms and produces smaller complement automata.
The remainder of the paper is organised as follows. After recalling some definitions and introducing our notation in Sect. 2, we present the complementation construction in Sect. 3 together with its complexity analysis and on-the-fly modification. In Sect. 4, we show a connection between our construction and rank-based constructions, followed by a correctness proof for our construction. The experimental evaluation is presented in Sect. 5.
2 Preliminaries
A (nondeterministic) Büchi automaton (NBA) is a tuple \(\mathcal {A}=(Q,\varSigma ,\delta ,I,F)\), where
-
Q is a finite set of states,
-
\(\varSigma \) is a finite alphabet,
-
\(\delta : Q \times \varSigma \rightarrow 2^Q\) is a transition function,
-
\(I \subseteq Q\) is a set of initial states, and
-
\(F \subseteq Q\) is a set of accepting states.
A run of an automaton \(\mathcal {A}\) over an infinite word \(w=w_0w_1\ldots \in \varSigma ^\omega \) is a finite or infinite sequence of states \(\rho =q_0q_1q_2\ldots \in Q^+\cup Q^\omega \) such that \(q_0\in I\) and \(q_{j+1}\in \delta (q_j,w_j)\) for each pair of adjacent states \(q_jq_{j+1}\) in \(\rho \). For a finite run \(\rho =q_0q_1q_2\ldots q_n\in Q^{n+1}\) we require that there is no transition for its last state, i.e. \(\delta (q_n,w_n)=\emptyset \), and we say that the run blocks. A run is accepting if \(q_j\in F\) holds for infinitely many j. A word w is accepted by \(\mathcal {A}\) if there exists an accepting run of \(\mathcal {A}\) over w. The language of an automaton \(\mathcal {A}\) is the set \(L(\mathcal {A})\) of all words accepted by \(\mathcal {A}\).
A complement of a Büchi automaton \(\mathcal {A}\) is a Büchi automaton \(\mathcal {C}\) over the same alphabet \(\varSigma \) that accepts the complement language, \(L(\mathcal {C})=\varSigma ^\omega \backslash L(\mathcal {A})\), of the language of \(\mathcal {A}\).
A Büchi automaton \(\mathcal {A}=(Q,\varSigma ,\delta ,I,F)\) is called complete if, for each state \(q\in Q\) and for each letter \(a\in \varSigma \), there exists at least one successor, i.e. \(|\delta (q,a)| \ge 1\). A Büchi automaton \(\mathcal {A}\) is unambiguous if, for each \(w\in L(\mathcal {A})\), there exists only one accepting run over w.
A state of a Büchi automaton \(\mathcal {A}=(Q,\varSigma ,\delta ,I,F)\) is called reachable if it occurs in some run for some word \(w \in \varSigma ^\omega \). \(\mathcal {A}=(Q,\varSigma ,\delta ,I,F)\) is called deterministic if it has only one initial state, i.e. if \(|I|=1\), and if, for each reachable state \(q\in Q\) and for each letter \(a\in \varSigma \), there exists at most one successor, i.e. \(|\delta (q,a)| \le 1\).
We are particularly interested in semi-deterministic automata. A Büchi automaton is semi-deterministic if it behaves deterministically from the first visit of an accepting state onward. Formally, a Büchi automaton \(\mathcal {A}=(Q,\varSigma ,\delta ,I,F)\) is a semi-deterministic Büchi automaton (SDBA) (also known as deterministic-in-the-limit) if, for each \(q_f\in F\), the automaton \((Q,\varSigma ,\delta ,\{q_f\},F)\) is deterministic.
Each semi-deterministic automaton can be divided into two parts: the part reachable from accepting states—which is completely deterministic—and the rest. Hence, one can alternatively define a semi-deterministic automaton such that the set of states  consists of two disjoint sets
consists of two disjoint sets  and
and  , where
, where  , and the transition relation
, and the transition relation  consists of three disjoint transition functions, namely
consists of three disjoint transition functions, namely

where the relation  is deterministic: for each
is deterministic: for each  and each \(a\in \varSigma \),
and each \(a\in \varSigma \),  . \(\delta \) can then be defined as
. \(\delta \) can then be defined as  if
if  and
and  if
if  . The elements of
. The elements of  are called transit edges. This alternative definition is captured in Fig. 1 and used in the following section.
are called transit edges. This alternative definition is captured in Fig. 1 and used in the following section.
3 Semi-deterministic Büchi Automata Complementation
First of all, we explain our complementation construction intuitively. Then we formulate it precisely and discuss the size of the resulting automata when the complementation is applied to semi-deterministic and deterministic Büchi automata. At the end, we briefly introduce the modification of our complementation construction for on-the-fly approach. The correctness is addressed in Sect. 4 after introducing the concept of level rankings and run graphs.
3.1 Relation of Runs to the Complement
Let \(\mathcal {A}=(Q,\varSigma ,\delta ,I,F)\) be an SDBA,  be the notation introduced in Fig. 1, and \(w=w_0w_1\ldots \in \varSigma ^\omega \) be an infinite word. Each run \(\rho \) of \(\mathcal {A}\) over w has one of the following properties:
be the notation introduced in Fig. 1, and \(w=w_0w_1\ldots \in \varSigma ^\omega \) be an infinite word. Each run \(\rho \) of \(\mathcal {A}\) over w has one of the following properties:
-
1.
\(\rho \) blocks,
-
2.
\(\rho \) stays forever in
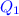 ,
, -
3.
\(\rho \) enters
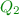 and stops visiting F at some point, or
and stops visiting F at some point, or -
4.
\(\rho \) is an accepting run.
Clearly, \(w\notin L(\mathcal {A})\) if and only if every run of \(\mathcal {A}\) over w has one of the first three properties. In the third case, we say that \(\rho \) is safe after visiting F for the last time (or since the moment it enters \(Q_2\) if it does not visit any accepting state at all).
In order to check whether \(w\in L(\mathcal {A})\) or not, one has to track all possible runs of \(\mathcal {A}\). After reading a finite prefix of w, the states reached by the corresponding prefixes of runs can be divided into three sets.
-
1.
The set
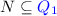 represents the runs that kept out of the deterministic part (N stands for nondeterministic) so far.
represents the runs that kept out of the deterministic part (N stands for nondeterministic) so far. -
2.
The set
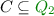 represents the runs that have entered the deterministic part and that are not safe. One has to check (hence the name C) if some of them will be prolonged into accepting runs in the future, or if all of the runs eventually block or become safe.
represents the runs that have entered the deterministic part and that are not safe. One has to check (hence the name C) if some of them will be prolonged into accepting runs in the future, or if all of the runs eventually block or become safe. -
3.
The set
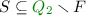 represents the safe runs.
represents the safe runs.
Clearly, every accepting run of \(\mathcal {A}\) stays in C after leaving N. On the other hand, if \(w\notin L(\mathcal {A})\), every infinite run either stays in N or eventually leaves C to S and thus does not stay in C forever.
3.2 NCSB Complementation Construction
In this section, we describe an efficient construction that produces, for a given SDBA \(\mathcal {A}\), a complement automaton \(\mathcal {C}\). The automaton \(\mathcal {C}\) has typically a low degree of non-determinism when compared to results of other complementation algorithms, and is always unambiguous. The complementation construction proposed here tracks the runs of \(\mathcal {A}\) using the well known powerset construction and guesses the right classification of runs into sets N, C, and S. Moreover, in order to check that no run stays forever in C, it uses one more set \(B\subseteq C\). The set B mimics the behaviour of C with one exception: it does not adopt the runs freshly coming to C via  . The size of B never increases until it becomes empty; then we say that a breakpoint is reached. After each breakpoint, B is set to track exactly the runs currently in C. To sum up, states of \(\mathcal {C}\) are quadruples (N, C, S, B)—hence the name NCSB complementation construction.
. The size of B never increases until it becomes empty; then we say that a breakpoint is reached. After each breakpoint, B is set to track exactly the runs currently in C. To sum up, states of \(\mathcal {C}\) are quadruples (N, C, S, B)—hence the name NCSB complementation construction.
After reading only a finite prefix of the input word w, the automaton cannot know whether or not some run is already safe, as this depends on the suffix of w. The automaton \(\mathcal {C}\) uses the guess-and-check strategy. Whenever a run \(\rho \) in C may freshly become safe (it is leaving an accepting state or it is entering \(Q_2\) via a transit edge), then the automaton \(\mathcal {C}\) makes a nondeterministic decision to move \(\rho \) to S or to leave it in C. The construction punishes every wrong decision:
-
in order to preserve correctness, a run of \(\mathcal {C}\) is blocked if \(\rho \) is moved to S too early (runs in S are not allowed to visit accepting states any more), and
-
in order to maintain unambiguity, \(\rho \) is allowed to move from C to S only when leaving an accepting state. Hence, if \(\rho \) misses the moment when it leaves an accepting state for the last time, it will stay in C forever and this particular run of \(\mathcal {C}\) cannot be accepting.
Before we formally describe the NCSB construction, we first naturally extend  , and
, and  to sets. For any
to sets. For any  , any \(a\in \varSigma \), and any set
, any \(a\in \varSigma \), and any set  or
or  , we set
, we set  .
.
With the provided intuition in mind, we define the complement automaton NBA \(\mathcal {C}= (P,\varSigma ,\delta ',I_\mathcal {C},F_\mathcal {C})\) as follows.
-
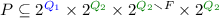 .
. -
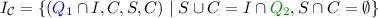 .
. -
\(F_\mathcal {C}= \{(N,C,S,B) \in P \mid B = \emptyset \}\).
-
\(\delta '\) is the transition function \(\delta ':P\times \varSigma \rightarrow 2^P\), such that \((N',C',S',B') \in \delta '\big ((N,C,S,B),a\big )\) iff
-
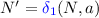 ,
, 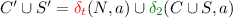 (intuition: tracing the reachable states correctly),
(intuition: tracing the reachable states correctly), -
\(C' \cap S' = \emptyset \) (intuition: a run in
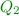 is either safe, or not),
is either safe, or not), -
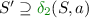 (intuition: safe runs must stay safe),
(intuition: safe runs must stay safe), -
 (intuition: only runs leaving an accepting state can become safe),
(intuition: only runs leaving an accepting state can become safe), -
for all \(q \in C \backslash F\),
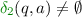 (intuition: otherwise the corresponding run was safe already and should have been moved to S earlier), and
(intuition: otherwise the corresponding run was safe already and should have been moved to S earlier), and -
if \(B = \emptyset \) then \(B' = C'\), and else
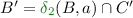 (intuition: breakpoint construction to check that no run stays in C forever).
(intuition: breakpoint construction to check that no run stays in C forever).
-
Note that the only source of nondeterminism of \(\delta '\) is when \(\mathcal {C}\) has to guess correctly whether or not a run \(\rho \) of \(\mathcal {A}\) is safe. Such situations arise in two cases, namely when the current state q of the run \(\rho \) satisfies
-
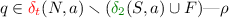 is freshly entering
is freshly entering 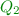 , and when
, and when -
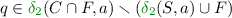 —\(\rho \) is leaving an accepting state.
—\(\rho \) is leaving an accepting state.
All other situations are determined, including runs that are currently in  (which belong to S) and runs that are currently in F (which belong to C).
(which belong to S) and runs that are currently in F (which belong to C).
3.3 Complexity
Let \(p=(N,C,S,B)\in P\) of \(\mathcal {C}\). Then
-
for a state
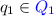 of \(\mathcal {A}\), \(q_1\) is either present or absent in N;
of \(\mathcal {A}\), \(q_1\) is either present or absent in N; -
for \(q_2\in F\), one of the following three options holds: \(q_2\) is only in C, \(q_2\) is both in C and B, or \(q_2\) is not present in p at all; and
-
for
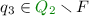 , one of the following four options holds: \(q_3\) is only in S, \(q_3\) is only in C, \(q_3\) is both in C and B, or \(q_3\) is not present in p at all.
, one of the following four options holds: \(q_3\) is only in S, \(q_3\) is only in C, \(q_3\) is both in C and B, or \(q_3\) is not present in p at all.
The size of P is thus bounded by  .
.
Let us note that, for deterministic automata (here we assume \(\mathcal {A}\) is complete and  is empty), the NCSB construction leads to an automaton similar to an automaton with \(2|Q|-|F|\) states produced by Kurshan’s construction [18]. To see the size of the automaton produced by our construction for a DBA, recall that a state (N, C, S, B) of the complement automaton encodes that exactly the states in \(N \cup C \cup S\) are reachable. For a DBA, \(N \cup C \cup S\) thus contains exactly one state q of Q. Moreover, N is empty and thus B coincides with C since B becomes empty together with C. If \(q\in F\), then it is in both B and C. If
is empty), the NCSB construction leads to an automaton similar to an automaton with \(2|Q|-|F|\) states produced by Kurshan’s construction [18]. To see the size of the automaton produced by our construction for a DBA, recall that a state (N, C, S, B) of the complement automaton encodes that exactly the states in \(N \cup C \cup S\) are reachable. For a DBA, \(N \cup C \cup S\) thus contains exactly one state q of Q. Moreover, N is empty and thus B coincides with C since B becomes empty together with C. If \(q\in F\), then it is in both B and C. If  , then it is either only in S, or in both B and C, leading to a size
, then it is either only in S, or in both B and C, leading to a size  .
.
3.4 Modification Suitable for On-the-fly Implementation
Some algorithms do not need to construct the whole complement automaton. For example, in order to verify that \(w\notin L(\mathcal {A})\) one only needs to built the accepting lasso in \(\mathcal {C}\) for w. Or when building a product with some other automaton (or Markov chain), it is unnecessary to build the part of \(\mathcal {C}\) which is not used in the product. Further, some tools work with implicitly encoded automata and/or query an SMT solver to check the presence of a transition in the automaton, which is expensive. Ultimate Büchi Automizer has both properties: it stores automata in an implicit form and builds a product of the complement with a program flowgraph. Such tools can greatly benefit from an on-the-fly complementation that does not rely on the knowledge of the whole input automaton.
Our complementation can be easily adapted for an on-the-fly implementation. Because we have no knowledge about  , and
, and  in this variation, the runs are held in N until they reach an accepting state, only then they are moved to C.
in this variation, the runs are held in N until they reach an accepting state, only then they are moved to C.
Technically, the “ ” from the definition of \(\delta '\) would be replaced by “\(N'=\delta (N,a)\backslash F\)” and for \(C'\) now holds \(C' \subseteq \delta (C,a) \cup (\delta (N,a)\cap F)\). The on-the-fly construction can therefore have up to
” from the definition of \(\delta '\) would be replaced by “\(N'=\delta (N,a)\backslash F\)” and for \(C'\) now holds \(C' \subseteq \delta (C,a) \cup (\delta (N,a)\cap F)\). The on-the-fly construction can therefore have up to  states.
states.
Note that the on-the-fly construction does not add any further nondeterminism to the construction. To the contrary, there is an injection of runs from the construction discussed in Sect. 3.2 to this on-the-fly construction. The correctness argument and the uniqueness argument for the accepting run which are given in Sect. 4 therefore need only very minor adjustments.
4 Level Rankings in Complementation and Correctness
We open this section by introduction of run graphs and level rankings. We then look at our construction through the level ranking lense and use the insights this provides for proving its correctness and unambiguity.
4.1 Complementation and Level Rankings
In [17], Kupferman and Vardi introduce level rankings as a witness for the absence of accepting runs of Büchi automata. They form the foundation of several complementation algorithms [12, 13, 17, 27, 29].
The set of all runs of a nondeterministic Büchi automaton \(\mathcal {A}=(\varSigma ,Q,I,\delta ,F)\) over a word w can be represented by a directed acyclic graph \(\mathcal G_w=(V,E)\), called the run graph of \(\mathcal {A}\) on w, with
-
vertices \(V \subseteq Q\times \omega \) such that \((q,i)\in V\) iff there is a run \(\rho = q_0 q_1 q_2 \ldots \) over \(\mathcal {A}\) on w with \(q_i=q\), and
-
edges \(E \subseteq (Q\times \omega ) \times (Q\times \omega )\) such that \(\big ((q,i),(q',i')\big )\in E\) iff \(i'=i+1\) and there is a run \(\rho = q_0 q_1 q_2 \ldots \) of \(\mathcal {A}\) over w with \(q_i=q\) and \(q_{i+1}=q'\).
The run graph \(\mathcal G_w\) is called rejecting if no path in \(\mathcal G_w\) satisfies the Büchi condition. That is, \(\mathcal G_w\) is rejecting iff w does not have any accepting run, and thus iff w is not in the language of \(\mathcal {A}\). \(\mathcal {A}\) can be complemented to a nondeterministic Büchi automaton \(\mathcal C\) that checks if \(\mathcal G_w\) is rejecting.
The property that \(\mathcal G_w\) is rejecting can be expressed in terms of ranks [17]. We call a vertex \((q,i)\in V\) of a graph \(\mathcal G=(V,E)\) safe, if no vertex reachable from (q, i) is accepting (that is, in \(F\times \omega \)), and finite, if the set of vertices reachable from (q, i) in \(\mathcal G\) is finite.
Based on these definitions, ranks can be assigned to the vertices of a rejecting run graph. We set \({\mathcal G_w}^0= \mathcal G_w\), and repeat the following procedure until a fixed point is reached, starting with \(i=1\):
-
Assign all safe vertices of \({\mathcal G_w}^{i-1}\) the rank i, and set \({\mathcal G_w}^{i}\) to \({\mathcal G_w}^{i-1}\) minus the vertices with rank i (that is, minus the safe vertices in \({\mathcal G_w}^{i-1}\)).
-
Assign all finite vertices of \({\mathcal G_w}^i\) the rank \(i+1\), and set \({\mathcal G_w}^{i+1}\) to \({\mathcal G_w}^i\) minus the vertices with rank \(i+1\) (that is, minus the finite vertices in \({\mathcal G_w}^i\)).
-
Increase i by 2.
A fixed point is reached in \(n+2\) stepsFootnote 2, and the ranks can be used to characterise the complement language of a nondeterministic Büchi automaton:
Proposition 1
[17] A nondeterministic Büchi automaton \(\mathcal {A}\) with n states rejects a word w iff \({\mathcal G_w}^{2n+2}\) is empty. \(\square \)
4.2 Ranks and Complementation of SDBAs
When considering the run graph for SBDAs, we only need to consider three ranks: 1, 2, and 3. What is more, the vertices  reachable from accepting vertices can only have rank 1 or rank 2 in a rejecting run graph.
reachable from accepting vertices can only have rank 1 or rank 2 in a rejecting run graph.
Proposition 2
A semi-deterministic Büchi automaton \(\mathcal {A}\) rejects a word w iff \({\mathcal G_w}^3\) is empty. This is the case iff \({\mathcal G_w}^2\) contains no vertex in  .
.
Proof
Let w be a word rejected by \(\mathcal S\). By construction, \({\mathcal G_w}^1\) contains no safe vertices. (Note that removing safe vertices does not introduce new safe vertices.)
Let us assume for contradiction that \({\mathcal G_w}^1\) contains a vertex  , which is not finite. As \((q_i,i)\) is not finite, there is an infinite run \(\rho = q_0q_1q_2 \ldots q_{i-1}q_iq_{i+1} \ldots \) of \(\mathcal {A}\) over w such that, for all \(j \ge i\), \((q_j,j)\) is a vertex in \({\mathcal G_w}^1\). This is because
, which is not finite. As \((q_i,i)\) is not finite, there is an infinite run \(\rho = q_0q_1q_2 \ldots q_{i-1}q_iq_{i+1} \ldots \) of \(\mathcal {A}\) over w such that, for all \(j \ge i\), \((q_j,j)\) is a vertex in \({\mathcal G_w}^1\). This is because  , the deterministic part of the SBDA, and \(\{(q_j,j) \mid j \ge i\}\) is therefore (1) determined by w and \((q_i,i)\), and (2) fully in \({\mathcal G_w}^1\), because otherwise \((q_i,i)\) would be finite.
, the deterministic part of the SBDA, and \(\{(q_j,j) \mid j \ge i\}\) is therefore (1) determined by w and \((q_i,i)\), and (2) fully in \({\mathcal G_w}^1\), because otherwise \((q_i,i)\) would be finite.
But if all vertices in \(\{(q_j,j) \mid j \ge i\}\) are in \({\mathcal G_w}^1\), then none of them is safe in \({\mathcal G_w}\). Using again that the tail \(q_iq_{i+1}q_{i+2} \ldots \) is unique and well defined (as  , the deterministic part of the SDBA), it follows that, for all \(j\ge i\), there is a \(k \ge j\) such that \(q_k\) is accepting. Consequently, \(\rho \) is accepting (contradiction).
, the deterministic part of the SDBA), it follows that, for all \(j\ge i\), there is a \(k \ge j\) such that \(q_k\) is accepting. Consequently, \(\rho \) is accepting (contradiction).
We have thus shown that, if \(\mathcal S\) rejects a word w, then \({\mathcal G_w}^2\) contains no state in  . This also implies that \({\mathcal G_w}^2\) contains no accepting vertices. Consequently, all vertices in \({\mathcal G_w}^2\) are safe. Consequently, \({\mathcal G_w}^3\) is empty. \(\square \)
. This also implies that \({\mathcal G_w}^2\) contains no accepting vertices. Consequently, all vertices in \({\mathcal G_w}^2\) are safe. Consequently, \({\mathcal G_w}^3\) is empty. \(\square \)
We now consider the NCSB construction from a level ranking perspective. We start with an intuition for the rational run \(\rho = (N_0,C_0,S_0,B_0) (N_1,C_1,S_1,B_1) (N_2,C_2,S_2,B_2) \ldots \) of \(\mathcal {C}\) over a word w rejected by \(\mathcal {A}\), where \((V,E)=\mathcal G_w\). A rational run is the unique accepting run of \(\mathcal {C}\) over w and it guesses the ranks precisely, that is:
-
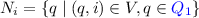 ,
, -
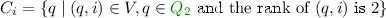 (we need to check that these states are finite in \({\mathcal {G}_w}^{2}\)),
(we need to check that these states are finite in \({\mathcal {G}_w}^{2}\)), -
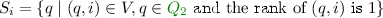 ,
, -
\(B_i \subseteq C_i\).
All runs of \(\mathcal {C}\) that differ on some i from the rational run will either block or will keep the wrongly guessed vertices with rank 1 in C and thus will be not accepting.
Note that the \(\mathcal {C}\) does not need to guess much. The development of the \(N_i\) is deterministic. The development of \(C_i \cup S_i\) is deterministic, \(S_i\) and \(C_i\) are disjoint, and states in F cannot be in \(S_i\). The \(B_i\) serve as a breakpoint construction, and the development of \(B_i\) is determined by the development of the \(C_i\). All that needs to be guessed is the point when a vertex becomes safe, and there is only a single correct guess.
4.3 Correctness
After reading only a finite prefix of an input word w, the automaton has to use its nondeterministic power to guess which reached state in  should be added to S. We now establish that the automaton \(\mathcal {C}\) is an unambiguous automaton that recognises the complement language of \(\mathcal {A}\) by showing
should be added to S. We now establish that the automaton \(\mathcal {C}\) is an unambiguous automaton that recognises the complement language of \(\mathcal {A}\) by showing
-
1.
\(\mathcal {C}\) does not accept a word that is accepted by \(\mathcal {A}\),
-
2.
for words that are not accepted by \(\mathcal {A}\), the run inferred from the level ranking discussed in Sect. 4.2 defines an accepting run, and
-
3.
for words w that are not accepted by \(\mathcal {A}\), this is the only accepting run of \(\mathcal {C}\) over w.
Lemma 1
Let \(\mathcal {A}\) be an SDBA, \(\mathcal {C}\) be constructed by the NCSB complementation of \(\mathcal {A}\), and \(w\in L(\mathcal {A})\) be a word in the language of \(\mathcal {A}\). Then \(\mathcal {C}\) does not accept w.
Proof
Let \(\rho =q_0q_1\ldots \) be an accepting run of \(\mathcal {A}\) over w, and let \(i\in \omega \) be an index such that \(q_i \in F\). Let us assume for contradiction that \(\rho '=(N_0,C_0,S_0,B_0)(N_1,C_1,S_1,B_1)\ldots (N_n,C_n,S_n,B_n)\ldots \) is an accepting run of \(\mathcal {C}\) over w. Clearly, \(q_i \in C_i\). It therefore holds, for all \(j\ge i\), that \(q_j \in C_j \cup S_j\).
We look at the following case distinction.
-
1.
For all \(j \ge i\), \(q_j \in C_j\). As \(\rho '\) is accepting, there is a breakpoint (\(B_j = \emptyset \)) for some \(j \ge i\). For such a j we have that \(q_{j+1} \in B_{j+1}\) and, moreover, that \(q_k \in B_k\) for all \(k \ge j+1\). Thus, \(B_k\ne \emptyset \) for all \(k\ge j+1\) and \(\rho '\) visits only finitely many accepting states (contradiction).
-
2.
There is a \(j \ge i\) such that \(q_j \in S_j\). But then \(q_k \in S_k\) holds for all \(k \ge j\) by construction. However, as \(\rho \) is accepting, there is an \(l\ge j\) such that \(q_l \in F\), which contradicts \(q_l \in S_l\) (contradiction). \(\square \)
Lemma 2
Let \(\mathcal {A}\) be an SDBA, \(\mathcal {C}\) be the automaton constructed by the NCSB complementation of \(\mathcal {A}\), \(w\notin L(\mathcal {A})\), and \((V,E)=\mathcal G_w\) be the run graph of \(\mathcal {A}\) on w. Then there is exactly one rational run of the form \(\rho = (N_0,C_0,S_0,B_0) (N_1,C_1,S_1,B_1) (N_2,C_2,S_2,B_2) \ldots \). This run is accepting.
Proof
It is easy to check that this defines exactly one infinite run: the updates of the N, C, and S components follow the rules for transitions from the definition of \(\mathcal {C}\), and the update of the B component is fully determined by the update of C and the previous value of B.
What remains is to show that the run is accepting. Let us assume for contradiction that there are only finitely many breakpoints reached, i.e. there is an index \(i \in \omega \), for which there is no \(j \ge i\), such that \(B_j = \emptyset \).
Now we have \(\emptyset \ne B_i \subseteq C_i = \{q \mid (q,i) \in V\) s.t.  and the rank of (q, i) is \(2\}\). The construction provides that, if there is no breakpoint on or after position i, then \(B_j\) is the set of states that correspond to vertices from \(Q\times \{j\}\) reachable in \({\mathcal G_w}^1\) from the vertices \(B_i \times \{i\}\). As there is no future breakpoint, there are infinitely many such vertices, and Königs lemma implies that there is an infinite path in \({\mathcal G_w}^1\) from at least one of the vertices in \(B_i \times \{i\}\). This provides a contradiction to the assumption that the rank of these vertices is 2, i.e. that they are finite in \({\mathcal G_w}^1\). \(\square \)
and the rank of (q, i) is \(2\}\). The construction provides that, if there is no breakpoint on or after position i, then \(B_j\) is the set of states that correspond to vertices from \(Q\times \{j\}\) reachable in \({\mathcal G_w}^1\) from the vertices \(B_i \times \{i\}\). As there is no future breakpoint, there are infinitely many such vertices, and Königs lemma implies that there is an infinite path in \({\mathcal G_w}^1\) from at least one of the vertices in \(B_i \times \{i\}\). This provides a contradiction to the assumption that the rank of these vertices is 2, i.e. that they are finite in \({\mathcal G_w}^1\). \(\square \)
Lemma 3
Let \(\mathcal {A}\) be an SDBA, \(\mathcal {C}\) be the automaton constructed by the NCSB complementation of \(\mathcal {A}\), \(w\notin L(\mathcal {A})\), and \((V,E)=\mathcal G_w\) be the run graph of \(\mathcal {A}\) on w. Let \(\rho = (N_0,C_0,S_0,B_0) (N_1,C_1,S_1,B_1) (N_2,C_2,S_2,B_2) \ldots \) be an infinite, non-rational run of \(\mathcal {C}\) over w that is, it does not satisfy
-
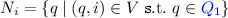 ,
, -
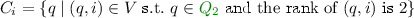 ,
, -
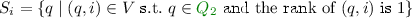 ,
,
for some i. Then \(\rho \) is rejecting.
Proof
As the N part always tracks the reachable states in  correctly by construction, and the \(C \cup S\) part always tracks the reachable states in
correctly by construction, and the \(C \cup S\) part always tracks the reachable states in  correctly by construction, we have one of the following two cases according to Proposition 2.
correctly by construction, we have one of the following two cases according to Proposition 2.
The first case is that there is a safe vertex \((q,i) \in V\) such that \(q \in C_i\). By construction, a unique maximal path \((q_i,i)(q_{i+1},i+1)(q_{i+2},i+2)(q_{i+3},i+3)\ldots \) for \(q_i = q\) exists in \(\mathcal G_w\), and this path does not contain any accepting state. By an inductive argument, for all vertices \((q_j,j)\) on this path, \(q_j \in C_j\). If the path is finite, \(\rho \) blocks at the end (due to the definition of the transition function of \(\mathcal {C}\)), which contradicts the assumption that the run \(\rho \) is infinite. Similarly, if the path is infinite, \(q_k\in B_k\) for some \(k \ge i\). Then \(q_j \in B_j\) for all \(j > k\) with \((q_j,j)\) on this path. Therefore, \(\rho \) cannot be accepting.
The second case is that there is a non-safe vertex in \((q,i) \in V\) such that \(q \in S_i\). (Note that this implies \(q \notin F\).) By construction, we get, for \(q_i = q\), a unique maximal path \((q_i,i)(q_{i+1},i+1)(q_{i+2},i+2)(q_{i+3},i+3)\ldots \) in \(\mathcal G_w\), and this path contains an accepting state \(q_k\). By an inductive argument, for all vertices \((q_j,j)\) on this path, \(q_j \in S_j\). But this implies \(q_k \in S_k\) (contradiction). \(\square \)
The first two lemmas provide the correctness of our complementation algorithm. Considering that no finite run is accepting, the third lemma establishes that \(\mathcal {C}\) is unambiguous.
Theorem 1
Let \(\mathcal {A}\) be an SDBA and \(\mathcal {C}\) be the automaton constructed by the NCSB complementation of \(\mathcal {A}\). Then \(\mathcal {C}\) is an unambiguous Büchi automaton that recognises the complement of the language of \(\mathcal {A}\).
5 Experimental Evaulation
This section compares the results of the NCSB complementation with these produced by well-known complementations for nondeterministic Büchi automata. All the automata, tools, scripts and commands used in the evaluation, and some further comparisons can be found at https://github.com/xblahoud/NCSB-Complementation.
5.1 Implementations of the NCSB Complementation
We implemented the NCSB complementation in two tools. One implementation is available in the Goal toolFootnote 3 [33]. Goal is a graphical interactive tool for omega automata, temporal logics, and games. It provides several Büchi complementation algorithms and was used in an extensive evaluation of these algorithms [32]. In the commandline version, the parameter for our construction is complement -m sdbw -a. The partition of the set Q into  and
and  is not a parameter, instead the implementation uses the set of all states that are reachable from some accepting state as
is not a parameter, instead the implementation uses the set of all states that are reachable from some accepting state as  .
.
Our second implementation is available in the Ultimate Automata Library. This library is used by the termination analyser Ultimate Büchi Automizer and other tools of the Ultimate program analysis frameworkFootnote 4. The implementation uses the on-the-fly construction discussed in Sect. 3.4. The library provides a language that allows users to define automata and a sequence of commands that should be executed by the library. This language is called automata script and an interpreter for this language is available via a web interfaceFootnote 5. The operation that implements the NCSB construction has the name buchiComplementNCSB.
5.2 Example Automata
For our evaluation, we took automata whose complementation was a subtask while the tool Ultimate Büchi Automizer was analysing the programs from the Termination category of the software verification competition SV-COMP 2015 [4]. We wrote each Büchi automaton that was semi-deterministic but not deterministic to a file in the Hanoi omega-automata format [2]. We obtained 106 semi-deterministic Büchi automata. Using the command autfilt –unique -H from the Spot library [10], we identified isomorphic automata and kept only the remaining 97 pairwise non-isomorphic ones.
By construction, all these automata behave deterministically only after the first visit of an accepting state. Hence the partition of the states Q into  and
and  is unique and the results of the construction presented in Sect. 3.2 and the results of the on-the-fly modification presented in Sect. 3.4 coincide.
is unique and the results of the construction presented in Sect. 3.2 and the results of the on-the-fly modification presented in Sect. 3.4 coincide.
5.3 Other Complementation Constructions
The known constructions for the complementation of nondeterministic Büchi automata can be classified into the following four categories.
-
Ramsey-based. Historically the first complementation construction introduced by Büchi [6] and later improved by Sistla, Vardi, and Wolper [31] in which a Ramsey-based combinatorial argument is involved.
-
Determinisation-based. A construction proposed by Safra [25] and later enhanced by Piterman [24] in which a state of a complement is represented by a Safra tree.
-
Rank-based. A construction introduced by Kupferman and Vardi [17] for which several optimisations [12, 13, 17, 27] have been proposed.
-
Slice-based. A construction [16] proposed by Kähler and Wilke that constructs complements accepting reduced split trees rather than run graphs.
For each of these categories, GOAL provides implementations that can be adjusted by various parameters. In our evaluation, we included one construction from each category. For the latter three categories, we took the arguments that were most successful in an extensive evaluation [32]. For the first category, we used additionally an optimisation that minimises the finite automata that are constructed during the complementation [5]. The commands that we used are listed in Table 1.
5.4 Evaluation
We applied the NCSB complementation and the four complementations of Table 1 to the 97 pairwise non-isomorphic SDBAs. All complementations were run on a laptop with an Intel Core i5 2.70 GHz CPU. We restricted the maximal heap space of the JVM to 8 GB (all complementations are implemented in Java) and used a timeout of 300 s. The results are depicted in Table 2 and Fig. 2.
For 91 out of 97 SDBAs, all implementations were able to compute a result. We refer to these 91 SDBAs as easy SDBAs, while the remaining six are referenced as difficult in the Table 2. For each complementation, we provide the cumulative numbers of states and transitions of all 91 easy complements. For each of the easy SDBAs, NCSB construction produces the complement with the smallest number of states. In Fig. 2, a size of the complement produced by the NCSB construction is compared to the size of the smallest complement produced by the constructions of Table 1 for each of the easy automata.
For the difficult SDBAs, at least one construction was not able to provide the result within the given time and memory limits. We provide the number of states of the computed complements for each of them. While there are two cases where the determinisation-based construction produced an automaton with less states than the NCSB construction, the number of transition was always smaller for the NCSB construction.
A common approach to mitigate the problem of large complementation results is to apply generic size reduction algorithm. Does our NCSB construction also outperform the other constructions if we apply size reduction techniques afterwards? In order to address this question, we applied the “simplification routines” of the Spot library [1] (in version 1.99.4a) to the complements. We run the command autfilt –small –high -B -H with a timeout of 300 s and obtained the results depicted in Table 3. For 75 SDBAs, all complements could be simplified within the timeout. For these we again provide the cumulative numbers of states and transitions before and after the simplifications. The column min shows how often each construction followed by simplification produced a complement with the minimal number of states. The column failure shows how often a timeout prevented a successful complementation or simplification. It is interesting to see that the simplifications were not able to reduce the number of transitions much for the NCSB construction, while they were able to reduce it by more than 20 % in case of the other complementations.
6 Conclusion
We have introduced an efficient complementation construction for semi-deterministic Büchi automata (SDBA). The results of our construction have two appealing properties: they are unambiguous and have less than \(4^n\) states. We have presented a modification of our construction suitable for implementation on-the-fly and showed that our construction can be seen as a specialised version of the rank-based construction for nondeterministic Büchi automata. We have implemented our construction in two tools and did an experimental evaluation on semi-deterministic Büchi automata produced by the termination analyser Ultimate Büchi Automizer. We have compared our construction to four known complementation constructions for (general) nondeterministic Büchi automata. The evaluation showed that our construction outperforms the existing constructions in the number of states and transitions.
Notes
- 1.
In model checking, one tests for emptiness the intersection of the automaton that recognises the runs of a system with the automaton that recognises the complement of the property language.
- 2.
It is common to use 0 as the minimal rank (i.e. to start with the finite vertices), but the correctness of the complementation does not rely on this. The proof in [17] refers to this case, and requires \(n+1\) steps. For our purpose, the minimal rank needs to be odd, i.e. we need to start with safe vertices.
- 3.
- 4.
- 5.
References
Babiak, T., Badie, T., Duret-Lutz, A., Křetínský, M., Strejček, J.: Compositional approach to suspension and other improvements to LTL translation. In: Bartocci, E., Ramakrishnan, C.R. (eds.) SPIN 2013. LNCS, vol. 7976, pp. 81–98. Springer, Heidelberg (2013)
Babiak, T., Blahoudek, F., Duret-Lutz, A., Klein, J., Křetínský, J., Müller, D., Parker, D., Strejček, J.: The Hanoi omega-automata format. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 479–486. Springer, Heidelberg (2015)
Benedikt, M., Lenhardt, R., Worrell, J.: LTL model checking of interval Markov chains. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013 (ETAPS 2013). LNCS, vol. 7795, pp. 32–46. Springer, Heidelberg (2013)
Beyer, D.: Software verification and verifiable witnesses. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 401–416. Springer, Heidelberg (2015)
Breuers, S., Löding, C., Olschewski, J.: Improved Ramsey-based Büchi complementation. In: Birkedal, L. (ed.) FOSSACS 2012. LNCS, vol. 7213, pp. 150–164. Springer, Heidelberg (2012)
Büchi, J.R.: On a decision method in restricted second order arithmetic. In: CLMpPS 1960, pp. 1–11. Stanford University Press (1962)
Bustan, D., Rubin, S., Vardi, M.Y.: Verifying \(\omega \)-regular properties of Markov chains. In: Alur, R., Peled, D.A. (eds.) CAV 2004. LNCS, vol. 3114, pp. 189–201. Springer, Heidelberg (2004)
Courcoubetis, C., Yannakakis, M.: The complexity of probabilistic verification. J. ACM 42(4), 857–907 (1995)
Dietsch, D., Heizmann, M., Langenfeld, V., Podelski, A.: Fairness modulo theory: a new approach to LTL software model checking. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 49–66. Springer, Heidelberg (2015)
Duret-Lutz, A., Poitrenaud, D., SPOT: An extensible model checking library using transition-based generalized Büchi automata. In: MASCOTS 2004, pp. 76–83. IEEE Computer Society (2004)
Fogarty, S., Kupferman, O., Wilke, T., Vardi, M.Y.: Unifying Büchi complementation constructions. Logical Methods Comput. Sci. 9(1), 1–25 (2013)
Friedgut, E., Kupferman, O., Vardi, M.Y.: Büchi complementation made tighter. Int. J. Found. Comput. Sci. 17(4), 851–868 (2006)
Gurumurthy, S., Kupferman, O., Somenzi, F., Vardi, M.Y.: On complementing nondeterministic Büchi automata. In: Geist, D., Tronci, E. (eds.) CHARME 2003. LNCS, vol. 2860, pp. 96–110. Springer, Heidelberg (2003)
Hahn, E.M., Li, G., Schewe, S., Turrini, A., Zhang, L.: Lazy probabilistic model checking without determinisation. In: CONCUR 2015. LIPIcs, vol. 42, pp. 354–367. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2015)
Heizmann, M., Hoenicke, J., Podelski, A.: Termination analysis by learning terminating programs. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 797–813. Springer, Heidelberg (2014)
Kähler, D., Wilke, T.: Complementation, disambiguation, and determinization of Büchi automata unified. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008, Part I. LNCS, vol. 5125, pp. 724–735. Springer, Heidelberg (2008)
Kupferman, O., Vardi, M.Y.: Weak alternating automata are not that weak. ACM Trans. Comput. Logic 2(2), 408–429 (2001)
Kurshan, R.P.: Computer-Aided Verification of Coordinating Processes: The Automata-Theoretic Approach. Princeton University Press, Princeton (1994)
McNaughton, R.: Testing and generating infinite sequences by a finite automaton. Inf. Control 9(5), 521–530 (1966)
Michel, M.: Complementation is more difficult with automata on infinite words. Technical report, CNET, Paris (Manuscript) (1988)
Miyano, S., Hayashi, T.: Alternating finite automata on \(\omega \)-words. Theor. Comput. Sci. 32(3), 321–330 (1984)
Muller, D.E.: Infinite sequences and finite machines. In: FOCS 1963, pp. 3–16. IEEE Computer Society Press (1963)
Pécuchet, J.-P.: On the complementation of Büchi automata. Theor. Comput. Sci. 47(3), 95–98 (1986)
Piterman, N.: From nondeterministic Büchi and Streett automata to deterministic parity automata. Logical Methods Comput. Sci. 3(3:5) (2007)
Safra, S.: On the complexity of omega-automata. In: FOCS 1988, pp. 319–327. IEEE Computer Society (1988)
Sakoda, W.J., Sipser, M.: Non-determinism and the size of two-way automata. In STOC 1978, pp. 274–286. ACM Press (1978)
Schewe, S.: Büchi complementation made tight. In: STACS 2009. LIPIcs, vol. 3, pp. 661–672. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2009)
Schewe, S.: Tighter bounds for the determinisation of Büchi automata. In: de Alfaro, L. (ed.) FOSSACS 2009. LNCS, vol. 5504, pp. 167–181. Springer, Heidelberg (2009)
Schewe, S., Varghese, T.: Tight bounds for the determinisation and complementation of generalised Büchi automata. In: Chakraborty, S., Mukund, M. (eds.) ATVA 2012. LNCS, vol. 7561, pp. 42–56. Springer, Heidelberg (2012)
Schewe, S., Varghese, T.: Tight bounds for complementing parity automata. In: Csuhaj-Varjú, E., Dietzfelbinger, M., Ésik, Z. (eds.) MFCS 2014, Part I. LNCS, vol. 8634, pp. 499–510. Springer, Heidelberg (2014)
Sistla, A.P., Vardi, M.Y., Wolper, P.: The complementation problem for Büchi automata with applications to temporal logic. Theor. Comput. Sci. 49(3), 217–239 (1987)
Tsai, M.-H., Fogarty, S., Vardi, M.Y., Tsay, Y.: State of Büchi complementation. Logical Methods Comput. Sci. 10(4:13) (2014)
Tsai, M.-H., Tsay, Y.-K., Hwang, Y.-S.: GOAL for Games, omega-automata, and logics. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 883–889. Springer, Heidelberg (2013)
Vardi, M.Y.: Automatic verification of probabilistic concurrent finite-state programs. In: FOCS 1985, pp. 327–338. IEEE Computer Society (1985)
Vardi, M.Y.: The Büchi complementation saga. In: Thomas, W., Weil, P. (eds.) STACS 2007. LNCS, vol. 4393, pp. 12–22. Springer, Heidelberg (2007)
Vardi, M.Y., Wolper, P.: An automata-theoretic approach to automatic program verification (preliminary report). In: LICS 1986, pp. 332–344. IEEE Computer Society (1986)
Yan, Q., Lower bounds for complementation of omega-automata via the full automata technique. Logical Methods Comput. Sci. 4(1: 5), 1–20 (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Blahoudek, F., Heizmann, M., Schewe, S., Strejček, J., Tsai, MH. (2016). Complementing Semi-deterministic Büchi Automata. In: Chechik, M., Raskin, JF. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2016. Lecture Notes in Computer Science(), vol 9636. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49674-9_49
Download citation
DOI: https://doi.org/10.1007/978-3-662-49674-9_49
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49673-2
Online ISBN: 978-3-662-49674-9
eBook Packages: Computer ScienceComputer Science (R0)






 is deterministic, accepting states are only in
is deterministic, accepting states are only in  , and
, and  lead from
lead from  to
to  .
.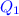 ,
,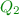 and stops visiting F at some point, or
and stops visiting F at some point, or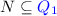 represents the runs that kept out of the deterministic part (N stands for nondeterministic) so far.
represents the runs that kept out of the deterministic part (N stands for nondeterministic) so far.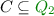 represents the runs that have entered the deterministic part and that are not safe. One has to check (hence the name C) if some of them will be prolonged into accepting runs in the future, or if all of the runs eventually block or become safe.
represents the runs that have entered the deterministic part and that are not safe. One has to check (hence the name C) if some of them will be prolonged into accepting runs in the future, or if all of the runs eventually block or become safe.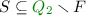 represents the safe runs.
represents the safe runs.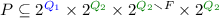 .
.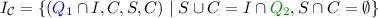 .
.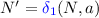 ,
, 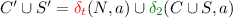 (intuition: tracing the reachable states correctly),
(intuition: tracing the reachable states correctly),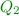 is either safe, or not),
is either safe, or not),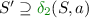 (intuition: safe runs must stay safe),
(intuition: safe runs must stay safe), (intuition: only runs leaving an accepting state can become safe),
(intuition: only runs leaving an accepting state can become safe),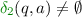 (intuition: otherwise the corresponding run was safe already and should have been moved to S earlier), and
(intuition: otherwise the corresponding run was safe already and should have been moved to S earlier), and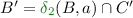 (intuition: breakpoint construction to check that no run stays in C forever).
(intuition: breakpoint construction to check that no run stays in C forever).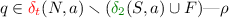 is freshly entering
is freshly entering 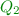 , and when
, and when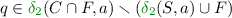 —
—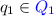 of
of 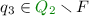 , one of the following four options holds:
, one of the following four options holds: 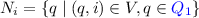 ,
,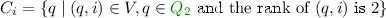 (we need to check that these states are finite in
(we need to check that these states are finite in 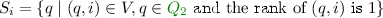 ,
,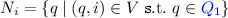 ,
,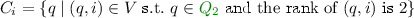 ,
,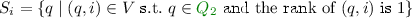 ,
,
