Weakest Precondition Reasoning for Expected Run–Times of Probabilistic Programs

Abstract

This paper presents a wp–style calculus for obtaining bounds on the expected run–time of probabilistic programs. Its application includes determining the (possibly infinite) expected termination time of a probabilistic program and proving positive almost–sure termination—does a program terminate with probability one in finite expected time? We provide several proof rules for bounding the run–time of loops, and prove the soundness of the approach with respect to a simple operational model. We show that our approach is a conservative extension of Nielson’s approach for reasoning about the run–time of deterministic programs. We analyze the expected run–time of some example programs including a one–dimensional random walk and the coupon collector problem.

This work was supported by the Excellence Initiative of the German federal and state government.

1 Introduction

Since the early days of computing, randomization has been an important tool for the construction of algorithms. It is typically used to convert a deterministic program with bad worst–case behavior into an efficient randomized algorithm that yields a correct output with high probability. The Rabin–Miller primality test, Freivalds’ matrix multiplication, and the random pivot selection in Hoare’s quicksort algorithm are prime examples. Randomized algorithms are conveniently described by probabilistic programs. On top of the usual language constructs, probabilistic programming languages offer the possibility of sampling values from a probability distribution. Sampling can be used in assignments as well as in Boolean guards.

The interest in probabilistic programs has recently been rapidly growing. This is mainly due to their wide applicability [10]. Probabilistic programs are for instance used in security to describe cryptographic constructions and security experiments. In machine learning they are used to describe distribution functions that are analyzed using Bayesian inference. The sample program

for instance flips a fair coin until observing the first heads (i.e. 0). It describes a geometric distribution with parameter .

The run–time of probabilistic programs is affected by the outcome of their coin tosses. Technically speaking, the run–time is a random variable, i.e.  it is $t_1$ with probability $p_1$, $t_2$ with probability $p_2$ and so on. An important measure that we consider over probabilistic programs is then their average or expected run–time (over all inputs). Reasoning about the expected run–time of probabilistic programs is surprisingly subtle and full of nuances. In classical sequential programs, a single diverging program run yields the program to have an infinite run–time. This is not true for probabilistic programs. They may admit arbitrarily long runs while having a finite expected run–time. The program $C_{geo}$, for instance, does admit arbitrarily long runs as for any n, the probability of not seeing a heads in the first n trials is always positive. The expected run–time of $C_{geo}$ is, however, finite.

In the classical setting, programs with finite run–times can be sequentially composed yielding a new program again with finite run–time. For probabilistic programs this does not hold in general. Consider the pair of programs

The loop in $C_1$ terminates on average in two iterations; it thus has a finite expected run–time. From any initial state in which x is non–negative, $C_2$ makes x iterations, and thus its expected run–time is finite, too. However, the program $C_1 ; C_2$ has an infinite expected run–time—even though it almost–surely terminates, i.e. it terminates with probability one. Other subtleties can occur as program run–times are very sensitive to variations in the probabilities occurring in the program.

Bounds on the expected run–time of randomized algorithms are typically obtained using a detailed analysis exploiting classical probability theory (on expectations or martingales) [9, 22]. This paper presents an alternative approach, based on formal program development and verification techniques. We propose a wp–style calculus à la Dijkstra for obtaining bounds on the expected run–time of probabilistic programs. The core of our calculus is the transformer $\textsf {ert}$, a quantitative variant of Dijkstra’s wp–transformer. For a program C, $\textsf {ert} \left[ {C}\right] \left( {f}\right) (\sigma )$ gives the expected run–time of C started in initial state $\sigma$ under the assumption that f captures the run–time of the computation following C. In particular, $\textsf {ert} \left[ {C}\right] \left( {\mathbf {0}}\right) (\sigma )$ gives the expected run–time of program $C$ on input $\sigma$ (where $\mathbf {0}$ is the constantly zero run–time). Transformer $\textsf {ert}$ is defined inductively on the program structure. We prove that our transformer conservatively extends Nielson’s approach [23] for reasoning about the run–time of deterministic programs. In addition we show that $\textsf {ert} \left[ {C}\right] \left( {f}\right) (\sigma )$ corresponds to the expected run–time in a simple operational model for our probabilistic programs based on Markov Decision Processes (MDPs). The main contribution is a set of proof rules for obtaining (upper and lower) bounds on the expected run–time of loops. We apply our approach for analyzing the expected run–time of some example programs including a one–dimensional random walk and the coupon collector problem [20].

We finally point out that our technique enables determining the (possibly infinite) expected time until termination of a probabilistic program and proving (universal) positive almost–sure termination—does a program terminate with probability one in finite expected time (on all inputs)? It has been recently shown [16] that the universal positive almost–sure termination problem is $\varPi ^0_3$–complete, and thus strictly harder to solve than the universal halting problem for deterministic programs. To the best of our knowledge, the formal verification framework in this paper is the first one that is proved sound and can handle both positive almost–sure termination and infinite expected run–times.

Related work. Several works apply wp–style– or Floyd–Hoare–style reasoning to study quantitative aspects of classical programs. Nielson [23, 24] provides a Hoare logic for determining upper bounds on the run–time of deterministic programs. Our approach applied to such programs yields the tightest upper bound on the run–time that can be derived using Nielson’s approach. Arthan et al. [1] provide a general framework for sound and complete Hoare–style logics, and show that an instance of their theory can be used to obtain upper bounds on the run–time of while programs. Hickey and Cohen [13] automate the average–case analysis of deterministic programs by generating a system of recurrence equations derived from a program whose efficiency is to be analyzed. They build on top of Kozen’s seminal work [18] on semantics of probabilistic programs. Berghammer and Müller–Olm [3] show how Hoare–style reasoning can be extended to obtain bounds on the closeness of results obtained using approximate algorithms to the optimal solution. Deriving space and time consumption of deterministic programs has also been considered by Hehner [11]. Formal reasoning about probabilistic programs goes back to Kozen [18], and has been developed further by Hehner [12] and McIver and Morgan [19]. The work by Celiku and McIver [5] is perhaps the closest to our paper. They provide a wp–calculus for obtaining performance properties of probabilistic programs, including upper bounds on expected run–times. Their focus is on refinement. They do neither provide a soundness result of their approach nor consider lower bounds. We believe that our transformer is simpler to work with in practice, too. Monniaux [21] exploits abstract interpretation to automatically prove the probabilistic termination of programs using exponential bounds on the tail of the distribution. His analysis can be used to prove the soundness of experimental statistical methods to determine the average run–time of probabilistic programs. Brazdil et al. [4] study the run–time of probabilistic programs with unbounded recursion by considering probabilistic pushdown automata (pPDAs). They show (using martingale theory) that for every pPDA the probability of performing a long run decreases exponentially (polynomially) in the length of the run, iff the pPDA has a finite (infinite) expected runtime. As opposed to our program verification technique, [4] considers reasoning at the operational level. Fioriti and Hermanns [8] recently proposed a typing scheme for deciding almost-sure termination. They showed, amongst others, that if a program is well-typed, then it almost surely terminates. This result does not cover positive almost-sure-termination.

Organization of the paper. Section 2 defines our probabilistic programming language. Section 3 presents the transformer $\textsf {ert}$ and studies its elementary properties such as continuity. Section 4 shows that the $\textsf {ert}$ transformer coincides with the expected run–time in an MDP that acts as operational model of our programs. Section 5 presents two sets of proof rules for obtaining upper and lower bounds on the expected run–time of loops. In Sect. 6, we show that the $\textsf {ert}$ transformer is a conservative extension of Nielson’s approach for obtaining upper bounds on deterministic programs. Section 7 discusses two case studies in detail. Section 8 concludes the paper.

The proofs of the main facts are included in the body of the paper. The remaining proofs and the calculations omitted in Sect. 7 are included in an extended version of the paper [17].

2 A Probabilistic Programming Language

In this section we present the probabilistic programming language used throughout this paper, together with its run–time model. To model probabilistic programs we employ a standard imperative language à la Dijkstra’s Guarded Command Language [7] with two distinguished features: we allow distribution expressions in assignments and guards to be probabilistic. For instance, we allow for probabilistic assignments like

$$ y \mathrel { \texttt {:} {\approx }} \mathtt {Unif}[1 \ldots x] $$

which endows variable y with a uniform distribution in the interval $[1\ldots x]$. We allow also for a program like

$$ x \mathrel { \texttt {:=} }0; \; \texttt {while} \, \big (p \cdot \! \langle \mathsf {true} \rangle + (1{-}p) \!\,\cdot \! \langle \mathsf {false} \rangle \big ) \, \{x \mathrel { \texttt {:=} }x+1 \} $$

which uses a probabilistic loop guard to simulate a geometric distribution with success probability p, i.e. the loop guard evaluates to $\mathsf {true}$ with probability p and to $\mathsf {false}$ with the remaining probability $1{-}p$.

Formally, the set of probabilistic programs pProgs is given by the grammar

$$ \begin{array}{rc@{~~}l@{\qquad }l} C ~::=~ &{} &{} \texttt {empty} &{} \text{ empty } \text{ program }\\ &{}\mid &{} \texttt {skip} &{} \text{ effectless } \text{ operation }\\ &{}\mid &{} \texttt {halt} &{} \text{ immediate } \text{ termination }\\ &{}\mid &{} x \mathrel { \texttt {:} {\approx }} \mu &{} \text{ probabilistic } \text{ assignment }\\ &{}\mid &{} C \texttt {;} \, C &{} \text{ sequential } \text{ composition }\\ &{}\mid &{} \left\{ {C}\right\} \mathrel {\Box }\left\{ {C}\right\} &{} \text{ non }\!\!-\!\!\text{ deterministic } \text{ choice }\\ &{}\mid &{} \texttt {if} \,(\xi )\,\{C \}\, \texttt {else} \,\{C \} &{} \text{ probabilistic } \text{ conditional }\\ &{}\mid &{} \texttt {while} \,(\xi )\,\{C \} &{} \text{ probabilistic } \text{ while } \text{ loop } \end{array} $$

Here x represents a program variable in $\mathsf {Var}$, $\mu$ a distribution expression in $\mathsf {DExp}$, and $\xi$ a distribution expression over the truth values, i.e.  a probabilistic guard, in $\mathsf {DExp}$. We assume distribution expressions in $\mathsf {DExp}$ to represent discrete probability distributions with a (possibly infinite) support of total probability mass 1. We use $p_1 \cdot \langle a_1 \rangle + \cdots + p_n \cdot \langle a_n \rangle$ to denote the distribution expression that assigns probability $p_i$ to $a_i$. For instance, the distribution expression represents the toss of a fair coin. Deterministic expressions over program variables such as $x-y$ or $x - y > 8$ are special instances of distribution expressions—they are understood as Dirac probability distributions¹.

To describe the different language constructs we first present some preliminaries. A program state $\sigma$ is a mapping from program variables to values in $\mathsf {Val}$. Let $\varSigma \triangleq \{\sigma \mid \sigma :\mathsf {Var} \rightarrow \mathsf {Val} \}$ be the set of program states. We assume an interpretation function $\llbracket {\,\cdot \,} \rrbracket :\mathsf {DExp} \rightarrow (\varSigma \rightarrow \mathcal {D}(\mathsf {Val}))$ for distribution expressions, $\mathcal {D}(\mathsf {Val})$ being the set of discrete probability distributions over $\mathsf {Val}$. For $\mu \in \mathsf {DExp}$, $\llbracket {\mu } \rrbracket$ maps each program state to a probability distribution of values. We use $\llbracket {\mu }\!:{v} \rrbracket$ as a shorthand for the function mapping each program state $\sigma$ to the probability that distribution $\llbracket {\mu } \rrbracket (\sigma )$ assigns to value v, i.e.  $\llbracket {\mu }\!:{v} \rrbracket (\sigma ) \triangleq \mathsf {Pr}_{\llbracket {\mu } \rrbracket (\sigma )}(v)$, where $\mathsf {Pr}$ denotes the probability operator on distributions over values.

We now present the effects of $\textsf {pProgs}$ programs and the run–time model that we adopt for them. $\texttt {empty}$ has no effect and its execution consumes no time. $\texttt {skip}$ has also no effect but consumes, in contrast to $\texttt {empty}$, one unit of time. $\texttt {halt}$ aborts any further program execution and consumes no time. $x \mathrel { \texttt {:} {\approx }} \mu$ is a probabilistic assignment that samples a value from $\llbracket {\mu } \rrbracket$ and assigns it to variable x; the sampling and assignment consume (altogether) one unit of time. $C_1 \texttt {;} \, C_2$ is the sequential composition of programs $C_1$ and $C_2$. $\left\{ {C_1}\right\} \mathrel {\Box }\left\{ {C_2}\right\}$ is a non–deterministic choice between programs $C_1$ and $C_2$; we take a demonic view where we assume that out of $C_1$ and $C_2$ we execute the program with the greatest run–time. $\texttt {if} \,(\xi )\,\{C_1\}\, \texttt {else} \,\{C_2\}$ is a probabilistic conditional branching: with probability $\llbracket {\xi }\!:{\mathsf {true}} \rrbracket$ program $C_1$ is executed, whereas with probability $\llbracket {\xi }\!:{\mathsf {false}} \rrbracket = 1{-}\llbracket {\xi }\!:{\mathsf {true}} \rrbracket$ program $C_2$ is executed; evaluating (or more rigorously, sampling a value from) the probabilistic guard requires an additional unit of time. $\texttt {while} \,(\xi )\,\{C\}$ is a probabilistic while loop: with probability $\llbracket {\xi }\!:{\mathsf {true}} \rrbracket$ the loop body C is executed followed by a recursive execution of the loop, whereas with probability $\llbracket {\xi }\!:{\mathsf {false}} \rrbracket$ the loop terminates; as for conditionals, each evaluation of the guard consumes one unit of time.

Example 1

(Race between tortoise and hare). The probabilistic program

adopted from [6], illustrates the use of the programming language. It models a race between a hare and a tortoise (variables h and t represent their respective positions). The tortoise starts with a lead of 30 and in each step advances one step forward. The hare with probability advances a random number of steps between 0 and 10 (governed by a uniform distribution) and with the remaining probability remains still. The race ends when the hare passes the tortoise. $\triangle$

We conclude this section by fixing some notational conventions. To keep our program notation consistent with standard usage, we use the standard symbol $\mathrel { \texttt {:=} }$ instead of $\mathrel { \texttt {:} {\approx }}$ for assignments whenever $\mu$ represents a Dirac distribution given by a deterministic expressions over program variables. For instance, in the program in Example 1 we write $t \mathrel { \texttt {:=} }t+1$ instead of $t \mathrel { \texttt {:} {\approx }} t+1$. Likewise, when $\xi$ is a probabilistic guard given as a deterministic Boolean expression over program variables, we use $\llbracket {\xi } \rrbracket$ to denote $\llbracket {\xi }\!:{\mathsf {true}} \rrbracket$ and $\llbracket {\lnot \xi } \rrbracket$ to denote $\llbracket {\xi }\!:{\mathsf {false}} \rrbracket$. For instance, we write $\llbracket {b=0} \rrbracket$ instead of $\llbracket {b=0}\!:{\mathsf {true}} \rrbracket$.

3 A Calculus of Expected Run–Times

Our goal is to associate to any program $C$ a function that maps each state $\sigma$ to the average or expected run–time of $C$ started in initial state $\sigma$. We use the functional space of run–times

to model such functions. Here, $\mathbb {R}_{{}\ge 0}^{\infty }$ represents the set of non–negative real values extended with $\infty$. We consider run–times as a mapping from program states to real numbers (or $\infty$) as the expected run–time of a program may depend on the initial program state.

We express the run–time of programs using a continuation–passing style by means of the transformer

$$ \textsf {ert} [\,\cdot \,]\!:\mathsf{{pProgs}} \rightarrow (\mathbb {T}\rightarrow \mathbb {T}). $$

Concretely, $\textsf {ert} \left[ {C}\right] \left( {f}\right) (\sigma )$ gives the expected run–time of program $C$ from state $\sigma$ assuming that f captures the run–time of the computation that follows $C$. Function f is usually referred to as continuation and can be thought of as being evaluated in the final states that are reached upon termination of C. Observe that, in particular, if we set f to the constantly zero run–time, $\textsf {ert} \left[ {C}\right] \left( {\mathbf {0}}\right) (\sigma )$ gives the expected run–time of program $C$ on input $\sigma$.

The transformer $\textsf {ert}$ is defined by induction on the structure of $C$ following the rules in Table 1. The rules are defined so as to correspond to the run–time model introduced in Sect. 2. That is, $\textsf {ert} \left[ {C}\right] \left( {\mathbf {0}}\right)$ captures the expected number of assignments, guard evaluations and $\texttt {skip}$ statements. Most rules in Table 1 are self–explanatory. $\textsf {ert} [ \texttt {empty} ]$ behaves as the identity since $\texttt {empty}$ does not modify the program state and its execution consumes no time. On the other hand, $\textsf {ert} [ \texttt {skip} ]$ adds one unit of time since this is the time required by the execution of $\texttt {skip}$. $\textsf {ert} [ \texttt {halt} ]$ yields always the constant run–time $\mathbf {0}$ since $\texttt {halt}$ aborts any subsequent program execution (making their run–time irrelevant) and consumes no time. The definition of $\textsf {ert}$ on random assignments is more involved: $\textsf {ert} \left[ {x \mathrel { \texttt {:} {\approx }} \mu }\right] \left( {f}\right) (\sigma ) = 1\,+\,\sum _{v} \textsf {Pr}_{\llbracket \mu \rrbracket (\sigma ) }(v) \cdot f(\sigma \left[ {x}/{v}\right] )$ is obtained by adding one unit of time (due to the distribution sampling and assignment of the value sampled) to the sum of the run–time of each possible subsequent execution, weighted according to their probabilities. $\textsf {ert} [C_1 \texttt {;} \, C_2]$ applies $\textsf {ert} [C_1]$ to the expected run–time obtained from the application of $\textsf {ert} [C_2]$. $\textsf {ert} [\left\{ {C_1}\right\} \mathrel {\Box }\left\{ {C_2}\right\} ]$ returns the maximum between the run–time of the two branches. $\textsf {ert} [ \texttt {if} \,(\xi )\,\{C_1\}\, \texttt {else} \,\{C_2\}]$ adds one unit of time (on account of the guard evaluation) to the weighted sum of the run–time of the two branches. Lastly, the $\textsf {ert}$ of loops is given as the least fixed point of a run–time transformer defined in terms of the run–time of the loop body.

Table 1. Rules for defining the expected run–time transformer $\textsf {ert}$. $\varvec{1}$ is the constant run–time $\lambda \sigma . 1$. ${\textsf {E}}_{\eta }\left( {h}\right) \triangleq \sum _{v} \textsf {Pr}_{\eta }(v) \cdot h(v)$ represents the expected value of (random variable) h w.r.t. distribution $\eta$. For $\sigma \in \varSigma$, $f\left[ {x}/{v}\right] (\sigma ) \triangleq f(\sigma \left[ {x}/{v}\right] )$, where $\sigma \left[ {x}/{v}\right]$ is the state obtained by updating in $\sigma$ the value of x to v. $\max \{f_1, f_2\} \triangleq \lambda \sigma .\max \{f_1(\sigma ), f_2(\sigma )\}$ represents the point–wise lifting of the $\max$ operator over $\mathbb {R}_{{}\ge 0}^{\infty }$ to the function space of run–times. represents the least fixed point of the transformer $F\!:\mathbb {T}\rightarrow \mathbb {T}$.

Remark. We stress that the above run–time model is a design decision for the sake of concreteness. All our developments can easily be adapted to capture alternative models. These include, for instance, the model where only the number of assignments in a program run or the model where only the number of loop iterations are of relevance. We can also capture more fine–grained models, where for instance the run–time of an assignment depends on the size of the distribution expression being sampled.

Example 2

(Truncated geometric distribution). To illustrate the effects of the $\textsf {ert}$ transformer consider the program in Fig. 1. It can be viewed as modeling a truncated geometric distribution: we repeatedly flip a fair coin until observing the first heads or completing the second unsuccessful trial. The calculation of the expected run–time $\textsf {ert} \left[ {C _{trunc}}\right] \left( {\mathbf {0}}\right)$ of program $C_{trunc}$ goes as follows:

$$\begin{aligned}&\textsf {ert} \left[ {C _{trunc}}\right] \left( {\mathbf {0}}\right) \\&~\quad =~ \mathbf {1} + \tfrac{1}{2} \cdot \textsf {ert} \left[ {{succ} \mathrel { \texttt {:=} }\mathsf {true}}\right] \left( {\mathbf {0}}\right) \\&\qquad \quad ~ \!+ \tfrac{1}{2} \cdot \textsf {ert} \left[ { \texttt {if} \,(\ldots )\,\{{succ\!} \mathrel { \texttt {:=} }\!\mathsf {true} \}\, \texttt {else} \,\{{succ\!} \mathrel { \texttt {:=} }\!\mathsf {false} \}}\right] \left( {\mathbf {0}}\right) \\&~\quad =~ \mathbf {1} + \tfrac{1}{2} \cdot \mathbf {1} + \tfrac{1}{2} \cdot \Bigl (\mathbf {1} + \tfrac{1}{2} \cdot \textsf {ert} \left[ {{succ} \mathrel { \texttt {:=} }\mathsf {true}}\right] \left( {\mathbf {0}}\right) + \tfrac{1}{2} \cdot \textsf {ert} \left[ {{succ} \mathrel { \texttt {:=} }\mathsf {false}}\right] \left( {\mathbf {0}}\right) \Bigr ) \\&~\quad =~ \mathbf {1} + \tfrac{1}{2} \cdot \mathbf {1} + \tfrac{1}{2} \cdot \Bigl (\mathbf {1} + \tfrac{1}{2} \cdot \mathbf {1} + \tfrac{1}{2} \cdot \mathbf {1} \Bigr ) ~=~ \mathbf {\tfrac{5}{2}} \end{aligned}$$

Therefore, the execution of $C _{trunc}$ takes, on average, 2.5 units of time.    $\triangle$

Fig. 1.

Program modeling a truncated geometric distribution

Note that the calculation of the expected run–time in the above example is straightforward as the program at hand is loop–free. Computing the run–time of loops requires the calculation of least fixed points, which is generally not feasible in practice. In Sect. 5, we present invariant–based proof rules for reasoning about the run–time of loops.

The $\textsf {ert}$ transformer enjoys several algebraic properties. To formally state these properties we make use of the point–wise order relation “$\preceq$” between run–times: given $f,g \in \mathbb {T}$, $f \preceq g$ iff $f(\sigma ) \le g(\sigma )$ for all states $\sigma \in \varSigma$.

Theorem 1

(Basic properties of the ert transformer). For any program $C \in \mathsf{{pProgs}}$, any constant run–time $\mathbf {k} = \lambda \sigma . k$ for $k \in \mathbb {R}_{{}\ge 0}$, any constant $r \in \mathbb {R}_{{}\ge 0}$, and any two run–times $f, g \in \mathbb {T}$ the following properties hold:

$$\begin{aligned} \begin{array}{l@{}l} Monotonicity\!: &{} f \preceq g ~\implies ~ \textsf {ert} \left[ {C}\right] \left( {f}\right) \,\preceq \, \textsf {ert} \left[ {C}\right] \left( {g}\right) ;\\[1ex] Propagation \; of \; &{} \textsf {ert} \left[ {C}\right] \left( {\mathbf {k} + f}\right) \,=\, \mathbf {k} + \textsf {ert} \left[ {C}\right] \left( {f}\right) \\ constants\!: &{} provided \; C \; is \; \texttt {halt} \!\!-\!\!free;\\[1ex] Preservation \; of \; \varvec{\infty }: &{} \textsf {ert} \left[ {C}\right] \left( {\infty }\right) \,=\, \infty \\ &{} provided \; C \; is \; \texttt {halt} \!\!-\!\!free;\\[1ex] Sub\!-\!additivity\!: &{} \textsf {ert} \left[ {C}\right] \left( {f + g}\right) \,\preceq \, \textsf {ert} \left[ {C}\right] \left( {f}\right) + \textsf {ert} \left[ {C}\right] \left( {g}\right) ;\\ &{} provided \; C \; is \; fully \; probabilistic;^2\\[1ex] Scaling\!: &{} \textsf {ert} \left[ {C}\right] \left( {r \cdot f}\right) \,\succeq \, \min \{1,\, r\} \cdot \textsf {ert} \left[ {C}\right] \left( {f}\right) ;\\ &{} \textsf {ert} \left[ {C}\right] \left( {r \cdot f}\right) \,\preceq \, \max \{1,\, r\} \cdot \textsf {ert} \left[ {C}\right] \left( {f}\right) . \end{array} \end{aligned}$$

$^{2}$A program is called fully probabilistic if it contains no non–deterministic choices.

Proof

Monotonicity follows from continuity (see Lemma 1 below). The remaining proofs proceed by induction on the program structure; see [17] for details.   $\square$

We conclude this section with a technical remark regarding the well–definedness of the $\textsf {ert}$ transformer. To guarantee that $\textsf {ert}$ is well–defined, we must show the existence of the least fixed points used to define the run–time of loops. To this end, we use a standard denotational semantics argument (see e.g.  [26, Chap. 5]): First we endow the set of run–times $\mathbb {T}$ with the structure of an $\omega$–complete partial order ($\omega$–cpo) with bottom element. Then we use a continuity argument to conclude the existence of such fixed points.

Recall that $\preceq$ denotes the point–wise comparison between run–times. It easily follows that $(\mathbb {T}, {\preceq })$ defines an $\omega$–cpo with bottom element $\varvec{0}= \lambda \sigma . 0$ where the supremum of an $\omega$–chain $f_1 \preceq f_2 \preceq \cdots$ in $\mathbb {T}$ is also given point–wise, i.e.  as $\sup \nolimits _{n}f_n \triangleq \lambda \sigma . \, \sup \nolimits _{n}f_n(\sigma )$. Now we are in a position to establish the continuity of the $\textsf {ert}$ transformer:

Lemma 1

(Continuity of the ert transformer). For every program $C$ and every $\omega$–chain of run–times $f_1 \preceq f_2 \preceq \cdots$,

$$ \textsf {ert} \left[ {C}\right] \left( {\sup \nolimits _{n}f_n}\right) ~=~ \sup \nolimits _{n} \textsf {ert} \left[ {C}\right] \left( {f_n}\right) . $$

Proof

By induction on the program structure; see [17] for details.    $\square$

Lemma 1 implies that for each program $C \in \textsf {pProgs}$, guard $\xi \in \mathsf {DExp}$, and run–time $f \in \mathbb {T}$, function $F_f(X) = \mathbf {1} + \llbracket {\xi }\!:{\mathsf {false}} \rrbracket \cdot f + \llbracket {\xi }\!:{\mathsf {true}} \rrbracket \cdot \textsf {ert} \left[ {C}\right] \left( {X}\right)$ is also continuous. The Kleene Fixed Point Theorem then ensures that the least fixed point $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) = \textsf {lfp} \,F_f$ exists and the expected run–time of loops is thus well-defined.

Finally, as the aforementioned function $F_f$ is frequently used in the remainder of the paper, we define:

Definition 1

(Characteristic functional of a loop). Given program $C \in \textsf {pProgs}$, probabilistic guard $\xi \in \mathsf {DExp}$, and run–time $f \in \mathbb {T}$, we call

$$ F_f^{\langle \xi , C \rangle }\!:\mathbb {T}\rightarrow \mathbb {T},~ X \mapsto \mathbf {1} + \llbracket {\xi }\!:{\mathsf {false}} \rrbracket \cdot f + \llbracket {\xi }\!:{\mathsf {true}} \rrbracket \cdot \textsf {ert} \left[ {C}\right] \left( {X}\right) $$

the characteristic functional of loop $\texttt {while} \,(\xi )\,\{C\}$ with respect to f.

When C and $\xi$ are understood from the context, we usually omit them and simply write $F_f$ for the characteristic functional associated to $\texttt {while} \,(\xi )\,\{C\}$ with respect to run–time f. Observe that under this definition, the $\textsf {ert}$ of loops can be recast as

$$ \textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) ~=~ \textsf {lfp} \,F_f^{\langle \xi , C \rangle }. $$

This concludes our presentation of the $\textsf {ert}$ transformer. In the next section we validate the transformer’s definition by showing a soundness result with respect to an operational model of programs.

4 An Operational Model for Expected Run–Times

We prove the soundness of the expected run–time transformer with respect to a simple operational model for our probabilistic programs. This model will be given in terms of a Markov Decision Process (MDP, for short) whose collected reward corresponds to the run–time. We first briefly recall all necessary notions. A more detailed treatment can be found in [2, Chap. 10]. A Markov Decision Process is a tuple $\mathfrak {M}= (\mathcal {S},\, Act ,\, \mathbf P ,\, s_0,\, rew )$ where $\mathcal {S}$ is a countable set of states, $Act$ is a (finite) set of actions, $\mathbf P \!:\mathcal {S} \times Act \times \mathcal {S} \rightarrow [0,\,\! 1]$ is the transition probability function such that for all states $s \in \mathcal {S}$ and actions $\alpha \in Act$,

$$\begin{aligned} \sum _{s' \in \mathcal {S}} \mathbf P (s,\alpha ,s') \in \{0,1\}~, \end{aligned}$$

$s_0 \in \mathcal {S}$ is the initial state, and $rew \!:\mathcal {S} \rightarrow \mathbb R_{\ge 0}$ is a reward function. Instead of $\mathbf P (s,\alpha ,s') = p$, we usually write ${s} \xrightarrow {\alpha } {s'} \vdash {p}$. An MDP $\mathfrak {M}$ is a Markov chain if no non–deterministic choice is possible, i.e. for each pair of states $s,s' \in \mathcal {S}$ there exists exactly one $\alpha \in Act$ with $\mathbf P (s,\alpha ,s') \ne 0$.

A scheduler for $\mathfrak {M}$ is a mapping $\mathfrak {S} \!:\mathcal {S} ^{+} \rightarrow Act$, where $\mathcal {S} ^{+}$ denotes the set of non–empty finite sequences of states. Intuitively, a scheduler resolves the non–determinism of an MDP by selecting an action for each possible sequence of states that has been visited so far. Hence, a scheduler $\mathfrak {S}$ induces a Markov chain which is denoted by $\mathfrak {M}_{\mathfrak {S}}$. In order to define the expected reward of an MDP, we first consider the reward collected along a path. Let $\text {Paths}^{\mathfrak {M}_{\mathfrak {S}}}$ ($\text {Paths}_{ fin }^{\mathfrak {M}}$) denote the set of all (finite) paths $\pi$ ($\hat{\pi }$) in $\mathfrak {M}_{\mathfrak {S}}$. Analogously, let $\text {Paths}^{\mathfrak {M}_{\mathfrak {S}}} (s)$ and $\text {Paths}_{ fin }^{\mathfrak {M}_{\mathfrak {S}}} (s)$ denote the set of all infinite and finite paths in $\mathfrak {M}_{\mathfrak {S}}$ starting in state $s \in \mathcal {S}$, respectively. For a finite path $\hat{\pi }= s_0\ldots s_n$, the cumulative reward of $\hat{\pi }$ is defined as

$$\begin{aligned} rew (\hat{\pi }) ~\triangleq ~ \sum _{k=0}^{n-1} rew (s_k). \end{aligned}$$

For an infinite path $\pi$, the cumulative reward of reaching a non–empty set of target states $T \subseteq \mathcal {S}$, is defined as $rew (\pi ,\Diamond T) \triangleq rew (\pi (0)\ldots \pi (n))$ if there exists an n such that $\pi (n) \in T$ and $\pi (i) \notin T$ for $0 \le i < n$ and $rew (\pi ,\Diamond T) \triangleq \infty$ otherwise. Moreover, we write $\varPi (s,T)$ to denote the set of all finite paths $\hat{\pi }\in \text {Paths}_{ fin }^{\mathfrak {M}_{\mathfrak {S}}} (s)$, $s \in \mathcal {S}$, with $\hat{\pi }(n) \in T$ for some $n \in \mathbb N$ and $\hat{\pi }(i) \notin T$ for $0 \le i < n$. The probability of a finite path $\hat{\pi }$ is

$$\begin{aligned} \mathrm {Pr}^{\mathfrak {M}_{\mathfrak {S}}}\{\hat{\pi }\} ~\triangleq ~ \prod _{k=0}^{|\hat{\pi }|-1} \mathbf P (s_k, \mathfrak {S} (s_1,\ldots ,s_k), s_{k+1}). \end{aligned}$$

The expected reward that an MDP $\mathfrak {M}$ eventually reaches a non–empty set of states $T \subseteq \mathcal {S}$ from a state $s \in \mathcal {S}$ is defined as follows. If

$$\begin{aligned} \inf _{\mathfrak S} \, \mathrm {Pr}^{\mathfrak {M}_{\mathfrak {S}}}\{s \models \Diamond T\} ~=~ \inf _{\mathfrak S} \, \sum _{\hat{\pi }\in \varPi (s,T)} \mathrm {Pr}^{\mathfrak {M}_{\mathfrak {S}}}\{\hat{\pi }\} ~<~ 1 \end{aligned}$$

then $\textsf {ExpRew} ^{\mathfrak {M}}\left( s \models \Diamond T\right) \triangleq \infty$. Otherwise,

$$\begin{aligned} \textsf {ExpRew} ^{\mathfrak {M}}\left( s \models \Diamond T\right) ~\triangleq ~ \sup _{\mathfrak {S}} \sum _{\hat{\pi }\in \varPi (s,T)} \mathrm {Pr}^{\mathfrak {M}_{\mathfrak {S}}}\{\hat{\pi }\} \cdot rew (\hat{\pi }). \end{aligned}$$

We are now in a position to define an operational model for our probabilistic programming language. Let $\downarrow$ denote a special symbol indicating successful termination of a program.

Definition 2

(The operational MDP of a program). Given program $C \in \mathsf{{pProgs}}$, initial program state $\sigma _0 \in \varSigma$, and continuation $f \in \mathbb {T}$, the operational MDP of C is given by $\mathfrak {M}^{f}_{\sigma _0}\llbracket C \rrbracket = (\mathcal {S},\, Act ,\, \mathbf P ,\, s_0,\, rew )$, where

• ,

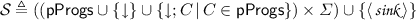• $Act \triangleq \{ L ,\, \tau ,\, R \}$,

• the transition probability function $\mathbf P$ is given by the rules in Fig. 2,

• $s_0 \triangleq \langle {C},\, {\sigma _0} \rangle$, and

• $rew :\mathcal {S} \rightarrow \mathbb R_{\ge 0}$ is the reward function defined according to Table 2.

Fig. 2.

Rules for the transition probability function of operational MDPs.

Since the initial state of the MDP $\mathfrak {M}^{f}_{\sigma _0}\llbracket C \rrbracket$ of a program $C$ with initial state $\sigma _0$ is uniquely given, instead of $\textsf {ExpRew} ^{\mathfrak {M}^{f}_{\sigma _0}\llbracket C \rrbracket }\left( \langle {C},\, {\sigma _0} \rangle \models \Diamond T\right)$ we simply write

$$\begin{aligned} \textsf {ExpRew} ^{\mathfrak {M}^{f}_{\sigma }\llbracket C \rrbracket }\left( T\right) . \end{aligned}$$

The rules in Fig. 2 defining the transition probability function of a program’s MDP are self–explanatory. Since only guard evaluations, assignments and $\texttt {skip}$ statements are assumed to consume time, i.e. have a positive reward, we assign a reward of 0 to all other program statements. Moreover, note that all states of the form $\langle { \texttt {empty} },\, {\sigma } \rangle$, $\langle {\downarrow },\, {\sigma } \rangle$ and are needed, because an operational MDP is defined with respect to a given continuation $f \in \mathbb {T}$. In case of $\langle { \texttt {empty} },\, {\sigma } \rangle$, a reward of 0 is collected and after that the program successfully terminates, i.e. enters state $\langle {\downarrow },\, {\sigma } \rangle$ where the continuation $f$ is collected as reward. In contrast, since no state other than is reachable from the unique sink state , the continuation $f$ is not taken into account if is reached without reaching a state $\langle {\downarrow },\, {\sigma } \rangle$ first. Hence the operational MDP directly enters from a state of the form $\langle { \texttt {halt} },\, {\sigma } \rangle$.

Table 2. Definition of the reward function $rew \!:\mathcal {S} \rightarrow \mathbb R_{\ge 0}$ of operational MDPs.

Example 3

(MDP of $C_{trunc}$ ). Recall the probabilistic program $C_{trunc}$ from Example 2. Figure 3 depicts the MDP $\mathfrak {M}^{f}_{\sigma }\llbracket C_{trunc} \rrbracket$ for an arbitrary fixed state $\sigma \in \varSigma$ and an arbitrary continuation $f \in \mathbb {T}$. Here labeled edges denote the value of the transition probability function for the respective states, while the reward of each state is provided in gray next to the state. To improve readability, edge labels are omitted if the probability of a transition is 1. Moreover, $\mathfrak {M}^{f}_{\sigma }\llbracket C_{trunc} \rrbracket$ is a Markov chain, because $C_{trunc}$ contains no non-deterministic choice.

A brief inspection of Fig. 3 reveals that $\mathfrak {M}^{f}_{\sigma }\llbracket C_{trunc} \rrbracket$ contains three finite paths $\hat{\pi }_{\mathsf {true}}$, $\hat{\pi }_{\mathsf {false} ~\mathsf {true}}$, $\hat{\pi }_{\mathsf {false} ~\mathsf {false}}$ that eventually reach state starting from the initial state $\langle {C _{trunc}},\, {\sigma } \rangle$. These paths correspond to the results of the two probabilistic guards in $C$. Hence the expected reward of $\mathfrak {M}^{f}_{\sigma }\llbracket C \rrbracket$ to eventually reach is given by

Observe that for $f = \mathbf {0}$, the expected reward $\textsf {ExpRew} ^{\mathfrak {M}^{f}_{\sigma }\llbracket C _{trunc} \rrbracket }\left( T\right)$ and the expected run–time $\textsf {ert} \left[ {C}\right] \left( {f}\right) (\sigma )$ (cf. Example 2) coincide, both yielding .    $\triangle$

The main result of this section is that $\textsf {ert}$ precisely captures the expected reward of the MDPs associated to our probabilistic programs.

Fig. 3.

The operational MDP $\mathfrak {M}^{f}_{\sigma }\llbracket C_{trunc} \rrbracket$ corresponding to the program in Example 3. $C'$ denotes the subprogram .

Theorem 2

(Soundness of the transformer). Let $\xi \in \mathsf {DExp}$, $C \in \mathsf{{pProgs}}$, and $f \in \mathbb {T}$. Then, for each $\sigma \in \varSigma$, we have

Proof

By induction on the program structure; see [17] for details.    $\square$

5 Expected Run–Time of Loops

Reasoning about the run–time of loop–free programs consists mostly of syntactic reasoning. The run–time of a loop, however, is given in terms of a least fixed point. It is thus obtained by fixed point iteration but need not be reached within a finite number of iterations. To overcome this problem we next study invariant–based proof rules for approximating the run–time of loops.

We present two families of proof rules which differ in the kind of the invariants they build on. In Sect. 5.1 we present a proof rule that rests on the presence of an invariant approximating the entire run–time of a loop in a global manner, while in Sect. 5.2 we present two proof rules that rely on a parametrized invariant that approximates the run–time of a loop in an incremental fashion. Finally in Sect. 5.3 we discuss how to improve the run–time bounds yielded by these proof rules.

5.1 Proof Rule Based on Global Invariants

The first proof rule that we study allows upper–bounding the expected run–time of loops and rests on the notion of upper invariants.

Definition 3

(Upper invariants). Let $f \in \mathbb {T}$, $C \in \mathsf{{pProgs}}$ and $\xi \in \mathsf {DExp}$. We say that $I \in \mathbb {T}$ is an upper invariant of loop $\texttt {while} \,(\xi )\,\{C\}$ with respect to f iff

$$\begin{aligned} \mathbf {1} + \llbracket {\xi }\!:{\mathsf {false}} \rrbracket \cdot f + \llbracket {\xi }\!:{\mathsf {true}} \rrbracket \cdot \textsf {ert} \left[ {C}\right] \left( {I}\right) ~\preceq I \end{aligned}$$

or, equivalently, iff $F_f^{\langle \xi , C \rangle } (I) \preceq I$, where $F_f^{\langle \xi , C \rangle }$ is the characteristic functional.

The presence of an upper invariant of a loop readily establishes an upper bound of the loop’s run–time.

Theorem 3

(Upper bounds from upper invariants). Let $f \in \mathbb {T}$, $C \in \mathsf{{pProgs}}$ and $\xi \in \mathsf {DExp}$. If $I \in \mathbb {T}$ is an upper invariant of $\texttt {while} \,(\xi )\,\{C\}$ with respect to f then

$$\begin{aligned} \textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) ~\preceq ~ I. \end{aligned}$$

Proof

The crux of the proof is an application of Park’s Theorem² [25] which, given that $F_f^{\langle \xi , C \rangle }$ is continuous (see Lemma 1), states that

$$ F_f^{\langle \xi , C \rangle } (I) \preceq I ~\implies ~ \textsf {lfp} \,F_f^{\langle \xi , C \rangle }\preceq I. $$

The left–hand side of the implication stands for I being an upper invariant, while the right–hand side stands for $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) \preceq I$.   $\square$

Notice that if the loop body C is itself loop–free, it is usually fairly easy to verify that some $I \in \mathbb {T}$ is an upper invariant, whereas inferring the invariant is—as in standard program verification—one of the most involved part of the verification effort.

Example 4

(Geometric distribution). Consider loop

From the calculations below we conclude that $I = \mathbf {1} + \llbracket {c = 1} \rrbracket \cdot \mathbf {4}$ is an upper invariant with respect to $\mathbf {0}$:

Then applying Theorem 3 we obtain

$$ \textsf {ert} \left[ {C_{\mathtt {geo}}}\right] \left( {\mathbf {0}}\right) ~\preceq ~\mathbf {1} + \llbracket {c = 1} \rrbracket \cdot \mathbf {4}. $$

In words, the expected run–time of $C_{\mathtt {geo}}$ is at most 5 from any initial state where $c=1$ and at most 1 from the remaining states. $\triangle$

The invariant–based technique to reason about the run–time of loops presented in Theorem 3 is complete in the sense that there always exists an upper invariant that establishes the exact run–time of the loop at hand.

Theorem 4

Let $f \in \mathbb {T}$, $C \in \mathsf{{pProgs}}$, $\xi \in \mathsf {DExp}$. Then there exists an upper invariant I of $\texttt {while} \,(\xi )\,\{C\}$ with respect to f such that ${ \textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) =I}$.

Proof

The result follows from showing that $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right)$ is itself an upper invariant. Since $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) = \textsf {lfp} \,F_f^{\langle \xi , C \rangle }$ this amounts to showing that

$$ F_f^{\langle \xi , C \rangle }\bigl (\, \textsf {lfp} \,F_f^{\langle \xi , C \rangle } \,\bigr ) ~\preceq ~ \textsf {lfp} \,F_f^{\langle \xi , C \rangle }~, $$

which holds by definition of $\textsf {lfp} \,$.   $\square$

Intuitively, the proof of this theorem shows that $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right)$ itself is the tightest upper invariant that the loop admits.

5.2 Proof Rules Based on Incremental Invariants

We now study a second family of proof rules which builds on the notion of $\omega$–invariants to establish both upper and lower bounds for the run–time of loops.

Definition 4

( $\omega$ –invariants). Let $f \in \mathbb {T}$, $C \in \mathsf{{pProgs}}$ and $\xi \in \mathsf {DExp}$. Moreover let $I_n \in \mathbb {T}$ be a run–time parametrized by $n \in \mathbb N$. We say that $I_n$ is a lower $\omega$ –invariant of loop $\texttt {while} \,(\xi )\,\{C\}$ with respect to f iff

$$ F_f^{\langle \xi , C \rangle } (\mathbf {0}) \succeq I_0 \qquad \text {and}\qquad F_f^{\langle \xi , C \rangle } (I_n) \succeq I_{n+1} \quad \text {for all}\; n \ge 0. $$

Dually, we say that $I_n$ is an upper $\omega$ –invariant iff

$$ F_f^{\langle \xi , C \rangle } (\mathbf {0}) \preceq I_0 \qquad \text {and}\qquad F_f^{\langle \xi , C \rangle } (I_n) \preceq I_{n+1} \quad \text {for all}\; n \ge 0. $$

Intuitively, a lower (resp. upper) $\omega$–invariant $I_n$ represents a lower (resp. upper) bound for the expected run–time of those program runs that finish within ${n+1}$ iterations, weighted according to their probabilities. Therefore we can use the asymptotic behavior of $I_n$ to approximate from below (resp. above) the expected run–time of the entire loop.

Theorem 5

(Bounds from) $\varvec{\omega }$ –invariants). Let $f \in \mathbb {T}$, $C \in \mathsf{{pProgs}}$, ${\xi \in \mathsf {DExp}}$.

• 1. If $I_n$ is a lower $\omega$–invariant of $\texttt {while} \,(\xi )\,\{C\}$ with respect to f and $\lim \limits _{n \rightarrow \infty } I_n$ exists³, then

  $$ \textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) \succeq \lim _{n \rightarrow \infty } I_n. $$

• 2. If $I_n$ is an upper $\omega$–invariant of $\texttt {while} \,(\xi )\,\{C\}$ with respect to f and $\lim \limits _{n \rightarrow \infty } I_n$ exists, then

  $$ \textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) \preceq \lim _{n \rightarrow \infty } I_n. $$

Proof

We prove only the case of lower $\omega$–invariants since the other case follows by a dual argument. Let $F_f$ be the characteristic functional of the loop with respect to f. Let $F_f^0 = \mathbf {0}$ and $F_f^{n+1} = F_f(F_f^{n})$. By the Kleene Fixed Point Theorem, $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) = \sup _n F_f^n$ and since $F_f^0 \preceq F_f^1 \preceq \ldots$ forms an $\omega$–chain, by the Monotone Sequence Theorem⁴, $\sup _n F_f^n = \lim _{n \rightarrow \infty } F_f^n$. Then the proof follows from showing that $F_f^{n+1} \succeq I_n$. We prove this by induction on n. The base case $F_f^{1} \succeq I_0$ holds because $I_n$ is a lower $\omega$–invariant. For the inductive case we reason as follows:

$$ F_f^{n+2} = F_f \bigl (F_f^{n+1}\bigr ) \succeq F_f (I_n) \succeq I_{n+1}. $$

Here the first inequality follows by I.H. and the monotonicity of $F_f$ (recall that $\textsf {ert} [C]$ is monotonic by Theorem 1), while the second inequality holds because $I_n$ is a lower $\omega$–invariant.   $\square$

Example 5

(Lower bounds for $C_{\mathtt {geo}}$ ). Reconsider loop $C_{\mathtt {geo}}$ from Example 4. Now we use Theorem 5.1. to show that $\mathbf {1} + \llbracket {c = 1} \rrbracket \cdot \mathbf {4}$ is also a lower bound of its run–time. To this end we first show that is a lower $\omega$–invariant of the loop with respect to $\mathbf {0}$:

Then from Theorem 5.1 we obtain

$$\begin{aligned} \textsf {ert} \left[ {C_{\mathtt {geo}}}\right] \left( {\mathbf {0}}\right) ~\succeq ~ \lim _{n \rightarrow \infty } \, \Bigl ( \mathbf {1} + \llbracket {c = 1} \rrbracket \cdot \bigl (\mathbf {4}-\tfrac{\mathbf {3}}{\mathbf {2}^n}\bigr ) \Bigr ) ~=~ \mathbf {1} + \llbracket {c = 1} \rrbracket \cdot \mathbf {4}. \end{aligned}$$

Combining this result with the upper bound $\textsf {ert} \left[ {C_{\mathtt {geo}}}\right] \left( {\mathbf {0}}\right) \preceq \mathbf {1} + \llbracket {c = 1} \rrbracket \cdot \mathbf {4}$ established in Example 4 we conclude that $\mathbf {1} + \llbracket {c = 1} \rrbracket \cdot \mathbf {4}$ is the exact run–time of $C_{\mathtt {geo}}$. Observe, however, that the above calculations show that $I_n$ is both a lower and an upper $\omega$–invariant (exact equalities $F_0(\mathbf {0})=I_0$ and $F_0(I_n)=I_{n+1}$ hold). Then we can apply Theorem 5.1 and 5.2 simultaneously to derive the exact run–time without having to resort to the result from Example 4.

Invariant Synthesis. In order to synthesize invariant , we proposed template $I_n = \mathbf {1} + \llbracket {c = 1} \rrbracket \cdot a_n$ and observed that under this template the definition of lower $\omega$–invariant reduces to $a_0 \le 1$, $a_{n+1} \le 2 + \tfrac{1}{2} a_n$, which is satisfied by . $\triangle$

Now we apply Theorem 5.1 to a program with infinite expected run–time.

Example 6

(Almost–sure termination at infinite expected run–time). Recall the program from the introduction:

Let $C_i$ denote the i-th line of C. We show that $\textsf {ert} \left[ {C}\right] \left( {\mathbf {0}}\right) \succeq \infty$.⁵ Since

$$ \textsf {ert} \left[ {C}\right] \left( {\mathbf {0}}\right) ~=~ \textsf {ert} \left[ {C_1}\right] \left( { \textsf {ert} \left[ {C_2}\right] \left( { \textsf {ert} \left[ {C_3}\right] \left( {\mathbf {0}}\right) }\right) }\right) $$

we start by showing that

$$ \textsf {ert} \left[ {C_3}\right] \left( {\mathbf {0}}\right) ~\succeq ~ \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x $$

using lower $\omega$–invariant $J_n = \mathbf {1} + \llbracket {n > x > 0} \rrbracket \cdot 2x + \llbracket {x \ge n} \rrbracket \cdot (2n-1)$. We omit here the details of verifying that $J_n$ is a lower $\omega$–invariant. Next we show that

$$\begin{aligned} \textsf {ert} \left[ {C_2}\right] \left( {\mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x}\right) ~\succeq ~ \mathbf {1}&{}+ \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr )\\&{}+ \llbracket {b = 1} \rrbracket \cdot \big (\mathbf {7} + \llbracket {x > 0} \rrbracket \cdot \varvec{\infty }\big ) \end{aligned}$$

by means of the lower $\omega$–invariant

$$ I_n ~=~ \mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) + \llbracket {b = 1} \rrbracket \cdot \Bigl ( \mathbf {7} - \mathbf {\tfrac{5}{2^n}} + n \cdot \llbracket {x > 0} \rrbracket \cdot 2x \Bigr ). $$

Let F be the characteristic functional of loop $C_2$ with respect to $\mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x$. The calculations to establish that $I_n$ is a lower $\omega$–invariant now go as follows:

$$\begin{aligned} F(\mathbf {0})&=~\mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) \\&\qquad \, \!\! + \llbracket {b = 1} \rrbracket \cdot \Bigl ( \mathbf {1} + \tfrac{1}{2} \cdot (\mathbf {1} + \mathbf {0}\left[ {x,b}/{2x,0}\right] ) + \tfrac{1}{2} \cdot (\mathbf {1} + \mathbf {0}\left[ {x,b}/{2x,1}\right] ) \Bigr )\\&=~\mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) + \llbracket {b = 1} \rrbracket \cdot \bigl ( \mathbf {1} + \tfrac{1}{2} \cdot \mathbf {1} + \tfrac{1}{2} \cdot \mathbf {1} \bigr )\\&=~\mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) + \llbracket {b = 1} \rrbracket \cdot \mathbf {2} ~=~I_0 ~\succeq ~ I_0\\[2ex] F(I_n)&=~\mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) \\&\;\; + \llbracket {b = 1} \rrbracket \!\cdot \! \Bigl ( \mathbf {1} + \tfrac{1}{2} \cdot (\mathbf {1} + I_n\left[ {x,b}/{2x,0}\right] ) + \tfrac{1}{2} \cdot (\mathbf {1} + I_n\left[ {x,b}/{2x,1}\right] ) \Bigr )\\&=~\mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) \\&\;\; + \llbracket {b = 1} \rrbracket \! \cdot \! \Bigl ( \mathbf {1} + \tfrac{1}{2} \cdot (\mathbf {3} + \llbracket {2x > 0} \rrbracket \cdot 4x) + \tfrac{1}{2} \!\cdot \! \Bigl ( \mathbf {9} - \mathbf {\tfrac{5}{2^n}} + n \cdot \llbracket {2x > 0} \rrbracket \cdot 4x \Bigr ) \Bigr )\\&=~\mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) \\&\;\; + \llbracket {b = 1} \rrbracket \!\cdot \! \Bigl (\mathbf {7} - \mathbf {\tfrac{5}{2^{n{+}1}}} + (n{+}1) \cdot \llbracket {x > 0} \rrbracket \cdot 2x \Bigr )\\&=~I_{n+1} ~\succeq ~ I_{n+1} \end{aligned}$$

Now we can complete the run–time analysis of program C:

$$\begin{aligned}&\textsf {ert} \left[ {C}\right] \left( {\mathbf {0}}\right) \\ ~&\qquad = \textsf {ert} \left[ {C_1}\right] \left( { \textsf {ert} \left[ {C_2}\right] \left( { \textsf {ert} \left[ {C_3}\right] \left( {\mathbf {0}}\right) }\right) }\right) \\ ~&\qquad \succeq \textsf {ert} \left[ {C_1}\right] \left( {\mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) + \llbracket {b = 1} \rrbracket \cdot \big ( \mathbf {7} + \llbracket {x > 0} \rrbracket \cdot \varvec{\infty }\big )}\right) \\ ~&\qquad = \textsf {ert} [x \mathrel { \texttt {:=} }1]\Big ( \textsf {ert} [b \mathrel { \texttt {:=} }1]\Big (\mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr )\\[-1ex]&\qquad \qquad \qquad \qquad \qquad \quad \quad \quad ~\,\, + \llbracket {b = 1} \rrbracket \cdot \big ( \mathbf {7} + \llbracket {x > 0} \rrbracket \cdot \varvec{\infty }\big )\Big )\Big )\\ ~&\qquad = \textsf {ert} \left[ { x \mathrel { \texttt {:=} }1}\right] \left( {\mathbf {8} + \llbracket {x > 0} \rrbracket \cdot \varvec{\infty }}\right) ~=~\mathbf {8} + \varvec{\infty }~=~ \varvec{\infty } \end{aligned}$$

Overall, we obtain that the expected run–time of the program C is infinite even though it terminates with probability one. Notice furthermore that sub–programs and $\texttt {while} \,(x > 0)\,\{x \mathrel { \texttt {:=} }x-1\}$ have expected run–time $\mathbf {1} + \llbracket {b} \rrbracket \cdot \mathbf {4}$ and $\mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2 x$, respectively, i.e. both have a finite expected run–time.

Invariant synthesis. In order to synthesize the $\omega$–invariant $I_n$ of loop $C_2$ we propose the template $I_n = \mathbf {1} + \llbracket {b \ne 1} \rrbracket \cdot \bigl ( \mathbf {1} + \llbracket {x > 0} \rrbracket \cdot 2x \bigr ) + \llbracket {b = 1} \rrbracket \cdot \bigl ( a_n + b_n \cdot \llbracket {x > 0} \rrbracket \cdot 2x \bigr )$ and from the definition of lower $\omega$–invariants we obtain $a_0 \le 2$, and $b_0 \le 0$, $b_{n+1} \le 1 + b_n$. These recurrences admit solutions and $b_n=n$. $\triangle$

As the proof rule based on upper invariants, the proof rules based on $\omega$-invariants are also complete: Given loop $\texttt {while} \,(\xi )\,\{C\}$ and run–time f, it is enough to consider the $\omega$-invariant $I_n = F_f^{n+1}$, where $F_f^{n}$ is defined as in the proof of Theorem 5 to yield the exact run–time $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right)$ from an application of Theorem 5. We formally capture this result by means of the following theorem:

Theorem 6

Let $f \in \mathbb {T}$, $C \in \mathsf{{pProgs}}$ and $\xi \in \mathsf {DExp}$. Then there exists a (both lower and upper) $\omega$–invariant $I_n$ of $\texttt {while} \,(\xi )\,\{C\}$ with respect to f such that ${ \textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) = \lim _{n \rightarrow \infty } I_n}$.

Theorem 6 together with Theorem 4 shows that the set of invariant–based proof rules presented in this section are complete. Next we study how to refine invariants to make the bounds that these proof rules yield more precise.

5.3 Refinement of Bounds

An important property of both upper and lower bounds of the run–time of loops is that they can be easily refined by repeated application of the characteristic functional.

Theorem 7

(Refinement of bounds). Let $f \in \mathbb {T}$, $C \in \mathsf{{pProgs}}$ and $\xi \in \mathsf {DExp}$. If I is an upper (resp. lower) bound of $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right)$ and $F_f^{\langle \xi , C \rangle }(I) \preceq I$ (resp. $F_f^{\langle \xi , C \rangle }(I) \succeq I$), then $F_f^{\langle \xi , C \rangle }(I)$ is also an upper (resp. lower) bound, at least as precise as I.

Proof

If I is an upper bound of $\textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right)$ we have $\textsf {lfp} \,F_f^{\langle \xi , C \rangle } \preceq I$. Then from the monotonicity of $F_f^{\langle \xi , C \rangle }$ (recall that $\textsf {ert}$ is monotonic by Theorem 1) and from $F_f^{\langle \xi , C \rangle }(I) \preceq I$ we obtain

$$ \textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) ~=~ \textsf {lfp} \,F_f^{\langle \xi , C \rangle } ~=~ F_f^{\langle \xi , C \rangle }( \textsf {lfp} \,F_f^{\langle \xi , C \rangle }) ~\preceq ~ F_f^{\langle \xi , C \rangle }(I) ~\preceq ~I, $$

which means that $F_f^{\langle \xi , C \rangle }(I)$ is also an upper bound, possibly tighter than I. The case for lower bounds is completely analogous.   $\square$

Notice that if I is an upper invariant of $\texttt {while} \,(\xi )\,\{C\}$ then I fulfills all necessary conditions of Theorem 7. In practice, Theorem 7 provides a means of iteratively improving the precision of bounds yielded by Theorems 3 and 5, as for instance for upper bounds we have

$$\begin{aligned} \textsf {ert} \left[ { \texttt {while} \,(\xi )\,\{C\}}\right] \left( {f}\right) ~\preceq ~ \cdots ~\preceq ~ F_f^{\langle \xi , C \rangle }\left( F_f^{\langle \xi , C \rangle }(I)\right) ~ \preceq ~ F_f^{\langle \xi , C \rangle }(I) ~\preceq I. \end{aligned}$$

If $I_n$ is an upper (resp. lower) $\omega$-invariant, applying Theorem 7 requires checking that $F_f^{\langle \xi , C \rangle }(L) \preceq L$ (resp. $F_f^{\langle \xi , C \rangle }(L) \succeq L$), where $L=\lim _{n \rightarrow \infty } I_n$. This proof obligation can be discharged by showing that $I_n$ forms an $\omega$-chain, i.e.  that $I_n \preceq I_{n+1}$ for all $n \in \mathbb N$.

6 Run–Time of Deterministic Programs

The notion of expected run–times as defined by $\textsf {ert}$ is clearly applicable to deterministic programs, i.e.  programs containing neither probabilistic guards nor probabilistic assignments nor non–deterministic choice operators. We show that the $\textsf {ert}$ of deterministic programs coincides with the tightest upper bound on the run–time that can be derived in an extension of Hoare logic [14] due to Nielson [23, 24].

In order to compare our notion of $\textsf {ert}$ to the aforementioned calculus we restrict our programming language to the language $\textsf {dProgs}$ of deterministic programs considered in [24] which is given by the following grammar:

$$\begin{aligned} C ~~::=~~&\texttt {skip} ~\;|\;~ x \mathrel { \texttt {:=} }E ~\;|\;~ C \texttt {;} \, C ~\;|\;~ \texttt {if} \,(\xi )\,\{C\}\, \texttt {else} \,\{C\} ~\;|\;~ \texttt {while} \,(\xi )\,\{C\}~, \end{aligned}$$

where E is a deterministic expression and $\xi$ is a deterministic guard, i.e. $\llbracket {E} \rrbracket (\sigma )$ and $\llbracket {\xi } \rrbracket (\sigma )$ are Dirac distributions for each $\sigma \in \varSigma$. For simplicity, we slightly abuse notation and write $\llbracket {E} \rrbracket (\sigma )$ to denote the unique value $v \in \mathsf {Val}$ such that $\llbracket {E}\!:{v} \rrbracket ({\sigma }) = 1$.

For deterministic programs, the MDP $\mathfrak {M}^{\mathbf {0}}_{\sigma }\llbracket C \rrbracket$ of a program $C \in \textsf {dProgs}$ and a program state $\sigma \in \varSigma$ is a labeled transition system. In particular, if a terminal state of the form $\langle {\downarrow },\, {\sigma '} \rangle$ is reachable from the initial state of $\mathfrak {M}^{\mathbf {0}}_{\sigma }\llbracket C \rrbracket$, it is unique. Hence we may capture the effect of a deterministic program by a partial function $\mathbb {C}\llbracket \,\cdot \, \rrbracket ({\,\cdot \,}) : \textsf {dProgs} \times \varSigma \rightharpoonup \varSigma$ mapping each $C \in \textsf {dProgs}$ and $\sigma \in \varSigma$ to a program state $\sigma ' \in \varSigma$ if and only if there exists a state $\langle {\downarrow },\, {\sigma '} \rangle$ that is reachable in the MDP $\mathfrak {M}^{\mathbf {0}}_{\sigma }\llbracket C \rrbracket$ from the initial state $\langle {C},\, {\sigma } \rangle$. Otherwise, $\mathbb {C}\llbracket C \rrbracket ({\sigma })$ is undefined.

Nielson [23, 24] developed an extension of the classical Hoare calculus for total correctness of programs in order to establish additionally upper bounds on the run–time of programs. Formally, a correctness property is of the form

$$\begin{aligned} \{~{P}~\}~{C}~\{~{E}~\Downarrow ~{Q}~\} ~, \end{aligned}$$

where $C \in \textsf {dProgs}$, E is a deterministic expression over the program variables, and P, Q are (first–order) assertions. Intuitively, $\{~{P}~\}~{C}~\{~{E}~\Downarrow ~{Q}~\}$ is valid, written $\models _{E}\{~{P}~\}~{C}~\{~{E}~\Downarrow ~{Q}~\}$, if and only if there exists a natural number k such that for each state $\sigma$ satisfying the precondition P, the program $C$ terminates after at most $k \cdot \llbracket {E} \rrbracket (\sigma )$ steps in a state satisfying postcondition Q. In particular, it should be noted that E is evaluated in the initial state $\sigma$.

Figure 4 is taken verbatim from [24] except for minor changes to match our notation. Most of the inference rules are self–explanatory extensions of the standard Hoare calculus for total correctness of deterministic programs [14] which is obtained by omitting the gray parts.

The run–time of $\texttt {skip}$ and $x \mathrel { \texttt {:=} }E$ is one time unit. Since guard evaluations are assumed to consume no time in this calculus, any upper bound on the run–time of both branches of a conditional is also an upper bound on the run–time of the conditional itself (cf. rule $[\text {if}]$). The rule of consequence allows to increase an already proven upper bound on the run–time by an arbitrary constant factor. Furthermore, the run–time of two sequentially composed programs $C _1$ and $C _2$ is, intuitively, the sum of their run–times $E_1$ and $E_2$. However, run–times are expressions which are evaluated in the initial state. Thus, the run–time of $C _2$ has to be expressed in the initial state of $C _1;C _2$. Technically, this is achieved by adding a fresh (and hence universally quantified) variable u that is an upper bound on $E_2$ and at the same time is equal to a new expression $E_2'$ in the precondition of $C _1;C _2$. Then, the run–time of $C _1;C _2$ is given by the sum $E_1 + E_2'$.

The same principle is applied to each loop iteration. Here, the run–time of the loop body is given by $E_1$ and the run–time of the remaining z loop iterations, $E'$, is expressed in the initial state by adding a fresh variable u. Then, any upper bound of $E \ge E_1 + E'$ is an upper bound on the run–time of z loop iterations.

We denote provability of a correctness property $\{~{P}~\}~{C}~\{~{E}~\Downarrow ~{Q}~\}$ and a total correctness property $\{~{P}~\}~{C}~\{~\Downarrow ~{Q}~\}$ in the standard Hoare calculus by $\vdash _{E}\{~{P}~\}~{C}~\{~{E}~\Downarrow ~{Q}~\}$ and $\vdash \{~{P}~\}~{C}~\{~\Downarrow ~{Q}~\}$, respectively.

Fig. 4.

Inference system for order of magnitude of run–time of deterministic programs according to Nielson [23].

Theorem 8

(Soundness of ert for deterministic programs). For all $C \in \textsf {dProgs}$ and assertions P, Q, we have

$$ \vdash \{~{P}~\}~{C}~\{~\Downarrow ~{Q}~\} \text { implies } \vdash _{E}\{~{P}~\}~{C}~\{~{ \textsf {ert} \left[ {C}\right] \left( {\mathbf {0}}\right) }~\Downarrow ~{Q}~\}. $$

Proof

By induction on the program structure; see [17] for details.

Intuitively, this theorem means that for every terminating deterministic program, the $\textsf {ert}$ is an upper bound on the run–time, i.e. $\textsf {ert}$ is sound with respect to the inference system shown in Fig. 4. The next theorem states that no tighter bound can be derived in this calculus. We cannot get a more precise relationship, since we assume guard evaluations to consume time.

Theorem 9

(Completeness of ert w.r.t. Nielson). For all $C \in \textsf {dProgs}$, assertions P, Q and deterministic expressions E, $\vdash _{E}\{~{P}~\}~{C}~\{~{E}~\Downarrow ~{Q}~\}$ implies that there exists a natural number k such that for all $\sigma \in \varSigma$ satisfying P, we have

$$\begin{aligned} \textsf {ert} \left[ {C}\right] \left( {\mathbf {0}}\right) (\sigma ) ~\le ~ k \cdot (\llbracket {E} \rrbracket (\sigma ))~. \end{aligned}$$

Proof

By induction on the program structure; see [17] for details.   $\square$

Theorem 8 together with Theorem 9 shows that our notion of $\textsf {ert}$ is a conservative extension of Nielson’s approach for reasoning about the run–time of deterministic programs. In particular, given a correctness proof of a deterministic program $C$ in Hoare logic, it suffices to compute $\textsf {ert} \left[ {C}\right] \left( {\varvec{0}}\right)$ in order to obtain a corresponding proof in Nielson’s proof system.

7 Case Studies

In this section we use our $\textsf {ert}$–calculus to analyze the run–time of two well–known randomized algorithms: the One–Dimensional (Symmetric) Random Walk and the Coupon Collector Problem.

7.1 One–Dimensional Random Walk

Consider program

which models a one–dimensional walk of a particle which starts at position ${x = 10}$ and moves with equal probability to the left or to the right in each turn. The random walk stops if the particle reaches position $x = 0$. It can be shown that the program terminates with probability one [15] but requires, on average, an infinite time to do so. We now apply our $\textsf {ert}$–calculus to formally derive this run–time assertion.

The expected run–time of $P_{rw}$ is given by

$$ \textsf {ert} \left[ {P_{rw}}\right] \left( {\varvec{0}}\right) ~=~ \textsf {ert} \left[ {x \mathrel { \texttt {:=} }10}\right] \left( { \textsf {ert} \left[ { \texttt {while} \,(x>0)\,\{C\}}\right] \left( {\varvec{0}}\right) }\right) ~, $$

where C stands for the probabilistic assignment in the loop body. Thus, we need to first determine run–time $\textsf {ert} \left[ { \texttt {while} \,(x > 0)\,\{C\}}\right] \left( {\varvec{0}}\right)$. To do so we propose

$$ I_n ~=~ \varvec{1}+ \llbracket {0 < x \le n} \rrbracket \cdot \varvec{\varvec{\infty }} $$

as a lower $\omega$–invariant of loop $\texttt {while} \,(x > 0)\,\{C\}$ with respect to $\mathbf {0}$; detailed calculations for verifying that $I_n$ is indeed a lower $\omega$–invariant can be found in the extended version of the paper [17]. Theorem 5 then states that

$$ \textsf {ert} \left[ { \texttt {while} \,(x > 0)\,\{C\}}\right] \left( {\varvec{0}}\right) \succeq \lim _{n \rightarrow \infty } \varvec{1}+ \llbracket {0 < x \le n} \rrbracket \cdot \varvec{\varvec{\infty }} = \varvec{1}+ \llbracket {0 < x} \rrbracket \cdot \varvec{\varvec{\infty }}. $$

Altogether we have

$$\begin{aligned} \textsf {ert} \left[ {P_{rw}}\right] \left( {\varvec{0}}\right)&~=~ \textsf {ert} \left[ {x \mathrel { \texttt {:=} }10}\right] \left( { \textsf {ert} \left[ { \texttt {while} \,(x>0)\,\{C\}}\right] \left( {\varvec{0}}\right) }\right) \\&~\succeq ~ \textsf {ert} \left[ {x \mathrel { \texttt {:=} }10}\right] \left( {\varvec{1}+ \llbracket {0 < x} \rrbracket \cdot \varvec{\varvec{\infty }}}\right) \\&~=~\mathbf {1} + (\mathbf {1} + \llbracket {0 < x} \rrbracket \cdot \varvec{\varvec{\infty }})\left[ {x}/{10}\right] \\&~=~\mathbf {1} + (\mathbf {1} + 1 \cdot \varvec{\varvec{\infty }}) ~=~ \varvec{\varvec{\infty }}, \end{aligned}$$

which says that $\textsf {ert} \left[ {P_{rw}}\right] \left( {\varvec{0}}\right) \succeq \varvec{\varvec{\infty }}$. Since the reverse inequality holds trivially, we conclude that $\textsf {ert} \left[ {P_{rw}}\right] \left( {\varvec{0}}\right) = \varvec{\varvec{\infty }}$.

7.2 The Coupon Collector Problem

Now we apply our $\textsf {ert}$–calculus to solve the Coupon Collector Problem. This problem arises from the following scenario⁶: Suppose each box of cereal contains one of N different coupons and once a consumer has collected a coupon of each type, he can trade them for a prize. The aim of the problem is determining the average number of cereal boxes the consumer should buy to collect all coupon types, assuming that each coupon type occurs with the same probability in the cereal boxes.

The problem can be modeled by program $C_{cp}$ below:

$$\begin{aligned}&{cp} \mathrel { \texttt {:=} }[0,\, \ldots ,\, 0] \texttt {;} \, i \mathrel { \texttt {:=} }1 \texttt {;} \, x \mathrel { \texttt {:=} }N\\&\texttt {while} \,(x > 0)\, \{\\&\qquad \texttt {while} \,( cp [i] \ne 0)\, \{ \\&\qquad \qquad i \mathrel { \texttt {:} {\approx }} \mathtt {Unif}[1 \ldots N] \\&\qquad \}; \\&\qquad cp [i] \mathrel { \texttt {:=} }1 \texttt {;} \, x \mathrel { \texttt {:=} }x-1\\&\} \end{aligned}$$

Array cp is initialized to 0 and whenever we obtain the first coupon of type i, we set cp[i] to 1. The outer loop is iterated N times and in each iteration we collect a new—unseen—coupon type. The collection of the new coupon type is performed by the inner loop.

We start the run–time analysis of $C_{cp}$ introducing some notation. Let $C _{ in }$ and $C _{ out }$, respectively, denote the inner and the outer loop of $C_{cp}$. Furthermore, let $\# col \triangleq \sum _{i=1}^{N} [ cp [i] \ne 0]$ denote the number of coupons that have already been collected.

Analysis of the inner loop. For analyzing the run–time of the outer loop we need to refer to the run–time of its body, with respect to an arbitrary continuation $g \in \mathbb {T}$. Therefore, we first analyze the run–time of the inner loop $C_{in}$. We propose the following lower and upper $\omega$–invariant for the inner loop $C_{in}$:

$$\begin{aligned} {J}_ n ^g ~=~ \mathbf {1} ~+~&[ cp [i] = 0] \cdot g \\ ~+~&[ cp [i] \ne 0] \cdot \sum _{k = 0}^{n}\left( \frac{\# col }{N}\right) ^k \biggl (\mathbf {2} + \frac{1}{N} \sum _{j=1}^{N} \, \llbracket { cp [j] =0} \rrbracket \cdot g[i/j]\biggr ). \end{aligned}$$

Moreover, we write $J^g$ for the same invariant where n is replaced by $\infty$. A detailed verification that $J_ n ^g$ is indeed a lower and upper $\omega$–invariant is provided in the extended version of the paper [17]. Theorem 5 now yields

Since the run–time of a deterministic assignment $x \mathrel { \texttt {:=} }E$ is

the expected run–time of the body of the outer loop reduces to

Analysis of the outer loop. Since program $C_{cp}$ terminates right after the execution of the outer loop $C_{out}$, we analyze the run–time of the outer loop $C_{out}$ with respect to continuation $\varvec{0}$, i.e.  $\textsf {ert} \left[ {C_{out}}\right] \left( {\mathbf {0}}\right)$. To this end we propose

$$\begin{aligned} I_{n}&~=~ \mathbf {1} + \sum _{\ell = 0}^{n} [x > \ell ] \cdot \biggl ( \mathbf {3} + [n \ne 0] + 2 \cdot \sum _{k=0}^{\infty } \left( \frac{\# col +\ell }{N} \right) ^{\! \!k} \,\biggr ) \\&\qquad - 2 \cdot [ cp [i] =0] \cdot [x > 0] \cdot \sum _{k=0}^{\infty } \left( \frac{\# col }{N} \right) ^{k} \end{aligned}$$

as both an upper and lower $\omega$–invariant of $C_{out}$ with respect to $\mathbf {0}$. A detailed verification that $I_n$ is an $\omega$-invariant is found in the extended version of the paper [17]. Now Theorem 5 yields

where I denotes the same invariant as $I_n$ with n replaced by $\infty$.

Analysis of the overall program. To obtain the overall expected run–time of program $C_{cp}$ we have to account for the initialization instructions before the outer loop. The calculations go as follows:

where denotes the $(N{-}1)$-th harmonic number. Since the harmonic numbers approach asymptotically to the natural logarithm, we conclude that the coupon collector algorithm $C_{{cp}}$ runs in expected time $\Theta (N \cdot \log (N))$.

8 Conclusion

We have studied a wp–style calculus for reasoning about the expected run–time and positive almost–sure termination of probabilistic programs. Our main contribution consists of several sound and complete proof rules for obtaining upper as well as lower bounds on the expected run–time of loops. We applied these rules to analyze the expected run–time of a variety of example programs including the well-known coupon collector problem. While finding invariants is, in general, a challenging task, we were able to guess correct invariants by considering a few loop unrollings most of the time. Hence, we believe that our proof rules are natural and widely applicable.

Moreover, we proved that our approach is a conservative extension of Nielson’s approach for reasoning about the run–time of deterministic programs and that our calculus is sound with respect to a simple operational model.