Abstract
It takes time for theoretical advances to get used in practical schemes. Anonymous credential schemes are no exception. For instance, existing schemes suited for real-world use lack formal, composable definitions, partly because they do not support straight-line extraction and rely on random oracles for their security arguments. To address this gap, we propose unlinkable redactable signatures (URS), a new building block for privacy-enhancing protocols, which we use to construct the first efficient UC-secure anonymous credential system that supports multiple issuers, selective disclosure of attributes, and pseudonyms. Our scheme is one of the first such systems for which both the size of a credential and its presentation proof are independent of the number of attributes issued in a credential. Moreover, our new credential scheme does not rely on random oracles. As an important intermediary step, we address the problem of building a functionality for a complex credential system that can cover many different features. Namely, we design a core building block for a single issuer that supports credential issuance and presentation with respect to pseudonyms and then show how to construct a full-fledged credential system with multiple issuers in a modular way. We expect this definitional approach to be of independent interest.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Structure preserving signatures
- Vector commitments
- Anonymous credentials
- Universal composability
- Groth-Sahai proofs
1 Introduction
Digital signature schemes are a fundamental cryptographic primitive. Besides their use for signing digital items, they are used as building blocks in more complex cryptographic schemes such as blind signatures [6, 42], group signatures [15, 52], direct anonymous attestation [20], electronic cash [40], voting schemes [48], adaptive oblivious transfer [23, 32], and anonymous credentials [12].
For protocols constructed like this to be efficient, special properties are demanded from a signature scheme, in particular when the protocol needs to achieve strong privacy properties. The most important such properties seem to be that the issuance of a signature and its later use in a protocol is unlinkable as well as that the scheme is able to sign multiple messages (without employing a hash function). The first signature scheme that met these requirements is a blind signature scheme by Brands [18]. The drawback of blind signatures, however, is that when using the signature later in a higher-level protocol it must typically be revealed so that a third party can be convinced of its validity. Thus, a signature can be used only once, which turns out to be quite limiting for applications such as group signatures, multi-show anonymous credentials, and compact e-cash [25].
Camenisch and Lysyanskaya [30, 31] were the first to design signature schemes (CL-signatures) overcoming these drawbacks. Their schemes are secure under the Strong RSA, the q-SDH, or the LRSW assumption, respectively, and allow for an alternative approach when using a signature in a protocol: instead of revealing the signature to a party, the user employs zero-knowledge proofs to convince the party that she possesses a valid signature. While in theory this is possible for any signature scheme, CL-signatures were the first that enabled efficient proofs using generalized Schnorr proofs of knowledge. This is due to the algebraic properties of CL-signatures, i.e., no hash function is applied to the message and the signature and message values are either exponents or group elements.
Since the introduction of CL-signatures, the area of privacy preserving protocols flourished considerably and numerous new protocols based on them have been proposed. This has also made it apparent, however, that CL-signatures still have a number of drawbacks:
-
1.
Random oracles. To make generalized Schnorr proofs of knowledge non-interactive (which is often required), one needs to resort to the Fiat-Shamir heuristic, i.e., to the random oracle model, and thus looses all provable security guarantees when the oracle is instantiated by a hash function [36].
-
2.
Straight-line extraction. When designing a protocol to be secure in the UC model [35], rewinding can not be used to prove security. As a result, witnesses in generalized Schnorr proofs of knowledge need to be encrypted under a public key encoded in the common reference string (CRS). As the witnesses (messages signed with CL-signatures) are discrete logarithms, this is rather expensive [26] and may render the overall protocol impractical.
-
3.
Linear size. When proving ownership of a CL-signature on many messages, all of them are needed for the verification of the signature and therefore a proof of possession of a signature will be linear in the number of messages.
A promising ingredient to overcome these drawbacks is the work by Groth and Sahai [45], who for the first time constructed efficient non-interactive zero-knowledge proofs (NIZK) without using random oracles, albeit for a limited set of languages. Indeed, the set of languages covered by these so-called GS-proofs does not include the ones covered by generalized Schnorr protocols and therefore many authors started to look for a compatible CL-signatures replacement, i.e., structure-preserving signature schemes [1–3]. Together with GS-proofs, these new schemes can also be used as signatures of knowledge [39] and thus are applicable in scenarios previously addressed with CL-signatures.
However, structure-preserving signatures still suffer in terms of performance when signing multiple messages (cf. drawback (3)), which is a typical requirement in applications such as anonymous credentials. Indeed, as for CL-signatures, the size of proofs with structure-preserving signatures grows linearly with the number of messages. As the constant factor for GS-proofs is larger than for generalized Schnorr proofs, structure-preserving signatures loose their attractiveness as a building block for such applications.
Our Contribution. In this paper, our goal is to address the three drawbacks of CL-signatures discussed above. To this end, we propose a new type of signature scheme, unlinkable redactable signatures (URS), in which one can redact message-signature pairs and reveal only their relevant parts each time they are used. Moreover, signatures in URS are unlinkable and the same message-signature pair can be redacted and revealed multiple times without being linked back to its origin. The real-world efficiency of URS is comparable to that of CL-signatures when a single message is signed and becomes superior when the number of messages signed grows. We view our contribution as threefold: First, in Sect. 2, we formally define URS. We present property-based security definitions for unlinkability and unforgeability and also a UC functionality for URS. Comparing the two definitions we find the seemingly common phenomenon that the functionality-based definition requires a key-registration process (allowing for the extraction of keys in the proof) while the property based definition per se does not require that. We validate our definitions by showing that an URS scheme satisfying strengthened property-based security definitions with key extraction securely implements our UC functionality.
Second, in Sect. 3, we construct an efficient URS scheme from vector commitments [37, 51, 56], structure-preserving signatures [2, 3], and (a minimal dose of) non-interactive proofs of knowledge (NIPoK), which in practice can be instantiated by witness-indistinguishable Groth-Sahai proofs [45]. As we are interested in practical efficiency, we instantiate our scheme with concrete building block that deliberately rely on stronger assumptions (see Sect. 4.3). However, if one is willing to accept a less efficient scheme, a CDH-based vector commitment scheme [37] secure under less strong assumptions. We show how to make use of algebraic properties in our building blocks to minimize the witness size of the NIPoK.
Third, in Sect. 4, to demonstrate the versatility of our URS scheme as a CL-signature scheme ‘replacement’, we employ it to design the first efficient universally composable anonymous credential system that supports multiple issuers, pseudonyms, and selective disclosure of attributes.
Anonymous credential systems usually need to support an ecosystem of different features. Therefore, a single ideal functionality providing all the features such as pseudonyms, selective attribute disclosure, predicates over attributes, revocation, inspection, etc. would be very complex and hard to both create and use in a modular way—not to mention credible security proofs.
Nevertheless, ideal functionalities are very attractive for modeling the complexity of anonymous credential schemes. Indeed an early seminal paper [29] attempted exactly this, but was foiled by drawback (2)—as well as by the immaturity of the UC framework at the time. To overcome this complexity, we present a flexible and modular approach for constructing UC-secure anonymous credentials. Namely, we design a core building block for a single issuer that supports credential issuance and presentation with respect to pseudonyms. We then show how to compose multiple such blocks to construct in a modular way a full-fledged credential system with multiple issuers.
Besides being composable, our system is also arguably one of the first schemes to support efficient non-interactive attribute disclosure with cost independent of the number of attributes issued without having to rely on random oracles. Even in the random oracle model this has been an elusive goal. Therefore, because of the composability and efficient selective disclose, our scheme is very attractive and quickly surpasses schemes based on blind signatures and CL-signatures [19, 31] when the number of attributes grows.
Related Work. We compare our signatures and credential schemes with other related work, a full comparison is deferred to the full paper [9]. As there are a multitude of papers on redactable, quotable, and sanitizable signatures [7, 21, 46, 58], we focus on the most influential definitional work and the most promising approaches in terms of efficiency.
A variety of signature schemes with flexible signing capabilities and strong privacy properties have been proposed [7, 8, 10, 14, 17, 34, 38]. While these works provide a fresh definitional approach, their schemes are very inefficient, especially when redacting a message vector with a large number of attributes. Some schemes built on vector commitments [51, 55] achieve better efficiency but only consider one-time-show credentials, and while the scheme in [51] is not defined formally, the scheme in [55] involves interaction.
The first efficient multi-show anonymous credential scheme is [29]. It was extended with efficient attribute disclosure [24] and had real-world exposure [20, 33]. It can, however, only be non-interactive in the random oracle model. Non-interactive credentials in the standard model have been built from P-signatures [12, 13]. An instantiation of our \({\mathsf {URS}}\) scheme, however, is almost twice more efficient than [12] despite the fact that the latter does not support signing multiple messages. Belenkiy et al. [11] show how to use the randomizability of P-signatures for delegation and Chow et al. [41] extend the randomizable group signatures scheme underlying [11] with a flexible attribute mechanism. Izabachène et al. [50] extends the work of [12] with vector commitments; their scheme is, however, not secure under our definitions. In independent work, Hanser and Slamanig [47] present a credential system with efficient (independent of the number of attributes) attribute disclosure. However, their system is only secure in the generic group model [43]. Furthermore, it uses hash function to encode attributes and thus does not enable efficient protocol design. None of these schemes is (universally) composable. Camenisch et al. [27] have recently proposed property-based definitions of anonymous credentials and of the necessary building blocks, given a construction and proved it secure. Their definitions turn out to be rather complex, indicating that for complex systems functionality-based definitions might be easier to handle. Indeed, for their definition of privacy, Camenisch et al. make use of what they call ‘filter’ which is very reminiscent of an ideal functionality. Finally, the construction they provide is based on CL-signatures and thus suffers from the drawbacks of that approach.
An important factor that is often neglected is the compatibility of schemes with zero-knowledge proofs to enable efficient protocol design. Because of its compatibility with Groth-Sahai proofs, efficiency and composability, immediate further applications of our URS scheme include efficient e-cash, credential-based key exchange, e-voting, auditing, and others.
2 Definitions of Unlinkable Redactable Signatures
Redactable signatures are an instance of homomorphic [7] or controlled-malleable signatures [38]. For our credentials application the most useful redaction operation is to selectively white-list or quote a subset of messages and their positions from a message vector of length n ([7] consider the quoting of sub-sentences). We denote the message space of all valid message vectors as \(\mathcal {M}\). We also refer to the redacted message as a quote of the original message. To distinguish the original vector from the quote of all messages we denote the original vector as \({\varvec{m}} = (1, m_1, \ldots , m_n)\) and a quote as \({\varvec{m}}_I = (2, m_1', \ldots , m_n')\). We represent each valid quoting transformation by a set \(I\subseteq [1,n]\) of message positions and denote quoting either by \(I({\varvec{m}})\) or \({\varvec{m}}_{I}\). We denote the i\(^\text {th}\) message element either by \({\varvec{m}}[i]\) or \(m_i\). A quote \({\varvec{m}}_{I}\) from \({\varvec{m}}\) is of the form
Note that the message itself already reveals whether it is a quote. Chase et al. [38] call such a scheme tiered and we refer to the vectors \({\varvec{m}}\) and \({\varvec{m}}_I\) as Tier 1 and Tier 2 vectors respectively. The vector \({\varvec{m}}_I\) can be sparse and can have a much shorter encoding than \({\varvec{m}}\). Finally, we define \({\mathsf {Zero}}({\varvec{m}}, I) = (1, \tilde{m}_1, \ldots , \tilde{m}_n)\), with \(\tilde{m}_j = m_j\) for \(j\in I\) and \(\tilde{m}_j = 0\) for \(j \notin I\). This should not be confused with the operator I that outputs a Tier 2 message.
2.1 Property-Based Definitions for Unlinkable Redactable Signatures
One can define the security of redactable signatures by instantiating controlled-malleable signature definitions for simulatability, simulation unforgeability, and simulation context-hiding of Chase et al. [38] with the quoting transformation class \(\mathcal {T}=\{I(\cdot )| I\subseteq [1..n]\}\) above. We prefer, however, to give our own unforgeability and unlinkability definitions that are more specific and do not rely on simulation and extraction. This makes them simpler and easier to prove, and thus more efficiently realizable. Together with key extractability they are nevertheless sufficient to realize the strong guarantees of our UC functionality.
Definition 1
(Unlinkable Redactable Signatures). An unlinkable redactable signature scheme \({\mathsf {URS}}\) consists of the following algorithms:
-
\({\mathsf {URS}}.{\mathsf {SGen}}(1^{\kappa }) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }} SP .\) \({\mathsf {SGen}}\) takes the security parameter \(1^{\kappa }\) as input and outputs the system parameters \( SP \).
-
\({\mathsf {URS}}.{\mathsf {Kg}}( SP ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}( pk , sk ).\) \({\mathsf {Kg}}\) takes the system parameters \( SP \) as an input and outputs public verification and private signing keys \(( pk , sk )\). The verification key \( pk \) defines the message space \(\mathcal {M}\).
-
\({\mathsf {URS}}.{\mathsf {Sign}}( sk , {\varvec{m}}) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}\sigma .\) \({\mathsf {Sign}}\) takes the signing key \( sk \) and a message \({\varvec{m}} \in \mathcal {M}\) as input and produces a signature \(\sigma \).
-
\({\mathsf {URS}}.{\mathsf {Derive}}( pk , I, {\varvec{m}}, \sigma ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}\sigma _I.\) \({\mathsf {Derive}}\) takes the public key \( pk \), a selection vector I, a message \({\varvec{m}}\) and a signature \(\sigma \) (both of Tier 1) as input. It produces a Tier 2 signature \(\sigma _I\) for \({\varvec{m}}_{I}\).
-
\({\mathsf {URS}}.{\mathsf {Verify}}( pk , \sigma , {\varvec{m}})\mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}0/1.\) \({\mathsf {Verify}}\) takes the verification key \( pk \), a signature \(\sigma \), and a message \({\varvec{m}}\) of Tier 1 or Tier 2 as input and checks the signature.
We omit the \({\mathsf {URS}}\) qualifier when it is clear from the context.
Correctness. Informally, correctness requires that for honestly generated keys, both honestly generated and honestly derived signatures must always verify.
Unforgeability. Unforgeability captures the requirement that an attacker, who is given Tier 1 and Tier 2 signatures on messages of his choice, should not be able to produce a signature on a message that is not derivable from the set of signed messages in his possession. More formally:
Definition 2
(Unforgeability). Let \({\mathsf {H}}\) output unique handles, for instance implemented using a counter. For a redactable signature scheme \({\mathsf {URS}}.\{{\mathsf {SGen}},{\mathsf {Kg}}, {\mathsf {Sign}},{\mathsf {Derive}},{\mathsf {Verify}}\}\), tables \(Q_1,Q_2,Q_3\), and an adversary \(\mathcal {A}\), consider the following game:
-
Step 1. \( SP \leftarrow {\mathsf {SGen}}(1^k); ( pk , sk )\xleftarrow {\$}{\mathsf {Kg}}( SP )\); \(Q_1, Q_2, Q_3\leftarrow \emptyset \).
-
Step 2. \(( {\varvec{m}}^*_I,\sigma ^*)\xleftarrow {\$}\mathcal {A}^{\mathcal{{O}}_{{\mathsf {Sign}}}(\cdot ),\mathcal{{O}}_{{\mathsf {Derive}}}(\cdot ,\cdot ), \mathcal{{O}}_{{\mathsf {Reveal}}}(\cdot )}( pk )\), where \(\mathcal{{O}}_{{\mathsf {Sign}}}\), \(\mathcal{{O}}_{{\mathsf {Derive}}}\), and \(\mathcal{{O}}_{{\mathsf {Reveal}}}\) behave as follows:
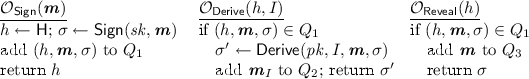
A signature scheme \({\mathsf {URS}}\) satisfies unforgeability if for all such PPT algorithms \(\mathcal {A}\) there exists a negligible function \(\nu (\cdot )\) such that in the above game the probability (over the random choices of \({\mathsf {Kg}}\), \({\mathsf {Sign}}\), \({\mathsf {Derive}}\) and \(\mathcal {A}\)) that \({\mathsf {Verify}}( pk ,\sigma ^*, {\varvec{m}}^*_I)=1\) and \(\forall {\varvec{m}}\in Q_3,\ {\varvec{m}}^*_I \ne {\varvec{m}}_{I}\), and \({\varvec{m}}^*_I \notin Q_2\) is less than \(\nu (\kappa )\).
Note that we do not consider a Tier 1 signature itself as a forgery. However, if the adversary manages to produce a valid Tier 1 signature on a message \({\varvec{m}}\) without calling \({\mathsf {Sign}}({\varvec{m}})\) and either \({\mathsf {Reveal}}(h)\) or \({\mathsf {Derive}}(h,I)\) on all subsets \(I\subseteq [1..n]\) for the corresponding handle h, he can use this Tier 1 signature to break unforgeability by deriving a Tier 2 signature from it.
Unlinkability. Informally, unlinkability ensures that an adversarial signer cannot distinguish which of two Tier 1 signatures of his choosing was used to derive a Tier 2 signature. More formally:
Definition 3
(Unlinkability). For the signature scheme \({\mathsf {URS}}.\{{\mathsf {SGen}}, {\mathsf {Kg}}, {\mathsf {Sign}}, {\mathsf {Derive}}, {\mathsf {Verify}}\}\) and a stateful adversary \(\mathcal {A}\), consider the following game:
-
Step 1. \( SP \leftarrow {\mathsf {SGen}}(1^k)\).
-
Step 2. \(( pk , I, {\varvec{m}}^{(0)}, {\varvec{m}}^{(1)}, \sigma ^{(0)}, \sigma ^{(1)})\xleftarrow {\$}\mathcal {A}( SP )\), where \( {\varvec{m}}^{(0)}_{I} = {\varvec{m}}^{(1)}_{I}\),
\({\mathsf {Verify}}( pk , \sigma ^{(0)}, {\varvec{m}}^{(0)}) = 1 \), and \({\mathsf {Verify}}( pk , \sigma ^{(1)}, {\varvec{m}}^{(1)} ) = 1\).
-
Step 3. Pick \(b \leftarrow \{0,1\}\) and form \(\sigma ^{(b)}_{I}\xleftarrow {\$}{\mathsf {Derive}}( pk ,I, {\varvec{m}}^{(b)}, \sigma ^{(b)})\).
-
Step 4. \(b'\xleftarrow {\$}\mathcal {A}(\sigma ^{(b)}_{I})\).
The signature scheme \({\mathsf {URS}}\) is unlinkable if for any polynomial time adversary \(\mathcal {A}\) there exists a negligible function \(\nu (\cdot )\) such that \( \Pr [b=b'] < \frac{1+ \nu (\kappa )}{2}\).
Note that this definition is very strong, as the adversary can even pick \( pk \).
2.2 Ideal Functionality for Unlinkable Redactable Signatures
We now give an alternative characterization of unlinkable redactable signatures using an ideal functionality \(\mathcal {F}_{\mathsf {URS}}\) defined as follows:

We point out some aspects of the ideal functionality. The functionality needs to output concrete values as signatures of messages and redacted signatures, as well as key material. To generate and verify these values, \({\mathcal {F}_{{\mathsf {URS}}}}\) requires the adversary/simulator \(\mathcal {SIM}\) to provide it with a number of polynomial-time algorithms. This is in line with how ideal functionalities for signatures, and in particular blind signatures, have been defined before [6, 35, 42, 49, 53]. We consider static corruptions of protocol machines, but allow the simulator to request the signing key at any time by sending the \(\mathtt{{leakSK}}\) message. This allows us to ensure that the privacy properties for users are still enforced even if the signer leaks its secret key. The functional and security properties are enforced by the functionality no matter how these (adversarial) algorithms compute the values. Unforgeability is enforced by the fact that \({\mathcal {F}_{{\mathsf {URS}}}}\) will output false (0) for verification queries for which the message (or a corresponding original message) has not been signed, provided that the signer is not corrupted and the signing key not leaked. (If the signer is corrupted statically, \((\mathtt{{keygen}},sid)\) will not be sent and hence \(kg \) not set and unforgeability not enforced.) Unlinkability of redacted signature is enforced by \({\mathcal {F}_{{\mathsf {URS}}}}\) as follows. It generates a fresh redacted signature only from those parts of the original message that are quoted, i.e., the hidden message parts are set to zero, and thus redacted signatures from \({\mathcal {F}_{{\mathsf {URS}}}}\) do not contain any information about the hidden parts of messages. More precisely, this is enforced for the keys generated by \({\mathcal {F}_{{\mathsf {URS}}}}\) and for any keys that an honest party successfully checked before generating a redacted signature. Unless mentioned otherwise, the reply of the functionality upon a failed check or verification is \(\bot \).
2.3 Key Registration and UC Realizability
We now want to construct a protocol \(\mathcal {R}_{{\mathsf {URS}}}\) that realizes \(\mathcal {F}_{{\mathsf {URS}}}\) using a \({\mathsf {URS}}\) scheme in the \(\mathcal {F}_{{{\mathsf {CRS}}}}\)-hybrid model where \( SP \) is the reference string and each call to \(\mathcal {F}_{{\mathsf {URS}}}\) is essentially replaced by running one of the algorithms of \({\mathsf {URS}}\). While this can be done (the detailed description of \(\mathcal {R}_{{\mathsf {URS}}}\) is given in the full version [9]), there are a number of hurdles that need to be overcome. These hurdles are quite typical and include, e.g., that we need to be able to extract the secret keys from the adversary to be able to simulate properly. They are, however, often treated only informally in security proofs. Here we want to make them explicit and treat them formally correct. So our goal is to prove a statement (Theorem) of the form:
If \({\mathsf {URS}}\) is correct, unforgeable, unlinkable, and X then \({\mathcal {R}_{{\mathsf {URS}}}}\) securely realizes \(\mathcal {F}_{{\mathsf {URS}}}\) in the \(\mathcal {F}_{{{\mathsf {CRS}}}}\) -hybrid model.
What do we have to require from X to make this theorem true? To prove the theorem we have to show indistinguishability between the ideal world and the real world. In the ideal world, an environment \(\mathcal {Z}\) interacts with the simulator \(\mathcal {SIM}\) and functionality \(\mathcal {F}_{{\mathsf {URS}}}\). In the real world, the environment \(\mathcal {Z}\) interacts with the real adversary \(\mathcal {A}\) and the protocol \(\mathcal {R}_{{\mathsf {URS}}}\).
We provide a tentative description of \(\mathcal {SIM}\) in the ideal world: when receiving the \((\mathtt{{initF}}, sid )\) message from \(\mathcal {F}_{{\mathsf {URS}}}\), it generates a trapdoor \({td}\) (in addition to \( SP \)) and returns \((\mathtt{{initF}}, { sid }, SP , {\mathsf {Kg}}, {\mathsf {Sign}}, {\mathsf {Derive}}, {\mathsf {Verify}})\). On receiving the \((\mathtt{{checkPK}}, sid , pk )\) message, is uses the trapdoor to extract the secret key \( sk \) and returns \( sk \) to \(\mathcal {F}_{{\mathsf {URS}}}\).
To make this work, we extend \({\mathsf {URS}}\) with several algorithms: \({{\mathsf {CheckPK}}}\) is run by \(\mathcal {R}_{{\mathsf {URS}}}\) on receiving a message \((\mathtt{{checkPK}}, sid , pk )\). \({\mathsf {SGenT}}\) and \({{\mathsf {ExtractKey}}}\) are the trapdoored parameter generation and key extraction algorithm for \(\mathcal {SIM}\). \(\mathsf {CheckKeys}\) is used to define what it means to extract a valid key.
-
\({\mathsf {URS}}.{{\mathsf {CheckPK}}}( pk ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}0/1.\) \({{\mathsf {CheckPK}}}\) is a deterministic algorithm that takes a public key \( pk \) as an input and checks that it is correctly formed. It outputs 1 if \( pk \) is correct, and 0 otherwise.
-
\({\mathsf {URS}}.{\mathsf {SGenT}}(1^{\kappa }) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}( SP , {td}).\) \({\mathsf {SGenT}}\) is a system parameters generation algorithm that takes the security parameter \(1^{\kappa }\) as input and outputs the system parameters \( SP \) and a trapdoor \({td}\) for the key extraction algorithm.
-
\({\mathsf {URS}}.{{\mathsf {ExtractKey}}}( pk , {td}) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }} sk .\) \({{\mathsf {ExtractKey}}}\) is an algorithm that takes a public key \( pk \) and a trapdoor \({td}\) as input. It extracts the corresponding secret key \( sk \) .
-
\({\mathsf {URS}}.\mathsf {CheckKeys}( pk , sk ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}0/1.\) \(\mathsf {CheckKeys}\) is an algorithm that takes a public \( pk \) and a private \( sk \) keys and checks if they constitute a valid signing key pair. It outputs 1 if they do, and 0 otherwise.
Strengthened Correctness requires that honestly generated keys, but also keys for which predicate \(\mathsf {CheckKeys}( pk , sk )\) holds can be used to create signatures that will verify. It moreover guarantees that \({{\mathsf {CheckPK}}}( pk )\) holds for honestly generated public keys.
Parameter Indistinguishability. Informally, parameter indistinguishability ensures that the \( SP \) produced by \({\mathsf {SGenT}}\) and \({\mathsf {SGen}}\) are computationally indistinguishable. It is formally defined as follows:
Definition 4
(Parameter Indistinguishability). A redactable signature scheme \({\mathsf {URS}}.\{{\mathsf {SGen}}, {\mathsf {Kg}}, {\mathsf {Sign}}, {\mathsf {Derive}},{\mathsf {Verify}}\}\) with alternative parameter generation \({\mathsf {SGenT}}\) is parameter indistinguishable if for any polynomial time adversary \(\mathcal {A}\) there exists a negligible function \(\nu (\cdot )\) such that \( \Pr [( SP _{0} , {td})\leftarrow {\mathsf {SGenT}}(1^k);\ SP _{1} \leftarrow {\mathsf {SGen}}(1^k);\ b\leftarrow \{0,1\};\ b' \leftarrow \mathcal {A}( SP _{b}) : b=b'] < \frac{1+ \nu (\kappa )}{2}. \)
Key Extractability. Informally, the key extractability ensures that if \({\mathsf {SGenT}}\) was run and if \({{\mathsf {CheckPK}}}\) outputs 1, then the extraction algorithm \({{\mathsf {ExtractKey}}}( pk , {td})\) will output a valid secret key \( sk \), i.e. \(\mathsf {CheckKeys}( pk , sk ) = 1\).
Definition 5
(Key Extractability). A redactable signature scheme \({\mathsf {URS}}.\{{\mathsf {SGen}}, {\mathsf {Kg}}, {\mathsf {Sign}}, {\mathsf {Derive}}, {\mathsf {Verify}}\}\) with additional algorithms \(({{\mathsf {CheckPK}}}, \;{\mathsf {SGenT}},\; \mathsf {CheckKeys},{{\mathsf {ExtractKey}}})\) is key extractable if \(\mathsf {CheckKeys}\) is correct and for any polynomial time adversary \(\mathcal {A}\) there exists a negligible function \(\nu (\cdot )\) such that \(\Pr [( SP , {td})\leftarrow {\mathsf {SGenT}}(1^k);\ pk \leftarrow \mathcal {A}( SP , {td});\ sk \leftarrow {{\mathsf {ExtractKey}}}( pk ,{td}): ({{\mathsf {CheckPK}}}( pk ) =1 \wedge \mathsf {CheckKeys}( pk , sk )=0) ) ] < \nu (\kappa )\).
Composable Unlinkability holds even when parameters in the unlinkability game are generated using \(( SP , {td})\leftarrow {\mathsf {SGenT}}(1^k)\) and \(\mathcal {A}\) is handed \({td}\). This allows for the use of the game in a hybrid argument when proving the security of the simulator. We note that in such an adapted unlinkability game the trapdoor \({td}\) must only enable key-extraction, and crucially does not allow the adversary to extract a Tier 1 signature from a Tier 2 signature (this would break unlinkability). In our instantiation this is achieved by splitting \( SP \) into several parts. The trapdoor is only generated for the part used for key extraction.
UC Realization. We prove that if an unlinkable redactable signature \({\mathsf {URS}}\) is correct, parameter indistinguishable, key extractable, unforgeable, and unlinkable, then \(\mathcal {R}_{{\mathsf {URS}}}\) securely realizes \(\mathcal {F}_{{\mathsf {URS}}}\). More formally, we have the following theorem (which is proven in the full version of this paper [9]).
Theorem 1
Let \({\mathsf {URS}}\) be an unlinkable redactable signature scheme. If \({\mathsf {URS}}\) is correct, parameter indistinguishable, key-extractable, unforgeable, and composable unlinkable then \({\mathcal {R}_{{\mathsf {URS}}}}\) securely realizes \(\mathcal {F}_{{\mathsf {URS}}}\) in the \(\mathcal {F}_{{{\mathsf {CRS}}}}\)-hybrid model.
3 The Construction of Our Redactable Signature Scheme
As a first step toward our full solution, we will construct an unforgeable and unlinkable URS scheme without key extraction. The scheme should be of independent interest, in case universal composability is not a design requirement. This isolation of key extraction, seemingly only needed for universal composition, is a nice feature of our definitions.
Let \(\mathcal{G}\) be a bilinear group generator that takes as an input security parameter \(1^\kappa \) and outputs the descriptions of multiplicative groups \( grp =(p,\mathbb {G},\tilde{\mathbb {G}},{\mathbb {G}_{t}}, e, G , \tilde{G} )\) where \(\mathbb {G}\), \(\tilde{\mathbb {G}}\), and \({\mathbb {G}_{t}}\) are groups of prime order p, e is an efficient, non-degenerating bilinear map \(e: \mathbb {G}\times \tilde{\mathbb {G}}\mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}{\mathbb {G}_{t}}\), and \( G \) and \( \tilde{G} \) are generators of the groups \(\mathbb {G}\) and \(\tilde{\mathbb {G}}\), respectively.
Our construction makes use of a structure preserving signature (SPS) scheme \({\mathsf {SPS}}.\{{\mathsf {Kg}}, {\mathsf {Sign}}, {\mathsf {Verify}}\}\) and a vector commitment scheme \({\mathsf {VC}}.\{{\mathsf {Setup}}, {\mathsf {Commit}}, {\mathsf {Open}},\!{\mathsf {Check}}\}\). We recall that the structure-preserving property of the signature scheme requires that verification keys, messages, and signatures are group elements and the verification predicate is a conjunction of pairing product equations. The intuition behind our construction is susceptibly simple: Use \({\mathsf {SPS}}.{\mathsf {Kg}}\) to generate a signing key pair and \({\mathsf {VC}}.{\mathsf {Setup}}\) to add commitment parameters to the public key. To sign a vector \({\varvec{m}}\), first, commit to \({\varvec{m}}\) and then sign the resulting commitment C. To derive a quote for a subset I of the messages, simply open the commitment to the messages in \({\varvec{m}}_I\). We verify a signature on a quote by verifying both the structure-preserving signature (\({\mathsf {SPS}}.{\mathsf {Verify}}\)) and checking the opening of the commitment (\({\mathsf {VC}}.{\mathsf {Check}}\)).
Such a scheme has, however, several shortcomings. First, it is linkable, as the same commitment is reused across multiple quotes of the same message. Even if both the underlying SPS scheme and the commitment scheme are individually re-randomizable, this seems hard to avoid as the unforgeability of the SPS scheme prevents randomization of the message. Second, such a construction is only heuristically secure. Existing vector commitments do not guarantee that multiple openings cannot be combined and mauled into an opening for a different sub-vector. We call vector commitment schemes that prevent this opening non-malleable. (Recently, [47] constructed an SPS scheme allowing for randomization within an equivalence class. However, their commitments cannot be opened to arbitrary vectors of \(\mathbb {Z}_p\) and are not provably opening non-malleable.)
Our main design goal is to address both of these weaknesses while avoiding a large performance overhead. Our main tool for this is an efficient non-interactive proof-of-knowledge. Intuitively, we hide the commitments and their openings, as well as a small part of the signature to achieve unlinkability. Hiding the commitment opening also helps solve the malleability problems for commitments. To achieve real-world efficiency we show how to exploit the re-randomizability of the SPS (and optionally the commitment scheme as described in the full version [9]).
Before describing our redactable signature scheme in more detail, we present a vector commitment scheme that uses a variant of polynomial commitments from [51]. While our changes are partly cosmetic, they simplify the assumption needed for opening non-malleability.
3.1 Vector Commitments Simplified
A vector of messages \({\varvec{m}}\in \mathbb {Z}_p^n\) is committed using a polynomial f(x) that has a value \(f(i)=m_i\) at the position i. In Lagrange form such a polynomial is a linear combination \(f(x)= \sum _{i=1}^n m_i f_i(x)\) of Lagrange basis polynomials \(f_i(x)=\prod _{j=0, j\ne i}^n \frac{x-j}{i-j}\). To batch-open a vector commitment for a position set \(I\subseteq \{1,\dots ,n\}\), one uses a polynomial \(f_{{I}}(x) = \sum _{i\in I} m_{i} f_{i}(x)\). For such a polynomial, it holds that \(f_{{I}}(i)=m_{i}\) for \(i\in I\); and \(f_{I}(0)=0\). (The additional root at 0 is necessary to achieve opening non-malleability). The reuse of the same Lagrange basis polynomials, which yields polynomials of not the lowest possible degree, reduces the number of variable bases in the equation of \({\mathsf {Check}}\) below and increases efficiency when used for the construction of bigger protocols such as anonymous credential. Also, note that \(f(x)-f_{{I}}(x)\) is divisible by the polynomial \(p_{I}(x)=x \cdot \prod _{i\in I}(x-i)\). We use the polynomial \(p(x) = x \cdot \prod _{i=1}^n (x-i)\) which is divisible by \(p_{I}(x)\) for any \(I\subseteq \{1,\dots ,n\}\) to randomize commitments to make them perfectly hiding.
Construction. We reuse the notation of Sect. 2 and use Tier 1 vectors \({\varvec{m}}\) for the vectors being committed and Tier 2 vectors \({\varvec{m}}_I\) for batch openings at positions I. We also let \( grp =(p,\mathbb {G}, \mathbb {\tilde{G}}, {\mathbb {G}_{t}}, e , G , \tilde{G} )\) be bilinear map parameters generated by a bilinear group generator \(\mathcal {G}(1^\kappa )\).
-
\({\mathsf {VC}}.{\mathsf {Setup}}( grp ).\) Pick \(\alpha \leftarrow \mathbb {Z}_p\) and compute \(( G _1, \tilde{G} _1,\ldots , G _{n+1}, \tilde{G} _{n+1})\), where \( G _i = G ^{(\alpha ^i)}\) and \( \tilde{G} _i = \tilde{G} ^{(\alpha ^i)}\). Output parameters \( pp = ( grp ,G_1, \tilde{G} _1,\ldots ,G_{n+1}, \tilde{G} _{n+1})\). Values \(G_1,\ldots ,G_{n+1}\) suffice to compute \(G^{\phi (\alpha )}\) for any polynomial \(\phi (x)\) of maximum degree \(n+1\) (and similarly for \( \tilde{G} ^{\phi (\alpha )}\)).
Furthermore, for the above defined \(f_i(x)\), p(x), and \(p_I(x)\), we implicitly define \(F_i=G^{f_i(\alpha )}\), \(P=G^{p(\alpha )}\), \(P_{I}= G^{p_{I(\alpha )}}\), and \(\tilde{P}_{I}= \tilde{G}^{p_{I(\alpha )}}\). These group elements can be computed from the parameters \( pp \).
-
\({\mathsf {VC}}.{\mathsf {Commit}}( pp , {\varvec{m}},r).\) Output \(C= \prod _{i=1}^{n} F_i^{m_i} P^r\).
-
\({\mathsf {VC}}.{\mathsf {Open}}( pp , I, {\varvec{m}}, r).\) Let \(w(x)= \frac{f(x)-f_{I}(x)+ r \cdot p(x)}{p_I(x)}\) and compute the witness \(W=G^{w(\alpha )}\) using parameters \( pp \).
-
\({\mathsf {VC}}.{\mathsf {Check}}( pp , C, {\varvec{m}}_{I}, W).\) Accept if \(e(C, \tilde{G} ) = e(W, \tilde{P}_{I}) e(\prod _{i\in I} F_{i}^{m_{i}}, \tilde{G} )\).
Note that \(p_I(x)\) always has the factor x. This is essential for achieving opening non-malleability. If \(p_I(x)\) would be 1 for \(I=\emptyset \), as in the original polynomial commitment scheme of [51], then C would be a valid batch opening witness for the empty set of messages.
Security Analysis. We require the commitment scheme to be complete, batch binding, and opening non-malleable. Completeness is standard for a commitment scheme follows easily from the following equation: \( e(C, \tilde{G} ) = e( G , \tilde{G} )^{f(\alpha )+r\cdot p(\alpha )} \!= e( G ,\tilde{P}_{I})^{\frac{f(\alpha )-f_I(\alpha )+r\cdot p(\alpha )}{p_I(\alpha )}} e( G , \tilde{G} )^{f_I(\alpha )} = e(W, \tilde{P}_{I}) e(\prod _{i\in I} F_{i}^{m_{i}}, \tilde{G} ). \)
Next, we define the batch binding and opening non-malleability properties:
Definition 6
(Batch Binding). For a vector commitment scheme \({\mathsf {VC}}.\{{\mathsf {Setup}},{\mathsf {Commit}},{\mathsf {Open}},{\mathsf {Check}}\}\) and an adversary \(\mathcal {A}\) consider the following game:
-
Step 1. \( grp \leftarrow \mathcal {G}(1^\kappa )\) and \( pp \leftarrow {\mathsf {VC}}.{\mathsf {Setup}}( grp )\)
-
Step 2. \(C,{\varvec{m}}_{I},W,{\varvec{m}}'_{I'}, W' \leftarrow \mathcal {A}( pp )\)
Then, the commitment scheme satisfies batch binding if for all such PPT algorithms \(\mathcal {A}\) there exists a negligible function \(\nu (\cdot )\) such that the probability (over the choices of \(\mathcal {G},{\mathsf {Setup}}, and\; \mathcal {A}\)) that \(1={\mathsf {VC}}.{\mathsf {Check}}( pp ,C,{\varvec{m}}_{I},W)={\mathsf {VC}}.{\mathsf {Check}}( pp ,C,{\varvec{m}}'_{I'},W')\) and that there exist \(i\in I \cap I'\) such that \(m_{i}\ne m'_{i}\) is at most \(\nu (\kappa )\). (Note that \({\varvec{m}}_I\) and \({\varvec{m}}'_{I'}\) are Tier 2 vectors, and thus encode the sets I and \(I'\) respectively.)
Definition 7
(Opening Non-malleability). For a vector commitment scheme \({\mathsf {VC}}.\{{\mathsf {Setup}},{\mathsf {Commit}},{\mathsf {Open}},{\mathsf {Check}}\}\) and an adversary \(\mathcal {A}\) consider the following game:
-
Step 1. \( grp \leftarrow \mathcal {G}(1^\kappa )\) and \( pp \leftarrow {\mathsf {VC}}.{\mathsf {Setup}}( grp )\)
-
Step 2. \({\varvec{m}}, I \leftarrow \mathcal {A}( pp )\)
-
Step 3. Pick random r, compute \(C\!\leftarrow \! {\mathsf {VC}}.{\mathsf {Commit}}( pp ,{\varvec{m}},r)\),
and \(W\! \leftarrow \! {\mathsf {VC}}.{\mathsf {Open}}( pp ,I ,{\varvec{m}},r)\).
-
Step 4. \(W',I' \leftarrow \mathcal {A}(C,W)\)
Then the commitment scheme satisfies opening non-malleability if for all such PPT algorithms \(\mathcal {A}\) there exists a negligible function \(\nu (\cdot )\) such that the probability (over the choices of \(\mathcal {G}\), \({\mathsf {Setup}}\), \({\mathsf {Commit}}\), and \(\mathcal {A}\) that \(1={\mathsf {VC}}.{\mathsf {Check}}( pp ,C,{\varvec{m}}_{I'},W')\), and \(I\ne I'\) is at most \(\nu (\kappa )\).
In the following theorems we make use of the n-BSDH assumption [44] and the n-RootDH assumption that are defined next. See the full version of this paper [9] for its generic group model proof. (We note that this assumption is only required for opening non-malleability, which is ignored by most existing constructions of anonymous credentials from vector commitments.)
Definition 8
(n-SDH Assumption). The n-strong Diffie-Hellman (n-SDH) assumption [16] states that there exists a \(\mathcal{G}\) that for all algorithms \(\mathcal {A}\), the following advantage
The n-BSDH assumption is defined identically to n-SDH except that now \(\mathcal {A}\) is challenged to compute \((c,e( G , \tilde{G} ^{1/(x+c)})\). Note that the n-BSDH assumption is already implied by the n-SDH assumption.
Definition 9
(n-RootDH Assumption).
For an adversary \(\mathcal {A}\) consider the following game:
-
Step 1. \( grp \leftarrow \mathcal {G}(1^\kappa )\)
-
Step 2. Pick random \(\alpha , r \leftarrow \mathbb {Z}_p^*\), compute \(X=(G^{\alpha \cdot \prod _{i=1}^n(\alpha -i)})^r\).
-
Step 3. \((J, state ) \leftarrow \mathcal {A}(G, \tilde{G} ,\{G^{\alpha ^i}, \tilde{G} ^{\alpha ^i}\}_{i=1}^{n+1},X)\)
-
Step 4. Compute \(Y=(G^{\prod _{i\in J}(\alpha -i)})^r\).
-
Step 5. \(J', Z \leftarrow \mathcal {A}( state , Y)\)
Then the group generator \(\mathcal {G}\) satisfies the n-RootDH assumption if for all such PPT algorithms \(\mathcal {A}\) there exists a negligible function \(\nu (\cdot )\) such that the probability (over the choices of \(\mathcal {G}\), \(\alpha \), r, and \(\mathcal {A}\) that J and \(J'\) are subsets of [1..n], \(J'\ne J\), and \(Z=(G^{\prod _{i\in J'}(\alpha -i)})^r\) is at most a negligible function \(\nu (\kappa )\).
Theorem 2
The commitment scheme \({\mathsf {VC}}\) defined above is batch binding under the \((n+1)\)-BSDH assumption. The proof is similar to that of [51] and can be found in the full version [9].
Theorem 3
The commitment scheme \({\mathsf {VC}}\) defined above is opening non-malleable under the n-RootDH assumption. The proofs can be found in the full version [9].
3.2 Non-interactive Zero-Knowledge and Witness Indistinguishable Proof Systems
Let R be an efficiently computable binary relation. For pairs \((W, Stmt ) \in R\) we call \( Stmt \) the statement and W the witness. Let \(\mathcal {L}\) be the language consisting of statements in R. A non-interactive zero-knowledge (NIZK) proof-of-knowledge system for a language \(\mathcal {L}\) consists of the following algorithms and protocols:
-
\(\varPi .{\mathsf {Setup}}( grp ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }} CRS .\) On input \( grp \leftarrow \ (1^{\kappa })\), it outputs common parameters (a common reference string) \( CRS \) for the proof system.
-
\(\varPi .{\mathsf {Prove}}( CRS , W, Stmt )\mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}\pi .\) On input a statement \( Stmt \) and a witness W, it generates a zero-knowledge proof \(\pi \) that the witness satisfies the statement.
-
\(\varPi .{\mathsf {Verify}}( CRS ,\pi , Stmt ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}0/1.\) On input \( Stmt \) and \(\pi \), it outputs 1 if \(\pi \) is valid, and 0 otherwise.
We explain the notation for the statements \( Stmt \). We call extractable (f-extractable [12]) witnesses that can be (only partially) extracted from the corresponding proof, respectively. To express the “extractability” property of the witnesses we use notation introduced by Camenisch et al. [28]. For the extractable witnesses we use the “knowledge” notation ( ), and for the f-extractable witnesses we use “existence” (
), and for the f-extractable witnesses we use “existence” ( ) notation. (If function f is constant, nothing can be extracted.) We define \(\mathfrak {K}\) as a set of extractable witnesses and \(\mathfrak {E}\) as a set of the witnesses that we can only prove existence about. We only consider proofs for multi-exponentiations (for existence) and pairing products (for existence and knowledge) equations. The following is an examplary statement:
) notation. (If function f is constant, nothing can be extracted.) We define \(\mathfrak {K}\) as a set of extractable witnesses and \(\mathfrak {E}\) as a set of the witnesses that we can only prove existence about. We only consider proofs for multi-exponentiations (for existence) and pairing products (for existence and knowledge) equations. The following is an examplary statement:

For simplicity of presentation, we do not explicitly specify public values of a statement as additional input to the algorithms, since they are clear from the description of the statement and the list of witnesses.
We employ different proof systems that are either witness indistinguishable or zero-knowledge in terms of privacy, and either extractable or simulation-extractable in term of soundness. For the security proofs we introduce the following algorithms:
-
\(\varPi .\mathsf{ExtSetup}( grp ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}( CRS , {td}_{ext}).\) On input \( grp \), it outputs a common reference string \( CRS \) and a trapdoor \({td}_\mathsf{ext}\) for extraction of valid witnesses from valid proofs. This is for witness-indistinguishable extractable proofs.
-
\(\varPi .\mathsf{SimSetup}( grp ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}( CRS , {td}_{ext}, {td}_{sim})\) It outputs a CRS and the extraction and simulation trapdoors. This is for proofs that are also zero-knowledge.
-
\(\varPi .\mathsf{SimProve}( CRS , {td}_\mathsf{sim}, Stmt )\mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}{\pi }.\) On input \( CRS \) and a trapdoor \({td}_{sim}\), it outputs a simulated proof \({\pi }\) such that \(\varPi .{\mathsf {Verify}}( CRS , \pi , Stmt )=1\).
-
\(\varPi .\mathsf{Extract}( CRS , {td}_\mathsf{ext}, \pi , Stmt ) \mathop {\rightarrow }\limits ^{{\scriptscriptstyle }}W.\) On input a proof \(\pi \) and a trapdoor \({td}_\mathsf{ext}\), it extracts a witness W that satisfies the statement \( Stmt \) of the proof \(\pi \).
For simulation-extractable NIZK proofs (that are non-malleable) we also allow an additional public input to the \({\mathsf {Prove}}, \mathsf{Extract}, \mathsf{SimProve}\), and \({\mathsf {Verify}}\) algorithms – a message (label) L, which is non-malleably attached to the proof (i.e. the signature of knowledge is computed on this message). We provide a formal definition below.
Definition 10
(Simulation Extractability). A proof system \(\varPi \) is called simulation extractable with labels if for any PPT adversary \(\mathcal {A}\) and security parameter \(\lambda \) there exists a negligible function \(\mathsf {negl}(\cdot )\) such that:
3.3 Our Redactable Signature Scheme
We construct our redactable signature scheme \({\mathsf {URS}}\) from a structure-preserving signature scheme \({\mathsf {SPS}}\), a vector commitment scheme \({\mathsf {VC}}\), and an extractable and witness-indistinguishable non-interactive proof-of-knowledge system \(\varPi \) described in the previous section. Some SPS and vector commitment schemes might also support randomization; we already discussed such a property for vector commitments in the last sub-section; for signatures we refer the reader to [2, 3]. We denote the randomization algorithm of signatures by \({\mathsf {SPS}}.{\mathsf {Rand}}\). We denote the randomizable elements of a SPS signature \(\varSigma \) by \(\psi _\texttt {rnd}(\varSigma )\) and the other elements by \(\psi _\texttt {wit}(\varSigma )\). (For a non-randomizable SPS signature \(\psi _\texttt {wit}(\varSigma )\) = \(\varSigma \).)
Our construction does not utilize any randomizability in the vector commitment scheme itself. In the full version [9] we analyze batch-binding and opening non-malleability in presence of such a randomization algorithm.
Construction.
-
\({\mathsf {URS}}.{\mathsf {SGen}}(1^{\kappa }).\) Compute \( grp \!\leftarrow \! \mathcal {G}(1^\kappa )\), \( pp \!\leftarrow \! {\mathsf {VC}}.{\mathsf {Setup}}( grp )\), \( CRS \!\leftarrow \! \varPi .{\mathsf {Setup}}( grp )\), output \( SP =( grp , pp , CRS )\).
-
\({\mathsf {URS}}.{\mathsf {Kg}}( SP ).\) Obtain \( grp \) from \( SP \), generate \(({ pk }_{sps},{ sk }_{sps})\leftarrow {\mathsf {SPS}}.{\mathsf {Kg}}( grp )\), output \( pk =({ pk }_{ sps }, SP )\) and \( sk =({ sk }_{ sps }, pk )\).
-
\({\mathsf {URS}}.{\mathsf {Sign}}( sk , {\varvec{m}}).\) Pick \(r\leftarrow \mathbb {Z}_p\), compute \(C={\mathsf {VC}}.{\mathsf {Commit}}( pp ,{\varvec{m}},r)\) and \(\varSigma \leftarrow {\mathsf {SPS}}.{\mathsf {Sign}}( sk _{sps},C)\), and return \(\sigma =(\varSigma ,C,r)\).
-
\({\mathsf {URS}}.{\mathsf {Derive}}( pk , I, {\varvec{m}}, \sigma ).\) First, compute \(W={\mathsf {VC}}.{\mathsf {Open}}( pp ,I,{\varvec{m}},r)\). Then, if a \({\mathsf {SPS}}.{{\mathsf {Rand}}}\) algorithm is present, randomize the signature as \(\varSigma '\leftarrow {\mathsf {SPS}}.{{\mathsf {Rand}}}( pk _{ sps },\varSigma )\); otherwise, set \({\varSigma }'\leftarrow \varSigma \). And compute the proof
 Return \(\sigma =(\psi _\texttt {rnd}({\varSigma }'),\pi )\) as the signature on \({\varvec{m}}_{I}\).
Return \(\sigma =(\psi _\texttt {rnd}({\varSigma }'),\pi )\) as the signature on \({\varvec{m}}_{I}\). -
\({\mathsf {URS}}.{\mathsf {Verify}}( pk , \sigma , {\varvec{m}}_{I}).\) Check that
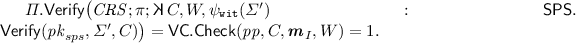
Theorem 4
\({\mathsf {URS}}\) is an unforgeable redactable signature scheme, if the SPS scheme is unforgeable, the vector commitment scheme satisfies the batch binding and opening non-malleability property, and the proof-of-knowledge system is extractable and witness indistinguishable. The proofs of Theorems 4 is provided in the full version [9].
Theorem 5
\({\mathsf {URS}}\) is an unlinkable redactable signature scheme if the proof-of-knowledge system is witness indistinguishable. The proofs are given in the full version of this paper [9].
Strengthened Scheme for an Universally Composable Construction. To be able to satisfy the UC functionality, we require an additional key-extraction property. We thus build an augmented redactable signature scheme \({\mathsf {URS}}\) from a redactable signature scheme \({\mathsf {URS}}^*\) (without key extraction) and a zero-knowledge non-interactive proof-of-knowledge system \(\varPi ^*\).
-
\({\mathsf {URS}}.{\mathsf {SGen}}(1^{\kappa }).\) Run \({ SP ^*}\leftarrow {\mathsf {URS}}^*.{{\mathsf {SGen}}}(1^{\kappa })\), get \( grp \) from \({ SP ^*}\), run \({ CRS _{sk}}\leftarrow \varPi ^*.{\mathsf {Setup}}( grp )\), and output \( SP =({ SP ^*},{ CRS _{sk}})\).
-
\({\mathsf {URS}}.{\mathsf {Kg}}( SP ).\) Obtain \( SP ^*\) and \( CRS _{sk}\) from \( SP \), sample randomness r, and run \(( pk ^*, sk ^*)\!\leftarrow {\mathsf {URS}}^*.{\mathsf {Kg}}( SP ^*;r)\). Compute the proof
 Output \( pk =( SP , pk ^*, \pi _{sk})\) and \( sk =( sk ^*, pk )\). We note that \({\mathsf {URS}}^*.{{\mathsf {Kg}}}( SP ^*;r)\) fixes the randomness of the a key generation algorithm.
Output \( pk =( SP , pk ^*, \pi _{sk})\) and \( sk =( sk ^*, pk )\). We note that \({\mathsf {URS}}^*.{{\mathsf {Kg}}}( SP ^*;r)\) fixes the randomness of the a key generation algorithm. -
\({\mathsf {URS}}.{{\mathsf {CheckPK}}}( SP , pk ).\) Check

\({\mathsf {Sign}}\), \({\mathsf {Derive}}\), \({\mathsf {Verify}}\) are almost unchanged and use \( pk ^*\) internally. \({\mathsf {SGenT}}\) and \({{\mathsf {ExtractKey}}}\) use the extraction setup and extractor of the proof system respectively, while \(\mathsf {CheckKeys}\) checks that the relation R holds for \( pk \) and \( sk \).
Note that Groth-Sahai proofs can be used to implement key-extraction by proving a binary, or n-ary decomposition of the secret key [57]. But this comes at a huge cost of more than 61,000 group elements at 128-bit security, even if this cost is only incurred once by every user per public key. We propose instead to use fully structure-preserving signatures (FSPS) [5] such that \( sk \) consists of group elements and can be easily extracted. FSPS for signing single group elements can be as cheap as 15 elements per signature and proofs of key possession consist of just 18 elements.
Theorem 6
The strengthened scheme \({\mathsf {URS}}\) is an unforgeable, unlinkable, and key extractable redactable signature scheme, if the underlying redactable signature scheme \({\mathsf {URS}}^*\) is unforgeable and unlinkable, and the proof-of-knowledge system \(\varPi ^*\) is zero-knowledge and extractable.
Unforgeability and unlinkability are corollaries of Theorem 4 and Theorem 5. Key-extractability follows directly from the extractability of the proof system.
Signing Group Elements as Additional Parts of the Message. While the presented redactable signature scheme can sign and quote a large number of values in \(\mathbb {Z}_p\) very efficiently, in certain applications, like the one presented in the next section, one might also need to sign a small number of additional group elements. In the \({\mathsf {Derive}}\) algorithm these elements will either be part of the derived message, and given in the clear after derivation, or be treated as part of the witness, i.e., hidden from the verifier. The detailed construction and the security proofs are given in the full version [9].
4 From Unlinkable Redactable Signatures to Anonymous Credentials
As we designed our UC-secure URS scheme as a building block for privacy-preserving protocols, anonymous credentials are a natural application. Indeed, an (unlinkable) redactable signature scheme is already a simple selective-disclosure credential system where the attributes issued to users are the messages signed in Tier 1 signatures and a user can later reveal a subset of her attributes by deriving a Tier 2 signature. However, in an anonymous credential system, users also require secret keys and pseudonyms (pseudonymous public keys), on which credentials can be issued and with respect to which credentials can be presented. This allows users to prove that they possess several credentials issued from different parties on the same secret key [19, 31].
In this section, we extend the functionality of \({{\mathsf {URS}}}\) in two ways: (1) we bind Tier 1 signatures to user secret keys in a way that prevents the derivation of signatures without knowledge of the secret and (2) we bind Tier 2 derived signatures to the unique context, \( cxt \) (nonce), to prevent replay attacks in which an attacker shows the same signature derived twice.
We first recall the algorithms of a multi-issuer anonymous credential system and then provide an instantiation using \({\mathsf {URS}}\). To be modular and to simplify the analysis, we then provide an ideal functionality for a single issuer. The functionality is carefully designed to self-compose naturally into a full-fledged credential system with multiple issuers. Finally, we provide a concrete instantiation of our generic construction and analyze its efficiency.
4.1 Algorithms of Our Anonymous Credential System
Let us first introduce the parties and the algorithms of a multi-issuer anonymous credential system supporting user attributes (cf. [19, 31]). Its protagonists are users (\(\mathcal {U}\)), issuers (\(\mathcal {I}\)), and verifiers (\(\mathcal {V}\)). Each user has a secret key \( X \), from which she can derive (cryptographic) pseudonyms \( P \). To get a credential issued, a user sends to the issuer a pseudonym \( P \) together with a (non-interactive) proof \(\pi _{ X , P }\) that she is privy to the underlying secret key. The issuer will then issue her a credential \( Cred \) on \( P \) containing the attributes \({\varvec{a}}\) the issuer vouches for. The user can then present the credential to a verifier under a potentially different pseudonym \(P'\) by sending, together with \(P'\), a (non-interactive) proof \(\pi _{ X , Cred }\) that she possesses a credential on the attributes \({\varvec{a}}_I\). Recall that I defines which attributes shall be revealed.
A credential system \({\mathsf {Cred}}\) defines a set of algorithms: a system parameters generation algorithm \({\mathsf {SGen}}\); an issuer setup algorithm \({\mathsf {Kg}}\); a user secret generation algorithm \({\mathsf {SecGen}}\); algorithms for pseudonym generation and verification \({\mathsf {NymGen}}\) and \({\mathsf {NymVerify}}\), respectively; an algorithm to request a credential \({\mathsf {RequestCred}}\); an algorithm for issuing a credential \({\mathsf {IssueCred}}\); an algorithm to check a newly issued credential for correctness \({\mathsf {CheckCred}}\); an algorithm to show a credential with respect to a pseudonym (to create a credential proof) \({\mathsf {Prove}}\); and an algorithm to verify a credential proof \({\mathsf {Verify}}\).
A more detailed discussion of these algorithms is given in the full version [9]. We instantiate these algorithms by adding support for user secrets, pseudonyms and contexts to our redactable signature scheme. Besides the \({{\mathsf {URS}}}\) algorithms, we use pseudonym generation and verification algorithms based on a structure preserving commitment scheme \({\mathsf {SPC}}\) and a hard relation to generate credential specific secrets. A hard relation has a generator \({\mathsf {K}}_{{\mathsf {R{gap}}}}\) that generates a witness \((X_ Cred \) and a public value \(Y_ Cred )\), and a verification algorithm \({\mathsf {V}}_{{\mathsf {R{gap}}}}\), such that it is easy to verify \((X_ Cred , Y_ Cred )\) but hard to compute \(X_ Cred \) from \(Y_ Cred \). This hardness is used to prevent a network adversary that observes the issuing protocol from impersonating the user.
Table 1 gives the construction of our credential scheme. We group the core credential algorithms into those used for setup, issuing and presentation. In our security definition and the proof we will make use of additional algorithms for simulation and extraction.
4.2 Ideal Functionality for Credentials
To tame the complexity of definitions for credential systems with many different issuers, we chose to give a definition \(\mathcal {F}_{\mathsf {Cred}}\) of a scheme for a single issuer only, that then can be used as building block to a a full-fledged credential system with multiple issuers. The single issuer functionally \(\mathcal {F}_{\mathsf {Cred}}\) will just allow users to get a credential on a pseudonym from the issuer and to prove ownership of a credential by the issuer w.r.t. a given pseudonym.
To serve as a secure building block, \(\mathcal {F}_{\mathsf {Cred}}\) must be carefully designed. On the one hand it must deal with the unforgeability of credentials and on the other hand it must provide the hooks such that colluding users cannot mix and match credentials from different issuers. To address the former \(\mathcal {F}_{\mathsf {Cred}}\) binds issued credentials to the respective users’ secret key X and for the latter \(\mathcal {F}_{\mathsf {Cred}}\) will enforce that credential proofs will not verify w.r.t. a pseudonym P unless a corresponding credential got issued to the X underlying that pseudonym. Then, provided adversarial users are unable to provide different X’s for the same pseudonym, credentials from different issuers issued to different users (i.e., different X’s) cannot be matched. As a consequence of this, the generation of user secret keys and pseudonyms is not done inside \(\mathcal {F}_{\mathsf {Cred}}\) but users are require to input their secret key X the pseudonym P (as cryptographic values) to \(\mathcal {F}_{\mathsf {Cred}}\) on the calls to get credentials issued or to generate a credential proof. Thus we assume that algorithms \(({\mathsf {SecGen}},{\mathsf {NymGen}},{\mathsf {NymVerify}})\) to generate user secret keys, to generate pseudonyms, and to verify pseudonyms are available. \(\mathcal {F}_{\mathsf {Cred}}\) is given \({\mathsf {NymVerify}}\) as an input parameter and will use this algorithm, to check the relation between P and X. For the security properties guaranteed by \(\mathcal {F}_{\mathsf {Cred}}\), we do not make any assumptions about the security properties of these algorithms. However, for the security of the overall credential scheme, pseudonym need to be commitments to X, i.e., to be binding and hiding w.r.t. X.
In the following we provide the definition of \(\mathcal {F}_{\mathsf {Cred}}\) and a protocol \(\mathcal {R}_{\mathsf {Cred}}\) that realizes \(\mathcal {F}_{\mathsf {Cred}}\) using \(\mathcal {F}_{{{\mathsf {CA}}}}\) and \(\mathcal {F}_{\mathsf {CRS}}\), assuming static corruptions.
Single Issuer Ideal Functionality. The starting point for our credential functionality is the ideal functionality of unlinkable redactable signatures, extended in a number of ways. Similar to \({\mathcal {F}_{{{\mathsf {URS}}}}}\) (and in line with other UC-functionalities such as \(\mathcal {F}_{\mathsf {sig}}\) that need to output cryptographic values), \({\mathcal {F}_{{\mathsf {Cred}}}}\) is handed a number of cryptographic algorithms by the simulator. These algorithms allow \({\mathcal {F}_{{\mathsf {Cred}}}}\) to produce cryptographic artifacts for proofs of credential ownership and attribute disclosure, to verify such proofs (when they are coming from the adversary), and to extract values from proofs. (We note that there are no artifacts for the credentials themselves.) While these algorithms can be completely adversarial, \({\mathcal {F}_{{\mathsf {Cred}}}}\) will enforce that algorithms and the artifacts produced by them) satisfy the required unforgeability and privacy properties. In fact, because of the privacy properties, \({\mathcal {F}_{{\mathsf {Cred}}}}\) needs to run these algorithms itself and cannot ask the simulator for the artifacts as is sometimes done (cf. \(\mathcal {F}_{{{\mathsf {URS}}}}\) and the UC-functionalities for blind signatures [6, 42]).
We now describe the steps of our ideal functionality \({\mathcal {F}_{{\mathsf {Cred}}}}\) (cf. Fig. 1) and explain the security properties it ensures and how it does so. Note that because we consider static corruption, \(\mathcal {F}_{\mathsf {Cred}}\) and \(\mathcal {SIM}\) are aware of which parties are corrupted.
\(\mathcal {F}_{\mathsf {Cred}}\) maintains two tables for bookkeeping: \(\mathcal {M}_{ ISS }\) stores information about issued credentials and \(\mathcal {M}_{ PRES }\) stores information about credentials that produced presentation proofs. It then handles requests as follows. Upon receiving a \((\mathtt{{keygen}}, { sid })\) message, \(\mathcal {F}_{\mathsf {Cred}}\) performs a setup by asking the simulator for the system parameters, the keys of the issuer, trapdoors, a set of algorithms and a list of corrupted parties. The message \((\mathtt{{leakSK}}, { sid })\) is handled in exactly the same way as for redactable signatures.
Next, upon receiving a \((\mathtt{{issueCred}}, { sid }, { qid }, \mathcal {U}, X , P , aux(P) )\) message from a user \(\mathcal {U}\), \(\mathcal {F}_{\mathsf {Cred}}\) initiates credential issuing by sending a corresponding message to the issuer specified in \({ sid }= (\mathcal {I},{ sid }')\). If \(\mathcal {I}\) responds to the request with a list of attributes \({\varvec{a}}\), \(\mathcal {F}_{\mathsf {Cred}}\) verifies that \( X , P ,\) and \( aux(P) \) form a valid pseudonym (i.e., \({\mathsf {NymVerify}}\) outputs 1), and, if so, records in \(\mathcal {M}_{ ISS }\) that a credential with attributes \({\varvec{a}}\) to user \(\mathcal {U}\) w.r.t. secret X has been issued.
Upon receiving a credential proof request in the form of a \((\mathtt{{proveCred}}, \ldots )\) message, \(\mathcal {F}_{\mathsf {Cred}}\) verifies whether the provided \( X , P ,\) and \( aux(P) \) form a valid pseudonym and whether a credential with attributes \({\varvec{a}}\) to user \(\mathcal {U}\) w.r.t. secret X has been issued. Then, \(\mathcal {F}_{\mathsf {Cred}}\) creates a cryptographic artifact for the proof using the \({\mathsf {Cred}}.{\mathsf {SimProve}}\) algorithm where no information that must not be revealed is input to the algorithm. This will guarantee the privacy properties of the credential proof for honest users. Furthermore, before outputting the proof to the user, \(\mathcal {F}_{\mathsf {Cred}}\) will verify it using \({\mathsf {Cred}}.{\mathsf {Verify}}\) as to ensure correctness.
Finally, upon receiving the \((\mathtt{{verifyCredProof}}, \ldots )\) message, \(\mathcal {F}_{\mathsf {Cred}}\) has to determine whether or not the proof should be accepted. Here we need to deal with unforgeability of credential proofs (and thus of credentials) if the issuer is honest and its secret key has not been leaked. Naturally, \(\mathcal {F}_{\mathsf {Cred}}\) should accept proofs that it has generated itself. Apart from that, \(\mathcal {F}_{\mathsf {Cred}}\) could in principle just accept all proofs for which the revealed attributes correspond to a credential that was issued. This would allow the adversary to also produce proofs that match credentials that were not issued to dishonest users but only to an honest user. To prevent this, we require an extraction algorithm \({\mathsf {Cred}}.{\mathsf {Extract}}\) which, on input a credential proof, will generate a user secret. Then, \(\mathcal {F}_{\mathsf {Cred}}\) will accept a credential proof only if the revealed attributes correspond to a credential that was issued to a corrupted users w.r.t. the \(X'\) extracted from the proof. That, however, would still allow (dishonest) users to mix and match their credentials. Therefore, \(\mathcal {F}_{\mathsf {Cred}}\) will accept the proofs only if the extracted \(X'\) underlies the pseudonym \(P'\) w.r.t. which the proof verifies. Therefore, \(\mathcal {F}_{\mathsf {Cred}}\) checks the latter using \({\mathsf {NymVerify}}\).
Realization of \(\mathcal {F}_{{\mathsf {Cred}}}\) . A protocol \(\mathcal {R}_{{\mathsf {Cred}}}\) that realizes \(\mathcal {F}_{{\mathsf {Cred}}}\) can be obtained from the algorithms described in Sect. 4.1 in the \((\mathcal {F}_{{{\mathsf {CRS}}}},\mathcal {F}_{{\mathsf {CA}}})\)-hybrid model where \( SP \) is the reference string and each call to \(\mathcal {F}_{{\mathsf {Cred}}}\) is replaced by running the corresponding algorithms. The detailed description of \(\mathcal {R}_{{\mathsf {Cred}}}\) is given in the full version [9].
For efficiency reasons related to the integration of pseudonyms (which requires zero-knowledge proofs and thus whitebox techniques), \(\mathcal {R}_{\mathsf {Cred}}\) does not use \(\mathcal {R}_{{{\mathsf {URS}}}}\) as a (blackbox) subroutine. We will, however, carefully align the internals of \(\mathcal {F}_{\mathsf {Cred}}\) and \(\mathcal {R}_{\mathsf {Cred}}\) with those of \(\mathcal {F}_{{{\mathsf {URS}}}}\) and \(\mathcal {R}_{{{\mathsf {URS}}}}\) respectively, such that we can use the UC emulation theorem in one of the hybrid steps of our security proof.
Theorem 7
Let \({{\mathsf {URS}}}\) be an unlinkable redactable signature scheme according to Definition 1, \({\mathsf {SPC}}\) be a structure-preserving commitment scheme, \({\mathsf {R{gap}}}\) be a verifiable relation, \(\varPi \) be a non-interactive proof of knowledge system. Then \({\mathcal {R}_{{\mathsf {Cred}}}}\) securely realizes \(\mathcal {F}_{{\mathsf {Cred}}}\) in the \((\mathcal {F}_{{{\mathsf {CRS}}}},\mathcal {F}_{{\mathsf {CA}}})\)-hybrid model if \({{\mathsf {URS}}}\) is correct, unlinkable, unforgeable, and key extractable, \({\mathsf {SPC}}\) is binding, the non-interactive proof-of-knowledge system is zero-knowledge and simulation extractable, and the \({\mathsf {R{gap}}}\) relation is hard. The proof is provided in the full version [9].
Building a Full-Fledged Credential System with Multiple Issuers. We now explain how to use our credential functionality to support multiple issuers using multiple sessions of \(\mathcal {F}_{\mathsf {Cred}}\), one for each issuer, together with algorithms \(({\mathsf {SecGen}},{\mathsf {NymGen}}, {\mathsf {NymVerify}})\) to generate user secret keys, to generate pseudonyms, and to verify pseudonyms. The pseudonyms are required to be both hiding and binding w.r.t. the user secret to provide privacy to the honest users and to prevent colluding users from sharing credentials unless they all user the same user secret. A user now can generate a user secret and different pseudonyms on them and then use multiple calls to the \(\mathcal {F}_{\mathsf {Cred}}\) instances for different issuers to get credentials on her pseudonyms. To compose a presentation proof that reveals attributes from different credentials, the user creates a pseudonym \( P '\) and uses the corresponding \(\mathcal {F}_{\mathsf {Cred}}\) instances to generate the required proofs with respect to this pseudonym. Because the pseudonym is the same in different proofs and each proof guarantees the same underlying secret in the credential and the pseudonym, the collection of these proofs together results in a single proof for multiple credentials. Each proof block guarantees unlinkability and unforgeability, and because the pseudonym is both binding and hiding this composed proof is also unforgeable and unlinkable with respect to other proof collections. The verification is done by querying the corresponding \(\mathcal {F}_{\mathsf {Cred}}\) instances for verification of each particular proof part and by checking that the pseudonym is the same in each proof part. A formal definition of a full-fledged credential scheme and proof that the scheme just sketched meets it is left as future work.
4.3 Instantiation and Efficiency Analysis
To analyze the efficiency of our scheme we consider a concrete instantiation scenario. We instantiate our non-interactive construction with Groth-Sahai proofs [45], the structure-preserving commitment scheme of [4], and our unlinkable redactable signature scheme presented in Sect. 3.3. We use disjunctive proofs to make the proof system simulation-extractable [22], see [54] for the efficient instantiation with 48 group elements overhead in the XDH setting that forms the basis of our efficiency analysis. As a hard relation we pick the Computational Diffie-Hellman problem. The URS scheme is instantiate with the fully structure-preserving signature scheme by Abe et al. [5], Groth-Sahai proofs, and the vector commitment scheme from Sect. 3.1. The proof of Theorem 8 follows from Theorems 6-7.
Theorem 8
The credential system described above securely realizes \(\mathcal {F}_{\mathsf {Cred}}\) defined in Sect. 4.2 if the SXDH, n-RootDH, n-BSDH, q-SDH, XDLIN, co-CDH, and DBP assumptions hold. Consult building blocks for definitions of assumptions.
We refer to the full version [9] for the comparison with prior work. We stress that the complexity of the \({\mathsf {Prove}}\) and \({\mathsf {Verify}}\) algorithms is independent of the number of all attributes contained in a credential.
The size of the credential proof is roughly 178 group elements (148 when using the SPS of [2] instead of FSPS). This means that the communication efficiency for showing a credential with respect to a pseudonym is around 11 KB (9 KB for SPS) at 128-bit security level, which is close to Idemix credentials [31] as the size of pairing groups is much smaller than the size of RSA groups and because the size of Idemix credential proofs is linear in the number of attributes. Besides, Idemix credentials do not provide such strong formal security guarantees, i.e. they require random oracles for non-interactive proofs and are not universally composable. Our non-UC scheme is comparable in efficiency with the credential system of Izabachène et al. [50] that has credential proofs of around 8 KB, while our UC scheme has larger proof sizes. Our scheme is much less efficient than the scheme of [47] but their scheme relies on hash functions in their construction and thus does not enable efficient protocol design.
Open Questions. We leave the construction of a scheme that achieves the same functionality as ours with the efficiency of [47]—perhaps using fully structure preserving signatures of equivalence classes—as an interesting open problem. Other interesting questions are exploiting the lack of opening non-malleability for attacks on existing constructions and efficiently basing the opening non-malleability property of vector commitments on a more standard cryptographic assumption than the n-RootDH assumption of Definition 9.
References
Abe, M., Chase, M., David, B., Kohlweiss, M., Nishimaki, R., Ohkubo, M.: Constant-size structure-preserving signatures: generic constructions and simple assumptions. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 4–24. Springer, Heidelberg (2012)
Abe, M., Fuchsbauer, G., Groth, J., Haralambiev, K., Ohkubo, M.: Structure-preserving signatures and commitments to group elements. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 209–236. Springer, Heidelberg (2010)
Abe, M., Groth, J., Haralambiev, K., Ohkubo, M.: Optimal structure-preserving signatures in asymmetric bilinear groups. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 649–666. Springer, Heidelberg (2011)
Abe, M., Haralambiev, K., Ohkubo, M.: Group to group commitments do not shrink. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 301–317. Springer, Heidelberg (2012)
Abe, M., Kohlweiss, M., Ohkubo, M., Tibouchi, M.: Fully structure-preserving signatures and shrinking commitments. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 35–65. Springer, Heidelberg (2015)
Abe, M., Ohkubo, M.: A framework for universally composable non-committing blind signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 435–450. Springer, Heidelberg (2009)
Ahn, J.H., Boneh, D., Camenisch, J., Hohenberger, S., Shelat, a, Waters, B.: Computing on authenticated data. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 1–20. Springer, Heidelberg (2012)
Attrapadung, N., Libert, B., Peters, T.: Computing on authenticated data: new privacy definitions and constructions. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 367–385. Springer, Heidelberg (2012)
Camenisch, J., Dubovitskaya, M., Haralambiev, K., Kohlweiss, K.: Composable & Modular Anonymous Credentials: Definitions and Practical Constructions. IACR Cryptology ePrint Archive, Report 2015/580
Backes, M., Meiser, S., Schröder, D.: Delegatable functional signatures. Cryptology ePrint Archive, Report 2013/408
Belenkiy, M., Camenisch, J., Chase, M., Kohlweiss, M., Lysyanskaya, A., Shacham, H.: Randomizable proofs and delegatable anonymous credentials. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 108–125. Springer, Heidelberg (2009)
Belenkiy, M., Chase, M., Kohlweiss, M., Lysyanskaya, A.: P-signatures and noninteractive anonymous credentials. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 356–374. Springer, Heidelberg (2008)
Belenkiy, M., Chase, M., Kohlweiss, M., Lysyanskaya, A.: Compact e-Cash and simulatable VRFs revisited. In: Shacham, H., Waters, B. (eds.) Pairing 2009. LNCS, vol. 5671, pp. 114–131. Springer, Heidelberg (2009)
Bellare, M., Fuchsbauer, G.: Policy-based signatures. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 520–537. Springer, Heidelberg (2014)
Bellare, M., Micciancio, D., Warinschi, B.: Foundations of group signatures: formal definitions, simplified requirements, and a construction based on general assumptions. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 614–629. Springer, Heidelberg (2003)
Boneh, D., Boyen, X.: Short signatures without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 56–73. Springer, Heidelberg (2004)
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014)
Brands, S.: Untraceable off-line cash in wallets with observers: extended abstract. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 302–318. Springer, Heidelberg (1994)
Brands, S.: Restrictive blinding of secret-key certificates. In: Guillou, L.C., Quisquater, J.-J. (eds.) EUROCRYPT 1995. LNCS, vol. 921, pp. 231–247. Springer, Heidelberg (1995)
Brickell, E.F., Camenisch, J., Chen, L.: Direct anonymous attestation. In: Atluri, V., Pfitzmann, B., McDaniel, P. (eds.) Proceedings of the 11th Conference on Computer and Communications Security, ACM CCS 2004, pp. 132–145. ACM Press, October 2004
Brzuska, C., Busch, H., Dagdelen, O., Fischlin, M., Franz, M., Katzenbeisser, S., Manulis, M., Onete, C., Peter, A., Poettering, B., Schröder, D.: Redactable signatures for tree-structured data: definitions and constructions. In: Zhou, J., Yung, M. (eds.) ACNS 2010. LNCS, vol. 6123, pp. 87–104. Springer, Heidelberg (2010)
Camenisch, J., Chandran, N., Shoup, V.: A public key encryption scheme secure against key dependent chosen plaintext and adaptive chosen ciphertext attacks. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 351–368. Springer, Heidelberg (2009)
Camenisch, J., Dubovitskaya, M., Neven, G., Zaverucha, G.M.: Oblivious transfer with hidden access control policies. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 192–209. Springer, Heidelberg (2011)
Camenisch, J., Groß, T.: Efficient attributes for anonymous credentials. In: Ning, P., Syverson, P.F., Jha, S. (eds.) Proceedings of the 15th Conference on Computer and Communications Security, ACM CCS 2008, pp. 345–356. ACM Press, October 2008
Camenisch, J.L., Hohenberger, S., Lysyanskaya, A.: Compact e-Cash. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 302–321. Springer, Heidelberg (2005)
Camenisch, J., Kiayias, A., Yung, M.: On the portability of generalized Schnorr proofs. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 425–442. Springer, Heidelberg (2009)
Camenisch, J., Krenn, S., Lehmann, A., Mikkelsen, G.L., Neven, G., Pedersen, M.: Formal treatment of privacy-enhancing credential systems. In: SAC 2015. Cryptology ePrint Archive, Report 2014/708
Camenisch, J., Krenn, S., Shoup, V.: A framework for practical universally composable zero-knowledge protocols. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 449–467. Springer, Heidelberg (2011)
Camenisch, J.L., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, p. 93. Springer, Heidelberg (2001)
Camenisch, J.L., Lysyanskaya, A.: A signature scheme with efficient protocols. In: Cimato, S., Galdi, C., Persiano, G. (eds.) SCN 2002. LNCS, vol. 2576, pp. 268–289. Springer, Heidelberg (2003)
Camenisch, J.L., Lysyanskaya, A.: Signature schemes and anonymous credentials from bilinear maps. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 56–72. Springer, Heidelberg (2004)
Camenisch, J.L., Neven, G., Shelat, A.: Simulatable adaptive oblivious transfer. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 573–590. Springer, Heidelberg (2007)
Camenisch, J., Van Herreweghen, E.: Design and implementation of the idemix anonymous credential system. In: Atluri, V. (ed.) Proceedings of the 9th Conference on Computer and Communications Security, ACM CCS 2002, pp. 21–30. ACM Press, November 2002
Canard, S., Lescuyer, R.: Protecting privacy by sanitizing personal data: a new approach to anonymous credentials. In: Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security, ASIACCS 2013, pp. 381–392. ACM, New York, NY, USA (2013)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd Annual Symposium on Foundations of Computer Science, pp. 136–145. IEEE Computer Society Press, October 2001
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited (preliminary version). In: Proceedings of the 30th Annual ACM Symposium on Theory of Computing, pp. 209–218. ACM Press, May 1998
Catalano, D., Fiore, D.: Vector commitments and their applications. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 55–72. Springer, Heidelberg (2013)
Chase, M., Kohlweiss, M., Lysyanskaya, A. , Meiklejohn, S.: Malleable signatures: new definitions and delegatable anonymous credentials. In: 2013 IEEE 27th Computer Security Foundations Symposium, IEEE (2014)
Chase, M., Lysyanskaya, A.: On signatures of knowledge. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 78–96. Springer, Heidelberg (2006)
Chaum, D., Fiat, A., Naor, M.: Untraceable electronic cash. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 319–327. Springer, Heidelberg (1990)
Chow, S.S.M., He, Y.J., Hui, L.C.K., Yiu, S.M.: SPICE - simple privacy-preserving identity-management for cloud environment. In: Bao, F., Samarati, P., Zhou, J. (eds.) ACNS 2012. LNCS, vol. 4731, pp. 516–543. Springer, Heidelberg (2012)
Fischlin, M.: Round-optimal composable blind signatures in the common reference string model. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 60–77. Springer, Heidelberg (2006)
Fuchsbauer, G., Hanser, C., Slamanig, D.: EUF-CMA-secure structure-preserving signatures on equivalence classes. Cryptology ePrint Archive, Report 2014/944
Goyal, V.: Reducing trust in the PKG in identity based cryptosystems. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 430–447. Springer, Heidelberg (2007)
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N.P. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008)
Haber, S., Hatano, Y., Honda, Y. , Horne, W., Miyazaki, K., Sander, T., Tezoku, S., Yao, D.: Efficient signature schemes supporting redaction, pseudonymization, and data deidentification. In: Abe, M., Gligor, V. (eds.) 3rd Conference on Computer and Communications Security, ASIACCS 2008, pp. 353–362. ACM Press, March 2008
Hanser, C., Slamanig, D.: Structure-preserving signatures on equivalence classes and their application to anonymous credentials. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 491–511. Springer, Heidelberg (2014)
Hirt, M., Sako, K.: Efficient receipt-free voting based on homomorphic encryption. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 539–556. Springer, Heidelberg (2000)
Hofheinz, D., Shoup, V.: GNUC: a new universal composability framework. J. Cryptol. 28, 423–508 (2015). IACR Cryptology ePrint Archive, Report 2011/303
Izabachène, M., Libert, B., Vergnaud, D.: Block-wise P-signatures and non-interactive anonymous credentials with efficient attributes. In: Chen, L. (ed.) IMACC 2011. LNCS, vol. 7089, pp. 431–450. Springer, Heidelberg (2011)
Kate, A., Zaverucha, G.M., Goldberg, I.: Constant-size commitments to polynomials and their applications. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 177–194. Springer, Heidelberg (2010)
Kiayias, A., Yung, M.: Group signatures with efficient concurrent join. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 198–214. Springer, Heidelberg (2005)
Kiayias, A., Zhou, H.-S.: Equivocal blind signatures and adaptive UC-security. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 340–355. Springer, Heidelberg (2008)
Kohlweiss, M., Miers, I.: Accountable tracing signatures. Cryptology ePrint Archive, Report 2014/824
Kohlweiss, M., Rial, A.: Optimally private access control. In: Proceedings of the 12th ACM Workshop on Privacy in the Electronic Society, WPES 2013, pp. 37–48, ACM, New York, NY, USA (2013)
Libert, B., Yung, M.: Concise mercurial vector commitments and independent zero-knowledge sets with short proofs. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 499–517. Springer, Heidelberg (2010)
Meiklejohn, S.: An extension of the groth-sahai proof system. Master’s thesis, Brown University (2009)
Nojima, R., Tamura, J., Kadobayashi, Y., Kikuchi, H.: A storage efficient redactable signature in the standard model. In: Samarati, P., Yung, M., Martinelli, F., Ardagna, C.A. (eds.) ISC 2009. LNCS, vol. 5735, pp. 326–337. Springer, Heidelberg (2009)
Acknowledgments
The authors would like to thank Sherman Chow and the anonymous reviewers for their helpful comments and suggestions. The research leading to these results was supported in part by the European Community’s Seventh Framework Programme for the project FutureID (grant agreement no. 318424).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 International Association for Cryptologc Research
About this paper
Cite this paper
Camenisch, J., Dubovitskaya, M., Haralambiev, K., Kohlweiss, M. (2015). Composable and Modular Anonymous Credentials: Definitions and Practical Constructions. In: Iwata, T., Cheon, J. (eds) Advances in Cryptology – ASIACRYPT 2015. ASIACRYPT 2015. Lecture Notes in Computer Science(), vol 9453. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48800-3_11
Download citation
DOI: https://doi.org/10.1007/978-3-662-48800-3_11
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-48799-0
Online ISBN: 978-3-662-48800-3
eBook Packages: Computer ScienceComputer Science (R0)




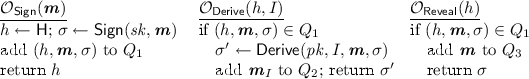
 Return
Return 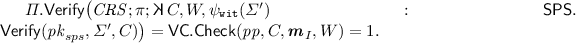
 Output
Output 
