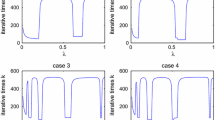
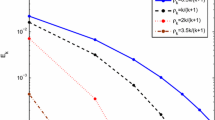
Abstract
The purpose of this paper is to introduce and study Ishikawa iterative algorithms for solving the SFP in the setting of infinite-dimensional Hilbert spaces. The main results presented in this paper improve and extend some recent results done by Xu [Iterative methods for the split feasibility problem in infinite-dimensional Hilbert space, Inverse Problems 26 (2010) 105018]. At the end we prove that the accumulation of errors in Ishikawa iterative CQ algorithm is bounded in certain range.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Ishikawa, S.: Fixed point and iteration of a nonexpansive mapping in a Banach spaces. Proc. Amer. Math. Soc. 73, 7365–7371 (1976)
Qin, X., Cho, Y.J., Kang, S.M.: Viscosity approximation methods for generalized equilibrium problems and fixed point with applicatons. Nonlinear Anal. 72, 99–12 (2010)
Xu, H.-K.: Iterative methods for the split feasibility problem in infinite-dimensional Hilbert space. Inverse Problems 26, 105018 (2010)
Xu, H.-K.: Averaged Mapping and the Gradient-Projection Algorithm (in press)
Xu, Y., Liu, Z., Shin Min, K.: Accumulation and conreol of random errors in the Ishikawa iterative process in arbitrary Banach space. Comput. Math. Appl.
Hundal, H.: An alternating projection that does not converge in norm. Nonlinear Anal. 57, 35–61 (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Dingping, W., Qibin, D., Erli, W., Hang, Z. (2013). The Split Feasibility Problem in Hilbert Space. In: Yang, G. (eds) Proceedings of the 2012 International Conference on Communication, Electronics and Automation Engineering. Advances in Intelligent Systems and Computing, vol 181. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-31698-2_161
Download citation
DOI: https://doi.org/10.1007/978-3-642-31698-2_161
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-31697-5
Online ISBN: 978-3-642-31698-2
eBook Packages: EngineeringEngineering (R0)