What Is Known About Vertex Cover Kernelization?

Abstract

We are pleased to dedicate this survey on kernelization of the Vertex Cover problem, to Professor Juraj Hromkovič on the occasion of his 60th birthday. The Vertex Cover problem is often referred to as the Drosophila of parameterized complexity. It enjoys a long history. New and worthy perspectives will always be demonstrated first with concrete results here. This survey discusses several research directions in Vertex Cover kernelization. The Barrier Degree of Vertex Cover is discussed. We have reduction rules that kernelize vertices of small degree, including in this paper new results that reduce graphs almost to minimum degree five. Can this process go on forever? What is the minimum vertex-degree barrier for polynomial-time kernelization? Assuming the ETH Hypothesis, there is a minimum degree barrier. The idea of automated kernelization is discussed. We here report the first experimental results of an AI-guided branching algorithm for Vertex Cover whose logic seems amenable for application in finding reduction rules to kernelize small-degree vertices. The survey highlights a central open problem in parameterized complexity. Happy Birthday, Juraj!

M. R. Fellows, L. Jaffke, A. I. Király and F. A. Rosamond—Acknowledge support from the Bergen Research Foundation (BFS).

1 Introduction and Preliminaries

A vertex cover of a graph is a subset of its vertices containing at least one endpoint of each of its edges. The Vertex Cover problem asks, given a graph G and an integer k, whether G contains a vertex cover of size at most k.

The study of the Vertex Cover problem lies at the roots of the theory of $\mathsf {NP}$-completeness: It is one of Karp’s 21 $\mathsf {NP}$-complete problems [46] and plays a central role in the monograph of Garey and Johnson [34]. However, interest in the Vertex Cover problem reaches far beyond pure theory. One reason is that it naturally models conflict resolution,¹ a problem occurring in numerous scientific disciplines, with an international workshop devoted to it [2]. Other applications include classification methods (see, e.g., [35]), computational biology (e.g., [13]), and various applications follow from the duality of Vertex Cover with the Clique problem (see, e.g., [1]). The latter finds numerous applications in fields such as computational biology and bioinformatics [9, 47, 48, 64, 71], computational chemistry [22, 52, 69] and electrical engineering [15, 39].

In parameterized/multivariate algorithmics [16, 20, 60], the objects of study are computational problems whose instances are additionally equipped with a integer k, the parameter, typically expressing some structural measure of the instance of the problem. The goal is to design algorithms for hard problems whose runtime confines the combinatorial explosion to the parameter k rather than the size of the input. A parameterized problem is called fixed-parameter tractable if it can be solved in time $f(k)\cdot n^{\mathcal {O}(1)}$ where f is some computable function, k the parameter and n the input size. The second central notion in the field of parameterized algorithms is that of a kernelization [19, 21, 27], a polynomial-time algorithm (usually described as a set of reduction rules) that takes as input an instance (I, k) of a parameterized problem and outputs an equivalent instance $(I', k')$, where $\left| I'\right| + k' \le g(k)$ for some computable function g.²

Kernelization (for the first time!) provided a theory of preprocessing with mathematically provable guarantees. On the other end, kernelization has immediate practical implications, as demonstrated by Karsten Weihe’s problem [66, 67] (see also [24, 25]) concerning the train systems in Europe. By the means of two simple reduction rules, graphs (instances) on 10, 000 vertices are reduced to equivalent instances whose connected components are of size at most 50, making the reduced instance solvable exactly even by brute force in reasonable time, after the preprocessing, even though the general problem is NP-hard. Similar reduction rules have been successfully applied in the context of cancer research [4] and spread of virus [23].

The notions of fixed-parameter tractability and kernelization are tightly linked. It has been shown by Cai et al. that a parameterized problem is fixed-parameter tractable if and only if it has a (polynomial-time) kernelization algorithm [10]. Kernelization for the Vertex Cover problem, which is often referred to as the Drosophila of parameterized complexity [20, 31, 37, 60], enjoys a long history. In 1993, the first kernel on $\mathcal {O}(k^2)$ vertices was obtained, and is accredited to Buss [8], with more refined reduction rules given in [3]. Kernels with a linear number of vertices were obtained in various ways. Using classic graph theoretic results, Chor et al. gave a kernel on 3k vertices [14] (see also [26]), a kernel on 2k vertices was obtained via an LP-relaxation by Chen et al. [11] and another kernel on 2k vertices without the use of linear programming was obtained by Dehne et al. [17]. The next series of improvements gave kernels on $2k - c$ vertices [62] and the current champion which is due to Lampis has $2k-c\log k$ vertices [51], where in the latter two c is any fixed constant. Another kernel on $2k - \mathcal {O}(\log k)$ vertices was observed in [58]. An experimental evaluation of several of the earlier kernels was carried out in [1].

There is no known subquadratic bound on the number of edges in any kernel for Vertex Cover, and the question whether such a kernel exists was a long standing open question in multivariate algorithmics. It was finally shown that up to logarithmic factors, Vertex Cover kernels with a quadratic number of edges are likely to be optimal: Dell and van Melkebeek, building on work of Bodlaender, Downey, Fellows and Hermelin [6, 7], also Fortnow and Santhanam [33], showed that there is no kernel on $\mathcal {O}(n^{2 - \varepsilon })$ bits, for any $\varepsilon > 0$, unless $\mathsf {NP} \subseteq \mathsf {coNP}/\mathsf {poly}$ [18]. The latter would imply that the polynomial hierarchy collapses to its third level [70] which is widely considered to be implausible by complexity theorists.³

In another line of research, following the parameter ecology program [29], the existence of kernels for Vertex Cover w.r.t. parameters that take on smaller values than the vertex cover number was studied. Such parameterizations are typically referred to as structural parameterizations of Vertex Cover. The first such result is due to Jansen and Bodlaender who gave a kernel on $\mathcal {O}(\ell ^3)$ vertices, where $\ell$ is the size of a feedback vertex set of the graph [45]. Further results include polynomial kernels where the parameter is the size of an odd cycle traversal or a König deletion set [50], the size of vertex deletion sets to maximum degree at most two [55], pseudoforest [32] and d-quasi forest [40]. Using the above mentioned lower bound machinery, it was shown that there is no kernel polynomial in the size of a vertex deletion set to chordal or perfect graphs unless $\mathsf {NP} \subseteq \mathsf {coNP}/\mathsf {poly}$ [5, 29].

As Vertex Cover is the primary intellectual “lab animal” in parameterized complexity, new and worthy perspectives will always be demonstrated first with concrete results here. We discuss several research directions in (Vertex Cover) kernelization. The first one is based on the observation that several reduction rules are known to kernelize vertices of small degree [8, 30, 63]; a natural question is whether this process can go on ‘forever’, i.e., whether we can find, for any fixed constant $d \in \mathbb {N}$, a set of reduction rules that kernelize in polynomial time to a reduced graph (the kernel) of minimum degree d. On the negative side, we observe that unless the Exponential-Time Hypothesis [42, 43] fails, this is not the case even if the exponent in the polynomial-time kernelization is some arbitrary function of d. On the positive side, we give a clear account of reduction rules for Vertex Cover that were first observed by Fellows and Stege [30] that kernelize instances to minimum degree ‘almost five’ (see Theorem 5 for the exact statement) and discuss how this question is closely related to finding faster fpt-algorithms for Vertex Cover, a question that lies at the very heart of parameterized complexity research.

In the light of the ongoing machine-learning and artificial intelligence revolution, one might wonder whether AI could assist in the search for new reduction rules of parameterized problems as well. While this question seems far out, we report first experimental results of an AI-guided branching algorithm for Vertex Cover whose logic seems amenable for application in finding new reduction rules to kernelize to increasing minimum degree.

The rest of this paper is organized as follows. In the remainder of this section, we give preliminary definitions and introduce the necessary background. In Sect. 2 we review some classic Vertex Cover kernels. Section 3 is devoted to the topic of kernelizing small-degree vertices. We there give a description of reduction rules observed by Fellows and Stege [30] (see also [63]). In Sect. 4 we report results on an AI-guided branching algorithm whose ideas might lay the foundations of automatically generated reduction rules for Vertex Cover. We conclude with an open problem in Sect. 5.

Technical Preliminaries and Notation. For two integers a and b with $a < b$, we let and for a positive integer a, we let .

Throughout the paper, each graph is finite, undirected and simple. Let G be a graph. We denote the vertex set of G by V(G) and the edge set of G by $E(G) \subseteq \left( {\begin{array}{c}V\\ 2\end{array}}\right)$. For a vertex $v \in V(G)$, we denote by N(v) the (open) neighborhood of G, i.e., . The degree of v is the size of the neighborhood of v, i.e., . We define the closed neighborhood of v as . For a set of vertices $W \subseteq V(G)$, we let and . For a set of vertices $\{v_1, \ldots , v_r\}$, we use the shorthand .

For two graphs G and H, we denote by $H \subseteq G$ that H is a subgraph of G, i.e. that $V(H) \subseteq V(G)$ and $E(H) \subseteq E(G)$. For a vertex set $X \subseteq V(G)$, we denote by G[X] the subgraph of G induced by X, i.e., . We let and we use the shorthand $G - v$ for $G - \{v\}$. Furthermore, we define for an edge set $F \subseteq E(G)$, and for a set $\bar{F} \subseteq \left( {\begin{array}{c}V(G)\\ 2\end{array}}\right)$, we let .

A subgraph $P \subseteq G$ is called a path if all its vertices have degree at most two in P and there are precisely two distinct vertices in V(P) that have degree one in P, called the endpoints of P. For $s, t \in V(G)$, a path is called (s, t)-path if it is a path with endpoints s and t.

We call two edges $e, f \in E(G)$ adjacent if they share an endpoint, i.e., if there exist vertices $v, w, x \in V(G)$ such that $e = \{v, w\}$ and $f = \{v, x\}$. A matching is a set of pairwise non-adjacent edges. A co-matching is a set of pairwise non-adjacent edges in the edge-complement of G, i.e., the graph whose vertex set is V(G) and whose edge set is the complement of E(G). We say that a matching (or co-matching) M saturates a set of vertices $W \subseteq V(G)$, if for all $v \in W$, there is a pair $\{v, w\} \in M$.

Given a set of vertices $X \subseteq V(G)$, we call the operation of adding to G a new vertex x with neighborhood N(X) and deleting all vertices in X the contraction of X.

Exponential-Time Hypothesis (${{{\textsf {\textit{ETH}}}}}$). In 2001, Impagliazzo and Paturi made a conjecture about the complexity of 3-Sat, the problem of determining whether a given Boolean formula in conjunctive normal form with clauses of size at most 3 has a satisfying assignment. This conjecture is known as the Exponential-Time Hypothesis (${{{\textsf {\textit{ETH}}}}}$) and has lead to a plethora of conditional lower bounds, see, e.g., the survey [53] or [16, Chap. 14]. Formally, $\textsf {ETH}$ can be stated as follows.⁴

Conjecture 1

(${{{\textsf {\textit{ETH}}}}}$ [42, 43]). There is an $\varepsilon > 0$ such that 3-Sat on n variables cannot be solved in time $\mathcal {O}^*(2^{\varepsilon n})$.

2 Standard Methods

In this section, we review some classic results in Vertex Cover kernelization. In particular, we discuss the Buss kernel [8] in Subsect. 2.1. Subsection 2.2 is devoted to the kernel based on the notion of a crown decomposition [14, 26] (see Definition 1). A linear-programming-based kernel [11] is discussed in Subsect. 2.3.

We would like to remark that the technical parts of the expositions given in the remainder of this section are based on [16, Sections 2.2.1, 2.3 and 2.5] and we refer to this text for several details.

2.1 Buss Kernelization

The first kernel for Vertex Cover appeared several years before the notion of kernelization was formally introduced and is attributed to Buss [8]. It relies on two observations. The first one is that by definition, there is no need to include an isolated vertex in a vertex cover, as it does not have any incident edges that need to be covered.

Reduction R.1

If G has an isolated vertex v, then reduce (G, k) to $(G - v, k)$.

The second observation is that, if G has a vertex v of degree more than k, then we have no choice but to include v in any size-k vertex cover of G: If we did not include v, we would have to include all of its at least $k+1$ neighbors, exceeding the budget of k vertices we are given. Hence, G has a vertex cover of size k if and only if $G - v$ has a vertex cover of size $k-1$, so we have observed that the following reduction rule is safe, meaning that the original instance is a Yes-instance if and only if the reduced instance is a Yes-instance.

Reduction R.2

If G has a vertex v with $\deg (v) > k$, then reduce (G, k) to $(G - v, k - 1)$.

Now, after exhaustively applying Reduction R.2, G has maximum degree at most k, so if G contains more than $k^2$ edges, then we are dealing with a No-instance: It is not possible to cover more than $k^2$ edges with k vertices of degree at most k. On the other hand, if (G, k) is a Yes-instance, then G has a vertex cover X of size at most k. After exhaustively applying Reduction R.1, G does not contain any isolated vertices so we can assume that every vertex of $V(G) \setminus X$ has a neighbor in X. Since the maximum degree of G is at most k, we can conclude that $\left| V(G) \setminus X\right| \le k^2$, which implies that $\left| V(G)\right| \le k^2 + k$. Hence, if G has more than $k^2+k$ vertices, we can again conclude that we are dealing with a No-instance. Since Reductions R.1 and R.2 clearly run in polynomial time, we have the following theorem.

Theorem 1

(Buss and Goldsmith [8]). Vertex Cover admits a kernel with at most $k^2 + k$ vertices and $k^2$ edges.

2.2 Crown Reduction

The key insight above was that any vertex of degree at least $k+1$ has to be contained in any size-k vertex cover of a graph. The kernel we present in this section follows a similar motivation. The goal is to identify a set of vertices that we can always assume to be contained in a size-k vertex cover of a graph. In other words, we want to find a set of vertices S, such that if G contains a vertex cover of size k then G contains a vertex cover of size k that contains S. The process of identifying such a set S is based on a structural decomposition of the input graph, called the crown decomposition. Formally, a crown decomposition is defined as follows and we illustrate it in Fig. 1.

Definition 1

(Crown Decomposition). Let G be a graph. A crown decomposition of G is a partition (C, H, B) of V(G), where C is called the crown, H the head and B the body, such that the following hold.

• (i) C is a non-empty independent set in G.

• (ii) There are no edges between vertices in C and vertices in B.

• (iii) G[C, H] contains a matching that saturates H.

Fig. 1.

Illustration of a crown decomposition (Definition 1). The fat edges in G[C, H] show a matching saturating H.

The motivation for using the above definition in Vertex Cover kernelization is as follows. Suppose we are given a crown decomposition (C, H, B) of G and consider the bipartite graph G[C, H]. Clearly, any vertex cover of G has to cover the edges in $G[C \cup H]$. However, by (iii) we know that there is a matching in G[C, H] saturating H, hence any vertex cover of G[H, C] has size at least $\left| H\right|$. On the other hand, H is a vertex cover of G[C, H] and since C is independent by (i), of $G[C \cup H]$. This allows us to conclude that G has a vertex cover of size k if and only if $G - (C \cup H)$ has a vertex cover of size $k - \left| H\right|$. Hence, the following reduction rule is safe.

Reduction R.3

If G has a crown decomposition (C, H, B), then reduce (G, k) to $(G - (C \cup H), k - \left| H\right| )$.

However, two questions remain. Namely whether we can find a crown decomposition of a graph in polynomial time and how to obtain the linear bound on the number of vertices in the resulting kernel. Both questions are answered by the following lemma whose proof is based on classic results in graph theory by König [49] and Hall [38], and polynomial-time algorithms for bipartite matching such as the classic algorithm due to Hopcroft and Karp [41].⁵

Lemma 1

(Lemma 2.14 in [16] based on [14]). Let G be a graph on at least $3k+1$ vertices. There is a polynomial-time algorithm that either

• (1) finds a matching of size at least $k+1$ in G; or

• (2) finds a crown decomposition of G.

Now, in Case 1 we can immediately conclude that (G, k) is a No-instance and in Case 2 we can apply Reduction R.3. By an exhaustive application of Lemma 1 in combination with Reduction R.3 (and Reduction R.1 to get rid of isolated vertices), we have the following theorem.

Theorem 2

(Chor et al. [14]). Vertex Cover admits a kernel with at most 3k vertices.

2.3 LP-Based Kernel

The Vertex Cover problem is one of many $\mathsf {NP}$-hard problems that can be expressed as an integer linear program [61], a fact which is commonly exploited in the field of approximation algorithms [65]. In this section, we show how to use linear programming to obtain a kernel for Vertex Cover on at most 2k vertices. We first recall how to formulate Vertex Cover as an integer linear program.

For each vertex $v \in V(G)$, we introduce a variable $x_v \in \{0, 1\}$ with the interpretation that $x_v = 1$ if and only if the vertex v is included in the vertex cover witnessed by a solution to the (integer) linear program. We can then formulate the constraints in a natural way, directly applying the definition of vertex covers: For each edge $uv \in E(G)$, the requirement that at least one of u and v has to be contained in the solution translates to the constraint $x_u + x_v \ge 1$. Since we are looking for a vertex cover of minimum size, the objective function minimizes the sum over all $x_v$’s.

$$\begin{aligned}&\min \sum _{v \in V(G)}x_v \nonumber \\ \text {subject to}\quad&x_u + x_v \ge 1 \quad \forall uv \in E(G) \end{aligned}$$

(1)

$$\begin{aligned}&x_v \in \{0, 1\}\, \quad \,\,\forall v \in V(G) \end{aligned}$$

(2)

To make the program feasible to compute, we relax the integrality constraints (2) to $x_v \in \mathbb {R}$, $x_v \ge 0$. (Note that we can drop the constraints $x_v \le 1$ since the objective function is a minimization.) The resulting linear program is solvable in polynomial time, but may not always return a feasible solution for the original Vertex Cover instance. However, we are chasing a different goal here, a kernelization algorithm.

Given an optimal solution $(x_v)_{v \in V(G)}$ of the (relaxed) linear program, we define the sets , , and . The key ingredient is the following theorem due to Nemhauser and Trotter [59].

Theorem 3

(Nemhauser and Trotter [59]). There is a minimum vertex cover X of G such that $V_1 \subseteq X \subseteq V_1 \cup V_{\frac{1}{2}}$.

We derive a reduction rule from Theorem 3. First, we note that in any Yes-instance of Vertex Cover, $\sum _{v \in V(G)} x_v \le k$. Furthermore, let X be a vertex cover of G of size k with $V_1 \subseteq X$ and $X \cap V_0 = \emptyset$ (whose existence is guaranteed by Theorem 3), then $X \setminus V_1$ is a vertex cover of $G - (V_0 \cup V_1)$ of size $k - \left| V_1\right|$. Conversely, if $G - (V_0 \cup V_1)$ has a vertex cover $X'$ of size $k'$, we observe that by the constraints (1), for any edge $vw \in E(G)$ with $v \in V_0$, we have that $w \in V_1$. Hence, $X' \cup V_1$ is a vertex cover of G of size $k' + \left| V_1\right|$. We have argued that the following reduction rule is safe.

Reduction R.4

Let $(x_v)_{v \in V(G)}$, $V_0$, $V_{\frac{1}{2}}$ and $V_1$ be as above. If $\sum _{v \in V(G)} x_v > k$, then conclude that we are dealing with a No-instance. Otherwise, reduce (G, k) to $(G - V_0 \cup V_1, k - \left| V_1\right| )$.

The number of vertices in the reduced instance after applying Reduction R.4 is

$$\begin{aligned} \left| V(G) \setminus (V_0 \cup V_1)\right| = \left| V_\frac{1}{2}\right| = \sum \nolimits _{v \in V_{\frac{1}{2}}} 2x_v \le 2 \cdot \sum \nolimits _{v \in V(G)} x_v \le 2k, \end{aligned}$$

so we have obtained the following kernel for Vertex Cover.⁶

Theorem 4

(Chen et al. [11]). Vertex Cover admits a kernel with at most 2k vertices.

3 Towards the Barrier – What Is the Maximum Minimum Vertex Degree of the Kernel that Can Be Achieved in Polynomial Time?

In the previous section, we have seen that by Reduction R.2 we can kernelize all vertices whose degree is larger than the target value k of the given vertex cover instance. Hence, after applying this rule exhaustively there will be no vertex of degree larger than k in the kernelized instance. But what about vertices of small degree? Vertices of degree zero, i.e., isolated vertices, can be removed from a Vertex Cover instance according to Reduction R.1. Furthermore, we will see below that there are fairly simple reduction rules that kernelize vertices of degree one and two (see Reductions R.5 and R.6). A natural question arises: Can this process go on ‘forever’, i.e., can we, for any fixed constant $d \in \mathbb {N}$, give a reduction rule that kernelizes all vertices of degree d from a given Vertex Cover instance?

The answer to this question is probably not—even if the degree of the polynomial in the runtime of the kernelization algorithm can depend on d: It is well-known (see, e.g., [16, 20, 28]) that unless $\textsf {ETH}$ fails, there is some barrier constant $\zeta _{VC}> 0$ such that the fastest possible algorithm for Vertex Cover runs in time $(1 + \zeta _{VC})^k \cdot n^{\mathcal {O}(1)}$. If we could kernelize Vertex Cover in polynomial time to arbitrarily large minimum degree, one could devise a straightforward branching algorithm that runs in time $(1 + \zeta _{VC}- \varepsilon )^k \cdot n^{\mathcal {O}(1)}$, for some $0< \varepsilon < \zeta _{VC}$, where $\varepsilon$ can be arbitrarily close to the value of $\zeta _{VC}$. We coin the corresponding integer $\delta _{VC}\in \mathbb {N}$ the barrier degree of Vertex Cover kernelization and now prove formally its existence (assuming $\textsf {ETH}$).

Proposition 1

Unless $\textsf {ETH}$ fails, there is some constant $\delta _{VC}\in \mathbb {N}$, such that Vertex Cover cannot be kernelized to instances of minimum degree $\delta _{VC}$.

Proof

Using standard arguments about branching algorithms (see, e.g., [16, Chap. 3]) one can show that there is an algorithm solving vertex cover in time $\lambda ^k \cdot n^{\mathcal {O}(1)}$, where $\lambda$ satisfies

$$\begin{aligned} \lambda \le \lambda ^d(\lambda -1), \end{aligned}$$

(3)

if the input graph always has a vertex of degree at least d to branch on. Now suppose that the statement of the proposition is false, then we can guarantee the existence of such a vertex for constant but arbitrarily large d (with only polynomial time overhead at each stage of the branching). Now let $\varepsilon > 0$ with $\varepsilon < \zeta _{VC}$. (Note that this implies that $\varepsilon < 1$ as $\zeta _{VC}< 0.2738$ [12].) We substitute $\lambda$ with $(1 + \varepsilon )$ in (3) and obtain:

$$\begin{aligned} 1 + \varepsilon&\le (1 + \varepsilon )^d \varepsilon \iff (1+\varepsilon )^d \ge \frac{1+\varepsilon }{\varepsilon } \iff d \log (1+ \varepsilon ) \ge \log \left( \frac{1+ \varepsilon }{\varepsilon }\right) \\ \iff d&\ge \frac{\log \left( \frac{1+ \varepsilon }{\varepsilon }\right) }{\log (1+\varepsilon )} = \frac{\log (1+\varepsilon ) - \log (\varepsilon )}{\log (1+\varepsilon )} = 1 - \frac{\log (\varepsilon )}{\log (1+\varepsilon )}. \end{aligned}$$

This shows that for any such $\varepsilon$, there is a constant $d_\varepsilon \in \mathbb {N}$ such that, if we could kernelize Vertex Cover to minimum degree $d_\varepsilon$, then we could solve it in $(1 + \varepsilon )^k \cdot n^{\mathcal {O}(1)}$ time, where $\varepsilon < \zeta _{VC}$ by our choice. This contradicts $\textsf {ETH}$ by, e.g., [28, Theorem 1].   $\square$

The proof of Proposition 1 also provides some very natural motivation for the question of kernelizing Vertex Cover to larger and larger minimum degree; such kernels immediately provide new $\mathsf {FPT}$-algorithms for the problem. In particular, kernelizing to minimum degree seven would already improve upon the current best known algorithm for Vertex Cover, yielding first progress in a very attractive research question in over a decade! We illustrate the runtime of such algorithms for several concrete values of d in Table 1.

In the remainder of this section, we present a set of reduction rules that were first observed by Fellows and Stege [30] to kernelize a vertex cover instance to minimum degree ‘almost five’, in the following sense: We show that a vertex can be kernelized if its degree is at most three or its degree is four and there are more than two edges between the vertices in its neighborhood.

Table 1. (Dependence on k of the) runtime of the resulting simple branching $\mathsf {FPT}$-algorithm when using a kernelization algorithm to minimum degree d, for several values of d, versus the current fastest known $\mathsf {FPT}$-algorithm for Vertex Cover [12].

We begin with a simple rule to deal with degree-one vertices and show that it is safe.

Reduction R.5

If G has a pendant edge $\{u, v\}$ with $\deg (u) = 1$, then reduce (G, k) to $(G - \{u, v\}, k-1)$.

Proposition 2

Reduction R.5 is safe, i.e., if G has a pendant edge $\{u, v\}$ with $\deg (u) = 1$, then G has a vertex cover of size k if and only if $G - \{u, v\}$ has a vertex cover of size $k-1$.

Proof

($\Rightarrow$) Suppose G has a vertex cover $X^*$ of size k. Since $\{u, v\}$ is an edge of G, at least one of u and v is contained in $X^*$. If $v \notin X^*$, then we let . Note that X is a vertex cover since v is the only neighbor of u. If $v \in X^*$, we simply let . Since $v \in X$, $X \setminus \{v\}$ is a vertex cover of $G - \{u, v\}$ of size $k-1$.

($\Leftarrow$) Let $X'$ be a vertex cover of $G - \{u, v\}$ of size $k-1$. We observe that any edge in $E(G) \setminus E(G - \{u, v\})$ is incident with v and conclude that $X' \cup \{v\}$ is a vertex cover of G of size k.   $\square$

Fig. 2.

Illustration of Reduction R.6. Note that, for our argument, it is immaterial whether the edge $\{a, b\}$ is present in G or not.

The next reduction rule takes care of vertices of degree two and is illustrated in Fig. 2.

Reduction R.6

If G has a vertex v with $\deg (v) = 2$, then reduce (G, k) to $(G', k-1)$, where $G'$ is the graph obtained from G by contracting N[v] to a single vertex.

Proposition 3

Reduction R.6 is safe, i.e., G has a vertex cover of size k if and only if $G'$ has a vertex cover of size $k-1$.

Proof

Throughout the proof, we denote the neighborhood of v in G by $N(v) = \{a, b\}$ and the vertex in $G'$ that was created due to the contraction of N[v] by $z_{N[v]}$.

($\Rightarrow$) We observe that each edge in $E(G') \setminus E(G)$ has an endpoint in $\{z_{N[v]}\} \cup N(a, b)$. Let X be a vertex cover of G of size k. If $X \cap N(v) = \emptyset$, then $\{v\} \cup N(a, b) \subseteq X$ and we can conclude that $X \setminus \{v\}$ is a vertex cover of $G'$. If $N(v) \subseteq X$, then is a vertex cover of $G'$. (Note that in this case, $X'$ has size at most $k-1$ as well.) If X contains precisely one vertex from N(v), assume w.l.o.g. that $X \cap N(v) = \{a\}$, then $v \in X$ (otherwise the edge $\{v, b\}$ is not covered), so $X \setminus \{v, a\} \cup \{z_{N[v]}\}$ is a vertex cover of $G'$ of size $k-1$.

($\Leftarrow$) Let $X'$ be a vertex cover of $G'$ of size $k-1$. We only have to distinguish the cases when $z_{N[v]} \in X'$ and when $z_{N[v]} \notin X'$. In the former case, $X' \setminus \{z_{N[v]}\} \cup \{a, b\}$ is a vertex cover of G, since each edge in $E(G) \setminus E(G')$ is incident with a vertex in $\{a, b\}$. In the latter case, $N(a, b) \subseteq X'$ since $z_{N[v]} \notin X'$, and we have that $X' \cup \{v\}$ is a vertex cover of G, as each edge in $E(G) \setminus E(G')$ has an endpoint in $\{v\} \cup N(a, b)$. In both cases, the size of the resulting vertex cover is k.   $\square$

Before we proceed with kernelizing vertices of degree larger than two, we require two auxiliary reduction rules. These will be crucially used to argue that we can exclude certain structures appearing in the subgraphs induced by the neighborhoods of small-degree vertices, and in the end will enable us to formulate reduction rules for vertices of degree three and several cases of degree-four vertices.

Fig. 3.

Illustration of the situation of Reduction R.7.

Reduction R.7

If G has two adjacent vertices u and v such that $N(v) \subseteq N[u]$, then reduce (G, k) to $(G - u, k - 1)$.

For an illustration of the situation of Reduction R.7, see Fig. 3.

Proposition 4

Reduction R.7 is safe, i.e., if G has two adjacent vertices u and v, and $N(v) \subseteq N[u]$, then G contains a vertex cover of size k if and only if $G - u$ has a vertex cover of size $k - 1$.

Proof

($\Rightarrow$) Suppose G has a vertex cover $X^*$ of size k. If $u \notin X^*$ then N(u) must be in $X^*$, so by assumption, it contains $N[v] \setminus \{u\}$. But then, is also a vertex cover of G of size k, so we can assume that $u \in X$. Then, $X \setminus \{u\}$ is a vertex cover of $G - u$ of size $k-1$.

($\Leftarrow$) is immediate since for any vertex cover $X'$ of $G - u$, $X' \cup \{u\}$ is a vertex cover of G.   $\square$

The following reduction rule captures [30, Reductions R.4 and R.5] and is illustrated in Fig. 4. Note that due to its complexity, it will only be executed for vertices whose degree is bounded by some fixed constant $\alpha$ (independent of k).

Reduction R.8

Suppose G has a vertex v such that the following hold. There is a partition $(C_1, C_2)$ of N(v) where

• (i) for $i \in [2]$, $G[C_i]$ is a clique.

Furthermore, there is a co-matching M of $G[C_1, C_2]$ such that

• (ii) M saturates $C_1$ and

• (iii) $G[V(M) \cap C_1, V(M)\cap C_2] + M$ is a complete bipartite graph.

Then, reduce (G, k) to $(G', k - \left| M\right| )$ where $G'$ is the graph obtained from G by deleting v and contracting all pairs in M.

Fig. 4.

Illustration of Reduction R.8. Non-edges in $G[C_1, C_2]$ are displayed with dotted lines and the bold dotted lines represent a co-matching in $G[C_1, C_2]$ saturating $C_1$.

Proposition 5

Reduction R.8 is safe, i.e., if its conditions are satisfied, then G contains a vertex cover of size k if and only if $G'$ contains a vertex cover of size $k - \left| M\right|$.

Proof

For $i \in [2]$, we let . For notational convenience, we will assume that the vertices that are kept in the contraction of the non-edges M are the vertices $M_1$ ($= C_1$, as M saturates $C_1$). Since by the assumption (i) of Reduction R.8, $C_1$ and $C_2$ induce cliques in G, we make

Observation 1

Any vertex cover in G has to use at least $\left| C_i\right| - 1$ vertices from $C_i$, where $i \in [2]$, and any vertex cover in $G'$ has to use at least $\left| C_1\right| - 1$ vertices from $C_1$.

We now prove the proposition by a case analysis on the structure of the intersection of vertex covers of G and $G'$ with $N_G(v)$ and $N_G(v) \setminus M_2$, respectively. Observation 1 will be used later to argue that we covered all possible cases.

Claim 1

G contains a vertex cover X of size k such that $N_G(v) \subseteq X$ if and only if $G'$ contains a vertex cover $X'$ of size $k - \left| M\right|$ where $N_G(v) \setminus M_2 \subseteq X'$.

Proof

($\Rightarrow$) Let X be a vertex cover of G of size k such that $N_G(v) \subseteq X$. (Note that we can assume that $v \notin X$.) We have that is a vertex cover of . By construction, any edge in $E(G') \setminus E(G^*)$ is incident with a vertex in $M_1 \subseteq X'$.

($\Leftarrow$) Let $X'$ be a vertex cover of $G'$ of size $k - \left| M\right|$ such that $N_G(v) \setminus M_2 \subseteq X'$. Then, is a vertex cover of G, since every edge in $E(G) \setminus E(G')$ is either incident with a vertex in $M_2$ or a neighbor of v. For the latter case, we observe that $N_G(v) \subseteq X$. $\lrcorner$

Claim 2

If G contains a vertex cover X of size k with $\left| C_i \setminus X\right| = 1$ for all $i \in [2]$, then $G'$ contains a vertex cover $X'$ of size at most $k - \left| M\right|$ with $\left| C_1 \setminus X'\right| \le 1$.

Proof

Let X be a vertex cover of G of size k and suppose that $C_1 \setminus X = \{v_1\}$ and $C_2 \setminus X = \{v_2\}$. We first observe that $v \in X$, since otherwise the edges $\{v, v_1\}$ and $\{v, v_2\}$ are not covered by X. By the same reasoning we have that $\{v_1, v_2\} \notin E(G)$.

Since M saturates $C_1$ by the assumption (ii) of Reduction R.8, we have that $v_1 \in M_1$. We prove the claim by a case analysis on the position of $v_2$.

• Case 1 $\varvec{(v_2 \notin M_2)}$: The assumption $v_2 \notin M_2$ implies that $M_2 \subseteq X$. We observe that is a vertex cover of the graph of size $k - \left| M\right| - 1$. Observe that $V(G^*) = V(G')$ and let . By construction, any edge in $E(G') \setminus E(G^*)$ is incident with a vertex in $M_1 \subseteq X'$, hence $X'$ is a vertex cover of $G'$ and clearly, $\left| X'\right| = k - \left| M\right|$.

• Case 2 $\varvec{(v_2 \in M_2)}$: In this case, 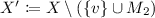is a vertex cover of the graph of size $k - \left| M\right|$. Let . Each edge $e' \in F'$ has an endpoint in $M_1$ by construction. If this endpoint is not $v_1$, then the edge $e'$ is covered by $X'$, since $M_1 \setminus \{v_1\} \subseteq X'$. We can assume that $e' = \{v_1, w\}$ for some $w \in N_{G'}(v_1)$. Since $\{v_1, v_2\} \notin E(G)$, $v_1, v_2 \in V(M)$ and by the assumption (iii) of Reduction R.8 ($G[M_1, M_2] + M$ is a complete bipartite graph), we can infer that $\{v_1, v_2\} \in M$. Hence, each neighbor of $v_1$ in $G'$ is either a neighbor of $v_1$ or $v_2$ in G. Since X is a vertex cover of G with $v_1, v_2 \notin X$, we have that

  $$ X' = X \cap V(G') \supseteq \left( N_G(v_1) \cup N_G(v_2) \right) \cap V(G') = N_{G'}(v_1) \ni w, $$

  so in this case, the edge $e' = \{v_1, w\}$ is covered by $X'$ as well.

This concludes the proof of the claim. $\lrcorner$

Note that, if G contains a vertex cover X of size k that misses precisely one vertex w from $N_G(v)$, then we have that $v \in X$ and we can change that vertex cover to which is also of size k and apply Claim 1 to conclude that $G'$ has a vertex cover of size (at most) $k - \left| M\right|$.

The next claim will complete the proof the proposition.

Claim 3

If $G'$ contains a vertex cover $X'$ of size $k - \left| M\right|$ with $\left| C_1 \setminus X'\right| = 1$, then G contains a vertex cover X of size k with $\left| C_i \setminus X\right| = 1$, for all $i \in [2]$.

Proof

Let $X'$ be a vertex cover of $G'$ of size $k - \left| M\right|$ with $C_1 \setminus X' = \{v_1\}$. Since M saturates $C_1$, we know that $v_1 \in M_1$. Let $v_2 \in M_2$ such that $\{v_1, v_2\} \in M$. We define

First note that X is of size k. Furthermore, any edge in $E(G) \setminus E(G')$ is either incident with v or with a vertex in $M_2$. The edges of the former type are clearly covered by X, since $v \in X$. Let $e \in E(G) \setminus E(G')$ be an edge incident with a vertex in $M_2$. If this vertex is not $v_2$, then it is in X, since $M_2 \setminus \{v_2\} \subseteq X$, so the edge e is covered. Otherwise, we have that $e = \{v_2, w\}$ for some $w \in N_G(v_2)$ and we observe the following. Any neighbor of $v_2$ in G is a neighbor of $v_1$ in $G'$ by construction. (Recall that $\{v_1, v_2\} \in M$.) Since $v_1 \notin X'$ and $X'$ is a vertex cover of $G'$ (and combining with previous observations), we know that $X \supseteq X' \supseteq N_{G'}(v_1) \supseteq N_G(v_2) \ni w$, so the edge $e = \{v_2, w\}$ is covered by X as well. $\lrcorner$

By Observation 1, Claims 1, 2, and 3 exhaust all possible cases and we have proved Proposition 5.   $\square$

We are now ready to kernelize degree-three vertices.

Reduction R.9

If none of the above reduction rules can be applied and G contains a vertex v of degree 3 with $N(v) = \{a, b, c\}$, then reduce (G, k) to $(G', k)$ where $G'$ is the graph on vertex set $V(G) \setminus \{v\}$ and edge set ${(E(G) \cap \left( {\begin{array}{c}V(G')\\ 2\end{array}}\right) ) \cup F}$, where

(4)

We illustrate the above reduction rule in Fig. 5.

Fig. 5.

Illustration of Reduction R.9.

Proposition 6

Reduction R.9 is safe, i.e., if its conditions are satisfied, then G contains a vertex cover of size k if and only if $G'$ contains a vertex cover of size k.

Proof

We first show that we can assume that there are no edges between the vertices in N(v).

Claim

If none of the above reduction rules can be applied, then $N(v) = \{a, b, c\}$ is an independent set in G.

Proof

If G[N(v)] contains at least two edges, then these two edges have a common endpoint, say $x \in N(v)$. But then, $N(v) \subseteq N[x]$, so we could have applied Reduction R.7, a contradiction. If G[N(v)] contains precisely one edge, assume w.l.o.g. that $\{a, b\} \in E(G)$, then we could have applied Reduction R.8 with $C_1 = \{c\}$, $C_2 = \{a, b\}$ and co-matching $M = \{\{a, c\}\}$, again a contradiction. $\lrcorner$

Due to the previous claim, we will assume that $N(v) = \{a, b, c\}$ is an independent set throughout the following.

Claim 4

If G has a vertex cover of size k, then $G'$ has a vertex cover of size at most k.

Proof

We first observe that, for each edge $e' \in E(G')$, either $e' \in E(G - v)$ or $e' \in F$. Hence, any vertex cover $X^*$ of $G - v$ is a vertex cover of $G'$ if each edge in F has an endpoint in $X^*$, since by definition, $X^*$ contains an endpoint of each edge in $E(G - v)$.

Let X be a vertex cover of G of size k. If $v \notin X$, then $N(v) = \{a, b, c\} \subseteq X$. By (4), each edge in F has at least one endpoint in $\{a, b, c\}$ and hence in X, so we can conclude that X is a vertex cover of $G'$ of size k.

Suppose $v \in X$ and note for the remainder of the proof that $X \setminus \{v\}$ is a vertex cover of $G-v$ of size $k-1$. We argue that we can assume that at most one vertex from N(v) is contained in X: For the case that $N(v) \subseteq X$, we can apply the same argument as above to conclude that $X \setminus \{v\}$ is a vertex cover of $G'$ of size $k-1$. If X contains precisely two vertices from $N(v) = \{a, b, c\}$, assume w.l.o.g. that $\{a, b\} \subseteq X$, then is a vertex cover of $G'$ of size k, since again, $X'$ contains N(v).

We assume that X contains at most one vertex from N(v). If X contains no vertex of N(v), then X must contain all of $N_G(a, b, c)$. Hence the only edges in F that are not covered by X – see (4) – are incident with the vertex b. Together with the fact that $X \setminus \{v\}$ is a vertex cover of $G - v$, we can conclude that $X \setminus \{v\} \cup \{b\}$ is a vertex cover of $G'$.

From now on, we assume that precisely one vertex of N(v) is contained in the vertex cover X of G. If $a \in X$, then $b, c \notin X$ and hence $N_G(b, c) \subseteq X$. Again, $X \setminus \{v\}$ is a vertex cover of $G - v$ and we observe that any edge in $e' \in F$ that does not have an endpoint in $X \setminus \{v\}$ is incident with the vertex c. By (4), either $e' = \{b, c\}$ or $e' = \{c, z\}$ for some $z \in N(a)$. We can conclude that $X \setminus \{v\} \cup \{c\}$ is a vertex cover of $G'$. The remaining cases can be argued for similarly: If $b \in X$, then $X \setminus \{v\} \cup \{a\}$ is a vertex cover of $G'$ and if $c \in X$, then $X \setminus \{v\} \cup \{b\}$ is a vertex cover of $G'$. $\lrcorner$

Claim 5

If $G'$ has a vertex cover of size k then G has a vertex cover of size k.

Proof

Throughout the following, let $X'$ be a vertex cover of $G'$ of size k. Since $\{a, b, c\}$ is not an independent set in $G'$, we know that $X'$ has to contain at least one vertex of $\{a, b, c\}$. If $\{a, b, c\} = N(v) \subseteq X'$, then $X'$ contains an endpoint of each edge in $E(G) \setminus E(G') = \left\{ \{v, x\} \mid x \in \{a, b, c\} \right\}$, so we can conclude that $X'$ is a vertex cover of G.

We now consider the cases when $X'$ contains precisely two vertices from $\{a, b, c\}$. If $\{a, b\} \subseteq X'$ and hence $c \notin X'$, then $X'$ contains $N_G(a)$ as well, to cover the edges between the vertex c and vertices in N(a). It follows that $X' \setminus \{a\}$ is a vertex cover of $G - v$. Since each edge in $E(G) \setminus E(G - v)$ is incident with v, we can conclude that $X' \setminus \{a\} \cup \{v\}$ is a vertex cover of G. By similar arguments we have that if $X' \cap \{a, b, c\} = \{b, c\}$, then $X' \setminus \{b\} \cup \{v\}$ is a vertex cover of G and if $X' \cap \{a, b, c\} = \{a, c\}$, then $X' \setminus \{c\} \cup \{v\}$ is a vertex cover of G.

It remains to argue the case when $X'$ contains precisely one vertex from $\{a, b, c\}$. Note that the only possible such case is when this vertex is b. If $X'$ contained only the vertex a (resp., c), then the edge $\{b, c\}$ (resp., $\{a, b\}$) would remain uncovered by $X'$. Suppose $X' \cap \{a, b, c\} = \{b\}$, so $a, c \notin X'$, implying that $N(a, b, c) \subseteq X'$. Hence, $X' \setminus \{b\}$ is a vertex cover of $G - v$ and $X' \setminus \{b\} \cup \{v\}$ is a vertex cover of G. $\lrcorner$

In the light of Claims 4 and 5, the proposition is proved.   $\square$

The next reduction rule kernelizes all vertices that have degree four and whose neighborhood induces a subgraph with more than two edges.

Fig. 6.

Illustration of Reduction R.10, with Reduction R.10.1 displayed at the top and Reduction R.10.2 displayed at the bottom.

Fig. 7.

In the left box, all pairwise non-isomorphic graphs on four vertices and three edges and in the right box, all pairwise non-isomorphic graphs on four vertices and four edges are shown.

Reduction R.10

If G contains a vertex v with degree four such that G[N(v)] has at least three edges and none of the above rules apply, then reduce (G, k) to $(G', k')$ according to one of the following cases (up to renaming the vertices in $N(v) = \{a, b, c, d\}$).

Reduction R.10.1

G[N(v)] is an (a, d)-path. In this case, let and $G'$ be the graph on vertex set $V(G) \setminus \{v\}$ and edge set $(E(G) \cap \left( {\begin{array}{c}V(G')\\ 2\end{array}}\right) ) \cup F$, where

(5)

Reduction R.10.2

$G[\{a, b, c\}]$ is a clique and d is isolated in G[N(v)]. In this case, and $G'$ is the graph on vertex set $V(G) \setminus \{v, d\}$ and edge set $(E(G) \cap \left( {\begin{array}{c}V(G')\\ 2\end{array}}\right) ) \cup F$, where

We illustrate Reductions R.10.1 and R.10.2 in Fig. 6.

Proposition 7

Reduction R.10 is safe, i.e., if its conditions are satisfied, then either Reduction R.10.1 or Reduction R.10.2 applies and G has a vertex cover of size k if and only if $G'$ has a vertex cover of size $k'$ (with $G'$ and $k'$ depending on the case that applies).

Proof

Throughout the proof, let $v \in V(G)$ denote the vertex satisfying the conditions of Reduction R.10. We first show that it is sufficient to consider the cases described in Reductions R.10.1 and R.10.2.

Claim

If G and v are as above and none of the above reduction rules can be applied, then one of the cases Reductions R.10.1 and R.10.2 applies.

Proof

If G[N(v)] contains at least five edges, then there has to be a vertex $x \in \{a, b, c, d\}$ which is incident with three of these edges. Hence, $N(v) \subseteq N[x]$ and we could have applied Reduction R.7, a contradiction. Suppose there are four edges in G[N(v)]. There are only two non-isomorphic graphs on four vertices and four edges, see the right hand side of Fig. 7. If G[N(v)] induces a $C_4$, assume w.l.o.g. that its vertices appear in the order $a-b-c-d-a$, then we can partition N(v) into cliques $C_2 = \{a, b\}$ and $C_1 = \{c, d\}$ and obtain a co-matching $M = \{\{a, c\}, \{b, d\}\}$ which satisfies the conditions of Reduction R.8, since M saturates $C_1$ and $G[C_1, C_2]+M$ is a complete bipartite graph: we have that $\{b, c\}, \{a, d\} \in E(G)$. If G[N(v)] induces an $H_4$, assume w.l.o.g. that the 3-cycle is ${a-b-c-a}$ and d is the pendant vertex adjacent to c, then we can partition N(v) into cliques $C_2 = \{a, b, c\}$ and $C_1 = \{d\}$ and have a co-matching $M = \{a, d\}$ saturating $C_1$. Hence, we could have applied Reduction R.8, a contradiction.

We can assume that G[N(v)] contains precisely three edges. There are three pairwise non-isomorphic graphs on four vertices and three edges, shown in the left-hand side of Fig. 7. If G[N(v)] induces a star ($S_4$) with center a, then we have that $N(v) \subseteq N[a]$, so we could have applied Reduction R.7, a contradiction. If G[N(v)] induces a $P_4$, we can apply Reduction R.10.1, if G[N(v)] induces a $K_3 \cup K_1$, then we can apply Reduction R.10.2. $\lrcorner$

We now prove that Reduction R.10.1 is safe.

Claim 6

If the conditions of Reduction R.10.1 hold, then G contains a vertex cover of size k if and only if $G'$ contains a vertex cover of size k.

Proof

($\Rightarrow$) Suppose G has a vertex cover X of size k. If $N(v) \subseteq X$, then every edge in $E(G') \setminus E(G)$ has at least one endpoint in X by construction, so X is a vertex cover of $G'$ as well. If X contains precisely three vertices of N(v), suppose w.l.o.g. that $X \cap N(v) = \{a, b, c\}$, then v has to be contained in X as well, otherwise the edge $\{v, d\}$ remains uncovered. Hence, $X \setminus \{v\} \cup \{d\} \supseteq N(v)$ is a vertex cover of $G'$ of size k.

From now on suppose that X contains precisely two vertices from N(v) and note that in all of the following cases, $v \in X$. The only vertex covers of G[N(v)] of size two are $\{b, c\}$, $\{a, c\}$ and $\{b, d\}$. First observe that any triple of vertices from $N_G(v)$ covers the edges $\left( {\begin{array}{c}N(v)\\ 2\end{array}}\right)$, so we do not have to consider them explicitly in the following discussion.

Suppose $X \cap N(v) = \{b, c\}$. Then, $N(a, d) \subseteq X$, so all edges in $E(G') \setminus E(G) \setminus \left( {\begin{array}{c}N(v)\\ 2\end{array}}\right)$ are covered by X. We can conclude that $X \setminus \{v\} \cup \{a\}$ (also $X \setminus \{v\} \cup \{d\}$) is a vertex cover of $G'$. If $X \cap N(v) = \{a, c\}$, then $N(b, d) \subseteq X$ and all edges in $E(G') \setminus E(G) \setminus \left( {\begin{array}{c}N(v)\\ 2\end{array}}\right)$ that are not covered by X are between d and N(a), so $X \setminus \{v\} \cup \{d\}$ is a vertex cover of $G'$. Similarly, if $X \cap N(v) = \{b, d\}$, then $X \setminus \{v\} \cup \{a\}$ is a vertex cover of $G'$.

Since G[N(v)] does not have a vertex cover of size at most 1, this concludes the proof of the first direction.

($\Leftarrow$) Since $N_G(v)$ is a clique in $G'$, any vertex cover of $G'$ contains at least three vertices from $N_G(v)$. Let $X'$ be a vertex cover of $G'$ of size k. If $N_G(v) \subseteq X'$, then $X'$ is also a vertex cover of G since each edge in $E(G) \setminus E(G')$ has an endpoint in $N_G(v)$. In the remainder, we can assume that $X'$ contains precisely three vertices from $N_G(v)$. Suppose ${X' \cap N_G(v) = \{a, b, c\}}$. Since $d \notin X'$, we have that $N(a, d) \subseteq X'$, hence all edges between a and N(a) are covered by $N(a) \subseteq X'$. Together with the observation that $\{b, c\}$ is a vertex cover of G[N(v)], we can conclude that $X' \setminus \{a\} \cup \{v\}$ is a vertex cover of G. If $X' \cap N_G(v) = \{a, b, d\}$, then $N(a, c) \subseteq X'$ since $c \notin X'$. By the same reasoning as before, we can observe that $X' \setminus \{a\} \cup \{v\}$ is a vertex cover of G. Similarly, if $X' \cap N_G(v) = \{b, c, d\}$ or if $X' \cap N_G(v) = \{a, c, d\}$ then we can argue that $X' \setminus \{d\} \cup \{v\}$ is a vertex cover of G. $\lrcorner$

We now prove the safeness of Reduction R.10.2.

Claim 7

If the conditions of Reduction R.10.2 hold, then G contains a vertex cover of size k if and only if $G'$ contains a vertex cover of size $k - 1$.

Proof

($\Rightarrow$) Let X be a vertex cover of G of size k. Observe that all edges in $E(G') \setminus E(G)$ have an endpoint in $\{a, b, c\}$ or in N(d). If $N_G(v) \subseteq X$, then X clearly contains a vertex cover of $G'$ of size at most $k-1$. Suppose X does not contain all of $N_G(v)$, implying that $v \in X$. Since $\{a, b, c\}$ is a clique in G, X contains at least two vertices from $\{a, b, c\}$, assume w.l.o.g. that $X \cap \{a, b, c\} = \{a, b\}$. If $d \in X$, then $X \setminus \{v, d\} \cup \{c\}$ is a vertex cover of $G'$ and if $d \notin X$, then $N(d) \subseteq X$, so X already covers all edges between $\{a, b, c\}$ and N(d), implying that $X \setminus \{v\}$ is a vertex cover of $G'$.

($\Leftarrow$) Let $X'$ be a vertex cover of $G'$ of size $k-1$. Since $G'[\{a, b, c\}]$ is a clique, $X'$ contains at least two vertices from $\{a, b, c\}$. If $\{a, b, c\} \subseteq X'$, then $X' \cup \{d\}$ is a vertex cover of G. If $X'$ contains precisely two vertices from $\{a, b, c\}$, then $N_G(d) \subseteq X'$, so all edges between d and N(d) (in G) are already covered by $X'$. We can conclude that in this case, $X' \cup \{v\}$ is a vertex cover of G. $\lrcorner$

This concludes the proof that Reduction R.10 is safe.   $\square$

It is easy to see that Reductions R.5, R.6, R.7, R.9 and R.10 can be executed in polynomial time. We observe (naively) that Reduction R.8 can be executed in time $\mathcal {O}\left( n \cdot 2^\alpha \cdot \alpha ! \cdot \alpha ^{\mathcal {O}(1)}\right)$, where $\alpha$ denotes the degree of the vertex v. Since for our arguments it is sufficient to apply Reduction R.8 for $\alpha \le 4$, we can assume that all its executions run in polynomial time as well. An exhaustive application of the reduction rules presented in this section therefore yields the following theorem.

Theorem 5

(cf. Fellows and Stege [30]). There is a polynomial-time algorithm that given an instance (G, k) of Vertex Cover outputs an equivalent instance $(G', k')$, where $k' \le k$,

• (I) the minimum degree of $G'$ is at least four and

• (II) for all vertices $v \in V(G')$ with $\deg _{G'}(v) = 4$, $G'[N(v)]$ contains at most two edges.

4 Automated Vertex Cover Kernelization

Many reduction rules for various problems are instances of the same class that can be described as “find a subgraph H with boundary X and replace it with a graph $H^*$”. For example, Reduction R.6 can be formulated as “find a $P_3$ (a, v, b) with boundary $\{a,b\}$ (a kind of “local surgery”) and replace it with $z_{N[v]}$”. Note however, that boundary connections might change during the replacement. Proposed reduction rules of this type can be checked in roughly $2^{|X|}$ times the time it takes to compute a minimum vertex cover in H and $H^*$.

Fig. 8.

Illustration of notation. (a) shows a graph ${G}\oplus {H}$ resulting from gluing G (darker background) and H (lighter background). (b) shows a vertex cover of ${G}\oplus {H}$ compatible with $\{2\}$, minimizing the intersection with V(H) and, thus, implying $P_{H}^G(\{2\})=4$. (c) shows a vertex cover S of ${G}\oplus {H}$ compatible with $\{0,1,2\}$, minimizing the intersection with V(H) and, thus, implying $P_{H}^G(\{0,1,2\})=3$. Note that S is not necessarily minimum or even minimal for ${G}\oplus {H}$. (d) and (e) show the same as (b) and (c) but with the graph $H'$ resulting from the application of Reduction R.7 to a vertex in H, proving $P_{H'}^G(X)=P_{H}^G(X)-1$ for $X\in \{\{2\}, \{0,1,2\}\}$.

Notation. See Fig. 8 for an illustration. Let G be a graph in which t non-isolated vertices $x_1,\ldots ,x_t$ are bijectively labeled with the integers in [t]. Then, we call G t-boundaried. If $\{x_1,\ldots ,x_t\}$ is an independent set in G, we call G strongly t-boundaried. For a t-boundaried graph H and a strongly t-boundaried graph G, we let ${{G}\oplus {H}}$ denote the result of gluing G and H, that is, identifying the vertices with the same label in the disjoint union of G and H. We call a set $S\subseteq V(G)$ compatible with a set $X\subseteq [t]$ in G if $N_G(x_i)\subseteq S \iff i\in X$ for all $i\in [t]$. Let $P_{H}^G:2^{[t]}\rightarrow \mathbb {N}$ be such that, for all $X\subseteq [t]$, $P_{H}^G(X)$ is the smallest number of vertices of H contained in any vertex cover S of ${G}\oplus {H}$ that is compatible with X in G (and $\infty$ if no such S exists). Then, we call $P_{H}^G$ the profile of H in G. It turns out that the profile is indeed independent of G, so we drop the superscript.

Lemma 2

Let G, $G'$ be strongly t-boundaried, let H be t-boundaried and let $X\subseteq [t]$. Then, $P_{H}^G(X)=P_{H}^{G'}(X)$ for all $X\subseteq [t]$.

Proof

Let $X\subseteq [t]$ and let S and $S'$ be vertex covers of ${G}\oplus {H}$ and ${G'}\oplus {H}$ that are compatible with X in G and $G'$, respectively, such that $|S\cap V(H)|$ and $|S'\cap V(H)|$ are minimum among all such vertex covers. To prove the claim, we show that is a vertex cover of ${{G}\oplus {H}}$. By symmetry, the same follows for S and $S'$ inversed, which then implies the lemma. Towards a contradiction, assume that ${G}\oplus {H}$ contains an edge uv such that $u,v\notin S^*$. Then, exactly one of u and v is in H as, otherwise, S is not a vertex cover of ${G}\oplus {H}$. Without loss of generality, let $u\in V(H)$ and $v\notin V(H)$. Thus, u is a boundary vertex $x_i$ and $v\notin S$. Since S and $S'$ are compatible with X in G and $G'$, respectively, we know that $N_G(x_i)\subseteq S \iff i\in X \iff N_{G'}(x_i)\subseteq S'$ and, as $v\in N_G(u)\setminus S$, we have $N_{G'}(u)\nsubseteq S'$. However, since $S'$ is a vertex cover of ${G'}\oplus {H}$, we have $u\in S'$, which contradicts $u\notin S^*$ since $u\in V(H)$.   $\square$

We observe that two t-boundaried graphs H and $H'$ with the same profile can be swapped for one another in any graph G without changing the size of an optimal vertex cover, that is, ${G}\oplus {H}$ and ${G}\oplus {H'}$ have the same vertex cover number. More generally, for any $c\in \mathbb {N}$, we say that H and $H'$ are c-equivalent if ${\forall _{X\subseteq [t]}\;P_{H}(X)=P_{H'}(X)+c}$. In this way, for any fixed size t, the profile gives rise to an equivalence relation on the set of t-boundaried graphs. This relation allows automated discovery of reduction rules that remove vertices with undesirable properties from the input graph. The idea is, for each induced subgraph H having an undesirable property $\varPi$, to replace H by some c-equivalent $H'$ that does not suffer from $\varPi$, while reducing k by c.

Lemma 3

Let G be strongly t-boundaried, let H and $H'$ be t-boundaried and c-equivalent for some $c\in \mathbb {N}$, and let $k\in \mathbb {N}$. Then, ${G}\oplus {H}$ has a vertex cover of size at most k if and only if ${G}\oplus {H'}$ has a vertex cover of size at most $k-c$.

Proof

As “$\Rightarrow$” is completely analogous to “$\Leftarrow$”, we only prove the latter. To this end, let S be a smallest vertex cover of ${G}\oplus {H}$ that, among all such vertex covers, minimizes $|S\cap V(H)|$. Let and note that S is compatible with X in G and $|S\cap V(H)|=P_{H}(X)$. Let $S'$ be a smallest vertex cover of ${G}\oplus {H'}$ that is compatible with X in G and, among all such vertex covers, minimizes $|S'\cap V(H')|$. As H and $H'$ are c-equivalent, we know that $|S\cap V(H)|=|S'\cap V(H')|+c$. We show that is a vertex cover of ${G}\oplus {H'}$ (clearly, $|S^*|\le |S\setminus V(H)|+|S'\cap V(H')|= |S\setminus V(H)| + |S\cap V(H)| + c = |S|+c$). Towards a contradiction, assume that there is an edge uv of ${G}\oplus {H'}$ with $u,v\notin S^*$. If $u,v\notin V(H')$, then S is not a vertex cover of ${G}\oplus {H}$ and, if $u,v\in V(H')$, then $S'$ is not a vertex cover of ${G}\oplus {H'}$. Thus, without loss of generality, $u\in V(H')$ and $v\notin V(H')$, implying that u is a boundary vertex $x_i$. Since $u\notin S^*$, we know that $u\notin S'$ and, since $S'$ is a vertex cover of ${G}\oplus {H'}$, we have $N_G(u)\subseteq S'$. Since $S'$ is compatible with X, we have $i\in X$ and, since S is compatible with X, we have $N_G(u)\subseteq S$, implying $v\in S$ which contradicts $v\notin S^*$ since $v\notin V(H)$.   $\square$

Given a t-boundaried graph H and a property $\varPi$, we can enumerate all t-boundaried graphs $H'$ that are c-equivalent to H for some c and that do not suffer from $\varPi$.

Two Examples. A proof-of-concept implementation⁷ was used to attack the remaining cases of degree-four vertices (see Sect. 3). For a given t-boundaried graph H or profile $P_{H}$ and a given number n, the implementation enumerates all strongly t-boundaried, n-vertex graphs $H'$ and outputs $H'$ if $P_{H}(X)=P_{H'}(X)$ for all $X\subseteq [t]$. Feeding the graphs displayed in Figs. 9a and 10a, the implementation yielded, in 5s and 6s, respectively, reduction rules that remove degree-four vertices whose neighborhood contains exactly two edges.

Fig. 9.

Illustration of Reduction R.11. (a) shows the degree-four vertex u with two edges in its neighborhood. A–D represent the sets of neighbors of 0–3, respectively, in the rest of the graph (A–D may mutually intersect or be empty). (b) shows the profile of (a) where the entry 3 at position $(A,\overline{B},C,D)$ means that three vertices are needed to cover all edges of (a), assuming all vertices in A, C, and D are already in the cover. Indeed, $\{u,1,2\}$ is a size-3 cover in this case. (c) shows a subgraph that is 0-equivalent to (a), that is, (b) is also the profile of (c).

Reduction R.11

Let G contain the 4-boundaried graph H depicted in Fig. 9a as an induced subgraph. Then, replace H by the 4-boundaried graph $H'$ depicted in Fig. 9c.

Fig. 10.

Illustration of Reduction R.12. (a) shows the degree-four vertex u with two edges in its neighborhood. A–D represent the sets of neighbors of 0–3, respectively, in the rest of the graph. (b) shows the profile of (a) where the entry 2 at position $(A,\overline{B},C,D)$ means that two vertices are needed to cover all edges of (a), assuming all vertices in A, C, and D are already in the cover. Indeed, $\{u,1\}$ is a size-2 cover in this case. (c) shows a subgraph that is 0-equivalent to (a), that is, (b) is also the profile of (c).

Reduction R.12

Let G contain the 4-boundaried graph H depicted in Fig. 10a as an induced subgraph. Then, replace H by the 4-boundaried graph $H'$ depicted in Fig. 10c.

By Lemma 3, correctness of Reductions R.11 and R.12 can be verified by convincing oneself that the profiles in Figs. 9 and 10 are indeed the profiles of the graphs of Figs. 9c and 10c, respectively (implying that the subgraphs are 0-equivalent).

Indeed, Reductions R.11 and R.12 cover all cases of degree-four vertices with two edges in the neighborhood, leaving only the cases of one and no edges in the neighborhood in order to be able to reduce to graphs of minimum degree five.

5 Conclusion and Open Problems

In Sect. 3, we have discussed the barrier degree constant $\delta _{VC}$ for Vertex Cover kernelization: We observed that, for some $\delta _{VC}\in \mathbb {N}$, Vertex Cover cannot be kernelized to instances of minimum degree $\delta _{VC}$ unless $\textsf {ETH}$ fails. In terms of $\mathsf {FPT}$ algorithms, the equivalent concept is that of the existence of the barrier constant $\zeta _{VC}> 0$ which is such that there is no algorithm for Vertex Cover running in time $(1 + \zeta _{VC})^k\cdot n^{\mathcal {O}(1)}$ modulo $\textsf {ETH}$ (e.g., [16, 20, 28]). So far it is only known that $\zeta _{VC}< 0.2738$ [12] and that $\delta _{VC}> 3$ (Sect. 3, see also [30]). However, observe that the question of determining the concrete value of $\delta _{VC}$ is much more tangible than the one of finding the value of $\zeta _{VC}$: Suppose one can show that a reduction rule that kernelizes degree-d vertices violates $\textsf {ETH}$, for some $d \in \mathbb {N}$. Then one might be able to adapt the gadgets used in that proof to show an $\textsf {ETH}$-violation via a reduction rule for degree $d+1, d+2, \ldots$ vertices as well. We pose: What is the exact value of $\delta _{VC}$?

The main theme of this paper has been to gather (from hitherto unpublished sources), carefully verify, and advance research on the question: to what minimum degree d can the (formidable naturally parameterized) Vertex Cover problem be kernelized to kernels of minimum degree d, even if the exponent of the polynomial running time bound grows wildly in d? ETH enforces a limit.