Abstract
Partial order reduction for timed systems is a challenging topic due to the dependencies among events induced by time acting as a global synchronization mechanism. So far, there has only been a limited success in finding practically applicable solutions yielding significant state space reductions. We suggest a working and efficient method to facilitate stubborn set reduction for timed systems with urgent behaviour. We first describe the framework in the general setting of timed labelled transition systems and then instantiate it to the case of timed-arc Petri nets. The basic idea is that we can employ classical untimed partial order reduction techniques as long as urgent behaviour is enforced. Our solution is implemented in the model checker TAPAAL and the feature is now broadly available to the users of the tool. By a series of larger case studies, we document the benefits of our method and its applicability to real-world scenarios.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Partial order reduction techniques for untimed systems, introduced by Godefroid, Peled, and Valmari in the nineties (see e.g. [6]), have since long proved successful in combating the notorious state space explosion problem. For timed systems, the success of partial order reduction has been significantly challenged by the strong dependencies between events caused by time as a global synchronizer. Only recently—and moreover in combination with approximate abstraction techniques—stubborn set techniques have demonstrated a true reduction potential for systems modelled by timed automata [23].
We pursue an orthogonal solution to the current partial order approaches for timed systems and, based on a stubborn set reduction [28, 39], we target a general class of timed systems with urgent behaviour. In a modular modelling approach for timed systems, urgency is needed to realistically model behaviour in a component that should be unobservable to other components [36]. Examples of such instantaneously evolving behaviours include, among others, cases like behaviour detection in a part of a sensor (whose duration is assumed to be negligible) or handling of release and completion of periodic tasks in a real-time operating system. We observe that focusing on the urgent part of the behaviour of a timed system allows us to exploit the full range of partial order reduction techniques already validated for untimed systems. This leads to an exact and broadly applicable reduction technique, which we shall demonstrate on a series of industrial case studies showing significant space and time reduction. In order to highlight the generality of the approach, we first describe our reduction technique in the setting of timed labelled transition systems. We shall then instantiate it to timed-arc Petri nets and implement and experimentally validate it in the model checker TAPAAL [19].
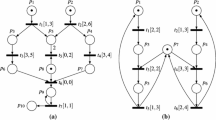
Let us now briefly introduce the model of timed-arc Peri nets and explain our reduction ideas. In timed-arc Petri nets, each token is associated with a nonnegative integer representing its age and input arcs to transitions contain intervals, restricting the ages of tokens available for transition firing (if an interval is missing, we assume the default interval \([0,\infty ]\) that accepts all token ages). In Fig. 1a we present a simple monitoring system modelled as a timed-arc Petri net. The system consists of two identical sensors where sensor i, \(i \in \{1,2\}\), is represented by the places \(b_i\) and \(m_i\), and the transitions \(s_i\) and \(r_i\). Once a token of age 0 is placed into the place \(b_i\), the sensor gets started by executing the transition \(s_i\) and moving the token from place \(b_i\) to \(m_i\) where the monitoring process starts. As the place \(b_i\) has an associated age invariant \(\le 0\), meaning that all tokens in \(b_i\) must be of age at most 0, no time delay is allowed and the firing of \(s_i\) becomes urgent. In the monitoring place \(m_i\) we have to delay one time unit before the transition \(r_i\) reporting the reading of the sensor becomes enabled. Due to the age invariant \(\le 1\) in the place \(m_i\), we cannot wait longer than one time unit, after which \(r_i\) becomes also urgent.
The places \(c_1\), \(c_2\) and \(c_3\) together with the transitions \(i_1\), \(i_2\) and t are used to control the initialization of the sensors. At the execution start, only the transition \(i_1\) is enabled and because it is an urgent transition (denoted by the white circle), no delay is initially possible and \(i_1\) must be fired immediately while removing the token of age 0 from \(c_1\) and placing a new token of age 0 into \(c_2\). At the same time, the first sensor gets started as \(i_1\) also places a fresh token of age 0 into \(b_1\). Now the control part of the net can decide to fire without any delay the transition \(i_2\) and start the second sensor, or it can delay one unit of time after which \(i_2\) becomes urgent due to the age invariant \(\le 1\) as the token in \(c_2\) is now of age 1. If \(i_2\) is fired now, it will place a fresh token of age 0 into \(b_2\). However, the token that is moved from \(c_2\) to \(c_3\) by the pair of transport arcs with the diamond-shaped arrow tips preserves its age 1, so now we have to wait precisely one more time unit before t becomes enabled. Moreover, before t can be fired, the places \(m_1\) and \(m_2\) must be empty as otherwise the firing of t is disabled due to inhibitor arcs with circle-shaped arrow tips.
In Fig. 1b we represent the reachable state space of the simple monitoring system where markings are represented using the notation like \(c_3:1 + b_2:2\) that stands for one token of age 1 in place \(c_3\) and one token of age 2 in place \(b_2\). The dashed boxes represent the markings that can be avoided during the state space exploration when we apply our partial order reduction method for checking if the termination transition t can become enabled from the initial marking. We can see that the partial order reduction is applied such that it preserves at least one path to all configurations where our goal is reached (transition t is enabled) and where time is not urgent anymore (i.e. to the configurations that allow the delay of 1 time unit). The basic idea of our approach is to apply the stubborn set reduction on the commutative diamonds where time is not allowed to elapse.
Related Work. Our stubborn set reduction is based on the work of Valmari et al. [28, 39]. We formulate their stubborn set method in the abstract framework of labelled transition systems with time and add further axioms for time elapsing in order to guarantee preservation of the reachability properties.
For Petri nets, Yoneda and Schlingloff [41] apply a partial order reduction to one-safe time Petri nets, however, as claimed in [38], the method is mainly suitable for small to medium models due to a computational overhead, confirmed also in [29]. The experimental evaluation in [41] shows only one selected example. Sloan and Buy [38] try to improve on the efficiency of the method, at the expense of considering only a rather limited model of simple time Petri nets where each transition has a statically assigned duration. Lilius [29] suggests to instead use alternative semantics of timed Petri nets to remove the issues related to the global nature of time, allowing him to apply directly the untimed partial order approaches. However, the semantics is nonstandard and no experiments are reported. Another approach is by Virbitskaite and Pokozy [40], who apply a partial order method on the region graph of bounded time Petri nets. Region graphs are in general not an efficient method for state space representation and the method is demonstrated only on a small buffer example with no further experimental validation. Recently, partial order techniques were suggested by André et al. for parametric time Petri nets [5], however, the approach is working only for safe and acyclic nets. Boucheneb and Barkaoui [12,13,14] discuss a partial order reduction technique for timed Petri nets based on contracted state class graphs and present a few examples on a prototype implementation (the authors do not refer to any publicly available tool). Their method is different from ours as it aims at adding timing constrains to the independence relation, but it does not exploit urgent behaviour. Moreover, the models of time Petri nets and timed-arc Petri nets are, even on the simplest nets, incomparable due to the different way to modelling time.
The fact that we are still lacking a practically applicable method for the time Petri net model is documented by a missing implementation of the technique in leading tools for time Petri net model checking like TINA [9] and Romeo [22]. We are not aware of any work on partial order reduction technique for the class of timed-arc Petri nets that we consider in this paper. This is likely because this class of nets provides even more complex timing behaviour, as we consider unbounded nets where each token carries its timing information (and needs a separate clock to remember the timing), while in time Petri nets timing is associated only to a priory fixed number of transitions in the net.
In the setting of timed automata [3], early work on partial order reduction includes Bengtsson et al. [8] and Minea [32] where they introduce the notion of local as well as global clocks but provide no experimental evaluation. Dams et al. [18] introduce the notion of covering in order to generalize dependencies but also here no empirical evaluation is provided. Lugiez, Niebert et al. [30, 34] study the notion of event zones (capturing time-durations between events) and use it to implement Mazurkiewicz-trace reductions. Salah et al. [37] introduce and implement an exact method based on merging zones resulting from different interleavings. The method achieves performance comparable with the approximate convex-hull abstraction which is by now superseded by the exact LU-abstraction [7]. Most recently, Hansen et al. [23] introduce a variant of stubborn sets for reducing an abstracted zone graph, thus in general offering overapproximate analysis. Our technique is orthogonal to the other approaches mentioned above; not only is the model different but also the application of our reduction gives exact results and is based on new reduction ideas. Finally, the idea of applying partial order reduction for independent events that happen at the same time appeared also in [15] where the authors, however, use a static method that declares actions as independent only if they do not communicate, do not emit signals and do not access any shared variables. Our realization of the method to the case of timed-arc Petri nets applies a dynamic (on-the-fly) reduction, while executing a detailed timing analysis that allows us to declare more transitions as independent—sometimes even in the case when they share resources.
2 Partial Order Reduction for Timed Systems
We shall now describe the general idea of our partial order reduction technique (based on stubborn sets [28, 39]) in terms of timed transition systems. We consider real-time delays in the rest of this section, as these results are not specific only to discrete time semantics. Let \(A \) be a given set of actions such that  where
where  stands for the set of nonnegative real numbers.
stands for the set of nonnegative real numbers.
Definition 1
(Timed Transition System). A timed transition system is a tuple \((S,s_0,\xrightarrow {})\) where S is a set of states, \(s_0\in S\) is the initial state, and  is the transition relation.
is the transition relation.
If \((s,\alpha ,s')\in \xrightarrow {} \) we write \(s\xrightarrow {\alpha } s'\). We implicitly assume that if \(s \xrightarrow {0} s'\) then \(s=s'\), i.e. zero time delays do not change the current state. The set of enabled actions at a state \(s \in S\) is defined as \(\mathsf {En}(s) {\mathop {=}\limits ^{\mathsf {def}}}\{ a \in A \mid \exists s' \in S.\ s \xrightarrow {a} s' \} \). Given a sequence of actions  we write \(s \xrightarrow {w} s'\) iff \(s \xrightarrow {\alpha _1} \dots \xrightarrow {\alpha _n} s'\). If there is a sequence w of length n such that \(s\xrightarrow {w} s'\), we also write \(s\xrightarrow {} ^n s'\). Finally, let \(\xrightarrow {} ^*\) be the reflexive and transitive closure of the relation \(\xrightarrow {} \) such that \(s \xrightarrow {} s'\) iff there is
we write \(s \xrightarrow {w} s'\) iff \(s \xrightarrow {\alpha _1} \dots \xrightarrow {\alpha _n} s'\). If there is a sequence w of length n such that \(s\xrightarrow {w} s'\), we also write \(s\xrightarrow {} ^n s'\). Finally, let \(\xrightarrow {} ^*\) be the reflexive and transitive closure of the relation \(\xrightarrow {} \) such that \(s \xrightarrow {} s'\) iff there is  and \(s \xrightarrow {\alpha } s'\).
and \(s \xrightarrow {\alpha } s'\).
For the rest of this section, we assume a fixed transition system \((S,s_0,\xrightarrow {})\) and a set of goal states \(G\subseteq S\). The reachability problem, given a timed transition system \((S,s_0,\xrightarrow {})\) and a set of goal states G, is to decide whether there is \(s' \in G\) such that \(s_0 \xrightarrow {} ^* s'\).
We now develop the theoretical foundations of stubborn sets for timed transition systems. A state \(s\in S\) is zero time if time can not elapse at s. We denote the zero time property of a state s by the predicate \(\mathsf {zt}(s)\) and define it as \(\mathsf {zt}(s)\) iff for all \(s'\in S\) and all  if \(s \xrightarrow {d} s'\) then \(d = 0\). A reduction of a timed transition system is a function \(\mathsf {St}: S \rightarrow 2^A \). A reduction defines a reduced transition relation \(\xrightarrow [\tiny \mathsf {St} ]{} \subseteq \xrightarrow {} \) such that \(s \xrightarrow [\tiny \mathsf {St} ]{\alpha } s'\) iff \(s \xrightarrow {\alpha } s'\) and
if \(s \xrightarrow {d} s'\) then \(d = 0\). A reduction of a timed transition system is a function \(\mathsf {St}: S \rightarrow 2^A \). A reduction defines a reduced transition relation \(\xrightarrow [\tiny \mathsf {St} ]{} \subseteq \xrightarrow {} \) such that \(s \xrightarrow [\tiny \mathsf {St} ]{\alpha } s'\) iff \(s \xrightarrow {\alpha } s'\) and  . For a given state \(s \in S\) we define \(\overline{\mathsf {St} (s)} {\mathop {=}\limits ^{\mathsf {def}}}A \setminus \mathsf {St} (s)\) as the set of all actions that are not in \(\mathsf {St} (s)\).
. For a given state \(s \in S\) we define \(\overline{\mathsf {St} (s)} {\mathop {=}\limits ^{\mathsf {def}}}A \setminus \mathsf {St} (s)\) as the set of all actions that are not in \(\mathsf {St} (s)\).
Definition 2
(Reachability Conditions). A reduction \(\mathsf {St} \) on a timed transition system \((S,s_0,\xrightarrow {})\) is reachability preserving if it satisfies the following four conditions.

Condition \(\mathcal {Z } \) declares that in a state where a delay is possible, all enabled actions become stubborn actions. Condition \(\mathcal {D } \) guarantees that in order to enable a time delay from a state where delaying is not allowed, a stubborn action must be executed. Similarly, Condition \(\mathcal {R }\) requires that a stubborn action must be executed before a goal state can be reached from a non-goal state. Finally, Condition \(\mathcal {W } \) allows us to commute stubborn actions with non-stubborn actions. The following theorem shows that reachability preserving reductions generate pruned transition systems where the reachability of goal states is preserved.
Theorem 1
(Shortest-Distance Reachability Preservation). Let \(\mathsf {St} \) be a reachability preserving reduction satisfying \(\mathcal {Z } \), \(\mathcal {D } \), \(\mathcal {R }\) and \(\mathcal {W } \). Let \(s \in S\). If \(s \xrightarrow {} ^n s'\) for some \(s' \in G\) then also \(s \xrightarrow [\tiny \mathsf {St} ]{} ^m s''\) for some \(s'' \in G\) where \(m \le n\).
Proof
We proceed by induction on n. Base step. If \(n=0\), then \(s=s'\) and \(m=n=0\). Inductive step. Let \(s_0\xrightarrow {\alpha _0} s_1\xrightarrow {\alpha _1} \dots \xrightarrow {\alpha _n} s_{n+1}\) where \(s_0 \not \in G\) and \(s_{n+1} \in G\). Without loss of generality we assume that for all i, \(0\le i\le n\), we have \(\alpha _i \ne 0\) (otherwise we can simply skip these 0-delay actions and get a shorter sequence). We have two cases. Case \(\lnot \mathsf {zt}(s_0)\): by condition \(\mathcal {Z } \) we have \(\mathsf {En}(s_0)\subseteq \mathsf {St} (s_0)\) and by the definition of \(\xrightarrow [\tiny \mathsf {St} ]{} \) we have \(s_0 \xrightarrow [\tiny \mathsf {St} ]{\alpha _0} s_1\) since  . By the induction hypothesis we have \(s_1 \xrightarrow [\tiny \mathsf {St} ]{} ^m s''\) with \(s''\in G\) and \(m \le n\) and \(m+1\le n+1\). Case \(\mathsf {zt}(s_0)\): let \(w=\alpha _0\alpha _1\dots \alpha _n\) and \(\alpha _i\) be such that \(\alpha _i\in \mathsf {St} (s_0)\) and for all \(k<i\) holds that \(\alpha _k\not \in \mathsf {St} (s_0)\), i.e. \(\alpha _i\) is the first stubborn action in w. Such an \(\alpha _i\) has to exist otherwise \(s_{n+1}\not \in G\) due to condition \(\mathcal {R }\). Because of condition \(\mathcal {D } \) we get \(\mathsf {zt}(s_k)\) for all k, \(0 \le k<i\), otherwise \(\alpha _i\) cannot be the first stubborn action in w. We can split w as \(w=u\alpha _iv\) with \(u\in \overline{\mathsf {St} (s_0)}^*\). Since all states in the path to \(s_i\) are zero time, by \(\mathcal {W } \) we can swap \(\alpha _i\) as \(s_0 \xrightarrow {\alpha _i} s'_1 \xrightarrow {u} s_i \xrightarrow {v} s'\) with \(|uv|=n\). Since \(\alpha _i\in \mathsf {St} (s_0)\) we get \(s_0 \xrightarrow [\tiny \mathsf {St} ]{\alpha _i} s'_1\) and by the induction hypothesis we have \(s'_1 \xrightarrow [\tiny \mathsf {St} ]{} ^m s''\) where \(s''\in G\), \(m \le n\), and \(m+1\le n+1\). \(\square \)
. By the induction hypothesis we have \(s_1 \xrightarrow [\tiny \mathsf {St} ]{} ^m s''\) with \(s''\in G\) and \(m \le n\) and \(m+1\le n+1\). Case \(\mathsf {zt}(s_0)\): let \(w=\alpha _0\alpha _1\dots \alpha _n\) and \(\alpha _i\) be such that \(\alpha _i\in \mathsf {St} (s_0)\) and for all \(k<i\) holds that \(\alpha _k\not \in \mathsf {St} (s_0)\), i.e. \(\alpha _i\) is the first stubborn action in w. Such an \(\alpha _i\) has to exist otherwise \(s_{n+1}\not \in G\) due to condition \(\mathcal {R }\). Because of condition \(\mathcal {D } \) we get \(\mathsf {zt}(s_k)\) for all k, \(0 \le k<i\), otherwise \(\alpha _i\) cannot be the first stubborn action in w. We can split w as \(w=u\alpha _iv\) with \(u\in \overline{\mathsf {St} (s_0)}^*\). Since all states in the path to \(s_i\) are zero time, by \(\mathcal {W } \) we can swap \(\alpha _i\) as \(s_0 \xrightarrow {\alpha _i} s'_1 \xrightarrow {u} s_i \xrightarrow {v} s'\) with \(|uv|=n\). Since \(\alpha _i\in \mathsf {St} (s_0)\) we get \(s_0 \xrightarrow [\tiny \mathsf {St} ]{\alpha _i} s'_1\) and by the induction hypothesis we have \(s'_1 \xrightarrow [\tiny \mathsf {St} ]{} ^m s''\) where \(s''\in G\), \(m \le n\), and \(m+1\le n+1\). \(\square \)
3 Timed-Arc Petri Nets
We shall now define the model of timed-arc Petri nets (as informally described in the introduction) together with a reachability logic and a few technical lemmas needed later on. Let \(\mathbb {N}_{0}= \mathbb {N} \cup \{0\}\) and \(\mathbb {N}_{0}^{\infty } = \mathbb {N}_{0}\cup \left\{ \infty \right\} \). We define the set of well-formed closed time intervals as \(\mathcal {I}{\mathop {=}\limits ^{\text {def}}}\{[a,b] \mid a \in \mathbb {N}_{0},b\in \mathbb {N}_{0}^{\infty }, a\le b \}\) and its subset \(\mathcal {I}^{\text {inv}}{\mathop {=}\limits ^{\text {def}}}\{[0,b] \mid b\in \mathbb {N}_{0}^{\infty } \}\) used in age invariants.
Definition 3
(Timed-Arc Petri Net). A timed-arc Petri net (TAPN) is a 9-tuple \(N = (P, T, T_{ urg }, IA , OA , g , w , Type , I )\) where
-
P is a finite set of places,
-
T is a finite set of transitions such that \(P \cap T = \emptyset \),
-
\(T_{ urg }\subseteq T\) is the set of urgent transitions,
-
\( IA \subseteq P \times T\) is a finite set of input arcs,
-
\( OA \subseteq T \times P\) is a finite set of output arcs,
-
\( g : IA \rightarrow \mathcal {I}\) is a time constraint function assigning guards (time intervals) to input arcs s.t.
-
if \((p,t) \in IA \) and \(t \in T_{ urg }\) then \( g ((p,t))=[0,\infty ]\),
-
-
\( w : IA \cup OA \rightarrow \mathbb {N}\) is a function assigning weights to input and output arcs,
-
\( Type : IA \cup OA \rightarrow \mathbf {{Types}}\) is a type function assigning a type to all arcs where \(\mathbf {{Types}}= \{ Normal , Inhib \} \cup \{ Transport _j\mid j \in \mathbb {N} \}\) such that
-
if \( Type (z) = Inhib \) then \(z \in IA \) and \( g (z)=[0,\infty ]\),
-
if \( Type ((p,t)) = Transport _j\) for some \((p,t) \in IA \) then there is exactly one \((t,p^{\prime }) \in OA \) such that \( Type ((t,p^{\prime })) = Transport _j\),
-
if \( Type ((t,p^{\prime })) = Transport _j\) for some \((t,p^{\prime }) \in OA \) then there is exactly one \((p,t) \in IA \) such that \( Type ((p,t)) = Transport _j\),
-
if \( Type ((p,t)) = Transport _j= Type ((t,p^{\prime }))\) then \( w ((p,t))= w ((t,p^{\prime }))\),
-
-
\( I : P \rightarrow \mathcal {I}^{inv}\) is a function assigning age invariants to places.
Note that for transport arcs we assume that they come in pairs (for each type \( Transport _j\)) and that their weights match. Also for inhibitor arcs and for input arcs to urgent transitions, we require that the guards are \([0,\infty ]\).
Before we give the formal semantics of the model, let us fix some notation. Let \(N = (P, T, T_{ urg }, IA , OA , g , w , Type , I )\) be a TAPN. We denote by \({}^\bullet x {\mathop {=}\limits ^{\text {def}}}\{y \in P \cup T \mid (y,x) \in IA \cup OA ,\ Type ((y,x)) \ne Inhib \}\) the preset of a transition or a place x. Similarly, the postset is defined as \(x^\bullet {\mathop {=}\limits ^{\text {def}}}\{y \in P \cup T \mid (x,y) \in ( IA \cup OA ) \}\). We denote by \({}^\circ t {\mathop {=}\limits ^{\text {def}}}\{ p \in P \mid (p,t) \in IA \wedge Type ((p,t)) = Inhib \}\) the inhibitor preset of a transition t. The inhibitor postset of a place p is defined as \(p^\circ {\mathop {=}\limits ^{\text {def}}}\{ t \in T \mid (p,t) \in IA \wedge Type ((p,t)) = Inhib \}\). Let \(\mathcal {B}(\mathbb {R}^{\ge 0})\) be the set of all finite multisets over \(\mathbb {R}^{\ge 0}\). A marking M on N is a function \(M : P \longrightarrow \mathcal {B}(\mathbb {R}^{\ge 0})\) where for every place \(p \in P\) and every token \(x \in M(p)\) we have \(x \in I (p)\), in other words all tokens have to satisfy the age invariants. The set of all markings in a net N is denoted by \(\mathcal {M}(N)\).
We write (p, x) to denote a token at a place p with the age \(x\in \mathbb {R}^{\ge 0}\). Then \(M=\{(p_1,x_1),(p_2,x_2),\dots ,(p_n,x_n)\}\) is a multiset representing a marking M with n tokens of ages \(x_i\) in places \(p_i\). We define the size of a marking as \(|M| = \sum _{p\in P}|M(p)|\) where |M(p)| is the number of tokens located in the place p. A marked TAPN \((N,M_0)\) is a TAPN N together with an initial marking \(M_0\) with all tokens of age 0.
Definition 4
(Enabledness). Let \(N = (P, T, T_{ urg }, IA , OA , g , w , Type , I )\) be a TAPN. We say that a transition \(t \in T\) is enabled in a marking M by the multisets of tokens \( In = \{(p,x_{p}^1), (p,x_{p}^2), \dots ,(p,x_{p}^{ w ((p,t))})\mid p \in {}^\bullet t\} \subseteq M\) and \( Out = \{ (p^{\prime },x_{p^{\prime }}^1), (p^{\prime },x_{p^{\prime }}^2), \dots ,(p^{\prime },x_{p^{\prime }}^{ w ((t,p^{\prime }))}) \mid p^{\prime } \in t^\bullet \}\) if
-
for all input arcs except the inhibitor arcs, the tokens from \( In \) satisfy the age guards of the arcs, i.e.
$$\forall p \in {}^\bullet t.\ x_p^i \in g ((p,t))\text { for }1\le i\le w((p,t)) $$ -
for any inhibitor arc pointing from a place p to the transition t, the number of tokens in p is smaller than the weight of the arc, i.e.
$$\forall (p,t) \in IA . Type ((p,t)) = Inhib \Rightarrow |M(p)|< w ((p,t))$$ -
for all input arcs and output arcs which constitute a transport arc, the age of the input token must be equal to the age of the output token and satisfy the invariant of the output place, i.e.
$$\begin{aligned}&\forall (p,t) \in IA . \forall (t,p^{\prime }) \in OA . Type ((p,t)) = Type ((t,p^{\prime })) = Transport _j\\&\Rightarrow \big ( x_p^i = x_{p^{\prime }}^i \wedge x_{p^{\prime }}^i \in I (p^{\prime })\big ) \text { for } 1\le i \le w((p,t)) \end{aligned}$$ -
for all normal output arcs, the age of the output token is 0, i.e.
$$\forall (t,p^{\prime }) \in OA . Type ((t,p^{\prime })) = Normal \Rightarrow x_{p^{\prime }}^i = 0 \text { for }1\le i \le w((t,p')).$$
A given marked TAPN \((N,M_0)\) defines a timed transition system \(T(N){\mathop {=}\limits ^{\text {def}}}(\mathcal {M}(N),M_0,\xrightarrow {})\) where the states are markings and the transitions are as follows.
-
If \(t\in T\) is enabled in a marking M by the multisets of tokens \( In \) and \( Out \) then t can fire and produce the marking \(M^{\prime } = (M \smallsetminus In ) \uplus Out \) where \(\uplus \) is the multiset sum operator and \(\smallsetminus \) is the multiset difference operator; we write \(M \xrightarrow {t} M^{\prime }\) for this action transition.
-
A time delay \(d \in \mathbb {N}_{0}\) is allowed in M if
-
\((x+d) \in I(p)\) for all \(p \in P\) and all \(x \in M(p)\), i.e. by delaying d time units no token violates any of the age invariants, and
-
if \(M {\mathop {\rightarrow }\limits ^{t}} M'\) for some \(t \in T_{ urg }\) then \(d=0\), i.e. enabled urgent transitions disallow time passing.
By delaying d time units in M we reach the marking \(M^{\prime }\) defined as \(M^{\prime }(p) = \{x+d \mid x \in M(p)\}\) for all \(p \in P\); we write \(M \xrightarrow {d} M^{\prime }\) for this delay transition.
-
Note that the semantics above defines the discrete-time semantics as the delays are restricted to nonnegative integers. It is well known that for timed-arc Petri nets with nonstrict intervals, the marking reachability problem on discrete and continuous time nets coincide [31]. This is, however, not the case for more complex properties like liveness that can be expressed in the CTL logic (for counter examples that can be expressed in CTL see e.g. [25]).
 , otherwise \(A_{M} (\varphi ) = \emptyset \))
, otherwise \(A_{M} (\varphi ) = \emptyset \))3.1 Reachability Logic and Interesting Sets of Transitions
We now describe a logic for expressing the properties of markings based on the number of tokens in places and transition enabledness, inspired by the logic used in the Model Checking Contest (MCC) Property Language [27]. Let \(N = (P, T, T_{ urg }, IA , OA , g , w , Type , I )\) be a TAPN. The formulae of the logic are given by the abstract syntax:
\(\varphi \,\, {:}{:}= \,\,{ deadlock }\, |\, t \, | \, e_1 \, \bowtie \, e_2 | \, \varphi _{1} \, \wedge \, \varphi _{2}\, | \, \varphi _{1}\, \vee \, \varphi _{2} \, | \, \lnot \varphi \)
\( e \,{:}{:}= \,\, c |\, p\, |\, e_1 \,\oplus \,e_2\)
where \(t \in T\), \(\bowtie \) \(\in \) \(\{<, \le , =, \ne , >, \ge \}\), \(c \in \mathbb {Z}\), \(p \in P\), and \(\oplus \in \{ +, -, * \}\). Let \(\varPhi \) be the set of all such formulae and let \(E_N\) be the set of arithmetic expressions over the net N. The semantics of \(\varphi \) in a marking \(M \in \mathcal {M}(N)\) is given by
assuming a standard semantics for Boolean operators and where the semantics of arithmetic expressions in a marking M is as follows: \( eval _{M}(c) = c\), \( eval _{M}(p) = |M(p)|\), and \( eval _{M}(e_{1} \oplus e_{2}) = eval _{M}(e_{1}) \oplus eval _{M}(e_{2})\).
Let \(\varphi \) be a formula. We are interested in the question, whether we can reach from the initial marking some of the goal markings from \(G_\varphi = \{ M \in \mathcal {M}(N) \mid M \models \varphi \}\). In order to guide the reduction such that transitions that lead to the goal markings are included in the generated stubborn set, we define the notion of interesting transitions for a marking M relative to \(\varphi \), and we let \(A_{M} (\varphi ) \subseteq T\) denote the set of interesting transitions. Formally, we shall require that whenever \(M \xrightarrow {w} M'\) via a sequence of transitions \(w= t_1t_2\dots t_n \in T^*\) where \(M \not \in G_\varphi \) and \(M' \in G_\varphi \), then there must exist i, \(1 \le i \le n\), such that \(t_i \in A_{M} (\varphi )\).
Table 1 gives a possible definition of \(A_{M} (\varphi )\). Let us remark that the definition is at several places nondeterministic, allowing for a variety of sets of interesting transitions. Table 1 uses the functions \( incr_M : E_N \rightarrow 2^T\) and \( decr_M : E_N \rightarrow 2^T\) defined in Table 2. These functions take as input an expression e, and return all transitions that can possibly, when fired, increase resp. decrease the evaluation of e. The following lemma formally states the required property of the functions \( incr_M \) and \( decr_M \).
Lemma 1
Let \(N = (P, T, T_{ urg }, IA , OA , g , w , Type , I )\) be a TAPN and \(M \in \mathcal {M}(N)\) a marking. Let \(e \in E_N\) and let \(M \xrightarrow {w} M'\) where \(w=t_1t_2\dots t_n \in T^*\).
-
If \( eval _{M}(e) < eval _{M'}(e)\) then there is i, \(1 \le i \le n\), such that \(t_i \in incr _{M}(e)\).
-
If \( eval _{M}(e) > eval _{M'}(e)\) then there is i, \(1 \le i \le n\), such that \(t_i \in decr _{M}(e)\).
We finish this section with the main technical lemma, showing that at least one interesting transition must be fired before we can reach a marking satisfying a given reachability formula.
Lemma 2
Let \(N = (P, T, T_{ urg }, IA , OA , g , w , Type , I )\) be a TAPN, let \(M \in \mathcal {M}(N)\) be its marking and let \(\varphi \in \varPhi \) be a given formula. If  and \(M\xrightarrow {w} M'\) where \(w \in \overline{A_{M} (\varphi )}^*\) then
and \(M\xrightarrow {w} M'\) where \(w \in \overline{A_{M} (\varphi )}^*\) then  .
.
4 Partial Order Reductions for TAPN
We are now ready to state the main theorem that provides sufficient syntax-driven conditions for a reduction in order to guarantee preservation of reachability. Let \(N = (P, T, T_{ urg }, IA , OA , g , w , Type , I )\) be a TAPN, let \(M \in \mathcal {M}(N)\) be a marking of N, and let \(\varphi \in \varPhi \) be a formula. We recall that \(A_{M} (\varphi )\) is the set of interesting transitions as defined earlier.
Theorem 2
(Reachability Preserving Closure). Let \(\mathsf {St} \) be a reduction such that for all \(M \in \mathcal {M}(N)\) it satisfies the following conditions.
-
1
If \(\lnot \mathsf {zt}(M)\) then \(\mathsf {En}(M) \subseteq \mathsf {St} (M)\).
-
2
If \(\mathsf {zt}(M)\) then \(A_{M} (\varphi ) \subseteq \mathsf {St} (M)\).
-
3
If \(\mathsf {zt}(M)\) then either
-
(a)
there is \(t \in T_{ urg }\cap \mathsf {En}(M) \cap \mathsf {St} (M)\) where \({}^\bullet ({}^\circ t) \subseteq \mathsf {St} (M)\), or
-
(b)
there is \(p \in P\) where \( I (p)=[a,b]\) and \(b \in M(p)\) such that \(t \in \mathsf {St} (M)\) for every \(t \in p^\bullet \) where \(b \in g ((p,t))\).
-
(a)
-
4
For all \(t \in \mathsf {St} (M) \setminus \mathsf {En}(M)\) either
-
(a)
there is \(p \in {}^\bullet t\) such that \(|\{x \in M(p) \mid x \in g ((p,t)) \}| < w((p,t))\) and
-
\(t' \in \mathsf {St} (M)\) for all \(t' \in {}^\bullet p\) where there is \(p' \in {}^\bullet t'\) with \( Type ((t',p)) = Type ((p',t')) = Transport _j\) and where \( g ((p',t')) \cap g ((p,t)) \ne \emptyset \), and
-
if \(0 \in g ((p,t))\) then also \({}^\bullet p \subseteq \mathsf {St} (M)\), or
-
-
(b)
there is \(p \in {}^\circ t\) where \(|M(p)| \ge w((p,t))\) such that
-
\(t' \in \mathsf {St} (M)\) for all \(t' \in p^\bullet \) where \(M(p) \cap g ((p,t')) \not =\emptyset \).
-
-
(a)
-
5
For all \(t \in \mathsf {St} (M) \cap \mathsf {En}(M)\) we have
-
(a)
\(t' \in \mathsf {St} (M)\) for every \(t' \in p^\bullet \) where \(p \in {}^\bullet t\) and \( g ((p,t)) \cap g ((p,t')) \ne \emptyset \), and
-
(b)
\((t^{\bullet })^\circ \subseteq \mathsf {St} (M)\).
-
(a)
Then \(\mathsf {St} \) satisfies \(\mathcal {Z } \), \(\mathcal {D } \), \(\mathcal {R }\), and \(\mathcal {W } \).
Cases for Condition 3
Let us now briefly discuss the conditions of Theorem 2. Clearly, Condition 1 ensures that if time can elapse, we include all enabled transitions into the stubborn set and Condition 2 guarantees that all interesting transitions (those that can potentially make the reachability proposition true) are included as well.
Condition 3 makes sure that if time elapsing is disabled then any transition that can possibly enable time elapsing will be added to the stubborn set. There are two situations how time progress can be disabled. Either, there is an urgent enabled transition, like the transition t in Fig. 2a. Since \(t_2\) can add a token to \(p_2\) and by that inhibit t, Condition 3a makes sure that \(t_2\) is added into the stubborn set in order to satisfy \(\mathcal {D } \). As \(t_1\) can remove the token of age 3 from \(p_1\) and hence disable t, we must add \(t_1\) to the stubborn set too (guaranteed by Condition 5a). The other situation when time gets stopped is when a place with an age invariant contains a token that disallows time passing, like in Fig. 2b where time is disabled because the place p has a token of age 5, which is the maximum possible age of tokens in p due to the age invariant. Since \(t_2\) can remove the token of age 5 from p, we include it to the stubborn set due to Condition 3b. On the other hand \(t_1\) does not have to be included in the stubborn set as its firing cannot remove the token of age 5 from p.
Condition 4 makes sure that an disabled stubborn transition can never be enabled by a non-stubborn transition. There are two reasons why a transition is disabled. Either, as in Fig. 3a where t is disabled, there is an insufficient number of tokens of appropriate age to fire the transition. In this case, Condition 4a makes sure that transitions that can add tokens of a suitable age via transport arcs are included in the stubborn set. This is the case for the transition \(t_1\) in our example, as [2, 5] has a nonempty intersection with [4, 6]. On the other hand, \(t_3\) does not have to be added. As the transition \(t_2\) only adds fresh tokens of age 0 to p via normal arcs, there is no need to add \(t_2\) into the stubborn set either. The other reason for a transition to be disabled is due to inhibitor arcs, as shown on the transition t in Fig. 3b. Condition 4b makes sure that \(t_1\) is added to the stubborn set, as it can enable t (the interval [6, 8] has a nonempty intersection with the tokens of age 6 and 7 in the place p). As this is not the case for \(t_2\), this transition can be left out from the stubborn set.
Cases for Condition 4
Cases for Condition 5

Finally, Condition 5 guarantees that enabled stubborn transitions can never disable any non-stubborn transitions. For an illustration, take a look at Fig. 4a and assume that t is an enabled stubborn transition. Firing of t can remove the token of age 4 from p and disable \(t_2\), hence \(t_2\) must become stubborn by Condition 5a in order to satisfy \(\mathcal {W } \). On the other hand, the intervals [6, 8] and [2, 5] have empty intersection, so there is no need to declare \(t_1\) as a stubborn transition. Moreover, firing of t can also disable the transition \(t_3\) due to the inhibitor arc, so we must add \(t_3\) to the stubborn set by Condition 5b.
The conditions of Theorem 2 can be turned into an iterative saturation algorithm for the construction of stubborn sets as shown in Algorithm 1. When running this algorithm for the net in our running example, we can reduce the state space exploration for fireability of the transition t as depicted in Fig. 1b. Our last theorem states that the algorithm returns stubborn subsets of enabled transitions that satisfy the four conditions of Theorem 1 and hence we preserve the reachability property as well as the minimum path to some reachable goal.
Theorem 3
Algorithm 1 terminates and returns \(\mathsf {St} (M) \cap \mathsf {En}(M)\) for some reduction \(\mathsf {St} \) that satisfies \(\mathcal {Z } \), \(\mathcal {D } \), \(\mathcal {R }\), and \(\mathcal {W } \).
5 Implementation and Experiments
We implemented our partial order method in C++ and integrated it within the model checker TAPAAL [19] and its discrete time engine verifydtapn [4, 11]. We evaluate our partial order reduction on a wide range of case studies.
PatientMonitoring. The patient monitoring system [17] models a medical system that through sensors periodically scans patient’s vital functions, making sure that abnormal situations are detected and reported within given deadlines. The timed-arc Petri net model was described in [17] for two sensors monitoring patient’s pulse rate and oxygen saturation level. We scale the case study by adding additional sensors. BloodTransfusion. This case study models a larger blood transfusion workflow [16], the benchmarking case study of the little-JIL language. The timed-arc Petri net model was described in [10] and we verify that the workflow is free of deadlocks (unless all sub-workflows correctly terminate). The problem is scaled by the number of patients receiving a blood transfusion. FireAlarm. This case study uses a modified (due to trade secrets) fire alarm system owned by a German company [20, 21]. It models a four-channel round-robin frequency-hopping transmission scheduling in order to ensure a reliable communication between a number of wireless sensors (by which the case study is scaled) and a central control unit. The protocol is based on time-division multiple access (TDMA) channel access and we verify that for a given frequency-jammer, it takes never more than three cycles before a fire alarm is communicated to the central unit. BAwPC. Business Activity with Participant Completion (BAwPC) is a web-service coordination protocol from WS-BA specification [33] that ensures a consistent agreement on the outcome of long-running distributed applications. In [26] it was shown that the protocol is flawed and a correct, enhanced variant was suggested. We model check this enhanced protocol and scale it by the capacity of the communication buffer. Fischer. Here we consider a classical Fischer’s protocol for ensuring mutual exclusion for a number of timed processes. The timed-arc Petri net model is taken from [2] and it is scaled by the number of processes. LynchShavit. This is another timed-based mutual exclusion algorithm by Lynch and Shavit, with the timed-arc Petri net model taken from [1] and scaled by the number of processes. MPEG2. This case study describes the workflow of the MPEG-2 video encoding algorithm run on a multicore processor (the timed-arc Petri net model was published in [35]) and we verify the maximum duration of the workflow. The model is scaled by the number of B frames in the IB\(^n\)P frame sequence. AlternatingBit. This is a classical case study of alternating bit protocol, based on the timed-arc Petri net model given in [24]. The purpose of the protocol is to ensure a safe communication between a sender and a receiver over an unreliable medium. Messages are time-stamped in order to compensate (via retransmission) for the possibility of losing messages. The case study is scaled by the maximum number of messages in transfer.
All experiments were run on AMD Opteron 6376 Processors with 500 GB memory. In Table 3 we compare the time to verify a model without (NORMAL) and with (POR) partial order reduction, the number of explored markings (in thousands) and the percentage of time and memory reduction. We can observe clear benefits of our technique on PatientMonitoring, BloodTransfusion and FireAlarm where we are both exponentially faster and explore only a fraction of all reachable markings. For example in FireAlarm, we are able to verify its correctness for all 125 sensors, as it is required by the German company [21]. This would be clearly unfeasible without the use of partial order reduction.
In BAwPC, we can notice that for the smallest instances, there is some computation overhead from computing the stubborn sets, however, it clearly pays off for the larger instances where the percentages of reduced state space are closely followed by the percentages of the verification times and in fact improve with the larger instances. Fischer and LynchShavit case studies demonstrate that even moderate reductions of the state space imply considerable reduction in the running time and computing the stubborn sets is well worth the extra effort.
MPEG2 is an example of a model that allows only negligible reduction of the state space size, and where we observe an actual slowdown in the running time due to the computation of the stubborn sets. Nevertheless, the overhead stays constant in the range of about 15%, even for increasing instance sizes. Finally, AlternatingBit protocol does not allow for any reduction of the state space (even though it contains age invariants) but the overhead in the running time is negligible.
We observed similar performance of our technique also for the cases where the reachability property does not hold and a counter example can be generated.
6 Conclusion
We suggested a simple, yet powerful and application-ready partial order reduction for timed systems. The reduction comes into effect as soon as the timed system enters an urgent configuration where time cannot elapse until a nonempty sequence of transitions gets executed. The method is implemented and fully integrated, including GUI support, into the open-source tool TAPAAL. We demonstrated its practical applicability on several case studies and conclude that computing the stubborn sets causes only a minimal overhead while providing large benefits for reducing the state space in numerous models. The method is not specific to stubborn reduction technique only and it preserves the shortest execution sequences. Moreover, once the time gets urgent, other classical (untimed) partial order approaches should be applicable too. Our method was instantiated to (unbounded) timed-arc Petri nets with discrete time semantics, however, we claim that the technique allows for general application to other modelling formalisms like timed automata and timed Petri nets, as well as an extension to continuous time. We are currently working on adapting the theory and providing an efficient implementation for UPPAAL-style timed automata with continuous time semantics.
References
Abdulla, P., Deneux, J., Mahata, P., Nylén, A.: Using forward reachability analysis for verification of timed Petri nets. Nord. J. Comput. 14, 1–42 (2007)
Abdulla, P.A., Nylén, A.: Timed Petri nets and BQOs. In: Colom, J.-M., Koutny, M. (eds.) ICATPN 2001. LNCS, vol. 2075, pp. 53–70. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45740-2_5
Alur, R., Dill, D.L.: A theory of timed automata. Theor. Comput. Sci. 126(2), 183–235 (1994)
Andersen, M., Gatten Larsen, H., Srba, J., Grund Sørensen, M., Haahr Taankvist, J.: Verification of liveness properties on closed timed-arc Petri nets. In: Kučera, A., Henzinger, T.A., Nešetřil, J., Vojnar, T., Antoš, D. (eds.) MEMICS 2012. LNCS, vol. 7721, pp. 69–81. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36046-6_8
André, E., Chatain, T., Rodríguez, C.: Preserving partial-order runs in parametric time Petri nets. ACM Trans. Embed. Comput. Syst. 16(2), 43:1–43:26 (2017)
Baier, C., Katoen, J.-P.: Principles of Model Checking. The MIT Press, Cambridge (2008)
Behrmann, G., Bouyer, P., Larsen, K.G., Pelánek, R.: Lower and upper bounds in zone-based abstractions of timed automata. STTT 8(3), 204–215 (2006)
Bengtsson, J., Jonsson, B., Lilius, J., Yi, W.: Partial order reductions for timed systems. In: Sangiorgi, D., de Simone, R. (eds.) CONCUR 1998. LNCS, vol. 1466, pp. 485–500. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055643
Berthomieu, B., Vernadat, F.: Time Petri nets analysis with TINA. In: Third International Conference on Quantitative Evaluation of Systems, pp. 123–124. IEEE Computer Society (2006)
Bertolini, C., Liu, Z., Srba, J.: Verification of timed healthcare workflows using component timed-arc Petri nets. In: Weber, J., Perseil, I. (eds.) FHIES 2012. LNCS, vol. 7789, pp. 19–36. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39088-3_2
Viesmose Birch, S., Stig Jacobsen, T., Jon Jensen, J., Moesgaard, C., Nørgaard Samuelsen, N., Srba, J.: Interval abstraction refinement for model checking of timed-arc Petri nets. In: Legay, A., Bozga, M. (eds.) FORMATS 2014. LNCS, vol. 8711, pp. 237–251. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10512-3_17
Boucheneb, H., Barkaoui, K.: Reducing interleaving semantics redundancy in reachability analysis of time Petri nets. ACM Trans. Embed. Comput. Syst. 12(1), 7:1–7:24 (2013)
Boucheneb, H., Barkaoui, K.: Stubborn sets for time Petri nets. ACM Trans. Embed. Comput. Syst. 14(1), 11:1–11:25 (2015)
Boucheneb, H., Barkaoui, K.: Delay-dependent partial order reduction technique for real time systems. Real-Time Syst. 54, 278–306 (2017)
Bozga, M., Graf, S., Ober, I., Ober, I., Sifakis, J.: The IF toolset. In: Bernardo, M., Corradini, F. (eds.) SFM-RT 2004. LNCS, vol. 3185, pp. 237–267. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30080-9_8
Christov, S., Avrunin, G., Clarke, A., Osterweil, L., Henneman, E.: A benchmark for evaluating software engineering techniques for improving medical processes. In: SEHC 2010, pp. 50–56. ACM (2010)
Cicirelli, F., Furfaro, A., Nigro, L.: Model checking time-dependent system specifications using time stream Petri nets and UPPAAL. Appl. Math. Comput. 218(16), 8160–8186 (2012)
Dams, D., Gerth, R., Knaack, B., Kuiper, R.: Partial-order reduction techniques for real-time model checking. Form. Asp. Comput. 10(5–6), 469–482 (1998)
David, A., Jacobsen, L., Jacobsen, M., Jørgensen, K.Y., Møller, M.H., Srba, J.: TAPAAL 2.0: integrated development environment for timed-arc Petri nets. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 492–497. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_36
Feo-Arenis, S., Westphal, B., Dietsch, D., Muñiz, M., Andisha, A.S.: The wireless fire alarm system: ensuring conformance to industrial standards through formal verification. In: Jones, C., Pihlajasaari, P., Sun, J. (eds.) FM 2014. LNCS, vol. 8442, pp. 658–672. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06410-9_44
Feo-Arenis, S., Westphal, B., Dietsch, D., Muñiz, M., Andisha, S., Podelski, A.: Ready for testing: ensuring conformance to industrial standards through formal verification. Form. Asp. Comput. 28(3), 499–527 (2016)
Gardey, G., Lime, D., Magnin, M., Roux, O.H.: Romeo: a tool for analyzing time Petri nets. In: Etessami, K., Rajamani, S.K. (eds.) CAV 2005. LNCS, vol. 3576, pp. 418–423. Springer, Heidelberg (2005). https://doi.org/10.1007/11513988_41
Hansen, H., Lin, S.-W., Liu, Y., Nguyen, T.K., Sun, J.: Diamonds are a girl’s best friend: partial order reduction for timed automata with abstractions. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 391–406. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_26
Jacobsen, L., Jacobsen, M., Møller, M.H., Srba, J.: Verification of timed-arc Petri Nets. In: Černá, I., Gyimóthy, T., Hromkovič, J., Jefferey, K., Králović, R., Vukolić, M., Wolf, S. (eds.) SOFSEM 2011. LNCS, vol. 6543, pp. 46–72. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18381-2_4
Jensen, P., Larsen, K., Srba, J.: Discrete and continuous strategies for timed-arc Petri net games. Int. J. Softw. Tools Technol. Transf. (STTT), 1–18 (2017, to appear). Online since September 2017
Marques Jr., A., Ravn, A., Srba, J., Vighio, S.: Model-checking web services business activity protocols. Int. J. Softw. Tools Technol. Transf. (STTT) 15(2), 125–147 (2012)
Kordon, F., Garavel, H., Hillah, L.M., Hulin-Hubard, F., Chiardo, G., Hamez, A., Jezequel, L., Miner, A., Meijer, J., Paviot-Adet, E., Racordon, D., Rodriguez, C., Rohr, C., Srba, J., Thierry-Mieg, Y., Trịnh, G., Wolf, K.: Complete Results for the 2016 Edition of the Model Checking Contest, June 2016. http://mcc.lip6.fr/2016/results.php
Kristensen, L.M., Schmidt, K., Valmari, A.: Question-guided stubborn set methods for state properties. Form. Methods Syst. Des. 29(3), 215–251 (2006)
Lilius, J.: Efficient state space search for time Petri nets. Electron. Notes Theo. Comput. Sci. 18, 113–133 (1998). MFCS 1998 Workshop on Concurrency
Lugiez, D., Niebert, P., Zennou, S.: A partial order semantics approach to the clock explosion problem of timed automata. Theor. Comput. Sci. 345(1), 27–59 (2005)
Mateo, J., Srba, J., Sørensen, M.: Soundness of timed-arc workflow nets in discrete and continuous-time semantics. Fundam. Inform. 140(1), 89–121 (2015)
Minea, M.: Partial order reduction for model checking of timed automata. In: Baeten, J.C.M., Mauw, S. (eds.) CONCUR 1999. LNCS, vol. 1664, pp. 431–446. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48320-9_30
Newcomer, E., Robinson, I.: Web services business activity (WS-businessactivity) version 1.2 (2009). http://docs.oasis-open.org/ws-tx/wstx-wsba-1.2-spec-os/wstx-wsba-1.2-spec-os.html
Niebert, P., Qu, H.: Adding invariants to event zone automata. In: Asarin, E., Bouyer, P. (eds.) FORMATS 2006. LNCS, vol. 4202, pp. 290–305. Springer, Heidelberg (2006). https://doi.org/10.1007/11867340_21
Pelayo, F., Cuartero, F., Valero, V., Macia, H., Pelayo, M.: Applying timed-arc Petri nets to improve the performance of the MPEG-2 encoding algorithm. In: 10th International Multimedia Modelling Conference, pp. 49–56. IEEE Computer Society (2004)
Perin, M., Faure, J.: Coupling timed plant and controller models with urgent transitions without introducing deadlocks. In: 17th International Conference on Emerging Technologies and Factory Automation (ETFA 2012), pp. 1–9. IEEE (2012)
Salah, R.B., Bozga, M., Maler, O.: On interleaving in timed automata. In: Baier, C., Hermanns, H. (eds.) CONCUR 2006. LNCS, vol. 4137, pp. 465–476. Springer, Heidelberg (2006). https://doi.org/10.1007/11817949_31
Sloan, R.H., Buy, U.: Stubborn sets for real-time Petri nets. Form. Methods Syst. Des. 11(1), 23–40 (1997)
Valmari, A., Hansen, H.: Stubborn set intuition explained. In: Koutny, M., Kleijn, J., Penczek, W. (eds.) Transactions on Petri Nets and Other Models of Concurrency XII. LNCS, vol. 10470, pp. 140–165. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-55862-1_7
Virbitskaite, I., Pokozy, E.: A partial order method for the verification of time Petri nets. In: Ciobanu, G., Păun, G. (eds.) FCT 1999. LNCS, vol. 1684, pp. 547–558. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48321-7_46
Yoneda, T., Schlingloff, B.-H.: Efficient verification of parallel real-time systems. Form. Methods Syst. Des. 11(2), 187–215 (1997)
Acknowledgements
We thank Mads Johannsen for his help with the GUI support for partial order reduction. The work was funded by the center IDEA4CPS, Innovation Fund Denmark center DiCyPS and ERC Advanced Grant LASSO. The last author is partially affiliated with FI MU in Brno.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis>This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara><SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Bønneland, F.M., Jensen, P.G., Larsen, K.G., Muñiz, M., Srba, J. (2018). Start Pruning When Time Gets Urgent: Partial Order Reduction for Timed Systems. In: Chockler, H., Weissenbacher, G. (eds) Computer Aided Verification. CAV 2018. Lecture Notes in Computer Science(), vol 10981. Springer, Cham. https://doi.org/10.1007/978-3-319-96145-3_28
Download citation
DOI: https://doi.org/10.1007/978-3-319-96145-3_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96144-6
Online ISBN: 978-3-319-96145-3
eBook Packages: Computer ScienceComputer Science (R0)