Abstract
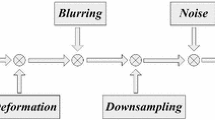
Considering that there is no edge constraint in general regularized algorithms, an improved super-resolution algorithm with additional regularization is presented. The Difference Curvature (DC) regularization which containing the image edge information is joined into the cost function, for further preserving the edge details at image reconstruction procedure. In each iteration, the DC regularization will extract the edge of high-resolution prediction frame and low-resolution observation frame. And the error between them is used to compensate the edge loss which may be smoothed by existing regularization. The reconstructed result is approximated to the original image by constraining the error between them. Then the optimum solution will be worked out by utilizing the steepest descent method. This approach is intended to constrain the edges of the image directly rather than simply avoiding the edge being smoothed. Comparing with other single regularization algorithms, experiment results indicate that the proposed algorithm can restore the edge details of reconstructed image well. And it also shows that various prior knowledge are important to image reconstruction process.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Tian, J., Ma, K.K.: A survey on super-resolution imaging. Signal Image Video Process. 5(3), 329–342 (2011)
Tsai, R.Y., Huang, T.S.: Multiframe image restoration and registration. In: Advances in Computer Vision and Image Processing, vol. 1 (1984)
Yu, X., Cen, X.: An image reconstruction approach in discrete cosine transform domain. In: International Congress on Image and Signal Processing, vol. 57, pp. 587–591. IEEE (2013)
Lama, R.K., Shin, S., Kang, M., Kwon, G.R., Choi, M.R.: Interpolation using wavelet transform and discrete cosine transform for high resolution display. In: IEEE International Conference on Consumer Electronics, pp. 184–186. IEEE (2016)
Nazren, A.R.A., Yaakob, S.N., Ngadiran, R., Hisham, M.B., Wafi, N.M.: Improving iterative back projection super resolution model via anisotropic diffusion edge enhancement. In: International Conference on Robotics, Automation and Sciences, pp. 1–4. IEEE (2017)
Tang, Z., Deng, M., Xiao, C., Yu, J.: Projection onto convex sets super-resolution image reconstruction based on wavelet bi-cubic interpolation. In: International Conference on Electronic and Mechanical Engineering and Information Technology, vol. 175, pp. 351–354. IEEE (2011)
Shen, H., Zhang, L., Huang, B., Li, P.: A map approach for joint motion estimation, segmentation, and super resolution. IEEE Trans. Image Process. 16(2), 479–490 (2007)
Irani, M., Peleg, S.: Improving resolution by image registration. Cvgip Graph. Models Image Process. 53(3), 231–239 (1991)
Stark, H., Oskoui, P.: High-resolution image recovery from image-plane arrays, using convex projections. J. Optical Soc. Am. Opt. Image Sci. 6(11), 1715 (1989)
Shao, W.Z., Wei, Z.H.: Super-resolution reconstruction based on generalized Huber-MRF image modeling. J. Softw. 18(10), 2434–2444 (2007)
Shao, W.Z., Deng, H.S., Wei, Z.H.: A posterior mean approach for MRF-based spatially adaptive multi-frame image super-resolution. Signal Image Video Process. 9(2), 437–449 (2015)
Zhang, X., Lam, E.Y., Wu, E.X., Wong, K.K.Y.: Application of Tikhonov regularization to super-resolution reconstruction of brain MRI images. In: Gao, X., Müller, H., Loomes, Martin J., Comley, R., Luo, S. (eds.) MIMI 2007. LNCS, vol. 4987, pp. 51–56. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-79490-5_8
Liu, W., Chen, Z., Chen, Y., Yao, R.: An ℓ1/2-BTV regularization algorithm for super-resolution. In: International Conference on Computer Science and Network Technology, pp. 1274–1281. IEEE (2016)
Mofidi, M., Hajghassem, H., Afifi, A.: An adaptive parameter estimation in a btv regularized image super-resolution reconstruction. Adv. Electr. Comput. Eng. 17(3), 3–10 (2017)
Chen, Q., Montesinos, P., Sun, Q.S., Peng, A.H., Xia, D.S.: Adaptive total variation denoising based on difference curvature. Image Vis. Comput. 28(3), 298–306 (2010)
Bai, X.B., Wang, K.Q., Wang, H.: Research on the classification of wood texture based on Gray Level Co-occurrence Matrix. J. Harbin Inst. Technol. 12, 021 (2005)
Hore, A., Ziou, D.: Image quality metrics: PSNR vs. SSIM. In: International Conference on Pattern Recognition, pp. 2366–2369. IEEE (2010)
Silvestre-Blanes, J.: Structural similarity image quality reliability: determining parameters and window size. Signal Process. 91(4), 1012–1020 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Luo, Z., Chen, D., Wang, X. (2018). Regularized Super-Resolution Reconstruction Based on Edge Prior. In: Huang, DS., Gromiha, M., Han, K., Hussain, A. (eds) Intelligent Computing Methodologies. ICIC 2018. Lecture Notes in Computer Science(), vol 10956. Springer, Cham. https://doi.org/10.1007/978-3-319-95957-3_44
Download citation
DOI: https://doi.org/10.1007/978-3-319-95957-3_44
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-95956-6
Online ISBN: 978-3-319-95957-3
eBook Packages: Computer ScienceComputer Science (R0)