Abstract
In this work we are interested in minimal complete sets of solutions for homogeneous linear diophantine equations. Such equations naturally arise during AC-unification—that is, unification in the presence of associative and commutative symbols. Minimal complete sets of solutions are for example required to compute AC-critical pairs. We present a verified solver for homogeneous linear diophantine equations that we formalized in Isabelle/HOL. Our work provides the basis for formalizing AC-unification and will eventually enable the certification of automated AC-confluence and AC-completion tools.
This work is supported by the Austrian Science Fund (FWF): project P27502.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Homogeneous linear diophantine equations
- Code generation
- Mechanized mathematics
- Verified code
- Isabelle/HOL
1 Introduction
(Syntactic) unification of two terms s and t, is the problem of finding a substitution \(\sigma \) that, applied to both terms, makes them syntactically equal: \(s\sigma = t\sigma \). For example, it is easily verified that  is a solution to the unification problem
is a solution to the unification problem  . Several syntactic unification algorithms are known, some of which have even been formalized in proof assistants.
. Several syntactic unification algorithms are known, some of which have even been formalized in proof assistants.
By throwing a set of equations E into the mix, we arrive at equational or E-unification, where we are interested in substitutions \(\sigma \) that make two given terms equivalent with respect to the equations in E, written \(s\sigma \approx _{E}t\sigma \). While for syntactic unification most general solutions, called most general unifiers, are unique, E-unification is distinctly more complex: depending on the specific set of equations, E-unification might be undecidable, have unique solutions, have minimal complete sets of solutions, etc.
For AC-unification we instantiate E from above to a set \(\textsf {AC}\) of associativity and commutativity equations for certain function symbols. For example, by taking  , we express that
, we express that  (which we write infix, for convenience) is the only associative and commutative function symbol. Obviously, the substitution \(\sigma \) from above is also a solution to the AC-unification problem
(which we write infix, for convenience) is the only associative and commutative function symbol. Obviously, the substitution \(\sigma \) from above is also a solution to the AC-unification problem  (since trivially
(since trivially  ). You might ask: is it the only one? It turns out that it is not. More specifically, there is a minimal complete set (see Sect. 2 for a formal definition) consisting of the five AC-unifiers:
). You might ask: is it the only one? It turns out that it is not. More specifically, there is a minimal complete set (see Sect. 2 for a formal definition) consisting of the five AC-unifiers:

But how can we compute it? The answer involves minimal complete sets of solutions for homogeneous linear diophantine equations (HLDEs for short). From the initial AC-unification problem  we derive the equation in Table 1, which basically tells us that, no matter what we substitute for
we derive the equation in Table 1, which basically tells us that, no matter what we substitute for  ,
,  , and
, and  , there have to be exactly twice as many occurrences of the AC-symbol
, there have to be exactly twice as many occurrences of the AC-symbol  in the substitutes for
in the substitutes for  and
and  than there are in the substitute for
than there are in the substitute for  .
.
The minimal complete set of solutions to this equation, labeled by fresh variables, is depicted in Table 1, where the numbers indicate how many occurrences of the corresponding fresh variable are contributed to the substitute for the variable in the respective column. The AC-symbol  is used to combine fresh variables occurring more than once. For example, the solution labeled by
is used to combine fresh variables occurring more than once. For example, the solution labeled by  contributes two occurrences of
contributes two occurrences of  to the substitute for
to the substitute for  and one occurrence of
and one occurrence of  to the substitute for
to the substitute for  , while not touching the substitute for
, while not touching the substitute for  at all.
at all.
Now each combination of solutions for which  ,
,  , and
, and  are all nonzeroFootnote 1 gives rise to an independent minimal AC-unifier (in general, given n solutions, there are \(2^n\) combinations, one for each subset of solutions). The unifiers above correspond to the combinations:
are all nonzeroFootnote 1 gives rise to an independent minimal AC-unifier (in general, given n solutions, there are \(2^n\) combinations, one for each subset of solutions). The unifiers above correspond to the combinations: We refer to the literature for details on how exactly we obtain unifiers from sets of solutions to HLDEs and why this works [1, 12]. Suffice it to say that minimal complete sets of solutions to HLDEs give rise to minimal complete sets of AC-unifiers.Footnote 2 The main application we have in mind, relying on minimal complete sets of AC-unifiers, is computing AC-critical pairs. This is for example useful for proving confluence of rewrite systems with and without AC-symbols [6, 10, 11] and required for normalized completion [8, 14].
We refer to the literature for details on how exactly we obtain unifiers from sets of solutions to HLDEs and why this works [1, 12]. Suffice it to say that minimal complete sets of solutions to HLDEs give rise to minimal complete sets of AC-unifiers.Footnote 2 The main application we have in mind, relying on minimal complete sets of AC-unifiers, is computing AC-critical pairs. This is for example useful for proving confluence of rewrite systems with and without AC-symbols [6, 10, 11] and required for normalized completion [8, 14].
In this paper we investigate how to compute minimal complete sets of solutions of HLDEs, with our focus on formal verification using a proof assistant. In other words, we are only interested in verified algorithms (that is, algorithms whose correctness has been machine-checked). More specifically, our contributions are as follows:
-
We give an Isabelle/HOL formalization of HLDEs and their minimal complete sets of solutions (Sect. 3).
-
We describe a simple algorithm that computes such minimal complete sets of solutions (Sect. 2) and discuss an easy correctness proof that we formalized in Isabelle/HOL (Sect. 4).
-
After several rounds of program transformations, making use of standard optimization techniques and improved bounds from the literature (Sect. 5), we obtain a more efficient solver (Sect. 6)—to the best of our knowledge, the first formally verified solver for HLDEs.
Our formalization is available in the Archive of Formal Proofs [9] (development version, changeset d5fabf1037f8). Through Isabelle’s code generation feature [4] a verified solver can be obtained from our formalization.
2 Main Ideas
For any formalization challenge it is a good idea to start from as simple a grounding as possible: trying to reduce the number of involved concepts to a bare minimum and to keep the complexity of involved proofs in check.
When formalizing an algorithm, once we have a provably correct implementation, we might still want to make it more efficient. Instead of doing all the (potentially hard) proofs again for a more efficient (and probably more involved) variant, we can often prove that the two variants are equivalent and thus carry over the correctness result from a simple implementation to an efficient one. This is also the general plan we follow for our formalized HLDE solver.
To make things simpler when computing minimal complete sets of solutions for an HLDE  (where
(where  and
and  are lists of coefficients and \(v \mathbin {\bullet }w\) denotes the dot product of two lists \(v = [v_1,\ldots ,v_k]\) and \(w = [w_1,\ldots ,w_k]\) defined by \(v_1w_1 + \cdots + v_kw_k\)), we split the task into three separate phases:
are lists of coefficients and \(v \mathbin {\bullet }w\) denotes the dot product of two lists \(v = [v_1,\ldots ,v_k]\) and \(w = [w_1,\ldots ,w_k]\) defined by \(v_1w_1 + \cdots + v_kw_k\)), we split the task into three separate phases:
-
generate a finite search-space that covers all potentially minimal solutions
-
check necessary criteria for minimal solutions (throwing away the rest)
-
minimize the remaining collection of candidates
Generate. For the first phase we make use of the fact that for every minimal solution  the entries of
the entries of  are bounded by the maximal coefficient in
are bounded by the maximal coefficient in  , while the entries of
, while the entries of  are bounded by the maximal coefficient in
are bounded by the maximal coefficient in  (which we will prove in Sect. 3).
(which we will prove in Sect. 3).
Moreover, we generate the search-space in reverse lexicographic order, where for arbitrary lists of numbers \(u = [u_1,\ldots ,u_k]\) and \(v = [v_1,\ldots ,v_k]\) we have \(u <_{\textsf {rlex}}v\) iff there is an \(i \le k\) such that \(u_i < v_i\) and \(u_j = v_j\) for all \(i < j \le k\). This allows for a simple recursive implementation and can be exploited in the minimization phase.
Assuming that x-entries of solutions are bounded by  and y-entries are bounded by
and y-entries are bounded by  , we can implement the generate-phase by the function
, we can implement the generate-phase by the function

where we use Haskell-like list comprehension and  is the standard tail function on lists dropping the first element—which in this case is the trivial (and non-minimal) solution consisting only of zeroes—and
is the standard tail function on lists dropping the first element—which in this case is the trivial (and non-minimal) solution consisting only of zeroes—and 
 computes all lists of natural numbers of length
computes all lists of natural numbers of length  whose entries are bounded by
whose entries are bounded by  , in reverse lexicographic order.
, in reverse lexicographic order.

Our initial example  can be represented by the two lists of coefficients
can be represented by the two lists of coefficients  and
and  and the corresponding search-space is generated by
and the corresponding search-space is generated by  , resulting in
, resulting in

Check. Probably the most obvious necessary condition for  to be a minimal solution is that it is actually a solution, that is,
to be a minimal solution is that it is actually a solution, that is,  (taking the later minimization phase into account, it is in fact also a sufficient condition). We can implement the check-phase, given two lists of coefficients
(taking the later minimization phase into account, it is in fact also a sufficient condition). We can implement the check-phase, given two lists of coefficients  and
and  , by
, by

using the standard filter function on lists that only preserves elements satisfying the given predicate.
For our initial example  computes the first two phases, resulting in
computes the first two phases, resulting in  .
.
Minimize. It is high time that we specify in what sense minimal solutions are to be minimal. To this end, we use the pointwise less-than-or-equal order \(\le _{\textsf {v}}\) on lists (whose strict part \(<_{\textsf {v}}\) is defined by \(x <_{\textsf {v}} y\) iff \(x \le _{\textsf {v}}y\) but not \(y \le _{\textsf {v}}x\)). Now minimization can be implemented by the function

where  is Isabelle/HOL’s list concatenation. This is also where we exploit the fact that the input to
is Isabelle/HOL’s list concatenation. This is also where we exploit the fact that the input to  is sorted in reverse lexicographic order: then, since
is sorted in reverse lexicographic order: then, since  is up front, we know that all elements of
is up front, we know that all elements of  are strictly greater with respect to \(<_{\textsf {rlex}}\); moreover, \(u <_{\textsf {v}} v\) implies \(u <_{\textsf {rlex}}v\) for all u and v; and thus,
are strictly greater with respect to \(<_{\textsf {rlex}}\); moreover, \(u <_{\textsf {v}} v\) implies \(u <_{\textsf {rlex}}v\) for all u and v; and thus,  is not \(<_{\textsf {v}}\)-greater than any element of
is not \(<_{\textsf {v}}\)-greater than any element of  , warranting that we put it in the resulting minimized list without further check.
, warranting that we put it in the resulting minimized list without further check.
A Simple Algorithm. Putting all three phases together we obtain a straightforward algorithm for computing all minimal solutions of an HLDE given by its lists of coefficients  and
and 

where  —which we sometimes write \(| xs |\)—computes the length of a list \( xs \). We will prove the correctness of
—which we sometimes write \(| xs |\)—computes the length of a list \( xs \). We will prove the correctness of  in Sect. 4.
in Sect. 4.
Performance Tuning. There are several potential performance improvements over the simple algorithm from above. In a first preparatory step, we categorize solutions into special and non-special solutions (Sect. 5). The former are minimal by construction and can thus be excluded from the minimization phase. For the latter, several necessary conditions are known that are monotone in the sense that all prefixes and suffixes of a list satisfy them whenever the list itself does. Now merging the generate and check phases by “pushing in” these conditions as far as possible has the potential to drastically cut down the explored search-space. We will discuss the details in Sect. 6.
3 An Isabelle/HOL Theory of HLDEs and Their Solutions
In this section, after putting our understanding of HLDEs and their solutions on firmer grounds, we obtain bounds on minimal solutions that serve as a basis for the two algorithms we present in later sections.
A homogeneous linear diophantine equation is an equation of the form

where coefficients  and
and  are fixed natural numbers. Moreover, we are only interested in solutions
are fixed natural numbers. Moreover, we are only interested in solutions  over the naturals.
over the naturals.
That means that all the required information can be encoded into two lists of natural numbers  and
and  . From now on, let
. From now on, let  and
and  be fixed, which is achieved by Isabelle’s locale mechanism in our formalization:Footnote 3
be fixed, which is achieved by Isabelle’s locale mechanism in our formalization:Footnote 3

In the locale, we also assume that  and
and  do not have any zero entries (which is useful for some proofs; note that arbitrary HLDEs can be transformed into equivalent HLDEs satisfying this assumption by dropping all zero-coefficients).
do not have any zero entries (which is useful for some proofs; note that arbitrary HLDEs can be transformed into equivalent HLDEs satisfying this assumption by dropping all zero-coefficients).
Solutions of the HLDE represented by  and
and  are those pairs of lists
are those pairs of lists  that satisfy
that satisfy  . Formally, the set of solutions
. Formally, the set of solutions  is given by
is given by

A solution is (pointwise) minimal iff there is no nonzero solution that is pointwise strictly smaller. The set of (pointwise) minimal solutions is given by

where we use the notation  to state that a list
to state that a list  is nonzero, that is, does not exclusively consist of zeroes. While the above definition might look asymmetric, since we only require
is nonzero, that is, does not exclusively consist of zeroes. While the above definition might look asymmetric, since we only require  and
and  to be nonzero, we actually also have that
to be nonzero, we actually also have that  and
and  are nonzero, because
are nonzero, because  and
and  are both solutions and
are both solutions and  and
and  do not contain any zeroes.
do not contain any zeroes.
Huet [5, Lemma 1] has shown that, given a minimal solution  , the entries of
, the entries of  and
and  are bounded by
are bounded by  and
and  , respectively. In preparation for the proof of this result, we prove the following auxiliary fact.
, respectively. In preparation for the proof of this result, we prove the following auxiliary fact.
Lemma 1
If x is a list of natural numbers of length n, then either
-
(1)
\(x_i \equiv 0 \pmod n\) for some \(1 \le i \le n\), or
-
(2)
\(x_i \equiv x_j \pmod n\) for some \(1 \le i < j \le n\).
Proof
Let X be the set of elements of x and  . If \(|M| < |X|\) then property (2) follows by the pigeonhole principle. Otherwise, \(|M| = |X|\) and either x contains already duplicates and we are done (again by establishing property (2)), or the elements of x are pairwise disjoint. In the latter case, we know that \(|M| = n\). Since all elements of M are less than n by construction, we obtain \(M = \{0,\ldots ,n-1\}\). This, in turn, means that property (1) is satisfied. \(\square \)
. If \(|M| < |X|\) then property (2) follows by the pigeonhole principle. Otherwise, \(|M| = |X|\) and either x contains already duplicates and we are done (again by establishing property (2)), or the elements of x are pairwise disjoint. In the latter case, we know that \(|M| = n\). Since all elements of M are less than n by construction, we obtain \(M = \{0,\ldots ,n-1\}\). This, in turn, means that property (1) is satisfied. \(\square \)
Now we are in a position to prove a variant of Huet’s Lemma 1 for improved bounds (which were, to the best of our knowledge, first mentioned by Clausen and Fortenbacher [2]), where, given two lists u and v of same length, we use  to denote
to denote  , that is, the maximum of those u-elements whose corresponding v-elements are nonzero.
, that is, the maximum of those u-elements whose corresponding v-elements are nonzero.
Lemma 2
Let  be a minimal solution. Then we have
be a minimal solution. Then we have  for all
for all  and
and  for all
for all  .
.
Proof
Since the two statements above are symmetric, we concentrate on the first one. Let  and assume that there is
and assume that there is  with
with  . We will show that this contradicts the minimality of
. We will show that this contradicts the minimality of  . We have
. We have

and thus  .
.
At this point we give an explicit construction for a corresponding existential statement in Huet’s original proof. The goal is to construct a pointwise increasing sequence of lists  such that for all
such that for all  we have (1)
we have (1)  and also (2)
and also (2)  . This is achieved by taking
. This is achieved by taking  where \(0_{n}\) denotes a list of n zeroes and we employ the auxiliary function
where \(0_{n}\) denotes a list of n zeroes and we employ the auxiliary function

that, given two lists y and v, increments v at the smallest position \(j\ge i\) such that \(v_j < y_j\) (if this is not possible, the result is v). Here \(x \mathbin {!} i\) denotes the ith element of list x and \(x[i:=v]\) a variant of list x, where the ith element is v.
As long as there is “enough space” (as guaranteed by  ), \({{{\varvec{u}}}^{i}}\) is pointwise smaller than
), \({{{\varvec{u}}}^{i}}\) is pointwise smaller than  and the sum of its elements is i for all
and the sum of its elements is i for all  , thereby satisfying both of the above properties.
, thereby satisfying both of the above properties.
Now we obtain a list u that in addition to (1) and (2) also satisfies (3)  . This is achieved by applying Lemma 1 to the list of natural numbers
. This is achieved by applying Lemma 1 to the list of natural numbers  , and analyzing the resulting cases. Either such a list is already in \({{{\varvec{u}}}^{}}\) and we are done, or \({{{\varvec{u}}}^{}}\) contains two lists \({{{\varvec{u}}}^{i}}\) and \({{{\varvec{u}}}^{j}}\) with \(i < j\), for which
, and analyzing the resulting cases. Either such a list is already in \({{{\varvec{u}}}^{}}\) and we are done, or \({{{\varvec{u}}}^{}}\) contains two lists \({{{\varvec{u}}}^{i}}\) and \({{{\varvec{u}}}^{j}}\) with \(i < j\), for which  holds. In the latter case, the pointwise subtraction
holds. In the latter case, the pointwise subtraction  satisfies properties (1) to (3).
satisfies properties (1) to (3).
Remember that  . Together with properties (1) and (2) we know
. Together with properties (1) and (2) we know

By (3), we further have  for some
for some  , showing that
, showing that  is strictly greater than the nonzero solution \((0_{|m|}[k:=c], u)\). Finally, a contradiction to the minimality of
is strictly greater than the nonzero solution \((0_{|m|}[k:=c], u)\). Finally, a contradiction to the minimality of  . \(\square \)
. \(\square \)
As a corollary, we obtain Huet’s result, namely that all  are bounded by
are bounded by  and all
and all  are bounded by
are bounded by  , since
, since  for all lists v and c.
for all lists v and c.
4 Certified Minimal Complete Sets of Solutions
Before we prove our algorithm from Sect. 2 correct, let us have a look at a characterization of the elements of  that we require in the process (where \(<_{\textsf {rlex}}\) as well as \(<_{\textsf {v}}\) are extended to pairs of lists by taking their concatenation).
that we require in the process (where \(<_{\textsf {rlex}}\) as well as \(<_{\textsf {v}}\) are extended to pairs of lists by taking their concatenation).
Lemma 3
 whenever \( xs \) is sorted with respect to \(<_{\textsf {rlex}}\).
whenever \( xs \) is sorted with respect to \(<_{\textsf {rlex}}\).
Proof
An easy induction over \( xs \) shows the direction from right to left. For the other direction, let x be an arbitrary but fixed element of  . Another easy induction over \( xs \) shows that then x is also in \( xs \). Thus it remains to show that there is no y in \( xs \) which is \(<_{\textsf {v}}\)-smaller than x. Assume that there is such a y for the sake of a contradiction and proceed by induction over \( xs \). If
. Another easy induction over \( xs \) shows that then x is also in \( xs \). Thus it remains to show that there is no y in \( xs \) which is \(<_{\textsf {v}}\)-smaller than x. Assume that there is such a y for the sake of a contradiction and proceed by induction over \( xs \). If  we are trivially done. Otherwise,
we are trivially done. Otherwise,  and when x is in
and when x is in  and y is in \( zs \), the result follows by IH. In the remaining cases either \(z = x\) or \(z = y\), but not both (since this would yield \(z <_{\textsf {v}} z\)). For the former we have \(x \le _{\textsf {rlex}}y\) by sortedness and for the latter we obtain \(y \not <_{\textsf {v}} x\) by the definition of
and y is in \( zs \), the result follows by IH. In the remaining cases either \(z = x\) or \(z = y\), but not both (since this would yield \(z <_{\textsf {v}} z\)). For the former we have \(x \le _{\textsf {rlex}}y\) by sortedness and for the latter we obtain \(y \not <_{\textsf {v}} x\) by the definition of  (since x is in
(since x is in  ), both contradicting \(y <_{\textsf {v}} x\). \(\square \)
), both contradicting \(y <_{\textsf {v}} x\). \(\square \)
In the remainder of this section, we will prove completeness (all minimal solutions are generated) and soundness (only minimal solutions are generated) of  .
.
Lemma 4
(Completeness).

Proof
Let  be a minimal solution. We use the abbreviations
be a minimal solution. We use the abbreviations  ,
,  , and
, and  . Then, by Lemma 3, we have
. Then, by Lemma 3, we have  . Note that
. Note that  is in C (which contains all solutions within the bounds provided by A and B, by construction) due to Lemma 2. Moreover,
is in C (which contains all solutions within the bounds provided by A and B, by construction) due to Lemma 2. Moreover,  for all \(y \in C\) follows from the minimality of
for all \(y \in C\) follows from the minimality of  , since C is clearly a subset of
, since C is clearly a subset of  . Together, the previous two statements conclude the proof. \(\square \)
. Together, the previous two statements conclude the proof. \(\square \)
Lemma 5
(Soundness).

Proof
Let  be in
be in  . According to the definition of
. According to the definition of  we have to show that
we have to show that  is in
is in  (which is trivial),
(which is trivial),  is nonzero, and that there is no \(<_{\textsf {v}}\)-smaller solution
is nonzero, and that there is no \(<_{\textsf {v}}\)-smaller solution  with nonzero
with nonzero  . Incidentally, the last part can be narrowed down to: there is no \(<_{\textsf {v}}\)-smaller minimal solution
. Incidentally, the last part can be narrowed down to: there is no \(<_{\textsf {v}}\)-smaller minimal solution  (since for every solution we can find a \(\le _{\textsf {v}}\)-smaller minimal solution by well-foundedness of \(<_{\textsf {v}}\), and the left component of minimal solutions is nonzero by definition).
(since for every solution we can find a \(\le _{\textsf {v}}\)-smaller minimal solution by well-foundedness of \(<_{\textsf {v}}\), and the left component of minimal solutions is nonzero by definition).
We start by showing that  is nonzero. Since there are no zeroes in
is nonzero. Since there are no zeroes in  and
and  , and
, and  is a solution,
is a solution,  can only be a zero-list if also
can only be a zero-list if also  is. However, the elements of
is. However, the elements of  are sorted in strictly increasing order with respect to \(<_{\textsf {rlex}}\) and the first one is already not the pair of zero-lists, by construction.
are sorted in strictly increasing order with respect to \(<_{\textsf {rlex}}\) and the first one is already not the pair of zero-lists, by construction.
Now, for the sake of a contradiction, assume that there is a minimal solution  . By Lemma 4, we obtain that
. By Lemma 4, we obtain that  is also in
is also in  . But then, due to its minimality,
. But then, due to its minimality,  is also in C (the same set we already used in the proof of Lemma 4). Moreover,
is also in C (the same set we already used in the proof of Lemma 4). Moreover,  is in C by construction. Together with Lemma 3 and
is in C by construction. Together with Lemma 3 and  , this results in the desired contradiction. \(\square \)
, this results in the desired contradiction. \(\square \)
As a corollary of the previous two results, we obtain that  computes exactly all minimal solutions, that is
computes exactly all minimal solutions, that is  .
.
5 Special and Non-special Solutions
For each pair of variable positions  and
and  , there is exactly one minimal solution such that only the x-entry at position
, there is exactly one minimal solution such that only the x-entry at position  and the y-entry at position
and the y-entry at position  are nonzero. Since all other entries are 0, the equation collapses to
are nonzero. Since all other entries are 0, the equation collapses to  . Taking the minimal solutions (by employing the least common multiple) of this equation, we solve for
. Taking the minimal solutions (by employing the least common multiple) of this equation, we solve for  and then for
and then for  and obtain the nonzero x-entry
and obtain the nonzero x-entry  and the nonzero y-entry
and the nonzero y-entry  , respectively. Given
, respectively. Given  and
and  , we obtain the special solution
, we obtain the special solution  where
where  is
is  and
and  is
is  .
.
All special solutions can be computed in advance and outside of our minimization phase, since special solutions are minimal (the only entries where a special solution could decrease are  and
and  , but those are minimal due to the properties of least common multiples). We compute all special solutions by the following function
, but those are minimal due to the properties of least common multiples). We compute all special solutions by the following function

where

We have already seen a relatively crude bound on minimal solutions in Sect. 3. A further bound, this time for minimal non-special solutions, follows.
Lemma 6
Let  be a non-special solution such that
be a non-special solution such that  and
and  for some
for some  and
and  . Then
. Then  is not minimal.
is not minimal.
Proof
Assume that  is a minimal solution and consider the special solution
is a minimal solution and consider the special solution  ). Due to
). Due to  and
and  we obviously have
we obviously have  . Since
. Since  is not special itself, we further obtain
is not special itself, we further obtain  , contradicting the supposed minimality of
, contradicting the supposed minimality of  . \(\square \)
. \(\square \)
This result allows us to avoid all candidates that are pointwise greater than or equal to some special solution during our generation phase, which is the motivation for the following functions for bounding the elements of non-special minimal solutions. The function  , bounding entries of
, bounding entries of  , is directly taken from Huet [5]. Moreover,
, is directly taken from Huet [5]. Moreover,  is our counterpart to
is our counterpart to  bounding entries of
bounding entries of  . As
. As  is symmetric to
is symmetric to  , we only give details for the latter, which is
, we only give details for the latter, which is

where  is defined by
is defined by

from which we can show that all minimal solutions satisfy the following bounds

where  ,
,  , and
, and  are mnemonic for bound on entries of right component, bound on sub dot product of left component, and bound on sub dot product of right component, respectively.
are mnemonic for bound on entries of right component, bound on sub dot product of left component, and bound on sub dot product of right component, respectively.
Lemma 7
Let  be a non-special minimal solution. Then, all of the following hold:
be a non-special minimal solution. Then, all of the following hold:
-
(1)
 ,
, -
(2)
 , and
, and -
(3)
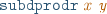 .
.
Proof
Property (1) directly corresponds to condition (c) of Huet. Thus, we refer to our formalization for details but note that this is where Lemma 6 is employed (apart from motivating the definitions of  and
and  in the first place).
in the first place).
Property (2), which is based on Huet’s condition (d), follows from  being a solution and the fact that the dot product cannot get larger by dropping (same length) suffixes from both operands.
being a solution and the fact that the dot product cannot get larger by dropping (same length) suffixes from both operands.
The last property (3) is based on condition (b) from Huet’s paper. Again, we refer to our formalization for details. \(\square \)
Given a bound B and a list of coefficients \( as \), the function  computes all pairs whose first component is a list \( xs \) of length \(| as |\) with entries at most B and whose second component is \( as \mathbin {\bullet } xs \). Note that the resulting list is sorted in reverse lexicographic order with respect to first components of pairs.Footnote 4
computes all pairs whose first component is a list \( xs \) of length \(| as |\) with entries at most B and whose second component is \( as \mathbin {\bullet } xs \). Note that the resulting list is sorted in reverse lexicographic order with respect to first components of pairs.Footnote 4

Example 1
For  (corresponding to the left-hand side coefficients of our initial example) and
(corresponding to the left-hand side coefficients of our initial example) and  the list computed by
the list computed by  is
is

Since for a potential solution  elements of
elements of  and of
and of  have different bounds, we employ
have different bounds, we employ

where

Note that the result of  is sorted with respect to \(<_{\textsf {rlex}}\). If we use
is sorted with respect to \(<_{\textsf {rlex}}\). If we use  and
and  as bounds for
as bounds for  and
and  , respectively, then
, respectively, then  takes care of the new generate phase.
takes care of the new generate phase.
The static bounds on individual candidate solutions we obtain from Lemma 2 can be checked by the predicate

The new check phase is based on the following predicate, which is a combination of these static bounds, the fact that we are only interested in solutions, and the three further bounds from Lemma 7

and implemented by  .
.
The new minimization phase finally, is still implemented by  , only that this time its input will often be a shorter list.
, only that this time its input will often be a shorter list.
Combining all three phases, non-special solutions are computed by

By including all special solutions we arrive at the intermediate algorithm  , which already separates special from non-special solutions, but still requires further optimization:
, which already separates special from non-special solutions, but still requires further optimization:

The proof that  correctly computes the set of minimal solutions, that is
correctly computes the set of minimal solutions, that is  , is somewhat complicated by the additional bounds, but structurally similar enough to the corresponding proof of
, is somewhat complicated by the additional bounds, but structurally similar enough to the corresponding proof of  that we refer the interested reader to our formalization.
that we refer the interested reader to our formalization.
Having covered the correctness of our algorithm, it is high time to turn towards performance issues.
6 A More Efficient Algorithm for Code Generation
While the list of non-special solutions computed in Sect. 5 lends itself to formalization (due to its separation of concerns regarding the generate and check phases), it may waste a lot of time on generating lists that will not pass the later checks.
Example 2
Recall our initial example with coefficients  and
and  . Let
. Let  and
and  . Then, the list generated by
. Then, the list generated by  contains for example a y-entry
contains for example a y-entry  . This is combined with all nine elements of
. This is combined with all nine elements of  (listed in Example 1) before filtering takes place, even though only a single x-entry, namely
(listed in Example 1) before filtering takes place, even though only a single x-entry, namely  , will survive the check phase (since all others exceed the bound
, will survive the check phase (since all others exceed the bound  for some entry).
for some entry).
We now proceed to a more efficient variant of  which computes the same results (alas, we cannot hope for better asymptotic behavior, since computing minimal complete sets of solutions of HLDEs is NP-complete).
which computes the same results (alas, we cannot hope for better asymptotic behavior, since computing minimal complete sets of solutions of HLDEs is NP-complete).
While all of the following has been formalized, we will not give any proofs here, due to their rather technical nature and a lack of further insights. We start with the locale

which takes a condition C, a bound B, and defines a function  that combines (to a certain extent)
that combines (to a certain extent)  and
and  from the previous section.
from the previous section.

Here, the auxiliary function  is defined by (note that termination of this function relies on the fact that there is an upper bound—namely B, as ensured by the first assumption of the locale—on the entries of the generated lists):
is defined by (note that termination of this function relies on the fact that there is an upper bound—namely B, as ensured by the first assumption of the locale—on the entries of the generated lists):

The idea of  is to length-incrementally (starting with rightmost elements) generates all lists whose elements are bounded by B, such that only intermediate results that satisfy C are computed.
is to length-incrementally (starting with rightmost elements) generates all lists whose elements are bounded by B, such that only intermediate results that satisfy C are computed.
For us, the crucial property of  is its connection to
is its connection to  , which is covered by the following result (for which we need the second locale assumption).
, which is covered by the following result (for which we need the second locale assumption).
Lemma 8

Where  ensures that \(|x| = |a|\), \(s = a \mathbin {\bullet }x\) and all non-empty suffixes of the list x (including x itself) satisfy condition C.
ensures that \(|x| = |a|\), \(s = a \mathbin {\bullet }x\) and all non-empty suffixes of the list x (including x itself) satisfy condition C.
Now we can define  in terms of two instantiations of the locale \({bounded\_gen\_check}\) (meaning that each time the locale parameters C and B are replaced by terms for which all assumptions of the locale are satisfied), using appropriate conditions \(C_1\), \(C_2\) and bounds \(B_1\), \(B_2\), respectively. This results in the two instances
in terms of two instantiations of the locale \({bounded\_gen\_check}\) (meaning that each time the locale parameters C and B are replaced by terms for which all assumptions of the locale are satisfied), using appropriate conditions \(C_1\), \(C_2\) and bounds \(B_1\), \(B_2\), respectively. This results in the two instances  and
and  of
of  , where
, where  receives a further parameter y, which stands for a fixed y-entry against which we are trying to generate x-entries.
receives a further parameter y, which stands for a fixed y-entry against which we are trying to generate x-entries.
To be more precise, we use the following instantiations

Combining  and
and  we obtain a function that computes candidate solutions as follows:
we obtain a function that computes candidate solutions as follows:

Using Lemma 8 it can be shown that  behaves exactly the same way as first generating candidates using
behaves exactly the same way as first generating candidates using  and then filtering them according to conditions \(C_1\) and \(C_2\).
and then filtering them according to conditions \(C_1\) and \(C_2\).

We further filter this list of candidate solutions in order to get rid of superfluous entries, resulting in the function  defined by
defined by

where  .
.
Extensionally  is equivalent to what
is equivalent to what  of our intermediate algorithm above does before minimization.
of our intermediate algorithm above does before minimization.
Lemma 9
Let  and
and  . Then
. Then

This finally allows us to use the following more efficient definition of  for code generation (of course all results on
for code generation (of course all results on  carry over, since extensionally the two versions of
carry over, since extensionally the two versions of  are the same, as shown by Lemma 9).
are the same, as shown by Lemma 9).

Generating the Solver. At this point we generate Haskell code for  (and also for the library functions
(and also for the library functions  and
and  , which will be used in our main file) by
, which will be used in our main file) by

(For this step a working Isabelle installation is required.)
The only missing part is the (hand written) main entry point to our program in Main.hs (it takes an HLDE as command line argument in Haskell syntax, makes sure that the coefficients are all nonzero, hands the input over to  , and prints the result):
, and prints the result):

A corresponding binary hlde can be compiled using the command (provided of course that our AFP entry and a Haskell compiler are both installed):

We conclude this section by an example run (joining output lines to save space):

7 Evaluation
We compare our verified algorithms—the simple algorithm (S) of Sect. 4, the intermediate algorithm of Sect. 5 (I), and the efficient algorithm of Sect. 6 (E)—with the fastest unverified implementation we are aware of: a graph algorithm (G) due to Clausen and Fortenbacher [2].
In Table 2 we give the resulting runtimes (in seconds) for computing minimal complete sets of solutions of a small set of benchmark HLDEs (in increasing order of number of solutions; column #sols): the first four lines cover our initial example and three slight modifications, while the remaining examples are taken from Clausen and Fortenbacher).
However, there are two caveats: on the one hand, the runtimes for G are direct transcriptions from Clausen and Fortenbacher (hence also the missing entries for the first four examples), that is, they where generated on hardware from more than two decades ago; on the other hand, G uses improved bounds for the search-space of potential solutions, which are not formalized and thus out of reach for our verified implementations.
Anyway, our initial motivation was to certify minimal complete sets of AC-unifiers. Which is, why we want to stress the following: already for the first four examples of Table 2 the number of AC-unifiers goes from five, over 13, then 981, up to 65 926 605. For the remaining examples we were not even able to compute the number of minimal AC-unifiers (running out of memory on 20 GB of RAM); remember that in the worst case for an elementary unification problem whose corresponding HLDE has n minimal solutions, the number of minimal AC unifiers is in the order of \(2^n\). Thus, applications that rely on minimal complete sets of AC-unifiers will most likely not succeed on examples that are much bigger than the one in line three of Table 2, rendering certification moot.
On the upside, we expect HLDEs arising from realistic examples involving AC-unification to be quite small, since the nesting level of AC-symbols restricts the length of a and b and the multiplicity of variables restricts individual entries.
8 Related Work
In the literature, there are basically three approaches for solving HLDEs: lexicographic algorithms, completion procedures, and graph theory based algorithms.
Already in the 1970s Huet devised an algorithm to generate the basis of solutions to homogeneous linear diophantine equations in a paper of the same title [5], the first instance of a lexicographic algorithm. Our formalization of HLDEs and bounds on minimal solutions is inspired by Huet’s elegant and short proofs. We also took up the idea of separating special and non-special solutions from Huet’s work. Moreover, the structure of our algorithm mostly corresponds to Huet’s informal description of his lexicographic algorithm: a striking difference is that we use a reverse lexicographic order. This facilities a construction relying on recursive list functions without the need of accumulating parameters. Compared to the beginning of our work, where we tried to stay with the standard lexicographic order, this turned out to lead to greatly simplified proofs.
In 1989, Lankford [7] proposed the first completion procedure solving HLDEs.
Fortenbacher and Clausen [2] give an accessible survey of these earlier approaches and in addition present the first graph theory based algorithm. They conclude that any of the existing algorithms is suitable for AC-unification: on the one hand there are huge performance differences for some big HLDEs; on the other hand AC-unification typically requires only relatively small instances; moreover, if the involved HLDEs grow too big the number of minimal AC-unifiers explodes massively, dwarfing the resource requirements for solving those HLDEs.
Later, Contejean and Devie [3] gave the first algorithm that was able to solve systems of linear diophantine equations (and is inspired by a geometric interpretation of the algorithm due to Fortenbacher and Clausen).
In contrast to our purely functional algorithm, all of the above approaches have a distinctively imperative flavor, and to the best of our knowledge, none of them have been formalized using a proof assistant.
9 Conclusions and Further Work
We had two main reasons for choosing a lexicographic algorithm (also keeping in mind that the problem being NP-complete, all approaches are asymptotically equivalent): (1) our ultimate goal is AC-unification and as Fortenbacher and Clausen [2] put it “How important are efficient algorithms which solve [HLDEs] for [AC-unification]? [...] any of the algorithms presented [...] might be chosen [...],” and (2) Huet’s lexicographic algorithm facilitates a simple purely functional implementation that is amenable to formalization.
Structure and Statistics. Our formalization comprises 3353 lines of code. These include 73 definitions and functions as well as 281 lemmas and theorems, most of which are proven using Isabelle’s Intelligible Semi-Automated Reasoning language Isar [13]. The formalization is structured into the following theory files:
-
List_Vector covering facts (about dot products, pointwise subtraction, several orderings, etc.) concerning vectors represented as lists of natural numbers.
-
Linear_Diophantine_Equations covering the abstract results on HLDEs discussed in Sect. 3.
-
Sorted_Wrt, Minimize_Wrt covering some facts about sortedness and minimization with respect to a given binary predicate.
-
Simple_Algorithm containing the simple algorithm of Sect. 2 and its correctness proof (Sect. 4).
-
Algorithm containing an intermediate algorithm (Sect. 5) that separates special from non-special solutions, as well as a more efficient variant (Sect. 6).
-
Solver_Code issuing a single command to generate Haskell code for
 and compiling it into a program hlde.
and compiling it into a program hlde.
Future Work. Our ultimate goal is of course to reuse the verified algorithm in an Isabelle/HOL formalization of AC-unification.
Another direction for future work is to further improve our algorithm. For example, the improved bounds  are discussed by Clausen and Fortenbacher [2]. Moreover, already Huet [5] mentions the optimization of explicitly computing
are discussed by Clausen and Fortenbacher [2]. Moreover, already Huet [5] mentions the optimization of explicitly computing  after
after  is fixed (which potentially divides the number of generated lists by the maximum value in
is fixed (which potentially divides the number of generated lists by the maximum value in  ).
).
Notes
- 1.
The “nonzero” condition naturally arises from the fact that substitutions cannot replace variables by nothing.
- 2.
Actually, this only holds for elementary AC-unification problems, which are those consisting only of variables and one specific AC-symbol. However, arbitrary AC-unification problems can be reduced to sets of elementary AC-unification problems.
- 3.
For technical reasons (regarding code generation) we actually have the two locales \(\textit{hlde-ops}\) and \(\textit{hlde}\) in our formalization.
- 4.
Also, in case you are wondering, the second component of the pairs will only play a role in Sect. 6, where it will avoid unnecessary recomputations of sub dot products. However, including these components already for
 serves the purpose of enabling later proofs of program transformations (or code equations as they are called in Isabelle).
serves the purpose of enabling later proofs of program transformations (or code equations as they are called in Isabelle).
References
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, New York (1998)
Clausen, M., Fortenbacher, A.: Efficient solution of linear diophantine equations. J. Symbolic Comput. 8(1), 201–216 (1989). https://doi.org/10.1016/S0747-7171(89)80025-2
Contejean, É., Devie, H.: An efficient incremental algorithm for solving systems of linear diophantine equations. Inf. Comput. 113(1), 143–172 (1994). https://doi.org/10.1006/inco.1994.1067
Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: Blume, M., Kobayashi, N., Vidal, G. (eds.) FLOPS 2010. LNCS, vol. 6009, pp. 103–117. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12251-4_9
Huet, G.: An algorithm to generate the basis of solutions to homogeneous linear diophantine equations. Inf. Process. Lett. 7(3), 144–147 (1978). https://doi.org/10.1016/0020-0190(78)90078-9
Klein, D., Hirokawa, N.: Confluence of non-left-linear TRSs via relative termination. In: Bjørner, N., Voronkov, A. (eds.) LPAR 2012. LNCS, vol. 7180, pp. 258–273. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28717-6_21
Lankford, D.: Non-negative integer basis algorithms for linear equations with integer coefficients. J. Autom. Reasoning 5(1), 25–35 (1989). https://doi.org/10.1007/BF00245019
Marché, C.: Normalized rewriting: an alternative to rewriting modulo a set of equations. J. Symbolic Comput. 21(3), 253–288 (1996). https://doi.org/10.1006/jsco.1996.0011
Meßner, F., Parsert, J., Schöpf, J., Sternagel, C.: Homogeneous Linear Diophantine Equations. The Archive of Formal Proofs, October 2017. https://devel.isa-afp.org/entries/Diophantine_Eqns_Lin_Hom.shtml, Formal proof development
Nagele, J., Felgenhauer, B., Middeldorp, A.: CSI: new evidence – a progress report. In: de Moura, L. (ed.) CADE 2017. LNCS (LNAI), vol. 10395, pp. 385–397. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63046-5_24
Shintani, K., Hirokawa, N.: CoLL: a confluence tool for left-linear term rewrite systems. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 127–136. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_8
Stickel, M.: A unification algorithm for associative-commutative functions. J. ACM 28(3), 423–434 (1981). https://doi.org/10.1145/322261.322262
Wenzel, M.: Isabelle/Isar - a versatile environment for human-readable formal proof documents. Ph.D. thesis, Institut für Informatik (2002)
Winkler, S., Middeldorp, A.: Normalized completion revisited. In: Proceedings of the 24th International Conference on Rewriting Techniques and Applications (RTA). Leibniz International Proceedings in Informatics, vol. 21, pp. 319–334. Schloss Dagstuhl (2013). https://doi.org/10.4230/LIPIcs.RTA.2013.319
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Meßner, F., Parsert, J., Schöpf, J., Sternagel, C. (2018). A Formally Verified Solver for Homogeneous Linear Diophantine Equations. In: Avigad, J., Mahboubi, A. (eds) Interactive Theorem Proving. ITP 2018. Lecture Notes in Computer Science(), vol 10895. Springer, Cham. https://doi.org/10.1007/978-3-319-94821-8_26
Download citation
DOI: https://doi.org/10.1007/978-3-319-94821-8_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94820-1
Online ISBN: 978-3-319-94821-8
eBook Packages: Computer ScienceComputer Science (R0)





 ,
, , and
, and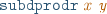 .
. and compiling it into a program
and compiling it into a program  serves the purpose of enabling later proofs of program transformations (or code equations as they are called in Isabelle).
serves the purpose of enabling later proofs of program transformations (or code equations as they are called in Isabelle).