Abstract
Recent work in the area of coordination models and collective adaptive systems promotes a view of distributed computations as functional blocks manipulating data structures spread over space and evolving over time. In this paper, we address expressiveness issues of such computations, and specifically focus on the field calculus, a prominent emerging language in this context. Based on the classical notion of event structure, we introduce the cone Turing machine as a ground for studying computability issues, and first use it to prove that field calculus is space-time universal. We then observe that, in the most general case, field calculus computations can be rather inefficient in the size of messages exchanged, but this can be remedied by an encoding to nearly similar computations with slower information speed. We capture this concept by a notion of delayed space-time universality, which we prove to hold for the set of message-efficient algorithms expressible by field calculus. As a corollary, it is derived that field calculus can implement with message-size efficiency all self-stabilising distributed algorithms.
This work has been partially supported by: EU Horizon 2020 project HyVar (www.hyvar-project.eu), GA No. 644298; ICT COST Action IC1402 ARVI (www.cost-arvi.eu); Ateneo/CSP D16D15000360005 project RunVar (runvar-project.di.unito.it). This document does not contain technology or technical data controlled under either U.S. International Traffic in Arms Regulation or U.S. Export Administration Regulations.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A traditional viewpoint in the engineering of coordination systems is to focus on the primitives by which a single coordinated device (or agent) interacts with others, either by point-to-point interaction, broadcast, or by means of some sort of mediator (a shared space, a channel, an orchestrator, and the like). A global coordination system is then designed as a protocol or workflow of interaction “acts”, regulating synchronisation of computational activities and the exchange of information through messages (among the many, e.g., see [8, 25]).
However, a number of recent works originated in the context of distributed intelligent systems (swarm intelligence, nature-inspired computing, multi-agent systems, self-adaptive and self-organising systems), and then impacting coordination models and languages as well, promote a higher abstraction of spatially-distributed collective adaptive systems. In these approaches, system coordination is expressed in terms of how the “collective” actually carries on an overall task, designed in terms of a spatio-temporal data structure to be produced as “output”. Works such as [4, 18] survey from various different viewpoints the many approaches that fall under this umbrella, and which we can classify in the following categories: methods that simplify programming of a collective by abstracting individual networked devices (e.g., TOTA [28], Hood [38], chemical models [36]), spatial patterns and languages (e.g., Growing Point Language [13], Origami Shape Language [30]), tools to summarise and stream information over regions of space and time (e.g., TinyDB [27] and Cougar [39]), and finally space-time computing models, e.g. targeting parallel computing (e.g., StarLisp [24], systolic computing [19]).
More recently, field-based computing through the field calculus [14, 15] and the generalised framework of aggregate programming [5, 34] combine and generalise over the above approaches, by viewing a distributed computation as a pure function, neglecting explicit indication of message-passing and rather focussing on the manipulation of data structures, spread over space and evolving over time. This is achieved by a small set of constructs equipped with a functional composition model that well supports the construction of complex system specifications. More generally, we see the field-calculus in terms of an evolution of distributed systems programming towards higher and higher declarative abstractions.
Some questions then naturally arise: which notions of universality emerge out of such a view of distributed computation? how can we characterise the expressiveness of a set of constructs used as building blocks to program distributed systems? how may non-functional aspects affect such notions? Classical Turing computability is not directly applicable to space-time distributed computations, as it does not capture relevant aspects such as the availability of information at given devices at given moments of time.
In this paper we address these issues by introducing the notions of cone Turing machine and space-time computability, and use them to prove a universality result for the field calculus–this notion of universality differs from others previously introduced for the field calculus [6], as it is performed in a discrete model rather than a continuous one, and it is more strongly connected to classical Turing computability. We also inspect efficiency aspects, since they deeply affect the “practical” notion of expressiveness: we find examples of space-time functions that would be realised only by field calculus programs that are “message-size-inefficient” (simply, message-inefficient henceforth)—i.e., that would rely on increasingly big messages as time passes and information moves around. However, we also find that for each such message-inefficient function there exists a “delayed” version with nearly similar behaviour: it features somewhat slower information speed across devices but can be implemented in a message-efficient way by field calculus. We capture this concept in terms of a stricter notion of delayed space-time universality, a property that holds for the set of message-efficient field calculus programs. As a corollary, we also derive an effective self-stabilisation universality result, stating that the field calculus is able to provide a message-efficient implementation for any self-stabilising distributed algorithm [15].
The remainder of this paper is organised as follows: Sect. 2 gives the main definitions of computability this paper is built upon; Sect. 3 introduces the field calculus and proves its universality; Sect. 4 shows a message-efficient but delayed encoding of computations, and discusses the notion of delayed space-time universality; Sect. 5 reviews related works and Sect. 6 concludes with final remarks. Figure 1 summarises the symbols and notations used throughout this paper.
2 Space-Time Computability
In order to ground a definition of “Turing-like” computability for distributed functions, two main ingredients are required: a mathematical space of functions, abstracting the essence of distributed computations, and a set of criteria for discarding impossible computations. The former can be achieved by translating the main features of distributed computations into mathematical objects: in this case, atomic computing events with communication through message passing. The latter can be achieved by combining physical requirements (i.e., causality) with classical computability requirements [6]. Accordingly, Sect. 2.1 formalises a space of distributed functions, and Sect. 2.2 introduces a Turing-like machine \(\text {TM}_{\textit{cone}}\) to ground computability.
2.1 Denotation of Space-Time Computations
A number of models have been proposed over the decades to ground distributed computations, each with a different viewpoint and purpose. Most of them boil down to two main ingredients: computational events, where actual actions take place, and messages that are exchanged to carry information between different events. These concepts can be formalised by the notion of event structure [23].
Definition 1
(Event Structure). An event structure \(\mathbf {E}= \langle E, \rightsquigarrow , < \rangle \) is a countable set of events \(E\) together with a neighbouring relation \(\rightsquigarrow \subseteq E\times E\) and a causality relation \(< \subseteq E\times E\), such that the transitive closure of \(\rightsquigarrow \) forms the irreflexive partial order < and the set \(\left\{ \epsilon ' \in E\mid ~ \epsilon ' < \epsilon \right\} \) is finite for each \(\epsilon \) (i.e., < is locally finite). We call \(\mathbf {ES}\) the set of all such event structures.
Note that the transitive closure condition on \(\rightsquigarrow \) also implies that \(\rightsquigarrow \) is asymmetric and irreflexive. A sample event structure is depicted in Fig. 2, showing how these relations partition events into “causal past,” “causal future,” and “concurrent” subsets with respect to any given event \(\epsilon \)—that is, respectively, events from which information can potentially be carried to \(\epsilon \) in a message, those to which information from \(\epsilon \) can be carried, and events informationally isolated from \(\epsilon \). Since < is uniquely induced by \(\rightsquigarrow \), we shall feel free to omit it whenever convenient, or use its weak form \(\le \).Footnote 1 Notice that since < is required to be irreflexive, \(\rightsquigarrow \) has to be an acyclic relation, thus inducing a directed acyclic graph (DAG) structure on \(E\). In fact, \(\mathbf {E}\) can be thought of as a DAG with a “neighbouring” relation (modelling message passing) and a “reachability” relation (modelling causal dependence). This kind of structure is also compatible with spaces of events equipped with special or general relativity metrics, considering \(\epsilon _1 \rightsquigarrow \epsilon _2\) to be possible only if \(\epsilon _1\) is in its causal past, i.e., is contained in or precedes the past light coneFootnote 2 of \(\epsilon _2\).
Notice that information about which device or devices might be performing that actual computation at each event is completely abstracted away: event structures aim to model which data may be available at every computational step, no matter on what device the computation may be happening. Thus a series of computations on the same device (whether it is fixed or mobile) can still be accurately modelled by a sequence of events \(\epsilon _1, \ldots , \epsilon _n\) such that \(\epsilon _i \rightsquigarrow \epsilon _{i+1}\), in which message passing is implemented simply by keeping data available on the device for subsequent computations.Footnote 3
The notion of event structure dates back several decades [23], and it has been used to relate many different distributed computation paradigm, such as Petri nets [31] or the actor model [21]: we now use them as a ground for space-time universality, building on these previous works. Even though the definition of event structure is usually given just in terms of the causality relation, we have also included the neighbouring relation since it is able to capture message passing details, which are usually needed to interpret actual distributed programs.
The notion of event structure is abstract, but well-suited to ground a semantics for space-time computations, intended as “elaborations of distributed data in a network of related events”: the causality ordering of events abstracts time, while the presence of concurrent events abstract spatial dislocation. Following [22], in the remainder of this paper overbar notation denotes metavariables over sequences and the empty sequence is \(\bullet \): e.g., we use \(\overline{\mathrm {\Phi }}\) for the sequence \(\mathrm {\Phi }_1, \ldots , \mathrm {\Phi }_n\). Similarly, formulas with sequences are duplicated for each set of sequence elements (sequences are assumed to have the same length): e.g., \(\overline{\mathrm {\Phi }}(\epsilon ) = \overline{\mathtt {v}}\) is a shorthand for \(\mathrm {\Phi }_1(\epsilon ) = \mathtt {v}_1, \ldots , \mathrm {\Phi }_n(\epsilon ) = \mathtt {v}_n\).
Definition 2
(Space-Time Values). Let \(\mathbf V \) be a denumerable universe of allowed computational values and \(\mathbf {E}\) be a given event structure. A space-time value \(\mathrm {\Phi }\) in \(\mathbf {E}\) is an annotation of the graph \(\mathbf {E}\) with labels in \(\mathbf V \), that is, a tuple \(\mathrm {\Phi }= \langle \mathbf {E}, f \rangle \) with \(f : E\rightarrow \mathbf V \), taking \(E\) as the set of events in \(\mathbf {E}\).
Definition 3
(Space-Time Functions). Let \(\mathbf V (\mathbf {E}) = \left\{ \langle \mathbf {E}, f \rangle \mid ~ f : E\rightarrow \mathbf V \right\} \) be the set of space-time values in an event structure \(\mathbf {E}\), and \(\mathbf V (*)= \bigcup _{\mathbf {E}\in \mathbf {ES}} \mathbf V (\mathbf {E})\) be the set of all space-time values in any event structure. Then, an n-ary space-time function in \(\mathbf {E}\) is a partial mapFootnote 4  and an n-ary space-time function is a partial map
and an n-ary space-time function is a partial map  , defined only for arguments belonging to a same \(\mathbf V (\mathbf {E})\) and such that for any \(\overline{\mathrm {\Phi }}\) in \(\mathbf V (\mathbf {E}) \cap \mathbf dom (\mathtt {f})\), \(\mathtt {f}(\overline{\mathrm {\Phi }}) \in \mathbf V (\mathbf {E})\).
, defined only for arguments belonging to a same \(\mathbf V (\mathbf {E})\) and such that for any \(\overline{\mathrm {\Phi }}\) in \(\mathbf V (\mathbf {E}) \cap \mathbf dom (\mathtt {f})\), \(\mathtt {f}(\overline{\mathrm {\Phi }}) \in \mathbf V (\mathbf {E})\).
A sample space-time value is depicted in Fig. 3. Notice that space-time values can be used to model data not only spatially distributed across devices, but also temporally distributed across time. In this way time-evolving inputs and, most importantly, intermediate results of computations (which are naturally time-dependent) are easily represented, attaining maximal generality while ensuring composability of behaviour. Furthermore, since space-time functions \(\mathtt {f}\) are partial maps, undefined values for \(\mathtt {f}(\overline{\mathrm {\Phi }})\) can model computations that are non-halting or otherwise failing on some event. We assume that a non-halting computation does not constitute a proper event, as it is not “observable” from the external world. The partial outcome of a computation \(\mathtt {f}\) that is non-halting on some event \(\epsilon \in \mathbf {E}\) can still be recovered by restricting \(\mathbf {E}\) to the largest \(\mathbf {E}' \subseteq \mathbf {E}\) on which \(\mathtt {f}\) is defined.
Most space-time functions, however, are not feasible in the physical world due to two main obstacles: inconsistencies between the causality relation and the required behaviour of the function (non-causal functions), and violation of classical constraints on computability (super-Turing functions). We shall see in the following subsection how to implement these two restrictions.
2.2 Cone Turing Machine
In order to define causality of a space-time function, it is necessary for the output value in each event \(\epsilon \) to depend only on input values in events \(\epsilon '\) which may have influenced \(\epsilon \), that is, such that \(\epsilon ' \le \epsilon \). This concept of causality can be captured by the definitions of event cone and cone function.Footnote 5
Definition 4
(Event Cone). An event cone is an event structure \(\mathbf {E}\) with a distinguished unique element \(\epsilon _\top \) which is the <-maximum in \(\mathbf {E}\), i.e., such that \(\forall \epsilon \in E~ \epsilon \le \epsilon _\top \). We call \(\mathbf {EC}\) the set of all such event structures.
Definition 5
(Restriction). Given an event structure \(\mathbf {E}\) and an event \(\epsilon \in E\), the \(\epsilon \)-cone in \(\mathbf {E}\), also called the restriction of \(\mathbf {E}\) to (the causal past of) \(\epsilon \), is defined as:
where \(E\upharpoonright \epsilon = \left\{ \epsilon ' \in E\mid ~ \epsilon ' \le \epsilon \right\} \). Analogously, given \(\mathrm {\Phi }\in \mathbf V (\mathbf {E})\) and \(\epsilon \in E\), the restriction of \(\mathrm {\Phi }\) to \(\epsilon \) is \(\mathrm {\Phi }\upharpoonright \epsilon = \langle E\upharpoonright \epsilon , \rightsquigarrow \cap \left( E\upharpoonright \epsilon \right) ^2, f \cap \left( E\upharpoonright \epsilon \right) \times \mathbf V \rangle \).
For example, the event structure formed by red events and by event \(\epsilon \) in Fig. 2 is an event cone, which is the restriction of the whole structure to \(\epsilon \).
Definition 6
(Cone Function). Let \(\mathbf V (\top )= \bigcup _{\mathbf {E}\in \mathbf {EC}} \mathbf V (\mathbf {E})\) be the set of all space-time values in any event cone. Then, an n-ary cone function is a partial map  defined only for arguments \(\overline{\mathrm {\Phi }}\) belonging to a same \(\mathbf V (\mathbf {E})\), and the space-time function
defined only for arguments \(\overline{\mathrm {\Phi }}\) belonging to a same \(\mathbf V (\mathbf {E})\), and the space-time function  induced by such \(\mathtt {f}_\top \) is such that given \(\overline{\mathrm {\Phi }}\in \mathbf V (\mathbf {E})\), \(\mathtt {f}(\overline{\mathrm {\Phi }}) = \langle \mathbf {E}, f \rangle \) where \(f(\epsilon ) = \mathtt {f}_\top (\overline{\mathrm {\Phi }}\upharpoonright \epsilon )\).Footnote 6
induced by such \(\mathtt {f}_\top \) is such that given \(\overline{\mathrm {\Phi }}\in \mathbf V (\mathbf {E})\), \(\mathtt {f}(\overline{\mathrm {\Phi }}) = \langle \mathbf {E}, f \rangle \) where \(f(\epsilon ) = \mathtt {f}_\top (\overline{\mathrm {\Phi }}\upharpoonright \epsilon )\).Footnote 6
Notice that the output of a cone function is not a map over space, but a single value in \(\mathbf V \), i.e., the value computed at the event \(\epsilon _\top \) on the basis of the history accessible to it in the cone. Note also that when inducing a space-time function, the same cone function is assumed to be applied in each event. However, space-time computations that apply different functions at different times can still be modelled by a single function with an extra input selecting the appropriate behaviour for each event. Since cone functions are able to represent any computation from causally-available inputs, causal space-time functions are precisely those which are induced by cone functions. Thus, computable space-time functions are those induced by a cone function that is computable, in the sense that it can be computed by a Turing Machine that operates over cones:
Definition 7
(Cone Turing Machine). Let A be an alphabet, \(\pi : \mathbf V \rightarrow A^*\) andFootnote 7 \(\pi ^\top : \mathbf V (\top )\rightarrow A^*\) be injective encodings of \(\mathbf V \) and \(\mathbf V (\top )\). A cone Turing machine \(\text {TM}_{\textit{cone}}^{\;\mathtt {f}}\) is a deterministic Turing machine with \(n+1\) tapes which given in its input tapes encodings \(\pi ^\top (\overline{\mathrm {\Phi }})\) of a sequence of space-time values in an event cone \(\mathbf {E}\), writes in its output tape an encoding \(\pi (\mathtt {v})\) of a value in \(\mathbf V \) (if it terminates). The cone function \(\mathtt {f}_\top \) induced by \(\text {TM}_{\textit{cone}}^{\;\mathtt {f}}\) is such that \(\mathtt {f}_\top (\overline{\mathrm {\Phi }}) = \mathtt {v}\) if and only if \(\text {TM}_{\textit{cone}}^{\;\mathtt {f}}\) terminates with output \(\pi (\mathtt {v})\) given inputs \(\pi ^\top (\overline{\mathrm {\Phi }})\). The space-time function \(\mathtt {f}\) induced by \(\text {TM}_{\textit{cone}}^{\;\mathtt {f}}\) is the one induced by the corresponding \(\mathtt {f}_\top \).
The specific choice of Turing machine formalisation in this definition is not significant, as all Turing machine formalisations are equivalent for purposes of determining computability, except insofar as its formulation simplifies connection with the field calculus in subsequent sections. The cone Turing machine can be accepted as a ground for space-time computability, since it processes all causally available data in each event in a Turing-complete way. Thus, a space-time function can be defined computable as per the following definition.
Definition 8
(Discrete Space-Time Computability). Let  be an n-ary space-time function. We say that \(\mathtt {f}\) is computable if and only if there exists a cone Turing machine \(\text {TM}_{\textit{cone}}^{\;\mathtt {f}}\) which induces \(\mathtt {f}\).
be an n-ary space-time function. We say that \(\mathtt {f}\) is computable if and only if there exists a cone Turing machine \(\text {TM}_{\textit{cone}}^{\;\mathtt {f}}\) which induces \(\mathtt {f}\).
Definition 9
(Space-Time Universality). A programming model (e.g., the field calculus) is space-time universal if and only if it is able to compute every space-time function that can be computed by a cone Turing machine.
3 Universality of Field Calculus
The field calculus is a tiny functional calculus capturing the essential elements of field computations, much as \(\lambda \)-calculus [12] captures the essence of functional computation and FJ [22] the essence of class-based object-oriented programming. Among other uses, it has been used to define reusable blocks of adaptive distributed algorithms [3, 5], and to define robustness properties [32, 34]. The defining property of computational fields is that they allow us to consider a computation from two different viewpoints: under a global viewpoint, a field is a distributed data structure manipulated by a network of devices, while under a local viewpoint it is just a single value, computed by a device on the basis of information gathered from neighbours. The translation between the two viewpoints is deterministic and automatic, abstracting away message-passing primitives.
Section 3.1 briefly presents the syntax and semantics of the field calculus from the local viewpoint, a detailed account of which can be found in [14, 15]. Section 3.2 extends the “event structure” formalism presented in Sect. 2, enabling convenient formalisation of properties used in the remainder of this paper. Section 3.3 shows that the field calculus is space-time universal, while outlining some inefficiencies that may occur in translating programs into it.
3.1 Field Calculus: Syntax and Semantics
We now present first-order field calculus [14] with a syntax inspired by recent DSL implementations [11] (in place of the prior Scheme-like formulation in [14]), plus a brief overview of its semantics under a local viewpoint. In our model, individual devices undergo computation in (local) asynchronous rounds (one per event): in each round, a device sleeps for some time, wakes up, gathers information about messages received from neighbours while sleeping, performs an evaluation of the program, and finally emits a message to all neighbours with information about the outcome of computation before going back to sleep.
The overall evolution of a network of devices is represented operationally through a small-step transition system \(\xrightarrow {\textit{act}} \) on network configurations \(N= \langle \textit{Env};\varPsi \rangle \), where \(\textit{Env}\) models the environmental conditions (i.e., network topology, inputs of sensors on each device) and \(\varPsi \) models the overall status of the devices in the network at a given time (as a map from device identifiers to environments \(\varTheta \)). Two types of transitions are considered: device firings \(N\xrightarrow {\delta } N'\), modelling a computational round performed by a device \(\delta \), and environment changes \(N\xrightarrow {\textit{env}} N'\), modelling any change in sensor data or network topology \(\textit{Env}\). Such a sequence of transitions can be mapped to a corresponding event structure, comprising an event \(\epsilon \) for each \(\xrightarrow {\delta } \) transition, with neighbouring relations \(\rightsquigarrow \) according to the network topology determined by \(\xrightarrow {\textit{env}} \) transitions. More precisely, an event \(\epsilon \) on device \(\delta \) (corresponding to a transition \(\langle \textit{Env};\varPsi _1\rangle \xrightarrow {\delta } \langle \textit{Env};\varPsi _2\rangle \)) has a neighbouring relation \(\rightsquigarrow \) to the first event \(\epsilon '\) on \(\delta '\) after \(\epsilon \) if and only if \(\delta \) is connected to \(\delta '\) in the network topology \(\textit{Env}\).
Operational semantics within a single device is formalised by the judgement “\(\delta ;\varTheta \vdash \mathtt {e}_{\mathtt {main}}\Downarrow \theta \)”, to be read “expression \(\mathtt {e}_{\mathtt {main}}\) evaluates to \(\theta \) on \(\delta \) with respect to environment \(\varTheta \)”, where \(\theta \) is an ordered tree of values tracking the results of all evaluated sub-expressions of \(\mathtt {e}_{\mathtt {main}}\), and \(\varTheta \) is a map from neighbour devices \(\delta _i\) (possibly including \(\delta \) itself) to the \(\theta _i\) produced in their last firing. Mapped into our language of space-time computation, \(\theta \) is the value of a space-time function at event \(\epsilon \) and \(\varTheta \) is the set of values of that function at events \(\epsilon ' \rightsquigarrow \epsilon \).
Figure 4 presents the syntax of field calculus.Footnote 8 A program \(\mathtt {P}\) consists of a sequence of function declarations and of a main expression \(\mathtt {e}\). A function declaration \(\mathtt {F}\) defines a (possibly recursive) function, with \(\mathtt {d}\) the function name, \(\overline{\mathtt {x}}\) the parameters and \(\mathtt {e}\) the body. An expression \(\mathtt {e}\) can be:
-
a variable \(\mathtt {x}\), either a function formal parameter or local to a \(\mathtt {let}\)- or \(\mathtt {rep}\)-expression;
-
a value \(\mathtt {v}\), either a local value (e.g., numbers, literals) defined through data constructors \(\mathtt {c}(\overline{\ell })\), or a neighbouring field value \(\phi \) (a map \( \overline{\delta }\mapsto \overline{\ell }\) from neighbours to local values) which is allowed to appear in intermediate computations but not in source programs;
-
a \(\mathtt {let}\)-expression \(\mathtt {let}\, \mathtt {x}= \mathtt {e}_0 \, \;\mathtt {in}\;\, \mathtt {e}\), which is evaluated by computing the value \(\mathtt {v}_0\) of \(\mathtt {e}_0\) and then yielding as result the value of the expression obtained from \(\mathtt {e}\) by replacing all the occurrences of the variable \(\mathtt {x}\) with the value \(\mathtt {v}_0\);
-
a function call \(\mathtt {f}(\overline{\mathtt {e}})\), where \(\mathtt {f}\) can be a declared function \(\mathtt {d}\) or a built-in function \(\mathtt {b}\), such as accessing sensors, mathematical and logical operators, or data structure operations;
-
a conditional branching \(\mathtt {if}(\mathtt {e}_1) \{ \mathtt {e}_2\} \{ \mathtt {e}_3\}\), where \(\mathtt {e}_1\) is a Boolean expression;
-
a \(\mathtt {nbr}\)-expression \(\mathtt {nbr}\{\mathtt {e}\}\), modelling neighbourhood interaction and producing a neighbouring field value \(\phi \) that represents an “observation map” from neighbours to their latest evaluation of \(\mathtt {e}\);
-
or a \(\mathtt {rep}\)-expression \(\mathtt {rep}(\mathtt {e}_1)\{(\mathtt {x}) \mathrm {\texttt {=>}}{} \mathtt {e}_2\}\), evolving a local state through time by evaluating an expression \(\mathtt {e}_2\), substituting variable \(\mathtt {x}\) with the value calculated for the \(\mathtt {rep}\)-expression at the previous computational round (in the first round \(\mathtt {x}\) is substituted with the value of \(\mathtt {e}_1\)). Although this first-order version of the calculus does not model anonymous functions (differently from the higher-order version in [15]), \((\mathtt {x}) \mathrm {\texttt {=>}}{} \mathtt {e}_2\) can be understood as an anonymous function with parameter \(\mathtt {x}\) and body \(\mathtt {e}_2\).
Values associated with data constructors \(\mathtt {c}\) of arity zero (e.g., literal values) are written by omitting the empty parentheses, i.e., we write \(\mathtt {c}\) instead of \(\mathtt {c}()\). In case \(\mathtt {b}\) is a binary built-in operator, we allow infix notation to enhance readability: e.g., we shall sometimes write \(1+2\) for \(+(1, 2)\).
A correct matching between messages exchanged and \(\mathtt {nbr}\) sub-expressions is ensured by a process called alignment, which navigates the value-trees \(\theta \) of neighbours in the environment \(\varTheta \) as sub-expressions of the main expression \(\mathtt {e}_{\mathtt {main}}\) are accessed. This process interacts subtly with branching statements \(\mathtt {if}(\mathtt {e}_1) \{ \mathtt {e}_2\} \{ \mathtt {e}_3\}\): since no matching of messages from different \(\mathtt {nbr}\) sub-expressions is allowed, computation of \(\mathtt {e}_2\) in devices that selected the first branch cannot interact with devices computing \(\mathtt {e}_3\). This effectively splits the computation into two fully isolated sub-networks (devices evaluating \(\mathtt {e}_1\) to \(\mathtt {True}\), and those evaluating it to \(\mathtt {False}\)).
3.2 Augmented Event Structures
In field calculus, as in most distributed computing paradigms, the semantics is device-dependent: in particular, neighbouring links \(\rightsquigarrow \) connecting subsequent events on the same device (state preservation) have a different role than links connecting events on different devices (message passing). This choice reflects practical implementation details of distributed computing networks, but it is not captured by the abstract concept of event structure (Definition 1).
However, it is still possible to use the framework in Sect. 2 for the field calculus. In fact, a function \(\mathtt {f}\) in field calculus always corresponds to a space-time function (Definition 3) with a number of extra input arguments (modelling environmental information) in each event:
-
the device \(\delta \) where the event takes place;Footnote 9
-
local sensor information (e.g., time clock, temperature, etc.);
-
relational sensor information (e.g., physical distance from other devices).
Note that relational sensor information is just a special case of local sensor information, in which the value returned is a map over neighbouring events.
Due to the special role played by these extra input parameters, it will be convenient to consider an event structure together with its associated environmental inputs to state the properties that will be investigated in the next sections:
Definition 10
(Augmented Event Structure). An augmented event structure is a tuple \(\mathbb {E}= \langle \mathbf {E}, \overline{\mathrm {\Phi }} \rangle \) consisting of an event structure \(\mathbf {E}\) together with a number of space-time values \(\overline{\mathrm {\Phi }}\) (including device information).Footnote 10
When functions are interpreted in augmented event structures, the provided space-time values are then supplied as inputs to the functions (or indirectly used to define sensor built-in functions).
3.3 Space-Time Universality
As outlined in Sect. 3.1, the field calculus operational semantics is defined through a set of syntax-directed rules, involving data available in (and computed by) events in the causal past of each firing event. Since the cone Turing machine can process inputs from arbitrary events in the causal past of the current event in a Turing-complete way, it follows that every space-time function that is computable for the field calculus is also computable for the cone Turing machine. Conversely, in order for the field calculus to be space-time universal it needs to be (i) Turing-complete for fully local computations and (ii) able to gather values from arbitrary events in the causal past. Condition (i) is easily matched by the field calculus, as it is assumed that built-in functions on local values, together with branching-expressions and recursive function declarations, provide the required Turing-completeness. Condition (ii) holds as shown by the following theorem.
Definition 11
(Rank). The rank of \(\epsilon \) in \(\mathbf {E}\) is the maximum length \({{\mathrm{rank}}}(\epsilon )\) of a path \(\epsilon _1 \rightsquigarrow \epsilon _2 \rightsquigarrow \ldots \epsilon \) ending in \(\epsilon \).
Definition 12
(Distance). The distance of \(\epsilon ' < \epsilon \) from \(\epsilon \) is the minimum length n of a path \(\epsilon ' = \epsilon _0 \rightsquigarrow \ldots \rightsquigarrow \epsilon _n = \epsilon \) connecting them.
Theorem 1
(Field Calculus Space-Time Universality). Let \(\mathtt {f}\) be a Turing computable cone function. Then there is a field calculus function \(\mathtt {f\_field}\) that produces the same outputs as \(\mathtt {f}\) in any augmented event structure including event information.
Proof
(sketch). Figure 5 shows a possible translation, assuming event information e as additional input. Function gather collects values of its arguments from causal past events into a labelled DAG, which is fed to the cone function \(\mathtt {f}\). The code is based on the following built-in functions, which we assume to be available.Footnote 11
- \(\texttt {pair}(\mathtt {v}_1, \mathtt {v}_2)\)::
-
constructs a pair \(\langle \mathtt {v}_1, \mathtt {v}_2 \rangle \).
- \(\texttt {1st}(\mathtt {v}), \texttt {2nd}(\mathtt {v})\)::
-
returns the first (resp. second) element of a pair \(\mathtt {v}\).
- \(\texttt {dag\_empty}()\)::
-
returns an empty DAG structure.
- \(\texttt {dag\_node}(\epsilon , \overline{\mathtt {v}})\)::
-
constructs a DAG consisting in a single node \(\epsilon \) with labels \(\overline{\mathtt {v}}\).
- \(\texttt {dag\_union}(G_1, G_2)\)::
-
returns \(G_1 \cup G_2\), merging duplicate entries of a same event.
- \(\texttt {dag\_join}(G, n)\)::
-
returns G with an added node n, connected to each sink of G.
- \(\texttt {unionhood}(G, \phi )\)::
-
computes the union of G with each neighbour graph in \(\phi \).
Whenever gather is called, it computes in next the result of joining the current node with neighbour dag values. If no neighbour is aligned to the current function call, \(\texttt {next} = \texttt {node}\) hence \(\texttt {dag}\) is returned. Otherwise, a recursive call is made with the enlarged graph \(\texttt {dag} \cup \texttt {next}\). Every event performs strictly more recursive calls than all of its neighbour events, so the recursion depth in event \(\epsilon \) is \({{\mathrm{rank}}}(\epsilon )\). On the n-th recursive call, values from events at distance \(\le n\) are computed and fed to the following recursive calls. Thus, gather collects values from all events \(\epsilon ' < \epsilon \).
4 Delayed and Stabilising Universality
In this section we address an efficiency shortcoming of the field calculus that concerns the size of messages exchanged across devices (Sect. 4.1), and accordingly draw more tailored notions of universality: a notion of delayed universality that relaxes temporal constraints of computation by which efficiency in message size can be practically recovered (Sect. 4.2) and stabilising universality that focusses on the ability of expressing all stabilising computations (Sect. 4.3).
4.1 On Message-Size Efficiency and Delays in Field Calculus
As shown in the proof of Theorem 1, function gather performs \({{\mathrm{rank}}}(\epsilon )\) recursive calls in each event \(\epsilon \), broadcasting an increasing part of the past event cone \(\mathbf {E}\upharpoonright \epsilon \) through expression \(\mathtt {nbr}\{\texttt {dag}\}\) in each of them. Thus, the total messages exchanged have \(O(\left|\mathbf {E}\upharpoonright \epsilon \right| \cdot {{\mathrm{rank}}}(\epsilon ))\) size, which is larger by a factor of \({{\mathrm{rank}}}(\epsilon )\) than what would be necessary in other distributed models of computation. In fact, a Turing machine would be able to receive full cone reconstructions \(\mathbf {E}\upharpoonright \epsilon '\) from neighbour events, join them and in turn broadcast a final reconstructed value by uniting them. This is not possible in field calculus due to its alignment mechanism: message exchange is bound to \(\mathtt {nbr}\)-expressions, which first send a message and then receive a response, whereas the previous procedure would require a program to first receive data in order to compute the message to be sent. This obstacle can be circumvented only by \(\mathtt {nbr}\) nesting (as in \(\mathtt {f\_field}\)), which leads to the larger message size. Not all field calculus computations require such nesting, though, only those requiring communication without delay, i.e., that access information in the past light cone of an event, as defined in the following.
Past light cones of events \(\epsilon _1\) and \(\epsilon _2\) in a sample augmented event structure. Note that the \(\epsilon _1\) (red) light cone includes device 2 twice, due to the break in state memory, while the \(\epsilon _2\) (green) light cone does not contain device 1, since all states in the event cone of \(\epsilon _2\) can take a path that includes state memory. (Color figure online)
Definition 13
(Past Light Cone). Let \(\mathbb {E}\) be an augmented event structure, \(\epsilon \) be an event. The past light cone \({{\mathrm{LC}}}(\epsilon )\) of \(\epsilon \) is the set of \(\epsilon '\) such that \(\epsilon ' < \epsilon \) and no path \(\epsilon ' = \epsilon _0 \rightsquigarrow \ldots \rightsquigarrow \epsilon _n = \epsilon \) passes through two events \(\epsilon _i\), \(\epsilon _j\) on a same device.
Figure 6 represents the past light cone of two given events. Intuitively, events are in the past light cone of \(\epsilon \) if they are barely able to reach \(\epsilon \), i.e., any delay of information propagation (i.e., “waiting” one round in a device) would break connection with them. In this case, communication is more fragile since \(\mathtt {rep}\) constructs are of no use: each form of communication enabled by \(\mathtt {rep}\) constructs requires waiting at least one round on a device. For a message to be exchanged from events \(\epsilon ' \in {{\mathrm{LC}}}(\epsilon )\), a field calculus program needs to execute a number of nested \(\mathtt {nbr}\) statements at least equal to their relative distance, each of them contributing to the overall message size.
4.2 Delayed Universality of the Field Calculus
For events sufficiently far from the past light cone, a slower and more light-weight pattern of data collection with respect to \(\mathtt {nbr}\) nesting can also be effective [3, 5]: the combined use of \(\mathtt {nbr}\) and \(\mathtt {rep}\) statements, as in the following.

In this highly common pattern of field calculus, data from the previous event on the same device is combined with data from the preceding event to each neighbour event. The data flow induced by this pattern is necessarily slower than that of \(\mathtt {nbr}\) nesting, however, it only requires a single \(\mathtt {nbr}\) statement and hence messages carrying on a single data—with no expansion with rank. As we shall show in Theorem 2, this pattern is also able to mimic the behaviour of any space-time computable function with a finite delay, provided that the event structure involved is persistent and fair.
Definition 14
(Persistence). An augmented event structure \(\mathbb {E}\) is persistent if and only if for each device \(\delta \), the events \(\epsilon \) in \(\mathbb {E}\) corresponding to that device form a totally ordered \(\rightsquigarrow \)-chain.
Definition 15
(Fairness). An augmented event structure \(\mathbb {E}\) is fair if and only if for each event \(\epsilon _0\) and device \(\delta \), there exists an event \(\epsilon \) on \(\delta \) such that \(\epsilon _0 < \epsilon \).
Notice that only countably infinite event structures can be fair.
Definition 16
(Delayed Functions). Let

be n-ary space-time functions. We say that \(\mathtt {g}\) is a delay of \(\mathtt {f}\) if and only if for each persistent and fair event structure \(\langle \mathbf {E}, \overline{\mathrm {\Phi }} \rangle \) there is a surjective and weakly increasingFootnote 12 map \(\pi : E\rightarrow E\) such that \(\mathtt {g}(\overline{\mathrm {\Phi }})(\epsilon ) = \mathtt {f}(\overline{\mathrm {\Phi }})(\pi (\epsilon ))\) for each \(\epsilon \).
Theorem 2
(Field Calculus Effective Delayed Universality). Let  be a computable space-time function. Then there exists a field calculus function \(\mathtt {f\_delayed}\) which executes a single \(\mathtt {nbr}\) statement and computes a space-time function
be a computable space-time function. Then there exists a field calculus function \(\mathtt {f\_delayed}\) which executes a single \(\mathtt {nbr}\) statement and computes a space-time function

which is a delay of \(\mathtt {f}\).
Proof
(sketch). Figure 7 shows a possible translation, assuming event information e as additional input. Function gather collects input values from past events into a labelled DAG, with an additional boolean label indicating whether all neighbours of the event are present in the graph. The DAG is then restricted to the most recent event for which the whole past event cone has already been gathered, and finally fed to the cone function \(\mathtt {f}\). The code is based on the same built-in functions used in Theorem 1, together with the following.
- \(\texttt {last\_event}(G, \epsilon )\)::
-
true iff \(\epsilon \) has no successor event in the same device in G.
- \(\texttt {next\_event}(G, \epsilon )\)::
-
returns the event \(\epsilon '\) following \(\epsilon \) in the same device in G.
- \(\texttt {dag\_restrict}(G, \epsilon )\)::
-
returns the restriction \(G \upharpoonright \epsilon \).
- \(\texttt {dag\_true}(G)\)::
-
true iff every node in G has \(\mathtt {True}\) as first label.
We assume all these functions are available, and that operator unionhood prefers label \(\mathtt {True}\) against \(\mathtt {False}\) when merging nodes with different labels.
Since the event structure is fair and persistent, data flow between devices is possible in many different ways: for any event \(\epsilon \) and device \(\delta \), we can find a path \(\epsilon \rightsquigarrow \ldots \rightsquigarrow \epsilon _\delta \) ending in \(\delta \) such that no two consecutive \(\rightsquigarrow \) crossing different devices are present. Thus, data about \(\epsilon \) is eventually gathered in \(\epsilon _\delta \).
The delay implied by the above translation is proportional to the hop-count diameter of the network considered: in fact, a transmission path is delayed by one round for every device crossing in it. In most cases, this delay is sufficiently small for the translation to be fruitfully used in practical applications [2, 3].
4.3 Stabilising Universality of the Field Calculus
Since field calculus is able to efficiently perform computations with a certain delay, it means that it can also efficiently perform those computations whose goal is expressed by the spatial computation limit to be eventually reached, as defined by the well-known classes of stabilising and self-stabilising programs [32].
Definition 17
(Stabilising Values). A space-time value \(\mathrm {\Phi }\) in an augmented event structure \(\mathbb {E}\) is stabilising if and only if for each device \(\delta \), there exists an event \(\epsilon _0\) on \(\delta \) such that for each subsequent \(\epsilon > \epsilon _0\) on \(\delta \), \(\mathrm {\Phi }(\epsilon ) = \mathrm {\Phi }(\epsilon _0)\).
The limit \(\lim (\mathrm {\Phi })\) of a stabilising value \(\mathrm {\Phi }\) is the map \(m : \mathbf D \rightarrow \mathbf V \) such that \(m(\delta ) = \mathtt {v}\) if for all \(\epsilon \) on \(\delta \) after a certain \(\epsilon _0\), \(\mathrm {\Phi }(\epsilon ) = \mathtt {v}\).
Definition 18
(Stabilising Structures). Given an event \(\epsilon \) in an augmented event structure \(\mathbb {E}\), the set \({{\mathrm{CD}}}(\epsilon )\) of connected devices in \(\epsilon \) is:
An augmented event structure \(\langle \mathbf {E}, \overline{\mathrm {\Phi }} \rangle \) is stabilising if and only if it is fair, persistent and both \(\overline{\mathrm {\Phi }}\) and \({{\mathrm{CD}}}\) (interpreted as a space-time value) are stabilising.
Definition 19
(Stabilising Functions). An n-ary space-time function  is stabilising if and only if given any stabilising augmented event structure \(\langle \mathbf {E}, \overline{\mathrm {\Phi }} \rangle \), the output \(\mathtt {f}(\overline{\mathrm {\Phi }})\) is stabilising. Two stabilising functions
is stabilising if and only if given any stabilising augmented event structure \(\langle \mathbf {E}, \overline{\mathrm {\Phi }} \rangle \), the output \(\mathtt {f}(\overline{\mathrm {\Phi }})\) is stabilising. Two stabilising functions

are equivalent if and only if given any stabilising augmented event structure \(\langle \mathbf {E}, \overline{\mathrm {\Phi }} \rangle \), their outputs have the same limits \(\lim (\mathtt {f}(\overline{\mathrm {\Phi }})) = \lim (\mathtt {g}(\overline{\mathrm {\Phi }}))\).
Theorem 3
(Delayed to Stabilising). Let  be a stabilising space-time function, and \(\mathtt {g}\) be a delay of \(\mathtt {f}\). Then \(\mathtt {g}\) is stabilising and equivalent to \(\mathtt {f}\).
be a stabilising space-time function, and \(\mathtt {g}\) be a delay of \(\mathtt {f}\). Then \(\mathtt {g}\) is stabilising and equivalent to \(\mathtt {f}\).
Proof
Let \(\delta \) be any device, and \(\epsilon \) be the first event on \(\delta \) such that the output of \(\mathtt {f}\) has stabilised to \(\mathtt {v}\) on \(\delta \) after \(\epsilon \). Let \(\pi : E\rightarrow E\) be the function such that \(\mathtt {g}\) is a delay of \(\mathtt {f}\) as in Definition 16, and let \(\epsilon '\) be such that \(\pi (\epsilon ') = \epsilon \) by surjectivity of \(\pi \). Then \(\mathtt {g}\) stabilises to \(\mathtt {v}\) on \(\delta \) after \(\epsilon '\), concluding the proof.
Combining Theorems 2 and 3, we directly obtain the following corollary.
Corollary 1
(Field Calculus Effective Stabilising Universality). Let  be a computable and stabilising space-time function. Then there exists a field calculus function \(\mathtt {f\_stabilising}\) which executes a single \(\mathtt {nbr}\) statement and computes a space-time function
be a computable and stabilising space-time function. Then there exists a field calculus function \(\mathtt {f\_stabilising}\) which executes a single \(\mathtt {nbr}\) statement and computes a space-time function

which is equivalent to \(\mathtt {f}\).
Stabilisation guarantees that a limit exists, but in general such a limit could highly depend on “transient environmental changes”. A stronger property, more useful in practical applications is self-stabilisation [1, 20, 26, 35], additionally guaranteeing full-independence to transient changes as defined in the following.
Definition 20
(Self-Stabilising Functions). An n-ary space-time function  is self-stabilising if and only if it is stabilising and given two stabilising event structures \(\langle \mathbf {E}, \overline{\mathrm {\Phi }}^1 \rangle \) and \(\langle \mathbf {E}, \overline{\mathrm {\Phi }}^2 \rangle \) such that \(\lim (\overline{\mathrm {\Phi }}^1) = \lim (\overline{\mathrm {\Phi }}^2)\) and \(\lim ({{\mathrm{CD}}}^1) = \lim ({{\mathrm{CD}}}^2)\), we have that \(\lim (\mathtt {f}(\overline{\mathrm {\Phi }}^1)) = \lim (\mathtt {f}(\overline{\mathrm {\Phi }}^2))\).
is self-stabilising if and only if it is stabilising and given two stabilising event structures \(\langle \mathbf {E}, \overline{\mathrm {\Phi }}^1 \rangle \) and \(\langle \mathbf {E}, \overline{\mathrm {\Phi }}^2 \rangle \) such that \(\lim (\overline{\mathrm {\Phi }}^1) = \lim (\overline{\mathrm {\Phi }}^2)\) and \(\lim ({{\mathrm{CD}}}^1) = \lim ({{\mathrm{CD}}}^2)\), we have that \(\lim (\mathtt {f}(\overline{\mathrm {\Phi }}^1)) = \lim (\mathtt {f}(\overline{\mathrm {\Phi }}^2))\).
Since self-stabilising functions are a subclass of stabilising functions, stabilising universality trivially implies self-stabilising universality.
5 Related Work
Studying the expressiveness of coordination models is a traditional topic in the field of coordination models and languages. As such, a good deal of literature exists that we here classify and compare with the notions defined in this paper.
A first thread of papers, which forms the majority of the available works, study expressiveness of coordination models using a traditional approach of concurrency theory based on the following conceptual steps: (i) isolating coordination primitives of existing models, (ii) developing a core calculus formalising how their semantics affect the coordination space (production/reception of messages, triggering of events or process continuations, injection/extraction of data-items/tuples), and finally (iii) drawing a bridge between the core calculus rewrite behaviour with the input/output behaviour of Turing machines, to inspect universality or compare expressiveness of different sets of primitives.
Notable examples of this approach include the study of expressiveness of Linda coordination primitives in [8], of event notification in data-driven languages in [9], of movement constructs in mobile environments in [10], and of timed coordination models in [25]. A slightly different approach is taken in [17], where the focus is expressiveness of a language for expressing coordination rules to program “the space of interaction”: the methodology is similar, but here expressiveness neglects the behaviour of coordinated entities, focussing just on the shared-space enacting coordination.
Other approaches start instead from the consideration that the dimension of interaction may require a more sophisticated machinery than comparison against Turing machines. A classical position paper following this line is Peter Wegner’s work in [37], which however did not turn into successful frameworks to study interaction models. Modular embedding is proposed in [16] as an empowering of standard embedding to compare relative expressiveness of concurrent languages, which has been largely used as a tool by the community studying the theory of concurrency.
The approach to universality and expressiveness presented in this paper sits in between the two macro approaches above. On the one hand, our notion of expressiveness is strictly linked to the classic Turing framework, and focusses on the global computation that a system of coordinated entities can carry on. Critically, however, it is based on denoting computations as event structures, a long-standing notion used to formalise distributed systems of various sorts [23, 29]. In this paradigm, each single node has the power of a Turing machine, all node execute the same behaviour, and what matters is the resulting spatio-temporal configuration of events, which describes the overall system execution and not just its final outcome. A somewhat similar stance is taken in [6, 7], in which field computations are considered as providing a space-time continuous effect, obtained with limit of density of devices and frequency of their operation going to infinity—an approach that we plan to soon connect with the one presented here.
6 Conclusions
In this paper, we proposed the cone Turing machine as a foundation for space-time computability in distributed systems based on event structures, and use it to study the expressiveness of field calculus. Field calculus is proved universal: but in practice, some computations can be ineffective for they would need exchange of messages with increasing size as time passes. By a form of abstraction which releases some constraints on temporal execution (i.e., accepting some delay), field calculus is shown instead to be both universal and message-size efficient. As a key corollary, we proved that field calculus can efficiently implement self-stabilising computations, a class of computations which lately received considerable interest [3, 20, 26, 33, 35].
In the future, we plan to further investigate the interplay of expressiveness and efficiency for relevant classes of distributed algorithms, both in a discrete and continuous setting, with the goal of designing new declarative programming constructs for distributed systems.
Notes
- 1.
The weak form of a partial order is defined as \(x \le y\) iff \(x < y\) or \(x = y\).
- 2.
In relativity, the past light cone of an event \(\epsilon _2\) comprises all events \(\epsilon _1\) such that photons produced by \(\epsilon _1\) reach the position of \(\epsilon _2\) at the time when \(\epsilon _2\) happens.
- 3.
Note that a computation in this model may be an arbitrarily complex action, so long as it is local: our later formulation will take each event to be an atomic execution of an entire round of a potentially complex program.
- 4.
With
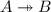 we denote the space of partial functions from A into B.
we denote the space of partial functions from A into B. - 5.
These concepts are closely linked to the notion of causality in physics and its definition in terms of light cones.
- 6.
We remark that whenever \(\mathtt {f}_\top (\overline{\mathrm {\Phi }}\upharpoonright \epsilon )\) is undefined for some \(\epsilon \) (the computation has not halted), we take \(\mathtt {f}(\overline{\mathrm {\Phi }})\) to be undefined as well.
- 7.
We denote with \(A^*\) the set of finite sequences of values from A.
- 8.
- 9.
We assume that device identifiers \(\delta \) are taken among a denumerable set \(\mathbf D \).
- 10.
We assume that a finite number of devices may occur in augmented event structures.
- 11.
All those functions except for unionhood are totally local, hence can be implemented through any Turing-complete set of built-in functions (e.g. the minimal zero, -, \(\mathtt {<}\)).
- 12.
A map \(\pi : E\rightarrow E\) is weakly increasing if and only if \(\epsilon _1< \epsilon _2 \Leftrightarrow \pi (\epsilon _1) < \pi (\epsilon _2)\).
References
Altisen, K., Corbineau, P., Devismes, S.: A framework for certified self-stabilization. In: Albert, E., Lanese, I. (eds.) FORTE 2016. LNCS, vol. 9688, pp. 36–51. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-39570-8_3
Audrito, G., Casadei, R., Damiani, F., Viroli, M.: Compositional blocks for optimal self-healing gradients. In: Self-Adaptive and Self-Organizing Systems (SASO), 2017, pp. 91–100. IEEE (2017)
Audrito, G., Damiani, F., Viroli, M.: Optimally-self-healing distributed gradient structures through bounded information speed. In: Jacquet, J.-M., Massink, M. (eds.) COORDINATION 2017. LNCS, vol. 10319, pp. 59–77. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-59746-1_4
Beal, J., Dulman, S., Usbeck, K., Viroli, M., Correll, N.: Organizing the aggregate: languages for spatial computing. In: Formal and Practical Aspects of Domain-Specific Languages: Recent Developments, Chap. 16, pp. 436–501. IGI Global (2013)
Beal, J., Pianini, D., Viroli, M.: Aggregate programming for the Internet of Things. IEEE Comput. 48(9), 22–30 (2015)
Beal, J., Viroli, M., Damiani, F.: Towards a unified model of spatial computing. In: 7th Spatial Computing Workshop (SCW 2014) (2014)
Beal, J., Viroli, M., Pianini, D., Damiani, F.: Self-adaptation to device distribution in the Internet of Things. TAAS 12(3), 12:1–12:29 (2017)
Busi, N., Gorrieri, R., Zavattaro, G.: On the expressiveness of Linda coordination primitives. Inf. Comput. 156(1–2), 90–121 (2000)
Busi, N., Zavattaro, G.: On the expressiveness of event notification in data-driven coordination languages. In: Smolka, G. (ed.) ESOP 2000. LNCS, vol. 1782, pp. 41–55. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46425-5_3
Busi, N., Zavattaro, G.: On the expressive power of movement and restriction in pure mobile ambients. Theor. Comput. Sci. 322(3), 477–515 (2004)
Casadei, R., Viroli, M.: Towards aggregate programming in Scala. In: First Workshop on Programming Models and Languages for Distributed Computing, PMLDC 2016, pp. 5:1–5:7. ACM, New York (2016)
Church, A.: A set of postulates for the foundation of logic. Ann. Math. 33(2), 346–366 (1932)
Coore, D.: Botanical computing: a developmental approach to generating inter connect topologies on an amorphous computer. Ph.D. thesis, MIT, Cambridge, MA, USA (1999)
Damiani, F., Viroli, M., Beal, J.: A type-sound calculus of computational fields. Sci. Comput. Program. 117, 17–44 (2016)
Damiani, F., Viroli, M., Pianini, D., Beal, J.: Code mobility meets self-organisation: a higher-order calculus of computational fields. In: Graf, S., Viswanathan, M. (eds.) FORTE 2015. LNCS, vol. 9039, pp. 113–128. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19195-9_8
Deboer, F., Palamidessi, C.: Embedding as a tool for language comparison. Inf. Comput. 108(1), 128–157 (1994)
Denti, E., Natali, A., Omicini, A.: On the expressive power of a language for programming coordination media. In: ACM SAC 1998, pp. 169–177 (1998)
Dobson, S., Denazis, S., Fernández, A., Gaïti, D., Gelenbe, E., Massacci, F., Nixon, P., Saffre, F., Schmidt, N., Zambonelli, F.: A survey of autonomic communications. TAAS 1(2), 223–259 (2006)
Engstrom, B.R., Cappello, P.R.: The SDEF programming system. J. Parallel Distrib. Comput. 7(2), 201–231 (1989)
Faghih, F., Bonakdarpour, B., Tixeuil, S., Kulkarni, S.: Specification-based synthesis of distributed self-stabilizing protocols. In: Albert, E., Lanese, I. (eds.) FORTE 2016. LNCS, vol. 9688, pp. 124–141. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-39570-8_9
Hewitt, C., Bishop, P.B., Steiger, R.: A universal modular ACTOR formalism for artificial intelligence. In: IJCAI 1973, pp. 235–245 (1973)
Igarashi, A., Pierce, B.C., Wadler, P.: Featherweight Java: a minimal core calculus for Java and GJ. ACM Trans. Program. Lang. Syst. 23(3), 396–450 (2001)
Lamport, L.: Time, clocks, and the ordering of events in a distributed system. Commun. ACM 21(7), 558–565 (1978)
Lasser, C., Massar, J., Miney, J., Dayton, L.: Starlisp Reference Manual. Thinking Machines Corporation, Cambridge (1988)
Linden, I., Jacquet, J., Bosschere, K.D., Brogi, A.: On the expressiveness of timed coordination models. Sci. Comput. Program. 61(2), 152–187 (2006)
Lluch-Lafuente, A., Loreti, M., Montanari, U.: Asynchronous distributed execution of fixpoint-based computational fields. CoRR abs/1610.00253 (2016)
Madden, S., Franklin, M.J., Hellerstein, J.M., Hong, W.: TAG: a Tiny AGgregation service for ad-hoc sensor networks. SIGOPS Oper. Syst. Rev. 36, 131–146 (2002)
Mamei, M., Zambonelli, F.: Programming pervasive and mobile computing applications: the TOTA approach. ACM Trans. Softw. Eng. Methodol. 18(4), 1–56 (2009)
Mattern, F., et al.: Virtual time and global states of distributed systems. Parallel Distrib. Algorithms 1(23), 215–226 (1989)
Nagpal, R.: Programmable self-assembly: constructing global shape using biologically-inspired local interactions and origami mathematics. Ph.D. thesis, MIT, Cambridge, MA, USA (2001)
Nielsen, M., Plotkin, G.D., Winskel, G.: Petri nets, event structures and domains, part I. Theor. Comput. Sci. 13, 85–108 (1981)
Pianini, D., Beal, J., Viroli, M.: Improving gossip dynamics through overlapping replicates. In: Lluch Lafuente, A., Proença, J. (eds.) COORDINATION 2016. LNCS, vol. 9686, pp. 192–207. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-39519-7_12
Viroli, M., Audrito, G., Beal, J., Damiani, F., Pianini, D.: Engineering resilient collective adaptive systems by self-stabilisation. ACM Trans. Model. Comput. Simul. 28(2), 16:1–16:28 (2018)
Viroli, M., Beal, J., Damiani, F., Pianini, D.: Efficient engineering of complex self-organising systems by self-stabilising fields. In: Self-Adaptive and Self-Organizing Systems (SASO), 2015, pp. 81–90. IEEE (2015)
Viroli, M., Damiani, F.: A calculus of self-stabilising computational fields. In: Kühn, E., Pugliese, R. (eds.) COORDINATION 2014. LNCS, vol. 8459, pp. 163–178. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43376-8_11
Viroli, M., Pianini, D., Montagna, S., Stevenson, G., Zambonelli, F.: A coordination model of pervasive service ecosystems. Sci. Comput. Program. 110, 3–22 (2015)
Wegner, P.: Why interaction is more powerful than algorithms. Commun. ACM 40(5), 80–91 (1997)
Whitehouse, K., Sharp, C., Brewer, E., Culler, D.: Hood: a neighborhood abstraction for sensor networks. In: Proceedings of the 2nd International Conference on Mobile Systems, Applications, and Services. ACM Press (2004)
Yao, Y., Gehrke, J.: The cougar approach to in-network query processing in sensor networks. SIGMOD Record 31, 9–18 (2002)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 IFIP International Federation for Information Processing
About this paper
Cite this paper
Audrito, G., Beal, J., Damiani, F., Viroli, M. (2018). Space-Time Universality of Field Calculus. In: Di Marzo Serugendo, G., Loreti, M. (eds) Coordination Models and Languages. COORDINATION 2018. Lecture Notes in Computer Science(), vol 10852. Springer, Cham. https://doi.org/10.1007/978-3-319-92408-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-92408-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-92407-6
Online ISBN: 978-3-319-92408-3
eBook Packages: Computer ScienceComputer Science (R0)











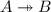 we denote the space of partial functions from A into B.
we denote the space of partial functions from A into B.